Wikipedia talk:WikiProject Mathematics/Archive/2015/Dec

PlanetMath Exchange dead or alive?

I'm trying to engage researchers in Sweden to be active contributors to Wikipedia. I will today talk to the department of Mathematics at Uppsala University. Some researchers from their department have earlier said that PlanetMath has the same function as Wikipedia has for other areas and that it might be more wise to be active on PlanetMath instead. It seems that a long time ago, people tried to do both, but what has happened since with the Exchange project? Olle Terenius (SLU) (talk) 10:48, 27 November 2015 (UTC)

Planetmath itself was dead for a long time. Now I see that the site seems to be back online. Sławomir
Biały 13:01, 27 November 2015 (UTC)

It seems to be far less active than Wikipedia, though. Try a search like Cauchy sequence and you will find the WP article at the top while PlanetMath is - hard to find. Also compare the PlanetMath article with Cauchy sequence. PlanetMath seems to be more oriented towards mathematicians than the general public, so the choice of platform may depend on who you wish to write for. RockMagnetist(talk) 13:52, 27 November 2015 (UTC)

At one point PlanetMath looked like a "mathier" to alternative Wikipedia (geared towards math students and mathematicians), but since then they lost a lot of contributors and were plagued by technical issues and switched hosts and software systems several times. At times the project looked almost dead and by now Wikipedia has long surpassed them in overall scope and quality.

Also note while Wikipedia writing style tends to be geared towards general audiences, we do in parallel also have a lot of material that doesn't really have the general audience as target bur rather scientists, math students or mathematicians. In that context it is also university classes and lecture notes as well as blogs by professional mathematician increasingly integrate Wikipedia to provide illustrations, explanations and background material. So even if you want to write primarily for math audiences WP is currently a better option than PlanetMath. In particular for professional mathematicians there is however also the option to contribute to Springer's (former) Encyclopedia of Mathematics, which has been turned into Wikiproject of sorts.--Kmhkmh (talk) 10:00, 3 December 2015 (UTC)

New AfC draft that may pique your interest

A new AfC draft has appeared: Draft:Quasi-exact-solvability. I have used my (somewhat rudimentary) TeX knowledge to clean up the draft, but a math check would be welcomed! Thanks all, /wia /tlk 19:10, 3 December 2015 (UTC)

Primary sources only? Boris Tsirelson (talk) 19:19, 3 December 2015 (UTC)

Here's a secondary source by Peter Olver. He's quite a respectable person in that area. Although the self-citation of User:Turbiner might appear to be a COI, Olver also cites quite a few of his papers, so I don't think we should be overly concerned about COI here. Sławomir
Biały 19:28, 3 December 2015 (UTC)

Cubic roots for complex numbers

Does anyone know how to solve ${\sqrt[{3}]{2\pm 11i}}=x+yi$ with the expression $x^{3}-3xy^{2}+(3x^{2}y-y^{3})i=2\pm 11i$

• without:

1. Any Guesses of the results at all
2. Any Use of De Moivre's formula

יהודה שמחה ולדמן (talk) 08:19, 2 December 2015 (UTC)

This question would be better suited at WP:Reference desk/Mathematics. Nevertheless, here is an answer.

Separating the real and the imaginary part and fixing the ± sign, this is a polynomial system of two equations of degree 3 in two unknowns. It has 9 complex solutions (normal by Bézout's theorem), 3 real solutions (normal for the cube roots of a complex number) and only one integer solution. For finding the real solutions, one may use the Maple function RootFinding[Isolate] (better here with option "output=interval"), which gives directly the integer solution and the two other real solutions. If you do not have access to Maple, you may find the integer solution by computing and factoring the resultant of the two equations with respect to one of the variables.

Another answer is the following: You are looking for the cube root of a Gaussian integer of norm 125 = 5³. If the cube root is a Gaussian integer, it should have the norm 5. This amounts thus to search the solution among the four Gaussian integers that have the norm 5. D.Lazard (talk) 10:04, 2 December 2015 (UTC)

With the considerable benefit of D.Lazard's comment, here are my thoughts. First fix the ± sign to be + for convenience. If you want minus, then just take the complex conjugate throughout.

Beginning with

$x^{3}-3xy^{2}=2$

$3x^{2}y-y^{3}=11\,,$

take the squares and add to get the square of the norm

$(x^{3}-3xy^{2})^{2}+(3x^{2}y-y^{3})^{2}=x^{6}-6x^{4}y^{2}+9x^{2}y^{4}+9x^{4}y^{2}-6x^{2}y^{4}+y^{6}=x^{6}+3x^{4}y^{2}+3x^{2}y^{4}+y^{6}=(x^{2}+y^{2})^{3}=2^{2}+11^{2}=4+121=125=5^{3}\,.$

And thus since x and y are real, we get

$x^{2}+y^{2}=5$

$y^{2}=5-x^{2}$

and substituting for y² in the first equation, we get

$4x^{3}-15x-2=0$

To solve this, we apply Newton's method which gives

$x_{n+1}={\frac {8x_{n}^{3}+2}{12x_{n}^{2}-15}}\,.$

The three roots are to be found in the three intervals into which the reals are divided by

${\frac {-{\sqrt {5}}}{2}}=-1.118034{\text{ and }}{\frac {\sqrt {5}}{2}}=+1.118034$

In the right-most interval, one can get an exact solution, namely x = 2.

y can be found from square-rooting 5 - x² and verifying that it is the correct root using the original equations. One of the three solutions is 2 + i. JRSpriggs (talk) 05:35, 4 December 2015 (UTC)

Multivariate trigonometric polynomial

Isn't it notable enough for being mentioned in "Trigonometric polynomial"? Boris Tsirelson (talk) 20:49, 3 December 2015 (UTC)

Are there sources for non-trivial content on this subject? Personally I know an interesting result about this subject, but I do not know if it has even been published. The property is the following: Let us define a multivariate trigonometric polynomial as a polynomial in trigonometric functions, whose arguments are linear forms with rational coefficients of one or several variables. There is no unique factorization for these trigonometric polynomials, because of $\sin(x)=2\sin(x/2)\cos(x/2)=4\sin(x/4)\cos(x/4)\cos(x/2)=\ldots$ However, these trigonometric polynomials have a well defined notion of greatest common divisor, and this gcd is effectively computable. This is easily provable by converting the trigonometric polynomials into Laurent polynomials in terms of $e^{ix_{j}/n_{j}}.$ It follows that fractions of such polynomials have a reduced form, which can be computed by dividing the numerator and the denominator by their gcd.

I learnt (or found) this property by providing a computational proof of Morley's trisector theorem, using trigonometry: expressing the length of one edge of Morley's equilateral triangle in term of trigonometric functions of the angles of the input triangle, multiplied by the radius of the circumscribed circle, one gets a rather complicated fraction of trigonometric polynomials of two of the angles (one angle is easily eliminated, using that the sum of the three angles is π). The reduced form of this fraction is a trigonometric polynomial, given in Morley's trisector theorem. As far as I know, no computer algebra system is able to simplify this fraction into a polynomial, although the above sketched algorithm is easy to implement.

I find this property and its application interesting as an Encyclopedic content. However, the lack of sources prevent to insert it in trigonometric polynomial, unless if there is a consensus for applying WP:IAR to this. D.Lazard (talk) 23:23, 3 December 2015 (UTC)

I think your interpretation is was not what the original question intended. I think the original question is about polynomials whose terms are products of sines and cosines evaluated at integer multiples of a coordinate (as in $\sin(2x)\cos(3y)\cos(-6z)$). An obvious reason for studying these is of course multivariate Fourier series. I'm certain reliable sources could be found and that it would make a good addition to the encyclopedia.

Regarding your property, I think it is partially surprising and partially unsurprising. The ring of entire functions does not have unique factorization (by the Weierstrass factorization theorem an entire function may be written as a product over its zeros, this product is generally infinite, and a UFD must admit finite factorizations), and your example $\sin x=2\sin(x/2)\cos(x/2)=4\sin(x/4)\cos(x/4)\cos(x/2)=\cdots$ has the same flavor. The ring of entire functions also has greatest common divisors (the ring is a Prüfer domain; it is clearly a domain, and it is easy to check that every ideal is invertible). Where I'm surprised is that I don't see any easy way to check that your ring admits greatest common divisors except through the Laurent polynomial argument you gave, and that argument results in computability of gcd's. It's quite nice! I wish it were written up somewhere so that it could be put into an article. Ozob (talk) 04:14, 4 December 2015 (UTC)

Yes, I meant $\sin(2x)\cos(3y)\cos(-6z),$ or equivalently (though not "equally") $\exp((2x+3y-6z)i)$ (or its real and imaginary parts). It seems there is no consensus about "the" degree of such thing, but anyway, trig polynomials are an algebra of functions, and every finite subset of the lattice gives a shift-invariant space of functions. Boris Tsirelson (talk) 06:48, 4 December 2015 (UTC)

restructuring inverse hyperbolic functions

Hi,

I did some restructuring at inverse hyperbolic functions, mostly moving the part about complex inverse hyperbolic functions to the end of the article, but I am wondering did i do every thing right and are there still other improvements to make.

Also editing this article did make me wonder:

• Are the addition, composition and other formulas also valid for complex numbers (and if not how do we add that to the article)
• Are there nice formulas for ln(x) = arsinh (...) = arcosh (...) = artanh (...) and so on?

Lets improve this article together :) WillemienH (talk) 11:08, 8 December 2015 (UTC)

There exists two pages about Inverse Limit and Inverse System

The two following pages seem to talk about very similar topics : https://en.wikipedia.org/wiki/Inverse_limit https://en.wikipedia.org/wiki/Inverse_system, in my opinion the second could be added as a part (the "category" point of view) of the first. --Tilwen (talk) 14:21, 9 December 2015 (UTC)

I agree. I've put tags suggesting merger from the latter to th former. -- Taku (talk) 20:54, 9 December 2015 (UTC)

False position method

• False position method (edit | talk | history | protect | delete | links | watch | logs | views)

A case is being made at the talk page that the title "false position" is a bad mistranslation of "regula falsi". Thoughts welcome. Johnuniq (talk) 23:37, 10 December 2015 (UTC)

Trigonometry of a tetrahedron

What should be done with Trigonometry of a tetrahedron? Michael Hardy (talk) 01:27, 12 December 2015 (UTC)

Merge into tetrahedron, I'd say. It even looks like most of the material is already there. Ozob (talk) 03:59, 12 December 2015 (UTC)

Yes, agree with merge, specifically the content of Trigonometry of a tetrahedron can be placed into the relevant sections of Tetrahedron#General properties. The tetrahedron article is not very long so article size is not a problem. M∧Ŝc²ħεИ_τlk 10:55, 13 December 2015 (UTC)

Einstein's proof of the Pythagorean theorem

I just created a new section presenting Einstein's stunningly simple proof of the Pythagorean theorem (which I learned just yesterday). Perhaps others can improve it. Michael Hardy (talk) 22:04, 12 December 2015 (UTC)

Wow! Surely someone should make a picture. Boris Tsirelson (talk) 22:11, 12 December 2015 (UTC)

Isn't this the same as the proof by similar triangles, given its own section earlier in the article? —David Eppstein (talk) 22:24, 12 December 2015 (UTC)

If it isn't, I don't understand it. And it doesn't seem to be a proof by dissection. Ozob (talk) 22:37, 12 December 2015 (UTC)

It might be. The proof seems incomplete without showing how the three facts of the penultimate sentence lead to AB^2 + AGamma^2 = BGamma^2.--Wikimedes (talk) 11:38, 13 December 2015 (UTC)

It's the same setup, but cuts to the chase a little more directly. There was a discussion of this proof at MathOverflow at [1] about two and a half years ago. Dick Palais gave the quick summary "It is clear that the areas of similar right triangles is proportional to the squares of corresponding sides---in particular to the squares of their hypotenuses. Dropping a perpendicular from the vertex of the right triangle onto the hypotenuse c divides it into two similar triangles with hypotenuses a and b, hence: kc^2 = ka^2 + k*b^2 so c^2 = a^2 + b^2". — Myasuda (talk) 14:27, 13 December 2015 (UTC)

Ah, it makes more sense now.

Palais says that Einstein "(re)discovered" this proof. Who originally discovered it? Ozob (talk) 16:21, 13 December 2015 (UTC)

Proof using similar triangles

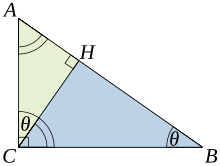
Here's what I think is really going on in the proof. Start with the diagram at right. Obviously

$AB^{2}=\left({\frac {1}{2}}AC\cdot BC\right)\cdot \left(2{\frac {AB}{AC}}{\frac {AB}{BC}}\right).$

The right hand side is the area of ABC times a proportionality factor. This proportionality factor is expressed in terms of ratios of side lengths, so it is a similarity invariant. Call this factor α. Then the above equation can be reexpressed as

$AB^{2}=\left({\frac {1}{2}}AC\cdot BC\right)\cdot \alpha ,$

and this equation holds with the same α for any triangle similar to ABC. Because the area of ABC is the sum of the areas of ACH and BCH, and because the triangles involved are all similar,

${\begin{aligned}AB^{2}&=\left({\frac {1}{2}}AH\cdot CH+{\frac {1}{2}}BH\cdot CH\right)\cdot \alpha \\&=\left({\frac {1}{2}}AH\cdot CH\right)\cdot \alpha +\left({\frac {1}{2}}BH\cdot CH\right)\cdot \alpha \\&=AC^{2}+BC^{2}.\end{aligned}}$

One does not need to introduce α to have a proof, but the point of the proof is really the similarity invariance of α.

The fact that the proof uses additivity of area makes it like a dissection proof, and the fact that it uses similarity of triangles to get at the square of the hypotenuse makes it like the similarity proof given in the article. It's not the same as either. Ozob (talk) 16:47, 13 December 2015 (UTC)

Indeed! Boris Tsirelson (talk) 17:32, 13 December 2015 (UTC)

"Area is additive" is itself not a simple claim — if the interior of a Jordan curve is split by a Jordan arc into two smaller areas, those areas might add up to less than the whole. See Osgood curve. In general, an additional assumption that the boundary is well-behaved (obviously true here) is needed. —David Eppstein (talk) 19:22, 13 December 2015 (UTC)

Would Einstein understand you?   :-)   Boris Tsirelson (talk) 19:32, 13 December 2015 (UTC)

Thanks Ozob, I get it now. Ozob's demonstration that the area of a right triangle is proportional to to its hypotenuse and that the constant of proportionality is the same for similar triangles is an essential part of the overall proof, yes?--Wikimedes (talk) 22:45, 13 December 2015 (UTC)

Well, it's trivially true that the area of any right triangle is proportional to the square of its hypotenuse (they're numbers, so you can divide them). What's important is that this constant is a similarity invariant. Initially this was surprising to me, but now I think it shouldn't be: Similarity classes of right triangles form a one parameter family, and both area and the square of the hypotenuse are degree two in the lengths of the legs of the triangle, so it's not surprising that they'd be related. Ozob (talk) 01:21, 14 December 2015 (UTC)

Oh, and I'm still curious as to the history of this proof. I'm not surprised that Einstein rediscovered it (he was, public image notwithstanding, good at math), but Palais says that the proof isn't original to him. Ozob (talk) 01:23, 14 December 2015 (UTC)

I could try asking Palais, if you think he knows more that could help. —David Eppstein (talk) 01:42, 14 December 2015 (UTC)

Einstein's name is the only name I've ever seen attached to this particular proof. I suspect that Palais put the parenthetical "re" before the word "discovered" to reflect that, considering the long history of the Pythagorean theorem, it wouldn't be surprising if at least one other person found the same proof prior to Einstein. But it probably wouldn't hurt to confirm by asking Palais if he meant something more. — Myasuda (talk) 01:58, 14 December 2015 (UTC)

Inline Greek letters

We routinely write things like this:

$\cos(\alpha +\beta )\,$

When done inline like this: $\cos(\alpha +\beta )\,$ then the characters appear in a font size sometimes three times that of the surrounding letters and often suffer from bizarre misalignments (but the size and alignment seems to depend on how the user's preferences are set). However, for the lower-case π we have a template enabling us to say that the area of a disk of radius r is πr², that last expression being coded as {{pi}}''r''². This suffers no such problems as those mentioned above, as far as I know. I don't know how to create such templates. How hard would it be to create such templates for other Greek letters? (I see that the template "alpha" currently rediects to a template called "alphabetize".) Michael Hardy (talk) 18:21, 15 December 2015 (UTC)

{{math|''β''}} generates β, just as {{math|''π''}} generates π, pretty close to the LaTeX formatting. The italics are necessary here; otherwise you get an upright beta, quite different from LaTeX. But the {{pi}} template is not italicized, and is I think identical to {{math|π}}/ π. —David Eppstein (talk) 18:29, 15 December 2015 (UTC)

Basel problem and Euler-Mascheroni constant

An editor is very insistent at Basel problem that trigonometric functions like $\sin x$ should be typeset as $sinx$. I reverted the original edit, citing WP:MOSMATH#Multi-letter names, and he reverted back, weirdly citing WP:BRD as if the onus were on me to justify the original consensus (even though I had already done so). I'm now at 3rr, and my edit has been reverted there again. This situation would benefit from other editors experienced in mathematics typesetting.

The same editor has pushed a similar set of edits through at Euler-Mascheroni constant, replacing the LaTeX $\gamma$ with the html γ, including things like $\gamma '$ → γ′. I assume the reason $\gamma$ is preferred is that it looks more like the LaTeX formulas that display on their own line, and so is consistent. In addition, the edit includes an obfuscation of the definition of the constant. Also, that edit did other weird things like replace an aligned equation with an unaligned onr. Sławomir
Biały 13:52, 15 December 2015 (UTC)

Yes, well, you could have not been at 3rr by not making BRD into a self-righteous thing ("you start the discussion!" "no, YOU start the discussion!"), something that is a very common WP communication problem. And indeed discussion on the talk page seems to be going nicely at the moment at Basel problem. I don't care so much about $\gamma$ versus γ (both are defensible). --JBL (talk) 14:08, 15 December 2015 (UTC)

I wasn't the one who brought up BRD. I made reasons for the revert very clear. The Basel one in particular explicitly violates the MOS. But gawd forbid Joel Lewis would ever want to look at content instead of smugly criticizing my behavior. Sławomir
Biały 14:35, 15 December 2015 (UTC)

It is not clear to me why your comment is so personal (have we had some unpleasant interaction in the past)? You posted about a conflict, requesting someone help you out because you had reached 3RR. A quick scan of the history of the relevant articles shows an inane pissing match about who is obligated to start the discussion in BRD. This sort of inanity is common on WP and counter-productive, and I suggested to you that you could avoid this problem easily (as could the other editor, but he's not here). There is no point in having a substantive discussion here because, as I noted, appropriate discussion is already taking place on the relevant talk pages and seems likely to result in an appropriate outcome (notably, not involving any formulas of the form $sinx$). --JBL (talk) 20:01, 15 December 2015 (UTC)

I just posted a comment about this on that editor's talk page. The fact that he used {{{sin(x)}}} rather than {sin(x)} suggests that the code may have come from one of those software packages on the web that generate TeX or MathJax code. Often they write code that looks as if a psychotic wrote it. Michael Hardy (talk) 18:06, 15 December 2015 (UTC)

Computational anatomy

New user Mim.cis (talk · contribs) identifies himself as Prof. Michael Miller from Johns Hopkins University, a pioneer in the field of Computational Anatomy. You can see him on Youtube here.

Some concern was caused because he started developing large amounts of mathematics in a sandbox, and it was not clear where this was going. You can read on User talk:Mim.cis the advice that he has been given, and at User talk:JohnCD/Archive 31#Questions re sandbox and User talk:JohnCD#Unrelated his replies and questions.

My initial worry that this was new original research was allayed by searching Google Scholar, in particular by finding this 1998 paper with 567 citations. It seems that Computational Anatomy is a real, and probably notable, subject.

Would people please look at User:Mim.cis/sandbox and advise: is there an article, or articles, in there? What should Prof. Miller do to progress it? Regards, JohnCD (talk) 22:32, 15 December 2015 (UTC)

There is certainly good content in there. What I think is the problem is that it is written like a survey article for people who are vaguely familiar with the area, and that is too high a level for Wikipedia. For example, after reading that page, I can tell you that CA is about diffeomorphisms and flows, and that it is somehow an infinite-dimensional version of what is classically done in kinematics with finite-dimensional Lie groups. But I cannot tell you what it has to do with anatomy. All I know about anatomy is that I'm made of bones, muscles, organs, and so on. I don't know where diffeomorphism groups enter. Conversely, I think someone who knew a lot about anatomy might know what a morphome is, but not what a diffeomorphism is or why they're interesting.

I believe that the right way to turn the sandbox into a Wikipedia article is to pitch it at two audiences: (1) Undergraduate mathematics majors, and (2) Undergraduate biology (or anatomy or pre-med) majors. This will require writing a lot more introductory material and rewriting most of the rest of the page. But without that, the sandbox will remain inappropriate for a Wikipedia article. Ozob (talk) 23:45, 15 December 2015 (UTC)

Pythagorean theorem again

There is a dispute about a small addition, which seems to caused by different notions of the nature of (good) encyclopedic writing, sourcing and WP:SYNTH. Comments/opinions would be appreciated at Talk:Pythagorean_theorem#explicit_sources_needed?--Kmhkmh (talk) 06:05, 16 December 2015 (UTC)

TeX error message

The code below gives me this error message:

Failed to parse (unknown function "\begin{array}"):

Nothing gets rendered; I see only the code.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/en.wikipedia.org/v1/":): {\displaystyle \begin{array}{ccl} n & \qquad & P_n(x) \\[6pt] \hline 0 & & 1 \\[6pt] 1 & & x \\[6pt] 2 & & \frac12 (3x^2-1) \\[6pt] 3 & & \frac12 (5x^3-3x) \\[6pt] 4 & & \frac18 (35x^4-30x^2+3) \\[6pt] 5 & & \frac18 (63x^5-70x^3+15x) \\[6pt] 6 & & \frac1{16} (231x^6-315x^4+105x^2-5) \\[6pt] 7 & & \frac1{16} (429x^7-693x^5+315x^3-35x) \\[6pt] 8 & & \frac1{128} (6435x^8-12012x^6+6930x^4-1260x^2+35) \\[6pt] 9 & & \frac 1 {128} (12155x^9-25740x^7+18018x^5-4620x^3+315x) \\[6pt] 10 & & \frac1{256} (46189x^{10}-109395x^8+90090x^6-30030x^4+3465x^2-63) \\ \hline \end{array} }

What's going on? Michael Hardy (talk) 17:36, 15 December 2015 (UTC)

I think its the [6pt] \hline. Compare

\begin{array}{ccl} n & \qquad & P_n(x) \\
\hline 0 & & 1 \\
[6pt] 1 & & x \\
[6pt] 2 & & \frac12 (3x^2-1) \\ 
\hline \end{array}

${\begin{array}{ccl}n&\qquad &P_{n}(x)\\\hline 0&&1\\[6pt]1&&x\\[6pt]2&&{\frac {1}{2}}(3x^{2}-1)\\\hline \end{array}}$

With

\begin{array}{ccl} n & \qquad & P_n(x) \\
[6pt] \hline 0 & & 1 \\
[6pt] 1 & & x \\
[6pt] 2 & & \frac12 (3x^2-1) \\ 
\hline \end{array}
</math>

Failed to parse (unknown function "\begin{array}"): {\displaystyle \begin{array}{ccl} n & \qquad & P_n(x) \\ [6pt] \hline 0 & & 1 \\ [6pt] 1 & & x \\ [6pt] 2 & & \frac12 (3x^2-1) \\ \hline \end{array} }

--Salix alba (talk): 00:39, 18 December 2015 (UTC)

Both work with PNG enabled, but with MathML+SVG, the first works and the second doesn't. Sławomir
Biały 10:53, 18 December 2015 (UTC)

AFC Draft for Review.. Draft:Regularized least squares

Could people take a look at Draft:Regularized least squares , reviewers often have problems determining whether mathematics related drafts are appropriate or not.21:26, 18 December 2015 (UTC)

Magic number

Please see and fix this.

• A selection: Magic number.

Thank you kindly.

Anna Frodesiak (talk) 23:39, 20 December 2015 (UTC)

Sorry, what is there to fix? I feel like there is some context that I'm missing. Ozob (talk) 01:19, 21 December 2015 (UTC)

Hi Ozob. See the article history. It started as a link to a CD, then removed, then to...., well, best see the history. It may be sorted out now. Best, Anna Frodesiak (talk) 01:27, 21 December 2015 (UTC)

If you are talking about "3" under List of numbers#Notable integers, I also do not see any problem. JRSpriggs (talk) 10:33, 21 December 2015 (UTC)

It was like this. Now it is fine. Thanks all! :) Anna Frodesiak (talk) 12:08, 21 December 2015 (UTC)

Math rendering suddenly very slow

I left a message saying the same thing in WP:VPT but maybe someone here knows something more: Rendering of mathematics using the "MathML with SVG or PNG fallback" preference option has become very slow today, to the point where I cannot view simple articles such as Centroid — after a long delay I instead get a Wikimedia Error page. If I switch to the default "PNG images" preference option for mathematics, rendering is fast. Anyone know what is going on and when it will be fixed? —David Eppstein (talk) 17:21, 14 December 2015 (UTC)

The topic was recently discussed as well at math portal of the Grman wikipedia (see de:Portal_Diskussion:Mathematik#Geschwindigkeit) and physikerwelt one of the developers posted a reply. Essentially he stated 2 things, firstly that some time earlier there was a bug causing a significant slowdown that has been fixed now and secondly he gave some average rendering times for math ml (per formula 50 ms for first time rendering and 5 ms for subsequent rendering), which are significantly slower than png rendering. I assume a formula is any single occurrence of <math></math> tags and we have some articles that might several 100 formulas easily, such formula heavy articles can be expected to load rather slowly when rendered for the first time. For my personal taste actually too slow to become the default solution.--Kmhkmh (talk) 03:05, 25 December 2015 (UTC)

Expanded formula tool in VisualEditor

The VisualEditor recently expanded the mathematics tool, and I'd like your feedback on the overall design, whether it seems to be working for you (browser/OS if it's not), and whether anything significant is missing. You don't actually need to opt in to VisualEditor in your preferences if you haven't already; just click here to play in my sandbox. Double-click on existing formulae to open them, or go to Insert > More > Formula to add new ones.

Feedback can be posted at WP:VisualEditor/Feedback (or here, if that's easier for you). Thanks, Whatamidoing (WMF) (talk) 20:41, 14 December 2015 (UTC)

Your question seems to be presupposing that mathematics editors here are actually using the Visual editor. But it appears to be still the case that VE is unable to create indented display-math formulas (using :<math> ... <math/>). This prevents it from being usable at all for mathematics articles, regardless of how featureful or whizzy it is. —David Eppstein (talk) 21:05, 14 December 2015 (UTC)

Actually, I presuppose only that the people most interested in and capable of providing feedback are likely to read this page.

As we have discussed before, wikitext technically doesn't have "indentation". (It probably should, but it doesn't.) ":<math>" is actually the second half of an HTML definition list, and consequently should not be used to adjust the visual display of mathematics formula (or anything else, including talk page comments). Doing so is a WP:ACCESS violation, and the product manager has refused to replicate that accessibility problem in the visual editor.

That said, I believe that the last time we talked about this, someone determined that indenting all math formula could be done with a single entry in CSS, thus both eliminating the accessibility problem for people who use screen readers and also making sure that the proper display happens on all articles, even if an editor forgets or removes it. Do you know why that hasn't happened yet?

And, finally, although the visual editor won't let you create such accessibility problems, it will let you edit pre-existing indented formulae. Whatamidoing (WMF) (talk) 21:14, 14 December 2015 (UTC)

My take on it is that wikitext *does* have indentation: almost every time editors use : without a previous ;, that's what they intend. The fact that the Wikimedia engine turns this good markup into semantically-bad html is not a problem with wikitext, nor a misunderstanding by the editors who wrote the markup; it is a bug in how the engine is implemented.

That said, you can track progress on the proposed math block display markup replacement at https://phabricator.wikimedia.org/T111712. I get the impression it's moving forward but not quite in place yet. Of course, persuading editors that they should use it in place of the simpler existing markup is yet another struggle that doesn't seem to have even started. —David Eppstein (talk) 21:32, 14 December 2015 (UTC)

More precisely, see [2]. I don't know whether or not anything has happened since then.

Thanks for your work on this, by the way. Ozob (talk) 21:38, 14 December 2015 (UTC)

I think a basic requirement of the software should be that it allows editing consistent with the manual of style. This embodies the ongoing consensus of the Wikipedia project, and is the product of many thousands of editors. Currently, the Manual of Style recommends "When displaying formulae on their own line, one should indent the line with one or more colons (:)" If anyone (e.g., the project manager in question) wishes to build consensus to change this, I would recommend starting an RfC (see WP:PAG). One possibility would be to recommend {{indent}} instead. Any proposed fix will probably involve a very large number of edits, so should be suggested with full community support. Sławomir
Biały 22:06, 14 December 2015 (UTC)

Every project has its own Manual of Style, and they often contradict each other on particular details. Consequently, it's not actually possible to write software so that it is consistent with all of the Manuals of Style.

I've done a lot of policy writing as a volunteer over the years (including the section of WP:PAG that you reference ;-), and for something like this, my usual recommendation is to change the guidance and not send a bot through to change everything instantly. It's less disruptive to add it to the AWB cleanup lists or to let it happen organically as editors update articles anyway (especially for the first few months – the worst case is deciding to change X to Y, running a bot through all the articles, and then deciding that it ought to have been changed to Y' instead. A delay for testing and double-checking is very helpful in that way). Whatamidoing (WMF) (talk) 18:33, 15 December 2015 (UTC)

I too would like a relatively formal RfC on this topic. I think it will be easy to find consensus, but because this guidance would affect so many articles, it's prudent to seek wider community feedback first. Assuming consensus is achieved for display="block", I agree that AWB is good mechanism to do the edits. Ozob (talk) 19:00, 15 December 2015 (UTC)

After looking at the dev discussions, the display="block" does seem like a reasonable option. It would be nice if the project were notified by a formal RfC before this was decided by dictum. There is enough hostility to the VE concept as an unasked-for fait accompli that relatively simple things like this would certainly help to rehabilitate its image. Sławomir
Biały 19:33, 15 December 2015 (UTC)

Ok, some actual feedback. This looks reasonably feature-complete and useful. I like the fact that I can go back and forth between editing using the gui and editing LaTeX code, with a real-time preview of the current formula. The "block" option in the options pane does seem to work, so my complaint above about not handling display math is invalid. (I didn't save so I have no idea how it encodes the result or whether it is compatible with our current MOS.)

The baselines on the names of the "standard numerical functions" buttons are uneven — function names with descenders but no ascenders (like exp) are aligned differently than ones that have ascenders but no descenders (like ln) which are in turn aligned differently than ones with neither (like cos). The "tanh" button name is cut off on both sides, because it's too wide for its button. (In Chrome on OS X, if it matters.) And why does log₁₀ need a separate button?

The "operators" section is missing \square and \ltimes. Maybe they're somewhere else? Also I didn't see \operatorname{...} anywhere — is it there and I missed it? Because it's very important for being able to define operators that aren't already predefined.

The organization is a little odd; I would have expected to find π in symbols and constants (but it's in only Greek letters), and I would not have expected to find vertical fractions and binomial coefficients in a section labeled as being about matrices. I would have expected some way to format Stirling numbers of the first kind and Stirling numbers of the second kind near binomial coefficients (they look the same but with square or curly braces instead of parens) but I don't see it.

In the logic section, I don't know what the difference between the vDash and models buttons is supposed to be; their labels look the same although they render in different sizes in the formula. I would usually want the "models" one in my editing but with the current interface I'm not going to be able to remember which one that is and would have to go back and forth looking at the TeX code to tell whether I had the right one. —David Eppstein (talk) 22:50, 14 December 2015 (UTC)

How does the formula editor scale? The plugin generates previews every time a formula is updated. It seems like this has the potential for generating a lot more queries than the servers can presently handle. Currently, the servers don't even seem to be able to handle very simple requests, such as rendering $\operatorname {this} \,\!$. Come to think of it, I'm not sure why the formula editor in WhatAmIDoing's sandbox works at all, when the rest of our math rendering doesn't seem to. Sławomir
Biały 04:03, 15 December 2015 (UTC)

Are you having the same MathML/SVG impossibly-slow rendering problems that I was noting in the previous section? If so, switch back to the default PNG view, it's much faster (despite also being even uglier). —David Eppstein (talk) 04:39, 15 December 2015 (UTC)

Someone asked about this a little while ago, and while I don't remember any of the details, the devs thought that scaling would not be a problem.

David, I'm not entirely sure which system they're using, but both are working for me. There's a delay of two or three seconds between clicking a button and seeing a new picture, regardless of which setting I use. (The typical lag probably depends somewhat upon where you are in the world.) Whatamidoing (WMF) (talk) 18:46, 15 December 2015 (UTC)

Replying the Slawekb. The reason the VE maths editor can work when normal editing has problems its that VE only uses the png rendering mode. You preference has no effect.--Salix alba (talk): 08:18, 25 December 2015 (UTC)

I've mentioned this at T118616. The big problem is that you can't see the rest of the page. If your working on some fairly complex sequence of equations then you often need the context, you may need to recall quite what the previous equation or variable was. The window is so big an not movable or resizable. This means you need perfect memory to be able to type a formula. --Salix alba (talk): 08:18, 25 December 2015 (UTC)

Jitse's bot

Jitse's bot has been inactive since June 17, 2015. The three pages, Wikipedia:WikiProject Mathematics/Current activity, Wikipedia:Pages needing attention/Mathematics/Lists, and Wikipedia:WikiProject Mathematics/Count have {{historical}}. There should be a replacement bot for these tasks. GeoffreyT2000 (talk) 01:41, 24 December 2015 (UTC)

I couldn't agree more. (Unfortunately, I myself am too busy, but if some editors have free time to spare, it should be possible to run a bot, say, at Wikipedia:Wikimedia Labs.) -- Taku (talk) 05:27, 24 December 2015 (UTC)

Yes, that is why civilization ceased to exist at that time. Michael Hardy (talk) 20:56, 24 December 2015 (UTC)

I have found the following page useful. It identifies new math articles:

User:Mathbot/Changes_to_mathlists

Michael Hardy (talk) 20:49, 27 December 2015 (UTC)

"things" or "concepts"

This edit would bear discussion. Are all of these _things_ concepts? What about all the other articles titled "List of things named after X"? Does every one of them list only _concepts_? If not, do we need to decide which should be edited in this way? Michael Hardy (talk) 21:09, 29 December 2015 (UTC)

. . . so we now have an isolated exception to this pattern. And in many of these cases it's obvious that not all of the _things_ are _concepts_. A machine is not a concept; a crater on the moon is not a concept. And I don't think a theorem or an equation is a concept. Something for which one can state a _definition_ is a concept. Michael Hardy (talk) 21:24, 29 December 2015 (UTC)

I moved the page back. Ozob (talk) 21:32, 29 December 2015 (UTC)

(after edit conflict) There is also Category:Lists of things named after people. I think this change to the pattern should be reverted, per the principle of least surprise, even though I can see the case that perhaps "concepts" is a better fit for this particular article. Sławomir
Biały 21:34, 29 December 2015 (UTC)

Maybe "topics" would work better, since this is what the article starts out with. "Things" is just so vague and should be avoided. --Are you freaking kidding me (talk) 01:40, 31 December 2015 (UTC)

If you want to make this change, I suggest that you try to organize an effort to move all articles and categories beginning with "List of things named after" to "List of topics named after". Perhaps you could ask about this on Wikipedia talk:Article titles. Ozob (talk) 02:31, 31 December 2015 (UTC)

I find "topics" to be an even poorer choice than "concepts". Although you find things to be too generic and vague, I would caution against changing it. If you do manage to find a non-objectionable alternative term, I'm pretty sure that it would be so esoteric that most of our readers (myself included) wouldn't know what you are talking about. Bill Cherowitzo (talk) 04:48, 31 December 2015 (UTC)

There's nothing wrong with "things" except that it's a word that comes from Germanic barbarians rather than civilized Romans and Greeks. It is broad and inclusive, and that is what is needed here. Michael Hardy (talk) 06:32, 31 December 2015 (UTC)

Draft:Paired transform and fast Fourier transform needs help

The draft author, who appears to be the primary author of most of the cited sources, seems impervious to advice from AFC reviewers. Perhaps he/she might be more receptive to advice from fellow mathematicians. Roger (Dodger67) (talk) 10:26, 26 December 2015 (UTC)

It is not clear to me that the content of the draft would meet Wikipedia's standards for notability, even if were written in an acceptable style. The article gives no secondary sources for this transform, making it of dubious interest. Ozob (talk) 17:24, 26 December 2015 (UTC)

@ Ozob please address your concerns to the draft author User:Amgrigoryan. Discussing it here without directly involving him is pointless. Roger (Dodger67) (talk) 08:19, 31 December 2015 (UTC)