Wikipedia talk:WikiProject Mathematics/Archive/2012/Aug

History of the function concept

The new article bearing this title is perhaps interesting. Some people implicitly believe that the concept of function that we know today is axiomatic and coeternal with the Father, but the true story is complicated and messy. Michael Hardy (talk) 12:28, 1 August 2012 (UTC)

Formalized form infobox experiment

A

Correct me if I am wrong in summarizing that the discussion we had at the Mizar system talk page raised two main concerns. The first is one of bias in favor of a particular formalized math system, in this case the Mizar system, violating WP:NPOV with respect to other competing systems. The second concern is that by granting permission to place these links we will be sanctioning en masse changes to almost all mathematical articles, which while may benefit a minority of readers, will probably not be of any benefit to the typical reader in the near future. One additional secondary concern was that if we want to expose the readers to formalized math it is better to develop it inside Wikimedia than sending the users to outside sources.

Before addressing these issues please allow me one personal note: I have an agenda. My agenda is to have formalized math accessible from Wikipedia mathematical articles. No more and no less. This is driven by a view that for some readers, like myself, reading code is more instructive than reading descriptive text. I am not here to write articles, but I am here to help build the best encyclopedia the world has ever seen.

I am not affiliated with any proof assistant and in fact my knowledge of Mizar is rather slim. My choice to promote the Mizar system was based on considerable groundwork I made in preparation for this initiative, but truth be told I like Coq much better. Without much understanding of how Wikipedia works, I made the judgment that the Mizar system is the one which is best suited to the task. I believe this choice can be defended on objective grounds, but seeking to avert single-purpose-account charges I will not attempt to do so here.

Next, the issues. Indeed, I realize now that Wikipedia cannot provide access to one particular formalized system, no matter its benefits, at the expense of other systems. Nor should it be in the business of picking winners. It must be either all in or all out. This does make the choice of inclusion much harder, but should not warrant, by itself, automatic submission to the deletion impulse. My answer to this concern is two-fold: yes, we will have to link to more than one system, and no, we cannot do so in the external links section. We will have to come up with some kind of infobox or an addition to an existing infobox that will accommodate these links and help keep the typical reader away from clicking them.

Second, clearly the initial scale of deployment is not to be left to individual decision making, but should result from the formation of consensus here, in the math project discussion forum. But consensus is built by discussion, so we will probably have to spend some time in deliberation. Thus, a measure of patience will be required and yes, a willingness to learn enough of a foreign formal language that it stops reading like gibberish. It is however not in the spirit of Wikipedia established policy to brush this initiative aside by not being willing to engage the other side.

Seeking compromise, I suggest that we limit the initial deployment to a small number of key non-trivial mathematical constructs, where access to a reference of formal definitions and properties can be most helpful to undergraduate math students who are working on problem sets. I further suggest that we try and measure take-up quantitatively and by field, by contacting professors and asking that they mention the links in class and ask students to make a note if they used them in the solution of a problem set. This experiment should be limited in time as well as scope, guaranteeing that the typical Wikipedia reader does not suffer too much.

Which brings us to the final concern of internal vs. external development of formal math structures. Frankly, I do not have much to say here. I wish I was in the position to help work on the developer side, but I am not. It does however seem odd to me to suggest that Wikimedia developers should put much efforts into something for which it is not clear if there is any need. First we need to establish that there is some demand for the product, then we go about building it. This seems common sense to me and provides additional impetus to running this experiment.

I thank you for taking the time to read this lengthy post and hope that I was able to address the main issues raised. Yaniv256 (talk) 21:12, 1 August 2012 (UTC)

If we are going to include Mizar system, Coq, or Metamath proofs by reference, then I think we should make sure that those proofs are available under the CC-BY-SA 3.0 License and the GFD License as are proofs contributed by other means.

I think that proof assistants are the wave of the future, but not the present or near future. They need to develop to the point that they can read proofs in English+TeX and translate them into their internal format (perhaps asking questions of the person running the program in the process). They do not appear to be there yet. JRSpriggs (talk) 04:34, 2 August 2012 (UTC)

Metamath is in the public domain, which is CC-BY-SA compatible. I can't speak to the others. CRGreathouse (t | c) 05:16, 2 August 2012 (UTC)

Formalization links
Structure	sigma-algebra
Definition in
Metamath	Coq	Mizar
Proof of properties
Metamath	Coq	Mizar
See automated proof checking for more information.

I know that Coq-Corn and the MML are open-source but I don't know much about which kind and if it is compatible. I'll have to look into it. Yaniv256 (talk) 06:26, 2 August 2012 (UTC)

To make the discussion concrete I am posting a prototype for the purposed infobox. Currently only the Mizar links will work, the others will just send you to Google. Yaniv256 (talk) 06:26, 2 August 2012 (UTC)

I am against the inclusion of formalized proofs in WP. Unless for "trivial" results they use to be too long to be read by humans. This is similar to the case of programs. On the other hand, for pages containing results that have been formally proved, we has to mention this with references (the non trivial computer aided proofs are usually published in scientific journals and/or conferences). D.Lazard (talk) 09:48, 2 August 2012 (UTC)

It's unclear to me exactly what is being proposed. Yaniv, are you suggesting that we add an infobox to lots of mathematics articles containing links to various proof assistants? I oppose this. The input to proof assistants is really not human readable, and adds nothing to the article. If you truly find it easier to read this kind of code than plain prose, and to understand its mathematical intent, then I applaud you. But that probably makes you one of a kind. Moreover, I should add that the consensus at Talk:Mizar system was decidedly against adding links to articles, largely because such links add nothing of value to the article. Now it is being proposed that a large infobox be added, taking up more valuable real estate with the same useless information. It seems most peculiar to me that you would think the consensus at Talk:Mizar system would support such an initiative. Sławomir Biały (talk) 12:03, 2 August 2012 (UTC)

That's pretty much my position too. It would be different if these systems were widely used and understood. That is if all, or at least a large number of mathematics educators used them to teach mathematics. But that would be reflected in mainstream sources: they should be used in many textbooks, and on many courses, in the same way. But this was not true when I was at university and I've seen nothing to suggest this has changed. These links are only relevant to the particular formal systems, not general mathematics articles.--JohnBlackburne^words_deeds 13:23, 2 August 2012 (UTC)

What I said on that talk page was I was against it as a general thing and pointed to WP:NOTDIRECTORY but would support such external links where formalized logic or proof seemed relevant, for example for things like variants of the axiom of choice. Sigma-algebra doesn't sound like something like that to me. 'Deployment' sounds exactly the opposite to what I was thinking of. Dmcq (talk) 14:26, 2 August 2012 (UTC)

I would support a small-scale experiment once the template is constructed. Add the template to a small number of articles where (as Dmcq says) formalized logic or proof seems relevant. CRGreathouse (t | c) 14:36, 2 August 2012 (UTC)

Please excuse my poor choice of words as I am not native to English. Let me be more precise: 7-9 pages, determined by consensus, for a period of 6 months. My choice to use sigma-algebra was probably misguided. Can I suggest that we defer the discussion of which pages to select until after we establish a consensus that running such an experiment would be desirable, in theory? Yaniv256 (talk) 19:17, 2 August 2012 (UTC)

I really don't see what all this is about. The articles in Wikipedia are all independent and there isn't really such things as experiments like this except to test out new Wikipedia features. I think you have some picture in your mind about Wikipedia that it is monolithic and organized. It isn't. Of course some people can discuss something but I think your best bet is just to go ahead and try it out, we'll all have forgotten whatever was here in six months, or at least I will as I have a dreadful memory and I don't suppose many others will care. Dmcq (talk) 20:02, 2 August 2012 (UTC)

Before attempts to try this, though, the box needs to be improved. In particular links to Wikipedia namespace (especially a redlink) from article space are not a good idea. —David Eppstein (talk) 20:41, 2 August 2012 (UTC)

Yes, that is true. Thanks! I changed it from WP:Formal math links to Help:Formal math links, which of course I will need to create before we will be done here. Any other suggestions? Yaniv256 (talk) 21:05, 2 August 2012 (UTC)

Still not good enough. Help: namespace is for help editing Wikipedia, not for explaining Wikipedia content, and should also not be linked from article space. See WP:SELFREF. —David Eppstein (talk) 21:28, 2 August 2012 (UTC)

What should I put then? Yaniv256 (talk) 21:36, 2 August 2012 (UTC)

Since we can only work in article space I think that the best we can do then is to just send readers to a page like Automated proof checking. They will have to work out the details by themselves. Formal proof and proof assistant are two other viable landing sites. Now that I took another look at these pages I see that I'll have to attend to them anyway, so don't judge them by their current form. Yaniv256 (talk) 00:39, 3 August 2012 (UTC)

Just link the title to one of those and remove the explanation at the bottom. People can click on things to find out. Dmcq (talk) 18:02, 3 August 2012 (UTC)

Sure, if you think that is better, thanks. Opening a new page and pasting prototype B. Yaniv256 (talk) 18:15, 3 August 2012 (UTC)

Maybe whats needed is a reference template like thouse at Wikipedia:WikiProject_Mathematics/Reference_resources#Citation templates?--Salix (talk): 04:26, 3 August 2012 (UTC)

I considered this option, but read in one of the guidelines that citations should only be used to support the text to the degree that one uses them in editing the text, and not as a way to hide external links. I could work on each page and edit it so as to find a way to place these links as citations, since they do count, in my mind, as quite reliable secondary sources. My concern, however, is that this might cause confusion to the typical reader, due to the fact that such citations would have to be placed in a way that somewhat obscures their nature and will not be consistent across pages. For this reason, in case someone would revert my citations, I fear that I will have little to say in defense, as I will probably agree with most of what they would have to say. Yaniv256 (talk) 16:32, 3 August 2012 (UTC)

The citation guidelines are irrelevant, as you note, as these are not being used as sources to what's already there. The relevant guidelines are the external links ones and those suggest that not even one of these should be added, never mind six, for the same reasons as given at Talk:Mizar system. If individual links are not appropriate then box highlighting them is especially so.--JohnBlackburne^words_deeds 18:34, 3 August 2012 (UTC)

B

Formalization links
Structure	sigma-algebra
Definition in
Metamath	Coq	Mizar
Proof of properties
Metamath	Coq	Mizar

Please excuse me. I thought the matter of legal compliance with the external links guidelines was behind us. My answer to these claims was and still is here. I fail to see a meaningful response to my arguments in the discussion we had, but then again I may be missing something. Since if this proposal is to fall due to legal objections we are all just wasting our time discussing it, I suggest we stop here and assert if John's argument does have consensual support. Yaniv256 (talk) 19:49, 3 August 2012 (UTC)

You just don't get it do you? Just because you think you are right does not mean others do. You have not convinced people of your case and those references would be removed if stuck on things like sigma algebra. The reason it would be okay for things like axiom of choice is because a person reading that might not know about it and would find it a useful link. A person reading about sigma algebra is very unlikely to find it of interest unless they were already deeply into that sort of business. Wikipedia is not a directory to other web sites or software or books, it is an encyclopaedia. We do not list every single book that defines sigma algebra so why on earth should we list Mizar? Dmcq (talk) 21:54, 3 August 2012 (UTC)

Thank you for making it clear. I will not waste your time any longer. Yaniv256 (talk) 22:17, 3 August 2012 (UTC)

Real-valued function prodded

Deletion of the article titled Real-valued function has been proposed on the grounds that it's been only a dictionary definition for several years and it's unclear what to redirect it to. A problem I see with this is that a large number of articles link to it. So: (1) Is there some appropriate redirect target; or (2) Can it be expanded so that it becomes a proper article? Michael Hardy (talk) 16:57, 31 July 2012 (UTC)

I don't see any problem with letting those links go red, and removing them bit by bit. Maybe someone could get them all with AWB? --Trovatore (talk) 17:42, 31 July 2012 (UTC)

That's a difficult question okay. I think developing real analysis and redirecting there might be best. The real question is what do we actually mean by real-valued function is it instead the old idea of smooth functions including 1/x which is actually a partial function? I guess real analysis would be better for covering more classical stuff too. Dmcq (talk) 17:59, 31 July 2012 (UTC)

I just don't see much value in linking the phrase real-valued function, in most cases. I think these links probably should be removed, independently of whether there's a canonical place to redirect the search term. --Trovatore (talk) 20:16, 31 July 2012 (UTC)

Why shouldn't "partial functions" be considered real-valued if their values are real numbers? Michael Hardy (talk) 12:38, 1 August 2012 (UTC)

I think expansion would be difficult (if someone had something to say, it probably would have been said by now). A reasonable redirect would be to function (mathematics)#Types of functions. The current definition is the first line of that section.Bill Cherowitzo (talk) 18:10, 31 July 2012 (UTC)

And by the way, I didn't do the redirect I suggested because I think that Trovatore is making a good point. I've seen far too many useless wikilinks in the math pages and I would count this one as one of those. I'm sure that some discussion of standards for wikilinks in mathematics pages has already occurred - so if someone could dig it up for review I would appreciate it. Bill Cherowitzo (talk) 02:38, 1 August 2012 (UTC)

Is there such a thing as a "cross-reference page" (or should we call it by some other name?) that links to various pages that may be of interest to those who follow a link like this one? I.e. Someone clicks on real-valued function and they see a page that might look something like this:

In mathematics, a real-valued function is a function whose values are real numbers. See:

• Function (mathematics)
• Real number
• Real analysis

This is a cross-reference page.

If such a thing doesn't exist, should we invent it (along with a template for the footnote, a style manual for them, and mentions and links within the other appropriate style manuals)? Michael Hardy (talk) 12:38, 1 August 2012 (UTC)

I've raised the topic of multiple-cross-reference pages here. Michael Hardy (talk) 13:37, 1 August 2012 (UTC)

For now I've made the article into a multiple-cross-reference page and created this manual, which currently has "essay" status. Michael Hardy (talk) 00:18, 3 August 2012 (UTC)

The Real analysis article has a heading called "Key concepts." Adding a short section there on Real-valued functions, perhaps covering some of the issues mentioned above, would seem appropriate and would make a good redirect target. --agr (talk) 00:36, 3 August 2012 (UTC)

But remember that real-valued functions occur not only in real analysis, but also in other areas of mathematics and the sciences, so that can't be the whole account of real-valued functions. Michael Hardy (talk) 19:37, 4 August 2012 (UTC)

What about adding Random variable as another entry?--Kmhkmh (talk) 03:18, 5 August 2012 (UTC)

There is some similarity in these two cases. "Real-valued function" is a function to real numbers from an unspecified domain. "Random variable" is a function from the sample space to an unspecified codomain. But these are not the same. "Random variable" is a historically important concept, discovered well before modern probability space approach, and must be retained as an article. Moreover, a half of probability theory is explained with various random variables (actually, even with random events as a special case of Boolean-valued random variables), with little consideration about codomains. Contrary, "real-valued function" is not anything historically significant, nor is it important in modern mathematics. BTW, I do not see much sense in these bizarre "multiple-cross-reference pages" and would prefer to see just a red link to avoid careless inbound links, rather than such an explanation of a trivial notion. Incnis Mrsi (talk) 12:42, 5 August 2012 (UTC)

My point was not to equate those 2 concepts, but rather that a random variable is one of the most important and most examples of a real valued function. That aside I'm not sure why you'd s real valued function si historically insignificant. There would be no calculus or real analysis without it and historically it actually stand for the development of the function/map concept itself. In fact many books simply treat function as a synonym for real valued function (or a subset of them since the domain is restricted to the reals as well), i.e. if some calculus or analysis primer speaks of functions, they usually mean real valued functions.--Kmhkmh (talk) 17:18, 6 August 2012 (UTC)

The phrase real-valued function appears to be nothing more than the sum of its parts: the two links real number and function (mathematics) should in effectively every case be sufficient. To allow articles, disambiguation pages, redirects or cross-reference pages for such phrases that have not acquired a distinct notable meaning seems to be inviting a proliferation of valueless pages. (I've also seen redirects for "common misspellings" that I feel should be removed.) I am not arguing against the concept of a Wikipedia:Multiple-cross-reference page, but to me it seems that real-valued function does not qualify. — Quondum^☏ 13:25, 5 August 2012 (UTC)

Why would you delete redirects from commonplace misspellings? Michael Hardy (talk) 16:25, 6 August 2012 (UTC)

A course like "Real functions", "functions of a real variable", "real analysis", etc., has been standard in U.S. mathematics for 80 years. A disambiguation page is useful, as Michael Hardy stated. Kiefer.Wolfowitz 17:08, 6 August 2012 (UTC)

+1--Kmhkmh (talk) 17:19, 6 August 2012 (UTC)

@Quondum : It's more than the sum of its parts in that (1) there are lots of existing links to the phrase; and (2) Someone who knows that "real" should redirect to "real number" and who also knows what a "value" of a function is might not know how locutions like "real-valued" are used, and "real-valued" is not a suitable article title.

When I create a new article, I always immediately create redirect pages from (1) alternative names, (2) alternative spellings and capitalizations, (3) common misspellings, (4) common misnomers. I also add hatnotes to other articles with similar names saying "This is about X. For Y, see [[Y]]." or the like.

@Kieffer : Of course I agree, except that "disambiguation page" isn't quite what this is, since links to it are appropriate and it's not about unrelated things bearing the same name. It more like a redirect but with multiple targets for the reader to choose among. Michael Hardy (talk) 15:50, 7 August 2012 (UTC)

Fundamental theorem of ideal theory in number fields

I created the article Fundamental theorem of ideal theory in number fields because this theorem is mentioned in Wieferich prime. Do others feel that this theorem should have an own article, or should I better include that information in Wieferich prime via a footnote? -- Toshio Yamaguchi (tlk−ctb) 07:10, 7 August 2012 (UTC)

This theorem appears in Dedekind domain#Some examples of Dedekind domains. Therefore a redirect to this link suffices. By the way, the Dedekind domains are just the rings in which this theorem hold and have mainly been introduced for the case of the integers in a number field. Therefore the lead of Dedekind domain should be expanded to mention this important example. D.Lazard (talk) 09:30, 7 August 2012 (UTC)

links to Hermite's identity

I deleted the "orphan" tag from Hermite's identity. Three articles link to it. But one of those is only a hatnote and otherwise the linking to it seems on the thin side. If someone can think of other articles that could appropriately link to it, could they add those links?

Also, it currently lacks references. Michael Hardy (talk) 15:21, 7 August 2012 (UTC)

I linked it from one other article that immediately came to mind. -- Toshio Yamaguchi (tlk−ctb) 15:53, 7 August 2012 (UTC)

Knights and knaves

The lead for this article credits Raymond Smullyan with the invention of "this type of puzzle". Not knowing much about history of logic puzzles, and suspecting that the puzzle has been around a lot longer than Smullyan's books, I thought this sounded like a rather generous claim. Can anyone check into how important Smullyan's contribution to the topic is? He is pretty old, and my sense that this is a problem from antiquity could just be wrong. Rschwieb (talk) 16:46, 7 August 2012 (UTC)

I have a book by Maurice Kraitchik ("Mathematical Recreations") dated 1943, well before Smullyan appears to have committed his Knights and Knaves to print, in which one of the first problems is one of exactly this type. Although I remember as a child finding something similar in one of my grandmother's Arthur Mee encyclopedias (which was old-fashioned even before she acquired it: 1870-ish I believe) which also had a puzzle along the same lines. So no way did Smullyan invent such a puzzle, although he may well have been a pioneer in giving an exhaustive workout to the genre. --Matt Westwood 21:34, 7 August 2012 (UTC)

Thanks for taking the pains to clear that up! Rschwieb (talk) 12:28, 9 August 2012 (UTC)

Proofs and sourcing of proofs in WP-articles

There is currently a developing discussion at WP:NOR which might be of interest/importance for editors here. It is at Wikipedia_talk:No_original_research#Original_mathematical_proofs_are_not_interpretations and in the next section as well.--Kmhkmh (talk) 15:31, 8 August 2012 (UTC)

Jitse's bot

Jitse's bot has done nothing in more than three days; the "current activities" page has not been updated. I don't see a lot of expression of alarm about that here. Is that because everyone else has directed their comments about it to Jitse Niesen, as I have, or could it be that I'm the only one who notices? Michael Hardy (talk) 18:36, 9 August 2012 (UTC)

I suspect there is not as much appreciation of the "current activities" page as would be useful. Once things get back to normal here, I may start posting a few highlights from that page here as they appear, along with a link to the page. Michael Hardy (talk) 00:41, 10 August 2012 (UTC)

August 9, 2012

Here are some new articles that do not (yet?) appear on the "current activities" page since Jitse's bot is down:

Added Douady–Earle extension

Added Perfectly orderable graph

Added Schizophrenic Number

Added Sumner's conjecture

Mathematicians:removed I. Bacharach

Mathematicians:removed Isadore M. Sheffer (is a redirect to Isador M. Sheffer)

Mathematicians:removed Jake Brown

Mathematicians:removed Peter Montgomery

Mathematicians:removed Robert Bryant

Mathematicians:added Isador M. Sheffer

Mathematicians:added Peter Montgomery (mathematician)

Mathematicians:added Robert Bryant (mathematician)

Michael Hardy (talk) 00:48, 10 August 2012 (UTC)

....and now the page has been updated for the first time since August 5th. Here's the list of new articles:

9 Aug: Christian of Prachatice, Cohen ring, Combining dimensions, Cone, Curta, Deal.II, Dedekind group, Douady–Earle extension, Equidissection, Isador M. Sheffer, J. W. Bruce, Matrix similarity, Mirsky's theorem, N. U. Prabhu, Orthogonal array, Perfect graph theorem, Perfectly orderable graph, Peter Montgomery (mathematician), Proper base change theorem, Regular tunings, Robbins' theorem, Robert Bryant (mathematician), Schizophrenic Number, Semiregular polytope, Smooth morphism, Sumner's conjecture, Trilinear polarity, Vizing's theorem, Zero order.

(Some may be newly recategorized articles rather than actually new articles.) So see if they need further work. Michael Hardy (talk) 02:44, 10 August 2012 (UTC)

Wikipedia:Featured article review/Infinite monkey theorem/archive2

This is a notification to interested editors that the article Infinite monkey theorem has been put up for featured article review for referencing and prose issues. — Crisco 1492 (talk) 03:56, 10 August 2012 (UTC)

Batrachion

AfD discussion at Wikipedia:Articles for deletion/Batrachion. Gandalf61 (talk) 21:16, 12 August 2012 (UTC)

Not a maths textbook, but an encyclopedia

The FAQ at the top of the page, asks "Why is it so difficult to learn mathematics from Wikipedia articles?", and suggests that it is because "Wikipedia is an encyclopedia, not a textbook [..] and not supposed to be pedagogic treatments of their topics".

To me, nearly every other subject in Wikipedia does read like a textbook summary. They all teach someone the basics of a subject. The one exception is maths, which despite my confidence to tertiary level, I find Wikipedia useless, because any attempt to include pedagogic examples are frowned upon.

Textbooks include 20 examples of a problem, and laboriously step through them. Surely this does not mean that we should exclude all examples? We readily include an image too illustrate a fact, but there can be no reason to exclude a stepped-through example, that also illustrates a fact.

Wikipedia is different to most other encyclopedias where space is not at a premium. I don't expect an article on, for example, Elementary algebra to be equal in length to a 500-page book. But I also don't expect it to exclude a couple of pages of examples, because a pedagogic approach is supposed to be bad. Maths articles are supposed to educate people, not exclude 95% of the readership who are expected to be able to learn something. --Iantresman (talk) 00:17, 13 August 2012 (UTC)

Do you have a particular example you were hoping to add to a particular page that was removed? If not, I'm not sure what sort of responses you're looking for. The number 1 reason that wikipedia math articles are not very accessible is that they tend to be written by specialists or other people with a relatively advanced math background, but as far as I can tell there's no organized campaign to prevent people from making math articles more accessible. --JBL (talk) 00:33, 13 August 2012 (UTC)

It also requires a specialist to make an advanced mathematics article accessible to lay persons. Most of the pedagogy we get is from WP:RANDY, and is of poor quality. I think this makes our more experienced editors believe that all pedagogy is bad. But I think we should aim for the quality of pedagogy in the Princeton Companion to Mathematics, written by specialists and aimed at a general audience. Sławomir Biały (talk) 12:41, 13 August 2012 (UTC)

Some math articles do include examples. But there are several reasons their use is limited.

1. Examples usually fail a strict reading of WP:V and WP:NOR. Making up our own examples to illustrate things leads to complaints when people demand specific sources for everything that is written. For lower level articles we might be able to directly quote some examples, although extensive copying would cause other complaints about excessive direct quotations.
2. The tone of examples tends to be nonencyclopedic. If we add an example with no explanation, people may not understand it at all. If we add the detailed explanation to help them, the article begins to read like a math textbook instead of an encyclopedia article - and the explanations again fail WP:V.
3. Even ignoring the verifiability problems, it's very hard to get agreement on which examples would be included. Everyone has their own pet way of presenting topics, and there is no easy way to find the "best" one. Even two authors of the same book have to go through lots of argument about how to phrase things. Finding agreement on unsourceable content in a wiki setting would be utterly impractical.
4. There's an entirely separate project, wikibooks, which is intended for pedagogical writing.

As a general principle, it is much more straightforward for us to focus on giving summaries of material, and leaving pedagogy to textbooks. — Carl (CBM · talk) 01:12, 13 August 2012 (UTC)

Comment: this type of issue has been raised a few times before. For example: Wikipedia_talk:WikiProject_Mathematics/Archive_69#wikipedia_is_a_great_source_of_info_for_just_about_anything.2C_with_one_exception:_mathematics., Wikipedia_talk:WikiProject_Mathematics/Archive_70#Accessibility_of_WP:Math_.28or_.22No.2C_I_don.27t_have_Dyscalculia_but_WP:Math_is_just_facts_and_proofs..22.29, Wikipedia_talk:WikiProject_Mathematics/Archive_18#General_Comment_about_Math_articles_from_a_non-mathematician, Wikipedia_talk:WikiProject_Mathematics/Archive_16#Request_from_Non-math_Person. Jowa fan (talk) 02:25, 13 August 2012 (UTC)

It may help the OP to realize that maths (and other specialist subjects, such as physics) are simply different from most other topics in an encyclopedia: the depth of coverage is far greater and more precise, and the average person has very little familiarity with the concepts. The overall result is that making a maths article pedagogical generally unavoidably detracts from it as a reference and vice versa. A bit like writing English articles for non-English readers would detract from them. — Quondum^☏ 04:24, 13 August 2012 (UTC)

Probably also worth suggesting that those who are wizards at mathematics are often not so good at writing encyclopedia articles to explain their knowledge. As a fairly frequent visitor to another (mathematics specialist) wiki, I hav seen the phenomenon whereby a page is written succinctly and smartly, so as to be readily understood by a newcomer (with solidly maintained links to concepts referenced), and then someone turns up who remarks, "This work is not rigorous and the examples are misleading" and replaces it with a much more difficult-to-follow exposition based on an axiomatic framework which is far from clearly explicated. This is not because the topic can not be explained in an easily-assimilable manner, so much as the fact that as the mathematician is so clever he can not believe that everyone in the world is so badly educated as not to understand a particular obscure symbology or terminology. When asked "Please explain your language," the answer that comes back is "Why should I, only a mathematician of my standing is clever enough to (be allowed to) know this." This (in my usually rubbish opinion) is not fully optimal.

Finding the balance is difficult, but not so difficult as to be impossible. Just because you can't do it doesn't mean to say it can't be done, however clever you think you are. --Matt Westwood 06:06, 13 August 2012 (UTC)

Imho editors often still thinking old print categories, when they treat this as an either-or-scenario. Since WP is not paper it is often possible to offer various approaches to the article's subject in different section, which have different levels of abstraction and accessibility.--Kmhkmh (talk) 13:06, 13 August 2012 (UTC)

Thanks for all the comments and links. Perhaps I'm over-reacting, or I misinterpreted the guidelines which I took to mean that articles should mostly exclude material that is (a) pedagogic, (b) textbook-like. Maybe the guidelines could be improved to suggest how an article can (i) be accessible (ii) include examples, without becoming a textbook, POV etc. --Iantresman (talk) 10:16, 13 August 2012 (UTC)

I think a balance is possible, but of course not so easy to achieve as there are many tradeoffs. I think most editors strive for this, but the primary value as a reference must not be sacrificed. The assumption of flexibility in an electronic medium may be a little misinterpreted: an article's length is severely constrained, and consequently pedagogy must in general be linked rather than included an added section. — Quondum^☏ 13:18, 13 August 2012 (UTC)

I guess that the more general an article (eg. algebra), the more problems we will have with space. But subdividing an article (eg. Solving a linear equations in two variables), should give us more space for explanations. So are we saying that in other words, divide and conquer? --Iantresman (talk) 17:05, 13 August 2012 (UTC)

It is not the place in an encyclopedia to teach how to solve a linear equation or a system of linear equations in two variables. This is done in high-school textbooks. In elementary algebra, the relevant information is that

• there are general methods to solve linear equations and systems in any number of variables,
• there are algorithms and computer programs that do that efficiently,
• if there are more variables than equations, then either there is no solution or an infinity
• etc.

The detailed explanation of the methods have to be referred to the articles on linear equations and systems. D.Lazard (talk) 17:45, 13 August 2012 (UTC)

Now I'm confused again. We have an article on the quadratic formula, which teaches people how to derived the quadratic formula, and even refers people to another article on how to do so using the Completing the square method, and articles on Solving quadratic equations with continued fractions. A strict reading of "Wikipedia is not a textbook" would exclude their approach.

So what I think you are saying, is that we don't go into detail in a general article like elementary algebra, but we might include that detail in separate relevant article. In which case we are not saying strictly that Wikipedia is not a textbook and can't teach like a textbook, but we may "teach", if follow the appropriate structure and style that does not read like a textbook. For example, L'Hôpital's rule includes just the kind of examples I would describe as pedagogic and textbook-like. --Iantresman (talk) 22:46, 13 August 2012 (UTC)

We can include an example as an illustration and it can include editor generated data just like an image but we need to be sure we don't include any new material - that they really are just illustrations and clearly seen to be such. We don't provide them in the sense of 'this is how you do it' but more as in 'here is an example illustrating what is being discussed'. Dmcq (talk) 23:11, 13 August 2012 (UTC)

I agree with Iantresman that many, if not most, articles on elementary math are written in a textbook-like style and do not follow the recommendations of MOS:MATH. This does not really bother me, if the reader may easily find the relevant information that an encyclopedia must provide. But it is frequently not the case. An example is the case of the division of the integers, there are the articles division (mathematics), long division, division algorithm, now moved to Euclidean division, remainder and modulo operation. The first article is overly detailed on notions that anybody, which is able to read Wikipedia, should know, but does not state clearly that there are two divisions between integers, the division that produces a rational number and the Euclidean division which produces a quotient and a remainder. The four other articles are related to the same notion of Euclidean division, but, although it is an ubiquitous notion, the reader can not have any idea of its main applications. As a consequence, all these articles are much less useful that they should be. Maybe a section on elementary math should be added to MOS:MATH? D.Lazard (talk) 09:54, 14 August 2012 (UTC)

I also think that an encyclopedia must provide certain information, but that some textbook-style examples may improve them. I'm certainly not suggesting that we replace the encylopedia style with textbook style. I would envision an article on division (mathematics) to be more "encylopedic" than an article on long division, which I would argue, can not avoid but include an example.

Since I am sure that no-one is suggesting that we never include examples, the question then becomes, how do we improve accessibility and include examples, without contravening "Wikipedia is not a textbook". --Iantresman (talk) 10:27, 14 August 2012 (UTC)

This is not a complete answer, but links to pages in Wikiversity and similar sites should be considered for filling this purpose when examples etc. start detracting from the main purpose as a reference. In all, I think the principle of retaining an article's utility as a reference could act as a guide for what level of examples/explanation is suitable. Within this constraint, accessibility should be maximized, possibly more in the sense of style of presentation (using more commonly understood definitions, avoiding unnecessarily obscure concepts, accessible language, etc.) than in the sense of pedagogy. As D.Lazard points out, articles have a tendency to morph in the direction of pedagogy at the expense of reference value of the topic. This is most acute in the articles that are elementary or topical enough to attract a large amount attention (e.g. Speed of light, Higgs boson, Division (mathematics)). The article Elementary algebra falls squarely in this zone. — Quondum^☏ 12:43, 14 August 2012 (UTC)

Gunther Schmidt

Deletion of Gunther Schmidt has been proposed on the grounds of lack of references. Can someone improve the article to the point where that objection doesn't apply? Or is it not worth keeping? Michael Hardy (talk) 00:21, 14 August 2012 (UTC)

David Eppstein did an edit on this after I posted what you see above, but he didn't delete the "prod" tag, and the article got deleted.

Two questions:

• Can references be added to support what the article says?
• Is it worth keeping as an article?

If so bit of further work might make it possible to restore it. Here's what the article said:

copied from deleted article:

Gunther Schmidt (born 1939) is a German mathematician whose research ranges from informatics of mathematics to mathematical logic. After studying mathematics at the University of Göttingen and the University of Munich, he worked from 1962 to 1988 at TU Munich (TUM) and 1988 until his retirement 2004 at Universität der Bundeswehr München.

Books

• Gunther Schmidt, 2010. Relational Mathematics. Cambridge University Press, ISBN 978-0-521-76268-7.
• Gunther Schmidt, Thomas Ströhlein, 1993. Relations and Graphs – Discrete Mathematics for Computer Scientists. Springer Verlag, ISBN 3-540-56254-0.
• Gunther Schmidt, Thomas Ströhlein, 1989. Relationen und Graphen – Mathematik für Informatiker. Springer Verlag, ISBN 3-540-50304-8.
• Manfred Broy, Gunther Schmidt, Eds. 1982. Theoretical Foundations of Programming Methodology. Reidel Publishers, ISBN 90-277-1460-6.

References

Weblinks

• Gunther Schmidt's web page in the Faculty of Informatics
• [1]

Category:German mathematicians Category:Living people Category:1939 births Category:University of Göttingen alumni Category:Ludwig Maximilian University of Munich alumni Category:Technical University Munich alumni Category:Bundeswehr University Munich alumni Category:German academics

end of copy of deleted article

I think that blpprod was the wrong reason to delete this article (almost certainly it could have been sourced adequately for verifiability) but the reason I didn't fight harder for it was that I was not certain he passed WP:PROF. Being a full professor with several books is suggestive but not conclusive. The strongest case for WP:PROF seems to be criterion #C1, significant impact within his discipline (as measured by citation counts, for instance) but in his case I was having a difficult time finding good citation counts because his name is so common. —David Eppstein (talk) 17:07, 14 August 2012 (UTC)

Mathematical Manuscripts of Karl Marx | References

Dear Members of the concerned community, I request you to consider adding the following to the References part of <http://en.wikipedia.org/wiki/Mathematical_manuscripts_of_Karl_Marx>:

Marx, Karl (1994)[1968], Yanovskaya, Sofya, ed.,Mathematical Manuscripts[complete English translation]together with a Special Supplement <http://cfcul.fc.ul.pt/varios/Karl_Marx_FINAL.pdf> Calcutta/Kolkata: Viswakos Parisad, I S B N 81-86210-00-8.

Regards. Pradip Baksi — Preceding unsigned comment added by 223.180.185.44 (talk) 03:58, 4 August 2012 (UTC)

I would have thought the ideologues in Soviet Russia and China would have gone out of their way to destroy pure mathematics with their Gradgrind type outlook, but it seemed to survive very well. Is there a story to be or already told about that? Dmcq (talk) 17:41, 6 August 2012 (UTC)

There's already a link. Why would we need another? Why is a Kolkata link hosted in Portugaul? What's Kolkata got to do with it anyway? What's the "special supplement"? linas (talk) 15:55, 18 August 2012 (UTC)

Elementary algebra GA review

I was reviewing Elementary algebra and then I found that the editors used textbook language, such as "Let's" which would be changed to "Let us," but that means let me teach you. Article sounds a lot like a Wikiversity page. I would appreciate a second opinion on this. Obtund^Talk 04:39, 4 August 2012 (UTC)

I think ""lets/let us" is unencyclopaedic. linas (talk) 15:57, 18 August 2012 (UTC)

How about the use of "we" as used in the Encyclopedia Britannica article on Elementary algebra --Iantresman (talk) 18:27, 18 August 2012 (UTC)

It's allowed by WP:FIRSTPERSON but the MOS says that "often rephrasing is preferable" and avoiding it is usually not difficult. For past discussions see e.g. Wikipedia talk:Manual of Style/Archive 95#"We" in mathematics. —David Eppstein (talk) 19:19, 18 August 2012 (UTC)

SVG output from graphics tools

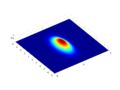
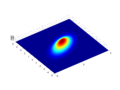
Hi, not an official part of this project (yet), but what you think of these SVG images I made based on MATLAB source code:

Exemplified in the Gaussian function article: New images:

• 
• 
• 

Old images:

• 
• 
• 

If you have any feedback (prefer the SVG or old versions) please let me know.

Zerodamage (talk) 19:20, 8 August 2012 (UTC)

Those look like nice improvements. One thing: in your images, there is a transparent background. I think for accessibility purposes people like there to be a solid background. Though I think this may have been a contentious point. You should check it out. RobHar (talk) 19:41, 8 August 2012 (UTC)

I agree that this is an improvement. I noticed that the svg makes the grid quantization visible (e.g. in the solid blue area) while the old png doesn't; I assume this is a deliberate choice, and I think it's a good idea e.g. to make it clearer why the central red-orange area has some jagginess. —David Eppstein (talk) 20:17, 8 August 2012 (UTC)

It is usual and easy to make a solid appearance of a transparent image. There are several more ways to do it via setting HTML/CSS background or superimposing of images. But it is, generally, impossible to make a transparent appearance of an opaque image. Do not add any background. The only thing I advice to change is width="100%" heignt="100%". Not so good in the context of Commons' web interface. Use concrete dimensions (such as 1050×787.5), please. Incnis Mrsi (talk) 20:18, 8 August 2012 (UTC)

Actually the jagedness is a sideeffect of the tools used. I looked at correcting it but decided it actually was advantageous for the images to preserve it. As for size code (100%), I'm assuming your referring to the SVG code; I will look into correcting that. Zerodamage (talk) 09:29, 9 August 2012 (UTC)

The images are annoyingly tiny. It would be great if all of the whitespace were removed, and they were rotated by 45 degrees so that the corners would not poke out and take up space. Make the central item, the point of interest, as large as possible! linas (talk) 16:22, 17 August 2012 (UTC)

List of reciprocity laws

Yet another link farm. -- Taku (talk) 20:32, 13 August 2012 (UTC)

The reciprocity law article seems like it is worth having to me. I don't see the need for a separate list of reciprocity laws. Sławomir Biały (talk) 00:22, 14 August 2012 (UTC)

I don't understand what is meant by calling it a "link farm", but in view of the content of the article titled reciprocity law, it's a duplicate that should redirect to the older article, as it now does. Michael Hardy (talk) 00:35, 14 August 2012 (UTC)

Sorry. It was a mistake. It has been corrected. -- Taku (talk) 02:01, 15 August 2012 (UTC)

Change the subject slightly, but I have been working on an article about Eisenstein Reciprocity, should be ready in a week or so. - Virginia-American (talk) 19:24, 17 August 2012 (UTC)

nLab cross-pollination

Anyone have any experience with movement of content between WPM and nLab? I notice that nLab has deeper/more extensive coverage of cat theory topics than WPM, and so I'm tempted to do some cut-n-paste effort from there to here, but am stymied slightly by the license, or rather lack there-of. The de facto license at nLab seems to be this, quoting from the home page: "Using content obtained from the nLab in your publications is free and encouraged if you acknowledge the source". That's it; I can find nothing more explicit. As far as I can tell, this hasn't been discussed on WPM before... Comments? linas (talk) 16:49, 17 August 2012 (UTC)

FYI, I've just created a template to help w/ ncatlab citations: so:

* {{nlab|id=simplex+category|title=Simplex category}}

will create the following text:

• Simplex category at the nLab

linas (talk) 19:22, 17 August 2012 (UTC)

Some parts of n-lab does seem to have original research. But if we're careful, the content dumping sounds like a good idea, only if we can do it as you noted. There is some discussion [2]. -- Taku (talk) 11:37, 18 August 2012 (UTC)

Apparently, the springer EOM has a CC-BY-SA/GFDL policy now, too, as long as one provides attribution. Someone dumped the whole contents of Neil Hitchin's 'magnetic monopole' into Magnetic monopole#Appendix... I am looking for an attribution template.... linas (talk) 14:13, 18 August 2012 (UTC)

Wait, you have to be careful. The only new content is unde cc-by-sa. From the main page:

"The original articles from the Encyclopaedia of Mathematics remain copyrighted to Springer but any new articles added and any changes made to existing articles within encyclopediaofmath.org will come under the Creative Commons Attribution Share-Alike License"

-- Taku (talk) 14:25, 18 August 2012 (UTC)

I had to read that 4 times, but I think they are actually saying that *all* content is CC-BY-SA/GFDL. The first few sentences make it sound like its only the new material, but later, they state that its all of the material. Or at least, that's what I got out of it after reading it over and over... So, FWIW, there is now a Template:SpringerEOM attribution. If this is wrong ... well, time for the wiki-lawyers to step in, as otehrwise, magnetic monopole is now in copyvio land ... linas (talk) 15:31, 18 August 2012 (UTC)

Finitely generated ring

I think I know enough algebra to know that there is no such thing as finitely generated ring (or every ring is finitely generated, namely by 1). Google search disagrees. I think people mean finitely generated k-algebras; so this should be redirected to finitely generated algebra in my opinion. But maybe someone knows better. -- Taku (talk) 20:46, 17 August 2012 (UTC)

Generally, when there is a term that can be used with R-algebra at the end, and is used with ring at the end instead, it's that one is speaking of Z-algebras. Similarly, a scheme is just a scheme over Z. Anyway, here the term "finitely generated ring" is defined on page 30 of Atiyah–Macdonald as indeed being a finitely generated Z-algebra. RobHar (talk) 04:08, 18 August 2012 (UTC)

Ok, this is very helpful. This answers my problem exactly; especially, the AM part. I will probably add a discussion f-gen in f-gen algebra unless someone else beats me do it. -- Taku (talk) 13:32, 18 August 2012 (UTC)

And just to preempt another conceivable use in the future: someone might use this term while working in a ring without unity. I think Rob's right though that most often it's going to be one of these screwy uses of "finite" that have been invented. Rschwieb (talk) 23:38, 19 August 2012 (UTC)

Stefan Banach

Volunteer Marek (talk · contribs) has been working hard on improving our article on Stefan Banach. The coverage of his education, mentorship, and life is now much better than it was, but the coverage of his mathematical contributions is still weak. Perhaps some project members whose interests run towards that kind of mathematics could help? —David Eppstein (talk) 00:11, 21 August 2012 (UTC)

His contributions section does seem short, but it looks like a good start to me. Maschen (talk) 14:42, 21 August 2012 (UTC)

List of zero terms

List of zero terms is also at AfD. Please comment there. Sławomir Biały (talk) 19:08, 28 July 2012 (UTC)

The treatment of zero in mathematics on Wikipedia is more generally a bit of a jumble. We have:

• 0 (number)#In mathematics,
• Zero (disambiguation)#Mathematics,
• Zero element,
• List of zero terms,

each giving a list of zero terms, each incomplete, with a lot of overlap.

Note also this curious pair of redirections:

• Non-zero → 0 (number),
• Nonzero  → Nonzero: The Logic of Human Destiny.

 --Lambiam 15:52, 29 July 2012 (UTC)

Now closed as merge to Zero element. I've done the merge but it could do with some eyes. I also had to split off Zero order as a seperate article which is very stubby.--Salix (talk): 11:33, 7 August 2012 (UTC)

See Talk:Zero order for some comments. Deltahedron (talk) 19:48, 18 August 2012 (UTC)

I have updated the article Zero order process to distinguish two separate meanings. Deltahedron (talk)

Normally when the same phrase is used for two different and unrelated meanings, we have two articles, with a hatnote linking one to the other. See WP:NOTDICT, in the last line of the table under "Major Differences". —David Eppstein (talk) 17:32, 22 August 2012 (UTC)

Feel free ... Deltahedron (talk) 19:01, 22 August 2012 (UTC)

New article feed

I've noticed your project was listed at User:AlexNewArtBot but was missing the ruleset, so the search was not carried out. I'ved added the rule (list all new articles with the string "math" in it, and hopefully that's all that was needed. If so, you should see this link turning blue soon, and then you may want to add it to your main page. See how we did it at our WP:SOCIOLOGY: Wikipedia:WikiProject_Sociology#New_article_feed. --_{Piotr Konieczny aka Prokonsul Piotrus| reply here} 18:18, 22 August 2012 (UTC)

Thanks, but mostly we depend on Mathbot (talk · contribs), Jitse's bot (talk · contribs) and Wikipedia:WikiProject Mathematics/Current activity instead. Rather than using syntactical analysis like that, it is based on the categories of the articles, so the two efforts may be complementary (both picking up ones missed by the other). —David Eppstein (talk) 18:22, 22 August 2012 (UTC)

Must y be an integer?

Take a look at this edit. If one adopts the definition

${\binom {n-y}{n}}={\frac {(n-y)(n-y-1)(n-y-2)\cdots (n-y-n+1)}{n!}}$

then this is well defined even if y is not an integer, and I'd have guessed the whole identity would still hold then. Maybe when I'm feeling less lazy I'll check it.

A good edit? Or not? Michael Hardy (talk) 16:38, 7 August 2012 (UTC)

If n > y >1 are integers, this binomial coefficient is null. Thus the series involved by this edit is finite. For small values of n, all factors are negative. It is not clear to me what the notation "choose" means in this case. On the other hand the formula you have written is clearly a polynomial in y, and thus defined for any n. Thus the edit is certainly not good. But it reveals that the involved formula has to be checked, as binomial coefficients are rarely used when all factors of the numerator are negative. D.Lazard (talk) 17:28, 7 August 2012 (UTC)

The last sentence is not entirely correct. For instance, the binomial series

$(1+x)^{\alpha }=\sum _{k=0}^{\infty }{\binom {\alpha }{k}}x^{k}$

is valid for any $\alpha \in \mathbb {R}$ and $|x|<1$.--LutzL (talk) 18:15, 7 August 2012 (UTC)

The expansion in question follows formally by expanding one factor of the integrand defining the beta function in a binomial series and integrating term by term. This would not require y to be an integer, though there would be some natural constraint on y to ensure convergence. Sławomir Biały (talk) 19:14, 7 August 2012 (UTC)

Yes, it uses ${\binom {y-1}{n}}=(-1)^{n}{\binom {n-y}{n}}$. Uniform convergence does not extend to the upper bound 1 of the integral, but I don't see a dependence on y. If convergence follows as some variation of the alternating harmonic series, then the argument should be valid for all y.--LutzL (talk) 19:55, 7 August 2012 (UTC)--Number of negative factors stabilizes.--LutzL (talk) 07:54, 8 August 2012 (UTC)

Well, the problem is that ${\binom {n-y}{n}}$ all (ultimately) have the same sign for fixed real y, so the series never converges on the real axis, except at $y\in \mathbb {N}$, where it's zero. Sławomir Biały (talk) 20:51, 7 August 2012 (UTC)

They all have the same sign, but it doesn't follow that the sum diverges. For example, if I'm not mistaken, ${\binom {n-1/2}{n}}$ grows like $c\cdot n^{-1/2}$, which certainly yields a convergent sum (as long as x isn't a negative integer). --JBL (talk) 22:52, 7 August 2012 (UTC)

Ah yes, of course. In general ${\binom {n-y}{n}}\sim n^{-y}/\Gamma (1-y)$. Sławomir Biały (talk) 00:50, 8 August 2012 (UTC)

Indeed, and convergence follows directly from the Raabe or Gauß tests, as long as $x,y>0$. For non-positive x or y even the defining integral would have a non-integrable singularity at t=0 or t=1.--LutzL (talk) 07:54, 8 August 2012 (UTC)

Presumably the formula in question is taken from a reliable source? What is that source and what does it say? Deltahedron (talk) 06:47, 8 August 2012 (UTC)

Knuth somewhere has a discussion of the binomial formula, perhaps in Volume One or Concrete Mathematics.... Sedgewick and Flajolet's 2-volume Analytic Combinatorics used to appear on the internet in draft form.Kiefer.Wolfowitz 10:01, 8 August 2012 (UTC)

2-volume ?? Their book, which is 1-volume, is available where it's been for years by following the link at Analytic combinatorics. — Preceding unsigned comment added by 2.97.22.242 (talk) 11:12, 8 August 2012 (UTC)

They wrote an earlier, simpler book on enumerative combinatorics (with a view towards algorithm analysis), perhaps as part of the same project. Kiefer.Wolfowitz 18:02, 21 August 2012 (UTC)

Mmm, Ok, I'll give you that one. 89.241.231.98 (talk) 03:33, 24 August 2012 (UTC)

Behrens–Fisher distribution

I've written this somewhat hastily scrawled user-space draft. I have in mind that with some further work it can evolve into something to be moved into the article space under the title Behrens–Fisher distribution (currently a redirect). In its early stages that will be maybe two or three times as long as the present draft. I'll be back to do more work on it. In the mean time, maybe others can improve it as well. Michael Hardy (talk) 03:40, 24 August 2012 (UTC)

Is there a mechanism for people to advertise userspace drafts of mathematical articles that they want others to look at (other than posting here of course)? It might be quite helpful. Deltahedron (talk) 03:45, 24 August 2012 (UTC)

Deltahedron: Probably not. Why not just link from here to there?

Michael Hardy: Good start to the article, though I probably will not be much help... Maschen (talk) 06:33, 24 August 2012 (UTC)

To Deltahedron, actually Wikipedia was supposed to be a place where you put your draft. But maybe nowadays it is more of a place for articles waiting for a peer review. One way to provide a mechanism (which doesn't exist to my knowledge) is to create a tag and ask people put it on their drafts. -- Taku (talk) 13:38, 24 August 2012 (UTC)

Sometimes with a fairly complicated article, one wants to make the draft somewhat complete before moving it to the article space. I might move it there soon with some tags saying some sections should get expanded. Michael Hardy (talk) 22:51, 24 August 2012 (UTC)

OK, it's moved to the article space. For now, it's an "orphan". Michael Hardy (talk) 23:35, 24 August 2012 (UTC)

Semi-Simplicial Sets and problems with that article

The whole thing with semi-simplicial sets is quite messy, so I'll start with a short history wrap-up

• 1950 Eilenberg and Zilber published the paper Semi-Simplicial Complexes and Singular Homology, where they defined a Semi-simplicial set as a collection of elements together with dimension and face-maps, which is what nowadays is commonly called a Delta set, and a Complete Semi-Simplicial Set as a Semi-Simplicial Set with degeneracy maps, which correponds to what today is most commonly called a Simplicial set
• 1967 Gabriel and Zismann published the book Calculus of Fractions and Homotopy Theory, where they used the term Simplicial Set to denote what Eilenberg and Zilber called complete Semi-Simplicial Set (they didn't use Semi-Simplicial- or Δ-Sets in this book).
• 1969 Rourke and Sanderson published the paper Δ-Sets I: Homotopy Theory. where they used the term Δ-Set for what Eilenberg and Zilber called Semi-Simplical Complex, css-set to describe what Eilenberg and Zilber called Complete Semi-Simplicial set, and Semi-Simplicial Complex as an umbrella term for Δ- and css-sets.
• 1997 Gelfand and Manin published the book Methods of Homological Algebra, where they refered to Semi-Simplicial sets as Triangulated Spaces (well, technically they call the geometric realization a triangulated space, and the combinatorial object the Triangualtion)
• 2008 Kozlov published the book Combinatorial Algebraic Topology, where he used the term trisp for Semi-Simplicial Sets, which is an abbreviation of Triangulated Space.

So, I think all this should be somehow incorporated into the Δ-Set article, though I'm not sure really sure what might be the best way to do so (and I don't know who coined which term originally). Moreover I'd say the article should be named after it's original name, i.e. Δ-Set should refer to semi-simplicial set, and not the other way round. And last but not least the article needs to be generally improved, e.g. by including the categorial definition (as a functor from Δ to Sets) for a semi-simplicial set. I'll might very well do that sometime, though. --Roman3 (talk) 12:19, 24 August 2012 (UTC)

The better math articles have a History section to them. I see nothing wrong with copying the above, more or less verbatim, into one of the two articles. Just make sure terms like trisp are not redlinks. linas (talk) 04:12, 25 August 2012 (UTC)

Suggested merges with dyadic product and outer product, into tensor product...

See talk:outer product, Dyadic Product and talk:Dyadic product. Opinions? At least a merge of dyadic product into outer product seems sensible to me and a few others. Maschen (talk) 14:30, 21 August 2012 (UTC)

Partial oppose. Outer product is concrete while tensor product is heavy on abstract nonsense. Kiefer.Wolfowitz 14:35, 21 August 2012 (UTC)

I was expecting this response, I'm not so fussed about merging outer into tensor product, but dyadic into outer could be done... Also Kronecker product should be left alone IMO. Maschen (talk) 14:38, 21 August 2012 (UTC)

"Dyadic product" is certainly the same thing as the article "outer product" currently describes. "Tensor product" is an operation on spaces (objects), not elements, but it is hardly possible to understand one without another. IMHO all content has to be merged, and outer product is about to be made a disambiguation page. Incnis Mrsi (talk) 14:39, 21 August 2012 (UTC)

Partial oppose, per Kiefer.Wolfowitz. I also think that the term "dyadics" is almost entirely obsolete, only appearing in very old textbooks. Sławomir Biały (talk)|

"Dyadic" is a very obsolete term, but that doesn't mean it can't be mentioned briefly in the merged articles (if they are), for historical awareness and completeness. It may be difficult to pull tensor product and outer product together, but certainly not dyadic and outer (also for which there is plenty of favour to merge on that talk page). Maschen (talk) 20:35, 21 August 2012 (UTC)

Let's summarize different merging possibilities:

1. Dyadic product + Outer product + Tensor product
2. Dyadic product + Outer product leaving Tensor product alone,
3. one proposal for: Dyadic product + Dyadics + Outer product,
4. everything on dyadics into one article, for pure historical interest: Dyadic tensor + Dyadic product + Dyadics, and optionally Outer product + Tensor product,

Which one(s)?... By all means we can't fall into the trap of pulling everything into one article... Maschen (talk) 20:56, 21 August 2012 (UTC)

I would say leave Tensor product and outer product articles alone for now, and merge all of the dyadic articles as you suggest in option 4. Sławomir Biały (talk) 22:35, 21 August 2012 (UTC)

P.S. Another thing to think about is how the article Kronecker product fits in with outer product. Sławomir Biały (talk) 22:35, 21 August 2012 (UTC)

Ok - that's reasonable. Kronecker product is a bit long and heavy to merge into anything though, and I think it should have its own article. If merged it will need a significant trim to just the lead definition and properties. Maschen (talk) 05:45, 22 August 2012 (UTC)

The term tensor product evidently refers not only to the tensor product of spaces, but also to the tensor product of elements (e.g. tensors such as vectors) within those spaces, as specifically addressed by section 2 of the article. (The tensor product of the spaces is the linear span of the tensor products of their elements.) The dyadic product and outer product are also mentioned in that article.

So I respectfully disagree with Incnis, Kiefer.Wolfowitz and Sławomir, and feel that Dyadic product, Outer product should be merged into and made into redirects to Tensor product#Tensor product of two tensors. Dyadic tensor and ***Dyadics should be merged into and redirected to Tensor as minimal historical notes. Note that outer product is equivalent to tensor product (i.e. it applies to an arbitrary pair of tensors over the same field, not only vectors), whereas dyadic product seems to refer specifically to vectors.

I do no know whether Tensor product or Outer product is the dominant term, but some reputable people use the first (e.g. Pertti Lounesto).

Dyadic is a disambiguation page, and so should not be merged.

The Kronecker product is in some sense the tensor (or outer) product of two order-2 tensors (the components are the same, except rearranged), put into the notation of matrices. It seems to me to be a clumsy way of representing a 4th-order tensor (product) using a rectangular matrix, and I think that link, the detail thereof in Tensor product should be trimmed to a mention and a link.

In summary, I think Tensor product already says mostly what it should, but should mention that the terminology and notation of dyadics and polyadics generally is obsolete, possibly in a historical section.

Disclaimer: I'm no expert, but browsing internet sources led me to this picture some while ago. — Quondum^☏ 08:48, 22 August 2012 (UTC)

Sorry I meant Dyadics - not the disambig page, links have been fixed. Fair points, although I prefer Sławomir's suggestion.

Out of interest, the tensor product article uses links in its headings, contrary to this guideline...

Should also add: I'm not going to actually merge anything (until consensus), but trying it out... Maschen (talk) 09:37, 22 August 2012 (UTC)

Even though outer products are an example of tensor products (assuming that a matrix is a rank-2 tensor), I think the Wikipedia articles outer product and tensor product serve different audiences. The outer product between vectors can be understood by people familiar with vectors in R^3 and matrices, while to understand tensor products you need to know some abstract algebra. I think it will be unnatural for one article to take both these audiences into account, so I prefer to have separate articles.

On dyadics, I don't see any harm in having an article on it, even though it's historical. In my opinion, all the dyadic articles should be merged into one. In particular, I see little reason for having a separate article on dyadic product. But I note that User:Crowsnest opposed this and I don't feel strongly about it either. I alerted this editor to the discussion here. -- Jitse Niesen (talk) 11:08, 22 August 2012 (UTC)

Due to a lack of time, I will not participate in the discussion. I expect there are enough knowledgeable editors around here to come to a nice solution. Wishing you a fruitful exchange of ideas, Crowsnest (talk) 20:46, 23 August 2012 (UTC)

I would like to voice my agreement with those who think that not everything should be merged to tensor product on grounds of different levels of concreteness/different audiences. (Of course these articles should link each other prominently.) Options 2 and 3 both seem like fine ideas to me. --JBL (talk) 13:50, 22 August 2012 (UTC)

As expected - there are conflicting views... All options 1-4 are in favour, although the slightly dominant consensus is 4 minus the merge outer product + tensor product...

The dyad articles are effectively merged, just waiting for more responses which may contain more valuable and subtle perspectives before inserting this into dyadic tensor... Maschen (talk) 06:01, 23 August 2012 (UTC)

It seems to me that there is actually disagreement on the meaning of the respective terms, and that the existing articles (esp. Outer product) misleadingly define simpler versions of what they really are. But since no-one seems to agree with me, I guess I should keep quiet. Besides, some of you may have direct experience in the field. — Quondum^☏ 09:53, 23 August 2012 (UTC)

I agree that all the articles dealing with dyadics, dyadic tensors, and dyadic product should be merged. The natural target for this merge would be (IMHO) dyadics, since the common factor here is the notation. The objects, and operation themselves are simply specially cases of tensors and tensor products, but what sets them aside is the historical notation and terminology surrounding them.

As for outer product that should probably be a disambuigation page, since that term can refer to a number of loosely related operations including the one currently described in outer product, exterior product, and even is some case cross product.

The tensor product article should be kept separate since that is a much more general operation than any of the others. (Which can be applied pretty much to anything which has some sort of module structure.)TR 12:51, 23 August 2012 (UTC)

I'll support TR. An article that focusses on dyadic terminology and notation (and related terms e.g. "polyadics" if notable) makes sense with an explanation of its relationship with more modern notation and terms, with a single "see also" to it link in Tensor and Tensor product. I'll need some study to comment properly on "outer product". Tensor and Tensor product can have these aspects offloaded if desired — Quondum^☏ 21:42, 23 August 2012 (UTC)

So there is no opposition to merge the dyadics articles... time to do it - see dyadics. Maschen (talk) 23:20, 23 August 2012 (UTC)

Here is a possible basis for turning outer product into a disambig page. By all means take, leave, and/or change it, just thought to give a head-start if anyone would like to actually reform the article in to a disambig page. Maschen (talk) 23:42, 23 August 2012 (UTC)

Support TR's position. Don't make the mistake of confusing "conceptually identical if you're trained in math" with "content is accessible to the lay audience". Insofar as the article serve different audiences, let them be. Also, be aware: the simpler the article, the more frequently it attracts incorrect edits from younger/inexperienced editors. Patrolling large articles is difficult. linas (talk) 03:53, 25 August 2012 (UTC)

As to DAB pages, please note: product (mathematics) already does the job; I don't see why we'd need another one. linas (talk) 03:59, 25 August 2012 (UTC)

On the potential DAB of outer product, we still need to resolve what to do with that title. Are you suggesting that product (mathematics) be expanded to give links to the various meanings of the term, and that outer product should become a redirect to it? (I'm not objecting). — Quondum^☏ 05:11, 25 August 2012 (UTC)

Another summary:

1. The point of changing outer product to this was to listify all of the links, then everything related to "outer product" people may expect from the title could be clicked to.
2. Redirecting outer product to product (mathematics) means outer product can't be linked in product (mathematics), but could still of course be listed/explained very briefly.
3. Linking from product (mathematics) to outer product would be wasteful.
4. Expanding product (mathematics) may not gain much, except for

• inserting the statement: "Some authors use the expression "outer product of tensors" as a synonym of "tensor product". The outer product is also a higher-order function in some computer programming languages such as APL and Mathematica."
• and link: Bra-ket notation for outer product.

Most of the other links in my draft are just "see also" links.

I'd say 2 and 4. Opinions? Maschen (talk) 18:44, 25 August 2012 (UTC)

Projective variety

Someone has to start the article someday and I just thought why not me today. I'm posting this since I don't mean to do it covertly. Right now, most of materials there overlap other elsewhere and it's not a balanced account, but I think it's not a good start, either.

About the title: "algebraic" is missing. It's because, in my real life, I never say "projective algebraic". The only concern would be ambiguity with "projective analytic". But by Chow's theorem this is actually not ambiguous. Right? -- Taku (talk) 00:33, 24 August 2012 (UTC)

More links could be added, right from the start "algebraic geometry" is not linked nor "topology" etc., I'll do that now. There is concern that if lots of effort goes into rewriting it this article, and it doesn't grow much, and still has plenty of overlap with other articles, then a similar event to recently merged dyadic articles (see above) could happen in the future - i.e. merged back into algebraic variety or whatever. At least a start though, good work. Maschen (talk) 06:30, 24 August 2012 (UTC)

Good going. It will be necessary to address the overlap with Algebraic geometry of projective spaces. Is there an article anywhere on the projective Nullstellensatz? Deltahedron (talk) 06:39, 24 August 2012 (UTC)

Maybe there isn't but see Hilbert's Nullstellensatz and Differential Nullstellensatz, probably close as can be... Maschen (talk) 06:50, 24 August 2012 (UTC)

To me, Algebraic geometry of projective spaces appears bizarre. What is it doing? Projective space seems like a natural space for the topic. Projective space shouldn't just focus on the topological and differential-geometric aspects, that's not balanced if more elementary and pedagogical. Some parts of it also overlap the Proj construction. Finally, the section "Morphisms to projective schemes" should move to projective variety. -- Taku (talk) 11:53, 24 August 2012 (UTC)

Are you sure that we don't already have a bunch of articles on this topic? Don't create a situation, where, like outer product and tensor product, someone will want to merge them all back together again in a few years. linas (talk) 04:07, 25 August 2012 (UTC)

There are some overlaps for sure. For example, Proj construction gives a very nice scheme-theoretic constriction and so there is no need to get into details in projective varieties. Also, some other subtopics (say GAGA) is covered adequately in its own article. On the other hand, I don't see this as an argument against having this article. It's an overview. To me, it's no brainer that this is an important topic and deserves its own article. In short, I believe it survives AFD :) -- Taku (talk) 11:47, 25 August 2012 (UTC)

Actually maybe some more concrete constructions could be useful (the red book does coordinate-non-free construction with explicit examples and something like should be included.) -- Taku (talk) 11:51, 25 August 2012 (UTC)

Just to provide an analogous situation to balance my previous view: there are many articles related to generalized dynamics - Analytical mechanics is the overview of many articles: principle of least action, Hamilton's principle, Lagrangian, Lagrangian mechanics, Hamiltonian, Hamiltonian mechanics, equations of motion, generalized coordinates, Euler-Lagrange equations... and all have plenty of mutual overlap (there are more physics examples, though will not clutter the space here). There is nothing wrong with an overview article, just be sure to reduce all overlap using WP:summary style, so it may be better to keep all concerete examples/derivations/details in whichever main articles are appropriate... and summarize everything in the overveiw. Maschen (talk) 21:17, 25 August 2012 (UTC)

Disambiguation help needed

Kernel (mathematics), Lie bracket, Adjoint representation, Generating set, and Covariant are currently among the disambiguation pages with the largest numbers of incoming links. Please help fix these. Cheers! bd2412 T 17:24, 23 August 2012 (UTC)

Kernel (mathematics), Lie bracket, Adjoint representation look fine, Generating set and Covariant need tidying up. I'll do that now. Maschen (talk) 20:21, 23 August 2012 (UTC)

Well generating set probably shouldn't be a dab page, it should probably be renamed to something like generator (mathematics) and turned into a real article. There is a fine line between being a DAB page, a list of related topics, and an article that explains why they are all related. Everything there is dealing with exactly one and the same concept of a generator, and not a bunch of unrelated things that happen to have the word 'generator' in them, yeah? So I am not at all convinced that "fixing" the incoming links is even the correct thing to do. linas (talk) 01:33, 26 August 2012 (UTC)

For generating set (now redirected to generator (mathematics)) - I extended slightly into article format and added the wikiproject maths/physics banners to talk:generator (mathematics) (change the settings if inaccurate). Maschen (talk) Maschen (talk) 09:16, 26 August 2012 (UTC)

I had looked at a few of them and it did seem to me that in many cases a link to a disambig or similar page was appropriate, i.e., there wasn't actually anything to be "fixed" in many cases. --JBL (talk) 02:06, 26 August 2012 (UTC)

Steiner point (disambiguation)

Steiner point now redirects to Steiner point (disambiguation). Should the title of the disambiguation page be changed simply to Steiner point? Michael Hardy (talk) 03:26, 26 August 2012 (UTC)

According to Wikipedia:Disambiguation#Naming the disambiguation page, yes. Deltahedron (talk) 06:01, 26 August 2012 (UTC)

 Done —David Eppstein (talk) 06:15, 26 August 2012 (UTC)

OK, next problem with this page: Which of the pages in the article space that link to it (other than redirects) are from hatnotes (so those links should remain intact) and which should get disambiguated? Michael Hardy (talk) 17:44, 26 August 2012 (UTC)

image:Shing-TungYau.jpg

File:Shing-TungYau.jpg is missing sourcing, and will be deleted soon. Does anyone know about this photo  ? -- 76.65.128.252 (talk) 12:50, 26 August 2012 (UTC)

Euclidean algorithm

There is a proposal to move Euclidean algorithm to Euclid's algorithm at Talk:Euclidean algorithm#Move?. Johnuniq (talk) 01:34, 28 August 2012 (UTC)

Daviddaved

Please look at this discussion. User:Daviddaved appears to be a mathematician. He is totally clueless about Wikipedia conventions and possibly about Wikipedia's purposes. _Some_ of his new articles may be worth keeping after some cleanup. Some may have copyright problems. He doesn't seem to notice things people post on his user talk page. Members of this WikiProject may be able to figure out which of his pages are worth keeping after cleanup. Michael Hardy (talk) 18:04, 30 August 2012 (UTC)

Isovolume problem

Isovolume problem is an "orphaned" article, i.e. no other articles link to it. If you know of other articles that ought to link to it, work on it. Michael Hardy (talk) 00:54, 31 August 2012 (UTC)

if isoperimetric inequality (section Isoperimetric inequality in higher dimensions) were not so technical, I would say, merge it there. Especially since the article is called 'isovolume problem' (= minimal surface given volume), but is actually about the isosurface problem (maximal volume given surface). The two are mathematically equivalent, but as the latter is really just a high-dimensional isoperimetric problem, the justification for a separate article is not so clear. Sasha (talk) 03:49, 31 August 2012 (UTC)

Merger proposal Equidistributed sequence

I suggest that Equidistribution theorem and Weyl's criterion could both be merged into Equidistributed sequence. I have just boldly merged Van der Corput theorem. Deltahedron (talk) 17:02, 26 August 2012 (UTC)

methinks, equidistributed sequence is already a bit long. Equidistribution theorem is a nice article with a historical overview which will be too long for a section of equidistributed sequence, why merge it?

As to Weyl's criterion, my objections are less firm (the main objection is that it is has connections beyond the field of equidistributed sequences, but perhaps it is not so crucial: if you succeed to make it a nice section of e.s., I will probably rescind my objections.

Sasha (talk) 19:18, 31 August 2012 (UTC)

Totally positive matrix

Totally positive matrix is a surprisingly neglected article. Work on it. Michael Hardy (talk) 02:47, 31 August 2012 (UTC)

Slightly expanded (emphasis on "RELIABLE" was to discourage pop sites like planetmath). Maschen (talk) 14:00, 31 August 2012 (UTC)