Wikipedia talk:WikiProject Mathematics/Archive/2019/Sep

Missing articles about Category:FEM elements

Serendipity element and Lagrange element are not created. --Sharouser (talk) 14:35, 1 September 2019 (UTC)

Punctuation epsilon–delta

Yet another occasion arises whose understanding requires one to realize that the "LaTeX" we use here is (many would say "obviously") not actual LaTeX.

${\begin{aligned}&\varepsilon -\delta \\&\varepsilon {-}\delta \\&\varepsilon {\text{-}}\delta \\&\varepsilon {\text{--}}\delta \end{aligned}}$

If the "LaTeX" code uses a hyphen, then the first form above is seen, with a minus sign rather than a hyphen.

The second form is with a minus sign enclosed in {curly braces} so the spacing appropriate when it is used as a binary operation symbol does not appear.

Thus: \varepsilon{-}\delta.

The third has this: \varepsilon\text{-}\delta. This causes an honest hyphen to appear.

The fourth has this: \varepsilon\text{--}\delta.

In our not-really-LaTeX system, this makes two hyphens appear. In genuine LaTeX, it would make an en-dash appear. In the non-TeX occurrences of this phrase in the article titled (ε, δ)-definition of limit, an en-dash is used.

Use of an actual en-dash in the not-really-LaTeX code results only in an error message.

Should we eschew our not-really-LaTeX software altogether for these occasions, or should we use one of the options above, or should we compromise and write

$\varepsilon$–$\delta$

or should we do something else? Michael Hardy (talk) 18:21, 31 August 2019 (UTC)

The solution is obvious: not to use the <math> tag when saying “ε–δ” which is essentially a human-language shorthand, not a scientific notation. But I know that many users stuck to LaTeX notation and call <math> on every imaginable pretext. Under a dire need to say “ε–δ” under LaTeX math mode one can say <math>\varepsilon\text{–}\delta</math> ↦ $\varepsilon {\text{–}}\delta$. Incnis Mrsi (talk) 18:49, 31 August 2019 (UTC)

@Incnis Mrsi: I could have sworn I hard tried \text{–} (with an actual en-dash) and that the result was an error message, but apparently it actually works. Michael Hardy (talk) 17:18, 2 September 2019 (UTC)

The solution that seems most obvious to me, to get an honest en-dash between the two symbols, is to go outside of math to do it. <math>\varepsilon</math>–<math>\delta</math> renders as $\varepsilon$–$\delta$. I don't see how that is in any way a compromise. —David Eppstein (talk) 17:22, 2 September 2019 (UTC)

I agree with David Eppstein (and this is also what I would do when actually writing a LaTeX document, i.e., I would type "... by the $\varepsilon$--$\delta$ definition ..."). The title of the article (ε, δ)-definition of limit suggests another (non-dash-based) resolution. --JBL (talk) 17:42, 2 September 2019 (UTC)

@Joel B. Lewis: That's exactly how I do it in actual LaTeX. I always hesitate to mix TeX with non-TeX notation in Wikipedia because of the many times they have failed to fit together well. Michael Hardy (talk) 21:01, 2 September 2019 (UTC)

$\varepsilon$--$\delta$ is probably what I'd do in an actual LaTeX document, too. XOR'easter (talk) 17:51, 2 September 2019 (UTC)

+1. Boris Tsirelson (talk) 18:33, 2 September 2019 (UTC)

A question about English grammar

The article titled Nonlocal operator begins like this:

In mathematics, a nonlocal operator is a mapping which maps functions on a topological space to functions, in such a way that the value of the output function at a given point cannot be determined solely from the values of the input function in any neighbourhood of any point. An example of a nonlocal operator is the Fourier transform.

Occasionally I think English-speaking mathematicians are not attentive enough to nuances of the use of the word any.

This function can take any number as an input.

is not quite the same as

This function can take every number as an input.

since in some contexts this might mean every number at the same time. But

Any function from R into whatever is blah blah blah.

means

Every function from R into whatever is blah blah blah.

Maybe this point is clearer if one thinks of the difference between

"Any member can preside over this meeting."

and

"Every member can preside over this meeting."

Now suppose you say

If it is the case that any function from R into whatever is blah blah blah then etc.etc.

That is in danger of being read as

If any function from R into whatever is blah blah blah then etc.etc.

and hence as

If there is any function from R into whatever is blah blah blah then etc.etc.

so that a universal quantifier in the writer's mind becomes an existential quantifier in the reader's mind. Merely writing "every" instead of "any" at the outset is all it takes to obviate this hazard.

Thus "any" can be universal in some contexts ("Anyone can do that.") and existential in others ("There isn't any." or "If anyone can run a 50 meters in three seconds, it's Usain Bolt.") The contexts in which it becomes existential seem to be these:

• Negative sentences: "I've never seen any examples of that."
• Questions: "Is there any money left?"
• Conditional clauses: "If there is any money left, donate it to Wikipedia."

How shall we apply this to the two occurrences of the word any in the passage quoted from Nonlocal operator? Michael Hardy (talk) 18:25, 27 August 2019 (UTC)

This topic is not in my expertise, but isn't there an extra quantification? Shouldn't the "of any" be changed to "the" or "the given"?

If you're asking/telling about the more general issue of imprecision in natural languages, then I'm not sure what the resolution is. Formal logic exists exactly to avoid that imprecision. Mgnbar (talk) 14:13, 3 September 2019 (UTC)

Square root of integers

The problem arose from WP:Articles for deletion/Square root of 10. What to do with the topic now, in light of the deletionist assault? Is a separate article warranted? If no separate, then my proposal, square root #Principal square roots of the positive integers, or something else? Incnis Mrsi (talk) 14:06, 3 September 2019 (UTC)

My knee-jerk reaction was, "This topic is basically (integers in) quadratic number fields, which are extremely important." But then I realized that we have Quadratic field for all that. What is the intended division of labor between the two articles? Is there a substantial body of knowledge specific to quadratic integers? The presence of reliable sources in that article suggests so, but I haven't examined them closely. Mgnbar (talk) 14:23, 3 September 2019 (UTC)

Properties like being Euclidean domain, being principal ideal domains, basis as free abelian group, and many others are more specific to quadratic integer rings than to quadratic fields, even if these properties are described in Quadratic field. D.Lazard (talk) 14:42, 3 September 2019 (UTC)

Integers are important far beyond ℚ[√D], if only due to such rings as Gauss ℤ[ i ], Eisenstein ℤ[³√1], and Dirichlet ℤ[ τ ] which is important for 5-fold rotational symmetry. Incnis Mrsi (talk) 14:51, 3 September 2019 (UTC)

@D.Lazard: what? Isn’t the usefulness of prime factorization to compute many of square roots of integers important? Incnis Mrsi (talk) 14:51, 3 September 2019 (UTC)

The computation of (approximations of) square roots of integers is not very different from that of real number, and belongs thus to Square root. Two things may belong to quadratic integers that are not there in any version: 1/ Computing the largest square-free factor of an integer (that is the smallest d generating a given $\mathbb {Q} ({\sqrt {d}})$). For that, no better algorithm is known than prime factorization. So a few lines in Quadratic integer suffices. 2/ Testing whether a quadratic integer is the square of a quadratic number, and, if yes, computing the square root. This is considered in Nested radical and would deserve to be linked here. D.Lazard (talk) 15:36, 3 September 2019 (UTC)

As “not very different from” – false, they are algebraic numbers and “integers”, after all. These facts are completely obscured after D.Lazard’s edits. Incnis Mrsi (talk) 16:06, 3 September 2019 (UTC)

Which edit(s) obscured anything? D.Lazard (talk) 16:54, 3 September 2019 (UTC)

Before the deletionist strike the topic redirected to that subsection. Now one can’t easily infer that square roots of integers are algebraic integers. Nor can the reader access √2, √3, √5, at least not in reasonable proximity of the request. The √10 thing is also removed, but it was not directly a D.’s fault. Incnis Mrsi (talk) 17:11, 3 September 2019 (UTC)

No redirect is needed for saying that the square roots of an integer are quadratic integers. I have added this to Square root. D.Lazard (talk) 18:19, 3 September 2019 (UTC)

What occasion could there be to write "square root of integers" rather than "square roots of integers" or "square root of an integer"? Michael Hardy (talk) 23:51, 4 September 2019 (UTC)

I followed the model of square root of negative numbers. For comparison, Special:PrefixIndex/square roots has nothing of the sort. Incnis Mrsi (talk) 04:44, 5 September 2019 (UTC)

So there exist more useless redirects from grammatically-faulty titles? Interesting, but not a good choice to use as a model. —David Eppstein (talk) 06:01, 5 September 2019 (UTC)

David Eppstein highly probably speaks English better than me by a large margin, hence WP:SOFIXIT. Incnis Mrsi (talk) 06:06, 5 September 2019 (UTC)

Math-related affiliate

Just a reminder about m:Wikimedia Community User Group Math, which any person who supports the group's goals is welcome to join. As of a few weeks ago, the group is one of the officially recognized m:affiliates of the Wikimedia Foundation. Whatamidoing (WMF) (talk) 00:29, 6 September 2019 (UTC)

Invariants and covariants

There is a problem with the disambiguation required for Michael Roberts (mathematician) in the previous thread: the link to a dab page is clearly intended to refer to covariants of invariant theory. The problem is that I have not found any mention of such a covariant in English Wikepedia. Do someone has an idea for solving the problem?

Here is what I remember on this subject: Let $f$ be a generic form in n variables (that is, its coefficients are indeterminates). The group GL(n) acts on the form by linear changes of variables. The discriminant of a form in two variables is an invariant. An invariant of GL(n) (or of a subgroup) is a polynomial in the coefficients of the form. A covariant is a form in the same variables, with coefficients polynomials in the coefficient of the given form, which is similarly invariant. For example, an invariant is a covariant of degree 0.

What precedes is clearly not sufficient, even for a stub. Again, any idea? D.Lazard (talk) 18:22, 9 September 2019 (UTC)

This is in fact about covariant transformations, or I miss something? Forms are tensors of special form. Incnis Mrsi (talk) 18:39, 9 September 2019 (UTC)

One possibility is to replace the phrase "covariants and invariants" with the phrase "invariant theory". (If there were a reference attached to this statement in the article then I would worry about accurately representing it, but since there is none ....) Also pinging the article author @Moonraker: to this discussion; possibly they can share some insight. --JBL (talk) 19:05, 9 September 2019 (UTC)

We do have the article “module of covariants”. — Taku (talk) 04:45, 10 September 2019 (UTC)

I have found two definitions of a covariant; one in Invariant of a binary form, and one in wikt:covariant, which is more general (not restricted to binary forms) and perfectly accurate. Therefore, I have created the redirect Covariant (invariant theory), I have disambiguated Michael Roberts (mathematician) by using this redirect, and added an entry in Covariance (disambiguation), that links to the redirect and contains a copy of dictionary definition. However, some questions deserve a further discussion;

• The new redirect is the only occurrence of the noun "covariant" in the dab page. This suggest creating a stub based on Wiktionary definition, called Covariant, and with a hatnote like "for the adjective uses, see Covariance (disambiguation)". What do you think?
• The fact that it vas so difficult to find this definition shows that a reorganization is needed for interlinking Invariant theory and all related articles. When this will be correctly done, it will probably appear that Invariant theory would need a complete rewrite, with possibly some merges and or splits.

D.Lazard (talk) 09:43, 10 September 2019 (UTC)

We already have definitions in a glossary; Glossary_of_invariant_theory has 42 uses of the term and and entry for covariant. --{{u|Mark viking}} {Talk} 17:27, 10 September 2019 (UTC)

The problem is that the definition given there is not understandable for most readers, and does not correspond to the usual definition (that of wikt:covariant and Invariant of a binary form). D.Lazard (talk) 18:10, 10 September 2019 (UTC)

I wouldn’t call a subminimal stub an article. See talk:Module_of_covariants #AG. Incnis Mrsi (talk) 18:20, 10 September 2019 (UTC)

(I have added an explanation on the notation as well as to a link to the article giving the definition. -- Taku (talk) 00:19, 11 September 2019 (UTC))

If I've opened up a smallish can of worms, I'm delighted. WP is full of holes where readers can't find easily, or can't find exactly, what they need, and every one filled is an improvement. Narky Blert (talk) 21:17, 10 September 2019 (UTC)

• First, as I recall, a covariant is something like a linear (multi-linear, polynomial) map that is invariant under the given group action. The basic idea is that you get more flexibility by working with maps not elements; i.e., you get more invariants to work with. (Module of covariants, I think, gives probably the most general definition of covariants.) So, given this, I don’t think redirecting covariant (invariant theory) to an invariant of a binary form is a good idea. I will make a library trip to find some refers (and do some edits).
• Generally speaking, Wikipedia is still weak in invariant theory topics (I don’t need to tell you why).
• Finally, yes, there is adjective “covariant” as in “covariant functor” and that has to be distinguished from. (So the disambig page is needed). — Taku (talk) 23:09, 10 September 2019 (UTC)

Thank you to JBL for pinging me. I am happy with what Taku says. Moonraker (talk) 21:43, 12 September 2019 (UTC)

Using a book that plagiarized Wikipedia as a Wikipedia source?

I've been editing trigonometry to address some of the problems it had in its GA review. In particular, much of it was unsourced or OR. I've been going through and deleting unsourced assertions and adding sources to everything else.

There was a section marked with 'more sources needed'. This sections was the 'applications' section, which has largely been unchanged since at least 2007: https://en.wikipedia.org/w/index.php?title=Trigonometry&oldid=122379664

I was going through and sourcing each 'application' one at a time, when I found a book that had all of them:

https://books.google.com/books?id=bENTBQAAQBAJ&pg=PA10&dq=trigonometry+audio+synthesis&hl=en&sa=X&ved=2ahUKEwjjtYeVgMzkAhUEt54KHXpECH4Q6AEwAHoECAYQAg#v=onepage&q=trigonometry%20audio%20synthesis&f=false

This is a Springer book where the authors have just copied and pasted the Wikipedia section, rearranging a few items.

I'm not too concerned that the authors have plagiarized this. My real question, though, is, would it be appropriate to use this book as a source for the whole list (as I've done for now), or would it be better to find sources that aren't plagiarized from Wikipedia itself?

Brirush (talk) 19:33, 12 September 2019 (UTC)

I think it's definitely better not to use sources that plagiarized from Wikipedia (or from elsewhere). XOR'easter (talk) 20:17, 12 September 2019 (UTC)

More definitively, Wikipedia policy prohibits using such sources. See WP:CIRCULAR. (Their preface credits Wikipedia, so this might count as properly-credited use of CC materials rather than straight-up plagiarism, but it makes no difference for its usability as a source.) —David Eppstein (talk) 20:18, 12 September 2019 (UTC)

It may also be worth adding {{Backwards copy}} to the articles, to prevent them being flagged as copy violation by Wikipedia. Certes (talk) 20:24, 12 September 2019 (UTC)

Thanks to both of you, this is very clear. Brirush (talk) 01:37, 13 September 2019 (UTC)

Articles with links to DAB pages

I have collected another batch of articles containing math(s)-related links to DAB pages which would benefit from expert attention. Search for 'disam' in read mode, and for '{{d' in edit mode; and if you solve one of these puzzles, post {{done}} here.

• Almost complex manifold  Done
• Chern's conjecture (affine geometry)  Done
• College Scholastic Ability Test  Done
• Color confinement  Done
• Complex manifold  Done
• Connectivism  Done
• Fractional quantum Hall effect  Done
• Geneviève Raugel  Done
• John W. Negele  Done
• Kummer surface  Done Jakob.scholbach (talk)
• Meta learning (computer science)  Done
• Michael Roberts (mathematician) → Covariant  Done (see next thread) D.Lazard (talk) 09:45, 10 September 2019 (UTC)
• n-sphere  Done
• Navier–Stokes equations → Stress tensor  Done
• Normal basis  Done Jakob.scholbach (talk)
• Polyvector field  Done Jakob.scholbach (talk)
• Random field  Done
• Transport coefficient → Stress tensor  Done
• Studentized range distribution  Done
• Two-dimensional electronic spectroscopy → Ensemble, Charge transfer  Done
• Variational multiscale method → Stress tensor  Done
• Whitehead's algorithm  Done (needed to create the redirect primitive element (free group), and to edit the linked dab page) D.Lazard (talk) 14:11, 9 September 2019 (UTC)
• Xiaohong Chen  Done

Thanks in advance, Narky Blert (talk) 02:58, 9 September 2019 (UTC)

I had to edit after a substandard fix in “almost complex manifold”. Please, look at a whole article, not only to narrow context. Don’t make job to earn green points. Incnis Mrsi (talk) 12:52, 9 September 2019 (UTC)

I'm going to stay polite, but please don't ask thanks for this rather aggressive pointing out of a perfectly correct (if maybe not optimal) edit that did not satisfy your opaque standards, and let me add that I have no idea what a green point is nor any desire to learn.

I'd also suggest you refrain from insulting people for petty motives. If you want to discuss math leave a message on the talk page of the article. jraimbau (talk) 11:15, 11 September 2019 (UTC)

The standards aren’t in fact “opaque”, it is MOS:LINKCLARITY. If Jean Raimbault wants to discuss my petty motives, then he can leave a message here, although it can become moot soon. Incnis Mrsi (talk) 11:51, 11 September 2019 (UTC)

Notice that Incnis Mrsi has been blocked for one month by Rschen7754 for incivility. JRSpriggs (talk) 03:06, 12 September 2019 (UTC)

Let us not escalate... Boris Tsirelson (talk) 04:45, 12 September 2019 (UTC)

Thanks for all your help and to Narky Blert for finding the problems. It looks as if the one unfixed link needs a physicist or engineer rather than a mathematician. Certes (talk) 12:22, 11 September 2019 (UTC)

Fixed the last one; it was referring to charge transfer in a CT complex --{{u|Mark viking}} {Talk} 07:37, 12 September 2019 (UTC)

I work on the assumption that mathematicians will be the people best-placed to determine the specific concepts which physicists, engineers, and the like have borrowed and misused.

(I'm an organic chemist. I'm allowed to say that sort of thing.) Narky Blert (talk) 19:37, 13 September 2019 (UTC)

Am engineer. Can agree, borrow and misuse math all the time. --Izno (talk) 20:20, 13 September 2019 (UTC)

What should an article for a branch of mathematics look like?

As I mentioned above, I've been reworking Trigonometry, focusing on organization and on removing OR and adding sources.

The page still looks skimpy, however, and I feel that more could be added (maybe separate sections on the properties of the graphs, on inverse functions, and perhaps fourier series/analysis?). I've been looking at other pages for inspiration, but I found to my surprise that no 'branch of mathematics' is currently a GA or a FA. Algebra, calculus, etc. are all below GA quality, and have some of the same problems that trigonometry has.

So I wanted to get some consensus before acting. What should 'big topic' articles like this cover? Is there any thing that you feel is necessary or standard for such articles? Is there any particularly good article in a related field that could be used as a template or inspiration? Brirush (talk) 02:42, 13 September 2019 (UTC)

You raise good questions. I think it is quite a challenge to be comprehensive, readable by non-experts and a reasonable length all at once for articles on general topics. One general article I like is Field (mathematics). It takes pains to be readable and concrete near the start of the article, but doesn't shy away from the more advanced topics later on. For trig, some ideas: I guess one of the first things to do is to figure out what goes in trigonometry and what goes in trigonometric functions. One might compare and contrast trigonometry, which is really about plane trigonometry, with spherical trigonometry, hyperbolic trigonometry and generalized trigonometry. Is there anything interesting about how trig has been or is currently taught? For applications, something more than just a long list of fields that use it might be good. Are there some particularly notable uses, maybe something from navigation or surveying? --{{u|Mark viking}} {Talk} 03:52, 13 September 2019 (UTC)

A detailed history section is a major plus! Edit: I see that trigonometry actually has a fairly well-developed one, with just a few citations that need to be added. — MarkH21 (talk) 07:03, 13 September 2019 (UTC)

Thanks for the work already done on Trigonometry. I completely agree with Mark viking's comments. A large part of my Wikipedia activity is devoted to improve in this way fundamental articles of Wikipedia (See my user talk for some of my main edits). IMO, we must distinguish articles about an area of mathematics, such as Trigonometry from articles about the fundamental concept(s) that are the basis of such an area, such as Trigonometric functions. Articles on areas must explain the motivations, the history, the limits of the area (when there is a consensus for that), and the relations with other areas. The objective is that a reader can gets an idea of the subject and find easily the related technical articles that he may need. An example of a very good such article is Number theory, although it needs many improvements (cosmetic, IMO) for being labeled GA. On the other hand, article on fundamental concepts must allow the reader to find the technical details that he needs, such as a formula that he has learnt and forgiven, or a related concept that he has heard about. This is in this spirit that I have recently edited Trigonometric functions (see [1]). In particular, other trigonometric functions than sine, cosine, and tangent are rarely used, except, maybe, in teaching; therefore, my edits limit the formulas given in the article to the most useful formulas relating sine, cosine, and tangent and refer to List of trigonometric identities for the less important formulas. However, the maintenance of such fundamental articles is a true problem, because of the numerous good faith editors who want to add their preferred minor aspect of the subject. For example, since my edits, a section on the expansion of trigonometric functions as infinite products has been added. IMO, such a section is confusing, and must be replaced by a simple link, as it gives too much emphasis on a non-fundamental result. D.Lazard (talk) 09:45, 13 September 2019 (UTC)

At the risk of putting words into D.Lazard's mouth, let me say it another way. Mathematical concepts have precise definitions. For example, a topology is a set of subsets satisfying certain axioms. However, mathematical disciplines are ill-defined and overlapping. For example, the discipline of topology heavily overlaps with geometry, analysis, algebra, etc. And Wikipedia should explain both concepts and disciplines. Mgnbar (talk) 12:16, 13 September 2019 (UTC)

I completely agree, and what I was saying is that rules for a good article (answer to the question in the heading) are different for disciplines and for concepts. D.Lazard (talk) 12:23, 13 September 2019 (UTC)

Agreed. And the citation process for the two is a bit different. For the concept of topology, one can cite the definition from Munkres' book Topology. For the discipline of topology, which topics can be included and excluded? If a topic appears in Munkres' Topology, then one can reasonably include it. If a topic does not appear, then one cannot reasonably exclude it. (The same problem exists for other sources and for combinations of sources.) So the discipline of topology has to be "defined" using examples. Mgnbar (talk) 16:34, 13 September 2019 (UTC)

This is maybe a bit of a quibble, but I don't think "concept" is the right word for topology in the sense of a collection of open sets, at least to distinguish it from topology as a discipline. Topology as a discipline is arguably still a concept. I think a better word would be "object" — the collection of open sets notion is a type of mathematical object, whereas the discipline is not (and indeed has no precise mathematical definition at all). --Trovatore (talk) 19:56, 13 September 2019 (UTC)

I've now completed my revision of Trigonometry. In the process, I've added several figures and tables, and almost doubled the size of the entry. I've tried to be careful and check for errors, but I would appreciate it if someone would look it over for mistakes, especially stray sentences from copy-and-paste or errors in the tables. If you feel any additions or removals are inappropriate, I can revert them. Thanks for the advice given above, it was extremely helpful.

Edit: The article itself isn't complete. As mentioned by someone else, it could use an overview of spherical/hyperbolic geometry. I'm not too familiar with spherical trigonometry, so I didn't attempt it.

Brirush (talk) 19:43, 13 September 2019 (UTC)

Trovatore: Topology is a class of mathematical objects, and topology (the discipline) is a sociological/anthropological object? Actually, I don't have strong opinions about the terminology. :) Mgnbar (talk) 20:44, 13 September 2019 (UTC)

I find that a useful proxy is whether you use a countable or uncountable noun. A topology (count noun) is a mathematical object, whereas topology (mass noun) is a discipline.

This is by the way the distinction we should use for a Boolean algebra (count noun, the structure) versus Boolean algebra (mass noun, the equational style). I fought the good fight on that point many years ago, with a somewhat unsatisfactory outcome, because of a participant with unusual foundational views. --Trovatore (talk) 21:29, 13 September 2019 (UTC)

​The page numbers in a lot of the references in trigonometry are given as the first half of a range. Surely this doesn't mean that the entire rest of the book after that page number is the relevant part. Would ff. work better? XOR'easter (talk) 18:40, 14 September 2019 (UTC)

Thank you, I was using https://reftag.appspot.com/ to convert google book links to Wikipedia citations. It had a few other idiosyncracies that I had to address (like using a non-existent 'coauthors' tag). I'll see if I can convert the page ranges to ff's! Brirush (talk) 22:53, 14 September 2019 (UTC)

Okay, I fixed it. I did not use ff after all, because I didn't realize it meant 'multiple pages', and when I found references, my technique was to find the exact page that had the quote I wanted, so it shouldn't need the subsequent pages. I changed it to single pages. Brirush (talk) 23:03, 14 September 2019 (UTC)

Thanks! I did some spot-checking and fixed a couple other glitches that were probably due to Google Books metadata weirdness. I'll try to check the page over more thoroughly soon. XOR'easter (talk) 23:58, 14 September 2019 (UTC)

Regarding the mathematics banner of the Category:Ordinal numbers

@Chongkian: See Category talk:Ordinal numbers. Chongkian (talk · contribs) removed the {{Maths banner}}. Apparently, he believes that {{WikiProject Numbers}} is sufficient. Is that appropriate?

I think that ordinals are relevant to Mathematics generally, not merely to the Numbers project. JRSpriggs (talk) 05:34, 15 September 2019 (UTC)

Sure! I've restored WPM there. Boris Tsirelson (talk) 09:21, 15 September 2019 (UTC)

From what I have found, generally there are WikiProject Mathematics ('math banner' or 'math rating'), WikiProject Statistics and WikiProject Numbers which are highly inter-related to each other. Whenever it is related to math in general, we shall use math banner or math rating, but if it is a more specific term of math (which is number or statistics), isnt that we should related it to its more 'specific' WikiProject category? 'Numbers' and 'statistics' are (and always be part of) 'mathematics'. That's the idea behind it for my reason. Same case like 'country', 'geography' or 'city'; 'geography' (or WikiProject Geography) shall be the default categorization first for all of administrative divisions (e.g. town, village, state, province), unless such particular article is about a country or city, then we shall put it under WikiProject Countries or WikiProject Cities respectively (because such WikiProjects do exist), and take out the 'parent' WikiProject which is WikiProject Geography. Villages shall be put under the general WikiProject Geography because up to this moment, there is no WikiProject Villages. Chongkian (talk) 10:03, 15 September 2019 (UTC)

It’s worth noting that WikiProject Numbers is only semi-active now. Also, statistics isn’t universally considered a branch of mathematics. — MarkH21 (talk) 10:18, 15 September 2019 (UTC)

Looking at WikiProject Numbers I fail to find there any interest to transfinite numbers. Thus, I'd say, it is THEIR decision, to treat "number" as "finite number". I just respect their (quite reasonable) decision. Boris Tsirelson (talk) 10:30, 15 September 2019 (UTC)

WikiProject Numbers has been concentrating on articles about integers by removing cruft (77 is the shirt number of Joe Minor-Leaguer), improving navigation templates and promoting their existence. Three years ago, 1 was the title of the article about the year AD 1. Certes (talk) 11:37, 15 September 2019 (UTC)

As a moderately active member of both projects, I don't remember any discussion of infinite numbers in the WikiProject Numbers page or notability guidelines. I don't believe 0.999... is tagged with WikiProject Numbers. — Arthur Rubin (talk) 17:30, 15 September 2019 (UTC)

The usual practice with project banners is to use all applicable ones, not to try to decide which is most applicable and use only that. —David Eppstein (talk) 17:56, 15 September 2019 (UTC)

I don't think WikiProject Numbers wants Ordinal number. As a fairly active member of both WPM and WPN, I don't think the charter of WPN includes infinite numbers. — Arthur Rubin (talk) 17:55, 16 September 2019 (UTC)

To Arthur: Then remove {{WikiProject Numbers}} from Category talk:Ordinal numbers and Category talk:Cardinal numbers. I do not feel qualified to do that since I am not a member of the numbers project. JRSpriggs (talk) 09:45, 17 September 2019 (UTC)

Hilbert's fourth problem article

Hi! The second sentence in this article in its current form seems to be somewhat mangled for me.

In one statement derived from the original, it was to find up to an isomorphism all geometries whose axioms system of the classical geometry (Euclidean, Hyperbolic and elliptic) if we drop the axioms of congruence involving the concept of the angle and add the systems with the `triangle inequality' regarded as an axiom.

Maybe this rewriting could be adequate:

In one statement derived from the original, it was to find up to an isomorphism all geometries that have an axiomatic system of classical geometry (Euclidean, Hyperbolic and elliptic), with those axioms of congruence that involve the concept of the angle dropped, and `triangle inequality', regarded as an axiom, added.

As I am not a professional, I would like to have an expert opinion before editing the article. Thank you in advance! --94.21.201.110 (talk) 11:17, 17 September 2019 (UTC)

Courtesy link: Hilbert's fourth problem. That is, indeed, incomprehensible. It used to be different, before a spate of edits by Vlasenko D in June. Probably those edits deserve some scrutiny (for English language usage at a minimum). --JBL (talk) 12:00, 17 September 2019 (UTC)

I agree. At least, the old version of the lead deserves to be immediately restored, although it could also be clarified. D.Lazard (talk) 13:49, 17 September 2019 (UTC)

Just why the initial letter in "hyperbolic" should be capital while that in "elliptic" is in lower case is unclear. Or to put it more bluntly, it shouldn't be. Michael Hardy (talk) 21:46, 18 September 2019 (UTC)

Portal:Mathematics

Proposal to delete all portals. The discussion is at Wikipedia:Village pump (proposals)#Proposal to delete Portal space. Voceditenore (talk) 08:55, 23 September 2019 (UTC)

Proposition of splitting Cubic function

I have opened a discussion on the suggestion of splitting Cubic function into Cubic function and Cubic equation. Feedback is welcome. D.Lazard (talk) 10:26, 24 September 2019 (UTC)

Pull the knotted part of the curve tight?

This discussion calls for experts, right? Boris Tsirelson (talk) 18:49, 19 September 2019 (UTC)

No, I don't think so: in the 2 years since the first comments were made, the caption has been changed and now does not suffer from the problem discussed there. --JBL (talk) 19:28, 19 September 2019 (UTC)

I see, thank you. Boris Tsirelson (talk) 19:49, 19 September 2019 (UTC)

(I agree with your comment there, incidentally -- Daqu was right about the error, the most recent comment looks wrong. But it is all moot as far as the article is concerned.) --JBL (talk) 20:47, 19 September 2019 (UTC)

Do you not need to require that the first (directional) derivative of the curve be continuous? I think that would be impossible if you just shrink it to a point. JRSpriggs (talk) 07:55, 20 September 2019 (UTC)

Feel free to find a verifiable source supporting your claims, if I am not to be considered as an expert. Quantum Knot (talk) 08:32, 20 September 2019 (UTC)

(to Quantum Knot) Such sources surely exist; can someone help to find them?

For now I've found this: This turns out to not be the correct notion of equivalence for knots - it would force all tame knots to be equivalent!. Boris Tsirelson (talk) 10:13, 20 September 2019 (UTC)

And this: For $m-n\leq 2$ this is not so: e.g., any knot $S^{1}\to \mathbb {R} ^{3}$ is PL isotopic to the unknot, but is not necessarily PL ambient isotopic to the unknot. Boris Tsirelson (talk) 10:24, 20 September 2019 (UTC)

And this: Secondly, surprisingly (and catastrophically), the way we have defined equivalence actually causes all knots to be equivalent to one another! “Gradually pulling the string tight” so that the knot shrinks to a point is a perfectly good continuous deformation between any knot and the unknot! (page 14)Boris Tsirelson (talk) 11:30, 20 September 2019 (UTC)

And this: The word "isotopy " refers to the deformation of the string. The word "ambient" refers to the fact that the string is being deformed through the three-dimensional space that it sits in. Note that in an ambient isotopy, we are not allowed to shrink a part of the knot down to a point, as in Figure 1.20, in order to be rid of the knot. (page 120) Boris Tsirelson (talk) 11:45, 20 September 2019 (UTC)

And this: Remark 1.5. All knots are trivial under continuous isotopy. (batchelor’s unknotting) Boris Tsirelson (talk) 11:52, 20 September 2019 (UTC)

Wow! The clue is the phrase "batchelor’s unknotting" (or "batchelor’s isotopy")! Google this, and you'll find easily a lot of required sources. So, I stop here; the problem is solved. (Should we create an article on this idea?) Boris Tsirelson (talk) 11:57, 20 September 2019 (UTC)

(to JRSpriggs) Sure, if we work in the space $\mathrm {Emb} ^{1}(S^{1},\mathbb {R} ^{3})$ of continuously differentiable embeddings, then the situation should be different. But differentiability is never mentioned in "Homotopy". Boris Tsirelson (talk) 10:02, 20 September 2019 (UTC)

Maybe "bachelor" rather than "batchelor"? Justin Roberts's discussion (your third link) is very nice. A less rigorous, more sociological explanation for why continuous deformations are the wrong idea is that no one would ever have introduced ambient isotopies into knot theory if continuous deformations sufficed. --JBL (talk) 20:13, 20 September 2019 (UTC)

I haven't tracked down an explicit reference, but this seems likely to be named after G. K. Batchelor, who studied knotted vortices in fluid dynamics. —David Eppstein (talk) 21:00, 20 September 2019 (UTC)

Huh, what do you know? --JBL (talk) 11:11, 24 September 2019 (UTC)

Minkowski fractal

(for context)

Image from "Fractal antenna"

Image from "Vicsek fractal"

See also: Talk:Fractal antenna/Archive 1 § Minkowski island/Vicsek fractal

There are currently redirects from Minkowski curve, Minkowski island, Minkowski sausage, and Minkowski fractal which lead to the article "Fractal antenna". An image given as an example of a fractal antenna design is labelled as a "Minkowski Island". Currently the term is in bold because the redirects indicate that it is a topic. However, an article about a subspecies of doves should probably redirect to an article about doves and not to an article about bird-shaped objects. It would be beneficial if an appropriate article was created to explain the Minkowski fractal, or if the redirects led to an article which explained the Minkowski fractal. The image is titled File:6452553 Vicsek Fractal Antenna.png, which implies that "Minkowski island" is an alternate name for the Vicsek fractal. "Vicsek fractal" does mention that the boundary is a variant of the Koch snowflake, and the "Koch snowflake" article contains a quadratic variant of the Koch curve labelled as the 'Minkowski Sausage', so one or both of the articles "Vicsek fractal" and "Koch snowflake" should probably contain the explanation. Hyacinth (talk) 04:08, 14 September 2019 (UTC)

See: Minkowski Sausage. Hyacinth (talk) 21:43, 24 September 2019 (UTC)

Not in Active WikiProjects category

I noticed that the Mathematics page doesn't appear on https://en.wikipedia.org/wiki/Category:Active_WikiProjects, which seems wrong. I'd fix it myself if I knew what I was doing, but I haven't edited a Wiki article before. Iyyl (talk) 01:37, 25 September 2019 (UTC)

I've added the project page to the category. Certes (talk) 10:49, 25 September 2019 (UTC)

Need help with images in Geometry

I've been working on geometry, trying to add references for every controversial statement and expanding stubs. In describing the branches of geometry, I had added an image for each branch. Now, the images are too big and too many to be aligned correctly, even after I deleted my image for Convex Geometry and shrank the others. I could use some expert opinion on the image layout. I haven't finished my edits (I plan on going over the applications section, and adding congruence, similarity, area and volume to the 'main concepts' section), but they shouldn't involve as many images. Thanks! Brirush (talk) 16:17, 25 September 2019 (UTC)

If you're looking for more room, the "Geometry lessons in the 20th century" image looks superfluous. And in the computational geometry section, a problem we can't solve with an efficient algorithm seems an odd choice for the illustration. —David Eppstein (talk) 16:27, 25 September 2019 (UTC)

I tried removing those two and it fixed the issue. Thank you, it completely resolved my problem! Brirush (talk) 16:55, 25 September 2019 (UTC)

Also, I am now finished contributing to geometry. I'd love if people looked it over and made any changes they see fit, or fix anything they feel I did incorrectly.Brirush (talk) 20:10, 25 September 2019 (UTC)

Thanks for your edits! A minor thing I noticed: the Munkres book is listed in the references twice (currently numbers 52 and 109). XOR'easter (talk) 02:33, 26 September 2019 (UTC)

That seemed easy enough to fix, so I made a go at it. --JBL (talk) 11:00, 26 September 2019 (UTC)

I appreciate both of you checking this out. Thanks! Brirush (talk) 12:54, 26 September 2019 (UTC)

How do you create mathematical illustrations?

Can someone give advice what software is useful for creating mathematical illustrations? I am currently working on fundamental group and would like to create some pictures illustrating some computations of pi_1's. For example, I would like to quickly illustrate the usage of the Seifert-van Kampen theoren by (schematically) drawing a genus 2 surface, and some loops on it, together with labelling and coloring the objects (so, nothing fancy). And of course the software should be free to use. Thanks for any advice. Jakob.scholbach (talk) 17:36, 24 September 2019 (UTC)

An example for the kind of illustration I want to create. Jakob.scholbach (talk) 17:37, 24 September 2019 (UTC)

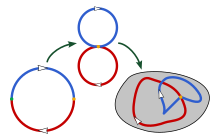
I don't think there is a definitive answer. For SVG illustrations, I tend to use inkscape (as was used in the illustration to the right) as a free alternative to illustrator. If you need the precision of a CAD program (e.g., dimensioning), I have used FreeCAD before and it was OK for my simple needs. Real programmers use tools like PostScript, PSTricks, MetaPost, or Asymptote (vector graphics language), but that can be a lot of work. --{{u|Mark viking}} {Talk} 18:04, 24 September 2019 (UTC)

I use Asymptote (unless the illustration is just a diagram); it takes time, but it gives nice results. Much better than PSTricks (that I used before; PostScript and MetaPost were beyond my patience). Especially on EoM; there a wikitext may contain <asy>some code for Asymptote</asy>; how nice: no separate file, no separate copyright, and anyone may look at the code, and change it "wiki-wiki"! (Well, anyone who knows Asy; but also our TeX code needs to be known...) My best example is here. Simpler examples: here, here,here. Still simpler:here,here,here,here. Though, really I prefer to write the asy code in separate files and transclude them, just for not intermixing wikitext and asycode (unless the asycode is quite short). Boris Tsirelson (talk) 20:11, 24 September 2019 (UTC)

Also, you may look at illustrations in "Space (mathematics)"; they are copied from "v:WikiJournal_of_Science/Spaces_in_mathematics"; there I was forced to create figures (unlike EoM), while the Asy code remains on my home computer (regretfully; ask me if you want to see it), and the corresponding SVG files are stored on Commons. Boris Tsirelson (talk) 20:27, 24 September 2019 (UTC)

I could help make the picture, if you'd be willing to delegate and had a sketch I could work from. I have some experience using Illustrator (and have a subscription for it) from my hobbies. Katja Berčič (talk) 15:09, 26 September 2019 (UTC)