Talk:Werner projection

Replace low-contrast images

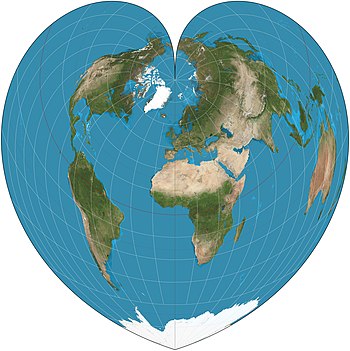
I will be replacing images on the various map projection pages. Presently many are on a satellite composite image from NASA that, while realistic, poorly demonstrates the projections because of dark color and low contrast. I have created a stylization of the same data with much brighter water areas and a light graticule to contrast. See the thumbnail of the example from another article. Some images on some pages are acceptable but differ stylistically from most articles; I will replace these also.

The images will be high resolution and antialiased, with 15° graticules for world projections, red, translucent equator, red tropics, and blue polar circles.

Please discuss agreement or objections over here (not this page). I intend to start these replacements on 13 August. Thank you. Strebe (talk) 22:48, 6 August 2011 (UTC)

File:Werner projection SW.jpg to appear as POTD

Hello! This is a note to let the editors of this article know that File:Werner projection SW.jpg will be appearing as picture of the day on February 14, 2015. You can view and edit the POTD blurb at Template:POTD/2015-02-14. If this article needs any attention or maintenance, it would be preferable if that could be done before its appearance on the Main Page. Thanks! — Crisco 1492 (talk) 13:49, 27 January 2015 (UTC)

Picture of the day

The Werner projection is a pseudoconic equal-area map projection. This cordiform (heart-shaped) projection originated in the 16th century. It is a limiting form of the Bonne projection. Distances along each parallel and along the central meridian are correct, as are all distances from the North Pole.Map: Strebe, using Geocart

Equidistant?

I have read various sources, and have not reached a firm conclusion, but I am not yet convinced that all distances are true from the North pole. Some sources claim that preserving all distances from a prescribed point and preserving areas is impossible. Can someone who understands this investigate the matter? If it is true, is the Werner projection unique in preserving both of these?--Leon (talk) 19:51, 21 March 2016 (UTC)

Hello Leon. It’s trivially true. The parallels are equally spaced circular arcs whose center is the north pole, which means they’re the correct distance from the north pole, which means anything from the north pole to any location on any parallel must be the right distance. What are “some sources”? I’ve never seen that, and if they exist, they’re wrong. Strebe (talk) 02:13, 22 March 2016 (UTC)

Well this is one such source. And an argument I've read, I cannot remember where, argues that if distances and areas are correct, scales are correct in both directions from the chosen centre and perpendicular to the chosen centre, which implies that there is no distortion and therefore the map is also conformal, which is impossible. What is the fallacy with this argument?

Back to the article, the combination of the two aforementioned properties sounds very distinguished. Are there any other projections combining these two properties?--Leon (talk) 08:36, 22 March 2016 (UTC)

The learnnc.org article is a little confused. The four traits it lists are sort of arbitrary; there's no particular reason to delineate those four as "the four". Meanwhile "equidistant" does not have a formal definition. By one definition, Werner is equidistant, but by others it is not, and regardless of what definition you choose, there will be maps not usually considered to be equidistant that are, or vice versa. But no matter what definition you choose, the explanation they give for equidistant is wrong. Nothing has correct distances between all points, yet the article does not qualify its description of equidistant with that fact. The same problem lies in the other argument you give. You don't even have to throw in equal-area or conformal: Distances are never correct on a map in the general sense. The argument's use of two directions is not well motivated; "two" directions are irrelevant. Sinusoidal projection, for example, is equal-area and has correct distances from the center along the equator and along the central meridian, but it's not equidistant by most definitions (although, it does have correct distances along all parallels, which could be argued is "equidistant", by some odd definition, though unrelated to the center point and axes from it).

As for Werner's place as (possibly) equidistant and also equal-area, no, it is not unique, since you could warp Werner by sliding the concentric arcs around the north pole in different amounts with respect to each other, neither destroying equivalence (the property of being equal-area), nor changing the distance any point is from center. There is an infinite amount of variations in sliding you could do, so this class is infinite. Other than this transformation, which always results in a more distorted map than Werner, I don't think there is another way to arrive at those two properties simultaneously. (Possibly there is some way if the point from which distances are correct is not a point when mapped, but stretched into an arc. I rather doubt that, though, for the same reasons it can't work if you stretch it into a straight line.) Strebe (talk) 17:51, 22 March 2016 (UTC)