Talk:Escape velocity/Archive 1

Archive 1

Overcomplicated??

I read thje entry here but got lost immediately. It becomes tangled from the outset. Can someone simplify? Here is a very elegant, simple and accurate definition in far fewer words:

If you throw an object straight up, it will rise until the the negative acceleration of gravity stops it, then returns it to Earth. Gravity's force diminishes as distance from the center of the Earth increases, however. So if you can throw the object with enough initial upward velocity so that gravity's decreasing force can never quite slow it to a complete stop, its decreasing velocity can always be just high enough to overcome gravity's pull. The initial velocity needed to achieve that condition is called escape velocity. From the surface of the Earth, escape velocity (ignoring air friction) is about 7 miles per second, or 25,000 miles per hour. Given that initial speed, an object needs no additional force applied to completely escape Earth's gravity. Answered by: Paul Walorski, B.A. Physics, Part-time Physics Instructor http://www.physlink.com/Education/AskExperts/ae158.cfm

LookingGlass (talk) 07:49, 17 July 2008 (UTC)

Units

Could someone write the escape velocities into units of mach as well as km/s? Thanks. -- Astudent 04:52 Apr 30, 2003 (UTC)

Umm, you do realize that mach pretty explicitly refers to a speed in an atmosphere, and when you're in an atmosphere, atmospheric drag is going to completely skew the escape velocities anyway, right? -- John Owens 06:13 Apr 30, 2003 (UTC)

First, the standard escape velocity value of 11.2 km/s is at the surface of the earth were the speed of sound is easily defined and well understood. Hence giving the Mach number of the escape velocity is a valid request. (At much higher altitudes, were the atmosphere is rarified, clearly the definition of the Mach number breaks down.) Second, to the layman, the speed of sound is just the speed of sound in air at approximately sea level in "standard" atmospheric conditions. The layman doesn't understand that it varies with temperature (among other things). So while you are technically correct, it would be helpful to the layperson if the escape velocity were related to the only "fast" speed they understand: the speed of sound at sea level. Since the speed of sound at sea level is 1225 km/hr, then the "Mach number" of the escape velocity at sea level would be (40320 km/hr)/(1225 km/hr) = 33. So the Mach number of the escape veloctiy is 33 at the surface of the earth (though, as the article points out, this is impossible to reach due to air drag and hence atmospheric heating). But there you go for whoever asked.Jrdx 01:40, 16 December 2006 (UTC)

---

This makes no sense....

(One complication is that virtually all astronomical objects rotate. The frame of reference must not rotate for that statement to be correct. Moreover, the gravitational slingshot effect sometimes involves transfer of energy to the projectile from the slingshot body that depends on the spatial relationship between projectile and body. The body loses some angular momentum -- possibly rotational as well as orbital -- adding kinetic energy to the projectile. Therefore, the complete gravitational field of the slingshot body must be included in the overall field, which then can no longer be approximatively treated as symmetric. Moreover, not only do escape velocities vary from place to place, they vary with time in such cases. Even moreso, they may sometimes depend on direction.)

Again, this makes no sense.....

(For reasons given above, computers may often have to be used to compute solar-system escape velocities to some desired precision.)

(One complication is that virtually all astronomical objects rotate.

Planets and stuff spin.

The frame of reference must not rotate for that statement to be correct.

Refers to "so that "velocity" is a misnomer; it is a scalar quantity and would more accurately be called "escape speed"". If you have a rotating frame of reference, then it will be a vector quantity rather than scalar, and it would be appropriate to call it a "velocity" after all. E.g., in computing the escape velocity for the solar system from a point on the Earth, or in its near vicinity, you would get different escape speeds depending on where in the Earth's gravitational field the object was, even if you calculate the velocity relative to the Sun's position rather than the Earth's ///_0\ [|_(CRAYOLA)_]> {'_'}  :Moreover, the gravitational slingshot effect sometimes involves transfer of energy to the projectile from the slingshot body that depends on the spatial relationship between projectile and body.

The Voyager spacecraft didn't have enough fuel to get out of the solar system under their own thrust; because they were given trajectories that gave them a significant boost from the slingshot effect at Jupiter & Saturn, that speed became greater than the escape velocity in that direction. If they'd just been given that much speed in a random direction, they would almost certainly still be orbiting the Sun.

The body loses some angular momentum -- possibly rotational as well as orbital -- adding kinetic energy to the projectile.

In the slingshot effect, some of the larger body's (call it a planet) momentum is transferred to the spacecraft. Because the planet has such greater mass, it's not measurable how much the planet is slowed down (or sped up, if you approach from the other direction). Mechanically, a slingshot can be considered much the same as a totally elastic collision between the planet and spacecraft; it's just that long-range gravity is the medium of the interaction, instead of close-up electromagnetic forces (Van der Waals, I think?). There can also be a minor component of acceleration from the tidal effects, which will affect the planet's rotation.

Therefore, the complete gravitational field of the slingshot body must be included in the overall field, which then can no longer be approximatively treated as symmetric. Moreover, not only do escape velocities vary from place to place, they vary with time in such cases. Even moreso, they may sometimes depend on direction.)

So for calculating an escape velocity from the Sun, you need to consider "lumps" in the gravitational field, such as moving planets, which will alter the speed needed to escape the system in different directions.

(For reasons given above, computers may often have to be used to compute solar-system escape velocities to some desired precision.)

I hope that from the above, it should be obvious (and not even in the way mathematicians say "it's obvious") why a computer would be helpful.

--John Owens 22:32, 2004 Feb 1 (UTC)

I'm pretty sure that there's a difference between escape velocity and the minimum velocity needed to escape a body at any particular time if you use slingshots and other dynamic effects like fuzzy orbits. They're not the same thing.WolfKeeper 00:53, 12 September 2007 (UTC)

---

This thing has way, way too many parenthetical remarks. If the information is important, just work it into the body of the article. --24.156.119.50 16:14, 28 Mar 2004 (UTC)

I'm inclined to agree. I just added a section; now maybe I'll go back and do a bit of rearranging of the earlier sections. Michael Hardy 22:40, 6 Sep 2004 (UTC)

---

I figure this article would really benefit from a brief table showing the escape velocities of major astronomical bodies (earth, luna, sun, mars, saturn, maybe our galaxy). -- Finlay McWalter | Talk 22:47, 25 Jul 2004 (UTC)

---

The notes say that this article needs to cite its sources - however, the vast majority of its discussion is mathematical development from first principles, and any normal undergraduate physics textbook is a "source" as such. It's kind of like asking for a citation for 2+2=4. Newton computed this without a source at all. Perhaps his Principia Mathematica should be cited as the source? With a note that it's best understood in the original Latin?

Jamey Fletcher 70.154.151.196 20:21, 24 December 2006 (UTC)

These two sentences need work

Someone added these two sentences in the first paragraph:

It is a theoretical quantity, because it assumes that an object is fired into space like a bullet. Instead propulsion is almost always used during the first part of the flight, and to "escape", at no time the escape velocity need to be attained.

Right at the beginning it says this is about objects that are not being propelled, so "the first part of the flight" during which propulsion is used is simply not relevant; this topic does not apply to it, but only to the later part where there is no propulsion. Moreover, it does not make sense to say "propulsion is almost always used", since a comet passing by the Earth that is not pulled into an orbit around the Earth escapes without propulsion, simply because it is always moving at a speed higher than the escape speed at whatever distance from Earth it's at. Moreover, there is no assumption about "being fired like a bullet", since the assumption, stated right in the first sentence, is that this whole thing applies only when there is no "propulsion". The last clause is ungrammatical; it says:

to "escape", at no time the escape velocity need to be attained.

What does that mean? Does it mean an object under propulsion can be lifted to an infinite height? If so, it's not relevant; this is only about objects not under propulsion. More precisely, it is about objects on which no forces act except the conservative gravitational field. How other objects behave, i.e., objects on which other, possibly non-conservative forces act, is simply not part of this topic. This topic treats only objects that are not propelled.

And what is meant by the words "It is a theoretical quantity"? I might have thought it means that in reality gravitational forces other than the Earth act on an object. But after the word "because" it then appears that something else was intended. Michael Hardy 14:43, 7 Sep 2004 (UTC)

Note that the escape velocity from the surface of Earth is not a speed that a spacecraft sent to outer space actually attains: while being propelled the height increases and the corresponding escape velocity decreases.

But if the spacecraft is not going to orbit Earth, but is being sent to photograph Uranus close-up, doesn't it actually go a lot faster than the escape speed at the surface? I seem to recall that the Apollo spacecraft going to the moon moved at something like 10 miles per second during the early part of the trip. Michael Hardy 22:45, 7 Sep 2004 (UTC)

I don't think so, [1] says 10.4 km/s (Earth Fixed Velocity).--Patrick 08:52, 8 Sep 2004 (UTC)

Urhixidur, please explain why this would not be correct:

(Considering the kinetic energies it may seem strange that a speed of 12 km/s (by itself corresponding to 72 MJ/kg) can increase the kinetic energy of the spacecraft from 450 to 900 MJ/kg, but the gain is at the expense of the Earth's kinetic energy, the launch will slightly slow down Earth.)

--Patrick 16:56, 8 Sep 2004 (UTC)

There is no mention of where the vehicle's energy is coming from, and it need not come from the Earth. Consider the Earth and the prepped vehicle as two distinct bodies, co-orbiting the Sun and in contact with each other. Assume the vehicle is at the Earth's far side from the Sun. The vehicle suddenly acquires the requisite extra 12 km/s of forward motion, possibly by ejecting part of its own mass at extremely high velocity in the opposite direction (I chose the vehicle's position so that the ejecta would not blast the Earth's surface and cause complications; here we assume the vehicle and its ejecta both "miss" the Earth itself). The vehicle will indeed eventually leave the solar system (its ejecta will do the same much faster, in all likelihood). In what way has this affected the Earth's momentum or energy? None whatsoever.

There is the matter of the gravitational influence of the vehicle on the Earth and vice-versa, but this can be neglected here. In fact, if you insist on not neglecting it, you'll notice that the vehicle, since it leaves *ahead* of Earth, will lose some of its energy to the Earth's benefit through gravitational interaction (it needs to escape the Earth as well as the Sun). Had the vehicle decided to leave in the opposite direction (which would require a 72 km/s delta-v!), its gravity would indeed slow the Earth very slightly.

The sentence as originally stated introduced a badly formed problem. Giving an object a velocity within a frame of reference gives it energy within that same frame (in this case 12 km/s translating to 72 MJ/kg). Switching to the Sun-centered frame, we see the object go from 30 km/s to 42 km/s and hence its energy go from 450 to 882 MJ/kg, a difference of 432 MJ/kg. Without specifying the rest of the system implicated (what imparted the extra velocity to our object?), we can't make any pronouncements.

Is this explanation clear enough?

Urhixidur 17:44, 2004 Sep 8 (UTC)

Interesting example. I have again considered the energies. Assume that the ejected mass is 1/n times the mass of the spacecraft, then it is ejected at a speed of 12n km/s relative to Earth. The apparent gain of 360 MJ per kg spacecraft can be explained by the fact that the kinetic energy, relative to Earth, of the ejected mass is 72n MJ per kg spacecraft, while relative to the solar system the energy only increases 72n - 360 MJ per kg spacecraft. With a large n as in your example it is clear that the large amount of energy to reach 42 km/s has to be produced anyway in the form of kinetic energy of ejected mass. I wonder whether there is a theoretical minimum amount of energy needed for the acceleration from 30 to 42 km/s; is it actually possible to use some kinetic energy of Earth, by "pushing it away"?.--Patrick 22:12, 8 Sep 2004 (UTC)

Assume, as you do, that the reaction mass (ejecta) is the fraction 1/n of the spacecraft's original mass. In the Earth frame, the initial kinetic energies are zero because nothing's moving. In the Sun frame, the kinetic energies are 450 MJ/kg for either parts (the reaction mass and payload parts). After the explosion, in the Earth frame we have the payload going one way with 72 MJ/kg (for the fraction (n-1)/n of the spacecraft's total mass) and the reaction mass going the other (at speed 12(n-1) km/s) with 72(n-1)² MJ/kg (note the square you missed). The overall (average) energy is 72(n-1) MJ/kg. This must have come from the explosives' potential chemical energy. In the Sun frame, we have the payload now going at 882 MJ/kg, and the reaction mass at 18(7-2n)² MJ/kg, average energy 18(21+4n) MJ/kg, delta 72(n-1) MJ/kg. Energy is conserved in translating between frames.

Urhixidur 22:53, 2004 Sep 8 (UTC)

OK, that seems the same; I used n for what you call n-1, and I expressed everything in kg payload (therefore I do not have the square).--Patrick 02:08, 9 Sep 2004 (UTC)

Say what?! Even if using a unit spacecraft mass, the square of the velocity is still in the picture. Assume n = 10; in that case the craft (9/10 of it) goes at 12 km/s whilst its reaction mass (1/10 of the original mass) goes at 12*9=108 km/s (conservation of momentum). The energy of the former is 72 MJ/kg whilst that of the latter is 5832 MJ/kg --its the square of the velocity, see...

Urhixidur 03:46, 2004 Sep 9 (UTC)

That is per kg reaction mass, for 1 kg payload we have 1/9 kg reaction mass.--Patrick 12:30, 9 Sep 2004 (UTC)

I'm not sure it's to the point, but exhaust speeds of 100 km/s are way, Way, WAY out there. See Spacecraft propulsion#Table of methods and their efficiencies. Normally it's the fuel that'd be 80–90% of the loaded ship.

Somewhere this needs the minimum escape speed from both the Earth & Sun = ${\sqrt {11.2^{2}+42.1^{2}}}-30=13.6\ \mathrm {km/s}$.

—wwoods 06:56, 9 Sep 2004 (UTC)

For rocket propulsion, yes, but this is a gedanken-experiment with "cannon propulsion". In combining Earth and Sun, you are quite right. Another approximation could be to work out the energy differential in moving to the edge of Earth's Hill sphere, and then let the Sun take over.

Urhixidur 11:39, 2004 Sep 9 (UTC)

speed vs velocity

what would be a better name for the phrase? escape velocity or escape speed? the article implies that speed is more accurate, as it is a scaler. i think this makes no sense, as escape velocity implies a speed to get off a planet, right? for the magnitute of the speed is to be at its minimum, doesn't the angle of launch need to be 90°? therefore it has a direction, and it is a vector quantity - so velocity is far more appropriate?

however i dont want to remove it from the article, as i am not sure i am right. comments? mastodon 22:20, 26 November 2005 (UTC)

The angle of lauch does not matter. That is why it is a scalar. (And scalar is the correct spelling. Michael Hardy 23:02, 26 November 2005 (UTC)

why not? if the angle was 45 degrees from the normal, a launched projectile would spend longer in the higher density part of the gravitational field, so would be more strongly attracted to the body, and would need more of a force, a greater magnitude of speed to escape. am i right? or am i not wrong?

Starting with the escape velocity, the velocity is a function of elevation (see parabolic trajectory). It is true that starting at an angle of 45 degrees the increase of altitude is slower, but also the decrease of speed, because in this case the gravity is not opposite to the velocity.--Patrick 01:07, 1 December 2005 (UTC)

also to be pedantic, as seems the trend (rolls eyes), if the angle was - say - 180° from the normal, the speed would need to be a little bit bigger to escape. comments? mastodon 23:12, 30 November 2005 (UTC)

It applies only when the parabolic orbit does not intersect the planet, hence, in the case of starting from the surface, if the direction is not downward (not lower than horizontal).--Patrick 00:29, 1 December 2005 (UTC)

I added some text about this in the orbit section.--Patrick 01:05, 1 December 2005 (UTC)

It's counterintuitive. The quickest way to understand this is to see that all you need is enough kinetic energy to lift you to infinite height, and that's finite because the field strength decreases fast enough as you go up. Michael Hardy 01:45, 1 December 2005 (UTC)

Question - shouldn't escape velocity = sqrt(2G/R) instead of sqrt(2GR)?

No, but you quoted the article wrong. The article said it was sqrt(2gR), where the "g" is lowercase, i.e., the acceleration of gravity at the earth's surface, or about 9.8 m/s². However, I think you are confused with the oft-given result (in fact, it was derived earlier in this article) that the escape velocity is equal to sqrt(2Gm_e/r), where m_e is the mass of the earth and the "g" is uppercase, i.e., the universal gravitational constant, or about 6.7x10^-11 Nm²/kg², and which is also correct. However, if you use the relation that g=Gm_e/r² (which is really the definition of g), you'll be able to go between these two equivalent expresssions for the escape velocity.Jrdx 02:32, 5 December 2006 (UTC)

I'm still not convinced it can be called speed. It seems to me that since velocity is a vector, only the part of the vector that is directly opposing gravity would be helping the object escape. The other part of the vector would only be causing it to spin around the larger body. Am I missing something? --Paulie Peña 23:33, 1 March 2006 (UTC)

Indeed, you are missing something. You are absolutely right that this result is counterintuitive. But think about the sum of kinetic energy and potential energy. If the projectile's kinetic energy at its present position is more than its potential energy at infinite distance from the planet, then it will escape. Michael Hardy 00:34, 2 March 2006 (UTC)

A large horizontal speed also helps the object escape.--Patrick 02:52, 2 March 2006 (UTC)

Correct. If the motion is ONLY horizontal, with sufficient speed the object will still escape. Michael Hardy 02:42, 5 December 2006 (UTC)

Speed and velocity have two very different meaning in physics. This topic cannot be changed to escape speed. Also assuming the escape velocity of earth, that is standing on the surface of the earth, is EV, then it doesn't matter which direction the object is moving. As long as it's velocity is >= EV, it will escape earth's gravitational pull. You can throw it straight up 0 degree, 45 degree angle or event straight down 180 degree angel assuming the object can pass thru earth. Proof. Assuming you throw a ball straight down with initial velocity of EV. As the ball goes toward center of earth, it's speed will increase due to gravity. As it is at the center of earth, the ball's speed will be at its greatest. Going past it, the speed will decrease because gravity is now pullling it back. As the ball reaches the surface at the other end, it's velocity of again be EV, and it will go straight up (or down if you want to look at it that way) toward the sky. If the object is throw horizontally at 90 degree angle, the ball should just orbit the earth. Think of satellites, they are always moving parpendicular to earth. If their direction of movement is tilted toward earth, they will fall to earth. If tilted away, they will move into space. This also answer the above question of 'large horizontal speed'. And proofs if it is thrown at 45 degree angle, it will still escape earth's gravity. --NYC 16:36, 13 March 2007 (UTC)

"Think of satellites, they are always moving parpendicular to earth" Well, doesn't really relate to article, but: the satellites are always moving in the direction of the earths surface at any point, and hence are actually moving in a direction tangent to it. --Freuga (talk) 00:22, 12 March 2008 (UTC)

Definition

Patrick, I disagree with your reverting to the previous version, claiming that mine was "not an improvement." I have run the two versions by a number of people, who all agree that my version is easier to read without losing any of the content. Of course we're talking about "physics," and of course it's for a given gravitational field. The current version is redundant. - Ztrawhcs.

"In physics" is the usual way to provide context. Escape velocity is a property of a gravitational field and a position, it does not depend on the object. Your version ignores dependence of position, and suggests dependence on the object. "its gravitational field" is also confusing. --Patrick 09:52, 27 January 2006 (UTC)

your version ... suggests dependence on the object ... Touche. Good point. I still think, however, that we need not completely sacrifice readability. The intro paragraph doesn't have to scare people away with its complexity. I can just imagine an entire generation of 10 year old would-be scientists seeing the wikipedia entry on Escape Velocity and turning away in brain-twisting horror, deciding never to become scientists but instead to become garbage men. I hope you're prepared to deal with that. Ztrawhcs 21:05, 2 August 2006 (UTC)

Newer results

Somebody should review the following references, our current data seems inexact:

• Annexed the number that appears in Wikipedia on escape velocity from Solar

System from Earth: 43.6 km/s. In agreement with my paper A note on Solar Escape Revisited * the correct figure is 16.6 km/s. When we get 43.6km/s or 13.6 km/s we neglect the recoil kinetic energy of the earth and that is nonnegligible in Sun's coordinate frame.

• The escape velocity from a position in a field with multiple sources is

derived from the total potential energy per kg at that position, relative to infinity. The potential energies for all sources can simply be added. For the escape velocity this results in the square root of the sum of the squares of the escape velocities of all sources separately.*

• For example, at the Earth's surface the escape velocity for the combination

Earth and Sun is √(11.2² + 42.1²) = 43.6 km/s. As a result, to leave the solar system requires a speed of 13.6 km/s relative to Earth in the direction of the Earth's orbital motion, since the speed is then added to the speed of 30 km/s of that motion.* Diaz-Jimenez_Anthony_P._French-MIT_Professor,_American_Journal_of_Physics,_56,_85,_1988 Diaz-Jimenez_Anthony_P._French-MIT_Professor,_American_Journal_of_Physics,_56,_86,_1988

(from OTRS) David.Monniaux 08:10, 16 February 2006 (UTC)

You mean 13.6 should be 16.6? How is that computed?--Patrick 02:44, 18 February 2006 (UTC)

Pr Diaz-Jimenez sent the Foundation several published papers that revisit the escape velocity. I can forward them to you by email (you can contact me with "send mail to"). David.Monniaux 09:23, 18 February 2006 (UTC)

Well what speed do e.g. rockets typically have to attain? If 16.6 is right then they would have to have attained that speed already. 203.218.86.162 09:28, 31 May 2006 (UTC)

formula in section 2

i have swopped the approx= and = because v is approximately the thing in the root, which exactly equals 11200. 203.218.86.162 09:28, 31 May 2006 (UTC)

Some of the formulea lack statements showing what the letter stand for, this is standard in consideration of equations. Unfortunatly, I do not know what the letters stand for, so I am not going to alter it. Can someone work this out?

--84.65.8.104 (talk) 05:24, 14 September 2009 (UTC)

Direction of rotation

I have added some clarifications on the direction of rotation of the body. Though rotation is not a must to account for the escape velocity, the direction in which the escaping body is launched is important, if the main body is rotating. --Wikicheng 04:06, 29 June 2006 (UTC)

Not at all. The escape velocity doesn't change. Rotation is irrelevant. The paragraph

"The escape velocity relative to the surface of a rotating body depends on direction in which the escaping body travels. For example, as the Earth's rotational velocity is 465 m/s to the east at the equator, a rocket launched tangentially from the Earth's equator to the east requires an initial velocity of about 10.735 km/s relative to Earth to escape whereas a rocket launched tangentially from the Earth's equator to the west requires an initial velocity of about 11.665 km/s relative to Earth. The surface velocity decreases with the cosine of the geographic latitude, so space launch facilities are often located as close to the equator as feasible, e.g. the American Cape Canaveral in Florida and the European Centre Spatial Guyanais, only 5 degrees from the equator in French Guiana."

should be deleted or atleast made clearer. What you are referring to is relative velocity. For example, if I am walking away from you at 1 m/s, I have a right to say it is you who are moving away from me at 1 m/s even thought you are standing perfectly still and it is I who is actually moving. The velocity difference between launching due east and west from Cape Canaveral is because Cape Canaveral is also moving. If you view the launch from the Sun, it would observe the rocket has the same velocity whether lauching due east or west with respect to Earth.

Also what does it mean "10.735 km/s relative to Earth to escape" and "11.665 km/s relative to Earth"? Did the author mean relative to where it is launched? It cannot be relative to Earth since relative to Earth means relative to center of Earth. --NYC 17:00 13, March 2007 (UTC)

Escape velocity 50 km above the surface of Venus

I'm working on the Colonization of Venus article right now, and part of it talks about floating cities at 50km above the surface where the atmospheric pressure and temperature are the same as Earth. What would be escape velocity be there? It doesn't seem like it would be that much different from the surface given that even 9000 km from Earth doesn't even halve the number. Venus rotates extremely slowly but these theoretical cities would be up where the wind velocity causes them to whip around the planet every four days. Mithridates 05:58, 9 August 2006 (UTC)

Gravity well

One section is named gravity well, yet it doesn't seem to have anything to do with gravity wells (which are things like black holes that distort spacetime as I understand from the article. Instead it's talking about a theoretical hole in a body through which an object can be dropped allowing it to reach the center. I believe the section needs to be renamed, perhaps someone with a good understanding of the concepts discussed there could find a more appropriate name? Richard001 08:59, 1 October 2006 (UTC)

Very, very late reply, but gravity wells are just the gravitational field around a planet or other body that has been mapped to a plane in three-dimensional space, where the curvature of that surface represents how strong the gravitational potential energy would be at all positive and negative Z coordinates above and below a corresponding XY coordinate on the plane; producing a hollow in the middle because potential energy builds as distance increases (the farther up a hill you go, the more potential energy you have, after all). It's merely a representation of the potential energy of gravity to allow humans to understand it and not an actual phenomenon. --Jtgibson (talk) 23:42, 27 January 2008 (UTC)

Could someone explain how you calculate the sqrt(2) and especially the sqrt(1.5) that are mentioned in the text. —Preceding unsigned comment added by 83.134.149.55 (talk) 19:12, 9 November 2008 (UTC)

The rocket misconception again

"In physics, escape velocity is the speed where the kinetic energy of an object is equal to the magnitude of its gravitational potential energy. Escape velocity only applies to objects that have no propulsion or thrust. An object under power, like a rocket, could leave the Earth's gravity at any speed." And yet the article then goes on to state that the escape velocity at earth is 11.2 km/s. If kinetic energy needs to equal gravitational potential energy, then how can you put a number on the escape velocity without knowing the mass of the particle that may or may not be escaping? -- kanzure (talk) 14:23, 7 March 2008 (UTC)

Edit. I note that mass cancels out. Perhaps this can be included in the article. -- kanzure (talk) 14:24, 7 March 2008 (UTC)

Rockets vs. Escape Velocity

I was pleased to find the first paragraph clearly stating that the concept of escape velocity only applies to non-self-powered objects.

But then in paragraph 4 we get "a rocket launched tangentially from the Earth's equator to the east requires an initial velocity of about 10.735 km/s relative to Earth to escape".

This seems to be a common misrepresentation in popular descriptions of space programs -- that rockets must achieve escape velocity to somehow "break free" of some imagined gravitational "barrier".

If I'm not mistaken, there's absolutely no requirement for escape velocity for a self-powered rocket -- fuel usage aside, it can take off at 1 mile per hour and just keep rising at 1 mile per hour for a thousand hours. No "barrier" to break through.

If that's accurate, the paragraph in question should be edited to describe an "unself-powered object like a bullet being shot" rather than a rocket taking off -- and a dedicated paragraph mentioning that rockets needing escape velocity is a common misconception seems advisable if the confusion is turning up even in this article.

Frankly, your remarks seem enormously confused. Rockets must indeed achieve escape velocity in order to escape. The fact that all this applies only to objects acted on by no forces except gravity does not make it inapplicable to rockets. Rockets cease to be "self-powered" when their engines stop firing, and then everything in this article applies. Certainly a rocket can continue to rise from the earth's surface at 1 mph for 1000 hours if it's got enough fuel, but what's that got to do with anything this article says? The article is about how the rocket (or other object) behaves when it's NOT doing that. The "misconception" you write of is not a mistconception at all. Michael Hardy 21:42, 19 January 2007 (UTC)

You're using the word "rocket" to mean "current rocket technology". I'm using the word "rocket" to mean "a self-powered projectile" in theoretical physics.

I'm saying it's confusing to start out with abstract theory -- where "self-powered projectile" is in contrast to "cannon ball" -- and then give a supposed illustration of that abstract theory with a device that is combining the two principals.

There needs to be an explanation about present-day rockets going into a ballistic phase at which point escape velocity comes into play.

The quote above is completely false in stating "requires an initial velocity" -- we've all seen rockets lumbering up off the launch pad.

And the point I actually came back here to bring up is, doesn't it take orbital velocity (so called) and not escape velocity (so called) to put a rocket (under ballistic propulsion) into an Earth-circling orbit?

Wouldn't leaving the Earth at escape velocity, ballistically, with no further power usage, send the rocket into an infinite parabolic or hyperbolic orbit, ending up somewhere Beyond Antares... (Not a good look for your weather satellite). —The preceding unsigned comment was added by 75.6.245.249 (talk) 10:27, 22 January 2007 (UTC).

Whether an object is self propelled or not, it has to reach the escape velocity to get out of earth's gravity. Please note that the escape velocity decreases with distance from earth. Once the object reaches the escape velocity for that height, it need not be self propelled any longer. If an object is self propelled to keep going at a steady rate of 10km/hr for a very very long time, eventually it reaches a point where the escape velocity is 10km/hr and it will be free from earth's gravity. At that moment, even if the self propulsion stops, the object will not return. If 5km per sec is the maximum velocity you can attain, then you need to take the object (using self propulsion or otherwise) to a height where the escape velocity is 5 km per sec, give it a velocity of 5 km per sec for it to escape. Basically, the object needs to be self propelled to a height where the velocity of the object crosses the escape velocity for that height-- WikiCheng | Talk 12:18, 22 January 2007 (UTC)

Constant propulsion problem

What will happen if an object is sent in the air from the Earth's surface with a speed less than escape velocity but with a constant propulsion force? Will it be able to escape earth gravity? Let see the problem under another angle for you to be sure you understand what I mean. Imagine we have a very long staircase which reaches the moon, by climbing it even by foot, will one be able to escape earth gravity and be in orbit?. Objects which do not reach the escape velocity speed fall on Earth because of the gravity resistance. But if there is a constant propulsion force, this resistance would be cancelled right? —The preceding unsigned comment was added by 24.201.98.14 (talk) 17:21, 22 January 2007 (UTC).

If you provide a constant propulsion force greater then gravity then you will escape. If you provide a propulsion force = to gravity and you have a none zero initial velocity, you will esacpe. If you had zero initial velocity you will remain where you are forever. If the propulsion force is less then gravity, you will fall. Simply put, if gravity is pulling it down, and you are pushing it up, if you are pushing harder then gravity, it will move up. If gravity is stronger it falls down. Initial speed is irrelevant. --NYC 17:16 13 March 2007 (UTC)

Derivations Section

There is a definite problem with the derivations section. There are two sections: one using g and r, and a second using G and M. The distinctions between these sections are redundant because g is derived from G, M, and r:

$g=GM/r$

In Physics, real Physics, the stuff that real world physicists work with, these two derivations are one and the same!

Stltcom 21:36, 13 July 2007 (UTC)Stltcom

Misconceptions

There is a quote in the misconceptions section that states the following: "A practical application that might involve an object leaving earth orbit at speeds much lower than the escape velocity is the hypothetical space elevator." I believe that this statement is incorrect. At the bottom of the tether, the object is in fact moving at relatively low speeds (the earth's surface at the equator is moving at roughly 1000 mph), but by the time it climbs to the end of the cable, it has accelerated to tangential speeds of thousands of miles per hour. In addition, at the end of the cable, the potential energy of the object is significantly less, which reduces the escape velocity. So the escape velocity decreases significantly, the object's velocity increases significantly, and theoretically the object could exceed the escape velocity with a sufficiently long tether. If the object leaves the end of the tether and no longer provides any propulsion of any kind, and if the object does in fact truely "escape" from the earth, then it has been accelerated to speeds in excess of the escape velocity. I believe the mistake made by whoever wrote that quote was in considering only the speed relative to the surface of the earth (the climbing speed). The fact that the frame of reference is rotating approximately once per day has a significant impact on the math that was not considered.

137.240.136.81 22:25, 11 September 2007 (UTC)

Further, I do not believe the included image adds anything to this article, in fact, the image chosen happens to be incorrect as the Space elevator requires a geosynchronous orbit and such an orbit cannot take place at a planet's pole. I'm removing the link to the image. -Verdatum (talk) 18:35, 27 November 2007 (UTC)

The misconception is actually like this: "The minimum escape speed is the speed an object must be going to get out of earths gravity well." This speed is around 25,000mph (whatever), however, you could really leave the earths gravity well at 5mph if you had a rocket to carry that much fuel. The misconception is that the escape speed needs to be understood as ballistic speed, that is, with nothing slowing it down except the acceleration of gravity. Of course, air resistance slows you down, but the physics idea usually neglects that. I have had to explain this to so many people (high school students mostly) who understood the idea to mean "You can never ever get out of earths gravity unless you are going 25,000mph (whatever)." —Preceding unsigned comment added by 129.93.28.91 (talk) 15:48, 17 April 2008 (UTC)

Should a "thing" attain escape velocity to orbit earth (or some other planet or star)? Giving it a tangential velocity is sufficient right? (of course this assumes that the planet's mass is concentrated at a single point 'like' a black hole.)````Ganesh

Wrong image

Isaac Newton's analysis of escape velocity. Projectiles A and B fall back to earth. Projectiles C and D achieve an orbit at a fixed height. Projectile E achieves escape velocity.

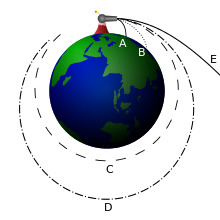
This image, which used to be at the top of the article, is not relevant. It shows objects being launched parallel to the surface of a planet. Escape velocity applies to objects launched directly away from a planet (perpendicular to the surface). I have removed the image. E James (talk) 22:25, 31 January 2008 (UTC)

I don't think you are correct. As the article tries to explain, escape velocity is more properly called escape speed. It doesn't matter in which direction the velocity vector initially points (as long as the resulting trajectory does not intersect the plane surface or atmosphere). The analysis only depends on the kinetic energy plus the potential energy being non-negative. I've restored the image.--agr (talk) 01:00, 1 February 2008 (UTC).

Yes, you are correct. I thought I had it figured out after reading the article and the discussion yesterday, but I was wrong. Thank you for restoring the image.

E James (talk) 17:09, 1 February 2008 (UTC)

I think the image's caption is incorrect, however: C does achieve an orbit with fixed height as claimed, but D does not. I'll edit the caption.

Laschatzer (talk) 16:37, 2 June 2008 (UTC)

Energy

I was always in pains to explain the concept of escape velocity. But I think it is best to express it as the minimal amount of energy (described as kinetic energy) to get free of earth attraction. So in space 'light-year' is a distance and 'escape velocity' is an amount of energy. Zadkin (talk) 11:14, 7 December 2008 (UTC)

A ladder

An astronaut using a ladder can escape at any speed. No matter how slowly. But no matter how slowly an astronaut climbs a ladder "out" of a black hole, all paths will lead inward. Even if that astronaut is very strong, there is no escape out of a black hole, because the gravity of the black hole makes all paths curve inwards. This has nothing to do with the escape velocity being larger than the speed of light. A black hole curves ALL paths inwards. Can this be made clearer in this article? 68.200.98.166 (talk) 02:42, 27 January 2010 (UTC)

1st and 2nd cosmic velocity

Although both these two entries redirect to this page, this page does not explain what it means 1st and 2nd cosmic velocity. I think it should. --Pavel Jelinek (talk) 15:15, 9 July 2010 (UTC)

Yes, good catch. Useful information can be found here, here and here. I have added a little sourced remark. Please do feel free to reword or elaborate, and move it to a more appropriate place, because I think it belongs a bit higher up in the article, perhaps somewhere in the overview section? DVdm (talk) 16:10, 9 July 2010 (UTC)

Misconceptions section: "leave the Earth's gravity"

This is addressed to Gr8xoz regarding my recent edit. I removed the paragraph because the statement

In fact a vehicle can leave the Earth's gravity at any speed less than the speed of light.

is ill-defined. What does it mean to "leave" gravity? This brings up the discussion of gravitational spheres of influence, which are unrelated to the escape velocity. The next sentences contradict the first one:

At higher altitudes, the local escape velocity is lower. But at the instant the propulsion stops, the vehicle can only escape if its speed is greater than or equal to the local escape velocity at that position.

So you can "leave" Earth's gravity at any speed you want, but you can only "escape" Earth's gravity at escape velocity or higher. This doesn't clear up misconceptions, it only introduces more confusion. Finally, the fact that the last sentence,

As is obvious from the equation, this speed approaches 0 as r becomes large.

declares itself to be "obvious" means it is superfluous and can be deleted. It's not a misconception either. Thoughts? MarcusMaximus (talk) 21:01, 14 December 2010 (UTC)

I see your point, an object can never leave the Earth's gravity since it never becomes zero. I do not see how the discussion of gravitational spheres of influence is relevant, it is just the volume where the gravity from a body dominates over the gravity of other bodies. I would suggest that

In fact a vehicle can leave the Earth's gravity at any speed less than the speed of light.

is changed to

In fact a vehicle can leave the Earth at any speed less than the speed of light.

This also solves the contradiction. I have made this change, is this solving the problem?

--Gr8xoz (talk) 21:47, 18 December 2010 (UTC)

What misconception is this paragraph trying to address? Maybe it would help to state it first. MarcusMaximus (talk) 06:09, 20 December 2010 (UTC)

Less than the speed of light?

It says in misconceptions "In fact a vehicle can leave the Earth at any speed less than the speed of light" As nothing can travel faster than the speed of light why is it necessary to qualify the sentence in this way? Also, as it stands, the sentence suggests that if a faster than light propulsion was possible you couldn't use it to leave the Earth.

I also have a problem with the sentence in the lead that says "The term escape velocity is actually a misnomer, as the concept refers to a scalar speed which is independent of direction." The sentence isn't complete as it doesn't say why the use of the term velocity is a misnomer. How about adding something like "whereas velocity is the measurement of the rate and direction of change in position of an object"? Richerman (talk) 22:07, 16 February 2011 (UTC)

As there has been no reply I've made the changes myself

I think this is a rather unimportant detail but "a vehicle can leave the Earth at any speed" could be interpreted as a statement saying that faster than light travel is possible at least if you are escaping from the earth. Gr8xoz (talk) 17:44, 20 February 2011 (UTC)

It is a small detail but adding unnecessary wording confuses the reader and makes them think they are missing something. I suppose you could interpret it that way but to follow that logic means that every time you talk about "any speed" you would have to qualify it "less than the speed of light". So, for instance, "there is no speed limit on this road so vehicles may travel at any speed less than the speed of light." Richerman (talk) 09:32, 21 February 2011 (UTC)

I agree with Richerman. The statement could also imply that if you travel at light speed you can't leave. The whole paragraph needs to be overhauled. MarcusMaximus (talk) 03:29, 23 February 2011 (UTC)

Escape Velocity of the Milky Way

I fear this has to be in error, as I would assume the gravitational pull of the entire galaxy would be more than the gravitational pull of the Sun (even from the surface of the Sol). Would this have to do with the Inverse Square Law perhaps? Due to you moving further and further away from the galactic core, the amount of "tug" exerted on you would decrease exponentially. Now that I think about it, it might be right, depending on where at you are in the Milky Way. Perhaps it needs to be worked out what the galactic escape velocity would be when near the center as opposed to our local region. I think that would help clarify the issue more than at current. Sardonicone (talk) 02:35, 21 May 2011 (UTC)

Escape velocity increases as you increase the mass of the object that you are "escaping" from (the "primary"), but decreases as you move further away from the centre of mass of that object. For a location outside of a spherically symmetric primary (on the surface of a planet, for example) we can calculate escape velocity exactly, and it turns our to be proportional to the square root of the primary's mass, and inversely proportional to the square root of distance from the centre of the primary. Calculating escape velocity relative to the Miky Way is much more complicated and uncertain because (a) we are inside the Milky Way; (b) it is not spherically symmetric; and (c) we don't even have a very accurate measure of the mass of the Milky Way. But according to astrophysicist and Nobel prize winner John C. Mather, the escape velocty from the centre of the Milky Way could be around 1,000 km/s [2]. Gandalf61 (talk) 11:12, 21 May 2011 (UTC)

Centres of Mass?

The equation Ve=root(2*G*M/r) doesn't work very well for trajectories that go or start near centres of mass. As it treats objects as point masses it frequently shows escape velocities crossing the speed of light- for instance at r= 9 cm for Earth, or r= 2.9 km for the sun. I know an equation for a distributed mass would solve this problem but is obviously far more complicated, I would love to see an equation that worked from mass centre - or even for non-spherical objects. :) Maybe there should be a section on centres of mass? Lucien86 (talk) 06:22, 15 August 2012 (UTC)

It's not the equation that breaks down, but the simplifying assumption of representing objects as point masses. A radius of 9 cm for an object the mass of the Earth, for example, is less than the Schwarzschild radius for that mass, so a value greater than the speed of light is entirely appropriate. In reality, this isn't much of an issue as all practical applications would already recognize that such a small radius would create a subterranean orbit. I don't think that there's much need for a new section; a sentence pointing out the shortcomings of the point mass assumption is more than sufficient. siafu (talk) 17:12, 15 August 2012 (UTC)

Luna I attained escape velocity?

I think the caption on the image of Luna I is at best misleading, if not flat-out wrong:

Luna 1, launched in 1959, was the first man-made object to achieve escape velocity from the Earth (see below table).[1]

And the table says for Earth V-sub-E is 11.2 km/s. So at what point did Luna I attain that speed? I would submit that it did not. As explained elsewhere in the article, it was not put into orbit in one, ballistic, push - it attained LEO (relatively) slowly, and from there attained the (local, lesser) V-sub-E.

robcranfill \a\t comcast.net

--130.76.32.214 (talk) 18:01, 2 October 2012 (UTC)

"As explained elsewhere in the article, it was not put into orbit in one, ballistic, push - it attained LEO (relatively) slowly, and from there attained the (local, lesser) V-sub-E."

Can you please post this section as I cannot find anything verifying this claim, especially not in relation to Luna 1. As the Luna 1 article states, it had no propulsion of its own. It was pushed to its final velocity by the R-7's third stage, almost certainly itself on a ballistic trajectory. There is no evidence that the third stage was in LEO prior to this or of a "slow" raising of Luna 1's orbit. What with, there's no EDS?!

Besides, the statement that Luna 1 achieved escape velocity is inline cited to a NASA archive, frankly I suspect they would know more than most the truth of the matter... ChiZeroOne (talk) 19:23, 2 October 2012 (UTC)

(edit conflict)Per the article on Luna 1,

Luna 1 became the first ever man-made object to reach the escape velocity of the Earth (what is also known as the second cosmic velocity), when it separated from its 1472 kg third stage.

Another way to look at the escape velocity is the minimum relative velocity that will allow travel beyond the gravitational influence of the body in question; i.e., it is not possible to exit the gravitional sphere of influence (even given infinite time) of the object without at some point reaching escape velocity. You note that the V_{E} will be less at high altitudes, but this does not mean that it is not a proper escape velocity. Escape velocity is defined by the current radius, so a theoretical escape velocity from a radius near the core of the Earth will be higher than it will at sea level, and it will be even lower in near the equator or from points at the top of mountains. siafu (talk) 19:25, 2 October 2012 (UTC)

Error

There seems to be an error in the condition of the formula

$v_{e}={\sqrt {\frac {2GM}{r}}}$.

Consider an example where the object to escape is a very light torus. By letting the point from which to escape approach the centre of gravity, the escape velocity can be made arbitrarily large. This is not correct.

One extra assertion making the formula correct, is to require that the gravitational force F imposed by the the body on the escaping object satisfies F = mMG/r^2 directed opposite of the escape path, for all points along its escape route. Here r is the distance from the point to the mass centre. Note that this is note satisfied close to the mass centre of he torus in the Example above. This is for example satisfied if the body to escape is a homogenous Ball and the escape starts outside the ball.

Jacco77 (talk) 15:40, 17 May 2011 (UTC)

In the overview section of the article, it states:

For the sake of simplicity, unless stated otherwise, we will assume that the scenario we are dealing with is that an object is attempting to escape from a uniform spherical planet by moving straight away (along a radial line away from the center of the planet), and that the only significant force acting on the moving object is the planet's gravity.

Obviously the case of a very light torus (or any torus) violates this assumption, and is not relevant to the development presented in the article. Similarly, this equation fails to account for various other perturbations (e.g. light pressure), and should be treated as a simplified theoretical model. You could add a short section discussing the shortcomings of this definition and the ways of dealing with situations that otherwise are not accurately treated by it if you like, as well. siafu (talk) 18:52, 17 May 2011 (UTC)

Thanks, missed that formulation. Perhaps I reacted to the formulation:

where G is the universal gravitational constant, M the mass of the planet, star or other body, and r the distance from the centre of gravity.

The "other body" part here made me think of more general bodies, such as a torus. Regarding the possible shortcomings section, I am not a physicist and the only shortcoming I could formulate is of the "pure old school mechanics" type formulated above, perhaps I could initiate such a section when I find time for it.Jacco77 (talk) 10:25, 18 May 2011 (UTC)

I added "for a spherically-symmetric body".--Patrick (talk) 22:41, 18 May 2011 (UTC)

I would like to point out this equation is valid only for points outside the said body. 62.197.226.110 (talk) 22:39, 8 October 2012 (UTC)

Reversion of rewrite

I have reverted a rewrite of the lead and Overview sections by Zedshort (talk · contribs) because it contained these sentences

"Escape velocity is a velocity in that it is the radial speed an object must have as it is directed radially away if it is to escape another mass's) gravitational pull. The escaping object may have an additional component of velocity normal to its radial velocity but in order to escape the planet's gravitational pull, it must have a speed in the radial direction at least as great in magnitude as the mass's "escape velocity"

which are simply wrong. The original Overview is correct when it says

"Escape velocity is actually a speed (not a velocity) because it does not specify a direction"

Escape velocity is independent of direction (ignoring effects of atmosphere, mountains etc.) - it is the same for a horizontally launched projectile (such as Newton's cannonball as for a vertically launched projectile. Gandalf61 (talk) 08:35, 2 July 2012 (UTC)

You are incorrect. Escape velocity is not just a speed but has a direction making it a vector quantity. The component of the speed in the radial direction must be equal to the escape velocity in magnitude. The direction of flight may be in any radial direction. I am speaking in terms of polar coordinates in which all radial lines away from a mass's center are in the radial direction. The escaping body may also have components of velocity in the phi and theta directions but those are at right angles to the radial direction and are of no consequence. It is the radial velocity magnitude that is of consequence. If a cannon ball is launched with a speed equal in magnitude to escape velocity and in a tangential direction it will lack the speed to "escape" the pull of the planet by a very small quantity. It will come close but be off by a small amount and will not escape the planets pull. If you don't understand polar coordinates you need to learn to use them. In addition your wholesale reverting of the other edits were inappropriate as they unrelated to the particular complaint about the use of the term "radial direction" and so were inappropriate.

The first sentence of a introduction should be easily comprehended but as it stood it was too advanced for 99% of the readers.

Be aware none of us own this article and if you are squatting on this and claim ownership you need to make room for others. I thoroughly understand the subject and don't make edits without giving it serious thought. The article is poorly written, full of redundancies and needs to be cleaned up and written in a clearer fashion. I am tempted to revert your reversion as you have changed my edits in a wholesale and inappropriate fashion. — Preceding unsigned comment added by Zedshort (talk • contribs) 14:12, July 2, 2012

The mistaken idea that escape velocity is a vector and depends on direction has been discussed before - see "Vector or scalar" above. If escape velocity were a vector then it couldn't be derived from a conservation of energy argument, since energy is a scalar.

Anyway, that was such a fundamental error on your part that it made me doubt the quality of the rest of your rewrite, and I didn't want to spend time disentangling the good from the bad. However, since you are now accusing me of "claiming ownerhsip" here, I will raise this issue at Wikipedia talk:WikiProject Physics, and see if other editors will step in and deal with it. Gandalf61 (talk) 14:53, 2 July 2012 (UTC)

No, Gandalf61 is correct, escape velocity is independent of direction, you simply have to reach that speed to be able to escape. Well caught.Teapeat (talk) 15:49, 2 July 2012 (UTC)

I agree with both the previous editors. Consider the pathalogical case - a satellite, height h above a planet has an escape velocity v 'towards the planet, not away from it. Assume that the planet has a hole through it and the satellite successfully passs through that hole and out the other side of the planet. When it gets to a height h on the other side, it will be travelling with a velocity v but away from the planet - it will escape in the wrong [?] direction. Martinvl (talk) 16:18, 2 July 2012 (UTC)

I assume that those who believe that the escape speed depends on direction do so on the ground that the object's angular momentum requires it to have some amount of tangential motion which uses up some of the energy. However, they fail to realize that as the object moves further and further from the gravitating mass, the amount of tangential motion and energy needed for that purpose (conserving angular momentum) declines towards zero. JRSpriggs (talk) 17:26, 2 July 2012 (UTC)

For what it's worth, the recently published physics textbook that I'm using (Sears and Zemansky's University Physics with Modern Physics, Thirteenth Edition, by Young and Freedman) doesn't even use the term escape velocity, instead saying "escape speed, the speed required for a body to escape completely from a planet." It goes on to talk about gravitational potential energy, satellites, and Newton's canon. Nowhere that I see does it say anything that would support Zedshort's claims. 786b6364 (talk) 17:54, 2 July 2012 (UTC)

The problem with this article is its lack of sources. For the escape velocity being independent of angle, there's for instance this one on pages 82 and 83:

• The projectile will escape to infinity provided that E >= 0; or equivalently that its velocity exceeds the escape velocity v_e = sqrt(2Rg). Note that this condition is independent of the angle of launch α (so long as we neglect atmospheric drag).

So this is just a matter of sourcing. - DVdm (talk) 18:38, 2 July 2012 (UTC)

I stand corrected. Thanks for the reference. I always though there would be a very small difference depending on the direction of launch. But I still believe the article contains redundancies and the first line should be one that draws the reader in with a simplified explanation rather than the pedantic one used at present. Zedshort (talk) 00:57, 3 July 2012 (UTC)

• I checked a couple of references: the Penguin Dictionary of Mathematics has a definition for Escape speed (escape velocity) and then defines it in terms of speed. The Oxford Concise Science dictionary has "escape velocity The minimum speed needed ...". Generally it seems that "escape velocity" is a misnomer and it is actually a scalar quantity, the direction is almost never specified. I'd be tempted to rename the page to be "escape speed" and add a redirect from "escape velocity" to the newly moved page, although maybe it isn't worth the effort. Anyway I think that you were correct to undo the changes as far as the direction goes, although some of the other changes that you reverted, which simplified the language, could have been kept. CodeTheorist (talk) 20:46, 2 July 2012 (UTC)

WP:COMMONNAME. While some sources are clearly using escape speed, I think escape velocity is still the more common term. Unless you can provide evidence to the contrary, I wouldn't move the page. 786b6364 (talk) 02:28, 3 July 2012 (UTC)

Agreed, I think that "escape velocity" is more common than "escape speed", although I have no hard evidence either way. So unfortunately we'll have to leave the page name as it is. CodeTheorist (talk) 12:28, 3 July 2012 (UTC)

It is called escape velocity because it clearly is a velocity. The escape 'speed' might theoretically work in any set direction but any real escape path is clearly limited to a single vector at any one moment and is therefore a velocity. Lucien86 (talk) 06:15, 15 August 2012 (UTC)

In real life it is a velocity, if you were to move at escape speed straight towards the surface of a planet, you would not escape. However mathematically it is a speed and not a velocity because 'escape speed' is just talking about the force of gravity, while hitting into the ground involves the electromagnetic force. So if you were to ignore all forces other than gravity, no matter what direction you move at escape speed, you will still escape. 150.104.193.122 (talk) 15:34, 7 January 2013 (UTC)

No, in real life it really is a speed, since it's derived from the energy equation, so travelling in any direction with the escape velocity will allow you to escape. If, hypothetically, there were a hole in the planet you're pointing at that you could pass through, you would still escape once you came out the other side because your total energy would be the same. Obviously this is ignoring all non-conservative effects (like atmospheric drag), but it really is a speed in all senses of the word, and the use of the word "velocity" is just by tradition. siafu (talk) 17:14, 7 January 2013 (UTC)

That's pretty much what I was saying, I was just explaining to all the people that say it's a velocity why it's not. — Preceding unsigned comment added by 24.136.39.217 (talk) 20:34, 7 January 2013 (UTC)

Name change

I suggest that the name of this page be changed to 'Escape speed'. As is disscussed above, escape speed is a speed and not a velocity. KingSupernova (talk) 15:40, 9 January 2013 (UTC)

While this is true, it's also true that the term is commonly referred to as "escape velocity" despite being a speed; for example, David Vallado's Fundamentals of Astrodynamics, probably the best-known and most popular textbook in the field, uses the term "escape velocity", as do the vast majority of sources. Per WP:COMMONNAME, policy is to use the common name for a thing, even if that name is less perfect than alternate, less common names. siafu (talk) 16:23, 9 January 2013 (UTC)

Removal of Misconception Section

This section has multiple issues. First, there's no source verifying this misconception even exists (I've never heard of it). Second and more seriously, the section is wrong. An object in orbit does need to reach escape velocity to "escape" orbit. While any additional increment in speed will cause it to leave its current orbit, if the velocity isn't great enough, it will simply assume a different orbit. Fell Gleaming^(talk) 01:27, 10 May 2010 (UTC)

LOL. So you're saying that if you have a vehicle doing 1m/s in orbit around the sun really high up in the Kuiper belt, that it needs solar surface escape velocity (618km/s) in order to escape from the Sun's gravity???- Wolfkeeper 01:44, 10 May 2010 (UTC)

It needs the full amount of energy as defined by (escape velocity KE) - (current KE), yes. I realize the original text is trying to state that, but it does so in an obfuscatory, confusing manner that is essentially incorrect as written. Also, in practical terms, one cannot escape earth's gravity at "any speed" ... the bare minimum of achieving NEO is required. (without invoking beanstalk-like methods). Furthermore, your reinsertion hasn't addressed the second point, which is that there is no source citation that such a misconception even exists.

Sorry, but you keep proving that the section is right about it being a misconception, by insisting that it's wrong!- Wolfkeeper 02:34, 10 May 2010 (UTC)

No, you've simply misread what I wrote. Escape KE - current KE = additional KE. Or, if you prefer, Current + Additional KE = Escape KE. Just as I said. Do you have a source that verifies this 'misconception' exists? And FYI, NEO and LEO are interchangeable terms...or were, at least, until asteroid mapping projects started preempting the NEO acronym. Fell Gleaming^(talk) 02:58, 10 May 2010 (UTC)

Fell Gleaming is incorrect about the energies. An object in a high orbit does not need the same kinetic energy to escape as an object in a low orbit. It needs the same total energy. So for example, let's call GM/R the SEKE ("surface escape kinetic energy"). An object in a circular orbit at a distance of n times the planet's radius has a potential energy of −SEKE/n and a kinetic energy of SEKE/(2n). It needs to add SEKE/(2n) of energy in order to escape. This is not equal to SEKE minus current kinetic energy (unless n=1).

But I agree with him that the section was not clear and I have rewritten it a bit.Eric Kvaalen (talk) 09:56, 12 February 2013 (UTC)

Good job. It has become much better now, but let's find some good source(s) for this. Otherwise this section will remain unstable. I have tagged the section. - DVdm (talk) 15:17, 12 February 2013 (UTC)

First, I think you mean LEO, not NEO, but you don't need to achieve LEO velocity to escape either; a rocket with enough stages can escape arbitrarily slowly; it's just horribly inefficient, but you can do it. There's absolutely no minimum speed to escape, you can leave the planet at 1 mile per hour, eventually the escape velocity comes down to 1 mph, and then you can turn the engine off. There's a minimum speed you need so you can escape with the engines *off* though, which depends on position in space (*local* escape velocity).- Wolfkeeper 02:34, 10 May 2010 (UTC)

Basically, an object needs sufficient total energy. The point is that an object high up in the Kuiper belt would have nearly enough (potential) energy already to escape, and it then needs very little kinetic energy to do so.- Wolfkeeper 02:34, 10 May 2010 (UTC)

If you want the section left in, and can find a source verifying the misconception exists, I'll be happy to rewrite it so its clear. Fell Gleaming^(talk) 02:16, 10 May 2010 (UTC)

FWIW, maybe you can do a very little something with this source (under the header The Great Escape). It is of course merely a letter by a certain Paul A. Delaney, Md (!) to some popular magazine, and a reply by Stuart F. Brown. DVdm (talk) 08:43, 10 May 2010 (UTC)

Misconception

The Misconception section currently starts with the following statement: "Contrary to what is sometimes asserted, a powered vehicle, such as a rocket, does not have to attain the escape velocity in order to leave orbit and escape to outer space." Per discussion previously on this talk page, this statement is not true. Per the definition of escape velocity, the speed required for escape to infinity drops off with distance; if an object travels away from the central body at constant body, escape velocity will drop until it is equal to the object's velocity. If the object does not reach this point (i.e., if it stops adding energy), it will not escape. What might be a true statement is that it's not necessary to achieve any particular escape velocity (i.e., escape velocity for any particular r) to escape the gravity well, but I rather doubt that that's a common misconception. siafu (talk) 01:14, 14 March 2013 (UTC)

Also, this statement is a bit misleading: "The gain in energy is equal to the speed (in a non-rotating coordinate system centred on the planet) times the momentum gain, and since the momentum gain depends only on the mass of fuel ejected (times the exhaust speed relative to the rocket), it is best to fire the engine when the speed is high. (See Oberth effect.) So to escape the earth, for example, the fuel use is minimized if the rocket first attains low Earth orbit as quickly as possible and then (perhaps later) executes one or more burns, always at the perigee of whatever orbit it is in at that stage, until it acquires enough energy to escape." The mention of low Earth orbit is a bit weird-- obviously you want to reach LEO as quickly as possible executing further burns, but for a number of reasons that much more important than the Oberth effect (like getting above the atmosphere); the Oberth effect is only really invokable in the reasoning for executing an escape burn at perigee rather than elsewhere in the orbit. I suggest rewording this as: "So to escape the earth, for example, the fuel use is minimized if the rocket executes one or more burns, always at the perigee of whatever orbit it is in at that stage, until it acquires enough energy to escape." I'm not against removing the text altogether, though, as it's starting to bear less relevance to the topic of escape velocity when pared down. siafu (talk) 01:24, 14 March 2013 (UTC)

Sources, sources, sources... - DVdm (talk) 06:55, 14 March 2013 (UTC)

The section has none. Maybe it should just be removed. siafu (talk) 16:05, 14 March 2013 (UTC)

No problem for me. - DVdm (talk) 16:54, 14 March 2013 (UTC)

Done. Also, were you asking me to provide sources for challenging the veracity of unsourced statements before? That doesn't make sense... siafu (talk) 02:39, 15 March 2013 (UTC)

Nono... I was just asking to provide sources for your suggested rewording, of course. Otherwise this would never end. Cheers and thanks. - DVdm (talk) 12:03, 15 March 2013 (UTC)

launch pad and Earth

The article says "For a mass equal to a Saturn V rocket, the escape velocity relative to the launch pad is 253.5 am/s (8 nanometers per year) faster than the escape velocity relative to the mutual center of mass. When the mass reaches the Andromeda galaxy the earth will have recoiled 500 m." This is a very odd statement I think because it initially talks of the the rocket in relation to the launch pad and then at the end it brings in the earth. So is the statement concerned with the reaction of the earth or the launch pad to the rocket?194.176.105.153 (talk) 15:45, 10 October 2013 (UTC)

Since the launchpad is (presumably) attached to the Earth, the two are equivalent. siafu (talk) 20:16, 10 October 2013 (UTC)

The above may be correct but I think it needs rewriting so that it is clear. I think the reference to the launch pad is an indication that the launch is from the surface of the earth which has a lower escape velocity than the mutual center of orbit of the earth and the rocket ready for launch. I think the point is then confused by the recoil which is another issue. I am currently finding this difficult to describe and write because the original statement has many confusing references to different objects and so it should be simplified. 194.176.105.153 (talk) 09:45, 11 October 2013 (UTC)

Deriving escape velocity using calculus should be dropped.

This section seems superfluous and overly complicated. I suggest that it is cut from the article.

The method for deriving the escape velocity is discussed sufficently in earlier sections where it states the escape velocity is derived from the kinetic energy at the surface being equal to the potential energy difference from the surface to infinity. This gives the formula

$v_{e}={\sqrt {\frac {2GM}{r}}}$

From the definition of g

$g={\frac {GM}{r^{2}}}$

you get the formula in terms of g and r only.

$v_{e}={\sqrt {2gr}}$

This is basic maths and doesn't require it's own section of derivation with a complicated argument. Similary for the rest of this section.

Neilljones (talk) 02:00, 13 March 2012 (UTC)

I agree. The energy deriv .ation is simpler and better because it shows that escape velocity is independent of initial direction or trajectory. The "Deriving escape velocity using calculus" section adds nothing to the article and should be removed. Gandalf61 (talk) 09:25, 13 March 2012 (UTC)

Agreed. Worse than not being useful, the section is also too far removed from the overarching "assume object moving away radially unless stated otherwise" statement at the beginning of the article. The statement being necessary at least in the second part of the article. This produces a section of derivations where important assumptions are not made clear. The section may be confusing, or worse wrong for someone preparing say a presentation. Zogwarg (talk) 05:53, 16 October 2013 (UTC)

Wrong hypothesis

There are a bunch of x-rays coming out of back holes. So the black holes escape gravity must be less than 299,792 km/s. Why don't you guys just learn the empirics first, and then the (often wrong) theories? --178.197.236.131 (talk) 11:55, 11 September 2013 (UTC)

The X-rays don't come out of the black holes. They are generated outside the event horizon by infalling charged particles. For further questions you better go the wp:reference desk/science. Here we discuss the article, not the content — see wp:talk page guidelines. Good luck. - DVdm (talk) 12:01, 11 September 2013 (UTC)

Told ya to learn, not to critise: http://en.wikipedia.org/wiki/Polar_jet --178.197.236.131 (talk) 12:03, 11 September 2013 (UTC)

DVdm is correct, and the article you have linked corroborates that. siafu (talk) 18:14, 11 September 2013 (UTC)

Oh yeah, let's quote it: "List of unsolved problems in physics - Why do the discs surrounding certain objects, such as the centersofactive galaxies, emit radiation jets along their polar axes?" But your answer was funny indeed, you just made my day. :D By the way DVdm just said another hypothesis, because we don't have any empirical data from where the jets are coming...they could also come directly out of the black holes core, so you may call it rather "drainage" than "hole". --178.197.224.215 (talk) 13:26, 22 December 2013 (UTC)

Fallacy?

Isn't this whole concept a bit...cocked up? The reach of gravity is infinite, isn't it? It just gets incredibly weak? If there were only two massive bodies in the universe (and no motive forces other than gravity), they would eventually collide, no matter how far apart they started. There is no "escape". There are simply greater forces and more prevalent gravity wells that counter gravity between distant masses. Applejuicefool (talk) 01:22, 2 September 2013 (UTC)

Perhaps a question for our wp:reference desk/science. This is where we discuss the article, not the subject — see wp:talk page guidelines. Good luck. - DVdm (talk) 07:24, 2 September 2013 (UTC)

If the kinetic energy of an object is greater than or equal to the gravitational potential energy, i.e. it has attained escape velocity, then no matter how long you wait the object has escaped and will keep going forever. In your specific (simplified) case, it is also possible that the two objects could never meet but orbit each other indefinitely. — Reatlas (talk) 06:30, 3 September 2013 (UTC)

It's difficult to understand why this proposition is wrong without a good understanding of calculus. For the same reason that Achilles will catch up with the turtle, there is indeed an actual limit in terms of speed away from each other that massive bodies will never be able to overcome. As they move away from each other, gravity will slow them down, but the force of gravity will also be getting weaker at the same time. siafu (talk) 14:51, 3 September 2013 (UTC)

I was taught in school that escape velocity is determined by the kinetic energy needed to lift an object from the surface of a body to "infinity". In a universe where gravity is an inverse-square force, this energy is finite. When gravity is an inverse-with-respect-to-distance force, as in the Planiverse, the energy is infinite. But that doesn't mean one can't travel from one planet to another.

This is a simple explanation (though, as pointed out, it helps to understand the integral calculus). Why the article doesn't start from such a simple explanation, I don't understand. This is rather a Rube Goldberg article -- explaining something simple in a complicated way. WilliamSommerwerck (talk) 18:08, 22 December 2013 (UTC)

Multiple sources

I find this section confusing. Let me give an example of why I don't understand this. Let's pretend that the earth is farther away from the sun than it really is, so that the escape velocity from the sun at this distance is 11.2 km/s, just as for the earth. So then we get that the escape velocity from sun/earth, with earth orbiting at this distance, would be sqrt(11.2^2 + 11.2^2) = 15.8 km/s. Now earth's (circular) orbital speed at this distance will be .7071*11.2 = 7.9 km/s, so we predict that we need to go at a speed of 15.8 - 7.9 = 7.9 km/s (relative to earth) in the direction of earth's orbit. But THIS IS LESS THAN EARTH'S ESCAPE VELOCITY! So, relative to the earth, the speed we need to start out with to go out to infinity is now LESS than it would be if the sun were not there?? Kier07 07:48, 4 September 2006 (UTC)

I didn't verify your number but I'll assuming they are correct. Then yes the velocity needed to escape Earth and Sun in your example is going to be less then the escape velocity of Earth alone. What the section doesn't say is, the object is allowed to "fall through" Earth. So your object starts up moving away from Earth at 7.9 km/s, eventually due to Earth's gravity, it will turn around and starting moving toward Earth. If the path doesn't collide with Earth, it will escape. If it's path collides with Earth, it's assumed to be able to fall throught it. The actualy path the object takes to escape is a swirl. It may swirl around Earth, or Sun depending on the initial conditions. Please also remember Earth is also moving so the object would not simply oscillate back and forth through Earth's center. --NYC 21:14, 14 March 2007 (UTC)

That is a good point, Kier07. I added some explanation why the original value is not enough. The newer version [3] is more plausible, but a source and/or an explanation is still needed.--Patrick (talk) 21:25, 31 January 2010 (UTC)

The current formula is also on http://www.physicsforums.com/showthread.php?t=16708, but the author hellfire says he/she is not sure.--Patrick (talk) 08:02, 1 February 2010 (UTC)

Firstly, what is this rubbish about the article needing 'multiple sources'? Maths doesn't need ANY sources, only logical correctness. Any Wikipedia article about a maths concept merely requires enough maths logic for the claims to be tested. Secondly, the article needs to begin with the CLEAR statement that 'escape velocity' is a mass-independent statement of the energy required for an object to escape a gravitational well. Escape velocity is a very clever statement of ENERGY requirements, not speed. In fact, an object cannot be given an instantaneous speed, so the speed referred to in an 'escape velocity' isn't even a special case, and the term confuses most people into thinking a rocket must reach at last this speed to leave the Earth. Of course, real rockets are based on the principle of diminished mass as the fuel providing thrust burns up. Since the term 'escape velocity' exists for practical reasons, shouldn't the article address the 'applied' aspects of the term as well? 77.98.38.164 (talk) 16:31, 17 April 2013 (UTC)

Re "Maths doesn't need ANY sources, only logical correctness", have a look at our rubbish policy in wp:NOR. - DVdm (talk) 17:35, 17 April 2013 (UTC)

The term Multiple Sources means Multiple Gravitational Sources. The question is: What radial velocity would a body launched from Earth need to escape both the Sun's and the Earth's gravitational fields. I haven't checked the numbers but I assume that the escape velocity for the Sun is that computed at the Earth's orbit. Virgil H. Soule (talk) 07:28, 25 January 2014 (UTC)

Escape velocities with respect to the sun

According to my calculation, with the below formula

$v_{e}={\sqrt {\frac {2GM}{r}}}$

I got these values:

at Mercury 47.9 km/s

at Venus 35.0 km/s

at Earth 29.8 km/s

at Mars 24.1 km/s

at Jupiter 13.1 km/s

at Saturn 9.6 km/s

at Uranus 6.8 km/s

at Neptune 5.4 km/s

It is not the same as in the table in the article. What is correct? --BIL (talk) 14:11, 18 February 2010 (UTC)

BIL, all your values are out by a factor of ${\sqrt {2}}$. You just missed the 2 in your calculations. Cosmogoblin (talk) 21:14, 1 November 2010 (UTC)

Point of clarification: The escape velocities given in the article are Surface Escape Velocities for each of the planets in the list. The velocities listed above presumably were computed at the mean orbital distance of each planet in the list. The two are completely different. Virgil H. Soule (talk) 07:28, 25 January 2014 (UTC)

Correction

I removed the following sentence from the lead:

A rocket moving out of a gravity well does not actually need to attain escape velocity to do so, but could achieve the same result at walking speed with a suitable mode of propulsion and sufficient fuel.

This is not true. In order to escape the gravitational pull of a body, a particle (or point-sized elephant) will at some point need to exceed the escape velocity somewhere along the trajectory. As the distance increase (r goes to infinity) the velocity will decress (v goes to zero); that is, you don't need to achieve the escape velocity for the orbital radius at which you started, but you will eventually cross the escape velocity or else fall back to the gravitational body, in some sort of orbit, once the opposing force (thrust) is removed. This restriction is only for constant values of escape velocity, and therefore only useful for ballistic trajectories, but it's not true to say that it does not apply to continuous (or at least non-instantaneous) thrust trajectories as well. siafu (talk) 00:07, 9 October 2012 (UTC)

I have undone that edit. Escape velocity is an initial velocity, allowing escape without further propulsion. The statement was obviously correct. In order to avoid this happening again, it would be nice to have a reference for it, but, as it is so trivially obvious, a ref may be hard to find. - DVdm (talk) 08:39, 9 October 2012 (UTC)

The statement is still incorrect; in order to escape, this velocity will be attained, otherwise escape simply won't happen. Escape velocity is also the velocity at which a continuous-propulsion craft can stop thrusting and coast to infinity, and if it does not ever cross this velocity threshold, it will remain in an orbit around the central body. I think you are confusing the situations in which escape velocity is a meaningful and useful quantity, with what is strictly speaking true. You can call it an initial velocity now, but there's no precondition on the equation derivation that says that this is required as calculating an escape velocity can be done for any value of r, whether the particle is "at rest" (wrt the central body) or moving at high relative speed. You'll have a hard time finding a reference for something that is incorrect, I'm afraid. siafu (talk) 14:53, 9 October 2012 (UTC)

Re "in order to escape, this velocity will be attained": It doesn't, because "this velocity" changes with location. As soon as you go a bit further out, the escape velocity gets less. When you change your location, "this velocity" is irrelevant and no longer exists. When you have unlimited propulsion, the limiting escape velocity is zero. And of course what you call "a continuous-propulsion craft" is essentially a propulsionless craft when it does "stop thrusting".

Input from others? - DVdm (talk) 15:34, 9 October 2012 (UTC)

Exactly; this is what I explained in the first place. Escape velocity is dependent on location, and this is exactly why the statement as written is incorrect-- "walking speed" will eventually be the escape velocity as you get far enough away. If you stop applying thrust just short of the point where your velocity exceeds the local escape velocity, you will not escape. I'm not advocating making the article more confusing with a complicated explanation of this, but it should not include assertions that are incorrect. siafu (talk) 15:47, 9 October 2012 (UTC)

I still think the statement is correct. If "could achieve the same result" refers to "could escape to infinity", then for all practical purposes the concept "escape velocity" is useless and irrelevant. With propulsion one can escape at any speed, and "walking" stands for "any" here. I see no problem with the statement, but obviously I would support replacing "walking" with "any" in the statement. - DVdm (talk) 16:00, 9 October 2012 (UTC)

The problem is that this statement is based on the choice of starting point to be a priveleged one. Starting from a very high orbit, the escape velocity is very low, and could even be walking speed. Starting from the surface of the Earth, it's very high. It's not providing any useful information to point out that you could do it ballistically or not. The use of "could escape to infinity" comes from the mathematical derivation itself, as the article (and any source describing escape velocity) says:

At its final state, it will be an infinite distance away from the planet, and its speed will be negligibly small and assumed to be 0.

I do not disagree that escape velocity is only meaningful when considering ballistic trajectories, since in a non-ballistic trajectory one need be safe in the knowledge that at some point your velocity will happen to equal the escape velocity. This is different from saying that it doesn't apply, because nothing in the mathematical assumptions involved in the escape velocity equation is violated in a non-ballistic case-- at least, not anything that isn't already untrue in reality for the ballistic trajectory. siafu (talk) 16:09, 9 October 2012 (UTC)

Yes, you are correct where you say that starting from a very high orbit, the escape velocity is very low, and could even be walking speed. So the "walking" should indeed be replaced with "any". No problem. - DVdm (talk) 16:26, 9 October 2012 (UTC)

Strictly speaking, the escape velocity for any body is zero at infinity. Virgil H. Soule (talk) 07:28, 25 January 2014 (UTC)

Definitions

Escape velocity is vector in the sense that it is always oriented away from the center of mass of a body in space. Gravitational potential energy is always oriented toward the center of mass and kinetic energy must be directed away to oppose it. Escape velocity is only of academic interest in defining the characteristics of a body in space. It has no real use in orbital mechanics. The escape velocities listed in the table are surface escape velocities for the bodies listed. In general, the Sun escape velocity is the only one that matters since vehicles launched on Earth-escape trajectories will typically enter an orbit around the Sun. A vehicle launched on a Mars tranfer orbit, for example, is in orbit around the sun. It should be noted that escape velocity can be defined at any radial distance from a body. The event horizon is effectively the surface of a black hole since anything interior to that is undefined.

Discussion of orbits or escape orbits should be separated from that of escape velocity. An escape orbit is a hyperbolic orbit with eccentricity greater than one. A parabolic orbit is unstable in that it may have eccentricity equal to one at some point but perturbations could cause it to become elliptical and closed at some other point. A body passing Jupiter, for example, can receive a gravitational assist that will insert it into a hyperbolic escape trajectory that would take it out of the solar system. A tangential launch or velocity-change maneuver could inject a vehicle into an escape orbit but usually is used to inject it into an elliptical orbit of some sort. The Apollo missions were launched on elliptical free-return trajectories. If a lunar injection maneuver wasn't performed on the Moon's backside, the vehicle would simply have looped around and returned to the Earth. To be captured by the Moon, the vehicle's velocity vector would have to be reduced in magnitude to the required Lunar orbital velocity.

The location of a launch site doesn't have much to do with escape velocity. An equatorial launch site is most desirable because it eliminates fuel that would be needed for plane-change maneuvers required to reach an equatorial orbit. Virgil H. Soule (talk) 16:40, 17 July 2013 (UTC)

We shouldn't get too far off topic, but many of the statements above are incorrect. Escape velocity is derived from conservation of energy, and is thus just a speed, and not a vector in any sense of the word. It is not at all true that escape velocity need be directed in any particular direction-- the assumption behind its derivation is that all forces acting in the system are conservative, so as long as nothing is done to violate that assumption (e.g. adding air drag or physically contacting the central body), pointing the velocity in any direction will result in orbital escape. Moreover, energy is never "directed" as it is also just a scalar. Think on it this way: pointing the velocity vector in the direction of the gravity gradient (i.e. towards the central body) will cause the orbiter to convert potential energy into kinetic energy as it gets closer, and then the reverse, converting kinetic into potential as it moves away, but the total energy is constant.

The definition of a hyperbolic orbit is an orbit where e > 1, so "An escape orbit is a hyperbolic orbit with eccentricity greater than one" is completely redundant and irrelevant. Parabolic orbits are unstable, yes, but this is a more technical statement in the domain of stability theory because small pertubations in a parabolic orbit will tend to push the system away from e = 1 rather than revert towards it; again, completely irrelevant to this page. Finally, an equatorial launch site makes a big difference, and not just because of plane-changing maneuvers. The speed of an object on the surface of the Earth relative to the center of of mass of the Earth is much greater than the speed of an object sitting on the pole; this additional speed that is provided "for free" is reflected in the smaller amount of fuel required to achieve escape velocity from the equator than from the poles. siafu (talk) 15:58, 18 July 2013 (UTC)

You didn't read what I wrote! Gravitational acceleration is a vector directed toward the center of mass of a body, always. To escape a body's gravity, another body must be accelerated radially away from the parent body and attain a certain radial velocity. This velocity is called Escape Velocity. The direction requirement makes escape velocity a vector. Escape Velocity is a purely hypothetical concept. This whole discussion has gotten all muddled up with talk of orbits and space launches and all that, which have nothing to do with escape velocity. The article itself has suffered as a result of all these misconceptions. It's really a very straight-forward subject. Virgil H. Soule (talk) 07:28, 25 January 2014 (UTC)

Vector or scalar

Velocity, by definition, is a vector. I've gone to some length to point out why escape velocity is also a vector. Please cite a reference when changing this. Thx Androstachys (talk) 13:54, 21 March 2011 (UTC)

You're the one claiming that the existing derivation (which is independent of direction) is incomplete and you're not citing any references.Rememberway (talk) 14:39, 21 March 2011 (UTC)

It's an energy conservation thing- once the vehicle has enough specific energy then it's leaving the gravity well- period. Energy doesn't care about direction.Rememberway (talk) 14:39, 21 March 2011 (UTC)

Androstachys, if you look at the "derivation" section of the article, you will see a mathematical proof that it's actually a scalar. Specifically, it's just a matter of whether the kinetic energy is at least as big as the potential energy at infinite distance. The whole thing follows from the fact that the sum of kinetic energy and potential energy remains constant. Kinetic energy is a scalar and depends in speed but not on direction. That proves that what matters here is only a scalar, not a vector. Michael Hardy (talk) 17:58, 21 March 2011 (UTC)

Unless your trajectory intersects the body from which you are escaping, or one of its moons. :) --agr (talk) 20:35, 21 March 2011 (UTC)

After almost 3 years this fallacy of regarding escape velocity as a misnomer persists - this does not place Wikipedia in a favourable light and must certainly cause sniggers of disbelief in the world of physics - please consult a professional astrophysicist and get this tragic mess cleaned up....Paul venter (talk) 20:36, 10 December 2014 (UTC)

Orbital Mechanics

"For an actual escape orbit a spacecraft is first placed in low Earth orbit (160–2,000 km) and then accelerated to the escape velocity at that altitude, which is a little less — about 10.9 km/s. The required change in speed, however, is far less because from a low Earth orbit the spacecraft already has a speed of approximately 8 km/s (28,800 km/h)." I added this.

However, an object in orbit is going the wrong direction, it's effective speed relative to moving away from the earth is zero. It would need to accelerate from zero to 10.9km/s perpendicular to the surface of the earth which would require a large amount of thrust. Capsela (talk) 14:08, 11 March 2016 (UTC)

References

The direction of travel is irrelevant in discussion of escape velocity. This is only an issue in this case if you're talking about speed relative to the surface of the Earth vs. speed relative to the center of the Earth. siafu (talk) 23:57, 11 March 2016 (UTC)

Relativistic Velocities

This page uses Newton's equation for kinetic energy: K = ½mv². This is OK for v << c. But what about when v is close to c? Shouldn't the Relativistic kinetic energy be used instead? Shawn H Corey (talk) 14:04, 27 March 2016 (UTC)

Yes, good point. See page 2-22 of http://www.eftaylor.com/pub/chapter2.pdf. The result is the same. I already added a little remark about this: [4]. - DVdm (talk) 14:12, 27 March 2016 (UTC)

You do realize this (if true) would ninja Event horizon and Black hole? Shawn H Corey (talk) 14:47, 27 March 2016 (UTC)

Yep, I made a slight tweak: [5]. - DVdm (talk) 14:53, 27 March 2016 (UTC)

Potential Energy

The use of the term Gravitational Potential Energy HERE is exactly opposite that used in the article of that name! Why in the world would you DO that??? Escape velocity of a small object in the gravitational field of a larger object is the velocity at which the small object's kinetic energy is sufficient to (reversibly, ideally) remove that object to an infinite distance from the larger object. Grav. P.E. is defined as the work available from an object at infinite distance from a larger object as it falls towards the larger object (ideally, reversibly), as such there should be no confusion. As a small object leaves a larger object, work must be done, the smaller object's kinetic energy of motion is converted to potential energy. At its escape velocity, there is just enough K.E. to deliver an object to a distance of ∞, leaving it motionless (i.e. without any K.E.). Escape velocity ignores air resistance and interactions with any other object.71.29.173.173 (talk) 16:43, 14 July 2016 (UTC)

Time of attaining escape velocity

The time of reaching escape velocity is finite, therefore there is no need that time tend to infinity.--188.26.22.131 (talk) 14:20, 17 June 2014 (UTC)

Escape velocity means that you integrate such that r = infinity can be reached with ultimate zero velocity. To get r(t) = infinity, you must integrate to t = infinity. The text was correct. I have reverted again. - DVdm (talk) 14:41, 17 June 2014 (UTC)

... but made an additional tweak. - DVdm (talk) 14:48, 17 June 2014 (UTC)

I think that something is dubious in this demonstration, as can be seen by contradiction. If the time required to escape is considered infinite, then the escape would never be completed. It is an asymptotic behaviour that is used in r tending to infinity, a mathematical condition to assure that r the distance from the central body can be as large as one wants. This means that in practice r is a finite sufficiently large value and it is reached in finite time.

Another aspect is that escape velocity should at least equal or be larger than orbital speed of an orbiting body, this increase involving a delta v budget. The limits of integration in speed should be therefore orbital speed v_o to escape velocity v_e and thus the final speed is not zero.--193.231.19.53 (talk) 12:03, 19 June 2014 (UTC)

From $\int _{v_{0}}^{v(t)}v\,dv=-\int _{r_{0}}^{r(t)}{\frac {GM}{r^{2}}}\,dr\,$ and

${\frac {v(t)^{2}}{2}}-{\frac {v_{0}^{2}}{2}}={\frac {GM}{r(t)}}-{\frac {GM}{r_{0}}}.\,$

an infinite time does not necessarily follow.--193.231.19.53 (talk) 12:17, 19 June 2014 (UTC)

Re "If the time required to escape is considered infinite, then the escape would never be completed": the idea of escape velocity is not "to complete the escape", but to be able to reach infinity before coming to rest. As far as I know, infinity is a place that cannot be reached in a finite time. - DVdm (talk) 12:35, 19 June 2014 (UTC)

References

I have used this source to replace the (unsourced) derivations in the article with a much simpler one. If we absolutely need more "exotic" derivations, let's first find good inline sources and discuss whether the article needs them. - DVdm (talk) 13:28, 19 June 2014 (UTC)

The new content of the section is much better. A numerical example would be useful to see what is the time required, for instance, for a satellite to escape from Earth's orbit? If we apply the previous example to the Moon, what thrust by rockets and delta-v budget would be necessary to escape orbiting Earth? It is already known that the orbit of the Moon gets larger and larger in time, even if extremely slowly.--193.231.19.53 (talk) 08:56, 24 June 2014 (UTC)

The time discussed here can be compared with the transfer time from Hohmann transfer orbit and bi-elliptic transfer.--193.231.19.53 (talk) 09:20, 24 June 2014 (UTC)

The "time required for a satellite to escape from Earth's orbit" is problematic. One instantaneous boost to the escape velocity is sufficient to escape from the orbit, but escaping from the gravitational influence would take an infinite time. - DVdm (talk) 09:43, 24 June 2014 (UTC)

Interesting aspects I notice here. What is the equivalent of one instantaneous boost to the escape velocity from the point of view of acceleration? Where does the gravitational influence of an astronomical body ends? Could the orbit of a satellite get progressively larger by each revolution before it reaching a zone where the gravitational influence of the larger body tends to zero? (For instance, what is the escape velocity of the Moon and how can it be reached, say, by instantaneous bust?) --82.137.9.111 (talk) 13:15, 28 August 2016 (UTC)

An object can never escape the gravitational influence of any other object in the (observable) Universe. However, we do talk about "spheres of influence" - the approximate region where an object's gravity is dominant. For example, the Earth's sphere of influence is about 1.5 million km, meaning that beyond that distance, the Sun's gravity is more important. This is only an approximation, but a very useful one, and actually used by space agencies in the initial planning of the orbits of real spacecraft.

As to your query about satellite orbits getting larger - the size of the orbit is determined by KE+PE, so the orbit won't get larger without some other source of energy to convert into additional KE+PE. With rockets, additional energy can be provided by chemical reactions. The Moon's orbit does actually increase, it recedes from the Earth by about 38mm per year; the energy source in this case is the Earth's rotational energy, so as the Moon drifts away, the Earth rotates more slowly (the length of the day increases). Cosmogoblin (talk) 11:21, 3 September 2016 (UTC)

Velocity is correct

From the formula given, and from the description of the reverse of the escape process, it seems clear that the term velocity is correct in that in the equation concerned it is a vector.

In very general terms, calculating the speed required for an escape posits at the least that there is a direction for it to take place in that provides a possibility of an escape taking place. If, for instance, the escaping object fires straight down, towards the center of the mass there is no such possibility. Although a common sense not a mathematical issue this illustrates the nonsense of the debate.

More specifically, the formula centres on the direction of escape being along a line passing through the centre of mass. If there is any deviation from this line then the formula will not hold, as after any given time the distance travelled from the centre of mass will become too little for the kinetic energy remaining in the escaping object to drive its escape.

I've started a new topic because I've deleted the paragraph. It seems to be being quoted all over the internet as an authority!! The arguments in the section Vector or scalar above by Michael Hardy do not seem pertinent. The formula given is uncontested, whether in the introduction or the derivation of it, and it contains only two variables: the mass of the object being escaped and the distance of the escaping object from its centre of mass. It seem obvious from the second of these that the resulting value for velocity is just that and not speed, for the reasons given. If it is considered scalar then it will only be correct at the instant considered and at none subsequently. That would generate an absurdity.

LookingGlass (talk) 10:58, 23 January 2016 (UTC)

I agree with the removal of that unsourced statement [6]. If someone feels strong about re-inserting it, they will surely find a few strong reliable sources for it. - DVdm (talk) 11:03, 23 January 2016 (UTC)

The above description of escape velocity as a vector is incorrect. The concept is derived from conservation of energy, which relies on the Euclidean norm of velocity, aka speed. While there are practical considerations in answering the question of whether or not a body having achieved escaped velocity will, in fact, actually escape the system, these arise from violations of the assumptions used to derive escape velocity. Specifically, the derivation assumes no non-conservative forces are present, and this is violated by non-elastic collisions and experiencing atmospheric drag. In the example cited, firing straight down towards the center of mass, the only reason escape would not happen because of a collision. If the heavier body were a point mass, and the orbiting body donut-shaped or somesuch, it would indeed be possible for a trajectory aimed directly "downward" to result in escape since the two bodies could pass each other by without colliding. siafu (talk) 11:32, 13 March 2016 (UTC)

Siafu is correct. Further, by firing toward the centre of mass, you have further to go and the escape "speed" increases; but the increase in required speed is exactly equal to the additional speed gained as you fall toward the centre. See gravity train for an interesting discussion on this. Cosmogoblin (talk) 11:26, 3 September 2016 (UTC)

Two suggestions for lead

1. The lead says

Given escape velocity perpendicular to a massive body, the object will move away from the body, slowing forever and approaching but never reaching zero speed.

But given the above discussion over the years on this talk page, perpendicularity or its absence is irrelevant. The perpendicularity assumption appears to be there to avoid the problem of colliding with Earth, but stating it like that leaves the false impression that the concept of escape velocity depends on perpendicularity. I would suggest that the sentence be replaced by

Given escape velocity at a direction pointing away from the ground of a massive body, the object will move away from the body, slowing forever and approaching but never reaching zero speed.

2. The opening sentence says

In physics, escape velocity is the minimum speed needed for an object to escape from the gravitational attraction of a massive body, without the aid of thrust, or suffering the resistance from friction.

But as has been mentioned on this talk page, you never "escape from the gravitational attraction" of anything, since gravity reaches out to infinity. I suggest this sentence be replaced by

In physics, escape velocity is the minimum speed needed for an object to escape from a massive body, in the sense of becoming neither on the surface nor in closed orbit of any radius no matter how great, without the aid of thrust, or suffering the resistance from friction.

Loraof (talk) 22:49, 1 January 2017 (UTC)

Interesting argument in (2) Loraof. I disagree in only a very pedantic way -- escape velocity is sufficient to escape from the gravitational influence of a body, since escape velocity is sufficient to reach an infinite distance.

I would content that the first sentence, prior to your edit, was simpler and no less correct; your contribution is useful, but could easily confuse a layperson fresh to the subject. I've made the first sentence a single paragraph, and merged your phrase into the second paragraph, as I think this provides an easier and more succinct introduction. Cosmogoblin (talk) 21:39, 10 April 2017 (UTC)

"System escape" is ill defined

The quantity "system escape" in the table, symbolized by v_te is confusing. Especially if one wants to know what is the velocity to escape the Sun's attraction from the radius of Earth. I've recently seen people believing it's the famous 11.2km/s which is obviously wrong, but this table doesn't help to understand if in this case it's ~42km/s or 16.2 km/s.

If escaping the Sun at 1AU needs 42 km/s, and the Sun represents 99.7% of the mass of the system, how come escaping all the bodies of the system is much smaller? Are there any undeclared assumptions here, like using gravity assist by the Moon or some other body? Is the velocity of the Earth around the Sun enough to reduce the required speed?

I don't know if it's practical to be explained in the text, but it does look like it could be a nice illustrative example with pedagogical value. — Preceding unsigned comment added by 147.96.22.43 (talk) 20:39, 3 May 2018 (UTC)

There is a reasonably clear explanation above the table in the section headed "Multiple Bodies". In energy terms, a speed less then 11.2 km/s at the Earth's surface will leave a projectile as a satellite of the earth. A speed greater than 11.2 km/s means the projectile has sufficient kinetic energy to escape from the Earth's gravitational influence, but it then becomes a satellite of the Sun unless its speed relative to the Sun is greater than 41.2 km/s. However, in addition to its speed relative to the Earth, the projectile also has the Earth's orbital speed relative to the Sun. Assuming it is launched in the right direction, it only needs an extra 16.6 km/2 on top of the Earth's orbital speed to achieve escape velocity relative to the Sun. Having escaped from the gravitational influence of the Sun, the projectile is still gravitationally bound to the our galaxy - after which calculations become more complex because our galaxy is not a single body, and because the influence of dark matter becomes significant at galactic length scales. Gandalf61 (talk) 15:24, 4 May 2018 (UTC)

Over my head

It escapes me how the first sentence does not already read:

In physics, escape velocity is the minimum speed needed for a [[ballistic object]] to escape from the gravitational influence of a massive body.

What am I missing, here? — MaxEnt 23:51, 17 May 2018 (UTC)

It should read like that. How about you edit the article accordingly? Arctic Gazelle (talk) 00:20, 2 September 2021 (UTC)

Multiple bodies section

It would be nice to get some references in this section so that readers interested in the derivation of this expression, and how the assumptions play into this result, have some leads.

207.38.134.235 (talk) 22:19, 16 January 2021 (UTC)

Yes, that would be nice. And necessary. I have tagged the section for sources. I will remove it per wp:NOR in a month or so. Thanks for having noticed. - DVdm (talk) 22:32, 16 January 2021 (UTC)

A month has gone by. I have removed the unsourced section. - DVdm (talk) 14:45, 16 February 2021 (UTC)

The section should be restored as this formula trivially follows from the previous section, namely the hyperbolic excess speed formula. Moreover, the next section uses the currently deleted formula for the system escape speed column. One can find full derivation from scratch in Italian, Russian, and Ukranian Wikipedias. The formula can also be found in Hendel, A. Z. Solar escape. The only difference is using the escape speed for the second body instead of the orbital speed; however, it is well-known and mentioned in this English article that they are proportional with the coefficient ${\sqrt {2}}$. Anton Lapounov (talk) 19:26, 8 December 2021 (UTC)