Talk:Diffraction grating
| This is the talk page for discussing improvements to the Diffraction grating article. This is not a forum for general discussion of the article's subject. |
Article policies
|
| Find sources: Google (books · news · scholar · free images · WP refs) · FENS · JSTOR · TWL |
| This It is of interest to the following WikiProjects: | ||||||||||||||||||
‹See TfM›
| ||||||||||||||||||
Vinyl diffraction grating
[edit]The jupiterscope is a wibbly vinyl diffraction grating that could be placed on a camera lens There are also candies with diffraction gratings pressed onto them to have vivild pure colors These are of note as the jupiterscope could make greasy glass also become a diffraction grating from the impression The candy reminds us that cheap nanoprinting on carbohydrates is possible
Gratuitous Science Jargon
[edit]The dimension and period of the grooves must be on the order of the wavelength in question.
- Why can't we just say "The size and spacing of the grooves must be the same as the light"? What purpose does explaining something with complicated terms serve?
echelle gratings
- ??? No link, no article, nothing. Only someone who already knows what these echelle gratings are would benefit from this comparison.Allywilson (talk) 16:39, 18 November 2007 (UTC)
A fundamental property of gratings is that the angle of deviation of all but one of the diffracted beams depends on the wavelength of the incident light.
- Lost us with "angle of deviation", "diffracted beams", "incident light". Seems like 2-3 words per sentence need links to their own article.
Therefore, a grating separates an incident polychromatic beam into its constituent wavelength components, i.e., it is dispersive
- "beam"? How is anything being a beam important to the fact that it is light? Is there a single instance in this article where you could not replace the word "beam" with "light"? "Constituent wavelength components" - colors. Just say colors. Then link "colors" to an article that explains how colors work, for those who need a more precise definition.
When groove spacing...
- Groove spacing finally makes an appearance, SIX or SEVEN paragraphs later! This should have been used in the first place. Now look what we have, two terms meaning the same thing, in the same article. Now we have inconsistency in addition to gratuitous jargon.
Booo science club! Hooray understanding! Viva la understandionne!
- "Why can't we just say "The size and spacing of the grooves must be the same as the light"? What purpose does explaining something with complicated terms serve?"
Because it isn't correct. 'Dimension' is easy to understand. 'Period' and 'order' in the context of science are also straightforward, anyone with any interest whatsoever in diffraction gratings will understand these.
- "echelle gratings"
Agreed. I'll put up an article or expansion request.
- "Lost us with "angle of deviation", "diffracted beams", "incident light". Seems like 2-3 words per sentence need links to their own article."
It would take a few minutes of research for any half-intelligent person to get up to speed here. Again, if you're anything to do with science, you should know these.
- ""beam"? How is anything being a beam important to the fact that it is light? Is there a single instance in this article where you could not replace the word "beam" with "light"? "Constituent wavelength components" - colors. Just say colors. Then link "colors" to an article that explains how colors work, for those who need a more precise definition."
Good grief, just do your homework. Nothing in this article is difficult to understand. Sojourner001 22:54, 18 January 2007 (UTC)
Incorrect Diffraction Equation
[edit]According to http://scienceworld.wolfram.com/physics/GratingEquation.html and some supplier's catalogs (www.thorlabs.com) the diffraction equation should be dsin(theta_incident)+dsin(theta_reflected)=m(lambda). There should be no minus sign. I'm not sure how to edit the equations, so I'll trust that someone else will do this. --128.196.213.163 21:59, 30 October 2006 (UTC)Anon
- I think it's just a problem with the sign of the angles. I tried to explain that in the article. -- Pgabolde
Unclear relation in equation
[edit]How are groove period and groove density related? Are they inverses of one another? The article leaves this unclear, but an inverse relation is implied when the units are compared... —The preceding unsigned comment was added by MyOwnLittlWorld (talk • contribs) 16:39, 27 February 2007 (UTC).
- Yes it's just the inverse. I clarified the article. -- Pgabolde
Incorrect Example?
[edit]
I don't think an LCD can cause a diffraction pattern, and am pretty sure if it could it wouldn't look like that. Is the picture instead an example of Newton's rings, caused by the close but imperfect separation between the LCD surface and the protective plastic screen? Atropos235 19:12, 18 February 2007 (UTC)
Agreed. The color pattern in the photograph, is in no way reminiscent of the pattern created by a periodic structure (like the pixels of an lcd in this case.). Also the spacing of the pixels is too large to produce significant diffraction effects with visible light. I would guess what we are seeing has to do with the polarization of light, passing through the polarizer in the LCD screen. Transparent plastics have the property that they can rotate the polarization of light with a degree depending on how much stress is applied to the material; this effect is also wavelength dependent. This could cause different regions to reflect different colors of light. --V. 03:36, 3 March 2007 (UTC)
- Since it's not clear whether the cell phone picture exhibits grating diffraction or not, I removed it for now. It looks like a thin-film effect to me. -- Pgabolde
Having seen similar patterns on the LCD of my own cellphone, I found that after cleaning its surface they disappeared. So, in my case, it does seem to be caused at least in part by a thin-film effect, produced by oil (from either my own body or something I handled) left on the surface by my fingers. I infer, partly from the wave-like images in the top part of the pictured LCD, that the thin-film and polarizer effects may both contribute to what we see.71.163.224.207 (talk) 19:25, 7 April 2016 (UTC) -- SlinkyManatee
- I would agree with that explanation, except the pattern and arrangement of the colors doesn't look to me like either. If I was to guess, I'd say we're looking at the reflection of an apple tree from underneath. Oh, and by the way, it is usually frowned upon to alter other people's comments on a talk page, even if it is to correct spelling and grammar. Zaereth (talk) 19:34, 7 April 2016 (UTC)
LCD screen definitely can make a diffraction. See my posting at
Isaacto (talk) 10:31, 31 January 2017 (UTC)
- I never doubted that they could, but nice photos. I simply doubt that's what this photo is showing. The reasoning is that the color scheme is all wrong. For diffraction I'd expect a smooth flow from one color to the next as the viewing angle changes, and by color I mean all the colors of the rainbow. For thin-film interference, I'd expect not the colors of the rainbow, but browns, turquois-greens, deep blues and magentas (not quite rainbow colors, due to the overlapping of certain wavelengths and not others). Thin-film coats invariable have a sort of metallic luster to them. What I would not expect is deep reds and leaf greens and sky blues all jumbled together. Upon further examination, my guess is still a blurry reflection of a plant, like maybe a rose bush. Zaereth (talk) 01:15, 1 February 2017 (UTC)
I also don't think the original photo is diffraction due to LCD. On the other hand, if LCD is not cited as an example I feel something is lost, since it is the diffraction grating that is available to about everybody, and can be easily measured and checked against the theory. 1.36.38.215 (talk) 13:47, 2 February 2017 (UTC)
- I agree completely, but the best way to do that is in the text. The images should be used carefully, as examples of what the writing is talking about, but they shouldn't be placed about all willy-nilly like a facebook page. They should bear some relevance to thye section where they're placed. The way to fix that problem is to simply write about it (easy part), but that requires going out and finding sources (hard part, in that most of us are just too darn lazy to go get them ourselves). You are most welcome to participate and add something about it. Zaereth (talk) 02:38, 3 February 2017 (UTC)
I've written a section, edit it like hell. I tried to put one of those photos as a demonstration, but couldn't get Wikipedia to be able to verify it as "suitable for Wikipedia Commons". Any hint is appreciated. 1.36.38.215 (talk) 14:29, 3 February 2017 (UTC)
- Awesome. Looks great to me. Now that you've planted a seed you can watch it grow. For photos, I personally find it best to just take my own. That avoids any copyright hassle. When I see something that could use a photo I try to create one that will provide a good demonstration. That's not always easy, though, because light and cameras don't always behave like you want them to. (In example, it took over 200 tries to get this photo of a laser's Gaussian profile, and I don't mean 200 photos, but trying everything I could to eliminate the laser speckle as much as possible.) If your photo is fair quality, adequately and honestly explained, there should be no problem uploading it. Just be sure you know what your photographing and don't try to pass it off a something else. In example, I was careful labeling this photo because it is merely simulating the laser in operation. In actual operation the beams wouldn't show up nearly as well. (That alone took about 30 tries, adjusting camera settings, laser intensity, and the fogginess of the room.) If you have further problems, someone on Wikimedia Commons should be able to assist you. Zaereth (talk) 21:56, 3 February 2017 (UTC)
I've uploaded the photo. I think it is more to do with insufficient information I've given to the image that I can't upload it initially. Thanks for your help! And let me know if you have any comments. Isaacto (talk) 04:46, 4 February 2017 (UTC)
lines-per-inch of a CD or a DVD
[edit]What is the lines-per-inch of a CD or a DVD?-69.87.204.209 21:02, 1 June 2007 (UTC)
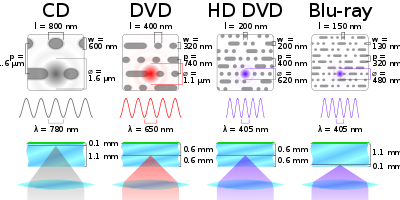
- According to compact disc#Physical details, "The distance between the tracks, the pitch, is 1.6 µm.". (1 track / 1.6 µm =~= 15 876 tracks-per-inch on CD).
- According to Blu-ray#Laser and optics, "This allows a reduction of the pit size from ... for DVD to ... for Blu-ray Disc... of the track pitch from 740 nm to 320 nm." (1 track / 740 nm =~= 33 867 tracks/inch on DVD) (1 track / 320 nm =~= 79 375 tracks/inch on Blu-ray).
- How does this information make this "diffraction grating" article better? --DavidCary (talk) 20:58, 15 October 2016 (UTC)
Intro sentence too hard
[edit]Does anyone feel up to the challenge of writing something easier to understand? If I didn't already know what to expect I wouldn't understand it. RJFJR 17:16, 14 June 2007 (UTC)
- Better now? Han-Kwang 18:30, 14 June 2007 (UTC)
- Much better. Thank you. RJFJR 22:23, 14 June 2007 (UTC)
Example of the cd/dvd
[edit]It is my understanding that it isthe thin film effect that causes interference patterns in reflected light from the dataside of cd's and dvd's and that the example on teh page needs to be removed.Allywilson (talk) 16:40, 18 November 2007 (UTC)
Editing of the article
[edit]I have re-arranged this article, and added some new bits to make it, I hope, more comprehensible, and to have a more logical structure.
The section on 'gratings as dispersive elements' is still a bit of a mish-mash, and I will do more work on this. I don't know enough about the manufacture of gratings to do anything with this section, but I suspect it is very sketchy and imcomplete Epzcaw (talk) 13:28, 26 May 2008 (UTC)
Diffraction efficiency
[edit]I believe that it is important to discuss the concept of diffraction efficiency either within this page or on a page of its own. I think it should be a section within this page. To those who don't know diffraction efficiency is what percent of the incident light is diffracted to a particular diffraction order in reflectance or transmitance (The efficiencies are generally different). Resonant gratings can be designed that for specific conditions (angle, wavelenth, polarization) the diffraction efficiency of a particular order will be 100%. Eranus (talk) 07:44, 24 July 2008 (UTC)
Diffraction from a photonic crystal point of view
[edit]This is a bit more for the physics students and not the classical way to view diffraction. Since gratings are periodic, one can use the formalism of solid state physics which deals with periodic structures on the atomic scale. Anyway a homegeneous surface can not change the momentum (propagation vector, k) parralel to the surface. This is the relation between translational symmetry and conservation of momentum. A periodic structure conserves only crystal mometnum also known as quasi momentum, it means that the momentum is conserved up to a reciprocal lattice vector K (1/peiod), so if the grating is periodic in the x direction and the structure is homogeneous in the y direction, then
where m is the diffraction order and n the refractive index in the region of diffraction (reflection or tansmition). The way form here to the grating formula is very short, all form symmetry point of view. Will be glad to hear opinions if this should be included (Of course better worded)Eranus (talk) 07:44, 24 July 2008 (UTC)
I certainly think the description of diffraction gratings which uses QED should be included or some form of explanation using photons - it's quite important to realise that this can't just be explained using waves.
Anon. —Preceding unsigned comment added by 92.15.40.214 (talk) 18:49, 7 August 2009 (UTC)
Hi, everyone. I'm new to this. To get the ball rolling on QED in this article, I've written up a little piece using Feynman's example in his book. However, I'm young, with much to learn in the wonderful field of quantum electrodymanics, in which I've just begun to swim—nearly all of my knowledge of it comes from Feynman's book. So please, edit the heck out of this, both in language and in content—it would be nice to see a quantum electrodynamical explanation of diffraction gratings here. Also, I'll scan the images from QED when I get the time.
QED (quantum electrodynamics) offers a derivation of the properties of a diffraction grating in terms of photons as particles. In short, QED models photons as following all paths from a source to a final point, each of which has a certain probability amplitude, which can be represented as a vector or complex number (equivalently), or as Richard Feynman simply calls them in his book on QED, "arrows". For the probability that a certain event will happen, one sums the probability amplitudes for all of the possible ways in which the event can occur, and then takes the square of the length of the result. The probability amplitude of a photon from a monochromatic source, in this case, is modeled as an arrow that spins rapidly until it is 'evaluated' at its final point. (The reason for the quotes around 'evaluated' is that this spinning is actually dependent on the time at which the photon would have left the monochromatic source, as the probability amplitudes of photons do not spin while they are in transit.) So, for example, for the probability that light will reflect off of a mirror, one sets the photon's probability amplitude spinning as it leaves the source, follows it to the mirror, and then to its final point (even for paths that do not involve bouncing off of the mirror at equal angles) and then 'evaluates' it at the final point; next, one sums these arrows (in a standard vector sum), and squares the length of the result for the probability that this photon will reflect off of the mirror. (For a simplification, the arrows representing these probability amplitudes are made an egual standard length though there are, in actuality, very minor variations.) The times these paths take are what determine the angle of the probability amplitude arrow, as they 'spin' at a constant rate (which is related to the frequency of the photon). Now, the times of the paths near the classical reflection site of the mirror will be nearly the same, so as a result the probability amplitudes will point in nearly the same direction—thus, they will have a sizable sum. As we examine the paths towards the edges of the mirror, we find that the times of nearby paths are quite different from each other, and thus we wind up summing vectors that cancel out quickly (see image). So, there is a higher probability that light will follow a near-classical reflection path than a path further out. However, a diffraction grating can be made out of this mirror, by scraping away areas near the edge of the mirror that usually cancel nearby amplitudes out—but now, since the photons would not reflect from the scraped-off portions, the probability amplitude pointing, say, to the right can have a sizable sum. Thus, this would let light of the right frequency sum to a larger probability amplitude (which, of course, then has its length squared for the probability that light will reflect from the selected region). This description of course involves many simplifications: a point source, a "surface" that light can reflect off of (thus neglecting the interactions with electrons) and so forth. However, this approximation is a reasonable one to illustrate a diffraction grating conceptually. Light of a different frequency can also use the same diffraction grating, but with a different final point.[1]
- ^ Feynman, Richard (1985). QED: The Strange Theory of Light and Matter. Princeton, New Jersey: Princeton University Press.
Trmwiki (talk) 21:58, 2 October 2011 (UTC)
Since none have objected so far, I'll go ahead and post this in the main article. Feel free to change anything, of course. Anyway. Thanks! — Preceding unsigned comment added by Trmwiki (talk • contribs) 22:00, 2 October 2011 (UTC)
Diffraction Gratings tutorial by J.M. Lerner and A. Thevenon
[edit]The tutorial is divided in the following section: Section 1: DIFFRACTION GRATINGS ? RULED & HOLOGRAPHIC Section 2: MONOCHROMATORS & SPECTROGRAPHS Section 3: SPECTROMETER THROUGHPUT & ETENDUE Section 4: OPTICAL SIGNAL?TO?NOISE RATIO AND STRAY LIGHT Section 5: THE RELATIONSHIP BETWEEN WAVELENGTH AND PIXEL POSITION ON AN ARRAY Section 6: ENTRANCE OPTICS
It is a tutorial, by J.M. Lerner and A. Thevenon, part of the HORIBA Jobin Yvon company website, on the optics of spectroscopy. It covers: diffraction gratings - ruled and holographic; monochromators and spectrographs; spectrometer throughput and etendue; optical signal-to-noise ratio and stray light; the relationship between wavelength and pixel position of an array; and entrance optics.
This article will be very helpful on the diffraction grating page as an external link (http://www.jobinyvon.com/SiteResources/Data/Templates/1divisional.asp?DocID=616&v1ID=&lang=) .Afrine (talk) 14:47, 21 November 2008 (UTC)
In nature
[edit]"Diffraction gratings are also present in nature. For example, the iridescent colors of peacock feathers, mother-of-pearl, butterfly wings, and some other insects are caused by very fine regular structures that diffract light, splitting it into its component colors." Does this also apply to other iridescent surfaces found in nature, like the leaves of some plants ? If not then what is the iridescence mechanism ? 77.100.112.34 (talk) 16:42, 10 September 2010 (UTC)
- The mechanism of iridescence is typically interference, whereas the diffraction grating reflects light of different color at different angles. Iridescence usually is caused not by regular structures that reflect light, but by placing two or more transparent surfaces parallel to each other, separated by a distance equal to some multiple of a wavelength of light. Iridescence is caused by the same thing which allows a Fabry-Perot interferometer to select certain colors by constructive interference, while eliminating other colors by destructive interference. The same effect allows a laser to work.
- As an example, a thin sheen of gasoline on top of a puddle of water does not produce fine lines, but rather produces a very thin layer with almost parallel refective surfaces, which causes interference. The thickness of the layer determines what color will be reflected back to you. Slight variations in thickness produce the different rainbow colors, which move and shift as the liquid flows. Light passing through at an angle "sees" the distance between layers as being thicker than light passing through at a perfect 90 degrees, so constructive interference will boost the colors of longer wavelengths as the viewing angle is increased. I hope that helps answer your question. Zaereth (talk) 17:46, 10 September 2010 (UTC)
- I did a little research here. The book Nature's palette: the science of plant color By David Webster Lee, page 255, says, "Structural coloration is common in animals, particularly in insects and birds, as in the peacock feather commented on by Robert Hooke. Such colors are almost always caused by thin-film interference. The iridescent green wing chevrons of the Rajah Brooke birdwing butterfly we encountered in Malaysian rainforests are produced in this way, by multilayered structures in the wingscales that interfere with visible light." He goes on to describe exactly how this happens, much like I've described above. Mother of pearl is definitely not iridescent from the effects produced by a diffraction grating> The only natural phenomenon I found where such regular structures exist to produce the very angle specific diffracted reflection on a scale large enough to be visible to us is a rainbow.
- Perhaps the unsupported statements from the article should be removed, because the sources so far contradict what it says. Zaereth (talk) 01:47, 11 September 2010 (UTC)
- I have made some changes the article to match the sources which I've found. If there are any questions or comments, please leave them here. I left out the stuff about a rainbow, however. Looking for a better source I found this site, http://physics.bu.edu/py106/notes/Diffraction.html . A rainbow is caused by dispersion, not diffraction. My bad. That site gives a good description of diffraction, and may be a good reference for the article. Zaereth (talk) 22:48, 14 September 2010 (UTC)
- The following posted here originally: http://en.wikipedia.org/w/index.php?title=Diffraction_grating&oldid=398524127 "I believe that butterfly wing color is due to regular diffraction patterns in their scales. See "Butterfly" : Butterflies are characterized by their scale-covered wings. The coloration of butterfly wings is created by minute scales. These scales are pigmented with melanins that give them blacks and browns, but blues, greens, reds and iridescence are usually created not by pigments but the microstructure of the scales. This structural coloration is the result of coherent scattering of light by the photonic crystal nature of the scales.[5][6][7]" I have no idea on the accuracy of this claim, but moved it to Discussion as it is more accurate here for the time being. Zklink (talk) 05:18, 7 December 2010 (UTC)
- The structures in the butterfly scales, at least as far as I have read, are thin-film structures (photonic crystals) and not so much diffraction. The easiest way to tell is to ask the question, does the iridescence produce the entire rainbow of colors as the viewing angle changes, or is the color change limited to just a few colors? Diffraction will spread out the entire spectrum, similar to the way a prism will. With thin-film interference, the constructive interference usually causes a change from one color to one other, (ie: from green to blue). The destructive interference eliminates the rest of the spectrum. The book Dynamic fields and waves By Andrew Norton gives a pretty good description of how thin-fim interference works in butterflies. On page 111, it shows an illustration of the structures in the butterfliy scales that causes such interference. (I'm not saying that there aren't cases where diffraction does play a role, but I haven't found them yet.) Zaereth (talk) 17:18, 7 December 2010 (UTC)
On the NASA astronomy picture of the day website, yesterday, was posted a photo of iridescent clouds, which are apparently caused by the diffraction grating phenomenon. I don't have any reliably sourced info on this, but if someone does, it may be worth adding to the article. Zaereth (talk) 20:44, 9 February 2011 (UTC)
Diagram urgently needed
[edit]Can anyone find a diagram to illustrate the grating equation explanation in the "Theory of Operation" section? In particular it should show the wavefronts and/or interference pattern in relation to the angle theta_i, which is hard to visualize from the text. (As well as d,lambda of course, and a value for m.) 84.227.237.33 (talk) 18:32, 3 April 2014 (UTC)
- Commons has an svg diagram derived from diagrams used by the German Wikipedia and a low-resolution gif used by the Dutch Wikipedia:
- The svg diagram has an α that does not occur in our text (which should be easy to remove) and "φ" instead of "θ" (which is easily changed, though). It also only shows one order but can be generalized by replacing "φ" by "θm" and "λ" by "mλ". The gif diagram could be recreated as an svg (with adjusted labeling), but that will obviously be more work. --Lambiam 11:28, 14 August 2014 (UTC)
Density plot
[edit]I don't understand what it is that is being depicted in the recently added "density plot" image. The density of what? What does the horizontal axis represent? Is the density of whatever it is represented by the colour value? It does not correspond to anything I see in the main text. --Lambiam 11:32, 14 August 2014 (UTC)
- I can't tell either what the picture is supposed to represent. There is nothing on the commons page or the photo caption to tell how the picture was created, what the vertical lines represent, nor anything else about what this has to do with gratings. A quick google search shows no other uses of the term "density plot" so I do not even know what this term means, unless it is the density of the grooves (but those don't look evenly spaced enough to be grooves). Perhaps the author can clarify what the picture is showing. Zaereth (talk) 23:43, 14 August 2014 (UTC)
The user who added the image has not responded and not edited for three months. I have now removed the image from the article. --Lambiam 06:52, 17 November 2014 (UTC)
Light bulb halo image
[edit]
Re [1] "What kind of grating produces radial spectral like this? There should be a page about it, but this article needs a figure showing a normal linearly dispersed spectrum."
- The effect will be well known to older photographers. See http://www.cokin.co.uk/pages/diffractor1.htm It's achieved (from dim memory) with a filter combination of small Fresnel prisms and a series of tiny diffraction gratings oriented with the prisms. The image description even gives the Cokin number as #42.
- I would agree though, it's not an illustrative image for an article on diffraction gratings to this level. A CD might be (another non-linear grating) as that is at least fairly familiar to readers as an object. Andy Dingley (talk) 16:31, 4 November 2015 (UTC)
No prisms involved Andy. The Cokin #042 diffraction grating pattern is more complex than one set of straight of parallel lines : it's twenty such sets superimposed, each offset by a rotation of 9o, producing 40 discrete linear radiating spectra. Natural Philo (talk) 00:17, 3 February 2016 (UTC)
- Thanks for the explanation. But if you (or someone else reading this) are committed to working on this page, then maybe you could find a figure better depicting the spectrum from a normal linear grating (as is dealt with mathematically in section 1). This is sort of done in the top of the figure comparing it to a prism, though I could imagine a better diagram. I looked through wikimedia commons and didn't find anything much better. The figures should try to explain the science, not possible artistic tangents of the principle.
- And changing the subject slightly, I did find this figure: [[2]] which graphically expresses the math in that section (but labelled with phi instead of theta) for the basic case of normal incidence and the first diffracted order. Interferometrist (talk) 20:34, 4 November 2015 (UTC)
- Now I see that someone has made the very same suggestion a year ago on this talk page 2 sections above here! Is anyone inclined to edit accordingly? Interferometrist (talk) 20:39, 4 November 2015 (UTC)
- That's difficult to do when the requested diagrams are not available. We're limited by the images we have at our disposal. I'd make one myself, but am just not qualified to get the math correct, so that's best left to someone who is. I would imagine you're looking for diagrams similar to what's represented here , or maybe a diagram showing how individual "rays" of white light are diffracted at different angles (the colored arrow approach), or even the whole thing represented as waves. Unfortunately, since this is a volunteer project, we just have to wait until someone either goes out and finds a free-use image, or until someone with both the graphics and technical knowledge comes along and makes one themselves.


- I did take these photos in a reflection diffraction-grating borrowed from one of my lasers, showing the line distribution. (In fact, the very same grating pictured green in the article.) It's very easy to get a beautiful photo of a source, like the fluorescent lamp, in individual spectral lines, so that the photo of the lamp is monochromatic. However, due to the high angle of the grating, getting all of the spectrum in one photo required a very small angular size, so the grating needed to be very close to the camera while the light source was rather far away. (I know that's not really what you're asking for, but wanted to show that simply "getting an image" is not always that easy. Any help is always appreciated.) Zaereth (talk) 22:57, 4 November 2015 (UTC)
- Alright, thanks. Yes I will try myself to produce an appropriate diagram. Give me some time. I also might try to work the one diagram explaining the diffraction angle into the math section. Interferometrist (talk) 17:49, 5 November 2015 (UTC)
External links modified
[edit]Hello fellow Wikipedians,
I have just modified one external link on Diffraction grating. Please take a moment to review my edit. If you have any questions, or need the bot to ignore the links, or the page altogether, please visit this simple FaQ for additional information. I made the following changes:
- Added archive https://web.archive.org/web/20140304074633/http://emlab.utep.edu/ee5390em21.htm to http://emlab.utep.edu/ee5390em21.htm
When you have finished reviewing my changes, please set the checked parameter below to true or failed to let others know (documentation at {{Sourcecheck}}).
This message was posted before February 2018. After February 2018, "External links modified" talk page sections are no longer generated or monitored by InternetArchiveBot. No special action is required regarding these talk page notices, other than regular verification using the archive tool instructions below. Editors have permission to delete these "External links modified" talk page sections if they want to de-clutter talk pages, but see the RfC before doing mass systematic removals. This message is updated dynamically through the template {{source check}} (last update: 5 June 2024).
- If you have discovered URLs which were erroneously considered dead by the bot, you can report them with this tool.
- If you found an error with any archives or the URLs themselves, you can fix them with this tool.
Cheers.—InternetArchiveBot (Report bug) 00:21, 13 December 2016 (UTC)
Rowland Ghosts
[edit]Important addition to Wikipedia needed: During my research on phase contrast microscopy I tumbled over the original work of F. Zernike (How I discovered Phase contrast) who said he was studying the so called "Rowland Ghosts" when he got his ingenious idea. Unfortunately the term Rowland Ghost is not classified and not yet part of the Wikipedia. It appears that the Rowland Ghosts are entangled with diffraction gratings. So please update that issue.
- If you know about Rowland Ghosts, to the extent where an article can be written, you could write an article on Rowland Ghosts.Migboy123 (talk) 01:24, 18 April 2019 (UTC)
- Never heard of him, but a quick google search shows that Rowland's Ghost haunts the old house on the site of Odell Castle in England.
- Seriously though, a Rowland ghost apparently occurs due to errors in the spacing of the ruling, which occur in repeating (harmonic) intervals every-so-many number of rules across the grating. It causes spectral lines to appear at either side of the parent line, where they shouldn't be. Not too unlike sundogs. It differs from other grating errors (also produced by different kinds of spacing errors) in the distance from the parent line, satellites will be much closer while Lyman ghosts much farther away.
- I think that adding a section on tolerances and errors (such as I did in the mirror article) is a wonderful idea. I don't have the time nor expertise to add it to the article myself, at least not today, but check out the book Optical Instruments Part 2 for more info, especially if you'd like to add something yourself. According to the book, grating manufacture is without a doubt the most high-precision, continuous manufacturing process ever carried out, requiring engines that can burnish (not cut) finely-spaced grooves with diamond tooling with a uniformity greater than 100 times the precision allowed by the screws and bearings of the machine. (It's really fascinating how they manage to do it, cutting groves so small they have to be measured with an interferometer.) Zaereth (talk) 02:09, 18 April 2019 (UTC)
Umbrella
[edit]
This article contains the (in my opinion) unrealistic statement "Diffraction colors also appear when one looks at a bright point source through a translucent fine-pitch umbrella-fabric covering". I have never seen diffraction colors through an umbrella, in contrast to when looking through fine silk fabric. An umbrella diffuses the light like frosted glass, whereas silk does not diffuse the light at all. An umbrella is opaque, whereas silk is semi-transparent. Silk and umbrellas contain 4 threads per mm, so the calculated separation between diffraction maxima is 0.13°. If the light is diffused over more than 0.13°, diffraction colors disappear. See the photo of screws seen through silk. The double contours are due to diffraction. In contrast, screws are invisible through an umbrella. Ceinturion (talk) 18:56, 22 May 2021 (UTC)
Brightness differences in left orders vs. right orders
[edit]I remember learning this long ago and have seen it for myself, yet I see no discussion of it on this Wikipedia page and have had no luck tracking down any online discussions of it after multiple Google searches. Why do/can diffraction gratings favor one side over the other, making either their left spectral patterns or their right spectral patterns brighter than the other side? 173.225.198.117 (talk) 21:32, 22 February 2024 (UTC)
- In a normal grating, the grooves are symmetrical, so they work equally well on left or right. In a blazed grating the grooves are not symmetrical, so they favor one side over the other. Zaereth (talk) 23:52, 22 February 2024 (UTC)
- The discussion there seems to indicate only one order and one wavelength are so favored: "[M]aximum optical power is concentrated in the desired diffraction order while the residual power in the other orders (particularly the zeroth) is minimized. Since this condition can only exactly be achieved for one wavelength, it is specified for which blaze wavelength the grating is optimized (or blazed)." I don't see how that expands to all lines in all of the orders on one side vs. the other. (Am I missing something?) 192.101.250.94 (talk) 19:47, 27 February 2024 (UTC)
- Isn't it obvious? Ok, for example, see this tutorial. In a normal grating, you have grooves that are semi-circular in shape separated by flat surfaces. Diffraction occurs due to the same phenomenon responsible for the double-slit experiment. Because the reflective/transmissive surfaces are flat, they work equally well on both sides, but losses occur due to the width of the grooves. In a blazed grating, the cross section is sawtooth shaped, and the flat reflective/transmissive surfaces all angle from the plane of the grating toward one side and not the other. Thus, whether from reflection or refraction, they favor one side over the other. And at just the right angle there really is no width to the grooves, which helps minimize losses. Zaereth (talk) 22:16, 27 February 2024 (UTC)




