Mathematics desk
< August 26	<< Jul \| August \| Sep >>	Current desk >

Welcome to the Wikipedia Mathematics Reference Desk Archives
The page you are currently viewing is an archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages.

August 27

"There will come a day when I'm either an ancestor to all living humans, or to none of them."

"There will come a day when I'm either an ancestor to all living humans, or to none of them." [1]

Does the math really work out behind this?

What if I, and all my offsprings, only have one child? Wouldn't the number of my living descendants be limited to the single digits at any given time? Given that the total fertility rate in my country is already 1.5 and is dropping fast, this scenario is becoming more likely by the day.My other car is a cadr (talk) 03:07, 27 August 2015 (UTC)[reply]

You are assuming that you will continue to have descendants and that other people also will. That's fine as a hypothetical case if the population remains large, but what the author might have in mind is that eventually our species will die out, and presumably not all in the same instant. If not, then there will be a time when there is a last human L. Then for any particular human H in our time, either L (now constituting the entire species) is a descendant of H, or L isn't. QED. --65.94.50.17 (talk) 04:01, 27 August 2015 (UTC)[reply]

The day arrives only almost surely, that is, with probability 1. HTH, Robinh (talk) 05:30, 27 August 2015 (UTC)[reply]

This speaks to the concept of Most recent common ancestor, but I am not sure if I agree with the sentiment here. Just looking at the picture from the article

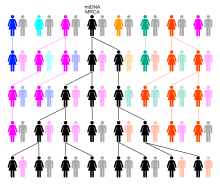
you can see plenty of "individuals" who are an ancestor to neither "all" or "none" living humans. So that day will surely come when the species dies out entirely, but until then, I don't see any reason why there can't be several "streams" of descendants during the lifetime of our species. Vespine (talk) 05:37, 27 August 2015 (UTC)[reply]

Identical ancestors point is more relevant here than Most recent common ancestor. If our species continues for thousands of generations and doesn't get extreme separation like space colonies without travel between them then it does seem very likely that all currently living people will either be an ancestor to all living humans, or to none of them. The scenario of getting exactly one reproducing child for numerous generations in a row is extremely unlikely. Over thousands of generations your descendants are almost certain to either die out, or branch out until they are all living humans. With our current travel activity and single planet, it wouldn't surprise me if it only took hundreds of generations. PrimeHunter (talk) 06:02, 27 August 2015 (UTC)[reply]

When the human species is extinct then you are an ancestor to all living humans, and to none of them. Bo Jacoby (talk) 13:32, 27 August 2015 (UTC).[reply]

The meaning of the strip is discussed at explainxkcd.com. AndrewWTaylor (talk) 13:39, 27 August 2015 (UTC)[reply]

@vespine: your scenario is possible, but has probability zero if the species continues forever (and if it doesn't, then you are the ancestor of noone). Robinh (talk) 06:09, 29 August 2015 (UTC)[reply]

Joining dots with lines

An arbitrary number of dots are joined by an arbitrary number of wiggly lines -- any number of lines can converge on any point, and the lines can be as wiggly and convoluted as desired, provided only that they do not cross one another. Is it always possible to rearrange the dots so that the lines can all become non-intersecting straight lines while preserving the essential structure of the diagram (i.e. which points are connected to which others)? I feel the answer should be 'yes', but I'm not 100% sure. 109.153.226.190 (talk) 11:49, 27 August 2015 (UTC)[reply]

Fary's theorem, I think. 129.234.195.173 (talk) 12:13, 27 August 2015 (UTC)[reply]

Thanks, yes, it seems to be more or less the same, although I see now that in my description I did not explicitly eliminate some cases that would cause the theorem not to apply (and the straight-line rearrangement to be obviously impossible), namely "loops" and more than one line connecting one pair of points. 109.153.226.190 (talk) 17:04, 27 August 2015 (UTC)[reply]