User:Trevithj/Negative feedback

This article is about feedback that opposes change. For unpleasant feedback, see negative criticism.

A simple feedback system. The feedback is negative if B is negative, so that A is processing the difference between input and output.

Negative feedback is the term widely used to describe the concept of automatic correction or goal-seeking behavior in many natural and artificial systems. The term comes from control theory, where correcting actions are based on a difference between desired and actual performance being fed back to a process. It is referred to as negative feedback because the difference involves in some sense subtracting the actual from the desired measures. General negative feedback systems are studied in control systems engineering.

Brief history

In mercury thermostats (circa 1600), negative feedback was used through the action of expanding columns of mercury to control vents in furnaces, maintaining a steady internal temperature.

In the invisible hand of the market metaphor of economic theory (1776), price movements provide a feedback mechanism to match supply and demand.

In centrifugal governors, negative feedback is used to maintain a near-constant speed of an engine, irrespective of the load or fuel-supply conditions.

In servomechanisms feedback is used to track either the speed or position of an output actuator to an input from a sensor, or from a user setting.

In audio amplifiers, negative feedback reduces distortion, minimises the effect of manufacturing variations in component parameters, and compensates for changes in characteristics due to temperature change.

In analog computing feedback around operational amplifiers is used to generate mathematical functions such as addition, subtraction, integration, differentiation, logarithm, and antilog functions.

In a phase locked loop feedback is used to maintain a generated alternating waveform in a constant phase to a reference signal. In many implementations the generated waveform is the output, but when used as a demodulator in a FM radio receiver, the error feedback voltage serves as the demodulated output signal. If there is a frequency divider between the generated waveform and the phase comparator, the device acts as a frequency multiplier.

In organisms, feedback enables various measures (eg body temperature, or blood sugar level) to be maintained within precise desired ranges by homeostatic processes.

History

Negative feedback as a control technique may be seen in the refinements of the water clock introduced by Ktesibios of Alexandria in the 3rd century BCE. Self-regulating mechanisms have existed since antiquity, and were used to maintain a constant level in the reservoirs of water clocks as early as 200 BCE.

The fly-ball governor is an early example of negative feedback.

Negative feedback was implemented in the 17th Century. Cornelius Drebbel had built thermostatically-controlled incubators and ovens in the early 1600s, and centrifugal governors were used to regulate the distance and pressure between millstones in windmills. James Watt patented a form of governor in 1788 to control the speed of his steam engine, and James Clerk Maxwell in 1868 described "component motions" associated with these governors that lead to a decrease in a disturbance or the amplitude of an oscillation.

The term "feedback" was well established by the 1920s, in reference to a means of boosting the gain of an electronic amplifier. Friis and Jensen described this action as "positive feedback" and made passing mention of a contrasting "negative feed-back action" in 1924. Harold Stephen Black detailed the use of negative feedback in electronic amplifiers in 1934, where he defined negative feedback as a type of coupling that reduced the gain of the amplifier, in the process greatly increasing its stability and bandwidth. Nyquist and Bode built on Black’s work to develop a theory of amplifier stability, but chose to define "negative" as applying to the polarity of the loop (rather than the effect on the gain), which gave rise to some confusion over basic definitions.

Early researchers in the area of cybernetics subsequently generalized the idea of negative feedback to cover any goal-seeking or purposeful behavior.

All purposeful behavior may be considered to require negative feed-back. If a goal is to be attained, some signals from the goal are necessary at some time to direct the behavior.

Cybernetics pioneer Norbert Wiener helped to formalize the concepts of feedback control, defining feedback in general as "the chain of the transmission and return of information", and negative feedback as the case when:

The information fed back to the control center tends to oppose the departure of the controlled from the controlling quantity...

While the view of feedback as any "circularity of action" helped to keep the theory simple and consistent, Ashby pointed out that, while it may clash with definitions that require a "materially evident" connection, "the exact definition of feedback is nowhere important". Ashby pointed out the limitations of the concept of "feedback":

The concept of 'feedback', so simple and natural in certain elementary cases, becomes artificial and of little use when the interconnections between the parts become more complex...Such complex systems cannot be treated as an interlaced set of more or less independent feedback circuits, but only as a whole. For understanding the general principles of dynamic systems, therefore, the concept of feedback is inadequate in itself. What is important is that complex systems, richly cross-connected internally, have complex behaviors, and that these behaviors can be goal-seeking in complex patterns.

Further confusion arose after BF Skinner introduced the terms positive and negative reinforcement, both of which can be considered negative feedback mechanisms in the sense that they try to minimize deviations from the desired behavior. In a similar context, Herold and Greller used the term "negative" to refer to the valence of the feedback: that is, cases where a subject receives an evaluation with an unpleasant emotional connotation.

A common theme for the 10 items [in the feedback analysis] is their valence, all representing negative feedback. Examples are being removed from a job or suffering some adverse consequence due to poor performance or receiving more or less direct indications of dissatisfaction from co-workers or the supervisor.

To reduce confusion, later authors have suggested alternative terms such as degenerative, self-correcting, balancing, or discrepancy-reducing in place of "negative".

Overview

Feedback loops in the human body

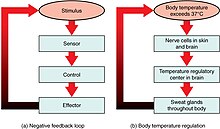
In many physical and biological systems, qualitatively different influences can oppose each other. For example, in biochemistry, one set of chemicals drives the system in a given direction, whereas another set of chemicals drives it in an opposing direction. If one or both of these opposing influences are non-linear, equilibrium point(s) result.

In biology, this process (in general, biochemical) is often referred to as homeostasis; whereas in mechanics, the more common term is equilibrium.

In engineering, mathematics and the physical, and biological sciences, common terms for the points around which the system gravitates include: attractors, stable states, eigenstates/eigenfunctions, equilibrium points, and setpoints.

In control theory, negative refers to the sign of the multiplier in mathematical models for feedback. In delta notation, −Δoutput is added to or mixed into the input. In multivariate systems, vectors help to illustrate how several influences can both partially complement and partially oppose each other.

Some authors, in particular with respect to modelling business systems, use negative to refer to the reduction in difference between the desired and actual behavior of a system. In a psychology context, on the other hand, negative refers to the valence of the feedback – attractive versus aversive, or praise versus criticism.

In contrast, positive feedback is feedback in which the system responds so as to increase the magnitude of any particular perturbation, resulting in amplification of the original signal instead of stabilization. Any system in which there is positive feedback together with a gain greater than one will result in a runaway situation. Both positive and negative feedback require a feedback loop to operate.

However, negative feedback systems can still be subject to oscillations. This is caused by the slight delays around any loop. Due to these delays the feedback signal of some frequencies can arrive one half cycle later which will have a similar effect to positive feedback and these frequencies can reinforce themselves and grow over time. This problem is often dealt with by attenuating or changing the phase of the problematic frequencies. Unless the system naturally has sufficient damping, many negative feedback systems have low pass filters or dampers fitted.

Some specific implementations

There are a large number of different examples of negative feedback and some are discussed below.

Error-controlled regulation

See also: Homeostasis and Allostasis

A regulator R adjusts the input to a system T so the monitored essential variables E are held to set-point values S that result in the desired system output despite disturbances D.

One use of feedback is to make a system (say T) self-regulating to minimize the effect of a disturbance (say D). Using a negative feedback loop, a measurement of some variable (for example, a process variable, say E) is subtracted from a required value (the 'set point') to estimate an operational error in system status, which is then used by a regulator (say R) to reduce the gap between the measurement and the required value. The regulator modifies the input to the system T according to its interpretation of the error in the status of the system. This error may be introduced by a variety of possible disturbances or 'upsets', some slow and some rapid. The regulation in such systems can range from a simple 'on-off' control to a more complex processing of the error signal.

It may be noted that the physical form of the signals in the system may change from point to point. So, for example, a disturbance (say, a change in weather) to the heat input to a house (as an example of the system T) is interpreted by a thermometer as a change in temperature (as an example of an 'essential variable' E), converted by the thermostat (a 'comparator') into an electrical error in status compared to the 'set point' S, and subsequently used by the regulator (containing a 'controller' that commands gas control valves and an ignitor) ultimately to change the heat provided by a furnace (an 'effector') to counter the initial weather-related disturbance in heat input to the house.

Negative feedback amplifier

Negative feedback amplifier using ideal unilateral elements. The feedback is negative if βA_OL> 0.

Main article: Negative feedback amplifier

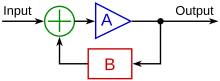
The figure shows a simplified block diagram of a negative feedback amplifier in which the feedback sets the overall ('closed-loop') amplifier gain at a value:

${\frac {O}{I}}={\frac {A_{OL}}{1+\beta A_{OL}}}\approx {\frac {1}{\beta }}$

where the approximate value assumes βA_OL >> 1, and 1/β as set by the feedback branch is independent of undesirable variations in the 'open-loop' gain A_OL (for example, due to manufacturing variations between units, or temperature effects upon components) provided only that this gain is sufficiently large.

The difference signal I–βO that is applied to the open-loop amplifier often is called the "error signal". This difference is given by:

$I-\beta O=I\left(1-\beta {\frac {O}{I}}\right)={\frac {I}{1+\beta A_{OL}}}.$

According to this equation, the 'error' is determined by three factors: the input signal I, the feedback fraction β, and the open-loop gain A_OL. Even though the negative feedback amplifier does not attempt to correct variations in the open-loop gain by opposing such changes, the feedback circuit does reduce their impact on the overall closed-loop system behavior.

The negative feedback amplifier was invented by Harold Stephen Black at Bell Laboratories in 1927, and granted a patent in 1937.

There are many advantages to feedback in amplifiers. For example, all electronic devices (among them, vacuum tubes, bipolar transistors, MOS transistors) exhibit some nonlinear behavior. Negative feedback corrects this failure by trading unused gain for higher linearity (lower distortion), substituting the smaller, but constant gain 1/β for the nonlinear but large gain A_OL. An amplifier with too large an open-loop gain, possibly in a specific frequency range, will result in a large feedback signal in that same range. This feedback signal, when subtracted from the original input, will act to reduce the input to the open-loop amplifier, thereby lowering the overall closed-loop gain. That is, the reduced input, although amplified again by the "too large" open-loop gain A_OL, results in an output signal that is amplified by only 1/β. Because the feedback network provides a value of β that is not amplitude dependent (that is, it provides a linear output, directly proportional to its input), the net result is a flattening (desensitizing) of the amplifier's gain over those frequencies such that, of course, βA_OL >> 1. Though feedback renders the gain much more predictable, amplifiers with negative feedback can oscillate. See the article on step response. They may even exhibit instability. Harry Nyquist of Bell Laboratories proposed the Nyquist stability criterion and the Nyquist plot to insure that behavior remains stable.

Operational amplifier circuits

Main article: Operational amplifier applications

A voltage amplifier using an operational amplifier to set the voltage across R₁ to V_in.

Almost all operational amplifier circuits employ negative feedback. Since the open-loop gain of an op-amp is extremely large, the tiniest of input signals would drive the output of the amplifier to one rail or the other in the absence of negative feedback. A simple example of the use of feedback is the op-amp voltage amplifier shown in the figure.

The idealized model of an operational amplifier assumes that the gain is infinite, the input impedances are infinite, and input offset currents and voltages are zero. Such an ideal amplifier would draw no current from the resistor divider. The infinite gain of the ideal op-amp means this feedback circuit would drive the voltage difference between the two op-amp inputs to zero. Consequently, the voltage gain of this circuit is derived as:

$V_{\text{out}}=\left(1+{\frac {R_{\text{2}}}{R_{\text{1}}}}\right)V_{\text{in}}\!\,$.

Practical op-amps are not ideal, but their input impedance is extremely high and they have very high gain. So the model of an ideal op-amp often suffices to understand circuit operation, putting aside assessment of non-ideal behaviors.

If the ideal op-amp is replaced by a realistic op-amp with a finite gain and other distortions, the unwanted disturbances in the amplifier properties that would appear in an open-loop operation of the op-amp are very well suppressed by the external circuit when the op-amp gain is large.

Mechanical engineering

In modern engineering, negative feedback loops are found in fuel injection systems and carburettors.

Control systems

Main article: Control systems

The ballcock or float valve uses negative feedback to control the water level in a cistern.

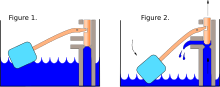
Examples of the use of negative feedback to control its system are: thermostat control, the phase-locked loop oscillator, the ballcock control of water level (see diagram at left), and temperature regulation in animals.

A simple and practical example is a thermostat. When the temperature in a heated room reaches a certain upper limit, the room heating is switched off so that the temperature begins to fall. When the temperature drops to a lower limit, the heating is switched on again. Provided the limits are close to each other, a steady room temperature is maintained. Similar control mechanisms are used in cooling systems, such as an air conditioner, a refrigerator, or a freezer.

Biology and chemistry

Control of endocrine hormones by negative feedback.

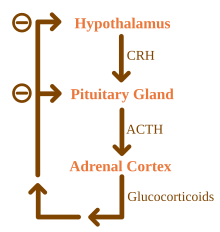
Some biological systems exhibit negative feedback such as the baroreflex in blood pressure regulation and erythropoiesis. Many biological process (e.g., in the human anatomy) use negative feedback. Examples of this are numerous, from the regulating of body temperature, to the regulating of blood glucose levels. The disruption of feedback loops can lead to undesirable results: in the case of blood glucose levels, if negative feedback fails, the glucose levels in the blood may begin to rise dramatically, thus resulting in diabetes.

For hormone secretion regulated by the negative feedback loop: when gland X releases hormone X, this stimulates target cells to release hormone Y. When there is an excess of hormone Y, gland X "senses" this and inhibits its release of hormone X. As shown in the figure, most endocrine hormones are controlled by a physiologic negative feedback inhibition loop, such as the glucocorticoids secreted by the adrenal cortex. The hypothalamus secretes corticotropin-releasing hormone (CRH), which directs the anterior pituitary gland to secrete adrenocorticotropic hormone (ACTH). In turn, ACTH directs the adrenal cortex to secrete glucocorticoids, such as cortisol. Glucocorticoids not only perform their respective functions throughout the body but also negatively affect the release of further stimulating secretions of both the hypothalamus and the pituitary gland, effectively reducing the output of glucocorticoids once a sufficient amount has been released.

Self-organization

Main articles: Self-organization and Emergence

Self-organization is the capability of certain systems "of organizing their own behavior or structure". There are many possible factors contributing to this capacity, and most often positive feedback is identified as a possible contributor. However, negative feedback also can play a role.

Economics

In economics, automatic stabilisers are government programs that are intended to work as negative feedback to dampen fluctuations in real GDP.

Free market economic theorists claim that the pricing mechanism operated to match supply and demand. However Norbert Wiener wrote in 1948:

"There is a belief current in many countries and elevated to the rank of an official article of faith in the United States that free competition is itself a homeostatic process... Unfortunately the evidence, such as it is, is against this simple-minded theory."