User:Tomruen/Uniform honeycombs
Appearance
This is a list of uniform tessellations in dimensions 2-8, constructed by vertex figures that are uniform polytopes with circumradii equal to 1.0.
Lattice refers to the vertex arrangement of a uniform tessellation/honeycomb. There are also dual lattices, which place vertices at the tessellation facet centers.
The number of vertices in the vertex figure is equal to the kissing number of the tessellation.
Circumradius 1 vertex figures
[edit]| BSA | Dim | Uniform polytope (vertex figure) | Vertices | Fam | Uniform tessellation | Tessellation, packing and vertex figure | Dual tessellation and facet |
|---|---|---|---|---|---|---|---|
| 2D | t0,1{3} expanded 2-simplex (hexagon) |
6 | honeycomb A2 lattice |
  
|
 
| ||
| 2D | {6} hexagon |
6 | H~2 | {3,6} H2 lattice | |||
| co | 3D | t0,2{3,3} expanded 3-simplex (cuboctahedron) |
12 | honeycomb A3 lattice |
  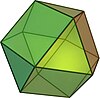
|
 
| |
| co | 3D | t1{3,4} rectified 3-orthoplex (cuboctahedron) |
12 | h{4,3,4} D3 lattice | |||
| spid | 4D | t0,3{3,3,3} expanded 4-simplex |
20 | honeycomb A4 lattice |

| ||
| tes | 4D | (4-4 duoprism (4-cube) |
16 | C~4 | t2{4,3,3,4} |

| |
| tes | 4D | {}x{4,3} cube prism (4-cube) |
16 | F~4 | t1{3,3,4,3} | ||
| ico | 4D | t1{3,3,4} rectified 4-orthoplex |
24 | h{4,3,3,4} D4 lattice |
 
|
 File:24-cell.svg File:24-cell.svg
| |
| ico | 4D | {3,4,3} (24-cell) |
24 | F~4 | {3,3,4,3} F4 lattice | ||
| scad | 5D | t0,4{3,3,3,3} expanded 5-simplex |
30 | honeycomb A5 lattice |

| ||
| squoct | 5D | {4}x{3,4} duoprism |
24 | C~5 | t2{4,3,3,3,4} | ||
| rat | 5D | t1{3,3,3,4} rectified 5-orthoplex |
40 | h{4,3,3,3,4} D5 lattice |

| ||
| stef | 6D | t0,5{3,3,3,3,3} expanded 6-simplex |
42 | honeycomb A6 lattice | |||
| squahex | 6D | {4}x{3,3,4} duoprism |
32 | t2{4,3,3,3,3,4} | |||
| octdip | 6D | {3,4}x{3,4} duoprism |
36 | t3{4,3,3,3,3,4} | |||
| rag | 6D | t1{3,3,3,3,4} rectified 6-orthoplex |
60 | h{4,3,3,3,3,4} D6 lattice |

| ||
| trittip | 6D | {3}x{3}x{3} triaprism |
27 | t2(2_22) honeycomb | |||
| nodeip | 6D | {}xt2{3,3,3,3} birectified 5-simplex prism |
40 | t1(2_22) honeycomb | |||
| mo | 6D | 1_22 |
72 | Gosset 2_22 honeycomb E6 lattice |
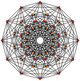
| ||
| 7D | t0,6{3,3,3,3,3,3} expanded 7-simplex |
56 | honeycomb A7 lattice | ||||
| 7D | {4}x{3,3,3,4} duoprism |
40 | t2{4,3,3,3,3,3,4} | ||||
| 7D | {3,4}x{3,3,4} duoprism |
48 | t3{4,3,3,3,3,3,4} | ||||
| rez | 7D | t1{3,3,3,3,3,4} rectified 7-orthoplex |
84 | h{4,3,3,3,3,3,4} D7 lattice |

| ||
| he | 7D | 0_33 trirectified 7-simplex |
70 | Gosset 1_33 honeycomb |
File:7-simplex t3.svg.png | ||
| 7D | {}x(1_31) | t1(331) honeycomb |
|||||
| 7D | {3}x(0_31) | t2(331) honeycomb |
|||||
| 7D | {3,3}x{3}x{} | t3(331) honeycomb |
|||||
| laq | 7D | 2_31 |
126 | Gosset 3_31 honeycomb E7 lattice |

| ||
| 8D | t0,7{3,3,3,3,3,3,3} expanded 8-simplex |
72 | honeycomb A8 lattice | ||||
| 8D | {4}x{3,3,3,3,4} duoprism |
48 | t2{4,3,3,3,3,3,3,4} | ||||
| 8D | {3,4}x{3,3,3,4} duoprism |
60 | t3{4,3,3,3,3,3,3,4} | ||||
| 8D | {3,3,4}x{3,3,4} duoprism |
64 | t4{4,3,3,3,3,3,3,4} | ||||
| rek | 8D | t1{3,3,3,3,3,3,4} rectified 8-orthoplex |
112 | h{4,3,3,3,3,3,3,4} D8 lattice |

| ||
| rene | 8D | 0_52 birectified 8-simplex |
84 | Gosset 1_52 honeycomb |

| ||
| roc prism | 8D | {} x 0_51 | 56 | t1(251) honeycomb |
|||
| hocto | 8D | 1_51 8-demicube |
128 | Gosset 2_51 honeycomb |
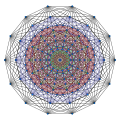
| ||
| 8D | {} x (3_21) | 112 | t1(521) honeycomb |
||||
| 8D | {3} x (2_21) | 81 | t2(521) honeycomb |
||||
| 8D | {3,3} x (1_21) | 48 | t3(521) honeycomb |
||||
| 8D | {3,3,3} x (0_21) | 50 | t4(521) honeycomb |
||||
| 8D | {3,3,3,3} x {3} x {} | 30 | t5(521) honeycomb |
||||
| fy | 8D | 4_21 polytope |
240 | Gosset 5_21 honeycomb E8 lattice |

| ||
Families =
[edit]Infinite Coxeter groups
[edit]Families of convex uniform tessellations are defined by Coxeter groups.
| n | eαn |
Alternated n-cubic[1] hδn |
n-cubic[2] δn |
Quartered n-cubic[3] qδn |
- | Hexagonal |
Aperigonal | |
|---|---|---|---|---|---|---|---|---|
| 1 | {∞}
| |||||||
| 2 | {6,3}
|
{4,4}
|
{6,3}
|
|||||
| 3 | q{4,3,4}
|
h{4,3,4}
|
{4,3,4}
|
|||||
| 4 | {3[5]}
|
{4,32,4}
|
{4,32,4}
|
q{4,32,4}
|
{3,4,3,3}
|
|||
| 5 | {3[6]}
|
h{4,33,4}
|
{4,33,4}
|
q{4,33,4}
|
||||
| 6 | {3[7]}
|
h{4,34,4}
|
{4,34,4}
|
q{4,34,4}
|
{32,2,2} | |||
| 7 | {3[8]}
|
h{4,35,4}
|
{4,35,4}
|
q{4,35,4}
|
{33,3,1}
|
|||
| 8 | {3[9]}
|
h{4,36,4}
|
{4,36,4}
|
q{4,36,4}
|
{35,2,1}
|
|||
| 9 | {3[10]}
|
h{4,37,4}
|
{4,37,4}
|
q{4,37,4}
|
{36,2,1}
|
|||
| 10 | ... | ... | ... | ... |


























