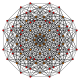
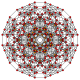
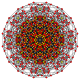
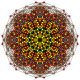
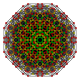
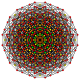
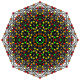
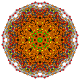
Rectified 7-simplexes
 7-simplex |
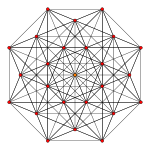 Rectified 7-simplex | |
 Birectified 7-simplex |
 Trirectified 7-simplex | |
| Orthogonal projections in A7 Coxeter plane | ||
|---|---|---|
In seven-dimensional geometry, a rectified 7-simplex is a convex uniform 7-polytope, being a rectification of the regular 7-simplex.
There are four unique degrees of rectifications, including the zeroth, the 7-simplex itself. Vertices of the rectified 7-simplex are located at the edge-centers of the 7-simplex. Vertices of the birectified 7-simplex are located in the triangular face centers of the 7-simplex. Vertices of the trirectified 7-simplex are located in the tetrahedral cell centers of the 7-simplex.
Rectified 7-simplex
[edit]| Rectified 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Coxeter symbol | 051 |
| Schläfli symbol | r{36} = {35,1} or |
| Coxeter diagrams | Or |
| 6-faces | 16 |
| 5-faces | 84 |
| 4-faces | 224 |
| Cells | 350 |
| Faces | 336 |
| Edges | 168 |
| Vertices | 28 |
| Vertex figure | 6-simplex prism |
| Petrie polygon | Octagon |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
The rectified 7-simplex is the edge figure of the 251 honeycomb. It is called 05,1 for its branching Coxeter-Dynkin diagram, shown as ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as S1
7.
Alternate names
[edit]- Rectified octaexon (Acronym: roc) (Jonathan Bowers)
Coordinates
[edit]The vertices of the rectified 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,0,0,0,1,1). This construction is based on facets of the rectified 8-orthoplex.
Images
[edit]| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | [5] | [4] | [3] |
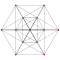
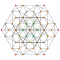
Birectified 7-simplex
[edit]| Birectified 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Coxeter symbol | 042 |
| Schläfli symbol | 2r{3,3,3,3,3,3} = {34,2} or |
| Coxeter diagrams | Or |
| 6-faces | 16: 8 r{35} 8 2r{35} |
| 5-faces | 112: 28 {34} 56 r{34} 28 2r{34} |
| 4-faces | 392: 168 {33} (56+168) r{33} |
| Cells | 770: (420+70) {3,3} 280 {3,4} |
| Faces | 840: (280+560) {3} |
| Edges | 420 |
| Vertices | 56 |
| Vertex figure | {3}x{3,3,3} |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as S2
7. It is also called 04,2 for its branching Coxeter-Dynkin diagram, shown as ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Alternate names
[edit]- Birectified octaexon (Acronym: broc) (Jonathan Bowers)
Coordinates
[edit]The vertices of the birectified 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,0,0,1,1,1). This construction is based on facets of the birectified 8-orthoplex.
Images
[edit]| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|
|
|
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | [5] | [4] | [3] |
Trirectified 7-simplex
[edit]| Trirectified 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Coxeter symbol | 033 |
| Schläfli symbol | 3r{36} = {33,3} or |
| Coxeter diagrams | Or |
| 6-faces | 16 2r{35} |
| 5-faces | 112 |
| 4-faces | 448 |
| Cells | 980 |
| Faces | 1120 |
| Edges | 560 |
| Vertices | 70 |
| Vertex figure | {3,3}x{3,3} |
| Coxeter group | A7×2, [[36]], order 80640 |
| Properties | convex, isotopic |
The trirectified 7-simplex is the intersection of two regular 7-simplexes in dual configuration.
E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as S3
7.
This polytope is the vertex figure of the 133 honeycomb. It is called 03,3 for its branching Coxeter-Dynkin diagram, shown as ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Alternate names
[edit]- Hexadecaexon (Acronym: he) (Jonathan Bowers)
Coordinates
[edit]The vertices of the trirectified 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,0,1,1,1,1). This construction is based on facets of the trirectified 8-orthoplex.
The trirectified 7-simplex is the intersection of two regular 7-simplices in dual configuration. This characterization yields simple coordinates for the vertices of a trirectified 7-simplex in 8-space: the 70 distinct permutations of (1,1,1,1,−1,−1,−1,-1).
Images
[edit]| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|
|

|
| Dihedral symmetry | [8] | [[7]] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|
|

|
| Dihedral symmetry | [[5]] | [4] | [[3]] |
Related polytopes
[edit]| Dim. | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| Name Coxeter |
Hexagon t{3} = {6} |
Octahedron r{3,3} = {31,1} = {3,4} |
Decachoron 2t{33} |
Dodecateron 2r{34} = {32,2} |
Tetradecapeton 3t{35} |
Hexadecaexon 3r{36} = {33,3} |
Octadecazetton 4t{37} |
| Images | 
|
 
|
 
|
|
|
 
|
 
|
| Vertex figure | ( )∨( ) |  { }×{ } |
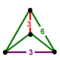 { }∨{ } |
 {3}×{3} |
 {3}∨{3} |
{3,3}×{3,3} | 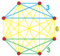 {3,3}∨{3,3} |
| Facets | {3} |
t{3,3} |
r{3,3,3} |
2t{3,3,3,3} |
2r{3,3,3,3,3} |
3t{3,3,3,3,3,3} | |
| As intersecting dual simplexes |
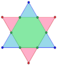 |
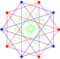 |
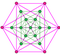 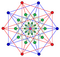 |
Related polytopes
[edit]These polytopes are three of 71 uniform 7-polytopes with A7 symmetry.
See also
[edit]References
[edit]- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
- Klitzing, Richard. "7D uniform polytopes (polyexa)". o3o3x3o3o3o3o - broc, o3x3o3o3o3o3o - roc, o3o3x3o3o3o3o - he