User:Reddwarf2956/Ratio of circumference to radius

Introduction

Circumference / radius = 2π

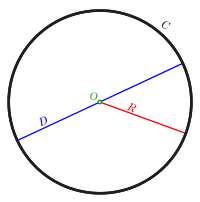
In mathematics, the Ratio of circumference to radius, is a fundamental mathematical constant, and has no formal glyph symbolism. The ratio of a circle's circumference to its radius, C/r, is ubiquitous in mathematics, engineering, and science. While the value is related to the period of many trigonometry functions including sine and cosine, the measure in radians of one complete revolution or turn is C/r. In computer programming the constant takes on many names and because of different word lengths many values.

A circle with radius of 1 unit has a circumference of 2π.

An arc of a circle with the same length as the radius of that circle corresponds to an angle of 1 radian. A full circle corresponds to a full turn, or approximately 6.28 radians, which are expressed here using the Greek letter tau (τ).

Relationship with unit circles and pi

Because the circumference of a circle is

${C}={2}\pi \cdot {r},\!$

the value C/r is equal to twice the number pi, 2π.

${C}/{r}={2}\pi .\!$

This ratio is the same as a unit circle which has radius of 1 to its circumference, 2π.

Area of a disk onion and triangle method with tau

Onion proof

Area of the disk via ring integration

Using calculus, we can sum the area incrementally, partitioning the disk into thin concentric rings like the layers of an onion. This is the method of shell integration in two dimensions. For an infinitesimally thin ring of the "onion" of radius t, the accumulated area is 𝜏t dt, the circumferential length of the ring times its infinitesimal width (you can approach this ring by a rectangle with width = 𝜏t and height = dt). This gives an elementary integral for a disk of radius r.

${\begin{aligned}\mathrm {Area} (r)&{}=\int _{0}^{r}\tau t\,dt\\&{}=\left[\tau {\frac {t^{2}}{2}}\right]_{t=0}^{r}\\&{}={\frac {1}{2}}\tau r^{2}.\end{aligned}}$

Triangle method

The circle and the triangle are equal in area.

Circle unwrapped to form a triangle

This approach is a slight modification of onion proof. Consider unwrapping the concentric circles to straight strips. This will form a right angled triangle with r as its height and 𝜏r (being the outer slice of onion) as its base.

Finding the area of this triangle will give the area of circle

${\begin{aligned}Area&{}={\frac {1}{2}}*base*height\\&{}={\frac {1}{2}}*\tau r*r\\&{}={\frac {1}{2}}\tau r^{2}\end{aligned}}$

The opposite and adjacent angles for this triangle are respectively in degrees 9.0430611...°, 80.956939...° and in radians 0.1578311..., 1.4129651....

Decimal Expansion and Continued fraction

The decimal expansion of Ratio of circumference to radius $C/r=2\pi$ and it is approximately equal to 6.283185307179586476925286766559005768394338798750211641949889184615632...OEIS: A019692. Continued fraction is found in OEIS: A058291 and is

$C/r=6+\textstyle {\frac {1}{3+\textstyle {\frac {1}{1+\textstyle {\frac {1}{1+\textstyle {\frac {1}{7+\textstyle {\frac {1}{2+\textstyle {\frac {1}{146+\textstyle {\frac {1}{3+\textstyle {\frac {1}{6+\textstyle {\frac {1}{1+\textstyle {\frac {1}{1+\ddots }}}}}}}}}}}}}}}}}}}}$

Trigonometry functions

Sine and cosine functions repeat with period C/r.

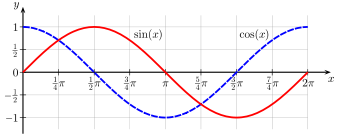
Most trigonometric functions are periodic functions with intervals of length C/r. The following tables shows the

Radians

It follows that the magnitude in radians of one complete revolution (360 degrees) is the length of the entire circumference, 2πr, divided by the radius, r, resulting in 2π.

${C}/{r}={2}\pi .\!$

Physics

Physical constants

http://en.wikipedia.org/wiki/Physical_constants

Reduced Planck constant

Computer Science

Support in programming languages

The constant tau is used in programming languages as names like twopi, two_pi, TWOPI, TWO_PI, .... The following table has the language and the value of the number.

Programming language	Name	Value
Fortran	TWOPI
OGRE	TWO_PI
Pascal	TwoPI	6.28318 53071 79586
Processing	TWO_PI TAU	6.28318 53071 79586 47693
Wiring	TWO_PI	6.28318 53071 79586 47693
Extreme Optimization Libraries	TwoPi	6.28318 53071 79586 47692 52867 66558
Haskell (module)
Python (PEP, bug)
Ruby (bug)

An example for Fortran: http://naif.jpl.nasa.gov/pub/naif/toolkit_docs/FORTRAN/spicelib/twopi.html .

Version numbering

The major/minor version numbers of Pugs converges to 2π (being reminiscent of TeX and METAFONT, which use a similar scheme); each significant digit in the minor version represents a successfully completed milestone. The third digit is incremented for each release. The current milestones are:

• 6.0: Initial release.
• 6.2: Basic IO and control flow elements; mutable variables; assignment.
• 6.28: Classes and traits.
• 6.283: Rules and Grammars.
• 6.2831: Type system and linking.
• 6.28318: Macros.
• 6.283185: Port Pugs to Perl 6, if needed.

History

In 1424, the Persian astronomer and mathematician, Jamshīd al-Kāshī (Kāshānī), correctly computed 2π to 9 sexagesimal digits. His value for 2π was 6;16,59,28,1,34,51,46,14,50. The decimal equivalent of this value to 17 digits is

$2\pi \approx 6.28318530717958648.\,$

In popular culture

Proposed Glyph Symbolism

Advocacy

An opinion column in The Mathematical Intelligencer, Robert Palais argued that π is "wrong" as a circle measure, and that a better value would be 2π, being the measure of the circle's circumference and the period of the sine, cosine, and complex exponential functions. He suggested a symbol like π but with three legs, $\pi \!\;\!\!\!\pi$, be used in place of 2π, demonstrating how it simplifies many mathematical formulas.

In 2010, Michael Hartl posted an essay called The Tau Manifesto on his personal website. In it, he proposed using the Greek letter tau (𝜏) to represent that number instead. Hartl argued that an existing symbol like 𝜏 would face fewer barriers to adoption than a new symbol like the "three-legged pi" proposed in the Intelligencer.

Criticism

The Pi Manifesto

Tau day, Tau time

The oldest known celebration for 'Tau Day' or '2 Pi Day' June 28.

A number of news outlets reported on "Tau Day", a holiday proposed in The Tau Manifesto' for June 28 to honor the number 2π. The Royal Institution of Australia's Tau Day celebration in 2011 featured the performance of a musical work based on tau.

According to the Massachusetts Institute of Technology's Dean of Admissions Stuart Schmill, "over [the] past year or so, there has been a bit of a debate in the math universe over which is a better number to use, whether it is Pi or Tau". Thus the school chose to inform 2012 applicants whether or not they were accepted on Pi Day at what MIT called Tau Time, 6:28 pm.

See also

• Turn (geometry)

External links

• example.com