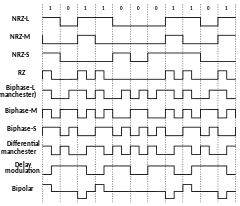
User:Rai282/Books/Modulation
Amplitude Modulation
[edit]
| Passband modulation |
|---|
 |
| Analog modulation |
| Digital modulation |
| Hierarchical modulation |
| Spread spectrum |
| See also |
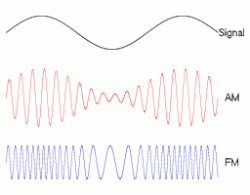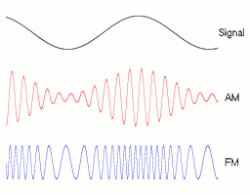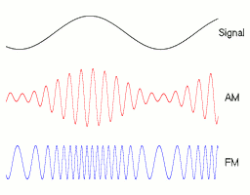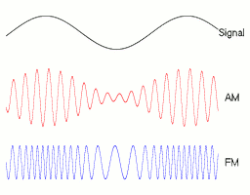
Amplitude modulation (AM) is a modulation technique used in electronic communication, most commonly for transmitting messages with a radio wave. In amplitude modulation, the amplitude (signal strength) of the wave is varied in proportion to that of the message signal, such as an audio signal. This technique contrasts with angle modulation, in which either the frequency of the carrier wave is varied, as in frequency modulation, or its phase, as in phase modulation.
AM was the earliest modulation method used for transmitting audio in radio broadcasting. It was developed during the first quarter of the 20th century beginning with Roberto Landell de Moura and Reginald Fessenden's radiotelephone experiments in 1900.[1] This original form of AM is sometimes called double-sideband amplitude modulation (DSBAM), because the standard method produces sidebands on either side of the carrier frequency. Single-sideband modulation uses bandpass filters to eliminate one of the sidebands and possibly the carrier signal, which improves the ratio of message power to total transmission power, reduces power handling requirements of line repeaters, and permits better bandwidth utilization of the transmission medium.
AM remains in use in many forms of communication in addition to AM broadcasting: shortwave radio, amateur radio, two-way radios, VHF aircraft radio, citizens band radio, and in computer modems in the form of QAM.
Foundation
[edit]In electronics, telecommunications and mechanics, modulation means varying some aspect of a continuous wave carrier signal with an information-bearing modulation waveform, such as an audio signal which represents sound, or a video signal which represents images. In this sense, the carrier wave, which has a much higher frequency than the message signal, carries the information. At the receiving station, the message signal is extracted from the modulated carrier by demodulation.
In general form, a modulation process of a sinusoidal carrier wave may be described by the following equation:[2]
- .
A(t) represents the time-varying amplitude of the sinusoidal carrier wave and the cosine-term is the carrier at its angular frequency , and the instantaneous phase deviation . This description directly provides the two major groups of modulation, amplitude modulation and angle modulation. In angle modulation, the term A(t) is constant and the second term of the equation has a functional relationship to the modulating message signal. Angle modulation provides two methods of modulation, frequency modulation and phase modulation.
In amplitude modulation, the angle term is held constant and the first term, A(t), of the equation has a functional relationship to the modulating message signal.
The modulating message signal may be analog in nature, or it may be a digital signal, in which case the technique is generally called amplitude-shift keying.
For example, in AM radio communication, a continuous wave radio-frequency signal has its amplitude modulated by an audio waveform before transmission. The message signal determines the envelope of the transmitted waveform. In the frequency domain, amplitude modulation produces a signal with power concentrated at the carrier frequency and two adjacent sidebands. Each sideband is equal in bandwidth to that of the modulating signal, and is a mirror image of the other. Standard AM is thus sometimes called "double-sideband amplitude modulation" (DSBAM).
A disadvantage of all amplitude modulation techniques, not only standard AM, is that the receiver amplifies and detects noise and electromagnetic interference in equal proportion to the signal. Increasing the received signal-to-noise ratio, say, by a factor of 10 (a 10 decibel improvement), thus would require increasing the transmitter power by a factor of 10. This is in contrast to frequency modulation (FM) and digital radio where the effect of such noise following demodulation is strongly reduced so long as the received signal is well above the threshold for reception. For this reason AM broadcast is not favored for music and high fidelity broadcasting, but rather for voice communications and broadcasts (sports, news, talk radio etc.).
AM is also inefficient in power usage; at least two-thirds of the power is concentrated in the carrier signal. The carrier signal contains none of the original information being transmitted (voice, video, data, etc.). However its presence provides a simple means of demodulation using envelope detection, providing a frequency and phase reference to extract the modulation from the sidebands. In some modulation systems based on AM, a lower transmitter power is required through partial or total elimination of the carrier component, however receivers for these signals are more complex because they must provide a precise carrier frequency reference signal (usually as shifted to the intermediate frequency) from a greatly reduced "pilot" carrier (in reduced-carrier transmission or DSB-RC) to use in the demodulation process. Even with the carrier eliminated in double-sideband suppressed-carrier transmission, carrier regeneration is possible using a Costas phase-locked loop. This does not work for single-sideband suppressed-carrier transmission (SSB-SC), leading to the characteristic "Donald Duck" sound from such receivers when slightly detuned. Single-sideband AM is nevertheless used widely in amateur radio and other voice communications because it has power and bandwidth efficiency (cutting the RF bandwidth in half compared to standard AM). On the other hand, in medium wave and short wave broadcasting, standard AM with the full carrier allows for reception using inexpensive receivers. The broadcaster absorbs the extra power cost to greatly increase potential audience.
Shift keying
[edit]A simple form of digital amplitude modulation which can be used for transmitting binary data is on–off keying, the simplest form of amplitude-shift keying, in which ones and zeros are represented by the presence or absence of a carrier. On–off keying is likewise used by radio amateurs to transmit Morse code where it is known as continuous wave (CW) operation, even though the transmission is not strictly "continuous". A more complex form of AM, quadrature amplitude modulation is now more commonly used with digital data, while making more efficient use of the available bandwidth.
Analog telephony
[edit]A simple form of amplitude modulation is the transmission of speech signals from a traditional analog telephone set using a common battery local loop.[3] The direct current provided by the central office battery is a carrier with a frequency of 0 Hz. It is modulated by a microphone (transmitter) in the telephone set according to the acoustic signal from the speaker. The result is a varying amplitude direct current, whose AC-component is the speech signal extracted at the central office for transmission to another subscriber.
Amplitude reference
[edit]An additional function provided by the carrier in standard AM, but which is lost in either single or double-sideband suppressed-carrier transmission, is that it provides an amplitude reference. In the receiver, the automatic gain control (AGC) responds to the carrier so that the reproduced audio level stays in a fixed proportion to the original modulation. On the other hand, with suppressed-carrier transmissions there is no transmitted power during pauses in the modulation, so the AGC must respond to peaks of the transmitted power during peaks in the modulation. This typically involves a so-called fast attack, slow decay circuit which holds the AGC level for a second or more following such peaks, in between syllables or short pauses in the program. This is very acceptable for communications radios, where compression of the audio aids intelligibility. However it is absolutely undesired for music or normal broadcast programming, where a faithful reproduction of the original program, including its varying modulation levels, is expected.
ITU type designations
[edit]In 1982, the International Telecommunication Union (ITU) designated the types of amplitude modulation:
| Designation | Description |
|---|---|
| A3E | double-sideband a full-carrier – the basic amplitude modulation scheme |
| R3E | single-sideband reduced-carrier |
| H3E | single-sideband full-carrier |
| J3E | single-sideband suppressed-carrier |
| B8E | independent-sideband emission |
| C3F | vestigial-sideband |
| Lincompex | linked compressor and expander (a submode of any of the above ITU Emission Modes) |
History
[edit]

Amplitude modulation was used in experiments of multiplex telegraph and telephone transmission in the late 1800s.[4] However, the practical development of this technology is identified with the period between 1900 and 1920 of radiotelephone transmission, that is, the effort to send audio signals by radio waves. The first radio transmitters, called spark gap transmitters, transmitted information by wireless telegraphy, using pulses of the carrier wave to spell out text messages in Morse code. They could not transmit audio because the carrier consisted of strings of damped waves, pulses of radio waves that declined to zero, and sounded like a buzz in receivers. In effect they were already amplitude modulated.
Continuous waves
[edit]The first AM transmission was made by Canadian-born American researcher Reginald Fessenden on 23 December 1900 using a spark gap transmitter with a specially designed high frequency 10 kHz interrupter, over a distance of one mile (1.6 km) at Cobb Island, Maryland, US. His first transmitted words were, "Hello. One, two, three, four. Is it snowing where you are, Mr. Thiessen?". The words were barely intelligible above the background buzz of the spark.[citation needed]
Fessenden was a significant figure in the development of AM radio. He was one of the first researchers to realize, from experiments like the above, that the existing technology for producing radio waves, the spark transmitter, was not usable for amplitude modulation, and that a new kind of transmitter, one that produced sinusoidal continuous waves, was needed. This was a radical idea at the time, because experts believed the impulsive spark was necessary to produce radio frequency waves, and Fessenden was ridiculed. He invented and helped develop one of the first continuous wave transmitters – the Alexanderson alternator, with which he made what is considered the first AM public entertainment broadcast on Christmas Eve, 1906. He also discovered the principle on which AM is based, heterodyning, and invented one of the first detectors able to rectify and receive AM, the electrolytic detector or "liquid baretter", in 1902. Other radio detectors invented for wireless telegraphy, such as the Fleming valve (1904) and the crystal detector (1906) also proved able to rectify AM signals, so the technological hurdle was generating AM waves; receiving them was not a problem.
Early technologies
[edit]Early experiments in AM radio transmission, conducted by Fessenden, Valdemar Poulsen, Ernst Ruhmer, Quirino Majorana, Charles Herrold, and Lee de Forest, were hampered by the lack of a technology for amplification. The first practical continuous wave AM transmitters were based on either the huge, expensive Alexanderson alternator, developed 1906–1910, or versions of the Poulsen arc transmitter (arc converter), invented in 1903. The modifications necessary to transmit AM were clumsy and resulted in very low quality audio. Modulation was usually accomplished by a carbon microphone inserted directly in the antenna or ground wire; its varying resistance varied the current to the antenna. The limited power handling ability of the microphone severely limited the power of the first radiotelephones; many of the microphones were water-cooled.
Vacuum tubes
[edit]The 1912 discovery of the amplifying ability of the Audion tube, invented in 1906 by Lee de Forest, solved these problems. The vacuum tube feedback oscillator, invented in 1912 by Edwin Armstrong and Alexander Meissner, was a cheap source of continuous waves and could be easily modulated to make an AM transmitter. Modulation did not have to be done at the output but could be applied to the signal before the final amplifier tube, so the microphone or other audio source didn't have to modulate a high-power radio signal. Wartime research greatly advanced the art of AM modulation, and after the war the availability of cheap tubes sparked a great increase in the number of radio stations experimenting with AM transmission of news or music. The vacuum tube was responsible for the rise of AM broadcasting around 1920, the first electronic mass communication medium. Amplitude modulation was virtually the only type used for radio broadcasting until FM broadcasting began after World War II.
At the same time as AM radio began, telephone companies such as AT&T were developing the other large application for AM: sending multiple telephone calls through a single wire by modulating them on separate carrier frequencies, called frequency division multiplexing.[4]
Single-sideband
[edit]In 1915, John Renshaw Carson formulated the first mathematical description of amplitude modulation, showing that a signal and carrier frequency combined in a nonlinear device creates a sideband on both sides of the carrier frequency. Passing the modulated signal through another nonlinear device can extract the original baseband signal.[4] His analysis also showed that only one sideband was necessary to transmit the audio signal, and Carson patented single-sideband modulation (SSB) on 1 December 1915.[4] This advanced variant of amplitude modulation was adopted by AT&T for longwave transatlantic telephone service beginning 7 January 1927. After WW-II, it was developed for military aircraft communication.
Analysis
[edit]
The carrier wave (sine wave) of frequency fc and amplitude A is expressed by
- .
The message signal, such as an audio signal that is used for modulating the carrier, is m(t), and has a frequency fm, much lower than fc:
- ,
where m is the amplitude sensitivity, M is the amplitude of modulation. If m < 1, (1 + m(t)/A) is always positive for undermodulation. If m > 1 then overmodulation occurs and reconstruction of message signal from the transmitted signal would lead in loss of original signal. Amplitude modulation results when the carrier c(t) is multiplied by the positive quantity (1 + m(t)/A):
In this simple case m is identical to the modulation index, discussed below. With m = 0.5 the amplitude modulated signal y(t) thus corresponds to the top graph (labelled "50% Modulation") in figure 4.
Using prosthaphaeresis identities, y(t) can be shown to be the sum of three sine waves:
Therefore, the modulated signal has three components: the carrier wave c(t) which is unchanged in frequency, and two sidebands with frequencies slightly above and below the carrier frequency fc.
Spectrum
[edit]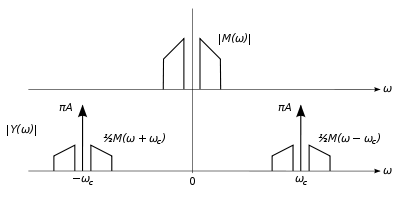
A useful modulation signal m(t) is usually more complex than a single sine wave, as treated above. However, by the principle of Fourier decomposition, m(t) can be expressed as the sum of a set of sine waves of various frequencies, amplitudes, and phases. Carrying out the multiplication of 1 + m(t) with c(t) as above, the result consists of a sum of sine waves. Again, the carrier c(t) is present unchanged, but each frequency component of m at fi has two sidebands at frequencies fc + fi and fc – fi. The collection of the former frequencies above the carrier frequency is known as the upper sideband, and those below constitute the lower sideband. The modulation m(t) may be considered to consist of an equal mix of positive and negative frequency components, as shown in the top of figure 2. One can view the sidebands as that modulation m(t) having simply been shifted in frequency by fc as depicted at the bottom right of figure 2.
The short-term spectrum of modulation, changing as it would for a human voice for instance, the frequency content (horizontal axis) may be plotted as a function of time (vertical axis), as in figure 3. It can again be seen that as the modulation frequency content varies, an upper sideband is generated according to those frequencies shifted above the carrier frequency, and the same content mirror-imaged in the lower sideband below the carrier frequency. At all times, the carrier itself remains constant, and of greater power than the total sideband power.
Power and spectrum efficiency
[edit]The RF bandwidth of an AM transmission (refer to figure 2, but only considering positive frequencies) is twice the bandwidth of the modulating (or "baseband") signal, since the upper and lower sidebands around the carrier frequency each have a bandwidth as wide as the highest modulating frequency. Although the bandwidth of an AM signal is narrower than one using frequency modulation (FM), it is twice as wide as single-sideband techniques; it thus may be viewed as spectrally inefficient. Within a frequency band, only half as many transmissions (or "channels") can thus be accommodated. For this reason analog television employs a variant of single-sideband (known as vestigial sideband, somewhat of a compromise in terms of bandwidth) in order to reduce the required channel spacing.
Another improvement over standard AM is obtained through reduction or suppression of the carrier component of the modulated spectrum. In figure 2 this is the spike in between the sidebands; even with full (100%) sine wave modulation, the power in the carrier component is twice that in the sidebands, yet it carries no unique information. Thus there is a great advantage in efficiency in reducing or totally suppressing the carrier, either in conjunction with elimination of one sideband (single-sideband suppressed-carrier transmission) or with both sidebands remaining (double sideband suppressed carrier). While these suppressed carrier transmissions are efficient in terms of transmitter power, they require more sophisticated receivers employing synchronous detection and regeneration of the carrier frequency. For that reason, standard AM continues to be widely used, especially in broadcast transmission, to allow for the use of inexpensive receivers using envelope detection. Even (analog) television, with a (largely) suppressed lower sideband, includes sufficient carrier power for use of envelope detection. But for communications systems where both transmitters and receivers can be optimized, suppression of both one sideband and the carrier represent a net advantage and are frequently employed.
A technique used widely in broadcast AM transmitters is an application of the Hapburg carrier, first proposed in the 1930s but impractical with the technology then available. During periods of low modulation the carrier power would be reduced and would return to full power during periods of high modulation levels. This has the effect of reducing the overall power demand of the transmitter and is most effective on speech type programmes. Various trade names are used for its implementation by the transmitter manufacturers from the late 80's onwards.
Modulation index
[edit]The AM modulation index is a measure based on the ratio of the modulation excursions of the RF signal to the level of the unmodulated carrier. It is thus defined as:
where and are the modulation amplitude and carrier amplitude, respectively; the modulation amplitude is the peak (positive or negative) change in the RF amplitude from its unmodulated value. Modulation index is normally expressed as a percentage, and may be displayed on a meter connected to an AM transmitter.
So if , carrier amplitude varies by 50% above (and below) its unmodulated level, as is shown in the first waveform, below. For , it varies by 100% as shown in the illustration below it. With 100% modulation the wave amplitude sometimes reaches zero, and this represents full modulation using standard AM and is often a target (in order to obtain the highest possible signal-to-noise ratio) but mustn't be exceeded. Increasing the modulating signal beyond that point, known as overmodulation, causes a standard AM modulator (see below) to fail, as the negative excursions of the wave envelope cannot become less than zero, resulting in distortion ("clipping") of the received modulation. Transmitters typically incorporate a limiter circuit to avoid overmodulation, and/or a compressor circuit (especially for voice communications) in order to still approach 100% modulation for maximum intelligibility above the noise. Such circuits are sometimes referred to as a vogad.
However it is possible to talk about a modulation index exceeding 100%, without introducing distortion, in the case of double-sideband reduced-carrier transmission. In that case, negative excursions beyond zero entail a reversal of the carrier phase, as shown in the third waveform below. This cannot be produced using the efficient high-level (output stage) modulation techniques (see below) which are widely used especially in high power broadcast transmitters. Rather, a special modulator produces such a waveform at a low level followed by a linear amplifier. What's more, a standard AM receiver using an envelope detector is incapable of properly demodulating such a signal. Rather, synchronous detection is required. Thus double-sideband transmission is generally not referred to as "AM" even though it generates an identical RF waveform as standard AM as long as the modulation index is below 100%. Such systems more often attempt a radical reduction of the carrier level compared to the sidebands (where the useful information is present) to the point of double-sideband suppressed-carrier transmission where the carrier is (ideally) reduced to zero. In all such cases the term "modulation index" loses its value as it refers to the ratio of the modulation amplitude to a rather small (or zero) remaining carrier amplitude.

Modulation methods
[edit]
Modulation circuit designs may be classified as low- or high-level (depending on whether they modulate in a low-power domain—followed by amplification for transmission—or in the high-power domain of the transmitted signal).[5]
Low-level generation
[edit]In modern radio systems, modulated signals are generated via digital signal processing (DSP). With DSP many types of AM are possible with software control (including DSB with carrier, SSB suppressed-carrier and independent sideband, or ISB). Calculated digital samples are converted to voltages with a digital-to-analog converter, typically at a frequency less than the desired RF-output frequency. The analog signal must then be shifted in frequency and linearly amplified to the desired frequency and power level (linear amplification must be used to prevent modulation distortion).[6] This low-level method for AM is used in many Amateur Radio transceivers.[7]
AM may also be generated at a low level, using analog methods described in the next section.
High-level generation
[edit]High-power AM transmitters (such as those used for AM broadcasting) are based on high-efficiency class-D and class-E power amplifier stages, modulated by varying the supply voltage.[8]
Older designs (for broadcast and amateur radio) also generate AM by controlling the gain of the transmitter's final amplifier (generally class-C, for efficiency). The following types are for vacuum tube transmitters (but similar options are available with transistors):[9][10]
- Plate modulation
- In plate modulation, the plate voltage of the RF amplifier is modulated with the audio signal. The audio power requirement is 50 percent of the RF-carrier power.
- Heising (constant-current) modulation
- RF amplifier plate voltage is fed through a choke (high-value inductor). The AM modulation tube plate is fed through the same inductor, so the modulator tube diverts current from the RF amplifier. The choke acts as a constant current source in the audio range. This system has a low power efficiency.
- Control grid modulation
- The operating bias and gain of the final RF amplifier can be controlled by varying the voltage of the control grid. This method requires little audio power, but care must be taken to reduce distortion.
- Clamp tube (screen grid) modulation
- The screen-grid bias may be controlled through a clamp tube, which reduces voltage according to the modulation signal. It is difficult to approach 100-percent modulation while maintaining low distortion with this system.
- Doherty modulation
- One tube provides the power under carrier conditions and another operates only for positive modulation peaks. Overall efficiency is good, and distortion is low.
- Outphasing modulation
- Two tubes are operated in parallel, but partially out of phase with each other. As they are differentially phase modulated their combined amplitude is greater or smaller. Efficiency is good and distortion low when properly adjusted.
- Pulse-width modulation (PWM) or pulse-duration modulation (PDM)
- A highly efficient high voltage power supply is applied to the tube plate. The output voltage of this supply is varied at an audio rate to follow the program. This system was pioneered by Hilmer Swanson and has a number of variations, all of which achieve high efficiency and sound quality.
- Digital methods
- The Harris Corporation obtained a patent for synthesizing a modulated high-power carrier wave from a set of digitally selected low-power amplifiers, running in phase at the same carrier frequency.[11][citation needed] The input signal is sampled by a conventional audio analog-to-digital converter (ADC), and fed to a digital exciter, which modulates overall transmitter output power by switching a series of low-power solid-state RF amplifiers on and off. The combined output drives the antenna system.
Demodulation methods
[edit]The simplest form of AM demodulator consists of a diode which is configured to act as envelope detector. Another type of demodulator, the product detector, can provide better-quality demodulation with additional circuit complexity.
See also
[edit]- AM stereo
- Shortwave radio
- Amplitude modulation signalling system (AMSS)
- Modulation sphere
- Types of radio emissions
- Airband
- DSB-SC
References
[edit]- ^ "Father Landell de Moura : Radio Broadcasting Pioneer : FABIO S. FLOSI : UNICAMP – University of Campinas, State of São Paulo" (PDF). Aminharadio.com. Archived (PDF) from the original on 2022-10-09. Retrieved 15 July 2018.
- ^ AT&T, Telecommunication Transmission Engineering, Volume 1—Principles, 2nd Edition, Bell Center for Technical Education (1977)
- ^ AT&T, Engineering and Operations in the Bell System (1984) p.211
- ^ a b c d Bray, John (2002). Innovation and the Communications Revolution: From the Victorian Pioneers to Broadband Internet. Inst. of Electrical Engineers. pp. 59, 61–62. ISBN 0852962185.
- ^ Atul P. Godse; U. A. Bakshi (2009). Communication Engineering. Technical Publications. p. 36. ISBN 978-81-8431-089-4.
- ^ Silver, Ward, ed. (2011). "Ch. 15 DSP and Software Radio Design". The ARRL Handbook for Radio Communications (Eighty-eighth ed.). American Radio Relay League. ISBN 978-0-87259-096-0.
- ^ Silver, Ward, ed. (2011). "Ch. 14 Transceivers". The ARRL Handbook for Radio Communications (Eighty-eighth ed.). American Radio Relay League. ISBN 978-0-87259-096-0.
- ^ Frederick H. Raab; et al. (May 2003). "RF and Microwave Power Amplifier and Transmitter Technologies – Part 2". High Frequency Design: 22ff. Archived from the original on 6 March 2016. Retrieved 8 September 2017.
- ^ Laurence Gray and Richard Graham (1961). Radio Transmitters. McGraw-Hill. pp. 141ff.
- ^ Cavell, Garrison C. Ed. (2018). National Association of Broadcasters Engineering Handbook, 11th Ed. Routledge. pp. 1099ff.
- ^ US 4580111, Swanson, Hilmer, "Amplitude modulation using digitally selected carrier amplifiers", published 1986-04-01, assigned to Harris Corp
Bibliography
[edit]- Newkirk, David and Karlquist, Rick (2004). Mixers, modulators and demodulators. In D. G. Reed (ed.), The ARRL Handbook for Radio Communications (81st ed.), pp. 15.1–15.36. Newington: ARRL. ISBN 0-87259-196-4.
External links
[edit]- Amplitude Modulation by Jakub Serych, Wolfram Demonstrations Project.
- Amplitude Modulation, by S Sastry.
- Amplitude Modulation, an introduction by Federation of American Scientists.
- Amplitude Modulation tutorial including related topics of modulators, demodulators, etc...
- Analog Modulation online interactive demonstration using Python in Google Colab Platform, by C Foh.
Frequency Modulation
[edit]| Passband modulation |
|---|
 |
| Analog modulation |
| Digital modulation |
| Hierarchical modulation |
| Spread spectrum |
| See also |


Frequency modulation (FM) is the encoding of information in a carrier wave by varying the instantaneous frequency of the wave. The technology is used in telecommunications, radio broadcasting, signal processing, and computing.
In analog frequency modulation, such as radio broadcasting, of an audio signal representing voice or music, the instantaneous frequency deviation, i.e. the difference between the frequency of the carrier and its center frequency, has a functional relation to the modulating signal amplitude.
Digital data can be encoded and transmitted with a type of frequency modulation known as frequency-shift keying (FSK), in which the instantaneous frequency of the carrier is shifted among a set of frequencies. The frequencies may represent digits, such as '0' and '1'. FSK is widely used in computer modems such as fax modems, telephone caller ID systems, garage door openers, and other low-frequency transmissions.[1] Radioteletype also uses FSK.[2]
Frequency modulation is widely used for FM radio broadcasting. It is also used in telemetry, radar, seismic prospecting, and monitoring newborns for seizures via EEG,[3] two-way radio systems, sound synthesis, magnetic tape-recording systems and some video-transmission systems. In radio transmission, an advantage of frequency modulation is that it has a larger signal-to-noise ratio and therefore rejects radio frequency interference better than an equal power amplitude modulation (AM) signal. For this reason, most music is broadcast over FM radio.
However, under severe enough multipath conditions it performs much more poorly than AM, with distinct high frequency noise artifacts that are audible with lower volumes and less complex tones.[citation needed] With high enough volume and carrier deviation audio distortion starts to occur that otherwise wouldn't be present without multipath or with an AM signal.[citation needed]
Frequency modulation and phase modulation are the two complementary principal methods of angle modulation; phase modulation is often used as an intermediate step to achieve frequency modulation. These methods contrast with amplitude modulation, in which the amplitude of the carrier wave varies, while the frequency and phase remain constant.
Theory
[edit]This section needs additional citations for verification. (November 2017) |
If the information to be transmitted (i.e., the baseband signal) is and the sinusoidal carrier is , where fc is the carrier's base frequency, and Ac is the carrier's amplitude, the modulator combines the carrier with the baseband data signal to get the transmitted signal:[4] [citation needed]
where , being the sensitivity of the frequency modulator and being the amplitude of the modulating signal or baseband signal.
In this equation, is the instantaneous frequency of the oscillator and is the frequency deviation, which represents the maximum shift away from fc in one direction, assuming xm(t) is limited to the range ±1.
It is important to realize that this process of integrating the instantaneous frequency to create an instantaneous phase is quite different from what the term "frequency modulation" naively implies, namely directly adding the modulating signal to the carrier frequency
which would result in a modulated signal that has spurious local minima and maxima that do not correspond to those of the carrier.
While most of the energy of the signal is contained within fc ± fΔ, it can be shown by Fourier analysis that a wider range of frequencies is required to precisely represent an FM signal. The frequency spectrum of an actual FM signal has components extending infinitely, although their amplitude decreases and higher-order components are often neglected in practical design problems.[5]
Sinusoidal baseband signal
[edit]Mathematically, a baseband modulating signal may be approximated by a sinusoidal continuous wave signal with a frequency fm. This method is also named as single-tone modulation. The integral of such a signal is:
In this case, the expression for y(t) above simplifies to:
where the amplitude of the modulating sinusoid is represented in the peak deviation (see frequency deviation).
The harmonic distribution of a sine wave carrier modulated by such a sinusoidal signal can be represented with Bessel functions; this provides the basis for a mathematical understanding of frequency modulation in the frequency domain.
Modulation index
[edit]As in other modulation systems, the modulation index indicates by how much the modulated variable varies around its unmodulated level. It relates to variations in the carrier frequency:
where is the highest frequency component present in the modulating signal xm(t), and is the peak frequency-deviation – i.e. the maximum deviation of the instantaneous frequency from the carrier frequency. For a sine wave modulation, the modulation index is seen to be the ratio of the peak frequency deviation of the carrier wave to the frequency of the modulating sine wave.
If , the modulation is called narrowband FM (NFM), and its bandwidth is approximately . Sometimes modulation index is considered NFM and other modulation indices are considered wideband FM (WFM or FM).
For digital modulation systems, for example, binary frequency shift keying (BFSK), where a binary signal modulates the carrier, the modulation index is given by:
where is the symbol period, and is used as the highest frequency of the modulating binary waveform by convention, even though it would be more accurate to say it is the highest fundamental of the modulating binary waveform. In the case of digital modulation, the carrier is never transmitted. Rather, one of two frequencies is transmitted, either or , depending on the binary state 0 or 1 of the modulation signal.
If , the modulation is called wideband FM and its bandwidth is approximately . While wideband FM uses more bandwidth, it can improve the signal-to-noise ratio significantly; for example, doubling the value of , while keeping constant, results in an eight-fold improvement in the signal-to-noise ratio.[6] (Compare this with chirp spread spectrum, which uses extremely wide frequency deviations to achieve processing gains comparable to traditional, better-known spread-spectrum modes).
With a tone-modulated FM wave, if the modulation frequency is held constant and the modulation index is increased, the (non-negligible) bandwidth of the FM signal increases but the spacing between spectra remains the same; some spectral components decrease in strength as others increase. If the frequency deviation is held constant and the modulation frequency increased, the spacing between spectra increases.
Frequency modulation can be classified as narrowband if the change in the carrier frequency is about the same as the signal frequency, or as wideband if the change in the carrier frequency is much higher (modulation index > 1) than the signal frequency.[7] For example, narrowband FM (NFM) is used for two-way radio systems such as Family Radio Service, in which the carrier is allowed to deviate only 2.5 kHz above and below the center frequency with speech signals of no more than 3.5 kHz bandwidth. Wideband FM is used for FM broadcasting, in which music and speech are transmitted with up to 75 kHz deviation from the center frequency and carry audio with up to a 20 kHz bandwidth and subcarriers up to 92 kHz.
Bessel functions
[edit]
For the case of a carrier modulated by a single sine wave, the resulting frequency spectrum can be calculated using Bessel functions of the first kind, as a function of the sideband number and the modulation index. The carrier and sideband amplitudes are illustrated for different modulation indices of FM signals. For particular values of the modulation index, the carrier amplitude becomes zero and all the signal power is in the sidebands.[5]
Since the sidebands are on both sides of the carrier, their count is doubled, and then multiplied by the modulating frequency to find the bandwidth. For example, 3 kHz deviation modulated by a 2.2 kHz audio tone produces a modulation index of 1.36. Suppose that we limit ourselves to only those sidebands that have a relative amplitude of at least 0.01. Then, examining the chart shows this modulation index will produce three sidebands. These three sidebands, when doubled, gives us (6 × 2.2 kHz) or a 13.2 kHz required bandwidth.
| Modulation index |
Sideband amplitude | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Carrier | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| 0.00 | 1.00 | ||||||||||||||||
| 0.25 | 0.98 | 0.12 | |||||||||||||||
| 0.5 | 0.94 | 0.24 | 0.03 | ||||||||||||||
| 1.0 | 0.77 | 0.44 | 0.11 | 0.02 | |||||||||||||
| 1.5 | 0.51 | 0.56 | 0.23 | 0.06 | 0.01 | ||||||||||||
| 2.0 | 0.22 | 0.58 | 0.35 | 0.13 | 0.03 | ||||||||||||
| 2.40483 | 0.00 | 0.52 | 0.43 | 0.20 | 0.06 | 0.02 | |||||||||||
| 2.5 | −0.05 | 0.50 | 0.45 | 0.22 | 0.07 | 0.02 | 0.01 | ||||||||||
| 3.0 | −0.26 | 0.34 | 0.49 | 0.31 | 0.13 | 0.04 | 0.01 | ||||||||||
| 4.0 | −0.40 | −0.07 | 0.36 | 0.43 | 0.28 | 0.13 | 0.05 | 0.02 | |||||||||
| 5.0 | −0.18 | −0.33 | 0.05 | 0.36 | 0.39 | 0.26 | 0.13 | 0.05 | 0.02 | ||||||||
| 5.52008 | 0.00 | −0.34 | −0.13 | 0.25 | 0.40 | 0.32 | 0.19 | 0.09 | 0.03 | 0.01 | |||||||
| 6.0 | 0.15 | −0.28 | −0.24 | 0.11 | 0.36 | 0.36 | 0.25 | 0.13 | 0.06 | 0.02 | |||||||
| 7.0 | 0.30 | 0.00 | −0.30 | −0.17 | 0.16 | 0.35 | 0.34 | 0.23 | 0.13 | 0.06 | 0.02 | ||||||
| 8.0 | 0.17 | 0.23 | −0.11 | −0.29 | −0.10 | 0.19 | 0.34 | 0.32 | 0.22 | 0.13 | 0.06 | 0.03 | |||||
| 8.65373 | 0.00 | 0.27 | 0.06 | −0.24 | −0.23 | 0.03 | 0.26 | 0.34 | 0.28 | 0.18 | 0.10 | 0.05 | 0.02 | ||||
| 9.0 | −0.09 | 0.25 | 0.14 | −0.18 | −0.27 | −0.06 | 0.20 | 0.33 | 0.31 | 0.21 | 0.12 | 0.06 | 0.03 | 0.01 | |||
| 10.0 | −0.25 | 0.04 | 0.25 | 0.06 | −0.22 | −0.23 | −0.01 | 0.22 | 0.32 | 0.29 | 0.21 | 0.12 | 0.06 | 0.03 | 0.01 | ||
| 12.0 | 0.05 | −0.22 | −0.08 | 0.20 | 0.18 | −0.07 | −0.24 | −0.17 | 0.05 | 0.23 | 0.30 | 0.27 | 0.20 | 0.12 | 0.07 | 0.03 | 0.01 |
Carson's rule
[edit]A rule of thumb, Carson's rule states that nearly all (≈98 percent) of the power of a frequency-modulated signal lies within a bandwidth of:
where , as defined above, is the peak deviation of the instantaneous frequency from the center carrier frequency , is the Modulation index which is the ratio of frequency deviation to highest frequency in the modulating signal and is the highest frequency in the modulating signal. Condition for application of Carson's rule is only sinusoidal signals. For non-sinusoidal signals:
where W is the highest frequency in the modulating signal but non-sinusoidal in nature and D is the Deviation ratio which is the ratio of frequency deviation to highest frequency of modulating non-sinusoidal signal.
Noise reduction
[edit]FM provides improved signal-to-noise ratio (SNR), as compared for example with AM. Compared with an optimum AM scheme, FM typically has poorer SNR below a certain signal level called the noise threshold, but above a higher level – the full improvement or full quieting threshold – the SNR is much improved over AM. The improvement depends on modulation level and deviation. For typical voice communications channels, improvements are typically 5–15 dB. FM broadcasting using wider deviation can achieve even greater improvements. Additional techniques, such as pre-emphasis of higher audio frequencies with corresponding de-emphasis in the receiver, are generally used to improve overall SNR in FM circuits. Since FM signals have constant amplitude, FM receivers normally have limiters that remove AM noise, further improving SNR.[8][9]
Implementation
[edit]Modulation
[edit]FM signals can be generated using either direct or indirect frequency modulation:
- Direct FM modulation can be achieved by directly feeding the message into the input of a voltage-controlled oscillator.
- For indirect FM modulation, the message signal is integrated to generate a phase-modulated signal. This is used to modulate a crystal-controlled oscillator, and the result is passed through a frequency multiplier to produce an FM signal. In this modulation, narrowband FM is generated leading to wideband FM later and hence the modulation is known as indirect FM modulation.[10]
Demodulation
[edit]
Many FM detector circuits exist. A common method for recovering the information signal is through a Foster–Seeley discriminator or ratio detector. A phase-locked loop can be used as an FM demodulator. Slope detection demodulates an FM signal by using a tuned circuit which has its resonant frequency slightly offset from the carrier. As the frequency rises and falls the tuned circuit provides a changing amplitude of response, converting FM to AM. AM receivers may detect some FM transmissions by this means, although it does not provide an efficient means of detection for FM broadcasts. In Software-Defined Radio implementations the demodulation may be carried out by using the Hilbert transform (implemented as a filter) to recover the instantaneous phase, and thereafter differentiating this phase (using another filter) to recover the instantaneous frequency. Alternatively, a complex mixer followed by a bandpass filter may be used to translate the signal to baseband, and then proceeding as before.
Applications
[edit]Doppler effect
[edit]When an echolocating bat approaches a target, its outgoing sounds return as echoes, which are Doppler-shifted upward in frequency. In certain species of bats, which produce constant frequency (CF) echolocation calls, the bats compensate for the Doppler shift by lowering their call frequency as they approach a target. This keeps the returning echo in the same frequency range of the normal echolocation call. This dynamic frequency modulation is called the Doppler Shift Compensation (DSC), and was discovered by Hans Schnitzler in 1968.
Magnetic tape storage
[edit]FM is also used at intermediate frequencies by analog VCR systems (including VHS) to record the luminance (black and white) portions of the video signal. Commonly, the chrominance component is recorded as a conventional AM signal, using the higher-frequency FM signal as bias. FM is the only feasible method of recording the luminance ("black-and-white") component of video to (and retrieving video from) magnetic tape without distortion; video signals have a large range of frequency components – from a few hertz to several megahertz, too wide for equalizers to work with due to electronic noise below −60 dB. FM also keeps the tape at saturation level, acting as a form of noise reduction; a limiter can mask variations in playback output, and the FM capture effect removes print-through and pre-echo. A continuous pilot-tone, if added to the signal – as was done on V2000 and many Hi-band formats – can keep mechanical jitter under control and assist timebase correction.
These FM systems are unusual, in that they have a ratio of carrier to maximum modulation frequency of less than two; contrast this with FM audio broadcasting, where the ratio is around 10,000. Consider, for example, a 6-MHz carrier modulated at a 3.5-MHz rate; by Bessel analysis, the first sidebands are on 9.5 and 2.5 MHz and the second sidebands are on 13 MHz and −1 MHz. The result is a reversed-phase sideband on +1 MHz; on demodulation, this results in unwanted output at 6 – 1 = 5 MHz. The system must be designed so that this unwanted output is reduced to an acceptable level.[11]
Sound
[edit]FM is also used at audio frequencies to synthesize sound. This technique, known as FM synthesis, was popularized by early digital synthesizers and became a standard feature in several generations of personal computer sound cards.
Radio
[edit]
Edwin Howard Armstrong (1890–1954) was an American electrical engineer who invented wideband frequency modulation (FM) radio.[12] He patented the regenerative circuit in 1914, the superheterodyne receiver in 1918 and the super-regenerative circuit in 1922.[13] Armstrong presented his paper, "A Method of Reducing Disturbances in Radio Signaling by a System of Frequency Modulation", (which first described FM radio) before the New York section of the Institute of Radio Engineers on November 6, 1935. The paper was published in 1936.[14]
As the name implies, wideband FM (WFM) requires a wider signal bandwidth than amplitude modulation by an equivalent modulating signal; this also makes the signal more robust against noise and interference. Frequency modulation is also more robust against signal-amplitude-fading phenomena. As a result, FM was chosen as the modulation standard for high frequency, high fidelity radio transmission, hence the term "FM radio" (although for many years the BBC called it "VHF radio" because commercial FM broadcasting uses part of the VHF band – the FM broadcast band). FM receivers employ a special detector for FM signals and exhibit a phenomenon known as the capture effect, in which the tuner "captures" the stronger of two stations on the same frequency while rejecting the other (compare this with a similar situation on an AM receiver, where both stations can be heard simultaneously). Frequency drift or a lack of selectivity may cause one station to be overtaken by another on an adjacent channel. Frequency drift was a problem in early (or inexpensive) receivers; inadequate selectivity may affect any tuner.
A wideband FM signal can also be used to carry a stereo signal; this is done with multiplexing and demultiplexing before and after the FM process. The FM modulation and demodulation process is identical in stereo and monaural processes.
FM is commonly used at VHF radio frequencies for high-fidelity broadcasts of music and speech. In broadcast services, where audio fidelity is important, wideband FM is generally used. Analog TV sound is also broadcast using FM. Narrowband FM is used for voice communications in commercial and amateur radio settings. In two-way radio, narrowband FM (NBFM) is used to conserve bandwidth for land mobile, marine mobile and other radio services.
A high-efficiency radio-frequency switching amplifier can be used to transmit FM signals (and other constant-amplitude signals). For a given signal strength (measured at the receiver antenna), switching amplifiers use less battery power and typically cost less than a linear amplifier. This gives FM another advantage over other modulation methods requiring linear amplifiers, such as AM and QAM.
There are reports that on October 5, 1924, Professor Mikhail A. Bonch-Bruevich, during a scientific and technical conversation in the Nizhny Novgorod Radio Laboratory, reported about his new method of telephony, based on a change in the period of oscillations. Demonstration of frequency modulation was carried out on the laboratory model.[15]
Hearing assistive technology
[edit]Frequency modulated systems are a widespread and commercially available assistive technology that make speech more understandable by improving the signal-to-noise ratio in the user's ear. They are also called auditory trainers, a term which refers to any sound amplification system not classified as a hearing aid. They intensify signal levels from the source by 15 to 20 decibels.[16] FM systems are used by hearing-impaired people as well as children whose listening is affected by disorders such as auditory processing disorder or ADHD.[17] For people with sensorineural hearing loss, FM systems result in better speech perception than hearing aids. They can be coupled with behind-the-ear hearing aids to allow the user to alternate the setting.[18] FM systems are more convenient and cost-effective than alternatives such as cochlear implants, but many users use FM systems infrequently due to their conspicuousness and need for recharging.[19]
See also
[edit]- Amplitude modulation
- Continuous-wave frequency-modulated radar
- Chirp
- FM broadcasting
- FM stereo
- FM-UWB (FM and Ultra Wideband)
- History of radio
- Modulation, for a list of other modulation techniques
- Phase modulation
References
[edit]- ^ Gibilisco, Stan (2002). Teach yourself electricity and electronics. McGraw-Hill Professional. p. 477. ISBN 978-0-07-137730-0.
morse-code frequency-shift-keying sent-using-fsk.
- ^ Rutledge, David B. (1999). The Electronics of Radio. Cambridge University Press. p. 310. ISBN 978-0-521-64645-1.
- ^ B. Boashash, editor, Time-Frequency Signal Analysis and Processing – A Comprehensive Reference, Elsevier Science, Oxford, 2003; ISBN 0-08-044335-4
- ^ Faruque, Saleh (2017). Radio Frequency Modulation Made Easy (PDF). Springer Cham. pp. 33–37. ISBN 978-3-319-41200-9.
- ^ a b T.G. Thomas, S. C. Sekhar Communication Theory, Tata-McGraw Hill 2005, ISBN 0-07-059091-5 p. 136
- ^ Der, Lawrence. "Frequency Modulation (FM) Tutorial" (PDF). Silicon Laboratories. S2CID 48672999. Archived from the original (PDF) on 2014-10-21. Retrieved 17 October 2019.
- ^ Lathi, B. P. (1968). Communication Systems, pp. 214–17. New York: John Wiley and Sons, ISBN 0-471-51832-8.
- ^ H. P. Westman, ed. (1970). Reference Data for Radio Engineers (Fifth ed.). Howard W. Sams & Co. pp. 21–11.
- ^ Alan Bloom (2010). "Chapter 8. Modulation". In H. Ward Silver; Mark J. Wilson (eds.). The ARRL Handbook for Radio Communications. American Radio Relay League. p. 8.7. ISBN 978-0-87259-146-2.
- ^ Haykin, Simon [Ed]. (2001). Communication Systems, 4th ed.
- ^ "FM Systems Of Exceptional Bandwidth" Proc. IEEE vol. 112, no. 9, p. 1664, September 1965
- ^ A. Michael Noll (2001). Principles of modern communications technology. Artech House. p. 104. ISBN 978-1580532846.
- ^ US 1342885
- ^ Armstrong, E. H. (May 1936). "A Method of Reducing Disturbances in Radio Signaling by a System of Frequency Modulation". Proceedings of the IRE. 24 (5). IRE: 689–740. doi:10.1109/JRPROC.1936.227383. S2CID 43628076.
- ^ Ф. Лбов. Новая система радиофона «Радиолюбитель». – 1924. – № 6. – С. 86.
- ^ ASHA Ad Hoc Committee on FM Systems (2002) [Original March 1994]. Guidelines for Fitting and Monitoring FM Systems (Technical report) (Revised ed.). American Speech–Language–Hearing Association. doi:10.1044/policy.GL2002-00010.
- ^ Schafer, Erin C.; Bryant, Danielle; Sanders, Katie; Baldus, Nicole; Algier, Katherine; Lewis, Audrey; Traber, Jordan; Layden, Paige; Amin, Aneeqa (June 1, 2014). "Fitting and Verification of Frequency Modulation on Children with Normal Hearing". Journal of the American Academy of Audiology. 25 (6): 529–540. doi:10.3766/jaaa.25.6.3. ISSN 1050-0545. PMID 25313543. EBSCOhost 107832936 – via EBSCOhost.
- ^ Lewis, M. Samantha; Crandall, Carl C.; Valente, Michael; Enrietto Horn, Jane (2004). "Speech perception in noise: directional microphones versus frequency modulation (FM) systems". Journal of the American Academy of Audiology. 15 (6): 426–439. doi:10.3766/jaaa.15.6.4. PMID 15341224.
- ^ McArdle, Rachel; Abrams, Harvey B.; Hnath Chisholm, Theresa (2005). "When Hearing Aids Go Bad: An FM Success Story". Journal of the American Academy of Audiology. 16 (10): 809–821. doi:10.3766/jaaa.16.10.5. EBSCOhost 106441304 – via EBSCOhost.
Further reading
[edit]- Carlson, A. Bruce (2001). Communication Systems. Science/Engineering/Math (4th ed.). McGraw-Hill. ISBN 978-0-07-011127-1.
- Frost, Gary L. (2010). Early FM Radio: Incremental technology in twentieth-century America. Baltimore, MD: Johns Hopkins University Press. ISBN 978-0-8018-9440-4.
- Seymour, Ken (2005) [1996]. "Frequency Modulation". The Electronics Handbook (2nd ed.). CRC Press. pp. 1188–1200. ISBN 0-8493-8345-5.
External links
[edit]- Analog Modulation online interactive demonstration using Python in Google Colab Platform, by C Foh.
Phase Modulation (PM)
[edit]| Passband modulation |
|---|
 |
| Analog modulation |
| Digital modulation |
| Hierarchical modulation |
| Spread spectrum |
| See also |
Phase modulation (PM) is a modulation pattern for conditioning communication signals for transmission. It encodes a message signal as variations in the instantaneous phase of a carrier wave. Phase modulation is one of the two principal forms of angle modulation, together with frequency modulation.
In phase modulation, the instantaneous amplitude of the baseband signal modifies the phase of the carrier signal keeping its amplitude and frequency constant. The phase of a carrier signal is modulated to follow the changing signal level (amplitude) of the message signal. The peak amplitude and the frequency of the carrier signal are maintained constant, but as the amplitude of the message signal changes, the phase of the carrier changes correspondingly.
Phase modulation is an integral part of many digital transmission coding schemes that underlie a wide range of technologies like Wi-Fi, GSM and satellite television. However it is not widely used for transmitting analog audio signals via radio waves.[why?] It is also used for signal and waveform generation in digital synthesizers, such as the Yamaha DX7, to implement FM synthesis. A related type of sound synthesis called phase distortion is used in the Casio CZ synthesizers.
Foundation
[edit]In general form, an analog modulation process of a sinusoidal carrier wave may be described by the following equation:[1]
- .
A(t) represents the time-varying amplitude of the sinusoidal carrier wave and the cosine-term is the carrier at its angular frequency , and the instantaneous phase deviation . This description directly provides the two major groups of modulation, amplitude modulation and angle modulation. In amplitude modulation, the angle term is held constant, while in angle modulation the term A(t) is constant and the second term of the equation has a functional relationship to the modulating message signal.
The functional form of the cosine term, which contains the expression of the instantaneous phase as its argument, provides the distinction of the two types of angle modulation, frequency modulation (FM) and phase modulation (PM).[2]

In FM the message signal causes a functional variation of the carrier frequency. These variations are controlled by both the frequency and the amplitude of the modulating wave.
In phase modulation, the instantaneous phase deviation (phase angle) of the carrier is controlled by the modulating waveform, such that the principal frequency remains constant.
In principle, the modulating signal in both frequency and phase modulation may either be analog in nature, or it may be digital.
The mathematics of the spectral behaviour reveals that there are two regions of particular interest:
- For small amplitude signals, PM is similar to amplitude modulation (AM) and exhibits its unfortunate doubling of baseband bandwidth and poor efficiency.
- For a single large sinusoidal signal, PM is similar to FM, and its bandwidth is approximately
- ,
Modulation index
[edit]As with other modulation indices, this quantity indicates by how much the modulated variable varies around its unmodulated level. It relates to the variations in the phase of the carrier signal:
where is the peak phase deviation. Compare to the modulation index for frequency modulation.
See also
[edit]- Automatic frequency control
- Modulation for a list of other modulation techniques
- Modulation sphere
- Polar modulation
- Electro-optic modulator for Pockel's Effect phase modulation for applying sidebands to a monochromatic wave
References
[edit]- ^ Klie, Robert H.; Bell Telephone Laboratories; AT&T (1977). Principles. Telecommunication Transmission Engineering. Vol. 1 (2nd ed.). Bell Center for Technical Education. ISBN 0-932764-13-4. OCLC 894686224.
- ^ Haykin, Simon (2001). Communication Systems. Wiley. p. 107. ISBN 0-471-17869-1.
Warning: Default sort key "Phase Modulation" overrides earlier default sort key "Amplitude Modulation".
Quadrature Amplitude Modulation (QAM)
[edit]This article may be too technical for most readers to understand. (June 2020) |
| Passband modulation |
|---|
 |
| Analog modulation |
| Digital modulation |
| Hierarchical modulation |
| Spread spectrum |
| See also |
Quadrature amplitude modulation (QAM) is the name of a family of digital modulation methods and a related family of analog modulation methods widely used in modern telecommunications to transmit information. It conveys two analog message signals, or two digital bit streams, by changing (modulating) the amplitudes of two carrier waves, using the amplitude-shift keying (ASK) digital modulation scheme or amplitude modulation (AM) analog modulation scheme. The two carrier waves are of the same frequency and are out of phase with each other by 90°, a condition known as orthogonality or quadrature. The transmitted signal is created by adding the two carrier waves together. At the receiver, the two waves can be coherently separated (demodulated) because of their orthogonality. Another key property is that the modulations are low-frequency/low-bandwidth waveforms compared to the carrier frequency, which is known as the narrowband assumption.
Phase modulation (analog PM) and phase-shift keying (digital PSK) can be regarded as a special case of QAM, where the amplitude of the transmitted signal is a constant, but its phase varies. This can also be extended to frequency modulation (FM) and frequency-shift keying (FSK), for these can be regarded as a special case of phase modulation[citation needed].
QAM is used extensively as a modulation scheme for digital communications systems, such as in 802.11 Wi-Fi standards. Arbitrarily high spectral efficiencies can be achieved with QAM by setting a suitable constellation size, limited only by the noise level and linearity of the communications channel.[1] QAM is being used in optical fiber systems as bit rates increase; QAM16 and QAM64 can be optically emulated with a three-path interferometer.[2][3]
Demodulation
[edit]
In a QAM signal, one carrier lags the other by 90°, and its amplitude modulation is customarily referred to as the in-phase component, denoted by I(t). The other modulating function is the quadrature component, Q(t). So the composite waveform is mathematically modeled as:
- or:
| (Eq.1) |
where fc is the carrier frequency. At the receiver, a coherent demodulator multiplies the received signal separately with both a cosine and sine signal to produce the received estimates of I(t) and Q(t). For example:
Using standard trigonometric identities, we can write this as:
Low-pass filtering r(t) removes the high frequency terms (containing 4πfct), leaving only the I(t) term. This filtered signal is unaffected by Q(t), showing that the in-phase component can be received independently of the quadrature component. Similarly, we can multiply sc(t) by a sine wave and then low-pass filter to extract Q(t).

The addition of two sinusoids is a linear operation that creates no new frequency components. So the bandwidth of the composite signal is comparable to the bandwidth of the DSB (double-sideband) components. Effectively, the spectral redundancy of DSB enables a doubling of the information capacity using this technique. This comes at the expense of demodulation complexity. In particular, a DSB signal has zero-crossings at a regular frequency, which makes it easy to recover the phase of the carrier sinusoid. It is said to be self-clocking. But the sender and receiver of a quadrature-modulated signal must share a clock or otherwise send a clock signal. If the clock phases drift apart, the demodulated I and Q signals bleed into each other, yielding crosstalk. In this context, the clock signal is called a "phase reference". Clock synchronization is typically achieved by transmitting a burst subcarrier or a pilot signal. The phase reference for NTSC, for example, is included within its colorburst signal.
Analog QAM is used in:
- NTSC and PAL analog color television systems, where the I- and Q-signals carry the components of chroma (colour) information. The QAM carrier phase is recovered from a special colorburst transmitted at the beginning of each scan line.
- C-QUAM ("Compatible QAM") is used in AM stereo radio to carry the stereo difference information.
Fourier analysis
[edit]Applying Euler's formula to the sinusoids in Eq.1, the positive-frequency portion of sc (or analytic representation) is:
where denotes the Fourier transform, and and are the transforms of I(t) and Q(t). This result represents the sum of two DSB-SC signals with the same center frequency. The factor of i (= eiπ/2) represents the 90° phase shift that enables their individual demodulations.
Digital QAM
[edit]

As in many digital modulation schemes, the constellation diagram is useful for QAM. In QAM, the constellation points are usually arranged in a square grid with equal vertical and horizontal spacing, although other configurations are possible (e.g. a hexagonal or triangular grid). In digital telecommunications the data is usually binary, so the number of points in the grid is typically a power of 2 (2, 4, 8, …), corresponding to the number of bits per symbol. The simplest and most commonly used QAM constellations consist of points arranged in a square, i.e. 16-QAM, 64-QAM and 256-QAM (even powers of two). Non-square constellations, such as Cross-QAM, can offer greater efficiency but are rarely used because of the cost of increased modem complexity.
By moving to a higher-order constellation, it is possible to transmit more bits per symbol. However, if the mean energy of the constellation is to remain the same (by way of making a fair comparison), the points must be closer together and are thus more susceptible to noise and other corruption; this results in a higher bit error rate and so higher-order QAM can deliver more data less reliably than lower-order QAM, for constant mean constellation energy. Using higher-order QAM without increasing the bit error rate requires a higher signal-to-noise ratio (SNR) by increasing signal energy, reducing noise, or both.
If data rates beyond those offered by 8-PSK are required, it is more usual to move to QAM since it achieves a greater distance between adjacent points in the I-Q plane by distributing the points more evenly. The complicating factor is that the points are no longer all the same amplitude and so the demodulator must now correctly detect both phase and amplitude, rather than just phase.
64-QAM and 256-QAM are often used in digital cable television and cable modem applications. In the United States, 64-QAM and 256-QAM are the mandated modulation schemes for digital cable (see QAM tuner) as standardised by the SCTE in the standard ANSI/SCTE 07 2013. In the UK, 64-QAM is used for digital terrestrial television (Freeview) whilst 256-QAM is used for Freeview-HD.

Communication systems designed to achieve very high levels of spectral efficiency usually employ very dense QAM constellations. For example, current Homeplug AV2 500-Mbit/s powerline Ethernet devices use 1024-QAM and 4096-QAM,[4] as well as future devices using ITU-T G.hn standard for networking over existing home wiring (coaxial cable, phone lines and power lines); 4096-QAM provides 12 bits/symbol. Another example is ADSL technology for copper twisted pairs, whose constellation size goes up to 32768-QAM (in ADSL terminology this is referred to as bit-loading, or bit per tone, 32768-QAM being equivalent to 15 bits per tone).[5]
Ultra-high capacity microwave backhaul systems also use 1024-QAM.[6] With 1024-QAM, adaptive coding and modulation (ACM) and XPIC, vendors can obtain gigabit capacity in a single 56 MHz channel.[6]
Interference and noise
[edit]In moving to a higher order QAM constellation (higher data rate and mode) in hostile RF/microwave QAM application environments, such as in broadcasting or telecommunications, multipath interference typically increases. There is a spreading of the spots in the constellation, decreasing the separation between adjacent states, making it difficult for the receiver to decode the signal appropriately. In other words, there is reduced noise immunity. There are several test parameter measurements which help determine an optimal QAM mode for a specific operating environment. The following three are most significant:[7]
- Carrier/interference ratio
- Carrier-to-noise ratio
- Threshold-to-noise ratio
See also
[edit]- Amplitude and phase-shift keying or asymmetric phase-shift keying (APSK)
- Carrierless amplitude phase modulation (CAP)
- Circle packing § Applications
- In-phase and quadrature components
- Modulation for other examples of modulation techniques
- Phase-shift keying
- QAM tuner for HDTV
- Random modulation
References
[edit]- ^ "Digital Modulation Efficiencies". Barnard Microsystems. Archived from the original on 2011-04-30.
- ^ "Ciena tests 200G via 16-QAM with Japan-U.S. Cable Network". lightwave. April 17, 2014. Retrieved 7 November 2016.
- ^ Kylia products Archived July 13, 2011, at the Wayback Machine, dwdm mux demux, 90 degree optical hybrid, d(q) psk demodulatorssingle polarization
- ^ "HomePlug® AV2 Technology" (PDF). www.homeplug.org. Archived from the original (PDF) on 2015-09-23.
- ^ "G.992.3 : Asymmetric digital subscriber line transceivers 2 (ADSL2)". www.itu.int. Constellation mapper - maximum number of bits per constellation BIMAX ≤ 15. Retrieved 2024-10-09.
{{cite web}}: CS1 maint: others (link) - ^ a b "TrangoLink Apex Orion - Trango Systems". www.trangosys.com. Archived from the original on 2012-03-15.
- ^ Howard Friedenberg and Sunil Naik. "Hitless Space Diversity STL Enables IP+Audio in Narrow STL Bands" (PDF). 2005 National Association of Broadcasters Annual Convention. Archived from the original (PDF) on March 23, 2006. Retrieved April 17, 2005.
Further reading
[edit]- Jonqyin (Russell) Sun "Linear diversity analysis for QAM in Rician fading channels", IEEE WOCC 2014
- John G. Proakis, "Digital Communications, 3rd Edition"
External links
[edit]- QAM Demodulation
- Interactive webdemo of QAM constellation with additive noise Institute of Telecommunicatons, University of Stuttgart
- QAM bit error rate for AWGN channel – online experiment
- How imperfections affect QAM constellation
- Microwave Phase Shifters Overview by Herley General Microwave
- Simulation of dual-polarization QPSK (DP-QPSK) for 100G optical transmission
Warning: Default sort key "Quadrature Amplitude Modulation" overrides earlier default sort key "Phase Modulation".
Space Modulation (SM)
[edit]| Passband modulation |
|---|
 |
| Analog modulation |
| Digital modulation |
| Hierarchical modulation |
| Spread spectrum |
| See also |
Space modulation is a radio amplitude modulation technique used in instrument landing systems (ILS) that incorporates the use of multiple antennas fed with various radio frequency powers and phases to create different depths of modulation within various volumes of three-dimensional airspace. This modulation method differs from internal modulation methods inside most other radio transmitters in that the phases and powers of the two individual signals mix within airspace, rather than in a modulator.
An aircraft with an on-board ILS receiver within the capture area of an ILS, (glideslope and localizer range), will detect varying depths of modulation according to the aircraft's position within that airspace, providing accurate positional information about the progress to the threshold.
Method used to determine aircraft position
[edit]The ILS uses two radio frequencies, one for each ground station (about 110 MHz for LOC and 330 MHz for the GS), to transmit two amplitude-modulated signals (90 Hz and 150 Hz), along the glidepath (GS) and the course (LOC) trajectories into airspace. It is this signal that is projected up from the runway which an aircraft employing an instrument approach uses to land.
The modulation depth of each 90 Hz and 150 Hz signal changes according to the deviation of the aircraft from the correct position for the aircraft to touchdown on the threshold. The difference between the two signal modulation depths is zero when the aircraft is on the correct course and glidepath on approach to the runway—i.e. No difference (zero DDM), produces no deviation from the middle indication of the instrument's needle within the cockpit of the aircraft.
See also
[edit]
Single-Sideband Modulation (SSB)
[edit]This article needs additional citations for verification. (July 2015) |

| Passband modulation |
|---|
 |
| Analog modulation |
| Digital modulation |
| Hierarchical modulation |
| Spread spectrum |
| See also |
In radio communications, single-sideband modulation (SSB) or single-sideband suppressed-carrier modulation (SSB-SC) is a type of modulation used to transmit information, such as an audio signal, by radio waves. A refinement of amplitude modulation, it uses transmitter power and bandwidth more efficiently. Amplitude modulation produces an output signal the bandwidth of which is twice the maximum frequency of the original baseband signal. Single-sideband modulation avoids this bandwidth increase, and the power wasted on a carrier, at the cost of increased device complexity and more difficult tuning at the receiver.
Basic concept
[edit]Radio transmitters work by mixing a radio frequency (RF) signal of a specific frequency, the carrier wave, with the audio signal to be broadcast. In AM transmitters this mixing usually takes place in the final RF amplifier (high level modulation). It is less common and much less efficient to do the mixing at low power and then amplify it in a linear amplifier. Either method produces a set of frequencies with a strong signal at the carrier frequency and with weaker signals at frequencies extending above and below the carrier frequency by the maximum frequency of the input signal. Thus the resulting signal has a spectrum whose bandwidth is twice the maximum frequency of the original input audio signal.
SSB takes advantage of the fact that the entire original signal is encoded in each of these "sidebands". Since a good receiver can extract the complete original signal from either the upper or lower sideband, it is not essential to transmit both sidebands plus the carrier. There are several methods for eliminating the carrier and one sideband from the transmitted signal. Producing this single sideband signal can be done at high level in the final amplifier stage as with AM [1] [2] but it is usually produced at a low power level and linearly amplified. The lower efficiency of linear amplification partially offsets the power advantage gained by eliminating the carrier and one sideband. Nevertheless, SSB transmissions use the available amplifier energy considerably more efficiently, providing longer-range transmission for the same power output. In addition, the occupied spectrum is less than half that of a full carrier AM signal.
SSB reception requires frequency stability and selectivity well beyond that of inexpensive AM receivers which is why broadcasters have seldom used it. In point-to-point communications where expensive receivers are in common use already they can successfully be adjusted to receive whichever sideband is being transmitted.
History
[edit]The first U.S. patent application for SSB modulation was filed on December 1, 1915, by John Renshaw Carson.[3] The U.S. Navy experimented with SSB over its radio circuits before World War I.[4][5] SSB first entered commercial service on January 7, 1927, on the longwave transatlantic public radiotelephone circuit between New York and London. The high power SSB transmitters were located at Rocky Point, New York, and Rugby, England. The receivers were in very quiet locations in Houlton, Maine, and Cupar, Scotland.[6]
SSB was also used over long-distance telephone lines, as part of a technique known as frequency-division multiplexing (FDM). FDM was pioneered by telephone companies in the 1930s. With this technology, many simultaneous voice channels could be transmitted on a single physical circuit, for example in L-carrier. With SSB, channels could be spaced (usually) only 4,000 Hz apart, while offering a speech bandwidth of nominally 300 Hz to 3,400 Hz.
Amateur radio operators began serious experimentation with SSB after World War II. The Strategic Air Command established SSB as the radio standard for its aircraft in 1957.[7] It has become a de facto standard for long-distance voice radio transmissions since then.
Mathematical formulation
[edit]
Single-sideband has the mathematical form of quadrature amplitude modulation (QAM) in the special case where one of the baseband waveforms is derived from the other, instead of being independent messages:
| (Eq.1) |
where is the message (real-valued), is its Hilbert transform, and is the radio carrier frequency.[8]
To understand this formula, we may express as the real part of a complex-valued function, with no loss of information:
where represents the imaginary unit. is the analytic representation of which means that it comprises only the positive-frequency components of :
where and are the respective Fourier transforms of and Therefore, the frequency-translated function contains only one side of Since it also has only positive-frequency components, its inverse Fourier transform is the analytic representation of
and again the real part of this expression causes no loss of information. With Euler's formula to expand we obtain Eq.1:
Coherent demodulation of to recover is the same as AM: multiply by and lowpass to remove the "double-frequency" components around frequency . If the demodulating carrier is not in the correct phase (cosine phase here), then the demodulated signal will be some linear combination of and , which is usually acceptable in voice communications (if the demodulation carrier frequency is not quite right, the phase will be drifting cyclically, which again is usually acceptable in voice communications if the frequency error is small enough, and amateur radio operators are sometimes tolerant of even larger frequency errors that cause unnatural-sounding pitch shifting effects).
Lower sideband
[edit]can also be recovered as the real part of the complex-conjugate, which represents the negative frequency portion of When is large enough that has no negative frequencies, the product is another analytic signal, whose real part is the actual lower-sideband transmission:
The sum of the two sideband signals is:
which is the classic model of suppressed-carrier double sideband AM.
Practical implementations
[edit]
Bandpass filtering
[edit]One method of producing an SSB signal is to remove one of the sidebands via filtering, leaving only either the upper sideband (USB), the sideband with the higher frequency, or less commonly the lower sideband (LSB), the sideband with the lower frequency. Most often, the carrier is reduced or removed entirely (suppressed), being referred to in full as single sideband suppressed carrier (SSBSC). Assuming both sidebands are symmetric, which is the case for a normal AM signal, no information is lost in the process. Since the final RF amplification is now concentrated in a single sideband, the effective power output is greater than in normal AM (the carrier and redundant sideband account for well over half of the power output of an AM transmitter). Though SSB uses substantially less bandwidth and power, it cannot be demodulated by a simple envelope detector like standard AM.
Hartley modulator
[edit]An alternate method of generation known as a Hartley modulator, named after R. V. L. Hartley, uses phasing to suppress the unwanted sideband. To generate an SSB signal with this method, two versions of the original signal are generated, mutually 90° out of phase for any single frequency within the operating bandwidth. Each one of these signals then modulates carrier waves (of one frequency) that are also 90° out of phase with each other. By either adding or subtracting the resulting signals, a lower or upper sideband signal results. A benefit of this approach is to allow an analytical expression for SSB signals, which can be used to understand effects such as synchronous detection of SSB.
Shifting the baseband signal 90° out of phase cannot be done simply by delaying it, as it contains a large range of frequencies. In analog circuits, a wideband 90-degree phase-difference network[9] is used. The method was popular in the days of vacuum tube radios, but later gained a bad reputation due to poorly adjusted commercial implementations. Modulation using this method is again gaining popularity in the homebrew and DSP fields. This method, utilizing the Hilbert transform to phase shift the baseband audio, can be done at low cost with digital circuitry.
Weaver modulator
[edit]Another variation, the Weaver modulator,[10] uses only lowpass filters and quadrature mixers, and is a favored method in digital implementations.
In Weaver's method, the band of interest is first translated to be centered at zero, conceptually by modulating a complex exponential with frequency in the middle of the voiceband, but implemented by a quadrature pair of sine and cosine modulators at that frequency (e.g. 2 kHz). This complex signal or pair of real signals is then lowpass filtered to remove the undesired sideband that is not centered at zero. Then, the single-sideband complex signal centered at zero is upconverted to a real signal, by another pair of quadrature mixers, to the desired center frequency.
Full, reduced, and suppressed-carrier SSB
[edit]Conventional amplitude-modulated signals can be considered wasteful of power and bandwidth because they contain a carrier signal and two identical sidebands. Therefore, SSB transmitters are generally designed to minimize the amplitude of the carrier signal. When the carrier is removed from the transmitted signal, it is called suppressed-carrier SSB.
However, in order for a receiver to reproduce the transmitted audio without distortion, it must be tuned to exactly the same frequency as the transmitter. Since this is difficult to achieve in practice, SSB transmissions can sound unnatural, and if the error in frequency is great enough, it can cause poor intelligibility. In order to correct this, a small amount of the original carrier signal can be transmitted so that receivers with the necessary circuitry to synchronize with the transmitted carrier can correctly demodulate the audio. This mode of transmission is called reduced-carrier single-sideband.
In other cases, it may be desirable to maintain some degree of compatibility with simple AM receivers, while still reducing the signal's bandwidth. This can be accomplished by transmitting single-sideband with a normal or slightly reduced carrier. This mode is called compatible (or full-carrier) SSB or amplitude modulation equivalent (AME). In typical AME systems, harmonic distortion can reach 25%, and intermodulation distortion can be much higher than normal, but minimizing distortion in receivers with envelope detectors is generally considered less important than allowing them to produce intelligible audio.
A second, and perhaps more correct, definition of "compatible single sideband" (CSSB) refers to a form of amplitude and phase modulation in which the carrier is transmitted along with a series of sidebands that are predominantly above or below the carrier term. Since phase modulation is present in the generation of the signal, energy is removed from the carrier term and redistributed into the sideband structure similar to that which occurs in analog frequency modulation. The signals feeding the phase modulator and the envelope modulator are further phase-shifted by 90° with respect to each other. This places the information terms in quadrature with each other; the Hilbert transform of information to be transmitted is utilized to cause constructive addition of one sideband and cancellation of the opposite primary sideband. Since phase modulation is employed, higher-order terms are also generated. Several methods have been employed to reduce the impact (amplitude) of most of these higher-order terms. In one system, the phase-modulated term is actually the log of the value of the carrier level plus the phase-shifted audio/information term. This produces an ideal CSSB signal, where at low modulation levels only a first-order term on one side of the carrier is predominant. As the modulation level is increased, the carrier level is reduced while a second-order term increases substantially in amplitude. At the point of 100% envelope modulation, 6 dB of power is removed from the carrier term, and the second-order term is identical in amplitude to carrier term. The first-order sideband has increased in level until it is now at the same level as the formerly unmodulated carrier. At the point of 100% modulation, the spectrum appears identical to a normal double-sideband AM transmission, with the center term (now the primary audio term) at a 0 dB reference level, and both terms on either side of the primary sideband at −6 dB. The difference is that what appears to be the carrier has shifted by the audio-frequency term towards the "sideband in use". At levels below 100% modulation, the sideband structure appears quite asymmetric. When voice is conveyed by a CSSB source of this type, low-frequency components are dominant, while higher-frequency terms are lower by as much as 20 dB at 3 kHz. The result is that the signal occupies approximately 1/2 the normal bandwidth of a full-carrier, DSB signal. There is one catch: the audio term utilized to phase-modulate the carrier is generated based on a log function that is biased by the carrier level. At negative 100% modulation, the term is driven to zero (0), and the modulator becomes undefined. Strict modulation control must be employed to maintain stability of the system and avoid splatter. This system is of Russian origin and was described in the late 1950s. It is uncertain whether it was ever deployed.
A second series of approaches was designed and patented by Leonard R. Kahn. The various Kahn systems removed the hard limit imposed by the use of the strict log function in the generation of the signal. Earlier Kahn systems utilized various methods to reduce the second-order term through the insertion of a predistortion component. One example of this method was also used to generate one of the Kahn independent-sideband (ISB) AM stereo signals. It was known as the STR-77 exciter method, having been introduced in 1977. Later, the system was further improved by use of an arcsine-based modulator that included a 1-0.52E term in the denominator of the arcsin generator equation. E represents the envelope term; roughly half the modulation term applied to the envelope modulator is utilized to reduce the second-order term of the arcsin "phase"-modulated path; thus reducing the second-order term in the undesired sideband. A multi-loop modulator/demodulator feedback approach was used to generate an accurate arcsin signal. This approach was introduced in 1984 and became known as the STR-84 method. It was sold by Kahn Research Laboratories; later, Kahn Communications, Inc. of NY. An additional audio processing device further improved the sideband structure by selectively applying pre-emphasis to the modulating signals. Since the envelope of all the signals described remains an exact copy of the information applied to the modulator, it can be demodulated without distortion by an envelope detector such as a simple diode. In a practical receiver, some distortion may be present, usually at a low level (in AM broadcast, always below 5%), due to sharp filtering and nonlinear group delay in the IF filters of the receiver, which act to truncate the compatibility sideband – those terms that are not the result of a linear process of simply envelope modulating the signal as would be the case in full-carrier DSB-AM – and rotation of phase of these compatibility terms such that they no longer cancel the quadrature distortion term caused by a first-order SSB term along with the carrier. The small amount of distortion caused by this effect is generally quite low and acceptable.
The Kahn CSSB method was also briefly used by Airphone as the modulation method employed for early consumer telephone calls that could be placed from an aircraft to ground. This was quickly supplanted by digital modulation methods to achieve even greater spectral efficiency.
While CSSB is seldom used today in the AM/MW broadcast bands worldwide, some amateur radio operators still experiment with it.
Demodulation
[edit]The front end of an SSB receiver is similar to that of an AM or FM receiver, consisting of a superheterodyne RF front end that produces a frequency-shifted version of the radio frequency (RF) signal within a standard intermediate frequency (IF) band.
To recover the original signal from the IF SSB signal, the single sideband must be frequency-shifted down to its original range of baseband frequencies, by using a product detector which mixes it with the output of a beat frequency oscillator (BFO). In other words, it is just another stage of heterodyning. For this to work, the BFO frequency must be exactly adjusted. If the BFO frequency is off, the output signal will be frequency-shifted (up or down), making speech sound strange and "Donald Duck"-like, or unintelligible.
For audio communications, there is a common agreement about the BFO oscillator shift of 1.7 kHz. A voice signal is sensitive to about 50 Hz shift, with up to 100 Hz still bearable. Some receivers use a carrier recovery system, which attempts to automatically lock on to the exact IF frequency. The carrier recovery doesn't solve the frequency shift. It gives better S/N ratio on the detector output.[citation needed]
As an example, consider an IF SSB signal centered at frequency = 45000 Hz. The baseband frequency it needs to be shifted to is = 2000 Hz. The BFO output waveform is . When the signal is multiplied by (aka heterodyned with) the BFO waveform, it shifts the signal to , and to , which is known as the beat frequency or image frequency. The objective is to choose an that results in = 2000 Hz. (The unwanted components at can be removed by a lowpass filter; for which an output transducer or the human ear may serve).
There are two choices for : 43000 Hz and 47000 Hz, called low-side and high-side injection. With high-side injection, the spectral components that were distributed around 45000 Hz will be distributed around 2000 Hz in the reverse order, also known as an inverted spectrum. That is in fact desirable when the IF spectrum is also inverted, because the BFO inversion restores the proper relationships. One reason for that is when the IF spectrum is the output of an inverting stage in the receiver. Another reason is when the SSB signal is actually a lower sideband, instead of an upper sideband. But if both reasons are true, then the IF spectrum is not inverted, and the non-inverting BFO (43000 Hz) should be used.
If is off by a small amount, then the beat frequency is not exactly , which can lead to the speech distortion mentioned earlier.
SSB as a speech-scrambling technique
[edit]SSB techniques can also be adapted to frequency-shift and frequency-invert baseband waveforms (voice inversion). This voice scrambling method was made by running the audio of one side band modulated audio sample through its opposite (e.g. running an LSB modulated audio sample through a radio running USB modulation). These effects were used, in conjunction with other filtering techniques, during World War II as a simple method for speech encryption. Radiotelephone conversations between the US and Britain were intercepted and "decrypted" by the Germans; they included some early conversations between Franklin D. Roosevelt and Churchill.[citation needed] In fact, the signals could be understood directly by trained operators. Largely to allow secure communications between Roosevelt and Churchill, the SIGSALY system of digital encryption was devised.
Today, such simple inversion-based speech encryption techniques are easily decrypted using simple techniques and are no longer regarded as secure.
Vestigial sideband (VSB)
[edit]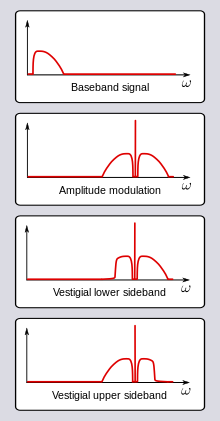
Limitation of single-sideband modulation being used for voice signals and not available for video/TV signals leads to the usage of vestigial sideband. A vestigial sideband (in radio communication) is a sideband that has been only partly cut off or suppressed. Television broadcasts (in analog video formats) use this method if the video is transmitted in AM, due to the large bandwidth used. It may also be used in digital transmission, such as the ATSC standardized 8VSB.
The broadcast or transport channel for TV in countries that use NTSC or ATSC has a bandwidth of 6 MHz. To conserve bandwidth, SSB would be desirable, but the video signal has significant low-frequency content (average brightness) and has rectangular synchronising pulses. The engineering compromise is vestigial-sideband transmission. In vestigial sideband, the full upper sideband of bandwidth W2 = 4.0 MHz is transmitted, but only W1 = 0.75 MHz of the lower sideband is transmitted, along with a carrier. The carrier frequency is 1.25 MHz above the lower edge of the 6 MHz wide channel. This effectively makes the system AM at low modulation frequencies and SSB at high modulation frequencies. The absence of the lower sideband components at high frequencies must be compensated for, and this is done in the IF amplifier.
Frequencies for LSB and USB in amateur radio voice communication
[edit]When single-sideband is used in amateur radio voice communications, it is common practice that for frequencies below 10 MHz, lower sideband (LSB) is used and for frequencies of 10 MHz and above, upper sideband (USB) is used.[11] For example, on the 40 m band, voice communications often take place around 7.100 MHz using LSB mode. On the 20 m band at 14.200 MHz, USB mode would be used.
An exception to this rule applies to the five discrete amateur channels on the 60-meter band (near 5.3 MHz) where FCC rules specifically require USB.[12]
Extended single sideband (eSSB)
[edit]Extended single sideband is any J3E (SSB-SC) mode that exceeds the audio bandwidth of standard or traditional 2.9 kHz SSB J3E modes (ITU 2K90J3E) to support higher-quality sound.
| Extended SSB modes | Bandwidth | Frequency response | ITU Designator |
|---|---|---|---|
| eSSB (Narrow-1a) | 3 kHz | 100 Hz ~ 3.10 kHz | 3K00J3E |
| eSSB (Narrow-1b) | 3 kHz | 50 Hz ~ 3.05 kHz | 3K00J3E |
| eSSB (Narrow-2) | 3.5 kHz | 50 Hz ~ 3.55 kHz | 3K50J3E |
| eSSB (Medium-1) | 4 kHz | 50 Hz ~ 4.05 kHz | 4K00J3E |
| eSSB (Medium-2) | 4.5 kHz | 50 Hz ~ 4.55 kHz | 4K50J3E |
| eSSB (Wide-1) | 5 kHz | 50 Hz ~ 5.05 kHz | 5K00J3E |
| eSSB (Wide-2) | 6 kHz | 50 Hz ~ 6.05 kHz | 6K00J3E |
Amplitude-companded single sideband (ACSSB) is a narrowband modulation method using a single sideband with a pilot tone, allowing an expander in the receiver to restore the amplitude that was severely compressed by the transmitter. It offers improved effective range over standard SSB modulation while simultaneously retaining backwards compatibility with standard SSB radios. ACSSB also offers reduced bandwidth and improved range for a given power level compared with narrow band FM modulation.
The generation of standard SSB modulation results in large envelope overshoots well above the average envelope level for a sinusoidal tone (even when the audio signal is peak-limited). The standard SSB envelope peaks are due to truncation of the spectrum and nonlinear phase distortion from the approximation errors of the practical implementation of the required Hilbert transform. It was recently shown that suitable overshoot compensation (so-called controlled-envelope single-sideband modulation or CESSB) achieves about 3.8 dB of peak reduction for speech transmission. This results in an effective average power increase of about 140%.[13] Although the generation of the CESSB signal can be integrated into the SSB modulator, it is feasible to separate the generation of the CESSB signal (e.g. in form of an external speech preprocessor) from a standard SSB radio. This requires that the standard SSB radio's modulator be linear-phase and have a sufficient bandwidth to pass the CESSB signal. If a standard SSB modulator meets these requirements, then the envelope control by the CESSB process is preserved.[14]
ITU designations
[edit]In 1982, the International Telecommunication Union (ITU) designated the types of amplitude modulation:
| Designation | Description |
|---|---|
| A3E | Double-sideband full-carrier – the basic amplitude-modulation scheme |
| R3E | Single-sideband reduced-carrier |
| H3E | Single-sideband full-carrier |
| J3E | Single-sideband suppressed-carrier |
| B8E | Independent-sideband emission |
| C3F | Vestigial-sideband |
| Lincompex | Linked compressor and expander |
See also
[edit]- ACSSB, amplitude-companded single sideband
- Independent sideband
- Modulation for other examples of modulation techniques
- Sideband for more general information about a sideband
References
[edit]- ^ Michael Murray Elliott (1953). Single sideband transmission by envelope elimination and restoration (Thesis). Naval Postgraduate School. hdl:10945/24839.
- ^ Leonard R Kahn (July 1952). "Single-sideband transmission by envelope elimination and restoration". Proceedings of the IRE. 40 (7): 803–806. doi:10.1109/JRPROC.1952.273844. S2CID 51669401.
- ^ US 1449382 John Carson/AT&T: "Method and Means for Signaling with High Frequency Waves" filed on December 1, 1915; granted on March 27, 1923
- ^ The History of Single Sideband Modulation Archived 2004-01-03 at the Wayback Machine, Ing. Peter Weber
- ^ IEEE, Early History of Single-Sideband Transmission, Oswald, A.A.
- ^ History Of Undersea Cables, (1927)
- ^ "Amateur Radio and the Rise of SSB" (PDF). National Association for Amateur Radio.
- ^ Tretter, Steven A. (1995). "Chapter 7, Eq 7.9". In Lucky, R.W. (ed.). Communication System Design Using DSP Algorithms. New York: Springer. p. 80. ISBN 0306450321.
- ^ Earthlink.net, listing numerous articles.
- ^ "A Third Method of Generation and Detection of Single-Sideband Signals" D K Weaver Jr. Proc. IRE, Dec. 1956
- ^ "BRATS – Advanced Amateur Radio Tuition Course". Brats-qth.org. Retrieved 2013-01-29.
- ^ "FCC Part 97 - Amateur Service rules" (PDF). www.fcc.gov.
- ^ "Controlled Envelope Single Sideband" (PDF). www.arrl.org. 2014-11-01. Retrieved 2017-01-15. by David L. Hershberger, W9GR, QEX, issue Nov./Dec. 2014, pp. 3–13.
- ^ "External Processing for Controlled Envelope Single Sideband" (PDF). www.arrl.org. 2016-01-01. Retrieved 2017-01-15. by David L. Hershberger, W9GR, QEX, issue Jan./Feb. 2016, pp. 9–12.
Sources
[edit]- Partly from Federal Standard 1037C in support of MIL-STD-188
Further reading
[edit]- Sgrignoli, G., W. Bretl, R. and Citta. (1995). "VSB modulation used for terrestrial and cable broadcasts." IEEE Transactions on Consumer Electronics. v. 41, issue 3, p. 367 - 382.
- J. Brittain, (1992). "Scanning the past: Ralph V.L. Hartley", Proc. IEEE, vol.80,p. 463.
- eSSB - Extended Single Sideband
Warning: Default sort key "Single-Sideband Modulation" overrides earlier default sort key "Quadrature Amplitude Modulation".
Digital Modulation
[edit]This article may be too technical for most readers to understand. (February 2017) |
| Passband modulation |
|---|
 |
| Analog modulation |
| Digital modulation |
| Hierarchical modulation |
| Spread spectrum |
| See also |

In electronics and telecommunications, modulation is the process of varying one or more properties of a periodic waveform, called the carrier signal, with a separate signal called the modulation signal that typically contains information to be transmitted.[1] For example, the modulation signal might be an audio signal representing sound from a microphone, a video signal representing moving images from a video camera, or a digital signal representing a sequence of binary digits, a bitstream from a computer.
This carrier wave usually has a much higher frequency than the message signal does. This is because it is impractical to transmit signals with low frequencies. Generally, to receive a radio wave one needs a radio antenna with length that is one-fourth of wavelength.[2] For low frequency radio waves, wavelength is on the scale of kilometers and building such a large antenna is not practical. In radio communication, the modulated carrier is transmitted through space as a radio wave to a radio receiver.
Another purpose of modulation is to transmit multiple channels of information through a single communication medium, using frequency-division multiplexing (FDM). For example, in cable television (which uses FDM), many carrier signals, each modulated with a different television channel, are transported through a single cable to customers. Since each carrier occupies a different frequency, the channels do not interfere with each other. At the destination end, the carrier signal is demodulated to extract the information bearing modulation signal.
A modulator is a device or circuit that performs modulation. A demodulator (sometimes detector) is a circuit that performs demodulation, the inverse of modulation. A modem (from modulator–demodulator), used in bidirectional communication, can perform both operations. The lower frequency band occupied by the modulation signal is called the baseband, while the higher frequency band occupied by the modulated carrier is called the passband.[citation needed]
In analog modulation, an analog modulation signal is "impressed" on the carrier. Examples are amplitude modulation (AM) in which the amplitude (strength) of the carrier wave is varied by the modulation signal, and frequency modulation (FM) in which the frequency of the carrier wave is varied by the modulation signal. These were the earliest types of modulation[citation needed], and are used to transmit an audio signal representing sound in AM and FM radio broadcasting. More recent systems use digital modulation, which impresses a digital signal consisting of a sequence of binary digits (bits), a bitstream, on the carrier, by means of mapping bits to elements from a discrete alphabet to be transmitted. This alphabet can consist of a set of real or complex numbers, or sequences, like oscillations of different frequencies, so-called frequency-shift keying (FSK) modulation. A more complicated digital modulation method that employs multiple carriers, orthogonal frequency-division multiplexing (OFDM), is used in WiFi networks, digital radio stations and digital cable television transmission.
Analog modulation methods
[edit]


In analog modulation, the modulation is applied continuously in response to the analog information signal. Common analog modulation techniques include:
- Amplitude modulation (AM) (here the amplitude of the carrier signal is varied in accordance with the instantaneous amplitude of the modulating signal)
- Double-sideband modulation (DSB)
- Double-sideband modulation with carrier (DSB-WC) (used on the AM radio broadcasting band)
- Double-sideband suppressed-carrier transmission (DSB-SC)
- Double-sideband reduced carrier transmission (DSB-RC)
- Single-sideband modulation (SSB, or SSB-AM)
- Single-sideband modulation with carrier (SSB-WC)
- Single-sideband modulation suppressed carrier modulation (SSB-SC)
- Vestigial sideband modulation (VSB, or VSB-AM)
- Quadrature amplitude modulation (QAM)
- Double-sideband modulation (DSB)
- Angle modulation, which is approximately constant envelope
- Frequency modulation (FM) (here the frequency of the carrier signal is varied in accordance with the instantaneous amplitude of the modulating signal)
- Phase modulation (PM) (here the phase shift of the carrier signal is varied in accordance with the instantaneous amplitude of the modulating signal)
- Transpositional Modulation (TM), in which the waveform inflection is modified resulting in a signal where each quarter cycle is transposed in the modulation process. TM is a pseudo-analog modulation (AM). Where an AM carrier also carries a phase variable phase f(ǿ). TM is f(AM,ǿ)
Digital modulation methods
[edit]In digital modulation, an analog carrier signal is modulated by a discrete signal. Digital modulation methods can be considered as digital-to-analog conversion and the corresponding demodulation or detection as analog-to-digital conversion. The changes in the carrier signal are chosen from a finite number of M alternative symbols (the modulation alphabet).

A simple example: A telephone line is designed for transferring audible sounds, for example, tones, and not digital bits (zeros and ones). Computers may, however, communicate over a telephone line by means of modems, which are representing the digital bits by tones, called symbols. If there are four alternative symbols (corresponding to a musical instrument that can generate four different tones, one at a time), the first symbol may represent the bit sequence 00, the second 01, the third 10 and the fourth 11. If the modem plays a melody consisting of 1000 tones per second, the symbol rate is 1000 symbols/second, or 1000 baud. Since each tone (i.e., symbol) represents a message consisting of two digital bits in this example, the bit rate is twice the symbol rate, i.e. 2000 bits per second.
According to one definition of digital signal,[3] the modulated signal is a digital signal. According to another definition, the modulation is a form of digital-to-analog conversion. Most textbooks would consider digital modulation schemes as a form of digital transmission, synonymous to data transmission; very few would consider it as analog transmission.[citation needed]
Fundamental digital modulation methods
[edit]The most fundamental digital modulation techniques are based on keying:
- PSK (phase-shift keying): a finite number of phases are used.
- FSK (frequency-shift keying): a finite number of frequencies are used.
- ASK (amplitude-shift keying): a finite number of amplitudes are used.
- QAM (quadrature amplitude modulation): a finite number of at least two phases and at least two amplitudes are used.
In QAM, an in-phase signal (or I, with one example being a cosine waveform) and a quadrature phase signal (or Q, with an example being a sine wave) are amplitude modulated with a finite number of amplitudes and then summed. It can be seen as a two-channel system, each channel using ASK. The resulting signal is equivalent to a combination of PSK and ASK.
In all of the above methods, each of these phases, frequencies or amplitudes are assigned a unique pattern of binary bits. Usually, each phase, frequency or amplitude encodes an equal number of bits. This number of bits comprises the symbol that is represented by the particular phase, frequency or amplitude.
If the alphabet consists of alternative symbols, each symbol represents a message consisting of N bits. If the symbol rate (also known as the baud rate) is symbols/second (or baud), the data rate is bit/second.
For example, with an alphabet consisting of 16 alternative symbols, each symbol represents 4 bits. Thus, the data rate is four times the baud rate.
In the case of PSK, ASK or QAM, where the carrier frequency of the modulated signal is constant, the modulation alphabet is often conveniently represented on a constellation diagram, showing the amplitude of the I signal at the x-axis, and the amplitude of the Q signal at the y-axis, for each symbol.
Modulator and detector principles of operation
[edit]PSK and ASK, and sometimes also FSK, are often generated and detected using the principle of QAM. The I and Q signals can be combined into a complex-valued signal I+jQ (where j is the imaginary unit). The resulting so called equivalent lowpass signal or equivalent baseband signal is a complex-valued representation of the real-valued modulated physical signal (the so-called passband signal or RF signal).
These are the general steps used by the modulator to transmit data:
- Group the incoming data bits into codewords, one for each symbol that will be transmitted.
- Map the codewords to attributes, for example, amplitudes of the I and Q signals (the equivalent low pass signal), or frequency or phase values.
- Adapt pulse shaping or some other filtering to limit the bandwidth and form the spectrum of the equivalent low pass signal, typically using digital signal processing.
- Perform digital to analog conversion (DAC) of the I and Q signals (since today all of the above is normally achieved using digital signal processing, DSP).
- Generate a high-frequency sine carrier waveform, and perhaps also a cosine quadrature component. Carry out the modulation, for example by multiplying the sine and cosine waveform with the I and Q signals, resulting in the equivalent low pass signal being frequency shifted to the modulated passband signal or RF signal. Sometimes this is achieved using DSP technology, for example direct digital synthesis using a waveform table, instead of analog signal processing. In that case, the above DAC step should be done after this step.
- Amplification and analog bandpass filtering to avoid harmonic distortion and periodic spectrum.
At the receiver side, the demodulator typically performs:
- Bandpass filtering.
- Automatic gain control, AGC (to compensate for attenuation, for example fading).
- Frequency shifting of the RF signal to the equivalent baseband I and Q signals, or to an intermediate frequency (IF) signal, by multiplying the RF signal with a local oscillator sine wave and cosine wave frequency (see the superheterodyne receiver principle).
- Sampling and analog-to-digital conversion (ADC) (sometimes before or instead of the above point, for example by means of undersampling).
- Equalization filtering, for example, a matched filter, compensation for multipath propagation, time spreading, phase distortion and frequency selective fading, to avoid intersymbol interference and symbol distortion.
- Detection of the amplitudes of the I and Q signals, or the frequency or phase of the IF signal.
- Quantization of the amplitudes, frequencies or phases to the nearest allowed symbol values.
- Mapping of the quantized amplitudes, frequencies or phases to codewords (bit groups).
- Parallel-to-serial conversion of the codewords into a bit stream.
- Pass the resultant bit stream on for further processing such as removal of any error-correcting codes.
As is common to all digital communication systems, the design of both the modulator and demodulator must be done simultaneously. Digital modulation schemes are possible because the transmitter-receiver pair has prior knowledge of how data is encoded and represented in the communications system. In all digital communication systems, both the modulator at the transmitter and the demodulator at the receiver are structured so that they perform inverse operations.
Asynchronous methods do not require a receiver reference clock signal that is phase synchronized with the sender carrier signal. In this case, modulation symbols (rather than bits, characters, or data packets) are asynchronously transferred. The opposite is synchronous modulation.
List of common digital modulation techniques
[edit]The most common digital modulation techniques are:
- Phase-shift keying (PSK)
- Binary PSK (BPSK), using M=2 symbols
- Quadrature PSK (QPSK), using M=4 symbols
- 8PSK, using M=8 symbols
- 16PSK, using M=16 symbols
- Differential PSK (DPSK)
- Differential QPSK (DQPSK)
- Offset QPSK (OQPSK)
- π/4–QPSK
- Frequency-shift keying (FSK)
- Audio frequency-shift keying (AFSK)
- Multi-frequency shift keying (M-ary FSK or MFSK)
- Dual-tone multi-frequency (DTMF)
- Amplitude-shift keying (ASK)
- On-off keying (OOK), the most common ASK form
- M-ary vestigial sideband modulation, for example 8VSB
- Quadrature amplitude modulation (QAM), a combination of PSK and ASK
- Polar modulation like QAM a combination of PSK and ASK[citation needed]
- Continuous phase modulation (CPM) methods
- Minimum-shift keying (MSK)
- Gaussian minimum-shift keying (GMSK)
- Continuous-phase frequency-shift keying (CPFSK)
- Orthogonal frequency-division multiplexing (OFDM) modulation
- Discrete multitone (DMT), including adaptive modulation and bit-loading
- Wavelet modulation
- Trellis coded modulation (TCM), also known as Trellis modulation
- Spread spectrum techniques
- Direct-sequence spread spectrum (DSSS)
- Chirp spread spectrum (CSS) according to IEEE 802.15.4a CSS uses pseudo-stochastic coding
- Frequency-hopping spread spectrum (FHSS) applies a special scheme for channel release
MSK and GMSK are particular cases of continuous phase modulation. Indeed, MSK is a particular case of the sub-family of CPM known as continuous-phase frequency-shift keying (CPFSK) which is defined by a rectangular frequency pulse (i.e. a linearly increasing phase pulse) of one-symbol-time duration (total response signaling).
OFDM is based on the idea of frequency-division multiplexing (FDM), but the multiplexed streams are all parts of a single original stream. The bit stream is split into several parallel data streams, each transferred over its own sub-carrier using some conventional digital modulation scheme. The modulated sub-carriers are summed to form an OFDM signal. This dividing and recombining help with handling channel impairments. OFDM is considered as a modulation technique rather than a multiplex technique since it transfers one bit stream over one communication channel using one sequence of so-called OFDM symbols. OFDM can be extended to multi-user channel access method in the orthogonal frequency-division multiple access (OFDMA) and multi-carrier code-division multiple access (MC-CDMA) schemes, allowing several users to share the same physical medium by giving different sub-carriers or spreading codes to different users.
Of the two kinds of RF power amplifier, switching amplifiers (Class D amplifiers) cost less and use less battery power than linear amplifiers of the same output power. However, they only work with relatively constant-amplitude-modulation signals such as angle modulation (FSK or PSK) and CDMA, but not with QAM and OFDM. Nevertheless, even though switching amplifiers are completely unsuitable for normal QAM constellations, often the QAM modulation principle are used to drive switching amplifiers with these FM and other waveforms, and sometimes QAM demodulators are used to receive the signals put out by these switching amplifiers.
Automatic digital modulation recognition (ADMR)
[edit]Automatic digital modulation recognition in intelligent communication systems is one of the most important issues in software-defined radio and cognitive radio. According to incremental expanse of intelligent receivers, automatic modulation recognition becomes a challenging topic in telecommunication systems and computer engineering. Such systems have many civil and military applications. Moreover, blind recognition of modulation type is an important problem in commercial systems, especially in software-defined radio. Usually in such systems, there are some extra information for system configuration, but considering blind approaches in intelligent receivers, we can reduce information overload and increase transmission performance. Obviously, with no knowledge of the transmitted data and many unknown parameters at the receiver, such as the signal power, carrier frequency and phase offsets, timing information, etc., blind identification of the modulation is made fairly difficult. This becomes even more challenging in real-world scenarios with multipath fading, frequency-selective and time-varying channels.[4]
There are two main approaches to automatic modulation recognition. The first approach uses likelihood-based methods to assign an input signal to a proper class. Another recent approach is based on feature extraction.
Digital baseband modulation
[edit]Digital baseband modulation changes the characteristics of a baseband signal, i.e., one without a carrier at a higher frequency.
This can be used as equivalent signal to be later frequency-converted to a carrier frequency, or for direct communication in baseband. The latter methods both involve relatively simple line codes, as often used in local buses, and complicated baseband signalling schemes such as used in DSL.
Pulse modulation methods
[edit]Pulse modulation schemes aim at transferring a narrowband analog signal over an analog baseband channel as a two-level signal by modulating a pulse wave. Some pulse modulation schemes also allow the narrowband analog signal to be transferred as a digital signal (i.e., as a quantized discrete-time signal) with a fixed bit rate, which can be transferred over an underlying digital transmission system, for example, some line code. These are not modulation schemes in the conventional sense since they are not channel coding schemes, but should be considered as source coding schemes, and in some cases analog-to-digital conversion techniques.
- Analog-over-analog methods
- Pulse-amplitude modulation (PAM)
- Pulse-width modulation (PWM) and pulse-depth modulation (PDM)
- Pulse-frequency modulation (PFM)
- Pulse-position modulation (PPM)
- Analog-over-digital methods
- Pulse-code modulation (PCM)
- Differential PCM (DPCM)
- Adaptive DPCM (ADPCM)
- Differential PCM (DPCM)
- Delta modulation (DM or Δ-modulation)
- Delta-sigma modulation (ΣΔ)
- Continuously variable slope delta modulation (CVSDM), also called adaptive delta modulation (ADM)
- Pulse-density modulation (PDM)
Miscellaneous modulation techniques
[edit]- The use of on-off keying to transmit Morse code at radio frequencies is known as continuous wave (CW) operation.
- Adaptive modulation
- Space modulation is a method whereby signals are modulated within airspace such as that used in instrument landing systems.
- The microwave auditory effect has been pulse modulated with audio waveforms to evoke understandable spoken numbers.[5][6][7]
See also
[edit]References
[edit]This article needs additional citations for verification. (June 2008) |
- ^ "How does modulation work? | Tait Radio Academy". Tait Radio Academy. 2014-10-22. Retrieved 2024-06-17.
- ^ Herrera, Rodrigo "Rod" (April 23, 2024). "General Antennas: What antenna length do I need for which frequency?". wimo.com. Retrieved June 19, 2024.
- ^ "Modulation Methods | Electronics Basics | ROHM". www.rohm.com. Retrieved 2020-05-15.
- ^
Dobre, Octavia A., Ali Abdi, Yeheskel Bar-Ness, and Wei Su. Communications, IET 1, no. 2 (2007): 137–156. (2007). "Survey of automatic modulation classification techniques: classical approaches and new trends" (PDF). IET Communications. 1 (2): 137–156. doi:10.1049/iet-com:20050176.
{{cite journal}}: CS1 maint: multiple names: authors list (link) CS1 maint: numeric names: authors list (link) - ^ Lin, James C. (August 20, 2021). Auditory Effects of Microwave Radiation. Chicago: Springer. p. 326. ISBN 978-3030645434.
- ^ Justesen, Don (March 1, 1975). "Microwaves and Behavior" (PDF). American Psychologist. Washington, D.C.: American Psychological Association. Archived from the original (PDF) on 2016-09-10. Retrieved October 5, 2021.
- ^ Justesen, Don (March 1, 1975). "Microwaves and Behavior". American Psychologist. Vol. 30, no. 3. Washington, D.C.: American Psychological Association. pp. 391–401. doi:10.1037/0003-066x.30.3.391. PMID 1137231. Retrieved October 15, 2021.
Further reading
[edit]- Multipliers vs. Modulators Analog Dialogue, June 2013
External links
[edit]- Interactive presentation of soft-demapping for AWGN-channel in a web-demo Institute of Telecommunications, University of Stuttgart
- Modem (Modulation and Demodulation)
- CodSim 2.0: Open source Virtual Laboratory for Digital Data Communications Model Department of Computer Architecture, University of Malaga. Simulates Digital line encodings and Digital Modulations. Written in HTML for any web browser.
Amplitude-Shift Keying (ASK)
[edit]Amplitude and Phase-Shift Keying (APSK)
[edit]Amplitude and Phase-Shift Keying
Continuous Phase Modulation (CPM)
[edit]Frequency-Shift Keying (FSK)
[edit]Multiple Frequency-Shift Keying (MFSK)
[edit]Multiple Frequency-Shift Keying
Minimum-Shift Keying (MSK)
[edit]On–Off Keying (OOK)
[edit]Pulse-Position Modulation (PPM)
[edit]Phase-Shift Keying (PSK)
[edit]Quadrature Amplitude Modulation (QAM)
[edit]This article may be too technical for most readers to understand. (June 2020) |
| Passband modulation |
|---|
 |
| Analog modulation |
| Digital modulation |
| Hierarchical modulation |
| Spread spectrum |
| See also |
Quadrature amplitude modulation (QAM) is the name of a family of digital modulation methods and a related family of analog modulation methods widely used in modern telecommunications to transmit information. It conveys two analog message signals, or two digital bit streams, by changing (modulating) the amplitudes of two carrier waves, using the amplitude-shift keying (ASK) digital modulation scheme or amplitude modulation (AM) analog modulation scheme. The two carrier waves are of the same frequency and are out of phase with each other by 90°, a condition known as orthogonality or quadrature. The transmitted signal is created by adding the two carrier waves together. At the receiver, the two waves can be coherently separated (demodulated) because of their orthogonality. Another key property is that the modulations are low-frequency/low-bandwidth waveforms compared to the carrier frequency, which is known as the narrowband assumption.
Phase modulation (analog PM) and phase-shift keying (digital PSK) can be regarded as a special case of QAM, where the amplitude of the transmitted signal is a constant, but its phase varies. This can also be extended to frequency modulation (FM) and frequency-shift keying (FSK), for these can be regarded as a special case of phase modulation[citation needed].
QAM is used extensively as a modulation scheme for digital communications systems, such as in 802.11 Wi-Fi standards. Arbitrarily high spectral efficiencies can be achieved with QAM by setting a suitable constellation size, limited only by the noise level and linearity of the communications channel.[1] QAM is being used in optical fiber systems as bit rates increase; QAM16 and QAM64 can be optically emulated with a three-path interferometer.[2][3]
Demodulation
[edit]
In a QAM signal, one carrier lags the other by 90°, and its amplitude modulation is customarily referred to as the in-phase component, denoted by I(t). The other modulating function is the quadrature component, Q(t). So the composite waveform is mathematically modeled as:
- or:
| (Eq.1) |
where fc is the carrier frequency. At the receiver, a coherent demodulator multiplies the received signal separately with both a cosine and sine signal to produce the received estimates of I(t) and Q(t). For example:
Using standard trigonometric identities, we can write this as:
Low-pass filtering r(t) removes the high frequency terms (containing 4πfct), leaving only the I(t) term. This filtered signal is unaffected by Q(t), showing that the in-phase component can be received independently of the quadrature component. Similarly, we can multiply sc(t) by a sine wave and then low-pass filter to extract Q(t).

The addition of two sinusoids is a linear operation that creates no new frequency components. So the bandwidth of the composite signal is comparable to the bandwidth of the DSB (double-sideband) components. Effectively, the spectral redundancy of DSB enables a doubling of the information capacity using this technique. This comes at the expense of demodulation complexity. In particular, a DSB signal has zero-crossings at a regular frequency, which makes it easy to recover the phase of the carrier sinusoid. It is said to be self-clocking. But the sender and receiver of a quadrature-modulated signal must share a clock or otherwise send a clock signal. If the clock phases drift apart, the demodulated I and Q signals bleed into each other, yielding crosstalk. In this context, the clock signal is called a "phase reference". Clock synchronization is typically achieved by transmitting a burst subcarrier or a pilot signal. The phase reference for NTSC, for example, is included within its colorburst signal.
Analog QAM is used in:
- NTSC and PAL analog color television systems, where the I- and Q-signals carry the components of chroma (colour) information. The QAM carrier phase is recovered from a special colorburst transmitted at the beginning of each scan line.
- C-QUAM ("Compatible QAM") is used in AM stereo radio to carry the stereo difference information.
Fourier analysis
[edit]Applying Euler's formula to the sinusoids in Eq.1, the positive-frequency portion of sc (or analytic representation) is:
where denotes the Fourier transform, and and are the transforms of I(t) and Q(t). This result represents the sum of two DSB-SC signals with the same center frequency. The factor of i (= eiπ/2) represents the 90° phase shift that enables their individual demodulations.
Digital QAM
[edit]

As in many digital modulation schemes, the constellation diagram is useful for QAM. In QAM, the constellation points are usually arranged in a square grid with equal vertical and horizontal spacing, although other configurations are possible (e.g. a hexagonal or triangular grid). In digital telecommunications the data is usually binary, so the number of points in the grid is typically a power of 2 (2, 4, 8, …), corresponding to the number of bits per symbol. The simplest and most commonly used QAM constellations consist of points arranged in a square, i.e. 16-QAM, 64-QAM and 256-QAM (even powers of two). Non-square constellations, such as Cross-QAM, can offer greater efficiency but are rarely used because of the cost of increased modem complexity.
By moving to a higher-order constellation, it is possible to transmit more bits per symbol. However, if the mean energy of the constellation is to remain the same (by way of making a fair comparison), the points must be closer together and are thus more susceptible to noise and other corruption; this results in a higher bit error rate and so higher-order QAM can deliver more data less reliably than lower-order QAM, for constant mean constellation energy. Using higher-order QAM without increasing the bit error rate requires a higher signal-to-noise ratio (SNR) by increasing signal energy, reducing noise, or both.
If data rates beyond those offered by 8-PSK are required, it is more usual to move to QAM since it achieves a greater distance between adjacent points in the I-Q plane by distributing the points more evenly. The complicating factor is that the points are no longer all the same amplitude and so the demodulator must now correctly detect both phase and amplitude, rather than just phase.
64-QAM and 256-QAM are often used in digital cable television and cable modem applications. In the United States, 64-QAM and 256-QAM are the mandated modulation schemes for digital cable (see QAM tuner) as standardised by the SCTE in the standard ANSI/SCTE 07 2013. In the UK, 64-QAM is used for digital terrestrial television (Freeview) whilst 256-QAM is used for Freeview-HD.

Communication systems designed to achieve very high levels of spectral efficiency usually employ very dense QAM constellations. For example, current Homeplug AV2 500-Mbit/s powerline Ethernet devices use 1024-QAM and 4096-QAM,[4] as well as future devices using ITU-T G.hn standard for networking over existing home wiring (coaxial cable, phone lines and power lines); 4096-QAM provides 12 bits/symbol. Another example is ADSL technology for copper twisted pairs, whose constellation size goes up to 32768-QAM (in ADSL terminology this is referred to as bit-loading, or bit per tone, 32768-QAM being equivalent to 15 bits per tone).[5]
Ultra-high capacity microwave backhaul systems also use 1024-QAM.[6] With 1024-QAM, adaptive coding and modulation (ACM) and XPIC, vendors can obtain gigabit capacity in a single 56 MHz channel.[6]
Interference and noise
[edit]In moving to a higher order QAM constellation (higher data rate and mode) in hostile RF/microwave QAM application environments, such as in broadcasting or telecommunications, multipath interference typically increases. There is a spreading of the spots in the constellation, decreasing the separation between adjacent states, making it difficult for the receiver to decode the signal appropriately. In other words, there is reduced noise immunity. There are several test parameter measurements which help determine an optimal QAM mode for a specific operating environment. The following three are most significant:[7]
- Carrier/interference ratio
- Carrier-to-noise ratio
- Threshold-to-noise ratio
See also
[edit]- Amplitude and phase-shift keying or asymmetric phase-shift keying (APSK)
- Carrierless amplitude phase modulation (CAP)
- Circle packing § Applications
- In-phase and quadrature components
- Modulation for other examples of modulation techniques
- Phase-shift keying
- QAM tuner for HDTV
- Random modulation
References
[edit]- ^ "Digital Modulation Efficiencies". Barnard Microsystems. Archived from the original on 2011-04-30.
- ^ "Ciena tests 200G via 16-QAM with Japan-U.S. Cable Network". lightwave. April 17, 2014. Retrieved 7 November 2016.
- ^ Kylia products Archived July 13, 2011, at the Wayback Machine, dwdm mux demux, 90 degree optical hybrid, d(q) psk demodulatorssingle polarization
- ^ "HomePlug® AV2 Technology" (PDF). www.homeplug.org. Archived from the original (PDF) on 2015-09-23.
- ^ "G.992.3 : Asymmetric digital subscriber line transceivers 2 (ADSL2)". www.itu.int. Constellation mapper - maximum number of bits per constellation BIMAX ≤ 15. Retrieved 2024-10-09.
{{cite web}}: CS1 maint: others (link) - ^ a b "TrangoLink Apex Orion - Trango Systems". www.trangosys.com. Archived from the original on 2012-03-15.
- ^ Howard Friedenberg and Sunil Naik. "Hitless Space Diversity STL Enables IP+Audio in Narrow STL Bands" (PDF). 2005 National Association of Broadcasters Annual Convention. Archived from the original (PDF) on March 23, 2006. Retrieved April 17, 2005.
Further reading
[edit]- Jonqyin (Russell) Sun "Linear diversity analysis for QAM in Rician fading channels", IEEE WOCC 2014
- John G. Proakis, "Digital Communications, 3rd Edition"
External links
[edit]- QAM Demodulation
- Interactive webdemo of QAM constellation with additive noise Institute of Telecommunicatons, University of Stuttgart
- QAM bit error rate for AWGN channel – online experiment
- How imperfections affect QAM constellation
- Microwave Phase Shifters Overview by Herley General Microwave
- Simulation of dual-polarization QPSK (DP-QPSK) for 100G optical transmission
Warning: Default sort key "Quadrature Amplitude Modulation" overrides earlier default sort key "Single-Sideband Modulation".
Single-Carrier FDMA (SC-FDE)
[edit]| Passband modulation |
|---|
 |
| Analog modulation |
| Digital modulation |
| Hierarchical modulation |
| Spread spectrum |
| See also |
Single-carrier FDMA (SC-FDMA) is a frequency-division multiple access scheme. Originally known as Carrier Interferometry, it is also called linearly precoded OFDMA (LP-OFDMA). Like other multiple access schemes (TDMA, FDMA, CDMA, OFDMA), it deals with the assignment of multiple users to a shared communication resource. SC-FDMA can be interpreted as a linearly precoded OFDMA scheme, in the sense that it has an additional DFT processing step preceding the conventional OFDMA processing.
SC-FDMA has drawn great attention as an attractive alternative to OFDMA, especially in the uplink communications where lower peak-to-average power ratio (PAPR) greatly benefits the mobile terminal in terms of transmit power efficiency and reduced cost of the power amplifier. This is where SC-FDMA gets its name from: it's an OFDM signal that mimics the characteristics of a single-carrier QAM signal.[1] It has been adopted as the uplink multiple access scheme in 3GPP Long Term Evolution (LTE), or Evolved UTRA (E-UTRA).[2][3][4]
The performance of SC-FDMA in relation to OFDMA has been the subject of various studies.[5][6][7] Although the performance gap is small, SC-FDMA's advantage of low PAPR makes it desirable for uplink wireless transmission in mobile communication systems, where transmitter power efficiency is of paramount importance.
Transmitter and receiver structure
[edit]The transmission processing of SC-FDMA is very similar to that of OFDMA. For each user, the sequence of bits transmitted is mapped to a complex constellation of symbols (BPSK, QPSK, or M-QAM). Then different transmitters (users) are assigned different Fourier coefficients. This assignment is carried out in the mapping and demapping blocks. The receiver side includes one demapping block, one IDFT block, and one detection block for each user signal to be received. Just like in OFDM, guard intervals (called cyclic prefixes) with cyclic repetition are introduced between blocks of symbols in view to efficiently eliminate inter-symbol interference from time spreading (caused by multi-path propagation) among the blocks.
In SC-FDMA, multiple access among users is made possible by assigning different users different sets of non-overlapping Fourier coefficients (sub-carriers). This is achieved at the transmitter by inserting (prior to IDFT) silent Fourier coefficients (at positions assigned to other users), and removing them on the receiver side after the DFT.

The distinguishing feature of SC-FDMA is that it leads to a single-carrier transmit signal, in contrast to OFDMA which is a multi-carrier transmission scheme. Subcarrier mapping can be classified into two types: localized mapping and distributed mapping. In localized mapping, the DFT outputs are mapped to a subset of consecutive subcarriers, thereby confining them to only a fraction of the system bandwidth. In distributed mapping, the DFT outputs of the input data are assigned to subcarriers over the entire bandwidth non-continuously, resulting in zero amplitude for the remaining subcarriers. A special case of distributed SC-FDMA is called interleaved SC-FDMA (IFDMA), where the occupied subcarriers are equally spaced over the entire bandwidth.[8]
Owing to its inherent single carrier structure, a prominent advantage of SC-FDMA over OFDM and OFDMA is that its transmit signal has a lower peak-to-average power ratio (PAPR), resulting in relaxed design parameters in the transmit path of a subscriber unit. Intuitively, the reason lies in the fact that where OFDM transmit symbols directly modulate multiple sub-carriers, SC-FDMA transmit symbols are first processed by an N-point DFT block.[9]
In OFDM, as well as SC-FDMA, equalization is achieved on the receiver side, after the DFT calculation, by multiplying each Fourier coefficient by a complex number. Thus, frequency-selective fading and phase distortion can be easily counteracted. The advantage is that frequency domain equalization using FFTs requires less computation than conventional time-domain equalization, which require multi-tap FIR or IIR-filters. Less computations result in less compounded round-off error, which can be viewed as numerical noise.
A related concept is the combination of a single carrier transmission with the single-carrier frequency-domain-equalization (SC-FDE) scheme.[10] The single carrier transmission, unlike SC-FDMA and OFDM, employs no IDFT or DFT at the transmitter, but introduces the cyclic prefix to transform the linear channel convolution into a circular one. After removing the cyclic prefix at the receiver, a DFT is applied to arrive in the frequency domain, where a simple single-carrier frequency-domain-equalization (SC-FDE) scheme can be employed, followed by the IDFT operation.

- DFT: Discrete Fourier Transform
- IDFT: Inverse Discrete Fourier Transform
- CP: Cyclic Prefix
- PS: Pulse Shaping
- DAC: Digital-to-analog converter
- RF: Radio Frequency signal
- ADC: Analog-to-digital converter
- LP-OFDMA: Linearly precoded OFDMA
Useful properties
[edit]- Low PAPR (crest factor)
- Low sensitivity to carrier frequency offset
- Less sensitive to non-linear distortion and hence, it allows the use of low-cost power amplifiers
- Greater robustness against spectral nulls
See also
[edit]References
[edit]- ^ "SC-FDMA vs. OFDM Modulation - MATLAB & Simulink". www.mathworks.com. Retrieved 2024-04-15.
- ^ Myung, Hyung; Lim, Junsung; Goodman, David (2006). "Single carrier FDMA for uplink wireless transmission" (PDF). IEEE Vehicular Technology Magazine. 1 (3): 30–38. doi:10.1109/MVT.2006.307304. S2CID 12743526.
- ^ Ekstrom, H.; Furuskar, A.; Karlsson, J.; Meyer, M.; Parkvall, S.; Torsner, J.; Wahlqvist, M. (2006). "Technical solutions for the 3G long-term evolution". IEEE Communications Magazine. 44 (3): 38–45. doi:10.1109/MCOM.2006.1607864. S2CID 1168131.
- ^ "Technical Specification Group Radio Access Network; Physical Layer Aspects for Evolved UTRA". 3rd Generation Partnership Project (3GPP).
- ^ Nisar, Muhammad Danish; Nottensteiner, Hans; Hindelang, Thomas (2007). "On Performance Limits of DFT Spread OFDM Systems". 2007 16th IST Mobile and Wireless Communications Summit (PDF). pp. 1–4. doi:10.1109/ISTMWC.2007.4299159. ISBN 978-1-4244-1662-2. S2CID 6077115.
- ^ Priyanto, Basuki E.; Codina, Humbert; Rene, Sergi; Sorensen, Troels B.; Mogensen, Preben (2007). "Initial Performance Evaluation of DFT-Spread OFDM Based SC-FDMA for UTRA LTE Uplink". 2007 IEEE 65th Vehicular Technology Conference - VTC2007-Spring. pp. 3175–3179. doi:10.1109/VETECS.2007.650. ISBN 978-1-4244-0266-3. S2CID 206836778.
- ^ Benvenuto, N.; Tomasin, S. (2002). "On the comparison between OFDM and single carrier modulation with a DFE using a frequency-domain feedforward filter". IEEE Transactions on Communications. 50 (6): 947–955. doi:10.1109/TCOMM.2002.1010614.
- ^ "SC-FDMA Single Carrier FDMA in LTE" (PDF). Ixia.
- ^ Myung, Hyung; Lim, Junsung; Goodman, David (2006). "Peak-To-Average Power Ratio of Single Carrier FDMA Signals with Pulse Shaping". 2006 IEEE 17th International Symposium on Personal, Indoor and Mobile Radio Communications. pp. 1–5. doi:10.1109/PIMRC.2006.254407. ISBN 1-4244-0329-4. S2CID 7457641.
- ^ Falconer, D.; Ariyavisitakul, S.L.; Benyamin-Seeyar, A.; Eidson, B. (2002). "Frequency domain equalization for single-carrier broadband wireless systems". IEEE Communications Magazine. 40 (4): 58–66. doi:10.1109/35.995852.
Trellis Coded Modulation (TCM)
[edit]Wavelet Modulation (WDM)
[edit]Hierarchical Modulation
[edit]This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. (February 2024) |
| Passband modulation |
|---|
 |
| Analog modulation |
| Digital modulation |
| Hierarchical modulation |
| Spread spectrum |
| See also |
Hierarchical modulation, also called layered modulation, is one of the signal processing techniques for multiplexing and modulating multiple data streams into one single symbol stream, where base-layer symbols and enhancement-layer symbols are synchronously overlaid before transmission.
Hierarchical modulation is particularly used to mitigate the cliff effect in digital television broadcast, particularly mobile TV, by providing a (lower quality) fallback signal in case of weak signals, allowing graceful degradation instead of complete signal loss. It has been widely proven and included in various standards, such as DVB-T, MediaFLO, UMB (Ultra Mobile Broadband, a new 3.5th generation mobile network standard developed by 3GPP2), and is under study for DVB-H.
Hierarchical modulation is also taken as one of the practical implementations of superposition precoding, which can help achieve the maximum sum rate of broadcast channels. When hierarchical-modulated signals are transmitted, users with good reception and advanced receivers can demodulate multiple layers. For a user with a conventional receiver or poor reception, it may only demodulate the data stream embedded in the base layer. With hierarchical modulation, a network operator can target users of different types with different services or QoS.
However, traditional hierarchical modulation suffers from serious inter-layer interference (ILI) with impact on the achievable symbol rate.
Example
[edit]
- ● 2 bits, QPSK
- ■ 4 bits, 64QAM
For example, the figure depicts a layering scheme with QPSK base layer, and a 64QAM enhancement layer. The first layer is 2 bits (represented by the green circles). The signal detector only needs to establish which quadrant the signal is in, to recover the value (which is '10', the green circle in the lower right corner). In better signal conditions, the detector can establish the phase and amplitude more precisely, to recover four more bits of data ('1101'). Thus, the base layer carries '10', and the enhancement layer carries '1101'.
Inter-layer interference
[edit]This section needs expansion. You can help by adding to it. (September 2009) |
For a hierarchically-modulated symbol with QPSK base layer and 16QAM enhancement layer, the base-layer throughput loss is up to about 1.5 bits/symbol with the total receive signal-to-noise ratio (SNR) at about 23 dB, about the minimum needed for the comparable non-hierarchical modulation, 64QAM. But unlayered 16QAM with the same SNR would approach full throughput. This means, due to ILI, about 1.5/4 = 37.5% loss of the base-layer achievable throughput. Furthermore, due to ILI and the imperfect demodulation of base-layer symbols, the demodulation error rate of higher-layer symbols increases too.
See also
[edit]- Link adaptation
- H.264 Scalable Video Coding
- H.265 scalability extensions (SHVC)
- AV1 Scalable video coding
- MPEG-4 SLS
- MPEG-5 Part 2 / Low Complexity Enhancement Video Coding / LC EVC
- DTS-HD MA
- Ogg Vorbis bitrate peeling
- WavPack hybrid mode
- JPEG 2000 SNR scalability
References
[edit]- H. Méric, J. Lacan, F. Arnal, G. Lesthievent, M.-L. Boucheret, Combining Adaptive Coding and Modulation With Hierarchical Modulation in Satcom Systems, IEEE Transactions on Broadcasting, Vol. 59, No. 4 (2013), pp 627-637.
- Shu Wang, Soonyil Kwon and Yi, B.K., On enhancing hierarchical modulation, IEEE International Symposium on Broadband Multimedia Systems and Broadcasting, March 31 2008-April 2 2008, Las Vegas, NV, (2008), pp. 1-6.
- Seamus O Leary, 'Hierarchical transmission and COFDM systems', Published in: IEEE Transactions on Broadcasting ( Volume: 43, Issue: 2, Jun 1997)Page(s): 166 - 174
External links
[edit]- Hierarchical Modulation Explained at the Wayback Machine (archived 2012-03-25)
- Hierarchical Modulation under DVB
Warning: Default sort key "Hierarchical Modulation" overrides earlier default sort key "Quadrature Amplitude Modulation".
Chirp Spread Spectrum (CSS)
[edit]
| Passband modulation |
|---|
 |
| Analog modulation |
| Digital modulation |
| Hierarchical modulation |
| Spread spectrum |
| See also |
| Multiplexing |
|---|
 |
| Analog modulation |
| Related topics |
In digital communications, chirp spread spectrum (CSS) is a spread spectrum technique that uses wideband linear frequency modulated chirp pulses to encode information.[1] A chirp is a sinusoidal signal whose frequency increases or decreases over time (often with a polynomial expression for the relationship between time and frequency).
Overview
[edit]As with other spread spectrum methods, chirp spread spectrum uses its entire allocated bandwidth to broadcast a signal, making it robust to channel noise. Further, because the chirps utilize a broad band of the spectrum, chirp spread spectrum is also resistant to multi-path fading even when operating at very low power. However, it is unlike direct-sequence spread spectrum (DSSS) or frequency-hopping spread spectrum (FHSS) in that it does not add any pseudo-random elements to the signal to help distinguish it from noise on the channel, instead relying on the linear nature of the chirp pulse. Additionally, chirp spread spectrum is resistant to the Doppler effect, which is typical in mobile radio applications.[2]
Uses
[edit]Chirp spread spectrum was originally designed to compete with ultra-wideband for precision ranging and low-rate wireless networks in the 2.45 GHz band. However, since the release of IEEE 802.15.4a (also known as IEEE 802.15.4a-2007), it is no longer actively being considered by the IEEE for standardization in the area of precision ranging.
Chirp spread spectrum is ideal for applications requiring low power usage and needing relatively low data rates (1 Mbit/s or less). In particular, IEEE 802.15.4a specifies CSS as a technique for use in low-rate wireless personal area networks (LR-WPAN). However, whereas IEEE 802.15.4-2006 standard specifies that WPANs encompass an area of 10 m or less, IEEE 802.15.4a-2007, specifies CSS as a physical layer to be used when longer ranges and devices moving at high speeds are part of your network. Nanotron's CSS implementation was actually seen to work at a range of 570 meters between devices.[3] Further, Nanotron's implementation can work at data rates of up to 2 Mbit/s - higher than specified in 802.15.4a.[4] Finally, the IEEE 802.15.4a PHY standard actually mixes CSS encoding techniques with differential phase shift keying modulation (DPSK) to achieve better data rates.
Chirp spread spectrum may also be used in the future for military applications as it is very difficult to detect and intercept when operating at low power.[5]
Very similar frequency swept waveforms are used in frequency modulated continuous wave radars to measure range (distance); an unmodulated continuous wave Doppler radar can only measure range-rate (relative velocity along the line of sight). FM-CW radars are very widely used as radio altimeters in aircraft.
One application of chirp spread spectrum is LoRa.[6][7]
See also
[edit]- Bluetooth
- IEEE 802.11
- IEEE 802.15.4
- IEEE 802.15.4a
- IEEE 802.16
- IEEE 802.20
- IEEE 802.22
- Spectral efficiency comparison table
- Zigbee
References
[edit]- ^ IEEE Computer Society, (August 31, 2007). IEEE Standard 802.15.4a-2007. New York, NY: IEEE.
- ^ Berni, A. J., & Gregg, W. D. (June 1973). On the utility of chirp modulation for digital signaling, IEEE Transactions on Communications. Volume COM-21, 748-751
- ^ http://www.autoid.org/SC31/wg5/06/WG5_200603_010_InfoCSS.ppt Archived 2007-10-21 at the Wayback Machine , Nanotron Mine Test: slide 22
- ^ Nanotron Technologies, (2007). nanoNET chirp based wireless networks. Retrieved from http://www.nanotron.com/EN/docs/WP/WP_CSS.pdf[permanent dead link]
- ^ The Revenge of Chirp Spread Spectrum, Military applications Archived 2008-05-15 at the Wayback Machine
- ^ "RF Modulation: Crash Course for Hackers". 28 January 2020.
- ^ Ikpehai, Augustine; Adebisi, Bamidele; Rabie, Khaled M.; Anoh, Kelvin; Ande, Ruth E.; Hammoudeh, Mohammad; Gacanin, Haris; Mbanaso, Uche M. (April 2019). "Low-Power Wide Area Network Technologies for Internet-of-Things: A Comparative Review". IEEE Internet of Things Journal. 6 (2): 2225–2240. doi:10.1109/JIOT.2018.2883728. ISSN 2327-4662. S2CID 69444615.
External links
[edit]- Download the 802.15 standards from IEEE
- IEEE 802.15 WPAN Low Rate Alternative PHY Task Group 4a (TG4a)
- Nanotron Technologies Frequently asked Questions page
- Nanotron Chirp Spread Spectrum page
- Nanotron nanoNET Chirp Based Wireless Networks[permanent dead link]
- About coexistence of IEEE 802.15.4aCSS with IEEE 802.11b/g (2.45 GHz WLAN)
Direct-Sequence Spread Spectrum (DSSS)
[edit]
| Passband modulation |
|---|
 |
| Analog modulation |
| Digital modulation |
| Hierarchical modulation |
| Spread spectrum |
| See also |
| Multiplexing |
|---|
 |
| Analog modulation |
| Related topics |
In telecommunications, direct-sequence spread spectrum (DSSS) is a spread-spectrum modulation technique primarily used to reduce overall signal interference. The direct-sequence modulation makes the transmitted signal wider in bandwidth than the information bandwidth. After the despreading or removal of the direct-sequence modulation in the receiver, the information bandwidth is restored, while the unintentional and intentional interference is substantially reduced.[1]
Swiss inventor, Gustav Guanella proposed a "means for and method of secret signals".[2] With DSSS, the message symbols are modulated by a sequence of complex values known as spreading sequence. Each element of the spreading sequence, a so-called chip, has a shorter duration than the original message symbols. The modulation of the message symbols scrambles and spreads the signal in the spectrum, and thereby results in a bandwidth of the spreading sequence. The smaller the chip duration, the larger the bandwidth of the resulting DSSS signal; more bandwidth multiplexed to the message signal results in better resistance against narrowband interference.[1][3]
Some practical and effective uses of DSSS include the code-division multiple access (CDMA) method, the IEEE 802.11b specification used in Wi-Fi networks, and the Global Positioning System.[4][5]
Transmission method
[edit]Direct-sequence spread-spectrum transmissions multiply the symbol sequence being transmitted with a spreading sequence that has a higher rate than the original message rate. Usually, sequences are chosen such that the resulting spectrum is spectrally white. Knowledge of the same sequence is used to reconstruct the original data at the receiving end. This is commonly implemented by the element-wise multiplication with the spreading sequence, followed by summation over a message symbol period. This process, despreading, is mathematically a correlation of the transmitted spreading sequence with the spreading sequence. In an AWGN channel, the despreaded signal's signal-to-noise ratio is increased by the spreading factor, which is the ratio of the spreading-sequence rate to the data rate.
While a transmitted DSSS signal occupies a wider bandwidth than the direct modulation of the original signal would require, its spectrum can be restricted by conventional pulse-shape filtering.
If an undesired transmitter transmits on the same channel but with a different spreading sequence, the despreading process reduces the power of that signal. This effect is the basis for the code-division multiple access (CDMA) method of multi-user medium access, which allows multiple transmitters to share the same channel within the limits of the cross-correlation properties of their spreading sequences.
Benefits
[edit]- Resistance to unintended or intended jamming
- Sharing of a single channel among multiple users
- Reduced signal/background-noise level hampers interception
- Determination of relative timing between transmitter and receiver
Uses
[edit]- The United States GPS, European Galileo and Russian GLONASS satellite navigation systems; earlier GLONASS used DSSS with a single spreading sequence in conjunction with FDMA, while later GLONASS used DSSS to achieve CDMA with multiple spreading sequences.
- DS-CDMA (Direct-Sequence Code Division Multiple Access) is a multiple access scheme based on DSSS, by spreading the signals from/to different users with different codes. It is the most widely used type of CDMA.
- Cordless phones operating in the 900 MHz, 2.4 GHz and 5.8 GHz bands
- IEEE 802.11b 2.4 GHz Wi-Fi, and its predecessor 802.11-1999. (Their successor 802.11g uses both OFDM and DSSS)
- Automatic meter reading
- IEEE 802.15.4 (used, e.g., as PHY and MAC layer for Zigbee, or, as the physical layer for WirelessHART)
- Radio-controlled model Automotive, Aeronautical and Marine vehicles
- Spread spectrum radar for covertness and resistance to jamming and spoofing
See also
[edit]- Complementary code keying
- Frequency-hopping spread spectrum
- Linear-feedback shift register
- Orthogonal frequency-division multiplexing
References
[edit]- ^ a b Torrieri, Don (2018). Principles of Spread-Spectrum Communication Systems, 4th ed.
- ^ "Espacenet - Bibliographic data". worldwide.espacenet.com. Retrieved 2020-12-02.
- ^ Stuber, Gordon L. (2017). Principles of Mobile Communication, 4th ed.
- ^ Rappaport, Theodore (2002). Wireless Communications Principles and Practice, 2nd ed.
- ^ Pratep, Misra; Enge, Per (2012). Global Positioning System: Signals, Measurements, and Performance, rev. 2nd ed.
- The Origins of Spread-Spectrum Communications
 This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22.
This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22.- NTIA Manual of Regulations and Procedures for Federal Radio Frequency Management
External links
[edit]Frequency-Hopping Spread Spectrum (FHSS)
[edit]Frequency-Hopping Spread Spectrum
Time-Hopping (THSS)
[edit]See Also
[edit]Capacity-Approaching Codes
[edit]Demodulation
[edit]This article needs additional citations for verification. (June 2009) |
| Passband modulation |
|---|
 |
| Analog modulation |
| Digital modulation |
| Hierarchical modulation |
| Spread spectrum |
| See also |
Demodulation is extracting the original information-bearing signal from a carrier wave. A demodulator is an electronic circuit (or computer program in a software-defined radio) that is used to recover the information content from the modulated carrier wave.[1] There are many types of modulation so there are many types of demodulators. The signal output from a demodulator may represent sound (an analog audio signal), images (an analog video signal) or binary data (a digital signal).
These terms are traditionally used in connection with radio receivers, but many other systems use many kinds of demodulators. For example, in a modem, which is a contraction of the terms modulator/demodulator, a demodulator is used to extract a serial digital data stream from a carrier signal which is used to carry it through a telephone line, coaxial cable, or optical fiber.
History
[edit]Demodulation was first used in radio receivers. In the wireless telegraphy radio systems used during the first 3 decades of radio (1884–1914) the transmitter did not communicate audio (sound) but transmitted information in the form of pulses of radio waves that represented text messages in Morse code.[citation needed] Therefore, the receiver merely had to detect the presence or absence of the radio signal, and produce a click sound. The device that did this was called a detector. The first detectors were coherers, simple devices that acted as a switch. The term detector stuck, was used for other types of demodulators and continues to be used to the present day for a demodulator in a radio receiver.
The first type of modulation used to transmit sound over radio waves was amplitude modulation (AM), invented by Reginald Fessenden around 1900. An AM radio signal can be demodulated by rectifying it to remove one side of the carrier, and then filtering to remove the radio-frequency component, leaving only the modulating audio component. This is equivalent to peak detection with a suitably long time constant. The amplitude of the recovered audio frequency varies with the modulating audio signal, so it can drive an earphone or an audio amplifier. Fessendon invented the first AM demodulator in 1904 called the electrolytic detector, consisting of a short needle dipping into a cup of dilute acid. The same year John Ambrose Fleming invented the Fleming valve or thermionic diode which could also rectify an AM signal.
Techniques
[edit]There are several ways of demodulation depending on how parameters of the base-band signal such as amplitude, frequency or phase are transmitted in the carrier signal. For example, for a signal modulated with a linear modulation like AM (amplitude modulation), we can use a synchronous detector. On the other hand, for a signal modulated with an angular modulation, we must use an FM (frequency modulation) demodulator or a PM (phase modulation) demodulator. Different kinds of circuits perform these functions.
Many techniques such as carrier recovery, clock recovery, bit slip, frame synchronization, rake receiver, pulse compression, Received Signal Strength Indication, error detection and correction, etc., are only performed by demodulators, although any specific demodulator may perform only some or none of these techniques.
Many things can act as a demodulator, if they pass the radio waves on nonlinearly.[2]
AM radio
[edit]An AM signal encodes the information into the carrier wave by varying its amplitude in direct sympathy with the analogue signal to be sent. There are two methods used to demodulate AM signals:
- The envelope detector is a very simple method of demodulation that does not require a coherent demodulator. It consists of a rectifier (anything that will pass current in one direction only) or other non-linear component that enhances one half of the received signal over the other and a low-pass filter. The rectifier may be in the form of a single diode or may be more complex. Many natural substances exhibit this rectification behaviour, which is why it was the earliest modulation and demodulation technique used in radio. The filter is usually an RC low-pass type but the filter function can sometimes be achieved by relying on the limited frequency response of the circuitry following the rectifier. The crystal set exploits the simplicity of AM modulation to produce a receiver with very few parts, using the crystal as the rectifier and the limited frequency response of the headphones as the filter.
- The product detector multiplies the incoming signal by the signal of a local oscillator with the same frequency and phase as the carrier of the incoming signal. After filtering, the original audio signal will result.
SSB is a form of AM in which the carrier is reduced or suppressed entirely, which require coherent demodulation. For further reading, see sideband.
FM radio
[edit]
Frequency modulation (FM) has numerous advantages over AM such as better fidelity and noise immunity. However, it is much more complex to both modulate and demodulate a carrier wave with FM, and AM predates it by several decades.
There are several common types of FM demodulators:
- The quadrature detector, which phase shifts the signal by 90 degrees and multiplies it with the unshifted version. One of the terms that drops out from this operation is the original information signal, which is selected and amplified.
- The signal is fed into a PLL and the error signal is used as the demodulated signal.
- The most common is a Foster–Seeley discriminator. This is composed of an electronic filter which decreases the amplitude of some frequencies relative to others, followed by an AM demodulator. If the filter response changes linearly with frequency, the final analog output will be proportional to the input frequency, as desired.
- A variant of the Foster–Seeley discriminator called the ratio detector[3]
- Another method uses two AM demodulators, one tuned to the high end of the band and the other to the low end, and feed the outputs into a difference amplifier. [citation needed]
- Using a digital signal processor, as used in software-defined radio.
PM
[edit]
QAM
[edit]QAM demodulation requires a coherent receiver. It uses two product detectors whose local reference signals are a quarter cycle apart in phase: one for the in-phase component and one for the quadrature component. The demodulator keeps these product detectors tuned to a continuous or intermittent pilot signal.
See also
[edit]References
[edit]- ^ "Demodulator - Definitions from Dictionary.com". dictionary.reference.com. Retrieved 2008-05-16.
- ^ Ghostly voices, New Scientist, 2 October 1999, retrieved 2017-04-25
- ^ "The ratio detector"
External links
[edit]- Demodulation chapter on All About Circuits
Line Coding
[edit]

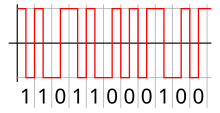



| Passband modulation |
|---|
 |
| Analog modulation |
| Digital modulation |
| Hierarchical modulation |
| Spread spectrum |
| See also |
In telecommunications, a line code is a pattern of voltage, current, or photons used to represent digital data transmitted down a communication channel or written to a storage medium. This repertoire of signals is usually called a constrained code in data storage systems.[1] Some signals are more prone to error than others as the physics of the communication channel or storage medium constrains the repertoire of signals that can be used reliably.[2]
Common line encodings are unipolar, polar, bipolar, and Manchester code.
Transmission and storage
[edit]After line coding, the signal is put through a physical communication channel, either a transmission medium or data storage medium.[3][4] The most common physical channels are:
- the line-coded signal can directly be put on a transmission line, in the form of variations of the voltage or current (often using differential signaling).
- the line-coded signal (the baseband signal) undergoes further pulse shaping (to reduce its frequency bandwidth) and then is modulated (to shift its frequency) to create an RF signal that can be sent through free space.
- the line-coded signal can be used to turn on and off a light source in free-space optical communication, most commonly used in an infrared remote control.
- the line-coded signal can be printed on paper to create a bar code.
- the line-coded signal can be converted to magnetized spots on a hard drive or tape drive.
- the line-coded signal can be converted to pits on an optical disc.
Some of the more common binary line codes include:
| Signal | Comments | 1 state | 0 state |
|---|---|---|---|
| NRZ–L | Non-return-to-zero level. This is the standard positive logic signal format used in digital circuits. | forces a high level | forces a low level |
| NRZ–M | Non-return-to-zero mark | forces a transition | does nothing (keeps sending the previous level) |
| NRZ–S | Non-return-to-zero space | does nothing (keeps sending the previous level) | forces a transition |
| RZ | Return to zero | goes high for half the bit period and returns to low | stays low for the entire period |
| Biphase–L | Manchester. Two consecutive bits of the same type force a transition at the beginning of a bit period. | forces a negative transition in the middle of the bit | forces a positive transition in the middle of the bit |
| Biphase–M | Variant of Differential Manchester. There is always a transition halfway between the conditioned transitions. | forces a transition | keeps level constant |
| Biphase–S | Differential Manchester used in Token Ring. There is always a transition halfway between the conditioned transitions. | keeps level constant | forces a transition |
| Differential Manchester (Alternative) | Need a Clock, always a transition in the middle of the clock period | is represented by no transition. | is represented by a transition at the beginning of the clock period. |
| Bipolar | The positive and negative pulses alternate. | forces a positive or negative pulse for half the bit period | keeps a zero level during bit period |

Each line code has advantages and disadvantages. Line codes are chosen to meet one or more of the following criteria:
- Minimize transmission hardware
- Facilitate synchronization
- Ease error detection and correction
- Achieve a target spectral density
- Eliminate a DC component
Disparity
[edit]Most long-distance communication channels cannot reliably transport a DC component. The DC component is also called the disparity, the bias, or the DC coefficient. The disparity of a bit pattern is the difference in the number of one bits vs the number of zero bits. The running disparity is the running total of the disparity of all previously transmitted bits.[5] The simplest possible line code, unipolar, gives too many errors on such systems, because it has an unbounded DC component.
Most line codes eliminate the DC component – such codes are called DC-balanced, zero-DC, or DC-free. There are three ways of eliminating the DC component:
- Use a constant-weight code. Each transmitted code word in a constant-weight code is designed such that every code word that contains some positive or negative levels also contains enough of the opposite levels, such that the average level over each code word is zero. Examples of constant-weight codes include Manchester code and Interleaved 2 of 5.
- Use a paired disparity code. Each code word in a paired disparity code that averages to a negative level is paired with another code word that averages to a positive level. The transmitter keeps track of the running DC buildup, and picks the code word that pushes the DC level back towards zero. The receiver is designed so that either code word of the pair decodes to the same data bits. Examples of paired disparity codes include alternate mark inversion, 8b/10b and 4B3T.
- Use a scrambler. For example, the scrambler specified in RFC 2615 for 64b/66b encoding.
Polarity
[edit]Bipolar line codes have two polarities, are generally implemented as RZ, and have a radix of three since there are three distinct output levels (negative, positive and zero). One of the principle advantages of this type of code is that it can eliminate any DC component. This is important if the signal must pass through a transformer or a long transmission line.
Unfortunately, several long-distance communication channels have polarity ambiguity. Polarity-insensitive line codes compensate in these channels.[6][7][8][9] There are three ways of providing unambiguous reception of 0 and 1 bits over such channels:
- Pair each code word with the polarity-inverse of that code word. The receiver is designed so that either code word of the pair decodes to the same data bits. Examples include alternate mark inversion, Differential Manchester encoding, coded mark inversion and Miller encoding.
- differential coding each symbol relative to the previous symbol. Examples include MLT-3 encoding and NRZI.
- Invert the whole stream when inverted syncwords are detected, perhaps using polarity switching
Run-length limited codes
[edit]For reliable clock recovery at the receiver, a run-length limitation may be imposed on the generated channel sequence, i.e., the maximum number of consecutive ones or zeros is bounded to a reasonable number. A clock period is recovered by observing transitions in the received sequence, so that a maximum run length guarantees sufficient transitions to assure clock recovery quality.
RLL codes are defined by four main parameters: m, n, d, k. The first two, m/n, refer to the rate of the code, while the remaining two specify the minimal d and maximal k number of zeroes between consecutive ones. This is used in both telecommunications and storage systems that move a medium past a fixed recording head.[10]
Specifically, RLL bounds the length of stretches (runs) of repeated bits during which the signal does not change. If the runs are too long, clock recovery is difficult; if they are too short, the high frequencies might be attenuated by the communications channel. By modulating the data, RLL reduces the timing uncertainty in decoding the stored data, which would lead to the possible erroneous insertion or removal of bits when reading the data back. This mechanism ensures that the boundaries between bits can always be accurately found (preventing bit slip), while efficiently using the media to reliably store the maximal amount of data in a given space.
Early disk drives used very simple encoding schemes, such as RLL (0,1) FM code, followed by RLL (1,3) MFM code which were widely used in hard disk drives until the mid-1980s and are still used in digital optical discs such as CD, DVD, MD, Hi-MD and Blu-ray using EFM and EFMPLus codes.[11] Higher density RLL (2,7) and RLL (1,7) codes became the de facto standards for hard disks by the early 1990s.[citation needed]
Synchronization
[edit]Line coding should make it possible for the receiver to synchronize itself to the phase of the received signal. If the clock recovery is not ideal, then the signal to be decoded will not be sampled at the optimal times. This will increase the probability of error in the received data.
Biphase line codes require at least one transition per bit time. This makes it easier to synchronize the transceivers and detect errors, however, the baud rate is greater than that of NRZ codes.
Other considerations
[edit]A line code will typically reflect technical requirements of the transmission medium, such as optical fiber or shielded twisted pair. These requirements are unique for each medium, because each one has different behavior related to interference, distortion, capacitance and attenuation.[12]
Common line codes
[edit]- 2B1Q
- 4B3T
- 4B5B
- 6b/8b encoding
- 8b/10b encoding
- 64b/66b encoding
- 128b/130b encoding
- Alternate mark inversion (AMI)
- Coded mark inversion (CMI)
- EFMPlus, used in DVDs
- Eight-to-fourteen modulation (EFM), used in compact discs
- Hamming code
- Hybrid ternary code
- Manchester code and differential Manchester
- Mark and space
- MLT-3 encoding
- Modified AMI codes: B8ZS, B6ZS, B3ZS, HDB3
- Modified frequency modulation, Miller encoding and delay encoding
- Non-return-to-zero (NRZ)
- Non-return-to-zero, inverted (NRZI)
- Pulse-position modulation (PPM)
- Return-to-zero (RZ)
- TC-PAM
Optical line codes
[edit]- Alternate-Phase Return-to-Zero (APRZ)
- Carrier-Suppressed Return-to-Zero (CSRZ)
- Three of Six, Fiber Optical (TS-FO)
See also
[edit]- Physical layer
- Self-synchronizing code and bit synchronization
References
[edit]- ^ K. Schouhamer Immink (2022). "Innovation in Constrained Codes". IEEE Communications Magazine. Retrieved 2022-10-05.
- ^ K. Schouhamer Immink (2001). "A Survey of Codes for Optical Disk Recording". IEEE Journal on Selected Areas in Communications. 19: 751–764. Retrieved 2018-02-05.
- ^ Karl Paulsen. "Coding for Magnetic Storage Mediums" Archived 2014-05-21 at the Wayback Machine.2007.
- ^ Abdullatif Glass; Nidhal Abdulaziz; and Eesa Bastaki (2007), "Slope line coding for telecommunication networks", IEEE International Conference on Signal Processing and Communication, Dubai: IEEE: 1537,
Line codes ... facilitates the transmission of data over telecommunication and computer networks and its storage in multimedia systems.
- ^ Jens Kröger (2014). "Data Transmission at High Rates via Kapton Flexprints for the Mu3e Experiment" (PDF). p. 16. Archived (PDF) from the original on 2022-10-09.
- ^ US 4387366, Peter E. K. Chow., "Code converter for polarity-insensitive transmission systems", published 1983
- ^ David A. Glanzer, "4.7 Polarity", Fieldbus Application Guide ... Wiring and Installation (PDF), Fieldbus Foundation, p. 10, archived (PDF) from the original on 2022-10-09
- ^
George C. Clark Jr.; J. Bibb Cain (2013). Error-Correction Coding for Digital Communications. Springer Science & Business Media. p. 255. ISBN 9781489921741.
When PSK data modulation is used, the potential exists for an ambiguity in the polarity of the received channel symbols. This problem can be solved in one of two ways. First ... a so-called transparent code. ...
- ^
Prakash C. Gupta (2013). Data Communications and Computer Networks. PHI Learning Pvt. Ltd. p. 13. ISBN 9788120348646.
Another benefit of differential encoding is its insensitivity to polarity of the signal. ... If the leads of a twisted pair are accidentally reversed...
- ^ Kees Schouhamer Immink (December 1990). "Runlength-Limited Sequences". Proceedings of the IEEE. 78 (11): 1745–1759. doi:10.1109/5.63306.
A detailed description is furnished of the limiting properties of runlength limited sequences.
- ^ Kees Schouhamer Immink (1995). "EFMPlus: The Coding Format of the MultiMedia Compact Disc". IEEE Transactions on Consumer Electronics. CE-41: 491–497.
A high-density alternative to EFM is described.
- ^ Dong, Jielin (2007). Network Dictionary. Javvin Technologies Inc. p. 284. ISBN 9781602670006.
 This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22. (in support of MIL-STD-188).
This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22. (in support of MIL-STD-188).
External links
[edit]- Line Coding Lecture No. 9
- Line Coding in Digital Communication
- CodSim 2.0: Open source simulator for Digital Data Communications Model at the University of Malaga written in HTML






![{\displaystyle {\begin{aligned}y(t)&=\left[1+{\frac {m(t)}{A}}\right]c(t)\\&=\left[1+m\cos \left(2\pi f_{m}t+\phi \right)\right]A\sin \left(2\pi f_{c}t\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/637cd857e4f781d6d7bbdb570fa8c227d64d4298)
![{\displaystyle y(t)=A\sin(2\pi f_{c}t)+{\frac {1}{2}}Am\left[\sin \left(2\pi \left[f_{c}+f_{m}\right]t+\phi \right)+\sin \left(2\pi \left[f_{c}-f_{m}\right]t-\phi \right)\right].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6540130eb862ec3332481d4f1730806e8352ba0)







![{\displaystyle {\begin{aligned}y(t)&=A_{c}\cos \left(2\pi \int _{0}^{t}f(\tau )d\tau \right)\\&=A_{c}\cos \left(2\pi \int _{0}^{t}\left[f_{c}+f_{\Delta }x_{m}(\tau )\right]d\tau \right)\\&=A_{c}\cos \left(2\pi f_{c}t+2\pi f_{\Delta }\int _{0}^{t}x_{m}(\tau )d\tau \right)\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a85546c0eab3462755f52bf3808a8b9f5083b38)





![{\displaystyle {\begin{aligned}y(t)&=A_{c}\cos \left(2\pi \left[f_{c}+f_{\Delta }x_{m}(t)\right]t\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33e21e0bf408a5afae4268fde1d3ec3d0ca150c3)


































![{\displaystyle {\begin{aligned}r(t)&={\tfrac {1}{2}}I(t)\left[1+\cos(4\pi f_{c}t)\right]-{\tfrac {1}{2}}Q(t)\sin(4\pi f_{c}t)\\&={\tfrac {1}{2}}I(t)+{\tfrac {1}{2}}\left[I(t)\cos(4\pi f_{c}t)-Q(t)\sin(4\pi f_{c}t)\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/548bd6eab15dcc86dd4f607025ffee024ce0c2c8)
![{\displaystyle s_{c}(t)_{+}={\tfrac {1}{2}}e^{i2\pi f_{c}t}[I(t)+iQ(t)]\quad {\stackrel {\mathcal {F}}{\Longrightarrow }}\quad {\tfrac {1}{2}}\left[{\widehat {I\ }}(f-f_{c})+e^{i\pi /2}{\widehat {Q}}(f-f_{c})\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/627a100c3a2b79e4267617288854c5123cb52494)



















![{\displaystyle {\begin{aligned}s_{\text{ssb}}(t)&=\operatorname {Re} \left\{s_{\mathrm {a} }(t)\cdot e^{j2\pi f_{0}t}\right\}\\&=\operatorname {Re} \left\{\,\left[s(t)+j\cdot {\widehat {s}}(t)\right]\cdot \left[\cos \left(2\pi f_{0}t\right)+j\cdot \sin \left(2\pi f_{0}t\right)\right]\,\right\}\\&=s(t)\cdot \cos \left(2\pi f_{0}t\right)-{\widehat {s}}(t)\cdot \sin \left(2\pi f_{0}t\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75792a0ac2bb0ee6213b5f329629648d7d68ee18)