User:Mpatel/sandbox/Black hole
{{Multiple issues | long = March 2008 | refimprove = October 2008 | restructure = October 2008 <!-- Too many short sections, per Wikipedia:Layout; non-unique section names, per WP:HEAD --> | jargon = October 2008 }}

| General relativity |
|---|
 |
A black hole is a region of space where mass is so concentrated that nearby matter or electromagnetic radiation (such as visible light) cannot escape the overwhelming gravitational field. The event horizon of a black hole marks the 'point of no return', a boundary that, if crossed, inevitably leads falling matter and radiation towards the central singularity.
Several types of black hole are thought to exist, their existence being theoretically predicted to arise as solutions of Einstein's field equations of general relativity, the currently accepted theory of gravitation. Black holes are generally believed to form from the collapse of massive stars. Others are thought to arise from quantum mechanical processes in the early universe.
Quantum mechanics research also indicates that, rather than holding captured matter forever, black holes may slowly leak a form of thermal energy called Hawking radiation and may well have a finite life.[2][3][4] Together with white holes, black holes are speculated to form wormholes, shortcuts through space and time. The as yet unknown theory of quantum gravity is believed to give the fully correct description of black holes.
Black holes are believed to reveal their presence through interaction with orbiting material. Recent observations of orbiting stars and gas indicate evidence for black holes.[5][6] Such observations have resulted in the general scientific consensus that, barring a breakdown in our understanding of nature, black holes do exist in our universe.[7]
History
[edit]The idea of a body so massive that even light could not escape was put forward by geologist John Michell in a letter written to Henry Cavendish in 1783 to the Royal Society:[8]
| “ | If the semi-diameter of a sphere of the same density as the Sun were to exceed that of the Sun in the proportion of 500 to 1, a body falling from an infinite height towards it would have acquired at its surface greater velocity than that of light, and consequently supposing light to be attracted by the same force in proportion to its vis inertiae, with other bodies, all light emitted from such a body would be made to return towards it by its own proper gravity. | ” |
| — John Michell | ||
This assumes that light is influenced by gravity in the same way as massive objects.
In 1796, mathematician Pierre-Simon Laplace promoted the same idea in the first and second editions of his book Exposition du système du Monde (it was removed from later editions).[9][10]
Such "dark stars" were largely ignored in the nineteenth century, since light was then thought to be a massless wave and therefore not influenced by gravity. Unlike the modern black hole concept, the object behind the horizon is assumed to be stable against collapse.
In 1915, Albert Einstein developed the theory of gravity called general relativity, having earlier shown that gravity does influence light (although light has zero rest mass,[citation needed] it is not the rest mass that is the source of gravity but the energy). A few months later, Karl Schwarzschild gave the solution for the gravitational field of a point mass and a spherical mass,[11] showing that a black hole could theoretically exist. The Schwarzschild radius is now known to be the radius of the event horizon of a non-rotating black hole, but this was not well understood at that time, for example Schwarzschild himself thought it was not physical. Johannes Droste, a student of Lorentz, independently gave the same solution for the point mass a few months after Schwarzschild and wrote more extensively about its properties.
In 1930, astrophysicist Subrahmanyan Chandrasekhar calculated using general relativity that a non-rotating body above 1.44 solar masses (the Chandrasekhar limit) would collapse,[citation needed] since no mechanism was known to prevent this. His arguments were opposed by Arthur Eddington, who believed that something would inevitably stop the collapse.[citation needed] Eddington was partly correct: a white dwarf slightly more massive than the Chandrasekhar limit will collapse into a neutron star.[citation needed] But in 1939, Robert Oppenheimer and others predicted that stars above approximately three solar masses (the Tolman-Oppenheimer-Volkoff limit) would collapse into black holes for the reasons presented by Chandrasekhar.[12]
Oppenheimer and his co-authors used Schwarzschild's system of coordinates (the only coordinates available in 1939), which produced mathematical singularities at the Schwarzschild radius, in other words the equations broke down at the Schwarzschild radius because some of the terms were infinite. This was interpreted as indicating that the Schwarzschild radius was the boundary of a "bubble" in which time "stopped". The collapsed stars were briefly known as "frozen stars",[citation needed] as the calculations indicated that an outside observer would see the surface of the star frozen in time at the instant where its collapse takes it inside the Schwarzschild radius. But many physicists[who?] could not accept the idea of time standing still inside the Schwarzschild radius, and there was little interest in the subject for over 20 years.[citation needed]
In 1958, David Finkelstein broke the deadlock over "stopped time" and introduced the concept of the event horizon by presenting Eddington-Finkelstein coordinates, which enabled him to show that "The Schwarzschild surface r = 2 m is not a singularity but acts as a perfect unidirectional membrane: causal influences can cross it in only one direction".[13] All theories up to this point, including Finkelstein's, covered only non-rotating, uncharged black holes.
In 1967, astronomers discovered pulsars,[14][15] and within a few years could show that the known pulsars were rapidly rotating neutron stars. Until that time, neutron stars were also regarded as just theoretical curiosities. So the discovery of pulsars awakened interest in all types of ultra-dense objects that might be formed by gravitational collapse.
Physicist John Wheeler is widely credited with coining the term black hole in his 1967 public lecture Our Universe: the Known and Unknown, as an alternative to the more cumbersome "gravitationally completely collapsed star". However, Wheeler insisted that someone else at the conference had coined the term and he had merely adopted it as useful shorthand. The term was also cited in a 1964 letter by Anne Ewing to the AAAS:[16]
According to Einstein’s general theory of relativity, as mass is added to a degenerate star a sudden collapse will take place and the intense gravitational field of the star will close in on itself. Such a star then forms a "black hole" in the universe.
The phrase had already entered the language years earlier as the Black Hole of Calcutta incident of 1756 in which 146 Europeans were locked up overnight in punishment cell of barracks at Fort William by Siraj ud-Daulah, and all but 23 perished.[17]
What makes it impossible to escape from black holes?
[edit]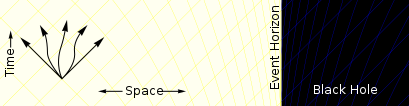 Far away from the black hole a particle can move in any direction. It is only restricted by the speed of light. |
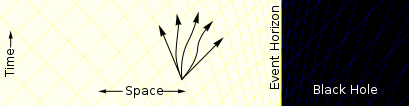 Closer to the black hole spacetime starts to deform. There are more paths going towards the black hole than paths moving away. |
 Inside of the event horizon all paths bring the particle closer to the center of the black hole. It is no longer possible for the particle to escape.[18] |
Popular accounts commonly try to explain the black hole phenomenon by using the concept of escape velocity, the speed needed for a vessel starting at the surface of a massive object to completely clear the object's gravitational field. It follows from Newton's law of gravity that a sufficiently dense object's escape velocity will equal or even exceed the speed of light. Citing that nothing can exceed the speed of light they then infer that nothing would be able to escape such a dense object.[19] However, the argument has a flaw in that it does not explain why light would be affected by a gravitating body or why it would not be able to escape. Nor does it give a satisfactory explanation for why a powered spaceship would not be able to break free.[20]
Two concepts introduced by Albert Einstein are needed to explain the phenomenon. The first is that time and space are not two independent concepts, but are interrelated forming a single continuum, spacetime. This continuum has some special properties. An object is not free to move around spacetime at will; it must always move forward in time and cannot change its position in space faster than the speed of light. This is the main result of the theory of special relativity.
The second concept is the base of general relativity; mass deforms the structure of this spacetime. The effect of a mass on spacetime can informally be described as tilting the direction of time towards the mass. As a result, objects tend to move towards masses. This is experienced as gravity. This tilting effect becomes more pronounced as the distance to the mass becomes smaller. At some point close to the mass, the tilting becomes so strong that all the possible paths an object can take lead towards the mass.[21] This implies that any object that crosses this point can no longer get further away from the mass, not even using powered flight. This point is called the event horizon.
Formation
[edit]From the exotic nature of black holes, it is natural to question if such bizarre objects could actually exist in nature or whether they are merely pathological solutions to Einstein's equations. In 1970, Hawking and Penrose showed using their singularity theorems that under generic conditions, black holes are expected to form.[22] Apart from the gravitational collapse of heavy objects such as stars, black holes could in principle also arise by more exotic means.
Gravitation collapse
[edit]Gravitational collapse occurs when an object's internal pressure is insufficient to resist its own gravity. For stars this usually occurs either because there is not enough "fuel" remaining to maintain its temperature, or because a star which would have been stable receives a lot of extra matter in a way which does not raise its core temperature. In either case, the star's temperature is no longer high enough to prevent it from collapsing under its own weight (the ideal gas law explains the connection between pressure, temperature, and volume).
The collapse may be stopped by the degeneracy pressure of the star's constituents, condensing the matter into an exotic denser state. The result is a type of compact star. the type depending on the mass of the remnant - the matter left over after changes triggered by the collapse (such as supernova or pulsations leading to a planetary nebula) have blown away the outer layers. This can be substantially less than the original star - remnants exceeding 5 solar masses are produced by stars which were over 20 solar masses before the collapse.[citation needed]
If the mass of the remnant exceeds ~2-4 solar masses (the Tolman-Oppenheimer-Volkoff limit), even the degeneracy pressure of neutrons is insufficient to stop the collapse.[23][24] After this, no known mechanism (except possibly quark degeneracy pressure, see quark star) is powerful enough to stop the collapse and the object will inevitably become a black hole.
This gravitational collapse of heavy stars is assumed to be responsible for the formation of most (if not all) stellar mass black holes.
Primordial black holes
[edit]Gravitational collapse requires great densities. Nowadays, such high densities are only found in stars, but in the early universe shortly after the big bang densities were much greater, possibly allowing for the creation of black holes. The high density alone is not enough to allow the formation of black holes since a uniform mass distribution will not allow the mass to bunch up. In order for primordial black holes to form in such a dense medium, there must be initial density perturbations which can then grow under their own gravity. Different models for the early universe vary widely in their predictions of the size of these perturbations. Various models predict the creation of black holes, ranging from a Planck mass to hundreds of thousands of solar masses.[25] Primordial black holes could thus account for the creation of any type of black hole.
Production in high energy collisions
[edit]Besides gravitational collapse, black holes could also be created in high energy collisions that produce sufficient density.[citation needed] Since classically black holes can be of any mass, micro black holes would be expected to form in any such process (no matter how low the energy). However, to date, no such events have been detected as a deficiency of the mass balance in particle accelerator experiments.[26] This suggests that there must be a lower limit for the mass of black holes.
Theoretically this boundary is expected to lie around the Planck mass (~1019 GeV/c2), where quantum effects are expected to make the theory of general relativity break down completely.[citation needed] This would put the creation of black holes firmly out of reach of any high energy process occurring on or near the Earth. Certain developments in quantum gravity however suggest that this bound could be much lower. Some braneworld scenarios for example put the Planck mass much lower, may be even as low as 1 TeV.[27] This would make it possible for micro black holes to be created in the high energy collisions occurring when cosmic rays hit the earth's atmosphere, or even maybe in the new Large Hadron Collider at CERN. These theories are however very speculative, and the creation of black holes in these processes is deemed unlikely by many specialists.[citation needed]
Growth
[edit]Once formed, a black hole can continue growing by absorbing additional matter. Any black hole will continually absorb interstellar dust from its direct surroundings and omnipresent cosmic background radiation, but neither of these processes should significantly affect the mass of a stellar black hole. More significant contributions can occur when the black hole is formed in a binary star system. After formation, the black hole can then absorb significant amounts of matter from its companion.[citation needed]
Much larger contributions can be obtained when a black hole merges with other stars or compact objects. The supermassive black holes suspected to exist in the center of most galaxies are expected to have formed from the coagulation of many smaller objects.[citation needed] The process has also been proposed as the origin of some intermediate-mass black holes.[citation needed]
Characterisation
[edit]The No-hair theorem
[edit]According to the "No Hair" theorem a black hole has only three independent physical properties: mass, charge and angular momentum.[28] Any two black holes that share the same values for these properties are indistinguishable. This contrasts with other astrophysical objects such as stars, which have very many—possibly infinitely many—parameters. Consequently, a great deal of information is lost when a star collapses to form a black hole. As information is preserved in most physical theories, the loss of information in black holes is puzzling. Physicists refer to this as the black hole information paradox.
The No Hair theorem makes assumptions about the nature of our universe and the matter within. Other assumptions lead to different conclusions. For example, if nature allows magnetic monopoles to exist—which appears to be theoretically possible, but has never been observed—then it should also be possible for black holes to have magnetic charge. If the universe has more than four dimensions (as string theories, a controversial but apparently possible class of theories, would require), or has a global anti-de Sitter structure, the theorem could fail completely, allowing many sorts of "hair". However, in our apparently four-dimensional, very nearly flat universe,[29] the theorem should hold.
Classification
[edit]By physical properties
[edit]The simplest black hole is one that has mass but neither charge nor angular momentum. These black holes are often referred to as Schwarzschild black holes after the physicist Karl Schwarzschild who discovered this solution in 1915.[11] It was the first non-trivial exact solution to the Einstein equations to be discovered, and according to Birkhoff's theorem, the only vacuum solution that is spherically symmetric. For real world physics this means that there is no observable difference between the gravitational field of such a black hole and that of any other spherical object of the same mass—for example a spherical star or planet—once one is in the empty space outside the object. The popular notion of a black hole "sucking in everything" in its surroundings is therefore incorrect; the external gravitational field, far from the event horizon, is essentially like that of ordinary massive bodies.
Electrically charged non-rotating black holes are described by the Reissner-Nordström solution, developed by Hans Reissner[30] and Gunnar Nordström.[31]
Mathematician Roy Kerr presented the Kerr solution in 1963, showing how this could be used to describe a rotating black hole.[32] In addition to its theoretical interest, Kerr's work made black holes more believable for astronomers, since black holes are formed from stars and all known stars rotate.
The most general known stationary black hole solution is the Kerr-Newman metric, discovered by physicist Ezra Newman et al[33][34] having both charge and angular momentum. All these general solutions share the property that they converge to the Schwarzschild solution at distances that are large compared to the ratio of charge and angular momentum to mass (in natural units).
While the mass of a black hole can take any positive value, the charge and angular momentum are constrained by the mass. In natural units , the total charge Q and the total angular momentum J are expected to satisfy Q2+(J/M)2 ≤ M2 for a black hole of mass M. Black holes saturating this inequality are called extremal. Solutions of Einstein's equations violating the inequality do exist, but do not have a horizon. These solutions have naked singularities and are deemed unphysical, as the cosmic censorship hypothesis rules out such singularities due to the generic gravitational collapse of realistic matter.[35] This is supported by numerical simulations.[36]
Due to the relatively large strength of the electromagnetic force, black holes forming from the collapse of stars are expected to retain the nearly neutral charge of the star. Rotation, however, is expected to be a common feature of compact objects, and the black-hole candidate binary X-ray source GRS 1915+105[37] appears to have an angular momentum near the maximum allowed value.
By mass
[edit]| Class | Mass | Size |
|---|---|---|
| Supermassive black hole | ~105 - 109 MSun | ~0.001 - 10 AU |
| Intermediate-mass black hole | ~103 MSun | ~103 km = REarth |
| Stellar-mass | ~10 MSun | ~30 km |
| Primordial black hole | up to ~MMoon | up to ~0.1 mm |
Black holes are commonly classified according to their mass, independent of angular momentum J.[citation needed] The size of a black hole, as determined by the radius of the event horizon, or Schwarzschild radius, is proportional to the mass through where is the Schwarzschild radius and is the mass of the Sun. A black hole's size and mass are thus simply related independent of rotation.[dubious – discuss] According to this criterion, black holes are classed as:
- Supermassive - contain hundreds of thousands to billions of solar masses. and are thought to exist in the center of most galaxies,[38][39] including the Milky Way.[40] They are believed to be responsible for active galactic nuclei, and presumably form either from the coalescence of smaller black holes, or by the accretion of stars and gas onto them. The largest known supermassive black hole is located in OJ 287 weighing in at 18 billion solar masses.[41]
- Intermediate - contain thousands of solar masses. They have been proposed as a possible power source for ultraluminous X-ray sources.[42] There is no known mechanism for them to form directly, so they likely form via collisions of lower mass black holes, either in the dense stellar cores of globular clusters or galaxies.[citation needed] Such creation events should produce intense bursts of gravitational waves, which may be observed soon.[citation needed] The boundary between super- and intermediate-mass black holes is a matter of convention. Their lower mass limit, the maximum mass for direct formation of a single black hole from collapse of a massive star, is poorly known at present.
- Stellar-mass black holes - have masses ranging from a lower limit of about 1.5–3.0 solar masses (the Tolman-Oppenheimer-Volkoff limit for the maximum mass of neutron stars) up to perhaps 15–20 solar masses. They are created by the collapse of individual stars, or by the coalescence (inevitable, due to gravitational radiation) of binary neutron stars. Stars may form with initial masses up to ≈100 solar masses, or possibly even higher, but these shed most of their outer massive layers during earlier phases of their evolution, either blown away in stellar winds during the red giant, AGB, and Wolf-Rayet stages, or expelled in supernova explosions for stars that turn into neutron stars or black holes. Being known mostly by theoretical models for late-stage stellar evolution, the upper limit for the mass of stellar-mass black holes is somewhat uncertain at present. The cores of still lighter stars form white dwarfs.
- Micro (also mini black holes) - have masses much less than that of a star. At these sizes, the effects of quantum mechanics are expected to come into play. There is no known mechanism for them to form via normal processes of stellar evolution, but certain inflationary scenarios predict their production during the early stages of the evolution of the universe.[citation needed] According to some theories of quantum gravity they may also be produced in the highly energetic reaction produced by cosmic rays hitting the atmosphere or even in particle accelerators such as the Large Hadron Collider.[citation needed] The theory of Hawking radiation predicts that such black holes will evaporate in bright flashes of gamma radiation. NASA's Fermi Gamma-ray Space Telescope satellite (formerly GLAST) launched in 2008 is searching for such flashes.[43]
Features
[edit]Event horizon
[edit]The defining feature of a black hole is the event horizon, a surface in spacetime that marks a point of no return. Once an object crosses this surface, it cannot return to the other side.[20] Consequently, anything inside this surface is completely hidden from outside observers. Other than this, the event horizon is a completely normal part of space with no special features that would allow someone falling into the black hole to know when they would cross the horizon.[20] The event horizon is not a solid surface, and does not obstruct or slow down matter or radiation that is traveling towards the region within the event horizon.
Outside the event horizon, the gravitational field is identical to the field produced by any other spherically symmetric object of the same mass.[20] The popular conception of black holes as "sucking" things in is misleading: objects can orbit black holes indefinitely, provided they stay outside the photon sphere (described below), and also ignoring the effects of gravitational radiation which causes orbiting objects to lose energy (similar to the effect of electromagnetic radiation).[44]
To a distant observer clocks near a black hole appear to tick more slowly than those further away from the black hole.[45] Due to this effect (known as gravitational time dilation) the distant observer will see an object falling into a black hole slow down as it approaches the event horizon, taking an infinite time to reach it.[citation needed] At the same time all process on this object slow down causing emitted light to appear redder an dimmer, an effect known as gravitational red shift.[citation needed] Eventually, the falling object becomes so dim that it can no longer be seen, at a point just before it reaches the event horizon.
From the falling object's viewpoint, distant objects generally appear blue-shifted due to the gravitational field of the black hole.[citation needed] This effect may be partly (or even entirely) negated by the Doppler red shift caused by the velocity with the distant object.[citation needed] For the object, nothing particularly special happens at the event horizon. In fact, there is no (local) way to determine whether the horizon has been passed or not.[20] An infalling object takes a finite proper time (i.e. measured by its own clock) to fall past the event horizon.[citation needed]
Singularity
[edit]According to general relativity, there is a space-time singularity at the center of a spherical black hole, which means an infinite space-time curvature. It means that, from the viewpoint of an observer falling into a black hole, in a finite time (at the end of his fall) a black hole's mass becomes entirely compressed into a region with zero volume, so its density becomes infinite.[citation needed] This zero-volume, infinitely dense region at the center of a black hole is called a gravitational singularity.
The singularity in a non-rotating black hole is a point, in other words it has zero length, width, and height. The singularity of a rotating black hole is smeared out to form a ring shape lying in the plane of rotation.[46] The ring still has no thickness and hence no volume.
The appearance of singularities in general relativity is commonly perceived as signaling the breakdown of the theory.[citation needed] This breakdown is not unexpected, as it occurs in a situation where quantum mechanical effects should become important, since densities are high and particle interactions should thus play a role. Unfortunately, to date it has not been possible to combine quantum and gravitation effects in a single theory. It is however quite generally expected that a theory of quantum gravity will feature black holes without singularities.[citation needed]
Formation of the singularity takes a finite (and very short) time only from the viewpoint of an infalling observer. From the standpoint of a distant observer, it takes infinite time to do so due to gravitational time dilation.
The difference in gravitational field at two points results in a tidal force, which, in a very strongly varying field causes an object to experience a large differential force in the direction of the gravitational source.[citation needed] Near black holes, the enormous tidal forces are expected to literally stretch and rip the object down to it's constituent atoms and elementary particles, a process called spaghettification. The strength of the tidal force of a black hole depends on how gravitational attraction changes with distance, rather than on the absolute force being felt. This means that small black holes cause spaghettification while infalling objects are still outside their event horizons, whereas objects falling into large, supermassive black holes may not be deformed or otherwise feel excessively large forces before passing the event horizon.[citation needed]
Photon sphere
[edit]The photon sphere is a spherical boundary of zero thickness such that photons moving along tangents to the sphere will be trapped in a circular orbit. For non-rotating black holes, the photon sphere has a radius 1.5 times the Schwarzschild radius.[citation needed] The orbits are dynamically unstable, hence any small perturbation (maybe caused by some infalling matter) will grow over time, either setting it on an outward trajectory escaping the black hole or on an inward spiral eventually crossing the event horizon.[citation needed]
While light can still escape from inside the photon sphere, any light that crosses the photon sphere on an inbound trajectory will be captured by the black hole.[citation needed] Hence any light reaching an outside observer from inside the photon sphere must have been emitted by objects inside the photon sphere but still outside of the event horizon.
Other compact objects, such as neutron stars, can also have photon spheres.[47] This follows because the gravitational field of an object does not depend on its actual size, hence any object that is smaller than 1.5 times the Schwarzschild radius corresponding to its mass will have a photon sphere.
Ergosphere
[edit]
Rotating black holes are surrounded by a region of spacetime in which it is impossible to stand still, called the ergosphere.[48] This is the result of a process known as frame-dragging; general relativity predicts that any rotating mass will tend to slightly "drag" along the spacetime immediately surrounding it. Any object near the rotating mass will tend to start moving in the direction of rotation. For a rotating black hole this effect becomes so strong near the event horizon that an object would have to move faster than the speed of light in the opposite direction to just stand still.
The ergosphere of black hole is bounded by
- on the outside, an oblate spheroid, which coincides with the event horizon at the poles and is noticeably wider around the "equator". This boundary is sometimes called the "ergosurface", but it is just a boundary and has no more solidity than the event horizon. At points exactly on the ergosurface, spacetime is "dragged around at the speed of light."
- on the inside, the (outer) event horizon.
Within the ergosphere, space-time is dragged around faster than light—general relativity forbids material objects to travel faster than light (so does special relativity), but allows regions of space-time to move faster than light relative to other regions of space-time.
Objects and radiation (including light) can stay in orbit within the ergosphere without falling to the center.[citation needed] But they cannot hover (remain stationary, as seen by an external observer), because that would require them to move backwards faster than light relative to their own regions of space-time, which are moving faster than light relative to an external observer.
Objects and radiation can also escape from the ergosphere. In fact the Penrose process predicts that objects will sometimes fly out of the ergosphere, obtaining the energy for this by "stealing" some of the black hole's rotational energy. If a large total mass of objects escapes in this way, the black hole will spin more slowly and may even stop spinning eventually.[citation needed]
Hawking radiation
[edit]In 1971, Stephen Hawking showed that the total area of the event horizons of any collection of classical black holes can never decrease, even if they collide and swallow each other; that is merge.[49] This is remarkably similar to the Second Law of Thermodynamics, with area playing the role of entropy. As classical objects with zero temperature it was assumed that black holes had zero entropy; the second law of thermodynamics would then be violated by an entropy-laden material entering the black hole, resulting in a decrease of the total entropy of the universe. Therefore, Jacob Bekenstein proposed that a black hole should have an entropy, and that it should be proportional to its horizon area. Since black holes do not classically emit radiation, the thermodynamic viewpoint seemed simply an analogy, since zero temperature implies infinite changes in entropy with any addition of heat, which implies infinite entropy. However, in 1974, Hawking applied quantum field theory to the curved spacetime around the event horizon and discovered that black holes emit Hawking radiation, a form of thermal radiation, allied to the Unruh effect, which implied they had a positive temperature. This strengthened the analogy between black hole dynamics and thermodynamics: using the first law of black hole mechanics, it follows that the entropy of a non-rotating black hole is one quarter the horizon area. This is a universal result and is extended to cosmological horizons such as in de Sitter space. It was later suggested[who?] that black holes are maximum-entropy objects, meaning that the maximum possible entropy of a region of space is the entropy of the largest black hole that can fit into it. This led to the holographic principle.
Hawking radiation reflects a characteristic temperature of the black hole, which can be calculated from its entropy. The more its temperature falls, the more massive a black hole becomes: the more energy a black hole absorbs, the colder it gets. A black hole with roughly the mass of the planet Mercury would have a temperature in equilibrium with the cosmic microwave background radiation (about 2.73 K). More massive than this, a black hole will be colder than the background radiation, and it will gain energy from the background faster than it gives energy up through Hawking radiation, becoming even colder still. However, for a less massive black hole the effect implies that the mass of the black hole will slowly evaporate with time, with the black hole becoming hotter and hotter as it does so. Although these effects are negligible for black holes massive enough to have been formed astronomically, they would rapidly become significant for hypothetical smaller black holes, where quantum-mechanical effects dominate. Indeed, small black holes are predicted to undergo runaway evaporation and eventually vanish in a burst of radiation.
Although general relativity can be used to perform a semi-classical calculation of black hole entropy, this situation is theoretically unsatisfying. In statistical mechanics, entropy is understood as counting the number of microscopic configurations of a system which have the same macroscopic qualities (such as mass, charge, pressure, etc.). But without a satisfactory theory of quantum gravity, one cannot perform such a computation for black holes. Some promise has been shown by string theory, however. There one posits that the microscopic degrees of freedom of the black hole are D-branes. By counting the states of D-branes with given charges and energy, the entropy for certain supersymmetric black holes has been reproduced. Extending the region of validity of these calculations is an ongoing area of research.
In 1974, Stephen Hawking showed that black holes are not entirely black but emit small amounts of thermal radiation.[50] He got this result by applying quantum field theory in a static black hole background. The result of his calculations is that a black hole should emit particles in a perfect black body spectrum. This effect has become known as Hawking radiation. Research from various directions suggests the theoretical validity of the effect.[51]
The temperature of the emitted black body spectrum is proportional to the surface gravity of the black hole. For a Schwarzschild black hole this is inversely proportional to the mass. Consequently, large black holes are very cold and emit very little radiation. A stellar black hole of 10 solar masses, for example, would have a Hawking temperature of several nanokelvin, much less than the 2.7K produced by the Cosmic Microwave Background. Micro black holes on the other hand could be quite bright producing high energy gamma rays.
Due to low Hawking temperature of stellar black holes, Hawking radiation has never been observed at any of the black hole candidates.
If Hawking's theory of black hole radiation is correct, then black holes are expected to emit a thermal spectrum of radiation, and thereby lose mass, by the equivalence of mass and energy.[50] Black holes will thus shrink and evaporate over time. The temperature of this spectrum (Hawking temperature) is proportional to the surface gravity of the black hole, which in turn is inversely proportional to the mass. Large black holes thus emit less radiation than small black holes.
A stellar black hole of 5 solar masses has a Hawking temperature of about 12 nanoKelvin. This is far less than the 2.7 K produced by the cosmic microwave background (CMB) radiation. Stellar mass (and larger) black holes thus receive more mass from the CMB than they emit through Hawking radiation and will thus grow instead of shrink. In order to have a Hawking temperature larger than 2.7 K (and thus be able to evaporate) a black hole needs to be lighter than the Moon (and thus have diameter of less than a tenth of a millimeter).
Rdaiation effects are expected to be very strong for very small black holes. Even a black hole that is heavy compared to a human would evaporate in an instant. A black hole the weight of a car (~ 10−24 m) would only take a nanosecond to evaporate, during which time it would briefly have a luminosity more than 200 times that of the sun. Lighter black holes are expected to evaporate even faster, for example a black hole of mass 1 TeV/c2 would take less than 10−88 seconds to evaporate completely. Of course, for such a small black hole quantum gravitation effects are expected to play an important role and could —although current developments in quantum gravity do not indicate so— hypothetically make such a small black hole stable.
Information loss paradox
[edit]An open question in fundamental physics is the so-called information loss paradox, or black hole unitarity paradox. Classically, the laws of physics are the same run forward or in reverse. That is, if the position and velocity of every particle in the universe were measured, we could (disregarding chaos) work backwards to discover the history of the universe arbitrarily far in the past. In quantum mechanics, this corresponds to a vital property called unitarity, which has to do with the conservation of probability.[52]
Black holes, however, might violate this rule. The position under classical general relativity is subtle but straightforward: because of the classical no hair theorem, we can never determine what went into the black hole. However, as seen from the outside, information is never actually destroyed, as matter falling into the black hole takes an infinite time to reach the event horizon.
Ideas about quantum gravity, on the other hand, suggest that there can only be a limited finite entropy (i.e. a maximum finite amount of information) associated with the space near the horizon; but the change in the entropy of the horizon plus the entropy of the Hawking radiation is always sufficient to take up all of the entropy of matter and energy falling into the black hole.
Many physicists are concerned however that this is still not sufficiently well understood. In particular, at a quantum level, is the quantum state of the Hawking radiation uniquely determined by the history of what has fallen into the black hole; and is the history of what has fallen into the black hole uniquely determined by the quantum state of the black hole and the radiation? This is what determinism, and unitarity, would require.
For a long time Stephen Hawking had opposed such ideas, holding to his original 1975 position that the Hawking radiation is entirely thermal and therefore entirely random, containing none of the information held in material the hole has swallowed in the past; this information he reasoned had been lost. However, on 21 July 2004 he presented a new argument, reversing his previous position.[53] On this new calculation, the entropy (and hence information) associated with the black hole escapes in the Hawking radiation itself. However, making sense of it, even in principle, is difficult until the black hole completes its evaporation. Until then it is impossible to relate in a 1:1 way the information in the Hawking radiation (embodied in its detailed internal correlations) to the initial state of the system. Once the black hole evaporates completely, such identification can be made, and unitarity is preserved.
By the time Hawking completed his calculation, it was already very clear from the AdS/CFT correspondence that black holes decay in a unitary way. This is because the fireballs in gauge theories, which are analogous to Hawking radiation, are unquestionably unitary. Hawking's new calculation has not been evaluated by the specialist scientific community, because the methods he uses are unfamiliar and of dubious consistency; but Hawking himself found it sufficiently convincing to pay out on a bet he had made in 1997 with Caltech physicist John Preskill, to considerable media interest.
Detection and evidence
[edit]Accretion disks and gas jets
[edit]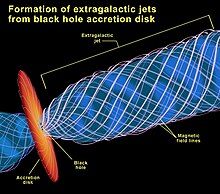
Most accretion disks and gas jets are not clear proof that a stellar-mass black hole is present, because other massive, ultra-dense objects such as neutron stars and white dwarfs cause accretion disks and gas jets to form and to behave in the same ways as those around black holes. But they can often help by telling astronomers where it might be worth looking for a black hole.
On the other hand, extremely large accretion disks and gas jets may be good evidence for the presence of supermassive black holes, because as far as we know any mass large enough to power these phenomena must be a black hole.
Strong radiation emissions
[edit]
Steady X-ray and gamma ray emissions also do not prove that a black hole is present, but can tell astronomers where it might be worth looking for one - and they have the advantage that they pass fairly easily through nebulae and gas clouds.
But strong, irregular emissions of X-rays, gamma rays and other electromagnetic radiation can help to prove that a massive, ultra-dense object is not a black hole, so that "black hole hunters" can move on to some other object. Neutron stars and other very dense stars have surfaces, and matter colliding with the surface at a high percentage of the speed of light will produce intense flares of radiation at irregular intervals. Black holes have no material surface, so the absence of irregular flares around a massive, ultra-dense object suggests that there is a good chance of finding a black hole there.
Intense but one-time gamma ray bursts (GRBs) may signal the birth of "new" black holes, because astrophysicists think that GRBs are caused either by the gravitational collapse of giant stars[54] or by collisions between neutron stars,[55] and both types of event involve sufficient mass and pressure to produce black holes. But it appears that a collision between a neutron star and a black hole can also cause a GRB,[56] so a GRB is not proof that a "new" black hole has been formed. All known GRBs come from outside our own galaxy, and most come from billions of light years away[57] so the black holes associated with them are actually billions of years old.
Astrophysicists such as Winter believe that some ultraluminous X-ray sources may be the accretion disks of intermediate-mass black holes.[58]
Quasars are thought to be the accretion disks of supermassive black holes, since no other known object is powerful enough to produce such strong emissions. Quasars produce strong emission across the electromagnetic spectrum, including UV, X-rays and gamma-rays and are visible at tremendous distances due to their high luminosity. Between 5 and 25% of quasars are "radio loud," so called because of their powerful radio emissions.[59]
Gravitational lensing
[edit]
A gravitational lens is formed when the light from a very distant, bright source (such as a quasar) is "bent" around a massive object (such as a black hole) between the source object and the observer. The process is known as gravitational lensing, and is one of the predictions of general relativity.
A source image behind the lens may appear as multiple images to the observer. In cases where the source, massive lensing object, and the observer lie in a straight line, the source will appear as a ring behind the massive object.
Gravitational lensing can be caused by objects other than black holes, because any very strong gravitational field will bend light rays. Some of these multiple-image effects are probably produced by distant galaxies.
Objects orbiting possible black holes
[edit]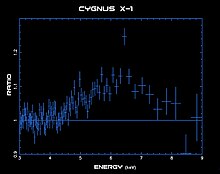
Objects orbiting black holes probe the gravitational field around the central object. An early example, discovered in the 1970s, is the accretion disk orbiting the putative black hole responsible for Cygnus X-1, a famous X-ray source. While the material itself cannot be seen directly, the X rays flicker on a millisecond time scale, as expected for hot clumpy material orbiting a ~10 solar-mass black hole just prior to accretion. The X-ray spectrum exhibits the characteristic shape expected for a disk of orbiting relativistic material, with an iron line, emitted at ~6.4 keV, broadened to the red (on the receding side of the disk) and to the blue (on the approaching side).
Another example is the star S2, seen orbiting the Galactic Center. Here the star is several light hours from the ~3.5×106 solar mass black hole, so its orbital motion can be plotted. Nothing is observed at the center of the observed orbit, the position of the black hole itself——as expected for a black object.
Determining the mass of black holes
[edit]Quasi-periodic oscillations can be used to determine the mass of black holes.[61] The technique uses a relationship between black holes and the inner part of their surrounding disks, where gas spirals inward before reaching the event horizon. As the gas collapses inwards, it radiates X-rays with an intensity that varies in a pattern that repeats itself over a nearly regular interval. This signal is the Quasi-Periodic Oscillation, or QPO. A QPO’s frequency depends on the black hole’s mass; the event horizon lies close in for small black holes, so the QPO has a higher frequency. For black holes with a larger mass, the event horizon is farther out, so the QPO frequency is lower.
Black hole candidates
[edit]Supermassive black holes at the centers of galaxies
[edit]
According to the American Astronomical Society, every large galaxy has a supermassive black hole at its center.[citation needed] The black hole’s mass is proportional to the mass of the host galaxy, suggesting that the two are linked very closely. The Hubble Space Telescope and ground-based telescopes in Hawaii were used in a large survey of galaxies.
For decades, astronomers have used the term "active galaxy" to describe galaxies with unusual characteristics, such as unusual spectral line emission and very strong radio emission.[62][63] However, theoretical and observational studies have shown that the active galactic nuclei (AGN) in these galaxies may contain supermassive black holes.[62][63] The models of these AGN consist of a central black hole that may be millions or billions of times more massive than the Sun; a disk of gas and dust called an accretion disk; and two jets that are perpendicular to the accretion disk.[63]
Although supermassive black holes are expected to be found in most AGN, only some galaxies' nuclei have been more carefully studied in attempts to both identify and measure the actual masses of the central supermassive black hole candidates. Some of the most notable galaxies with supermassive black hole candidates include the Andromeda Galaxy, M32, M87, NGC 3115, NGC 3377, NGC 4258, and the Sombrero Galaxy.[64]
Astronomers are confident that our own Milky Way galaxy has a supermassive black hole at its center, in a region called Sagittarius A*:
- A star called S2 (star) follows an elliptical orbit with a period of 15.2 years and a pericenter (closest) distance of 17 light hours from the central object.
- The first estimates indicated that the central object contains 2.6M (2.6 million) solar masses and has a radius of less than 17 light hours. Only a black hole can contain such a vast mass in such a small volume.
- Further observations[65] strengthened the case for a black hole, by showing that the central object's mass is about 3.7M solar masses and its radius no more than 6.25 light-hours.
Intermediate-mass black holes in globular clusters
[edit]In 2002, the Hubble Space Telescope produced observations indicating that globular clusters named M15 and G1 may contain intermediate-mass black holes.[66][67] This interpretation is based on the sizes and periods of the orbits of the stars in the globular clusters. But the Hubble evidence is not conclusive, since a group of neutron stars could cause similar observations. Until recent discoveries, many astronomers thought that the complex gravitational interactions in globular clusters would eject newly-formed black holes.
In November 2004 a team of astronomers reported the discovery of the first well-confirmed intermediate-mass black hole in our Galaxy, orbiting three light-years from Sagittarius A*. This black hole of 1,300 solar masses is within a cluster of seven stars, possibly the remnant of a massive star cluster that has been stripped down by the Galactic Centre.[68][69] This observation may add support to the idea that supermassive black holes grow by absorbing nearby smaller black holes and stars.
In January 2007, researchers at the University of Southampton in the United Kingdom reported finding a black hole, possibly of about 10 solar masses, in a globular cluster associated with a galaxy named NGC 4472, some 55 million light-years away.[70][71]
Stellar-mass black holes in the Milky Way
[edit]
The Milky Way galaxy contains several probable stellar-mass black holes which are closer to Earth than the suspected supermassive black hole in the Sagittarius A* region. These candidates are all members of X-ray binary systems in which the denser object draws matter from its partner via an accretion disk. The probable black holes in these pairs range from three to more than a dozen solar masses.[72][73] The most distant stellar-mass black hole detected is a member of a binary system located in the Messier 33 galaxy.[74]
In 1971, Louise Webster and Paul Murdin, at the Royal Greenwich Observatory,[75] and Charles Thomas Bolton, working independently at the University of Toronto's David Dunlap Observatory,[76] observed HDE 226868 wobble, as if orbiting around an invisible but massive companion. Further analysis led to the declaration that the companion, Cygnus X-1, was in fact a black hole.[77][78]
Micro black holes
[edit]There is theoretically no smallest size for a black hole.[citation needed] Stephen Hawking theorized that primordial black holes could evaporate and shrink to become micro black holes.[citation needed] Searches for evaporating primordial black holes are proposed for the GLAST satellite, launched in 2008. However, if micro black holes can be created by other means, such as by cosmic ray impacts or in colliders, that does not imply that they must evaporate.
The formation of black hole analogs on Earth in particle accelerators has been reported.[citation needed] These analogs are not the same as gravitational black holes, but are vital testing grounds for quantum theories of gravity.[79]
They act like black holes because of the correspondence between the theory of the strong nuclear force, which has nothing to do with gravity, and the quantum theory of gravity. They are similar because both are described by string theory. So the formation and disintegration of a fireball in quark gluon plasma can be interpreted in black hole language. The fireball at the Relativistic Heavy Ion Collider (RHIC) is a phenomenon which is closely analogous to a black hole, and many of its physical properties can be correctly predicted using this analogy. The fireball, however, is not a gravitational object. It is presently unknown whether the much more energetic Large Hadron Collider (LHC) would be capable of producing the speculative large extra dimension micro black hole, as many theorists have suggested.[80]
Alternative models
[edit]Several alternative models, which behave like a black hole but avoid the singularity, have been proposed. However, most researchers judge these concepts artificial, as they are more complicated but do not give near term observable differences from black holes (see Occam's razor). The most prominent alternative theory is the Gravastar.
In March 2005, physicist George Chapline at the Lawrence Livermore National Laboratory in California proposed that black holes do not exist, and that objects currently thought to be black holes are actually dark-energy stars. He draws this conclusion from some quantum mechanical analyses. Although his proposal currently has little support in the physics community, it was widely reported by the media.[81][82] A similar theory about the non-existence of black holes was later developed by a group of physicists at Case Western Reserve University in June 2007.[83]
Among the alternate models are magnetospheric eternally collapsing objects, clusters of elementary particles[84] (e.g., boson stars[85]), fermion balls,[86] self-gravitating, degenerate heavy neutrinos[87] and even clusters of very low mass (~0.04 solar mass) black holes.[84]
References
[edit]- ^ Kraus, Ute (2005-03-20). "Step by Step into a Black Hole".
- ^ Hawking, Stephen (1974). "Black Hole Explosions". Nature. 248: 30–31. doi:10.1038/248030a0.
- ^ McDonald, Kirk T. (1998), Hawking-Unruh Radiation and Radiation of a Uniformly Accelerated Charge (PDF)
- ^ Hawking & Penrose 1996, p. 44.
- ^ "Gamma-rays from Black Holes and Neutron Stars". NASA/Goddard Space Flight Center.
- ^ Remillard, Ronald A.; McClintock, Jeffrey E. (2006), "X-ray Properties of Black-Hole Binaries", Ann.Rev.Astron.Astrophys., 44: 49–92.
- ^ Celotti, A.; Miller, J.C.; Sciama, D.W. (1999), "Astrophysical evidence for the existence of black holes", Class. Quant. Grav., 16.
- ^ Michell, J. (1784), "On the Means of Discovering the Distance, Magnitude, &c. of the Fixed Stars, in Consequence of the Diminution of the Velocity of Their Light, in Case Such a Diminution Should be Found to Take Place in any of Them, and Such Other Data Should be Procured from Observations, as Would be Farther Necessary for That Purpose", Phil. Trans. R. Soc. (London), 74: 35–57.
- ^ "Dark Stars (1783)". Thinkquest. Retrieved 2008-05-28.
- ^ Laplace; see Israel, Werner (1987), "Dark stars: the evolution of an idea", in Hawking, Stephen W. & Israel, Werner, 300 Years of Gravitation, Cambridge University Press, Sec. 7.4
- ^ a b Schwarzschild, Karl (1916), "Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie", Sitzungsber. Preuss. Akad. D. Wiss.: 189–196 and Schwarzschild, Karl (1916), "Über das Gravitationsfeld eines Kugel aus inkompressibler Flüssigkeit nach der Einsteinschen Theorie", Sitzungsber. Preuss. Akad. D. Wiss.: 424–434.
- ^ On Massive Neutron Cores, J. R. Oppenheimer and G. M. Volkoff, Physical Review 55, #374 (15 February 1939), pp. 374–381.
- ^ D. Finkelstein (1958). "Past-Future Asymmetry of the Gravitational Field of a Point Particle". Phys. Rev. 110: 965–967.
- ^ Hewish, Antony (1968). "Observation of a Rapidly Pulsating Radio Source". Nature. 217: 709–713. doi:10.1038/217709a0. Retrieved 2007-07-06.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Pilkington, J D H (1968). "Observations of some further Pulsed Radio Sources" (PDF). Nature. 218: 126–129. doi:10.1038/218126a0. Retrieved 2007-07-06.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Michael Quinion. "Black Hole". World Wide Words. Retrieved 2008-06-17.
- ^ "Online Etymology Dictionary".
- ^ The diagrams here are effectively Finkelstein diagrams using an advanced time parameter. Compare to (Hawking & Ellis 1973, figure 23ii).
- ^ An example of this reasoning can be found on this website created by students from Tufts university.
- ^ a b c d e Carroll 2004, p. 222.
- ^ Townsend, P.K., Black Holes, p. 18. Lecture notes for a Cambridge Part III course.
- ^ Hawking, S.W.; Penrose, R. (1970), "The Singularities of Gravitational Collapse and Cosmology", Proc.Roy.Soc.Lon, 314 (1519): 529–548, JSTOR 2416467
- ^ Static Solutions of Einstein's Field Equations for Spheres of Fluid, Richard C. Tolman, Physical Review 55, #374 (February 15, 1939), pp. 364–373.
- ^ On Massive Neutron Cores, J. R. Oppenheimer and G. M. Volkoff, Physical Review 55, #374 (February 15, 1939), pp. 374–381.
- ^ Carr, B.J. (2005), "Primordial Black Holes: Do They Exist and Are They Useful?", Proceedings of "Inflating Horizon of Particle Astrophysics and Cosmology", Universal Academy Press Inc and Yamada Science Foundation
- ^ Giddings, Steven B.; Thomas, Scott (2002), "High Energy Colliders as Black Hole Factories: The End of Short Distance Physics", Phys.Rev. D, 65 (056010)
- ^ Arkani-Hamed, Nima; Dimopoulos, Savas; Dvali, Gia (1998), "The Hierarchy Problem and New Dimensions at a Millimeter", Phys.Lett. B, 429: 263–272
- ^ Heusler, M. (1998), "Stationary Black Holes: Uniqueness and Beyond", Living Rev. Relativity, 1 (6)
- ^ Hinshaw, G.; et al. (2008), Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Data Processing, Sky Maps, and Basic Results
{{citation}}: Explicit use of et al. in:|author=(help). - ^ Reissner, H (1916). "Über die Eigengravitation des elektrischen Feldes nach der Einstein'schen Theorie". Annalen der Physik. 50: 106–120. doi:10.1002/andp.19163550905.
- ^ Nordström, G (1918). "On the Energy of the Gravitational Field in Einstein's Theory". Verhandl. Koninkl. Ned. Akad. Wetenschap., Afdel. Natuurk., Amsterdam. 26: 1201–1208.
- ^ "R. P. Kerr, "Gravitational field of a spinning mass as an example of algebraically special metrics", Phys. Rev. Lett. 11, 237 (1963)".
- ^ Newman, Ezra and Janis, Allen. "Note on the Kerr Spinning-Particle Metric," Journal of Mathematical Physics, volume 6, pages 915-917 (1965).
- ^ Newman, Ezra et al. "Metric of a Rotating, Charged Mass," Journal of Mathematical Physics, volume 6, pages 918-919 (1965).
- ^ For a review see Wald, Robert. M. (1997), Gravitational Collapse and Cosmic Censorship.
- ^ For a discussion of these numerical simulations see Berger, Beverly K. (2002), "Numerical Approaches to Spacetime Singularities", Living Rev. Relativity, 5, retrieved 2007-08-04.
- ^ McClintock, Jeffrey E.; Shafee, Rebecca; Narayan, Ramesh; Remillard, Ronald A.; Davis, Shane W.; Li, Li-Xin (2006), "The Spin of the Near-Extreme Kerr Black Hole GRS 1915+105", Astrophys.J., 652: 518–539.
- ^ Antonucci, R. (1993). "Unified Models for Active Galactic Nuclei and Quasars". Annual Reviews in Astronomy and Astrophysics. 31 (1): 473–521. doi:10.1146/annurev.aa.31.090193.002353.
- ^ Urry, C. (1995). "Unified Schemes for Radio-Loud Active Galactic Nuclei". Publications of the Astronomical Society of the Pacific. 107: 803–845. doi:10.1086/133630.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Schödel, R. (2002). "A star in a 15.2-year orbit around the supermassive black hole at the centre of the Milky Way". Nature. 419 (6908): 694–696. doi:10.1038/nature01121.
{{cite journal}}: Cite has empty unknown parameter:|month=(help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Valtonen, M.J.; et al. (2008), "A massive binary black-hole system in OJ 287 and a test of general relativity", Nature, 452: 851, doi:10.1038/nature06896
{{citation}}: Explicit use of et al. in:|last2=(help) - ^ Maccarone, T.J.; et al. (2007), "A black hole in a globular cluster", Nature, 455: 183–185, doi:10.1038/nature05434
{{citation}}: Explicit use of et al. in:|last2=(help) - ^ "NASA's GLAST Burst Monitor Team Hard at Work Fine-Tuning Instrument and Operations". NASA. 2008-07-28.
- ^ Carroll 2004, sec. 5.4 and Carroll 2004, sec. 7.6.
- ^ Carroll 2004, p. 217
- ^ Carroll 2004, p. 262.
- ^ Nemiroff, Robert J. (1993), "Visual distortions near a neutron star and black hole", American Journal of Physics, 61: 619
- ^ Carroll 2004, p. 264
- ^ Stephen Hawking A Brief History of Time, 1998, ISBN 0-553-38016-8
- ^ a b Hawking, S.W. (1974), "Black hole explosions?", Nature, 248: 30–31, doi:10.1038/248030a0
- ^ Page, Ron N. (2005), "Hawking Radiation and Black Hole Thermodynamics", New.J.Phys., 7 (203): 203, doi:10.1088/1367-2630/7/1/203
- ^ "Does God Play Dice? Archived Lecture by Professor Steven Hawking, Department of Applied Mathematics and Theoretical Physics (DAMTP) University of Caimbridge". Retrieved 2007-09-07.
- ^ "Hawking changes his mind about black holes". News@Nature.com. Retrieved 2006-03-25.
- ^ Bloom, J.S., Kulkarni, S. R., & Djorgovski, S. G. (2002). "The Observed Offset Distribution of Gamma-Ray Bursts from Their Host Galaxies: A Robust Clue to the Nature of the Progenitors". Astronomical Journal. 123: 1111–1148.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Blinnikov, S.; et al. (1984). "Exploding Neutron Stars in Close Binaries". Soviet Astronomy Letters. 10: 177.
{{cite journal}}: Explicit use of et al. in:|author=(help) - ^ Lattimer, J. M. and Schramm, D. N. (1976). "The tidal disruption of neutron stars by black holes in close binaries". Astrophysical Journal. 210: 549.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Paczynski, B. (1995). "How Far Away Are Gamma-Ray Bursters?". Publications of the Astronomical Society of the Pacific. 107: 1167.
- ^ Winter, L.M., Mushotzky, R.F. and Reynolds, C.S. (2005, revised 2006). "XMM-Newton Archival Study of the ULX Population in Nearby Galaxies". Astrophysical Journal. 649: 730.
{{cite journal}}: Check date values in:|date=(help)CS1 maint: multiple names: authors list (link) - ^ Jiang, L., Fan, X., Ivezić, Ž., Richards, G.~T., Schneider, D.~P., Strauss, M.~A., Kelly, B.~C. (2007). "The Radio-Loud Fraction of Quasars is a Strong Function of Redshift and Optical Luminosity". Astrophysical Journal. 656: 680–690.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Staff (August 30, 2006). "More Images of Cygnus X-1, XTE J1650-500 & GX 339-4". Harvard-Smithsonian Center for Astrophysics/Chandra X-ray Center. Retrieved 2008-03-30.
- ^ "NASA scientists identify smallest known black hole".
- ^ a b J. H. Krolik (1999). Active Galactic Nuclei. Princeton, New Jersey: Princeton University Press. ISBN 0-691-01151-6.
- ^ a b c L. S. Sparke, J. S. Gallagher III (2000). Galaxies in the Universe: An Introduction. Cambridge: Cambridge University Press. ISBN 0-521-59704-4.
{{cite book}}: Check|isbn=value: checksum (help) - ^ J. Kormendy, D. Richstone (1995). "Inward Bound---The Search For Supermassive Black Holes In Galactic Nuclei". Annual Reviews of Astronomy and Astrophysics. 33: 581–624. doi:10.1146/annurev.aa.33.090195.003053.
- ^ Ghez, A. M. (2005). "Stellar Orbits around the Galactic Center Black Hole". The Astrophysical Journal. 620 (2): 744–757. doi:10.1086/427175. Retrieved 2008-05-10.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help); Unknown parameter|month=ignored (help) - ^ Gerssen, Joris (2002). "Hubble Space Telescope Evidence for an Intermediate-Mass Black Hole in the Globular Cluster M15. II. Kinematic Analysis and Dynamical Modeling". The Astronomical Journal. 124 (6): 3270–3288. doi:10.1086/344584.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help); Unknown parameter|month=ignored (help) - ^ "Hubble Discovers Black Holes in Unexpected Places". HubbelSite. 2002-09-17. Retrieved 2007-10-31.
- ^ "Second black hole found at the centre of our Galaxy". NatureNews. doi:10.1038/news041108-2. Retrieved 2006-03-25.
- ^ Maillard, J.P.; Paumard, T.; Stolovy, S.R.; Rigaut, F. (2004), "The nature of the Galactic Center source IRS 13 revealed by high spatial resolution in the infrared", Astron.Astrophys., 423: 155–167, doi:10.1051/0004-6361:20034147
- ^ http://xxx.lanl.gov/abs/0805.2952
- ^ Maccarone, Thomas J.; Kundu, Arunav; Zepf, Stephen E.; Rhode, Katherine L. (2007), "A black hole in a globular cluster", Nature, 445: 183–185, doi:10.1038/nature05434
- ^ Casares, J. (2006). Observational evidence for stellar mass black holes. Proceedings of IAU Symposium 238: "Black Holes: From Stars to Galaxies -Across the Range of Masses".
- ^ Garcia, M.R.; Miller, J. M.; McClintock, J. E.; King, A. R.; Orosz, J. (2003), "Resolved Jets and Long Period Black Hole Novae", Astrophys.J., 591: 388–396, doi:10.1086/375218
- ^ Orosz, J.A.; et al. (2007). "A 15.65 solar mass black hole in an eclipsing binary in the nearby spiral galaxy Messier 33" (subscription required). Nature. 449: 872–875. doi:10.1038/nature06218.
{{cite journal}}: Explicit use of et al. in:|author=(help) - ^ Webster, B. Louise (1972). "Cygnus X-1—a Spectroscopic Binary with a Heavy Companion?". Nature. 235 (2): 37–38. doi:10.1038/235037a0. Retrieved 2008-03-10.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Bolton, C. T. (1972). "Identification of Cygnus X-1 with HDE 226868". Nature. 235 (2): 271–273. doi:10.1038/235271b0. Retrieved 2008-03-10.
- ^ Rolston, Bruce (10 November 1997). "The First Black Hole". University of Toronto. Retrieved 2008-03-11.
- ^ Shipman, H. L. (1975). "The implausible history of triple star models for Cygnus X-1 Evidence for a black hole". Astrophysical Letters. 16 (1): 9–12. Retrieved 2008-03-11.
- ^ Nastase, Horatiu (2005). "The RHIC fireball as a dual black hole". arXiv:hep-th/0501068.
- ^ See Safety of particle collisions at the Large Hadron Collider for a more in depth discussion.
- ^ "Black holes 'do not exist'". News@Nature.com. Retrieved 2006-03-25.
- ^ Chapline, G. (2005). "Dark Energy Stars". Proceedings of the Texas Conference on Relativistic Astrophysics, Stanford, CA, December. 2004. arXiv:astro-ph/0503200.
- ^ Cool, Heidi (2007-06-20). "Black holes don't exist, Case physicists report". Case Western Reserve University. Retrieved 2007-07-02.
- ^ a b Maoz, Eyal (1998). "Dynamical Constraints On Alternatives To Supermassive Black Holes In Galactic Nuclei". The Astrophysical Journal Letters. 494 (2): L181–L184. doi:10.1086/311194.
- ^ Torres, Diego F.; Capozziello, S.; Lambiase, G. (2000). "A supermassive boson star at the galactic center?". Physical Review D. 62 (10). arXiv:astro-ph/0004064. doi:10.1103/PhysRevD.62.104012.
- ^ Munyaneza, F.; Viollier, R. D. (2001). "The motion of stars near the Galactic center: A comparison of the black hole and fermion ball scenarios". The Astrophysical Journal. 564 (2002): 274–283. arXiv:astro-ph/0103466. doi:10.1086/323949.
- ^ Tsiklauri, David; Viollier, Raoul D. (1998). "Dark matter concentration in the galactic center". The Astrophysical Journal. 500 (2): 591. arXiv:astro-ph/9805273. doi:10.1086/305753.
Further reading
[edit]Popular reading
[edit]- Ferguson, Kitty (1991), Black Holes in Space-Time, Watts Franklin, ISBN 0-531-12524-6.
- Hawking, Stephen (1988), A Brief History of Time, Bantam Books, Inc, ISBN 0-553-38016-8.
- Hawking, Stephen; Penrose, Roger (1996), The Nature of Space and Time, Princeton University Press, ISBN 0-691-03791-2
{{citation}}: Check|isbn=value: checksum (help). - Melia, Fulvio (2003), The Black Hole at the Center of Our Galaxy, Princeton U Press, ISBN 978-0-691-09505-9.
- Melia, Fulvio (2003), The Edge of Infinity. Supermassive Black Holes in the Universe, Cambridge U Press, ISBN 978-0-521-81405-8.
- Pickover, Clifford (1998), Black Holes: A Traveler's Guide, Wiley, John & Sons, Inc, ISBN 0-471-19704-1.
- Thorne, Kip S. (1994), Black Holes and Time Warps, Norton, W. W. & Company, Inc, ISBN 0-393-31276-3.
University textbooks and monographs
[edit]- Carroll, Sean M. (2004), Spacetime and Geometry, Addison Wesley, ISBN 0-8053-8732-3, the lecture notes on which the book was based are available for free from Sean Carroll's website.
- Carter, B. (1973), "Black hole equilibrium states", in DeWitt, B.S.; DeWitt, C. (eds.), Black Holes.
- Chandrasekhar, Subrahmanyan (1999), Mathematical Theory of Black Holes, Oxford University Press, ISBN 0-19-850370-9.
- Frolov, V.P.; Novikov, I.D. (1998), Black hole physics.
- Hawking, S.W.; Ellis, G.F.R. (1973), [[The Large Scale Structure of Spacetime]], Cambridge University Press, ISBN 0521099064
{{citation}}: URL–wikilink conflict (help). - Melia, Fulvio (2007), The Galactic Supermassive Black Hole, Princeton U Press, ISBN 978-0-691-13129-0.
- Taylor, Edwin F.; Wheeler, John Archibald (2000), Exploring Black Holes, Addison Wesley Longman, ISBN 0-201-38423-X.
- Thorne, Kip S.; Misner, Charles; Wheeler, John (1973), Gravitation, W. H. Freeman and Company, ISBN 0-7167-0344-0.
- Wald, Robert M. (1992), Space, Time, and Gravity: The Theory of the Big Bang and Black Holes, University of Chicago Press, ISBN 0-226-87029-4.
Research papers
[edit]- Hawking, S.W. (2005), Information Loss in Black Holes. Stephen Hawking's purported solution to the black hole unitarity paradox, first reported at a conference in July 2004.
- Ghez, A.M.; Salim, S.; Hornstein, S.D.; Tanner, A.; Lu, J.R.; Morris, M.; Becklin, E.E.; Duchene, G. (2005), "Stellar orbits around the Galactic Center black hole", Astrophysics J., 620
{{citation}}: Unknown parameter|etal=ignored (help). More accurate mass and position for the black hole at the centre of the Milky Way. - Hughes, S.A. (2005), Trust but verify: the case for astrophysical black holes. Lecture notes from 2005 SLAC Summer Institute.
External links
[edit]- Black Hole confirmed in Milky Way retrieved Dec 10, 2008
- Yale University Video Lecture: Introduction to Black Holes at Google Video
- Black Holes: Gravity's Relentless Pull - Award-winning interactive multimedia Web site about the physics and astronomy of black holes from the Space Telescope Science Institute
- FAQ on black holes
- Schwarzschild Geometry on Andrew Hamilton’s website
- Tufts University: Student Project (Great Kid's Section)
- Movie of Black Hole Candidate from Max Planck Institute
- UT Brownsville Group Simulates Spinning Black-Hole Binaries
- Black Hole Research News on ScienceDaily
- Scientific American Magazine (July 2003 Issue) The Galactic Odd Couple - giant black holes and stellar baby booms
- Scientific American Magazine (May 2005 Issue) Quantum Black Holes
- SPACE.com All About Black Holes - News, Features and Interesting Original Videos
- Black Holes Intro - Introduction to Black Holes
- Advanced Mathematics of Black Hole Evaporation
- HowStuffWorks: How Black Holes Work - Easy to consume guide to Black Holes
- Ted Bunn's Black Holes FAQ explains in simple language some other consequences of the way in which black holes bend space-time.
- Is the Mass of Black Holes Limited? - The Future of Things article
{{Black holes}}
[[Category:Black holes|Black holes]]
[[Category:Dark matter]]
[[Category:Relativity]]





