Template:Regular hyperbolic tiling table/sandbox
Appearance
| Regular hyperbolic tiling table | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Spherical (improper/Platonic)/Euclidean/hyperbolic (Poincaré disc: compact/paracompact/noncompact) tessellations with their Schläfli symbol | ||||||||||||
| p \ q | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... | ∞ | ... | iπ/λ |
| 1 |  {1,1} |
{1,2} |
{1,3} |
{1,4} |
{1,5} |
{1,6} |
{1,7} |
{1,8} |
{1,∞} |
{1,iπ/λ} | ||
| 2 | 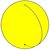 {2,1} |
 {2,2} |
 {2,3} |
 {2,4} |
 {2,5} |
 {2,6} |
 {2,7} |
 {2,8} |
 {2,∞} |
 {2,iπ/λ} | ||
| 3 | {3,1} |
 {3,2} |
 {3,3} |
 {3,4} |
 {3,5} |
 {3,6} |
 {3,7} |
 {3,8} |
 {3,∞} |
 {3,iπ/λ} | ||
| 4 | {4,1} |
 {4,2} |
 {4,3} |
 {4,4} |
 {4,5} |
 {4,6} |
 {4,7} |
 {4,8} |
 {4,∞} |
 {4,iπ/λ} | ||
| 5 | {5,1} |
 {5,2} |
 {5,3} |
 {5,4} |
 {5,5} |
 {5,6} |
 {5,7} |
 {5,8} |
 {5,∞} |
 {5,iπ/λ} | ||
| 6 | {6,1} |
 {6,2} |
 {6,3} |
 {6,4} |
 {6,5} |
 {6,6} |
 {6,7} |
 {6,8} |
 {6,∞} |
 {6,iπ/λ} | ||
| 7 | {7,1} |
{7,2} |
 {7,3} |
 {7,4} |
 {7,5} |
 {7,6} |
 {7,7} |
{7,8} |
 {7,∞} |
{7,iπ/λ} | ||
| 8 | {8,1} |
{8,2} |
 {8,3} |
 {8,4} |
 {8,5} |
 {8,6} |
 {8,7} |
 {8,8} |
 {8,∞} |
{8,iπ/λ} | ||
| ... | ||||||||||||
| ∞ | {∞,1} |
 {∞,2} |
 {∞,3} |
 {∞,4} |
 {∞,5} |
 {∞,6} |
 {∞,7} |
 {∞,8} |
 {∞,∞} |
 {∞,iπ/λ} | ||
| ... | ||||||||||||
| iπ/λ | {iπ/λ,1} |
 {iπ/λ,2} |
 {iπ/λ,3} |
 {iπ/λ,4} |
 {iπ/λ,5} |
 {iπ/λ,6} |
{iπ/λ,7} |
{iπ/λ,8} |
 {iπ/λ,∞} |
 {iπ/λ,iπ/λ} | ||
| This is the template sandbox page for Template:Regular hyperbolic tiling table (diff). |
