Talk:Trigonometric functions/Archive 1

Archive 1

Archive 2

Archive 3

"Jump start"

The "Jump start" section is...um...out of place, to say the least, and I don't see how it helps. May I suggest people spend some time to get a feel for the style of articles here before plunging headfirst? Revolver 07:45, 17 Sep 2004 (UTC)

First of all i have to admit it is incoherent with the otherwise strong technical representation of the article, and it certainly can in no way claim to be correct from a abstract mathematical attidude. However it shall help pupils (perhaps even some undergraduates) to get a better 'grip' of what angles are as well as trigonometric functions. I noticed that minors soon loose the connection to the simple explanation of the triangle subscribed in the unit circle and treat angles as if they were something highly abstract, thus often try to avoid them or misuse them although angles if seen from a simple point of view could be treated with the same simplicity as say the add operation of scalars (or something else which is mathematically banal). Perhaps we should make a own page out of this: 'angles in simple terms' or something like that. One thing is for sure however that it misfits here, and this will only be a temporary measure, as i too would dislike to see something such non-technical in a article where you expect the opposite. I intend to put some images to that sometime later. Hope my intentions became a bit clearer :) --Slicky 19:18, Sep 17, 2004 (UTC)

My primary concern had to do with style. The jump start section is written more in the style of a conversational undergraduate lecture transcribed to paper. While this may be good for an oral lecture, it doesn't translate well to an encyclopedia article, and it kind of goes against style standards of wikipedia. Moreover, the issues you raise about student understanding or interpretation seem to me to have more to do with angles, and perhaps the straightforward geometric treatment could be emphasised more there. As to your contention of the problem (e.g. calc students who seem to "forget" that trig functions have geometric interpretations), I certainly know what you're talking about. But it seems to me the best way to address this in articles is simply to give a strong presentation of the simpler geometric interpretation. And I think this is done well in the beginning of the article. I think it's the best we can do, is present information and make it accessible. Of course, to show HOW simple interpretation is useful falls under this. But, to explicitly point out this choice and drive home its merits, seems to me to reflect a pedagogical invasion. That part is really the teacher's responsibility, and if they don't do it, it's their fault, not ours. Revolver 07:52, 18 Sep 2004 (UTC)

Okay i outsourced this article now by creating a new one, titled as trigonometry in simple terms and put a link at the bottom beside the others. I never actually intended to mix those articles, however as you might have noticed i am relatively new as a wikipedian (although i am a joyful wikipedia user since years), and i fancy the idea of free information since well..... my earliest days. A coherent style and technically strong formulation is the key to gain a large audience, however the typical 'calc students' are left out and rapidly loose their interest in maths more and more, as their own mind-build universe of mathematical consistency crumbles more and more until they are seeking out for anything (subject-related) that avoids math as much as possible, without beeing aware that mathematics is the key to everything. Therefore i think it could help one or another to actually find back to the path of maths, not with the intention to make them fit enough to become a mathematical theorist but to at least apply it with grace and delight and make extensive use of it in technical studies/research. To put the emphasis of this rant into one sentence and conclude what i began to say: I deem it important that there are also articles that are less mathematical, less correct and provide much less information in much more words for those not-so inclined. (But frankly if i haven't misunderstood you entirely it seems to me as if you too second that, and i totally agree with you in that coherence in any article should be preserved to the utmost possible extend).--Slicky 18:13, Sep 18, 2004 (UTC)

You might want to see the articles trigonometry and applications of trigonometry. The latter esp. might overlap with some things you're trying to do. As for calc students tuning out math because it is presented with a coherent style and technically strong formulation...how else should it be presented? With a confused, jumbled style and technically weak and ambiguous formulation?? I'm sorry, I feel for students, but at some point they just have to accept the nature of math and the nature of studying math. Math is an exact science; if you can't handle its precision, then maybe it's not for you. I don't know what the "path of math" is. If it is motivation, certainly I agree, but I don't think this conflicts with a coherent style and technically strong formulation. The two approaches are not at war with each other. Ideally, even a theoretical presentation should be given with "grace and delight". I think this is an effect of the Bourbaki school that still affects advanced math textbooks. As for the one sentence conclusion: I do think what you're asking for is important, I just feel it belongs more at a place like Wikibooks, not an encyclopedia. Encyclopedia articles (IMO) should be reference tools and introductions to subjects, but not pedagogical tools. I do not expect to gain a true understand of molecular biology or biochemistry from wikipedia articles, e.g., but I do expect it to be invaluable reference and guide while in a class or self-study. Revolver 04:48, 19 Sep 2004 (UTC)

At further contemplation the only conclusion that i came up with is to agree with you, that wikipedia is not the right place for such over-simplified and thus partly incorrect (regarding the expressions) written articles/entries. (I actually thought how i would respond whilst i am seeking for something and end up reading some introductory stuff for minors wich lacks depth in every way, as i actually used wikipedia a lot for further research on topics that were not comprehensively enough covered in books or not at all.) So there definitely should be a clear boarderline between exactly in-depth entries and entries that are more personal and just excerpts (the latter one surely misfits for a place like wikipedia, except user pages of course ;) ). For now I'll take it off and perhaps reshape it into a somewhat better formulated and more comprehensive bookentry in wikipedia out of it. BTW: With 'The path of math' i just meant to have a certain fascination and respect for math, even if you just use it as a tool (applied maths for instance in exp. physics/physical chemistry,..), because we wouldn't be where we are without it. (oh and forgive my lazy upper-case placing) --Slicky 07:24, Sep 19, 2004 (UTC)

TODO List

Could someone proficient with Latex, edit all text-typed formulae and expressions into a Latex meta-description. That would improve the readability a lot and would ensure a better experience as we strive towarads browser-native MathML support. --Slicky 10:48, Sep 16, 2004 (UTC)

Could someone add, when it is first mentioned, an explanation as to what the set of zero's actually is? ---Crusty007 23:11, 18 March 2007 (UTC)

Done. Good idea! Cheers, Doctormatt 01:46, 19 March 2007 (UTC)

Domain of cotan

cotan(x)=cos(x)/sin(x)

cotan(x)=1/tan(x)

The first of these is defined where cos(x)=0; the second is not. Does the domain of cotan include values of x for which cos(x)=0 or not?

Brianjd 08:36, Sep 12, 2004 (UTC)

The short answer to your question is that the confusion evaporates if we follow the convention that 1/∞ = 0 and 1/0 = ∞. If that bothers you, then the answer is that the domain is the same, and the identity holds everywhere that both sides are defined. If you want to use cot(x) = 1/tan(x) as a definition, then you should do it piecewise, using this where cos(x) is not 0, and then "plugging in the right value" when it is. Revolver 07:52, 18 Sep 2004 (UTC)

Notation of Inverses

which notation is more common for inverses: arcsin or sin^-1 ? Which came first? -- Tarquin 12:00 Mar 6, 2003 (UTC)

The notation f^-1 always means the inverse of f, never the multiplicative inverse of f. In programming we obviously have to use arcsin; I don't know about other places.

Brianjd 08:33, Sep 12, 2004 (UTC)

The confusion is over f^-1(x) which always means the inverse of f, versus f(x)^-1 which means the multiplicative inverse. The ambiguity is when sin^2(x) entered convention not as sin(sin(x)) but (sin(x))^2, probably due to even more confusion with sin(x^2) Obscurans 13:21, 28 April 2007 (UTC)

Etymology of Sine

…the modern word "sine" comes from a mistranslation of the Hindu jiva.

That seems farfetched and thus potentially interesting—please tell us more! What does jiva mean in Hindu? What's your source on this? The standard etymology of English sine is derivation from Latin sinus [curve, bend], which is pretty suggestive of the 'curvaceous' shape of the sinusoid. Merriam-Webster supports me in this. So what's wrong with the well-known, logical and sensible explanation?
—Herbee 20:56, 2004 Mar 25 (UTC)

It's not that Webster is wrong, per se—the English "sine" does come from sinus—but the reason why sinus was used is apparently much more interesting than you assume. My source is Carl B. Boyer, A History of Mathematics, 2nd ed. (see references). He writes (p. 209):

...Thus was born, apparently in India, the predecessor of the modern trigonometric function known as the sine of an angle; and the introduction of the sine function represents the chief contribution of the Siddhantas to the history of mathematics. Although it is generally assumed that the change from the whole chord to the half chord took place in India, it has been suggested by Paul Tannery, the leading historian of science at the turn of the century, that this transformation of trigonometry may have occurred at Alexandria during the post-Ptolemaic period. Whether or not this suggestion has merit, there is no doubt that it was through the Hindus, and not the Greeks, that our use of the half chord has been derived; and our word "sine," through misadventure in translation (see below), has descended from the Hindu name, jiva.

The "(see below)" I think refers to a much later section (p. 252) on translations of Arabic mathematics in Europe in the 12th century. There, Boyer writes:

It was Robert of Chester's translation from the Arabic that resulted in our word "sine." The Hindus had given the name jiva to the half-chord in trigonometry, and the Arabs had taken this over as jiba. In the Arabic language there is also the word jaib meaning "bay" or "inlet." When Robert of Chester came to translate the technical word jiba, he seems to have confused this with the word jaib (perhaps because vowels were omitted); hence, he used the word sinus, the Latin word for "bay" or "inlet." Sometimes the more specific phrase sinus rectus, or "vertical sine," was used; hence, the phrase sinus versus, or our "versed sine," was applied to the "sagitta," or the "sine turned on its side."

By the way, assuming an etymology of sinus for sine because of the "curvaceous shape" of the sine (from the other meaning of sinus for "curve," in particular the curved shape of a draped toga or garment) is probably an anachronism. Plots of the sine function ala analytic geometry didn't come until centuries after Chester. On the other hand, Chester may have mistakenly thought that "bay" alluded to the subtended arc; I'm just speculating, though. Steven G. Johnson 22:18, 25 Mar 2004 (UTC)

A little note in arabic. the letter representing V in arabic is very rarely used. The reason for this is i think its not actually ORIGINALLY recognized. Not even in the alphabetic of the language. I think it was the simplest thing to translate the letter "V" into a "B". further more jiba is hard to pronounce in a sentince describing an angle, and therefor might have led the arabs changing the order to better siute their pronounciation. Also the creation of new vocabulary of the word "bay". Also taking into account all of the other trigmetical words are synchronized in a way. Its all speculation but the following example in pronounciation should clerify things:

short forms used when talking math, like tan : tangent
sin : jaib : ja
cos : jata : jata

(recently the extra arabic letters have been un-officialy imported into english letters. using this i can represent the three variations of the english letter T into T , 6 , '6(the " ' " representing 6 but with a dot) as arabicly pronounced letters) based on this

tan : '6il : '6a
cot : '6ata : '6ata

I hope the resemblense can be noticed. this is also implemented in the last 2 of the original 6 common trignometical functions. Another example of missing arabic letters other than "V" is the letter "P". Which you can sence in 80% of the english speaking arabs, when talking to them you can hear words like "broblem" and so forth.

Note that the "versed sine" is 1–cos(&theta) = distance from the center of the chord to the center of the arc. I'm guessing that rectus and versus here refer to what we would now call the y and x coordinates, assuming that they originally drew a circle and measured the angle from the horizontal...Boyer doesn't say, however. Further evidence for this is the fact, according to the OED, that "sagitta", originally a synonym for the versed sine, is also an obsolete synonym for abscissa. sagitta is Latin for "arrow", and according to the OED's citations this is a visual metaphor for the versed sine (if you see the arc as the bow, the chord as the string, and the versed sine as the arrow shaft). Note that Wikipedia could use a short entry on versed sine. Steven G. Johnson 21:55, 25 Mar 2004 (UTC)

If you search for "jaib sinus" online, you find a number of other sources that confirm Boyer's etymology, notably:

• Eli Maor, Trigonometric Delights, ch. 3: "Six Functions Come of Age" (Princeton Univ. Press, 1998).
• Trigonometric functions (MacTutor History of Mathematics Archive)
• Amartya Sen, "Not Frog, But Falcon", The Times of India (Jan. 9, 2003).
• Prof. L. A. Smoller, The birth of trigonometry

Maor attributes the sinus translation to Gherardo of Cremona (c. 1150) instead of Robert of Chester (although he doesn't explicitly say Gherardo was "first"). Boyer, however, describes how both Robert of Chester and Gherardo of Cremona, along with several others, were contemporaries who were gathered together in Toledo by the archbishop there, where a school of translation was developed. Boyer says that Robert made the first translation of e.g. the Koran and of al-Khwarizmi's Algebra, among other things. Boyer also says, however, that most of these works are not dated, so it is possible that there is some uncertainty over who first translated the trigonometric work.

Maor also says that, although the first use of half-chords was in the Siddhanta, the first explicit reference to the sine function was in the Aryabhatiya a century later. There, Aryabhata the elder uses the term ardha-jya, which means "half-chord", which he later shortens to jya or jiva.

Some of these online works, especially the Maor book, seem quite nice. It would be great if some of this information could make its way into Wikipedia. —Steven G. Johnson 02:48, Mar 26, 2004 (UTC)

The page on the "Birth of Trigonometry" gives a good explanation. To quote:

From India the sine function was introduced to the Arab world in the 8th century, where the term jya was transliterated into jiba or jyb. Early Latin translations of Arabic mathematical treatises mistook jiba for the Arabic word jaib, which can mean the opening of a woman's garment at the neck. Accordingly, jaib was translated into the Latin sinus, which can mean "fold" (in a garment), "bosom," "bay," or even "curve." Hence our word "sine."

With the reference being originally from "The Crest of the Peacock: The Non-European Roots of Mathematics, new ed. (Princeton, NJ: Princeton University Press, 1991, 2000), p. 282." --AJ Mas 05:49, 14 November 2005 (UTC)

Etymology of inverse functions

Is there any interesting history of the names "arcsin," "arccos," et cetera, that could be included?

About CSC

Is there anyone from Computer Sciences Corporation?

perhaps you will be willing to write an article that introduces your company :)

"Using only geometry and properties of limits, it can be shown that the derivative of sine is cosine and the derivative of cosine is negative sine. One can then use the theory of Taylor series to show that the following identities hold for all real numbers x:"

This statement is false. I show a proof for this that does not use geometry or properties of limits on the trig identity article. I am removing the word only. --Dissipate 06:11, 28 Jun 2004 (UTC)

I assume you're talking about the "linear differential equations" approach to prove d(sin x)/dx = cos(x). I have some comments about that, but first, I would point out that I think you misread what I wrote. If you read it carefully, all that it claims is that "There exists a method which shows that the derivative of sine is cosine and of cosine is negative sine, and which only uses geometry and the properties of limits". I made no such claim that this method was ITSELF the only method to solve the problem. I only made an existence statement, not a uniqueness statement.

But it doesn't matter much, because even the proof you suggest uses geometry and limits. Moreover, ANY PROOF MUST USE EACH OF THESE, for the simple reasons (1) if sine and cosine are to be defined indepedently of infinite series, or analytic methods, say, then they have to be defined geometrically; in my method, they are the real and imaginary parts of a point on the unit circle (or, x- and y-coordinates) parametrised by the circle's arc length, (2) the problem asks us to find a derivative...since a derivative is defined using limits, by definition we must use limits at some point.

I don't think your method at the other article is wrong...I think it's been misinterpreted. The point at which you use geometry and limits in one fell swoop is when you sneak in the result on the solutions of linear diff eqs. The problem here is that to prove (check) that this is the right solution requires knowing the derivatives of sine and cosine, so we're assuming what we're trying to prove. But, the argument is important and instructive. The diff eq itself along with the initial conditions can be "proven" informally using physics/vector ideas, (see Tristan Needham's book), i.e. the eqs come from a geometric conception of sine and cosine independent of analysis. Then, roughly the same argument (it's probably a bit different) will get you d(sin x)/dx = cos(x), using only properties of limits, or at worst, elementary properties of derivatives. Then, you have another "definition" of sine/cosine -- you define them as the solns of the IVP, and this definition is justified by the informal physics/vector analogy. It's an important way to look at it.

Revolver 09:26, 28 Jun 2004 (UTC)

Revolver: you are right, I misinterpreted. I thought you meant only infinite series and those two limits specifically on the trig identity page.--Dissipate 03:02, 29 Jun 2004 (UTC)

Multiple of 3 deg

Is it true that you can calculate the exact value of the sin or cos of any multiple of 3 deg (π / 60), as stated in this article? This looks to me like a typo for multiples of thirty degrees, which I would agree can be done by hand. Can anyone work out sin (39 deg) exactly by hand? (no calculators allowed) Ian Cairns 23:58, 4 Jul 2004 (UTC)

This is done at exact trigonometric constants, although I haven't personally checked every identity. Revolver 04:21, 7 Jul 2004 (UTC)

It is true, although such calculations may not be feasible. This may be done by seeing that for x = 36°, -cos(x) = cos(4x), using the double angle formulas and solving the resulting quartic with Ferrari's method. Then one may use the half angle formula to obtain the sine of 15°, which is equal to the cosine of 75°. Using the double angle formula for cosines will obtain the cosine of 72°, and the subtraction formula (along with Pythagorean identities) gives the cosine of 3°, from which any multiple may be obtained. Scythe33 18:05, 30 August 2005 (UTC)

Image problem?

In Internet Explorer 5.50 for Windows 95, the "all six trig functions" image thumbnail appears black with only the colored lines and trig function names visible (not the circle or black letters). Could this be a transparency problem? Weird thing is, the full-size version looks fine. - dcljr 05:46, 11 Oct 2004 (UTC)

Other problems

In the Computing section, I've corrected the mistaken claim that calculators use "the Taylor series described below or a similar method" to calculate the trig functions. Actually, the method they use is nothing like a Taylor series (as far as I know); it's called the CORDIC method.

I've never looked at this in detail, but if I understand correctly, CORDIC is mainly used in only very low-end embedded hardware and FPGAs that lacks multiplication units.

Compared to other approaches, CORDIC is a clear winner when a hardware multiplier is unavailable (e.g. in a microcontroller) or when you want to save the gates required to implement one (e.g. in an FPGA). On the other hand, when a hardware multiplier is available (e.g. in a DSP microprocessor), table-lookup methods and good old-fashioned power series are generally faster than CORDIC.[1]

So, I don't think your edit is correct.—Steven G. Johnson 23:40, Oct 27, 2004 (UTC)

I found a review paper (Kantabutra, 1996) that gives an overview of the different techniques, with many references. On modern general-purpose CPUs, a combination of coarse table lookup with some kind of polynomial approximation or interpolation seems to be the dominant technique. I've updated the article accordingly. —Steven G. Johnson 01:14, Oct 28, 2004 (UTC)

More importantly, consider this excerpt from the same section:

Using the [[Pythagorean theorem]],
''c'' = &radic;(a<sup>2</sup> + b<sup>2</sup>) =
&radic;2. This is illustrated in the following figure:
<br>

Therefore,
:<math>\sin \left(45^\circ\right) = ...

Umm... where's the figure? (The article's been this way since at least January 2004! Am I missing something here?) - dcljr 06:27, 11 Oct 2004 (UTC)

Arabic words Jiba and Jaib (and TeX)

I have added the Arabic spellings of Jiba and Jaib (they're the same). Thanks for fixing my link to Arabic alphabet I will now slowly help with TeX issues.

Query

Sinusoidal redirects here for some reason, although it's a hearing problem. Is this a bad redirect, or does Sinusoidal exist as a mathematical term as well?

Sinusoidal is indeed a mathematical term (it's even non-mathematical English: repeatedly wavy or curvy). It means roughly: varying in the manner of a sine wave.

The article at tinnitus does intend to point here (via redirect at sinusoidal) but what they are trying to say isn't clear to me. It could mean that the sound is a pure tone (pure tones have intensity verse time that is a sine function) but it is saying something about beats... I'm not sure what they are trying to say. Someone who knows what they are trying to say may want to clear that up.RJFJR 00:47, Dec 30, 2004 (UTC)

"Generality"

The article says that

They may be defined as ratios of two sides of a right triangle containing the angle, or, more generally, as ratios of coordinates of points on the unit circle, or, more generally still, as infinite series, or equally generally, as solutions of certain differential equations.

This had me scratching my head wondering in what sense the later definitions were more general. I'm guessing this is referring to the domains of the functions: 0 to pi/2 in the first case, all reals in the second, and all complex numbers in the third and fourth. This was not clear though. Josh Cherry 02:36, 15 Apr 2005 (UTC)

relations

I don't think it is useful to give the relations before giving the definitions. The cannot be used as definitions as is claimed unless you define at least one. --MarSch 18:23, 24 Jun 2005 (UTC)

Law of Sines Edit Requested

I request that the Ambiguous case for the law of sines be addressed in the article. Guardian of Light 6 July 2005 13:39 (UTC)

Arctan with two arguments

Is it worth mentioning that many computer languages have an additional inverse trigonometric function, called atan2 in C, used for polar coordinate calculations? Provided x and y are not both zero, it is defined by atan2(y,x)=t where t is the unique angle in [-π,π] such that x=cos t, y=sin t. This would be of practical value for computer science students seeking quick online help, but I don't want to mess with a featured article. --JahJah 10:09, 20 August 2005 (UTC)

That description is not quite right. The function is not restricted to cases where x^2 + y^2 = 1. In all other cases it is not true that x=cos t and y = sin t (x and y can even be bigger than 1 or smaller than -1). Josh Cherry 13:28, 20 August 2005 (UTC)

You're right. Do you think it is appropriate for inclusion? --JahJah 13:37, 20 August 2005 (UTC)

I think it should be included. salte 13:17, 4 December 2006 (UTC)

Another vote for inclusion here. Arctan with just one argument sucks. It's like, so pre-computer-age. --Oolong 14:55, 27 January 2007 (UTC)

Already discussed in Inverse trigonometric function. —Steven G. Johnson 21:03, 27 January 2007 (UTC)

Cotangent

I found the formula:

$\cot {x}=\sum _{n=-\infty }^{\infty }{\frac {1}{x+n\pi }}$

but don't know how to fit it in the article. Any suggestions?Scythe33 22:15, 24 August 2005 (UTC)

Maybe over at Trigonometric identity? --noösfractal 03:40, 25 August 2005 (UTC)

rational sine/cosine

If a sine or cosine of a rational angle (in degrees) is rational, then it has to be either -1, -0.5, 0, 0.5 or 1. All the other sines and cosines of rational angles are irrational. Is this fact known and is it written in this article?

Algorithm for Implementation

The following page explains an algorithm used to implement COSINE and another for SINE.

Sine and Cosine Function

Is there are good way to include the algorithm and would it be of interest to include it, rather than simply leaving it as an external reference?

That's the Taylor series expansion, which is already described in the article. (By itself, it's not suitable for serious use in computation, however. See the section on computation.) —Steven G. Johnson 17:07, 14 November 2005 (UTC)

complex angles

i have a math reference dictionary that says sin is "best defined as a complex function by the power series..." you know what i'm talking about. do that mean you can have complex inputs? i.e. angles? because that just sounds absurd, it's like saying negative distance in the context of negative energy, only negative energy is actually predicted actually i remembered that sinh(x)=-isin(ix). i can rule out the possibility of the book making a mistake now.

Complex angles exsists. yes it is fully possible to calculate the sine and cosine values of a complex angle. T.Stokke 19:39, 12 July 2007 (UTC)

Properties and applications new image

Hi, I was messing around with a little trig function plotting program I was writing in VB. I noticed an interesting shape that loops and meets itself in the center.

This is the image.

Do you think this would be a good addition to add below the "Functions based on sine and cosine can make appealing pictures." picture on the page? I could add axes and chance the colour scheme etc to make it more appealing.

It uses the equation:

$(x(\theta )\,,y(\theta ))=\sin(5\theta )\,,{\frac {\sin(8\theta )}{\cos(4\theta )}}$

It also follows an interesting rule relating to the coefficients and the number of loops it makes.

Do you think this would be a good addition to the page? -- Haddock420 16:53, 17 December 2005 (UTC)

Yes, I think it would be nice. In case you're curious, you can use the trigonometric identity sin(2x) = 2 sin(x) cos(x) to rewrite the equation as

$(x(\theta )\,,y(\theta ))=(\sin(5\theta )\,,2\sin(4\theta )).$

Figures of this form are known as Lissajous figures. I hope you're not too disappointed that your discovery is not new; it's happened to me a lot. -- Jitse Niesen (talk) 18:16, 17 December 2005 (UTC)

Slope definitions

How does the slope definitions section get away with not actually giving the slope definitions? Hehe. My algebra is a little rusty, so I have probably forked up the signs here:

Sin theta = rise/radius = rise/sqrt(rise^2+run^2) = rise/|rise| sqrt(1+(run/rise)^2)

So we see that

The slope definitions:

• Sin theta = + or - 1/sqrt(1+m^-2)
• Cos theta = + or - 1/sqrt(1+m^2)
• Tan theta = m

This is of course consistant with

Tan theta = Sin theta/Cos theta = sqrt(1+m^2)/sqrt(1+1/m^2) = sqrt(m^2*((1+m^-2)/(1+m-^2))) = sqrt(m^2)

Could some trigonomexperts verify/fix and add this stuff? --Intangir 21:17, 3 January 2006 (UTC)

Incorrect series formulae?

I found that the given series formula for tangent produces significant error for larger values of x, even at high N. Using Matlab, I computed 100 data points over $[0,0.9\pi /2]$ with the series and plotted the resulting error vs. the built-in function. I did this in a loop with N incrementing. The series converged (the error function stopped noticeably changing after N=15), but it was not even close to agreement.

Even if this was round-off error on the part of Matlab (seems unlikely for N<50), the formula still seems to be missing a factor of 1/6. For example, when N=1, the coefficient for the term is $2^{2}(2^{2}-1)U_{1}/2!=4\cdot 3\cdot 1/2=6\neq 1$, while the page implies a coefficient of "1" for the first term of the series. And, isn't there supposed to be a $(-1)^{N-1}$ term somewhere?

I am not an expert on this, but it seems that the "up/down" function is an approximation of the Bernoulli number which is found in other treatments. Can anyone explain these inconsistencies?

69.124.9.75 15:10, 21 January 2006 (UTC) Brandon

The up/down numbers are related to the even Bernoulli numbers, but they are not an approximation.

You were completely right that the series from the article were incorrect. Strange though, as I seem to recall checking them against MathWorld. Anyway, I now copied the series from MathWorld and checked that the first couple of terms agree, and I also checked it against Abramowitz and Stegun.

Thank you very much for bringing this to my attention. -- Jitse Niesen (talk) 16:51, 21 January 2006 (UTC)

Additional Functions

I have seen mention of the "versed cosine", "coversine", "versed cosecant", and "excosecant" on what appears to be a Russian website. Should these be included? (I think they would complete the symmetry within the image presenting eight other trigonometric functions.) (Also, I think pairing "excosecant" with "vercosine", or even "coexsecant" with "coversine", would be more symmetric than pairing "coversine" with "excosecant".) Zeroparallax 09:05, 5 February 2006 (UTC)

These functions are rare enough in modern use that only versine and exsecant need to be mentioned briefly here, and their variants can be described on the linked pages. (Indeed, see versine already.) And, as far as I can tell, "coversine" is far more common than "vercosine"; language is not always symmetric, I'm afraid. —Steven G. Johnson 19:09, 5 February 2006 (UTC)

Recent edits to "History" section

I notice that User:Jagged 85 has been making substantial edits to the "History" section, emphasizing the contributions of Indian mathematicians. I'm concerned, however, because he/she is providing zero references for the information added, such as supposed developments by the Babylonians and developments of the Taylor series in India 400 years before Euler.

The old version adhered pretty closely to the account by Boyer (see the references), and made no mention of e.g. Madhava that I can recall.

Please provide sources for substantial new historical claims.

—Steven G. Johnson 06:11, 28 February 2006 (UTC)

Citations

I think this article requires more inline citaions; escpecially becuase it is a featured article. Kilo-Lima ^{Vous pouvez parler} 21:09, 11 March 2006 (UTC)

suggestions

One of the things this article seems to be missing is a graph on a cartesian plane of the tangent function. Also, the fact that the cotangent of an angle is the same as the arctangent of that same angle has not been made clear.

I have created a graph of tan(x) at Image:Tangent.svg if someone wants to include it in the article.

Image sizes

I just reverted a part of this edit. The edit message was "let users pick their own thumb size in user preferences unless there is a specific reason not to". I do think there's a specific reason in this case—the text in the thumbs should be readable for a default user (i.e. a user who has the default thumbnail size). –Gustavb 03:59, 2 April 2006 (UTC)

Dead link

Trigonometric functions of angles 0° to 90° by degree in the links at the end of article is dead.

Thank you, now fixed. -- Jitse Niesen (talk) 06:29, 3 April 2006 (UTC)

The trig hand link is also bad. Instead of showing the pic it scolds and warns, evidently expecting an image upload. I did not look at the source. translator 20:10, 13 July 2007 (UTC)

Oops

I accidentally messed up a math expression halfway down the page, I'm not sure what I did and I'm not sure how to revert, can someone please fix my mistake? --Monguin61 23:39, 12 April 2006 (UTC)

I fixed it, nevermind, sorry --Monguin61 23:55, 12 April 2006 (UTC)

Confused about divergence statement

What am I misunderstanding in this statement near the end of Unit-circle Definitions?

From these constructions, it is easy to see that the secant and tangent functions diverge as θ approaches π/2 (90 degrees)

Why does one not say that the functions CONverge (toward infinity) as θ approaches π/2? Their proportional difference is nowhere greater than it is near 0 nor smaller than it is near π/2, no? This relationship (however it might properly be described) is instantly apparent in a unit-circle diagram that normalizes the tangent to vertical, as an earlier version of the diagram seems to have done some years back.

66.32.190.156 07:33, 5 June 2006 (UTC) AldenG

Confusion resolved. From the article on convergence, it emerges that when two functions approach equality at a common limit-value, they are said to converge -- unless the limit value is infinity or negative infinity, in which case they are said to diverge.

66.32.177.66 16:23, 19 June 2006 (UTC) AldenG

Archive 1

Archive 2

Archive 3

Better unit circle definition

Isn't the whole beauty of the unit circle definition that you can avoid mentioning angles altogether? This is the approach used in Lipman Bers' Calculus textbook (volume one):

1. Define the unit circle.

2. The length of the unit circle is 2pi.

3. Define P(\theta) to be a point on the circle of length \theta, obtained by moving counter-clockwise from (1,0)

4. Define sin and cos as follows for point P(\theta) = (x,y): sin(\theta) = y cos(\theta) = x

5. Derive properties of sin and cos from the geometry of the unit circle (e.g. sin^2+cos^2 = 1 because x and y are on the unit circle)

6. Expand the definition to right triangles by defining a coordinate system in which the length of the hypotenuse is 1 (the radius of the unit circle) and the origin is...

7. Expand sin and cos to all triangles

So you've described theta as a distance along the unit circle instead of an angle. So why is that such a wonderful idea? Dmcq (talk) 17:16, 9 January 2012 (UTC)

Note that the definition of angle is arc length scaled to a unit circle, so this isn't even really a change, it is just avoiding defining a word. — Steven G. Johnson (talk) 17:25, 9 January 2012 (UTC)

Replacing the image of the sawtooth wave

I've created a replacement for the image File:Sawtooth Fourier Analysis.JPG which is in the periodic functions section of this article. Here it is:

I'll wait for a day or two before putting it in to make sure I'm not stepping on anyone's toes. Of course I'll modify the caption too because it is not quite right for the new animation.

4dhayman (talk) 00:07, 21 February 2012 (UTC)

Looks good to me. The caption is far too long anyway: anything over two or three lines should be made into article content, where it is easier to read and is better integrated into the article.--JohnBlackburne^words_deeds 00:45, 21 February 2012 (UTC)

Okay, thanks, I'll go ahead and put it in then. No harm done if someone wants it reverted later. 4dhayman (talk) 01:07, 21 February 2012 (UTC)

Placement of sin 18°

Should sin 18° not be placed in the list alongside 15°, 54° and 75°, because it is as complex as sin 54°? — Preceding unsigned comment added by 86.13.216.157 (talk) 02:22, 4 May 2012 (UTC)

They are in numerical order in the individual tables, not according to complexity. They were rearranged into numeric order before I read this. Dmcq (talk) 10:44, 4 May 2012 (UTC)

tan 90°

I see in the tables that tan 90° is listed as infinity. While tan(x) approaches infinity as x approaches 90° degrees, tan(90°) is not defined as it involves sin(90°) / cos(90°) = 1/0 and anything divided by zero is not defined. 83.70.170.48 (talk) 13:13, 9 May 2012 (UTC)

It says below the table that "projective infinity" is the intended meaning. Some mention of a pole of order 1 would also be helpful.--LutzL (talk) 14:36, 9 May 2012 (UTC)

I do accept the meaning, and the fact that certain published tables list it as infinity, but the fact that the article states cot(x) = 1/tan(x) and tan(x) = infinity, cot(x) would therefor be 1/inf (zero) and not infinity. These functions are undefined at an angle of 90°, due to divide-by-zero problems. 83.70.170.48 (talk) 13:06, 10 May 2012 (UTC)

Connection to the inner product

In between Inverse functions and Properties and applications, I'd like to add a very short section titled Connection to the inner product:

In an inner product space, the angle between two non-zero vectors is defined to be

$\operatorname {angle} (x,y)=\arccos {\frac {\langle x,y\rangle }{\|x\|\cdot \|y\|}}.$

Any objections? -- UKoch (talk) 14:39, 17 October 2012 (UTC)

I have now added the section--as a subsection of Inverse functions, since it refers to the arccos function. -- UKoch (talk) 18:28, 5 December 2012 (UTC)

Suggest adding figure numbers to all of the figures

Earlier today, I reverted a good-faith edit by 112.211.202.47 who found the "a, b, h" labeling in the text to be totally obscure, so he/she subsituted "o" (meaning "opposite") for "a" and "a" (meaning "adjacent") for "b". This attempt by 112.211.202.47 to clarify things actually worsened the confusion.

The real problem is that there is often little or no obvious connection between text and figures, which were drawn by different people and use different labeling conventions.

I suggest giving the illustrations figure numbers.

PRO: Numbering the figures will allow them to be unambiguously referred to in the text.

CON: I am not aware of any automatic numbering templates that will keep text numbering and figuring numbering in sync. If figures are added or deleted, a laborious search needs to be made through the text to make sure that all numbers match.

I believe that the PRO advantages outweigh the CONs. If a consensus agrees with me, I will add figure numbers.

Example articles that I have worked on that have required figure numbering include Interferometry, Michelson interferometer, Mach–Zehnder interferometer, Quadratic equation, Kaufmann–Bucherer–Neumann experiments, and so forth. A common feature of these articles has been the need to reference multiple figures from diverse points in the text. I believe that Trigonometric functions has the same requirement. Stigmatella aurantiaca (talk) 02:15, 2 July 2013 (UTC)

Is the massive animated figure appropriate?

There is a very large, very animated figure next to the section on the relationship to the exponential and complex numbers. This figure seems to me to be both (1) almost entirely original research and (2) using very unencyclopaedic language (ie "thru"). I don't think it makes a good addition to the article, not least because moving images very rarely are, and I think it should be removed, per policy on OR and appropriate language. Any disagreement? Quantum Burrito (talk) 22:32, 7 December 2013 (UTC)

trignometry is a life key — Preceding unsigned comment added by K.sarankathiravan (talk • contribs) 15:12, 23 January 2014 (UTC)

New animation, explaining sine and cosine as related to the unit circle, with their respective graphs

Cos, sin and the unit circle.

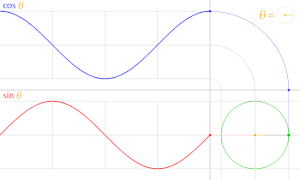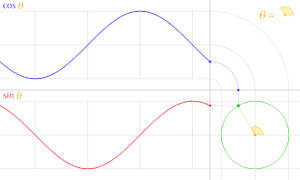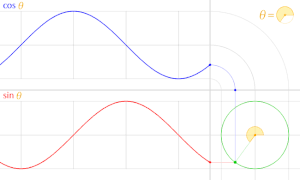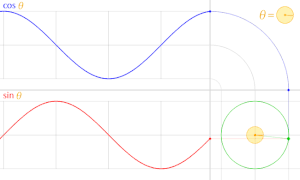
For what it's worth, I recently made this animation explaining cosine and sine in terms of the unit circle. Please, read the image's description on the image's page (just click the image) before making any remarks.

This is the only representation of both functions and their relation to the unit circle I could figure out that would:

1. Show the graph of both sin(θ) and cos(θ) in the usual orientation, where the horizontal axis represents θ and the vertical the value of the function.

2. The graphs shown, when animated, would not be drawn inverted when θ increases (the point in the unit circle moves counter-clockwise, as usual).

The "bent" way I used to represent cosine was necessary in order to have the graph y = cos(θ) in the usual orientation, condition 1 above, otherwise it would have to be vertical, and users would have to "tilt their heads" in order to see the graph properly. This not only would be very lazy, but it would be a terrible idea because:

• There would be a huge, empty square between both graphs. The animation frame would be too large, and mostly empty space. This space would not be useful for anything else that wouldn't be conveyed better in the accompanying article or image description.

• There would be no way to compare both graphs at once.

Therefore, his odd format is justified. Notice that this bend could be done either to the left or to the right. However, if to the right, the graphs would be drawn backwards in the animation, as they would be drawn from the left, and not to the right, as it is currently. This breaks condition 2, mentioned earlier.

I'm not sure if everyone would be OK with including this animation in the article. I couldn't figure where to place it anyway. So, for now, I'm just letting you guys know this animation exists. Cheers! — LucasVB | Talk 16:22, 16 March 2014 (UTC)

I've added this to the page—Love, Kelvinsong talk 16:05, 26 June 2014 (UTC)

Graphs!

I mean like, really, don't you feel this article could use some graphs, like of all the functions? Their absence is quite silly. I think there used to be some, what happened to them? Aoru (talk) 15:33, 26 June 2014 (UTC)

They are all condensed into one graph in the section Trigonometric functions#Unit-circle definitions. See File:Trigonometric_functions.svg. JRSpriggs (talk) 04:56, 27 June 2014 (UTC)

radians section is confused

The radians section is confused. There are real difficulties in the notion of "measure" of an angle, in the sense of associating a real number to an angle. Dieudonné has a careful discussion of this in his book LInear Algebra and Geometry, in which he concludes that it is impossible to measure an angle without making use of the complex exponential function. Another less explicit example of this is how most complex analysis textbooks use the power series definitions of cosine and sine to define the argument of a complex number, via the complex logarithm, and use that to measure angles.

A radian has to be dimensionless if you are going to plug it into a power series. Therefore this discussion contradicts the other sections of the article. The other sections are fairly careful to avoid saying that theta is a real number. If theta is an arclength, it has dimensions of length, but then theta squared has dimensions of length squared, so the power series expansion for sine makes no sense and certainly does not produce a ratio. In reality, angles are dimensionless, and the ratios of the sides of triangles are also dimensionless, so the other sections of this article succeed in avoiding the trap which this section falls into.

There is more than one way to fix this. Define radians as the dimensionless real number that makes sine satisfy the usual differential equation, or the usual Euler's formula, or the usual power series.

The arc length of the unit circle cannot be rigorously defined without using the integral calculus...actually, Jordan, in his Cours d'Analyse, is careful to define rectifiable curve and do enough integral calculus to define arclengths analytically right before deriving the derivatives of sine and cosine. Modern texts are usually not so careful and thus fall into a logical circle. Euclid was unable to study arclength as a real number, only areas, which is why it was left to Archimedes to introduce an extra axiom, about convexity, to study the arclength of the circle. (See Dieksterhuis on Archimedes, for example. Also Heath's commentaries.) 98.109.232.157 (talk) 05:02, 1 September 2014 (UTC)

If Θ is an angle specified in any desired system (degrees, grad, fractions of a straight angle, or whatever), then

$\alpha =\lim _{n\to \infty }\left(n\cdot \sin \left({\frac {\Theta }{n}}\right)\right)=\lim _{n\to \infty }\left(n\cdot \tan \left({\frac {\Theta }{n}}\right)\right)$

is that same angle in radians. So there is no problem defining it. JRSpriggs (talk) 10:26, 1 September 2014 (UTC)

(sin x)^2+(cos x)^2=1 =

when x is > or equal than 1 the following examples are true.I don't know if this is original research or not but it states that for all integers bigger than one, examples a)and b), the hypotenuse which faces the angle of right angle triangles is one, and 90 degrees for the angle and in radian 90 degrees is${\frac {pi}{2}}.$ . I don't see these examples listed in article named trigonometric functions.

a)$f(x)={\frac {1}{x}}+{\frac {x-1}{x}}=1$

b)$f(x)=\sin ^{-1}{\sqrt {\frac {1}{x}}}+\cos ^{-1}{\sqrt {\frac {x-1}{x}}}=?$

c)${\sqrt {\frac {x-1}{x}}}$ where ${\sqrt {(}}x-1)$is included in$\tan ^{-1}{\sqrt {(}}x-1)$

199.7.157.18 (talk) 21:42, 3 September 2014 (UTC)

"Alternatively, all of the basic trigonometric functions can be defined in terms of a unit circle centered at O"

I could not find this from the book, please provide proper referencing. — Preceding unsigned comment added by Bastasie (talk • contribs) 19:25, 23 April 2014 (UTC)

That part not changed, its without the reference for the figure below:

https://en.wikipedia.org/wiki/Trigonometric_functions#mediaviewer/File:Circle-trig6.svg

although its extremely familiar to me — Preceding unsigned comment added by Bastasie (talk • contribs) 16:19, 25 October 2014 (UTC)

Check my work

Although it borders on original research, I based this off the following work, which I believe to be rather straightforward (and the power series solution works because the tangent function is analytic around the origin):

The tangent function satisfies the differential equation ${\frac {dy}{dx}}=1+y^{2}$ with initial value $y(0)=0$, as mentioned in the article. Seek a power series solution in the form $y=\tan(x)=\sum _{k=0}^{\infty }a_{k}x^{k}$. Differentiate it once and substitute into the equation:

$\sum _{k=0}^{\infty }ka_{k}x^{k-1}=1+(\sum _{k=0}^{\infty }a_{k}x^{k})^{2}$

Apply the Cauchy product to the right hand side and subtract one from both sides:

$-1+\sum _{k=0}^{\infty }ka_{k}x^{k-1}=\sum _{k=0}^{\infty }x^{k}\sum _{j=0}^{k}a_{k-j}a_{j}$.

Because $a_{0}=0$ (because of the initial condition):

$-1+\sum _{k=1}^{\infty }ka_{k}x^{k-1}=\sum _{k=0}^{\infty }x^{k}\sum _{j=0}^{k}a_{k-j}a_{j}$.

Detach the first (k=1) term from the left side:

$-1+a_{1}+\sum _{k=2}^{\infty }ka_{k}x^{k-1}=\sum _{k=0}^{\infty }x^{k}\sum _{j=0}^{k}a_{k-j}a_{j}$.

At x=0, the right hand side is zero and so are all the terms on the left side, which implies that $a_{1}=1$ (my justification of this is a bit shaky because this is only at one particular value of x; however ${\frac {d}{dx}}\tan(x)\vert _{x=0}=1$ is another way of justifying this value of that coefficient, albeit with what I see as an additional initial condition, which can of course be derived separately using the properties of sine and cosine). This just leaves

$\sum _{k=2}^{\infty }ka_{k}x^{k-1}=\sum _{k=0}^{\infty }x^{k}\sum _{j=0}^{k}a_{k-j}a_{j}$

Equating terms of equal power gives

$a_{k+1}(k+1)=\sum _{j=0}^{k}a_{k-j}a_{j}$

$a_{k+1}={\frac {\sum _{j=0}^{k}a_{k-j}a_{j}}{k+1}}$.

From this and the fact that we already found that $a_{0}=0,a_{1}=1$, the terms I find match those given in the article:

$\tan(x)=x+{\frac {1}{3}}x^{3}+{\frac {2}{15}}x^{5}+{\frac {17}{315}}x^{7}\cdots$

To complete this assertion rigorously would require a proof by induction that the terms I find here match those given in the article, but it answers the question of how to algorithmically find the series directly as posed in an HTML comment in that section.--Jasper Deng (talk) 21:14, 13 January 2015 (UTC)

τ vs. π

A recent edit (diff) has changed the identities in the table at Trigonometric functions#Right-angled triangle definitions to use τ rather than π. When I reverted the first edit with that change, my summary was "τ is good but Wikipedia follows the mainstream and does not try to show a better way". Is there something I'm missing to justify using τ here? I'm aware that a number of people regard τ as much better (see pi#In popular culture), but is there a reason to use a symbol that would be a mystery to many readers here? Johnuniq (talk) 22:33, 12 February 2013 (UTC)

(Replies 2 years later) Hello. I'm sorry that I made that edit. I was watching Vi Hart and Numberphile videos, and I got really serious about т. I will always use π on wikipedia from now on. Max Buskirk (talk) 21:53, 16 February 2015 (UTC)

Circular reasoning in "significance of radians" subsection

In this section, an argument is presented which concludes that sine and cosine only obey the differential equations for sine and cosine when their parameter is measured in radians. The support for this claim, however, relies on the assumption that the parameter x in f(x) is in radians. If x is measured in degrees, and the derivative taken with respect to x, the differential equations for sine and cosine still hold. That is, there is nothing about the differential equation definition which fixes the dimensions of the parameter, as long as the parameter is a dimensionless quantity (radians or degrees both work perfectly well). I'll give this a week before I make any edits. Rangdor (talk) 00:50, 14 April 2015 (UTC)

The sine of an angle in radians and the sine of an angle in degrees are two different functions. To calculate the derivative of the sine, one uses the formula for the sine of the sum of two angles:

$\sin(x+h)=\sin x\cos h+\cos x\sin h$

${\frac {d\sin }{dx}}(x)=\lim _{h\to 0}{\frac {\sin(x+h)-\sin x}{h}}=\sin x\lim _{h\to 0}{\frac {\cos h-1}{h}}+\cos x\lim _{h\to 0}{\frac {\sin h}{h}}\,.$

To get the desired result of cosine, we need:

$\lim _{h\to 0}{\frac {\cos h-1}{h}}=0$

$\lim _{h\to 0}{\frac {\sin h}{h}}=1\,.$

The later result is only possible if h is given in radians, not degrees. JRSpriggs (talk) 10:51, 14 April 2015 (UTC)

sin(1°)

It is possible to express the value of sin(1°) analytically. It can be obtained by solving the cubic equation, sin(3°) = 3sin(1°)-4sin³(1°). Therefore, trigonometric functions of all angles of integer degrees can be expressed analytically. --Roland 19:51, 10 June 2013 (UTC)

The request is for an explicit expression, not an implicit one as you propose. There is not explicit solution for this cubic equation. All rational fractions of pi resp. all angles of rational degree can be implicitely expressed as a solution of an algebraic equation.--LutzL (talk) 17:25, 11 June 2013 (UTC)

Yes, there is. Cubic equations can be solved analytically. Please refer to http://en.wikipedia.org/wiki/Cubic_equation#Roots_of_a_cubic_function

A website actually gives the solution: http://www.intmath.com/blog/how-do-you-find-exact-values-for-the-sine-of-all-angles/6212 --Roland 21:59, 11 June 2013 (UTC)

You are completely right, there is an analytical expression for sin(1°), which is sin(1°) (understood as the evaluation of the series). But the thread starter obviously wanted an algebraic expression, i.e., one only involving roots in addition to the usual arithmetic operations.--LutzL (talk) 18:07, 2 July 2013 (UTC)

Additionally, if you check the analytical formula for the root of the cubic equation, then you will see that you need an auxillary analytical number to express the solutions. Which is, ... , wait, ... , wait, ... , wait for it, ... , yes, exactly sin(1°).--LutzL (talk) 11:47, 3 July 2013 (UTC)

The linked article expresses, in a very complicated way, the trivial fact that cos(1°)+i*sin(1°) is one of the cubic roots of cos(3°)+i*sin(3°). However, there is no way to express this cubic root using only arithmetic operations and roots of positive real numbers.--LutzL (talk) 12:08, 3 July 2013 (UTC)

The implication in the article is that sin(1°) can be evaluated without computing trigonometric functions. As noted above, this is false; so it would be better to remove this paragraph as misleading. I have done so. cffk (talk) 16:39, 14 December 2015 (UTC)

No, this is true, sin(1°) can be evaluated without computing trigonometric functions. It can be evaluated by arithmetic operations, including square and cube roots (through Cardano formula. I have thus restored this paragraph and added some clarification. D.Lazard (talk) 17:16, 14 December 2015 (UTC)

Surely the evaluation of the cube root of a complex number involves trigonometry? For example the real part of the cube root of 3 + 4i is 5^(1/3)*cos(atan(3/4)/3). Can you write it in a form that doesn't involve trigonometric functions (without popping back into the complex plane)? cffk (talk) 18:18, 14 December 2015 (UTC)

The article Root-finding algorithm provides many (much more than ten) methods for computing the roots (including the complex ones) of a polynomial. All may apply to computing cube roots (equation $x^{3}=a$), and none involve any trigonometric function nor polar coordinates in the complex plane. This is related with the fundamental theorem of algebra, which has nothing to do with trigonometry. D.Lazard (talk) 21:08, 14 December 2015 (UTC)

But, these root-finding methods are all iterative ones! Surely the point of the paragraph in question was that sin(1°) can be computed in finite terms using the basic arithmetic operations and extracting real roots.

In addition, if this is an allowed method, why bother mentioning the Cardano formula? You could just solve the original cubic equation. Better yet, why not just solve the "simpler" polynomial x^180 + 1 = 0. cffk (talk) 21:31, 14 December 2015 (UTC)

I see that Trigonometric constants expressed in real radicals provides a useful summary: "All trigonometric numbers—sines or cosines of rational multiples of 360°—are algebraic numbers (solutions of polynomial equations with integer coefficients); but not all of these are expressible in terms of real radicals. When they are, they are expressible more specifically in terms of square roots." cffk (talk) 22:25, 14 December 2015 (UTC)

You are right about iterative methods. In fact, everything depends on what is chosen as basic arithmetic operations. Even square roots require iterative methods for being evaluated. The formulas of this section do not compute the values of trigonometric functions, but express them in terms of a finite number of symbols. in the formulas for angles multiple of 3° theses symbols are the integers, the symbols for addition, subtraction, multiplication and division, and square roots. As this is not sufficient for representing every number, people used to introduce other symbols (or other numbers), such as n-th roots (real or possibly complex), Bring radicals, algebraic numbers, and finally real and complex numbers. They were interested in characterizing the smallest class to which belongs the numbers that are widely considered. The relevant facts, here, are: sin(x) and cos(x) are expressible in terms of square roots if x is an integer multiple of 1°. They are expressible in terms of square roots and non-real cube roots if x is an integer multiple of 1°. They are expressible in terms of n-th roots (and therefore algebraic) if x is the product of 1° by a rational number (this is a non-elementary consequence of Galois theory). Otherwise, either x (measured in degrees) or both sin(x) and cos(x) are transcendental numbers (this is a corollary of Baker's theorem, 1967).

IMO, these results are more useful than the useless formulas for angles that are multiple of 3°. Maybe, I'll edit the article for inserting these results, when I'll get some time for that. D.Lazard (talk) 10:49, 15 December 2015 (UTC)

Your changes have improved the article, thanks. However, now the paragraph about solving a cubic to get sin(1°) is even more out of place. You can't list sin(1°) under "Explicit values" when its evaluation requires either an iterative method or trigonometry to compute a complex cube root. I recommend removing this paragraph again (but leave the earlier passage which says that sin(1°) is an algebraic number). Finally, please remember that there is a serviceable, if somewhat awkward, direct method for computing square roots by hand which generates the digits one at a time. cffk (talk) 15:33, 16 December 2015 (UTC)

"Value" and "evaluation" are ambiguous word to which, it seems that you give your own meaning. In fact, I understand that, for you, a value is a numerical approximation. Formally this is not true, as a value of sin(1°) must be equal to sin(1°), which is not the case of any approximation. On the other hand, it seems that you not consider as a value the expression for sin(3°) given in the article, while most mathematicians consider it as an admissible value. Nevertheless I have edited the article for replacing "value" by "expression" for avoiding any confusion. D.Lazard (talk) 17:05, 16 December 2015 (UTC)

My objection is that the expression for sin(1°) is implicit because, when writing it out as a real expression, it necessarily involves other trigonometric functions (see also the comments by LutzL above). A secondary objection is that this is an altogether useless result which just serves to clutter the article and to confuse the reader. cffk (talk) 18:32, 16 December 2015 (UTC)

I'm still dubious about the wisdom of listing sin 1° as having an explicit value. However, if the article is going to list any expression, let's, at least, make it as simple as possible. So I've replaced the messy business of solving a cubic equation with two simple expressions for sin 1°. This makes it plain that these definitions are circular. cffk (talk) 15:21, 19 December 2015 (UTC)

There is no definition in this section; so there is no circular definition. Moreover, one cannot say that a 90th root is something simple. On the other hand, the formula that you give is smart way to avoid using Cardano formula while getting a very similar result. It has also the advantage that it may generalized to a proof that the sine and cosine of any rational angle may be expressed in terms of nth roots. I'll edit this new version for clarifying that this is not circular and provide a (useless) explicit expression of sin 1° in terms of radicals. D.Lazard (talk) 23:03, 19 December 2015 (UTC)

Find a degree of a ratio without a calculator?

While not using a calculator, after learning how to find a non perfect square root (example: square root of 19 is in between 4 and 5, so as you keep using a number in between and squaring it until you are close enough to 19), I'm stumped on finding the degree value when you have opposite, adjacent, and/or hypotenuse. Here is an example:

sin(x) = 1/2

Solve for x without a calculator and/or prior knowledge (obvious, like avoid saying things like a square root of 100 is 10 without showing your work).

Joeleoj123 (talk) 12:35, 31 October 2016 (UTC)

In general, solving sin(x) = c to find x without using a calculator or trigonometric tables will be very difficult. But for the particular case sin(x) = 1/2 you can draw a right-angled triangle with hypotenuse length 2 and opposite side length 1, and then realize that this is one half of an equilateral triangle. Gandalf61 (talk) 12:46, 31 October 2016 (UTC)

Image placement

Several paragraphs of the section titled "Unit-circle definitions" talk about an "image to the right". However, at least on my computer monitor, the correspinding image is not placed to the right but actually on the next screen page (and even in the next section of the article). Can something be done about the placement of these images? – Tea2min (talk) 09:12, 17 February 2017 (UTC)

The article used the body of the article for providing information that belong to figure captions. I have solved the point by several edits for making the body of the section self-contained, moving the image that you mention to the top of the section, and using the same notation in the body and in the image (and other cleaning up that are not directly related to your complaint). Further work is still needed, in particular to create a section "Graphs", which is blatantly lacking. D.Lazard (talk) 12:00, 17 February 2017 (UTC)

External links modified

Hello fellow Wikipedians,

I have just modified one external link on Trigonometric functions. Please take a moment to review my edit. If you have any questions, or need the bot to ignore the links, or the page altogether, please visit this simple FaQ for additional information. I made the following changes:

• Added archive https://web.archive.org/web/20040404234808/http://www.pupress.princeton.edu/books/maor/ to http://www.pupress.princeton.edu/books/maor/

When you have finished reviewing my changes, you may follow the instructions on the template below to fix any issues with the URLs.

This message was posted before February 2018. After February 2018, "External links modified" talk page sections are no longer generated or monitored by InternetArchiveBot. No special action is required regarding these talk page notices, other than regular verification using the archive tool instructions below. Editors have permission to delete these "External links modified" talk page sections if they want to de-clutter talk pages, but see the RfC before doing mass systematic removals. This message is updated dynamically through the template {{source check}} (last update: 5 June 2024).

• If you have discovered URLs which were erroneously considered dead by the bot, you can report them with this tool.
• If you found an error with any archives or the URLs themselves, you can fix them with this tool.

Cheers.—InternetArchiveBot (Report bug) 21:38, 20 May 2017 (UTC)

Edits of December 2017

@D.Lazard::I implore you not to make any more edits to the main article for the rest of the day in your time region.@D.Lazard:: Please, just for the rest of your day. My edits and your edits have conflicted twice, which made me lost my work. And Why did you delete my proof of the fact that tanθ is the ordinate of B, cotθ is the abscissa of C, secθ is the abscissa of E, and cscθ is the ordinate of D? This morning and afternoon, my work of editing this article was interrupted twice by something that required me to leave the computer. That was why you could see some errors in my edits, because I couldn't finish my edit. Now I have time to finish it.Onmaditque (talk) 11:44, 30 December 2017 (UTC)

To editor Onmaditque: Please place new discussions in new sections at bottom of talk pages (automatically done by button "New section" at the top of talk pages).

In case of edit conflict, you should not lost your work: it suffices to follow the instructions of the edit-conflict page. Otherwise, you can go back to your last edit page, and copy the implied sentence(s) for pasting it (them) either in a new edit page, that may be your WP:sandbox page or the page that you were editing.

I have removed your proof for several reasons. Firstly it does not add anything useful to the article (see MOS:MATH#Proofs). Secondly, a succession of formulas without linking words is not a proof. Thirdly, you use vector notation, that should be too technical for most readers. By the way every proof should use geometric arguments, and the clearest proof depends on the geometric background of the reader. Thus any proof should be confusing for some readers, while no proof will add anything for understanding trigonometric functions (which are the subject). Thus it is better to not have a proof here.

About edit conflicts: Please provide edit summaries, and when you are planning further edits on the same part of the article, say it in the edit summary. D.Lazard (talk) 12:28, 30 December 2017 (UTC)

@D.Lazard:: Thank you for providing the reasons of removing my proof. I totally agree with these reasons,but I would like to ask why you reverted my two edits after DVdm? I think I fixed some inaccuracies in my edits. For example, I changed "the smallest period" in the sentence "The smallest period is π for the tangent and the cotangent and 2π for the four other trigonometric functions" to "the smallest positive period (called the primitive period)". Since the period of a periodic function can be negative, strictly speaking, a periodic function does not have the smallest period. It is also more accurate to say "That is, the identities

${\begin{aligned}\tan \theta &=\tan(\theta +k\pi )\,,\\\cot \theta &=\cot(\theta +k\pi )\,,\end{aligned}}$

hold for any angle θ and any integer k." than to say "that is

${\begin{aligned}\tan \theta &=\tan(\theta +k\pi )\,,\\\cot \theta &=\cot(\theta +k\pi )\,,\end{aligned}}$

for any integer k." What's more, I kept most of your words in my latest revision (the one before your reversion).I feel that you reverted my edits without even reading it. Neither did you provide a definite reason. What did you mean by "non-explained edits"? Remember "BRD is not a valid excuse for reverting good-faith efforts to improve a page simply because you don't like the changes" or even because you think your revision is the best.Onmaditque (talk) 06:53, 31 December 2017 (UTC)

You never provide any edit summary. This may be acceptable for minor edits that are easy to check. This is not for edits like yours, which require a careful check for knowing if they really improve the article, and for understanding their motivations. That is what I mean with "non-explained edits". This would be a sufficient reason for reverting your last edits. But there are several other reasons:

• A change of section heading requires a consensus a soon as some one disagree with it. This is the case here.
• Your edits are badly formatted and do not respect WP:MOS (using "&" instead of "and"; symbols for points sometimes in italic, sometimes not; displayed formula transformed into a non-breaking long formula; ...)
• The mention of "primitive period" is confusing here, as the term is used only in some branches of mathematics, and other terms are used elsewhere. Moreover, if you look where Primitive period redirects, you will see that it is not a good idea to suggest searching this phrase. Nevertheless, I could agree with your concern about "smallest", and I have added "positive" for clarification.
• About adding "for any angle" or changing "smallest period" into "smallest positive period": A mathematical text written for being understandable by a large audience cannot be formally correct. Therefore, a lack of accuracy is acceptable, and even recommended, if it is not mathematically wrong, if nobody would be confused by it, and if a better accuracy would make reading more difficult. It is why I have omitted "for any angle". For "smallest period", I am convinced that nobody would be confused, but I agree that it is mathematically incorrect, and deserves to be fixed, since this would not really complicate the sentence.

As you can see, it is not that I do not "like" your edits, it is that I disagree with them. Thus BRD applies fully. Nevertheless, I acknowledge that these are good faith edits. Otherwise, I would not have taken so much time for discussing them. D.Lazard (talk) 10:48, 31 December 2017 (UTC)

Edits of January 2018

@D.Lazard:: Thank you for providing the reasons of reverting my edits. Your words made me know more about how to edit Wikipedia properly. There are some issues with your revision of the article that I would like to discuss with you.The term “identity” in the sentence “As a rotation of an angle of ±2π is the identity, point A is the same for two angles that differ from an integer multiple of 2π” is confusing, since the term is too technical for most readers to understand its meaning. Moreover, “two angles that differ from an integer multiple of 2π” means “two angles that do not equal an integer multiple of 2π”, so the original phrase “two angles that differ from an integer multiple of 2π” does not make much sense. In order to make the sentence easier to understand, I suggest that you rewrite it like this: “As a rotation of an angle of ±2π does not change the position or size of a shape, Point A is the same for two angles whose difference is an integer multiple of 2π”. --Onmaditque (talk) 01:02, 7 January 2018 (UTC)

Many thanks for your recent edits, which clearly improve my version. D.Lazard (talk) 15:13, 7 January 2018 (UTC)

Removing of section "Computation"

I will remove section "Computation" for the following reasons. It is written in the form of an essay rather than in encyclopedic style. It WP:original synthesis mixing in an indiscriminate way some very elementary special cases, methods used before availability of computers, and methods used in old computers. The methods that are used presently by builtin functions in computers software are not even mentioned. Also IEEE 754 (which recommend the application of the norm to sine and cosine), and methods for very high precision are not mentioned. So the only true information that a non-specialist reader can extract from this section is that methods exist for the computation.

A section on methods for computing trigonometric functions could be useful if it describes the methods that are presently used in computers, but the present section is not a convenient starting point for that, and I guess that it would be too technical for this article. So WP:TNT seems the best way to proceed. D.Lazard (talk) 14:04, 26 April 2019 (UTC)

I support your initiative. Good information is available at Exact trigonometric constants so it should be linked, either in “See also” or elsewhere in the article. Dolphin (t) 06:10, 27 April 2019 (UTC)

This article is already linked in section "Algebraic value" under its main name "Trigonometric constants expressed in real radicals". D.Lazard (talk) 07:45, 27 April 2019 (UTC)

Thanks! Dolphin (t) 08:41, 27 April 2019 (UTC)

Basic identities

Does this section really belong in this article? This article is ostensibly about trigonometric functions. There is already an article, List of trigonometric identities, for identities. I think this section should either be removed or at least minimized.—Anita5192 (talk) 16:21, 14 August 2019 (UTC)

IMO, this section must contain only the basic identities that everyone who manipulates trigonometric functions must know and use. So for minimizing it, I see nothing else to remove than the formulas involving csc, sec, and ctg, which are not used in practice (using other trig. functions than sin, cos and tan makes every real-world computation much more difficult, because of too many choices). Also, the antiderivatives are useful in practice only for sin and cos, as, except for very simple expressions, the first thing to do for integrating is to convert everything into sin and cos.

On the other hand, the most important basic identities must be kept here, as it is here that a reader comes naturally for refreshing his memory of them. D.Lazard (talk) 17:12, 14 August 2019 (UTC)

sinh and cosh

This article uses sinh and cosh without defining them or linking to a page with a definition. — Preceding unsigned comment added by Subcelestial (talk • contribs) 17:43, 15 November 2019 (UTC)

 Fixed, with some text improvement. D.Lazard (talk) 18:02, 15 November 2019 (UTC)

Who got rid of the Exsecant, Versine, and Excosecant?

These are also trigonometric functions.Eshaan11 (talk) 13:42, 5 May 2020 (UTC)

... and they are mentioned at the end of the history section, which is their right place, as explained there. D.Lazard (talk) 14:05, 5 May 2020 (UTC)

My minor edits

@D.Lazard: What are the problems with my edits except a capitalization of "degrees"? Thanks Santosh L (talk) 04:22, 17 June 2020 (UTC)

Counterclockwise is typically one word. Although the hyphenated form is attested, there's no need to change it. Also, your changing of "expressed in" to "taken as" is awkward at best. –Deacon Vorbis (carbon • videos) 04:26, 17 June 2020 (UTC)

Asymptote oversight?

I'm surprised that there's no mention at all of how the tangent function has a vertical asymptote at θ = (k + ⁠1/2⁠)π, as it's what clearly delineates tan from sin and cos. Tangent (function) redirects here so I think it deserves mentioning, but I'm not sure on the best place for it as this article is quite dense already. Snizzbut (talk) 16:16, 28 February 2021 (UTC)

Good point. Also, the basic properties as functions of trigonometric functions were also lacking. I have added them, with a figure, at the beginning of section "In calculus". D.Lazard (talk) 17:24, 28 February 2021 (UTC)

Values of zero in table?

In the "Simple algebraic values," is there some reason not to show zeroes for the sine and tangent of 0°, and for the cosine and cotangent of 90°? Right now, those spaces are blank. That seems odd, considering that other spaces on the table show infinity; that's an arguable point--the zeroes are not. Uporządnicki (talk) 13:52, 19 August 2021 (UTC)

 Done. I replaced the tagged zeros with templates as in the first column. See [2]. - DVdm (talk) 14:05, 19 August 2021 (UTC)

Test:

"<math>0</math>" produces "$0$" (nothing), where "{{math|0}}" produces "0".

"<math>1</math>" produces "$1$".

"<math>00</math>" produces "$00$".

"<math>01</math>" produces "$01$".

"<math>0=0</math>" produces "$0=0$".

"<math> 0</math>" produces "$0$". HA, we need a space!

Strange - DVdm (talk) 14:10, 19 August 2021 (UTC)

For consistency, I went back to "<math> 0</math>" with the spaces: [3]. - DVdm (talk) 14:33, 19 August 2021 (UTC)

Silly me! I was just going to go in and type "0"! Uporządnicki (talk) 16:37, 19 August 2021 (UTC)

Not silly, as it seems to produce the same as "{{math|0}}". I tried that but that would give inconsistent results when rendering math as PNG. I've asked at Wikipedia:Village pump (technical)#Math 0. Let's see what they say... - DVdm (talk) 17:07, 19 August 2021 (UTC)

Update. Known bug, introduced today: Phab:T288846#7294135, [4] - DVdm (talk) 21:28, 19 August 2021 (UTC)

Well, I meant "silly me" ironically--tongue-in-cheek suggesting that it was silly to think of trying the obvious: I want to show 0, type 0. I'll have to take your word for it that it will raise some sort of problem in Papua-New Guinea. Uporządnicki (talk) 11:54, 20 August 2021 (UTC)

Article

i wanted to learn something - completely impossible from this article, this is just a reference for those who know all of this material already. — Preceding unsigned comment added by 108.84.184.142 (talk) 21:44, 10 March 2013 (UTC)

• i agree, the definition is supposed to be comprehensible without too much reference or dependence on other "terms". it was obviously written by those who already understand the subject and can't intuit how to explain it for those who don't. 197.134.147.164 (talk) 11:03, 15 May 2013 (UTC)

• I also agree. This article seems to cry out for a bold rewrite. Stigmatella aurantiaca (talk) 02:27, 2 July 2013 (UTC)

• I also agree. It is so disappointing that there are no surface plots of the absolute value for the complex trig functions. This "Domain coloring" is lame and impossible to decipher (it is completely ridiculous that I have to ask maple or mathematica to gain a reasonable quantitative understanding) 69.131.208.241 (talk) 21:49, 24 November 2021 (UTC).

The domain coloring method is "lame"? Please explain. It is true, though, that the type of the coloring used in the article (introduced by the user Nschloe) is very non-standard. A1E6 (talk) 16:43, 25 November 2021 (UTC)

I would like to point out that an encyclopedia article is not supposed to be the first place to learn about something. First consult a textbook, then for things that a textbook might leave out, or might get wrong, or might be slanted about, then go consult the encyclopedia. Or, first consult the encyclopedia in order to get a very vague and general idea of what is involved in the topic, what it is about, and a list of textbooks or sources in its bibliography. So these comments are invalid. 98.109.232.157 (talk) 05:06, 1 September 2014 (UTC)

OK, almost eight years old, but this statement is too outrageously ridiculous to leave alone. OF COURSE, an encyclopedia is supposed to be the first place to learn about something. That's exactly why people used to buy Encyclopedia Britannica, Encyclopedia Americana, Colliers, Funk & Wagnalls ... A question would come up in the family--that's where they'd go to look; Mom and Dad would encourage the kids to look things up. And yes, I think that if an encyclopedia is supposed to be general interest (which I think Wikipedia is) and not a specialist reference for specialists, it should make an effort to say what a thing is about in some way--at least as much as the topic will allow--that anybody can understand it. On tech and math subjects, Wikipedia falls woefully short in that regard. Uporządnicki (talk) 14:42, 30 April 2021 (UTC)

Wikipedia is a "reference" (can a math reference even be labeled as "non-specialist"?), not a textbook (WP:NOTTEXTBOOK). Sometimes, the articles are too technical and are marked as such, but that rarely happens. This article is not one of them and the editors are doing their best to make the article understandable. But I don't think it's possible to write a math reference so that anybody can understand it. A1E6 (talk) 16:38, 25 November 2021 (UTC)

Boy I hope that is not the purpose of Wikipedia. That would make it pretty useless. 4 July 2017 (JCBoone) — Preceding unsigned comment added by Joseph C Boone (talk • contribs) 21:50, 4 July 2017 (UTC)

Unit Circle Diagram

Contains a number of errors. I'm not in a good position (ie. edit SVGs) to correct them. The value for sixty degrees is given as

$\sin {\frac {\pi }{3}}=\sin 60^{\circ }={\frac {\sqrt {3}}{2}}={\frac {1}{2}}$

which is not the case. It's correct in the table next to the diagram. Mwasheim (talk) 14:55, 9 April 2023 (UTC)

Sorry, in my understanding it says:

$(\cos ,\sin )({\frac {\pi }{3}})=(\cos ,\sin )(60^{\circ })=({\frac {1}{2}},{\frac {\sqrt {3}}{2}})$,

which is correct. –Nomen4Omen (talk) 15:08, 9 April 2023 (UTC)

Um, that is correct. Hmm. I was busy converting between radians and degrees and didn't read the legend carefully enough. Thanks! Mwasheim (talk) 15:21, 9 April 2023 (UTC)

as an aside, I wonder if it would help people sitting there with calculators which use radians (ie. all?) to specify that sin 90 is generally sin(rad(90)) on calculators?