Talk:Set (mathematics)/Archive 2
| This is an archive of past discussions about Set (mathematics). Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page. |
| Archive 1 | Archive 2 | Archive 3 |
Set as an abstract object
I disagree (rather strongly) with this edit. A set is indeed abstract, but most people don't know what "abstract" is mathematically, and if anything, the concept of set is abstract enough (the irony) that we better don't mention that very thing in the first sentence.
There's been a long argument between me and Pontiff Greg Bard on my talk page about this (User talk:Oleg Alexandrov#a set is an abstract object) with a third party, JackSchmidt, putting in a third opinion which I will quote below. Other comments?
- (The comment below is originally from User talk:Oleg Alexandrov.)
- (Hopefully I am not butting in.) The edit appears fairly minor, and probably the two positions can be merged easily. I can agree that "a set is an abstract object" is one of the first things we learn about sets, since they are quite often once of the first "abstract" things you study in math (using mathematical language here). I think the part of the edit that makes the article less simple is linking to rather refined, though fundamental, philosophical articles in the lead of an article on a mathematical subject. Since set theory, especially naive set theory, has caused quite an examination of the philosophical foundations of mathematics, such links are appropriate *somewhere* in the article. I think the only concern is that it not be in what is more or less the opening sentence.
- Could both agree to "In mathematics, a set is an abstract object that can be thought of as any collection of distinct objects considered as a whole." as the opening sentence (with only the single wikilink), and then an addition, perhaps to the Definition section (so quite fundamental to the article, and appearing quite early), links to the philosophical concepts being used somewhat informally there? I think the tone in that section is quite suitable for wiki-links to the philosophical articles that provide a sounder understanding of the terms. Alternatively one could follow a somewhat common style of having a two or three paragraph lead that has sentences for what it is, what it is used for, its history, its foundation, and its generalizations. I think a very short lead is much nicer, and that editing in the Definition section would probably reach consensus more quickly, but I don't see any insurmountable trouble with expanding the lead. JackSchmidt (talk) 06:08, 5 February 2008 (UTC)
- I still disagree the first sentence of the article is the place to settle such fine points. Oleg Alexandrov (talk) 06:24, 5 February 2008 (UTC)
- I hope the proposed solution does not seek to settle such fine points in the opening sentence, merely it provides text both parties can agree on. I was hoping that the word "abstract" itself is not a problem, merely the attempt to say specifically what we mean by this word in the opening sentence.
- Apparently the word "abstract" is not considered a general-service word, wiktionary:simple:abstract, but I think we were taught this word in k-6th grade, but certainly in 7-12th. Again hopefully we can agree the word itself is not a problem, merely being too formal about the word in the first sentence is worrisome to Oleg Alexandrov and others, and not fundamentally important to Greg Bard and others. The addition to the definition section should provide philosophical context for "object", and if any fine points need to be settled, there should be a section on such things. JackSchmidt (talk) 06:55, 5 February 2008 (UTC)
- I still disagree the first sentence of the article is the place to settle such fine points. Oleg Alexandrov (talk) 06:24, 5 February 2008 (UTC)
- I am not so concerned with object (philosophy) as a link. It is there so as to distinguish from the mention of "abstract object" (and it was working well in that capacity). It was linked because it was an appropriate wikilink to a term which was already in the article, which would benefit the article as a wikilink. My main concern is calling something what it is. I don't think we need to point out in every biography that "Abraham Lincoln, was a human being, who..." Because, although that fact is equally fundamental to the concept of Lincoln, it is also sufficiently obvious to everyone. For such a concept as set, I would think that we would want all the tools at our disposal to say what it is on that fundamental non-obvious level.
- Oleg, please observe: "most people don't know what "abstract" is mathematically," Where does the idea ever come from that every single point about the thing has to be "mathematical"? I already told you that mathematicians do not have the monopoly on the study of this thing. The first step to working interdisciplinarily is admitting that we have an interdisciplinary subject. Please ease up on the grip over these type of articles. Your statement also supports the thesis that it should be elucidated upon, not omitted.
- Abstract objects are not made more abstract by identifying them as "abstract objects." They are made less abstract. This would seem to be a self evident principle (about language, not set). I am sorry Oleg, but it is on this ground that I will be reinserting that phrase. Please reconsider your opening remark above.
- Where does the idea come from that it might be okay to have this as the first sentence, but it would be better to wikilink abstract object somewhere else in the article? The guideline on wp says that the first instance of a term should be wikilinked, but not the others. So exactly why would this be an exception? It is an exception which is consistent with all of the rest of the de-emphasizing, mitigating, and outright denial of the logical (metalogical/metamathematical/philosophical,etc) foundations of these concepts which I am endeavoring to insert. It is a POV issue, and a I wish the mathematicians were more conciliatory, rather than hostile to these foundations (which invariably, they don't find important at all.) Be well, Pontiff Greg Bard (talk) 17:23, 5 February 2008 (UTC)
- Every mathematical object is abstract, so saying that any particular one is abstract is unnecessary. Worse it is misleading since it gives the false impression that some mathematical objects are concrete. I strongly support the current formulation, over the proposed one. Paul August ☎ 18:33, 5 February 2008 (UTC)
- Paul, the last sentence says that set theory can be viewed as foundational to the rest. That means we do not need to identify every single abstract object as such --just the most important ones. Please reconsider. Please consider what I have said above about the hostility to these concepts. Why does everybody feel so strongly? I find that troubling, and closed minded. Be well. Pontiff Greg Bard (talk) 19:02, 5 February 2008 (UTC)
- Saying that a set consists of objects, with object linking to object (philosophy), does seem rather confusing since that article says that object has different meanings, including some that are simply wrong in the context "a set consists of objects". Similarly, I don't see how a link to abstract object helps the reader to understand what a set is. Saying that a set is an abstract object, while its elements are objects, is confusing because it implies that a set is more abstract than its elements. Greg, I think that what you're calling hostility against logical/philosophical ideas is in fact hostility against your logical/philosophical ideas. -- Jitse Niesen (talk) 20:21, 5 February 2008 (UTC)
- I tried to find a compromise between the two positions. I think my text is slightly better than the previous one and Gregbard's, but like Jitse I find the links misleading. We could, perhaps, replace the two occurrences of "object" in the sentence by "thing". I think this would give the wikilinks a context in which only philosophically minded people would click them; which seems to be exactly what we need here. --Hans Adler (talk) 20:32, 5 February 2008 (UTC)
- I think that the original version is better — and so I've restored it per Hans' edit summary. Paul August ☎ 20:36, 5 February 2008 (UTC)
- Can you explain what you didn't like, so we can move towards a consensus? Somehow I feel that my version was slightly clearer, but I can't really say why. (I am not talking about the links here.) --Hans Adler (talk) 20:42, 5 February 2008 (UTC)
- In my opinion it is simpler, more elegant, easier to understand, and as I said above, does not contain the unnecessary and misleading term "abstract". Paul August ☎ 20:47, 5 February 2008 (UTC)
- I think I see now what I like about my version: It starts with the problem. We have a bunch of things, and we want to do mathematics with them. So we just pretend that all the things together are one thing. The old version sounds as if mathematicians had discovered sets lying around somewhere, not knowing what to do with them, and then one day a bright guy discovered that you can think of them as just a collection of objects. This seems to make them more mysterious. --Hans Adler (talk) 20:58, 5 February 2008 (UTC)
- Moreover, "In mathematics, a set can be thought of…" sounds as if it should be continued with something like "whereas in law, a set is…". My point here is that we seem to have developped Wikipedia jargon for this kind of situation, in which we stress the fact that the word has several meanings a bit more than we should. --Hans Adler (talk) 21:59, 5 February 2008 (UTC)
- In my opinion it is simpler, more elegant, easier to understand, and as I said above, does not contain the unnecessary and misleading term "abstract". Paul August ☎ 20:47, 5 February 2008 (UTC)
- Can you explain what you didn't like, so we can move towards a consensus? Somehow I feel that my version was slightly clearer, but I can't really say why. (I am not talking about the links here.) --Hans Adler (talk) 20:42, 5 February 2008 (UTC)
- I think that the original version is better — and so I've restored it per Hans' edit summary. Paul August ☎ 20:36, 5 February 2008 (UTC)
- I tried to find a compromise between the two positions. I think my text is slightly better than the previous one and Gregbard's, but like Jitse I find the links misleading. We could, perhaps, replace the two occurrences of "object" in the sentence by "thing". I think this would give the wikilinks a context in which only philosophically minded people would click them; which seems to be exactly what we need here. --Hans Adler (talk) 20:32, 5 February 2008 (UTC)
- Saying that a set consists of objects, with object linking to object (philosophy), does seem rather confusing since that article says that object has different meanings, including some that are simply wrong in the context "a set consists of objects". Similarly, I don't see how a link to abstract object helps the reader to understand what a set is. Saying that a set is an abstract object, while its elements are objects, is confusing because it implies that a set is more abstract than its elements. Greg, I think that what you're calling hostility against logical/philosophical ideas is in fact hostility against your logical/philosophical ideas. -- Jitse Niesen (talk) 20:21, 5 February 2008 (UTC)
- Paul, the last sentence says that set theory can be viewed as foundational to the rest. That means we do not need to identify every single abstract object as such --just the most important ones. Please reconsider. Please consider what I have said above about the hostility to these concepts. Why does everybody feel so strongly? I find that troubling, and closed minded. Be well. Pontiff Greg Bard (talk) 19:02, 5 February 2008 (UTC)
Perhaps it helps to have all the versions together here. Feel free to add new versions.
- In mathematics, a set can be thought of as any collection of distinct objects considered as a whole. [Traditional version]
- A set is an abstract object. It can be thought of as any collection of distinct objects considered as a whole. [Gregbard's version]
- In mathematics, any collection of distinct objects can be treated as a new abstract object, called a set. [Hans' version]
--Hans Adler (talk) 20:49, 5 February 2008 (UTC)
- The question whether sets are abstract or not is somewhat subtle; see Penelope Maddy, and Realism in Mathematics (p. 2) on Google books. As it stands, the article is essentially a fork of naive set theory. I would rather see this article cover sets more broadly, including philosophical issues such as concreteness. I am not in a good position myself yet to write that material here, though. — Carl (CBM · talk) 00:15, 6 February 2008 (UTC)
- Going beyond naive set theory is a worthy goal. However, starting the article with a rather obfuscated first sentence (sorry Greg and Hans) is probably not the way to go. Adding another short paragraph in the introduction about deeper issues (without getting too technical) could be a good idea. Oleg Alexandrov (talk) 04:02, 6 February 2008 (UTC)
- I agree that the first sentence is not the place for fine points. What about simply "In mathematics, a set is a collection of distinct objects." — Carl (CBM · talk) 04:46, 6 February 2008 (UTC)
- Going beyond naive set theory is a worthy goal. However, starting the article with a rather obfuscated first sentence (sorry Greg and Hans) is probably not the way to go. Adding another short paragraph in the introduction about deeper issues (without getting too technical) could be a good idea. Oleg Alexandrov (talk) 04:02, 6 February 2008 (UTC)
- I have to concur with the position that the introductory sentence should not be intimidating and should not be the result of a complex compromise between mathematicians and philosophers. If need be, a sentence can be added to point out that formal definitions of the notion can be tricky but the development of these ideas should be explained later in the article. Linking to Object (philosophy or abstract object is a bad idea. Most readers come in thinking they have a good intuitive idea of what a set is and are told from the get go "you're not even close, you moron". Pichpich (talk) 19:30, 6 February 2008 (UTC)
- When I tried reading David Hume's A Treatise of Human Nature for the first time at age 16, right from the "get go" I got the message "you're not even close, you moron." This turned out to be one of the most intellectually edifying experiences in my life, forcing me to new educational heights. Some subjects are just plain harder than others; and for many people, higher mathematics is one such subject.
- That said, I like Hans Adler's suggestion best from the list above, though we might also consider:
- In mathematics, a set is any abstract object consisting of a collection of distinct (abstract or concrete) objects.
- That said, I like Hans Adler's suggestion best from the list above, though we might also consider:
- However, Carl raises a good point about the status of realism in mathematics. While I may think that such realists are misguided, it is surely not a settled issue. And if they are correct, then no mathematical objects are abstract (unless, of course, a mind independent realm of mathematical forms would still count as abstract in a relevant sense—a very real possibility). Given this, we might consider:
- In mathematics, any collection of distinct objects can be treated as a new object, called a set. [rewrite of Hans' version]
- In mathematics, a set is any object consisting of a collection of distinct (abstract or concrete) objects. [rewrite of my version]
- Regardless, I find the "traditional version" unnecessarily awkward, and I think it would be appropriate to replace it. Postmodern Beatnik (talk) 16:23, 13 February 2008 (UTC)
- Try to think from the point of view of the reader who never heard of sets before. Tell him in plain language what a set is. Trying to go to the fine points before even giving the reader a chance to get an idea about the topic is not good I think. Oleg Alexandrov (talk) —Preceding comment was added at 03:35, 14 February 2008 (UTC)
- Well, I'm not a mathematician and I'm not confused by calling a set an abstract object. Indeed, I doubt the concept of being an abstract object is too difficult for a reasonably intelligent person. And the lead section is supposed to sum up the article. If the bottom line on sets is that they are abstract objects consisting of a collection of other objects (either abstract or concrete) then that's what the lead section should say. Postmodern Beatnik (talk) 20:21, 19 February 2008 (UTC)
- You're trying to put too many ideas in one sentence. Again, that's too much to swallow to somebody who never talked about sets before. You're very welcome to add a second paragraph to the introduction elaborating on the abstractness issue, it just should not be in the first sentence. Oleg Alexandrov (talk) 05:23, 20 February 2008 (UTC)
- Well, I'm not a mathematician and I'm not confused by calling a set an abstract object. Indeed, I doubt the concept of being an abstract object is too difficult for a reasonably intelligent person. And the lead section is supposed to sum up the article. If the bottom line on sets is that they are abstract objects consisting of a collection of other objects (either abstract or concrete) then that's what the lead section should say. Postmodern Beatnik (talk) 20:21, 19 February 2008 (UTC)
- Try to think from the point of view of the reader who never heard of sets before. Tell him in plain language what a set is. Trying to go to the fine points before even giving the reader a chance to get an idea about the topic is not good I think. Oleg Alexandrov (talk) —Preceding comment was added at 03:35, 14 February 2008 (UTC)
- However, Carl raises a good point about the status of realism in mathematics. While I may think that such realists are misguided, it is surely not a settled issue. And if they are correct, then no mathematical objects are abstract (unless, of course, a mind independent realm of mathematical forms would still count as abstract in a relevant sense—a very real possibility). Given this, we might consider:
I have given ten diverse sources that identify a set as an abstract object. There are sources here from mathematical logic, and various other disciplines which would seem to elevate the appropriate level of emphasis.
- Identifying a particular abstract object and calling it an "abstract object" helps us understand something fundamental about the object, and makes it possible for us to talk about it intelligently.
- There is nothing "misleading" about calling a set an "abstract object." The opposite is true: we are leading people to think appropriately about this concept by identifying it as such.
- The "set" is probably the most famous "abstract object" there is. In almost any account of what is an abstract object, the "set" is usually given as the first example, or portrayed as the paragon of an example of such.
- At least one of these references opens a chapter "A set is an abstract object."
I hope we can see our way to working with it. Be well. Pontiff Greg Bard (talk) 10:23, 4 March 2008 (UTC)
- As I pointed out above, those who advocate realism in mathematics (such as Penelope Maddy did, at least at one point) say that sets are not abstract objects, but concrete ones. The abstract/concrete nature of sets would be well served by a paragraph in the article, but not by a single sentence in the lede that glosses over the issue or treats it as settled. Also, I'll point out that there are very few other mathematics articles that begin by pointing out that the obejcts at hand are abstract. We don't see:
- A ring (mathematics) is an abstract object..
- A fibre bundle is an abstract object..
- A category (mathematics) is an abstract object...
- and so on.
- I started that section on the nature of sets; I'm sure it can be filled out some more. I changed the lede to refer down to that section, and to point out that the issue of abstractness is not completely clear. — Carl (CBM · talk) 14:25, 4 March 2008 (UTC)
- The lede looks all right. I'm just glad this is in there pretty close to the start. In the case of these others you mention, I would point out that not every abstract object needs to be explicated in this way, however some of the most important ones should be. In the case of ring I notice that there are wikilinks as follows:
- ring --> Algebraic structure --> set --> abstract object
- This type of arrangement is fine with me. This way people have a chance of nailing this down if they explore deeply enough. Pontiff Greg Bard (talk) 00:12, 5 March 2008 (UTC)
- The thing is looking pretty good in my view. My only notes are the following: "In philosophy" implies that there is some world of philosophy that is separate from the rest of the world. This is a general complaint I have about WP. If it is supposed to be true in one field or another it is supposed to be true for all rational beings (especially in logic!) I think we should find some other way to insert a wikilink to mathematics, or logic or whatever; otherwise it just seems like a gratuitous way to insert "philosophy" into the article which I don't see as necessary. The other issue I am observing, but in which I do not have any special knowledge is the Maddy position. It doesn't say in her article that she believes sets are concrete, it says "can be." I was not able to make the stronger statement as it is worded now because of that. If you are sure, then that's that for me Carl. Are you absolutely sure? Her position doesn't make complete sense to me as presented (but that's ok). Be well, Pontiff Greg Bard (talk) 23:57, 12 March 2008 (UTC)
- A key role of the lede is to establish context. The term "abstract" is not used here in the naive English meaning, but the specialized meaning from philosophy. Compare other mathematics articles, for example center (group) which starts out "In abstract algebra..." even though abstract algebra is the only setting in which the center of a group is studied.
- I seem to remember some of Maddy's book is on google books. I am no expert in her philosophy, but I can get the book from the library and look at it. — Carl (CBM · talk) 01:40, 13 March 2008 (UTC)
- Well I don't see this "set" edit as the beginning of a revolution in rearranging every lede of all the articles that begin that way. However, I think we should use that format in some places, and not others. "In food science, a sandwich is ..." would be ridiculous. I think other people enjoy sets other than mathematicians. So that's my perspective on why I think it's an issue. Pontiff Greg Bard (talk) 03:56, 13 March 2008 (UTC)
- Constructions like "In rocket science, lettuce is any green plant other than eruca sativa" are a bit strange, but then large bodies of text like encyclopedias are allowed to have some idiosyncracies. In this case the qualifier "in philosophy" is appropriate because when people think about whether sets are abstract or concrete they are really doing philosophy, and without the qualifier readers might think that mathematicians (as such) are concerned about this. They are not. I think most of us are not interested in such points at all. This is not something we teach, or read or write about, and at least in my experience it is also not something we talk about at parties. I think raising the issue in the lede of set (mathematics) at all gives it undue weight, but I don't object so long as it is properly qualified so that people know they needn't look up the meaning of "abstract" just to understand one of the most fundamental notions in mathematics. --Hans Adler (talk) 08:18, 13 March 2008 (UTC)
Preserved histories
Set (mathematics)
* (cur) (last) 22:23, 17 September 2008 Redirect fixer (Talk | contribs | block) (32 bytes) (Set has been moved; it now redirects to Set (mathematical).) (rollback | undo) * (cur) (last) 17:35, 18 April 2002 AxelBoldt (Talk | contribs | block) (Moving back to Set) (undo) * (cur) (last) 12:12, 9 April 2002 Zundark (Talk | contribs | block) (moved from Mathematical_set) (undo) * (cur) (last) 23:20, 2 April 2002 Toby (Talk | contribs | block) m (undo) * (cur) (last) 00:34, 27 March 2002 213.253.39.214 (Talk | block) (Russell's paradox) (undo) * (cur) (last) 00:33, 27 March 2002 213.253.39.214 (Talk | block) (Russell's Paradox) (undo) * (cur) (last) 10:21, 26 March 2002 -- April (Talk | contribs | block) m (move math useage here)
— Preceding unsigned comment added by Dcoetzee (talk • contribs) 23:45, 17 September 2008 (UTC)
Move
User:DionysosProteus has rather boldly moved set to set (mathematical) and redirected set to set (disambiguation). Now I admit it's not completely implausible that set should be a disambiguation page, but I think it was a bit excessive to suddenly move a long-standing article with no discussion.
Anyway here are my specific concerns:
- Yes, set has a huge number of meanings, but most of them are rather marginal as topics for an encyclopedia article. I'd go so far as to say that the mathematical meaning is the one, by an enormous margin, most worthy of an article. This is a bit reminiscent of the QED debate — quantum electrodynamics is not the meaning most known to most people, but it is by far the one most important to treat in an encyclopedia article.
- Even if the move were correct, the name set (mathematical) is wrong; by WP convention it would be set (mathematics).
- Similarly, if set is to point to the disambiguation page, then the disambiguation page should simply be called set, not set (disambiguation). --Trovatore (talk) 22:35, 17 September 2008 (UTC)
- I was bold? Wikipedia told to be so. Points 2 & 3 are fine but #1 isn't. Sets on films and in theatres, the sets of a tennis match, and a DJ's set are not marginal meanings. I would think it's doubtful that something like a "head-count" of instances in which most people use the word in everyday life would bring its mathematical usage out on top. Not sure by what critera the mathematical meaning is more significant for an encyclopedia than these cultural definitions. Mathematics is more "important" than Drama or the Cinema? Not sure what evidence would settle the question either way. I should think that the first line of the disambig page: "Set has 464 separate definitions in the Oxford English Dictionary, the most of any English word; its full definition comprises 10,000 words making it the longest definition in the OED" should argue for a disambig at Set. DionysosProteus (talk) 22:45, 17 September 2008 (UTC)
- I think Trovatore's point was that it's not everyday usage that matters, it's encyclopaedic value. For example, no-one would write an article on tennis sets (we have one on tennis scoring which discusses the concept) even though they are probably talked about more often than mathematical sets. --Tango (talk) 22:50, 17 September 2008 (UTC)
- Everyone thinks that WP:BOLD is a license to try anything. Fewer have actually read the guideline. Please read it. Geometry guy 23:05, 17 September 2008 (UTC)
- It pretty much is a license to try anything, as long as you don't mind people reverting you. --Tango (talk) 23:17, 17 September 2008 (UTC)
- So you haven't read it either, then. Geometry guy 23:22, 17 September 2008 (UTC)
- For a radical edit, the bold-revert-discuss protocol would be fine here. The move ought to be reverted pending discussion (even though, as I say, it's not implausible that the discussion would come out in favor). But now that can't be done without admin-deleting set. That's why WP:BOLD specifically mentions page moves as a place to be careful. --Trovatore (talk) 23:24, 17 September 2008 (UTC)
- It pretty much is a license to try anything, as long as you don't mind people reverting you. --Tango (talk) 23:17, 17 September 2008 (UTC)
- Everyone thinks that WP:BOLD is a license to try anything. Fewer have actually read the guideline. Please read it. Geometry guy 23:05, 17 September 2008 (UTC)
- I think Trovatore's point was that it's not everyday usage that matters, it's encyclopaedic value. For example, no-one would write an article on tennis sets (we have one on tennis scoring which discusses the concept) even though they are probably talked about more often than mathematical sets. --Tango (talk) 22:50, 17 September 2008 (UTC)
- I was bold? Wikipedia told to be so. Points 2 & 3 are fine but #1 isn't. Sets on films and in theatres, the sets of a tennis match, and a DJ's set are not marginal meanings. I would think it's doubtful that something like a "head-count" of instances in which most people use the word in everyday life would bring its mathematical usage out on top. Not sure by what critera the mathematical meaning is more significant for an encyclopedia than these cultural definitions. Mathematics is more "important" than Drama or the Cinema? Not sure what evidence would settle the question either way. I should think that the first line of the disambig page: "Set has 464 separate definitions in the Oxford English Dictionary, the most of any English word; its full definition comprises 10,000 words making it the longest definition in the OED" should argue for a disambig at Set. DionysosProteus (talk) 22:45, 17 September 2008 (UTC)
Support move but fix up with proper names: Set (mathematics) for maths version and Set for disambig page. I don't think there is an overwheling case for the mathematical meaning being overwhelmingly the most significant. Last month views were Set 28748, Set_(mythology) 18911. It will be a pain to fix all the redirects, but I can't see a long term problem. --Salix alba (talk) 23:38, 17 September 2008 (UTC)
- I was skeptical of this move, but I'm willing to entertain the possibility that the mythological meaning is common enough to support make the primary page a dab page. Dcoetzee 23:43, 17 September 2008 (UTC)
- Given the large number of meanings of set, I'm willing to buy the arguments thus far...but let me ask Salix alba to clarify his. Apple Inc. gets a comparable number of page views (83,500) compared to Apple (116,000); note this is a smaller disparity than pointed out for the examples of set. Should Apple thus become a disambiguation page? --C S (talk) 01:35, 18 September 2008 (UTC)
- That is a good point. I think the argument in that case goes the other way. Between apple and Apple computer, it's clear that the fruit is the "principal" meaning: the computer company is named after the fruit. No such argument applies in the case of mathematical sets, tennis sets, the Egyptian god of the dead, etc.
- Furthermore, the principle of least surprise argues for apple to refer to the fruit. A reader who arrives at apple hoping to find Apple Computer but who finds red fruit instead will instantly understand exactly what happened. But someone getting a mathematics article when they wanted the Egyptian god of the dead (or vice versa) is more likely to be puzzled and surprised.
- I don't know what Salix Alba's idea was, but that's how I would argue it. I hope this has been of some value. -- Dominus (talk) 03:55, 18 September 2008 (UTC)
- It has certainly convinced me that making Set a disambiguation page was a good idea. (Even though I think it was done a bit too boldly.) --Hans Adler (talk) 13:20, 18 September 2008 (UTC)
- The "Principle of least surprise" is something I can understand in establishing a "primary" meaning or lack of one. It's certainly a good argument to use here as in the case of apple and many others. That's why I'm willing to "buy" the move, even if the "primary" is just a wiktionary entry, that may be less surprising than being sent to a mathematics page. A disambiguation page certainly makes sense here. I think Salix Alba's page view argument, however, is a red herring. Just like the large number of people viewing Apple Inc may first find they are directed to Apple, it may be that the large number viewing the mythological set are fully aware why they were first sent to a mathematical article. Surprise is in the eye of the beholder. Perhaps it's natural to think the mathematical set is the least surprising of all the Wikipedia entries to be sent to, but I can't help but think most people would view a "collection" or disambiguation as the most natural result. --C S (talk) 10:25, 19 September 2008 (UTC)
I've now moved Set (disambiguation) to Set.--Salix alba (talk) 17:47, 19 September 2008 (UTC)
- This has created about a thousand incorrect links. Please fix them. (And next time, please fix them before doing the move.) --Zundark (talk) 18:11, 19 September 2008 (UTC)
- I'm going through them now, folks can help if they want (see AWB). Quite a few did not really want to link to Set (mathematics), many just want to link to the more general English word for collection rather than a more technical meaning and others want Set (computer science), a "set of cards". Philisophical and linguistic uses are the trickiest. --Salix alba (talk) 23:08, 19 September 2008 (UTC)
Box-fixing
I didn't think this was controversial, but when 95% of our readers use standard versions of IE with no extra fonts, I think it is us who should be conforming to their needs. IE does support empty set and intersection characters, but not union or subset. I've replaced any union characters with a capital U (which looks pretty good in a sans serif font) and I replaced some subset symbols with "is a subset of", and others with images using math tags. I'd advise similar practices be followed in other articles. Note that if you set your preferences to "HTML if possible", the formulas in math tags should be rendered correctly as HTML for people with browsers supporting all these characters. Deco 20:56, 11 July 2005 (UTC)
Box Fixing Redux
Someone PLEASE tell me we can do better than peppering the article with images to fix the "symbol/box/font" problem! Unicode should be ubiquitous by now. Can not everyone read these symbols? ⋂ ⋃ ∈ ∉ —24.176.175.202 (talk • contribs) 15 January 2008
- Hello. I am using IE 7.0, and all of those symbols appear as boxes.
- --Bob K (talk) 14:32, 19 January 2009 (UTC)
- Eureka! I just changed Times New Roman to Lucida Sans Unicode in a pull down menu at Tools -> Internet Options -> Fonts -> Webpage Font:, and now the symbols work.
- --Bob K (talk) 14:49, 19 January 2009 (UTC)
It never ends
Quote from NBG theory:
Category theory
The ontology of NBG provides scaffolding for speaking about "large objects" without risking paradox. In some developments of category theory, for instance, a "large category" is defined as one whose objects make up a proper class, with the same being true of its morphisms. A "small category", on the other hand, is one whose objects and morphisms are members of some set. We can thus easily speak of the "category of all sets" or "category of all small categories" without risking paradox. Those categories are large, of course. There is no "category of all categories" since it would have to contain the category of small categories, although yet another ontological extension can enable one to talk formally about such a "category" (see for example the "quasicategory of all categories" of Adámek et al (1990), whose objects and morphisms form a "proper conglomerate"). On whether an ontology including classes as well as sets is adequate for category theory, see Muller (2001).
/quote
The 3 main paradoxes of set theory (Cantor Burali-Forti Russel's) have caused people to develop axioms to avoid such abominations. However to me, and I believe many other people, it still seems appropriate to use unrestricted comprehension on collections. So for this matter it is sensible to talk about the "hyper-set" of all sets (which is simply a dupe for class), and "hyperclass". If we take the empty set in von Neumann's universe construction to be the von Neumann universe, and naively assume "power collections" exist (I'm not sure if this can be put into an axiom), it's highly intuitive to think of the "2nd von Neumann universe" as the hyperclass of all classes. Now we don't have to end here. Indeed for any successor ordinal α we can define a hyper-α-class from the previous ordinal, and for limit ordinals define the hyper-α-class to be the union of all hyper-β-class where β<α. What we have now is a von Neumann universe of hyper von Neumann universes. Again, why stop here? We can keep going and going and whenever you suggest something that contains "everything" we can go further... It never ends. Any comments?--Standard Oil (talk) 03:48, 20 February 2009 (UTC)
- The talk page is for discussion about improvements to the article (see WP:TALK). This material is not suitable for inclusion because it is not the subject of a reliable, published source on set theory (see Wikipedia:No original research). Dcoetzee 03:54, 20 February 2009 (UTC)
Which is it?
These sentences:
For instance, the set of real numbers has greater cardinality than the set of natural numbers. However, it can be shown that the cardinality of (which is to say, the number of points on) a straight line is the same as the cardinality of any segment of that line, of the entire plane, and indeed of any finite-dimensional Euclidean space.
Seem to be in contradiction. The first asserts that |N| is less than |R|, but the second seems to explain why that wouldn't be the case because the cardinality of a segment of a line is the same as the cardinality of the whole line. Am I reading this wrong? —Memotype::T 00:00, 12 March 2009 (UTC)
- Every segment of a line that is nontrivial in the sense that it contains more than one point has the same cardinality as R. Did you confuse "segment" with "sequence"? --Hans Adler (talk) 00:45, 12 March 2009 (UTC)
- No, but what you just said contradicts the assertion that the set of real numbers has greater cardinality as the set of natural numbers — both are equally infinite, no?. —Memotype::T 03:56, 12 March 2009 (UTC)
- No. Where do you see a contradiction in what Hans said? The set of natural numbers is not a segment of the real line, so the fact that every nontrivial segment (interval) taken from the line has the same cardinality as the line itself, does not contradict the fact that that cardinality is strictly greater than the cardinality of the naturals. --Trovatore (talk) 07:42, 12 March 2009 (UTC)
- The cardinality of an infinite subset of the line has nothing to do with whether it stretches infinitely in one or both directions. The only thing that matters (for the kind of tame subsets we usually have in mind) is whether it contains a full segment. In fact, for any such segment it's easy to transform it into the full line, in such a way that for every point in the full line there is exactly one point in the segment. --Hans Adler (talk) 08:43, 12 March 2009 (UTC)
- No, but what you just said contradicts the assertion that the set of real numbers has greater cardinality as the set of natural numbers — both are equally infinite, no?. —Memotype::T 03:56, 12 March 2009 (UTC)
- I kind of see, but I'm still a bit confused. When we say "cardinality" we mean the number of members in a set, right? The number of members in the set of natural numbers is infinite, and so it the number of members in the real numbers set, no? Thus, how does it make sense to say the cardinality of natural numbers is less than the cardinality of real numbers? —Memotype::T 22:47, 12 March 2009 (UTC)
- Both are infinite, but the set of reals is a bigger sort of infinite. A lot of people have a preconceived notion that there's no such thing as "a bigger sort of infinite", but there is, there really really is. You have to unlearn that prejudice and move on. --Trovatore (talk) 00:59, 13 March 2009 (UTC)
- Actually, I don't agree with that because it's a platonist statement. The "bigger sort of infinite" is only a fiction that is convenient (perhaps even necessary) for mathematicians. It doesn't really reflect any phenomena that we can observe in the real world; after all, so far as we know the universe is really finite, i.e. it has finite diameter and contains only a finite number of particles etc. In the real world, even a line segment contains only finitely many distinguishable points. But if we want to talk about all natural numbers, we need infinity, and if we want to talk about all sets of natural numbers we need the "bigger sort of infinity". Without being able to talk about these things we mathematicians would be deprived of most of the beautiful objects that we are studying. --Hans Adler (talk) 02:27, 13 March 2009 (UTC)
- I am, of course, speaking as a mathematical realist (sometimes imprecisely called Platonist). --Trovatore (talk) 05:15, 14 March 2009 (UTC)
- Perhaps it would be better to say "it's a bigger infinite cardinal", which is an extremely well defined concept, unlike "infinity". It's far easier just to say "infinity" and assume people can work out what you mean from context, though. --Tango (talk) 21:27, 14 March 2009 (UTC)
- Actually, I don't agree with that because it's a platonist statement. The "bigger sort of infinite" is only a fiction that is convenient (perhaps even necessary) for mathematicians. It doesn't really reflect any phenomena that we can observe in the real world; after all, so far as we know the universe is really finite, i.e. it has finite diameter and contains only a finite number of particles etc. In the real world, even a line segment contains only finitely many distinguishable points. But if we want to talk about all natural numbers, we need infinity, and if we want to talk about all sets of natural numbers we need the "bigger sort of infinity". Without being able to talk about these things we mathematicians would be deprived of most of the beautiful objects that we are studying. --Hans Adler (talk) 02:27, 13 March 2009 (UTC)
- Both are infinite, but the set of reals is a bigger sort of infinite. A lot of people have a preconceived notion that there's no such thing as "a bigger sort of infinite", but there is, there really really is. You have to unlearn that prejudice and move on. --Trovatore (talk) 00:59, 13 March 2009 (UTC)
- I kind of see, but I'm still a bit confused. When we say "cardinality" we mean the number of members in a set, right? The number of members in the set of natural numbers is infinite, and so it the number of members in the real numbers set, no? Thus, how does it make sense to say the cardinality of natural numbers is less than the cardinality of real numbers? —Memotype::T 22:47, 12 March 2009 (UTC)
Determinate member?
Is there such a thing? I expect there is, and I've got the name wrong. What I mean is a set with various members, but with one dominant (is that the word) member, a member which if taken away means the set no longer exists, even if all the rest are still there. Is such a collection then in fact a set? I'm thinking of the Solar System which is defined as, "The Solar System consists of the Sun and all those objects bound to it by gravity". Which, I think, is an intensional definition. Of course if you take the Sun away, that is the same as taking everything else away, and the set still exists - it's just the Sun with an empty set of objects orbiting it. Anyway, you can see I don't usually work with any mathematics, but I hope I have enough intuition to understand simpler answers on this!! HarryAlffa (talk) 15:46, 8 May 2009 (UTC)
- The term doesn't exist and the concept makes no sense. Removing any member of a set always gives a set as a result. Examples: {a,b, c} \ {a} = {b, c}, {a} \ {a} = the empty set. Removing the Sun from the set consisting of the Sun and all objects bound to the Sun by gravity, gives the set of all objects bound to the Sun by gravity. Paul August ☎ 20:00, 8 May 2009 (UTC)
- I thought I'd pretty much expressed the same thing on removing members from the set - or at least tried to! The Intensional definition is, "The Solar System consists of the Sun and all those objects bound to it by gravity". What can be said of the Sun in this set, besides being a member? I think this is the question behind my ignorant musings. HarryAlffa (talk) 20:25, 8 May 2009 (UTC)
- In talking of the Solar System I'm wondering if saying, "The Sun determines the Solar System", means what I think it means - and can I link the word "determines" to a nice article in the Set Theory category? HarryAlffa (talk) 20:25, 8 May 2009 (UTC)
- You are talking about aspects that mathematicians usually ignore; from a mathematical point of view an intensionally defined set is exactly same set as the extensionally defined set with the same elements. (See axiom of extensionality.) It's not at all clear what "taking the Sun away" is supposed to mean on the level of abstraction on which mathematicians work. Presumably you mean you are changing the world somehow, but before you have clarified everything a mathematician can't really say much about your problem. Thinking about the possible clarifications, or pretending that they are unnecessary and trying to get away with it, all of this is in the domain of philosophy, while this is primarily a mathematical article and if you ask a question here you are most likely to get responses from mathematicians. --Hans Adler (talk) 20:45, 8 May 2009 (UTC)
- Well, I would quibble with some details. The distinction between extensional and intensional collections is actually quite important to mathematicians — it's precisely the confusion between them that leads to the classical antinomies, such as Russell's paradox. Roughly speaking, sets are extensional (arbitrary lists of things where you don't care about their order or multiplicity), whereas classes are intensional (defined by a rule). Sometimes the intensional notion comes up implicitly, as when you have a code for a Borel set, and for certain purposes you want to consider the sets coded by that code in different models as being "the same", even though they don't have the same elements.
- However I agree with Hans that sets as mathematicians think about them don't typically involve physical objects such as the Sun. --Trovatore (talk) 21:13, 8 May 2009 (UTC)
- The difference between extensional and intensional definitions becomes important when you have a "functorial" situation in the widest sense, e.g. when you extend or restrict your set-theoretical universe. HarryAlffa's question seems to be related to this, but it's way too vague to be sure. And in any case I am not away of any such notion of "determining", under any name, in set theory (for which I am not an expert, though). --Hans Adler (talk) 21:45, 8 May 2009 (UTC)
- There at least I agree with you: I can't think of any way to interpret the phrase the Sun determines the Solar System with a technical set-theoretic notion of determine. --Trovatore (talk) 22:00, 8 May 2009 (UTC)
- The difference between extensional and intensional definitions becomes important when you have a "functorial" situation in the widest sense, e.g. when you extend or restrict your set-theoretical universe. HarryAlffa's question seems to be related to this, but it's way too vague to be sure. And in any case I am not away of any such notion of "determining", under any name, in set theory (for which I am not an expert, though). --Hans Adler (talk) 21:45, 8 May 2009 (UTC)
- You are talking about aspects that mathematicians usually ignore; from a mathematical point of view an intensionally defined set is exactly same set as the extensionally defined set with the same elements. (See axiom of extensionality.) It's not at all clear what "taking the Sun away" is supposed to mean on the level of abstraction on which mathematicians work. Presumably you mean you are changing the world somehow, but before you have clarified everything a mathematician can't really say much about your problem. Thinking about the possible clarifications, or pretending that they are unnecessary and trying to get away with it, all of this is in the domain of philosophy, while this is primarily a mathematical article and if you ask a question here you are most likely to get responses from mathematicians. --Hans Adler (talk) 20:45, 8 May 2009 (UTC)
Ok! Thanks guys! I got interested if there was some concept of the sort I've tried to describe, but this is a side-track really of my real-world first desire of providing an explanation of my use of the word determines in, "The Sun determines the Solar System". What I'm trying to convey here is that it's the properties of the Sun from which all the other properties of the Solar System flow; if the Solar mass was different, then the orbits of all the planets would be different etc. etc. I think that's what my use of determines means here, and I think it's a nice way of putting it. Does it make sense to describe, as an intensional definition, "The Solar System consists of the Sun and all those objects bound to it by gravity"? In short, does anything in Set theory have anything informative to convey to an ordinary reader about these two phrases? Or indeed that they are correct phrases to use? I hope I'm not boring you with this! HarryAlffa (talk) 15:25, 9 May 2009 (UTC)
- I think what you are looking for is a map (mathematics) (or "function"). Most non-mathematicians are only used to functions from numbers to numbers, but the concept is much more general. Consider the map f that associates to every object x the set f(x) of all objects that are bound to x by gravity. Then the Solar System is f(Sun). This map makes some of your assumptions explicit. --Hans Adler (talk) 15:39, 9 May 2009 (UTC)
- Ah! That sounds like an exact answer for the definition! I will check it out forthwith! HarryAlffa (talk) 18:10, 9 May 2009 (UTC)
- You've pretty much described the function above, and I understand that, I'm not sure about linking to function though for the definition, I think the intensional definition would be more accessible to a general reader. HarryAlffa (talk) 18:21, 9 May 2009 (UTC)
- Honestly, sorry to argue with Hans, I don't see that it addresses the issue at all. Functions also can be viewed from an intensional or extensional perspective, and they are quite different things: An extensional function, the kind we mostly deal with in set theory, is an arbitrary association between objects, whereas an intensional one is a rule for picking out an object given an object. --Trovatore (talk) 18:24, 9 May 2009 (UTC)
Venn diagrams
I changed some graphics in the article from files like this  into files like this
into files like this  .
.
Using several (maybee more beautiful) colours, the old diagrams are less clear than those simply using white and red. The reality knows only two possibilities: An area belongs to the set or not. There is nothing in between, and the diagrams should reflect that.
All the more, most of the old diagrams lack the margin standing for the universe. For a blackboard scetch this might be acceptable, but not for an encyclopedia. A set diagram without a universe is simply false - not only for sets containing the intersection of both complements.
--Tilman Piesk (talk) 20:48, 2 February 2008 (UTC)
- Apart from the original slides being prettier, I find them more clear since the background and foreground have different colors. Oleg Alexandrov (talk) 01:02, 3 February 2008 (UTC)
- This discussion is based on a unfortunately common confusion between the work of Leonhard Euler (viz., the Euler diagram) and the work of John Venn (viz., the Venn diagram).
- Euler diagrams, in every application, have no "margin standing for the universe".
- By contrast, the defining and specific feature of a Venn diagram is the presence of "margin standing for the universe" (it must be understood that, historically, Venn diagrams are Euler-diagrams-as-improved-by-Venn).
- Thus, any claim that a set of circles, standing alone, with no surrounding margin, is a "Venn diagram" is not only plainly wrong but is, also, a sign of complete ignorance of the history, significance, graphic conventions, and the application of such diagrams -- all of which were, in their origin, attempting to improve on the conventions for graphical representations of logical reasoning statements that had been first proposed by Gottfried Leibniz. Thus, it is obviously imperative that:
- (1) Anything labelled Venn diagram must have a "margin standing for the universe"; and
- (2) Anything that does not have a "margin standing for the universe" must be labelled a Euler diagram.149.171.240.78 (talk) 02:16, 3 February 2008 (UTC)
- Is this A\B? Is A on the right?
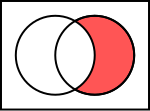
- Since "relative complement"/"set-theoretic difference"/"subtraction" is not a symmetric, it is important to label A and B. To me, the graphic intuitively looks like B\A, not A\B.
- mjk (talk) 10:01, 25 January 2010 (UTC)
- I've changed to the A\B diagram and changed the comment below so it goes with the text beside it. Dmcq (talk) 12:58, 25 January 2010 (UTC)
Blackboard Bold vs Bold
I don't know if this is a degeneration led from the web, but I've never seen the noted sets (such as ) represented by anything other than blackboard bold before. Why is mere embolding (such as N) being treated as the preferred font? NathanZook (talk) 02:25, 21 April 2010 (UTC)
- Bold alone was the traditional way, actually; blackboard bold was not available in professional typesetting until TeX. In this case, there are two concerns:
- Almost everyone can see bold letters in their browser, but people may not have fonts with blackboard bold characters. So we would have to use images to display blackboard bold, which looks worse than just bold. See WP:MOSMATH#Blackboard_bold for more on this
- This article is meant for a very general reader, who will probably not be familiar with blackboard bold anyway.
- I am sure that we have some Wikipedia articles that use blackboard bold; it's very hard to ensure 100% consistency. But regular bold seems like the best choice here. — Carl (CBM · talk) 02:53, 21 April 2010 (UTC)
Special characters template
We don't usually add the {{SpecialChars}} template to mathematics articles. This template contradicts the WP:LAYOUT guideline, and to the best of my knowledge no guideline whatsoever even suggests using the special characters template. So I have removed it (for the third time) from this article. If it really truly belongs here, then a special case needs to be made for adding it to this article (as opposed to the many other mathematics articles on Wikipedia). My opinion is that the template should only be added if it serves some encyclopedic value, e.g., if a significant portion of the article in question is actually about a character set. In the case of this article, its presence disrupts the contents of the article, and should be removed. Sławomir Biały (talk) 11:50, 14 May 2010 (UTC)
English name for set
Recently I am reading some older sources about the set theory (specially Huntington's The Continuum..., and Jourdain's translation of few Cantor's famous 1895–7 articles (ISBN 978-0486600451)). I see that authors use different names for set {Huntington - "class"; Jourdain - "aggregate"), and I guess that name "set" came into English later, of course most probably from German 'Cantorian' original die Mendge'. Is this true, and is it known when this naming was first used? I have also to figure it out, when name for set was first used, (and by whom) in my native language. --xJaM (talk) 13:55, 21 January 2011 (UTC)
Limits of subsets
It is usefull to know that A_{n} \uparrow A means A_{n} \supseteq A_{n+1} and A = \bigcup_{n=1}^{\infty}A_{n}. Simirarly A_{n} \downarrow A means A_{n+1} \supseteq A_{n} and A = \bigcap_{n=1}^{\infty}A_{n}. —Preceding unsigned comment added by Boucekv (talk • contribs) 11:24, 5 May 2011 (UTC)
Sets in Statistics
I have just come across Sets in Statistics while patrolling new pages. A lot of the content looks to be duplicated with this article, but might there be something to be gained from a merge? Best — Mr. Stradivarius ♫ 10:40, 21 December 2011 (UTC)
Well-defined sets
I have deleted some examples that are not aligned with the well-definedness of sets: For example, A = {1, 2, red} does not constitute a set under a well-defined universal set. The union or intersection with such a set is not well-defined, either. — Preceding unsigned comment added by 139.179.156.138 (talk) 12:22, 29 September 2013 (UTC)
- It's been a while since you wrote that, but it is a well-defined set in the universe of (a) numbers and colors or (b) strings of ASCII characters. — Arthur Rubin (talk) 09:11, 25 March 2014 (UTC)
Confusing part about uniqueness of sets
As someone who's just learning set theory, I found this part of the article confusing: "Every element of a set must be unique; no two members may be identical. (A multiset is a generalized concept of a set that relaxes this criterion.) All set operations preserve this property. The order in which the elements of a set or multiset are listed is irrelevant (unlike for a sequence or tuple). Combining these two ideas into an example
- {6, 11} = {11, 6} = {11, 6, 6, 11}"
The right-hand side of this equation certainly looks to me like something that violates the uniqueness property. If it's not just me that finds that notation confusing, perhaps someone could add an extra line explaining it... — Preceding unsigned comment added by Monsterman222 (talk • contribs) 08:12, 25 March 2014 (UTC)
- The elements of a set are unique, so the representation is not unique. I don't knowhow to expalin it, though. Any ideas? — Arthur Rubin (talk) 09:12, 25 March 2014 (UTC)
Bolzano and the term "set"
Article sez:
- The term "set" was coined by Bolzano in his work The Paradoxes of the Infinite.
Is that really accurate? Bolzano was writing in German. Assuming he did in fact coin the term (a point for which I have no independent confirmation but am willing to believe), the term he coined was not "set" but Menge. Right? And the translation from Menge in German to "set" in English is not so canonical that another word might not have been chosen. For example, English wiktionary gives 1. quantity 2. crowd 3. (mathematics) set. I'm not saying Bolzano's contribution here should be overlooked, but I think it may be a little imprecise to say he coined the term "set". --Trovatore (talk) 22:25, 30 April 2014 (UTC)
- I have made an edit that addresses this problem. It's certainly possible that a more elegant solution exists. --Trovatore (talk) 22:44, 30 April 2014 (UTC)
mathematicks
3 kinds of set — Preceding unsigned comment added by 210.4.62.23 (talk) 10:13, 5 June 2014 (UTC)
3kinds of set
3 kinds of set — Preceding unsigned comment added by 210.4.62.23 (talk) 10:15, 5 June 2014 (UTC)
Definition
I'm happy with the first conjunct of
- the notion of a "set" is taken as an undefined primitive in axiomatic set theory, and its properties are defined by the Zermelo–Fraenkel axioms
but not the second. There are set theories other than Zermelo–Fraenkel! 86.177.102.36 (talk) 18:14, 26 April 2015 (UTC)
- Indeed, axiomatic set theory can be something else than Zermelo-Fraenkel. Correcting. Ladislav Mecir (talk) 23:05, 15 September 2016 (UTC)
Cantor and paradoxes (again)
This seems to come up over and over, and in fact several of our articles (the worst is probably naive set theory) are seriously problematic on this point.
It is not in fact at all clear that Cantor's informal conception of set, correctly understood, leads to the classical antinomies (the Russell paradox, the Cantor paradox, the Burali-Forti paradox). Gottlob Frege's system was definitely refuted by these paradoxes, but Cantor's was not precisely enough stated to make it clear one way or the other. If you read Contributions to the Foundation of the Theory of Transfinite Numbers, with a bit of historical perspective/bias, it seems very like what would later be called the von Neumann hierarchy, which does not (as far as anyone knows) admit the paradoxes.
Wang Hao took the position that Cantor's theory was not paradoxical. Maria Frápolli, as I understand it, claims to identify a progression in Cantor's thought, with an earlier theory that was paradoxical, and a later one that may not have been.
In any case, while it is not clear that "a gathering together of definite objects of our perception" is paradoxical, what is clear is that it is not a formal mathematical statement, and that by itself probably justifies the claim that it was "inadequate for formal mathematics", as our article states. --Trovatore (talk) 08:22, 16 September 2016 (UTC)
- Does it anywhere say here that Cantor's informal conception of set leads to the classical antinomies (the Russell paradox, the Cantor paradox, the Burali-Forti paradox)? Naive set theory seems to be fairly neutral on that point. The mentioned problems definitely arise when unrestricted comprehension is assumed. Perhaps this should be pointed out. But drawing conclusions these days that Cantor's theory way not paradoxical is just as ridiculous as claiming the opposite (since Cantor wasn't precise enough for anyone to draw conclusions). Cantor was a hero, but not a prophet. I think it would be wrong if the words "paradox" and Cantor are disallowed in the same article. YohanN7 (talk) 09:33, 16 September 2016 (UTC)
- I think that the statement is fine. Of course, there are plenty of references that claim Cantor's set theory was inconsistent as well, but as Yohan says we don't say anything about consistency in the article. We way that Cantor's definition was inadequate and that contemporary theories instead take "set" as an undefined notion. That claim seems fine to me: in fact, nobody uses Cantor's metaphysical approach anymore (no more "inconsistent multiplicities" etc) and instead "set" is treated as an undefined term. — Carl (CBM · talk) 11:37, 16 September 2016 (UTC)
- Sorry, I probably didn't give adequate context. I was explaining my revert of this edit. --Trovatore (talk) 17:17, 16 September 2016 (UTC)
Definition again
Recently, the lead was changed to say that a set is a well-defined collection of objects. I can accept that the article contains a section called "Definition", but going from there to say that it is well defined is too much. "Set" is an undefined primitive notion. A reference for this (if contested) could be Halmos. YohanN7 (talk) 10:06, 1 November 2016 (UTC)
I see now that the "definition" insists on "well-defined" too. Then it says "objects could be anything". Cantors "definition" of set does not boil down to "a thingie is a set if and only if this and that" in a well-defined manner. YohanN7 (talk) 10:06, 1 November 2016 (UTC)
- So first of all the claim in the article does not seem to be that the notion of set is well-defined, but rather that each individual set is well-defined.
- But actually that claim is less supportable. It can be argued that "set" is, if not well-defined, then at least well-specified, because of the canonical isomorphism between equal levels of the von Neumann hierarchy, however ∈ is interpreted. The statement as given, unfortunately, suggests that each individual set is determined by a defining formula, which is not true in any non-trivial sense.
- I think what Cantor wrote was neither one; rather, the objects of the set were supposedly "well-defined". But I don't think this meant they had definitions. It just meant that the objects were supposed to be particular things. A particular object in a set is not supposed to be one thing for me and a different thing for you, or one thing today and a different thing tomorrow. That's how I've always read it, anyway.
- In any case I agree that the current usage of "well-defined" is confusing (and also not supported by Cantor's phrase), and should be changed or removed. --Trovatore (talk) 17:27, 1 November 2016 (UTC)
- I think that reading "well-defined collection of objects" as a statement about definability of the set notion is a misunderstading. In my opinion, what Cantor meant by claiming that a set contains "definite" objects is that the set membership is definite, in other words, that the set is not "fuzzy". However, if the formulation causes this kind of misunderstanding, it is probably not optimal. Ladislav Mecir (talk) 20:15, 1 November 2016 (UTC)
- Yes, I think you and I are saying more or less the same thing here.
- This is the line from the Beiträge, as translated into English by Jourdain:
- By an "aggregate" (Menge) we are to understand any collection into a whole (Zusammenfassung su einem Ganzen) M of definite and separate objects m of our intuition or our thought.
- This is a formulation that actually holds up really well to the present day. I think it would be an excellent basis for the definition in this article, provided we scrupulously avoid inviting the inference that it in itself leads to the paradoxes (though the view that it does lead to them should certainly be discussed).
- I suspect that someone in the history of this article, or perhaps some writings that influenced someone writing this article, improperly reformulated "collection of definite objects" to "well-defined collection of objects". We should also make it clear that "definite" objects are not necessarily definable. --Trovatore (talk) 22:41, 1 November 2016 (UTC)
- I agree. It is not well-defined in any mathematical sense, but certainly not ill-defined either in any precise mathematical sense. It is just informal. Maybe also note somewhere that common axiomatic set theories make no attempt at a definition of "set" either. YohanN7 (talk) 10:02, 2 November 2016 (UTC)
- There are three separate things on the table here: (1) The well-defininedness of the notion of set; (2) the well-definedness of any particular set; (3) the objects being "definite and separate".
- I think whoever wrote the language in dispute was conflating (2) and (3), whereas you, Yohan, are conflating (1) and (2). But they are three completely separate things. --Trovatore (talk) 16:01, 2 November 2016 (UTC)
- Possibly. But I am actually referring to what I perceive of, in ordinary language, as the idea of set, not any particular set. Thus (1), not (2) if you ask me. I write "Set is an undefined primitive notion" in my first post, where I think I am clear about what I mean. Whether notion is an established concept different from ordinary language idea, I don't know. YohanN7 (talk) 13:30, 9 November 2016 (UTC)
- I acknowledge that my last sentence in my first post touches on item (2), but I hope I don't conflate the items
 . I am concerned mostly with item (1). YohanN7 (talk) 14:08, 9 November 2016 (UTC)
. I am concerned mostly with item (1). YohanN7 (talk) 14:08, 9 November 2016 (UTC)
- I agree. It is not well-defined in any mathematical sense, but certainly not ill-defined either in any precise mathematical sense. It is just informal. Maybe also note somewhere that common axiomatic set theories make no attempt at a definition of "set" either. YohanN7 (talk) 10:02, 2 November 2016 (UTC)
Adequacy
The text "Cantor's definition turned out to be inadequate for formal mathematics" is certainly true. However, in my opinion, it is also misleading. I think that the formulation "Cantor's definition turned out to be inadequate" is less misleading. Ladislav Mecir (talk) 07:29, 9 November 2016 (UTC)
- I don't entirely agree. Cantor's formulation in the Beitraege (at least, as translated by Jourdain) is essentially the modern conception, though less fully explained. To me that makes it problematic to say that it "turned out to be inadequate", especially if the reader assumes that the paradoxes are the reason it "turned out" that way — the paradoxes do not attach to this notion.
- It is true of course that those few words of Cantor are not really enough to do much with, without further explanation. At the very least, you need to talk about treating sets as individuals, and collecting them into other sets, and you need to explain the ordinals. If that's what you mean, I don't disagree. But the "turned out" wording is still problematic. Suggest another alternative, maybe? --Trovatore (talk) 21:43, 3 December 2016 (UTC)
- 'To me that makes it problematic to say that it "turned out to be inadequate"' - For the definition to be adequate, it should be useful as a criterium whether some object is a set. To that you note: "It is true of course that those few words of Cantor are not really enough to do much with". To confirm it, let's try: is the collection of all sets a set? If we consult Cantor's works, we may get Cantor's answer to this question. However, the formulation mentioned as "the Cantor's definition" in the article, i.e., the formulation you call "those few words" is not adequate for that. This is known and discussed in reputable sources. Ladislav Mecir (talk) 23:00, 3 December 2016 (UTC)
- By an "aggregate" {Menge) we are to understand any collection into a whole {Zusanivienfassung zu einem Ganzen) M of definite and separate objects m of our intuition or our thought.
- So no, the collection of all sets is not a set. In order to collect them into a whole, they have to be there in the first place. If you collect the ones you already have, then that is a new set, which was therefore not collected.
- In any case, I agree that this may not be entirely fully specified by that one sentence. But it is, I think, Cantor's intended conception, and it does avoid the paradoxes.
- My main concern here is to avoid giving the impression that the paradoxes are the reason this definition is "inadequate". If we can find a way to clearly avoid that, then it shouldn't be a problem. --Trovatore (talk) 00:07, 4 December 2016 (UTC)
- Notes:
- the term is Zusammenfassung
- "So no, the collection of all sets is not a set. In order to collect them into a whole, they have to be there in the first place." - you are trying to input your understanding of Cantor's work to the formulation. However, the formulation mentions "objects of our thought", and what forbids you, me, or anyone else to think about sets? Once we do, they are "objects of our thought", and no additional condition in the "few words" prevents you, me, or anyone else to ask whether their collection is a set, and whether the formulation in question gives us a definite answer. Also note that the existence of a universal set alone does not lead to paradoxes. Ladislav Mecir (talk) 07:48, 4 December 2016 (UTC)
- Notes:
- 'To me that makes it problematic to say that it "turned out to be inadequate"' - For the definition to be adequate, it should be useful as a criterium whether some object is a set. To that you note: "It is true of course that those few words of Cantor are not really enough to do much with". To confirm it, let's try: is the collection of all sets a set? If we consult Cantor's works, we may get Cantor's answer to this question. However, the formulation mentioned as "the Cantor's definition" in the article, i.e., the formulation you call "those few words" is not adequate for that. This is known and discussed in reputable sources. Ladislav Mecir (talk) 23:00, 3 December 2016 (UTC)
well-defined
I'm a bit worried about the usage of the term "well-defined" when giving an informal definition of set. I recognize that it's common to mention it, but I think it has to be done carefully.
Here's how Cantor put it (as translated by Jourdain), and it's still pretty good, if understood correctly:
- By an "aggregate" (Menge) we are to understand any collection into a whole (Zusammenfassung zu einem Ganzen) M of definite and separate objects m of our intuition or thought.
Now, the first thing to note is that the term "definite" is applied to the objects, not to the collection. So saying "a set is a well-defined..." misses that point.
Perhaps more importantly, "definite" here doesn't mean that either the collection or the objects have definitions. It means that they're not vague. For any one of the objects, it's an exact thing, with no fuzzy edges. It may or may not have a name that lets us talk about it, but anything either is or is not that object. And similarly for the collection — any object is or is not an element of the collection; nothing is sort-of-in-sort-of-out.
That's an important thing to get across, but "well-defined" isn't a good way to get it across. It suggests that the collection or the objects must have a definition, which is not necessarily true. --Trovatore (talk) 22:20, 6 November 2017 (UTC)
Changes from adding references
I've been adding references to this article and changing things when I can't find references too them.
In particular, I changed the opening line from "collection of well-defined, distinct objects" to "well-defined collection of distinct objects", because I could find no references for the former, but many for the latter.
A much larger change is regarding extensional and intensional definitions. Again, it was very difficult to find anything on extensional and intensional definitions in mathematics, using that terminology. Almost all such references were philosophical texts, and this is an article for (introductory) mathematics (as contrasted to the more advanced set theory article.
I found many, many references discussing 'roster notation' vs 'set-builder notation'. And so I've re-written the section to reflect that. Like anything newly-written, it's not that good, so I'd love for future editors to touch it up and fix it and do whatever they want with it.
- The reference given for this line: "In roster notation, listing a member repeatedly does not change the set, for example, the set {11, 6, 6} is identical to the set {11, 6}" does not say this. — Preceding unsigned comment added by Moksifu (talk • contribs) 22:13, 28 November 2019 (UTC)
But overall, I believe that, according to the sources, we should move from 'extension/intension' definitions to the 'roster/set-builder' notation, and have made changes accordingly. Brirush (talk) 18:53, 27 September 2019 (UTC)
- I agree, given that 'extensional/intensional definition' had no references. (I guess, extensional and intensional equality of set expressions could be distinguished, the former applying if the denoted sets contain the same elements, and the latter if the expressions are syntactically equal.) - As for "well-defined", that property should go without saying anywhere in mathematics, so it wouldn't matter where the adjective is placed or omitted. - Jochen Burghardt (talk) 20:42, 28 September 2019 (UTC)
- "Well-defined collection" is actually a particularly poor formulation, even if it's been used a lot, because it suggests that the collection needs to have a definition (that is, an expressible rule that decides whether or not a given object is in the set), whereas the important point is that the objects themselves (and their elementhood in the set) are not vague or indeterminate. Surely we can find sources that are more careful about this sort of thing; I think the "well-defined collection" is simply sloppy language, not a deliberate attempt to identify a different concept.
- We should not avoid philosophical sources. Among branches of mathematics, set theory is one of a very few that are the most philosophy-adjacent, both in terms of content and history. --Trovatore (talk) 23:38, 28 September 2019 (UTC)
- I think you have perfectly valid points. My main goal has been to take 'Top Importance' math articles and give them proper citations. While I agree that 'well-defined' doesn't make perfect sense for describing sets, it's in by far the majority of books I've found. In fact, searching 'well-defined' and 'set' in google books gives page after page of "well-defined collection" and I so far haven't found a single source that mentions the elements being well-defined. But I won't revert anything if you make changes! After all, many of the best math sources are not available or searchable on google books, and I don't have access to a research library at this time.
- As for the philosophy sources, I agree, and I've kept in those sources that mentioned 'intension' and 'extension' and added another. This area is beyond me, though, so it could use help from an expert in philosophy! My current plans are to add more sources to the later sections over the week.Brirush (talk) 00:25, 29 September 2019 (UTC)
Retrofit talk-page year headers/subpages
17-Nov-09: I have added subheaders above as "Topics from 2002-2006" (etc.) to emphasize the dates of topics in the talk-page. Older topics might still apply, but using the year headers helps to focus on more current issues as well. The topic-year boundaries were located by searching from bottom for the prior year#. Afterward, I dated/named unsigned comments and moved 1 entry (titled "Images") into date order for 2007 & 2008.
Then I added "Talk-page subpages" at the TOC. -Wikid77 (talk) 19:07, 17 November 2009 (UTC)
- This might have been standard in 2009 (although given the person who implemented it, I doubt it) but it's super-plus nonstandard now; I am reversing it and adding standard archiving to the page. --JBL (talk) 16:31, 16 May 2020 (UTC)


