Talk:Radar altimeter

what if the plane banks?

I have a question: what happens if an aircraft makes a turn, and in the process, banks? Logically, the altimeters will point sideways, and the height that they measure will increase, even to infinite when a plane banks 90° . What if the plane pulss up or dives? Are these altimeters stabilized? From what i read, most passenger jets have an altimeter to the left and one to the right. Are their different measurements used to calculate the angle of banking? And what if the terrain isn't flat? How do altimeters know wether the reading that comes from the roof of a skyscraper is the right one, or the one from the adjacent street? Are radar altimeters controlled by barometric altimeters to check for sudden and unlogical changes in altitude? This article leaves me with a lot of questions. Can sombody who knows the matter well enough provide answers to these questions please? thanks. -karelke- —Preceding unsigned comment added by 193.190.253.150 (talk) 19:28, 4 March 2009 (UTC)

You would only have a problem during bank if you had a very sharp (directional) beam. If the beam is wider, some part that goes, wlog, to the left as seen from the airplane, will strike the ground first, directly under the plane as seen from the ground, bounce back first, and, in the end, give a correct reading even during bank. And "sudden and unlogical changes in altitude (values shown)" do indeed happen if the terrain is not flat. As I understand it, a famous example is Funchal Airport, where the altimeter reading suddenly drops quite a bit when the airplane comes over the runway from the sea, which is quite a bit lower. (And if you bank 90° during approach, an incorrect altimeter reading will be the least of your problems.) ospalh (talk) 21:14, 7 March 2009 (UTC)

Frequency change?

I don't see how this

Alternatively, the change in frequency of the wave can be measured, the greater the shift the further the distance travelled. This method can achieve much better accuracy than the aforementioned for the same outlay and radar altimeters that use frequency modulation are industry standard.

is supposed to work. Frequency changes with distance traveled? That's news to me. Could someone pleas clarify? ospalh (talk) 20:40, 7 March 2009 (UTC)

The German page mentions FMCW, sounds reasonable, but a link would still be nice. ospalh (talk) 09:05, 8 March 2009 (UTC)

 Done. Since all commercial radio altimeters in the US -- and so, I suspect, nearly all radio altimeters in general -- use FMCW, I started a section in this article about FMCW. Still needs work. I hope in the meantime the link in that section -- as ospalh suggested -- to our FMCW article gives an adequate explanation. --DavidCary (talk) 01:43, 25 January 2014 (UTC)

primary term

Please discuss the term priority of the term Radar altimeter versus the term common to aviation applications radio altimeter. 75.210.125.201 (talk) 03:15, 28 April 2013 (UTC)

Removed content

A significant section of this article was added in 2014 and really has nothing to do with the topic of radar altimeters, but is related to geodesy. I'm placing the content here so it can be mored to a more appropriate article.

Pulse-limited altimetry

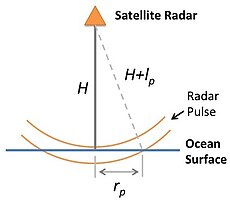
Consider a radar pulse emanating from a radar beacon traveling downwards and interacting with a flat ocean surface. The following figure shows an illustration of the vertical cross-section and top-down view of the radar pulse (adapted from ) .

The radar altimeter measures the return power of the radar pulse that's reflected off the land/ocean surface. The temporal evolution of the reflected radar pulse is interpreted in order to estimate the distance between the radar altimeter and the reflecting surface; surface irregularities can also be estimated. The expected return pulse can be derived from a few basic mathematical considerations.

From the previous illustration of the radar pulse vertical cross-section, the radius of the outer edge can be found using the Pythagorean theorem:

$H^{2}+r_{p}^{2}=(H+l_{p})^{2}=H^{2}+l_{p}^{2}+2Hl_{p}$

where r_p is the leading edge of the pulse. If we assume l_p² is small and can be neglected then we can solve for r_p as:

$r_{p}=(2Hl_{p})^{\frac {1}{2}}=(Hct_{p})^{\frac {1}{2}}$

The time evolution of the return power measured from the footprint of the radar signal reflecting off the ocean/land surface can be described in three parts: (1) the time before the pulse arrives, (2) the time after the beginning of the pulses arrival and before of the tail of the pulse has arrived, and (3) after the tail of the pulse has arrived. The power function can then be expressed functionally as:

$P(t)={\begin{cases}0&t<t_{o}\\\pi r^{2}(t)&t_{o}<t<t_{o}+t_{p}\\\pi [r^{2}(t)-r^{2}(t-t_{p})]&t>t_{o}+t_{p}\\\end{cases}}$

Using the equation for r_p and normalizing by the peak power yields:

$P(t)={\begin{cases}0&t<t_{o}\\{\frac {t-t_{o}}{t_{p}}}&t_{o}<t<t_{o}+t_{p}\\\ 1&t>t_{o}+t_{p}\\\end{cases}}$

This following plot demonstrates the power function for a radar wave pulse. The power function should be constant with time after the full pulse reaches the ocean/land surface (at (t-t_o)/t_p = 1), however the power will actually decrease with time w.r.t the illumination pattern of the radar on the ocean/land surface.

Delay-Doppler (or SAR) altimetry

The primary difference between delay-doppler (or Synthetic Aperture Radar) and pulse-limited altimetry is that delay-doppler altimetry looks at a smaller section of the pulse-limited radar footprint, but emits far more pulse signals to give the effect of covering the same footprint as pulse-limited but with better resolution. The top-down view in the figure below shows the decreased footprint size of the delay-doppler signal.

In order to determine the power signal of the delay-doppler radar as a function of time, we'll need to assume that the footprint of the pulsed radar is small enough to be considered two rectangles of width W. This allows the power function to be similarly (see Pulse-limited section above) written as:

$P(t)={\begin{cases}0&t<t_{o}\\\ 2Wr(t)&t_{o}<t<t_{o}+t_{p}\\\ 2W[r(t)-r(t-t_{p})]&t>t_{o}+t_{p}\\\end{cases}}$

Using the equation for the radius derived in the previous section (see Pulse-limited section above), the power vs. time function, normalized by the time relative to the arrival time at the leading edge, $t'=t-t_{o}$, becomes:

$P(t')={\begin{cases}0&t'<0\\\ ({\frac {t'}{t_{p}}})^{\frac {1}{2}}&0<t'<t_{p}\\\ ({\frac {t'}{t_{p}}})^{\frac {1}{2}}-({\frac {t'}{t'-t_{p}}})^{\frac {1}{2}}&t'>t_{p}\\\end{cases}}$

An illustration of the normalized power vs. time function is shown below:

There are two primary advantages that the delay-doppler method has over the traditional pulse-limited altimeter. First, the radar footprint is covering less area so the radar pulse emitted by the satellite requires much less power. It covers the radar footprint using more frequent, but less power consuming radar pulses. Secondly, the return waveform has a more complex signature allowing the arrival time of the pulse to be more accurately constrained.

Error budget

The following list notes the error sources associated with radar altimetry measurements:

Tides - Tidal variations are much larger than the dynamic variations in sea surface height. Because tidal periods can be on the order of diurnal and semidiurnal, the tides create an aliased frequency in the temporal variations in the sea level height that must be removed.

Electromagnetic Bias - There is a sea state bias where the troughs of waves tend to focus waves back to the radar, while the crests of the waves scatter waves away from the radar.

Ionosphere - The ionosphere can also impose a delay on the radar return signal, where electron plasma in the ionosphere slow down the group velocity of the radar pulse. The electron density in the ionosphere varies throughout the day, complicating the ionosphere correction.

Dry Troposphere - Refraction from the dry gas component of the atmosphere create a signal delay in the radar, but a correction can be approximated using the Saastamoinen formula: ΔRdry= -0.02277Po*(1+0.0026cos2φ) where Po is the sea level pressure in Pascal and φ the latitude.

Wet Troposphere - Water vapor can also cause a delay in the radar signal which can be more difficult to correct. A delay correction for the total water column in the radar measurement can be accounted for using output from meteorological models, like ECMWF and NCEP.

Icecap - There have been cases of hazard caused to airplanes flying over an icecap, by their radar altimeters displaying the height above the underlying bedrock instead of the height above the ice.

Ambiguous about GPS altimeter issue

The article CLAIMS that since 2012 GPS is not suitable for altimeter measurements, and radar altimeters must be used. This statement as it stands is nonsense at least as far as guidance is concerned, a great deal of engineering effort went into establishing elevated accuracy standards for GPS altimeter accuracy in the WAAS and GBAS systems here in the United States for all manner of precision approaches, and these approaches are still on the books. There are other subsystems (GPWS?) that may use either radar altimeters or conventional air data systems with Pitot tubes, there's also the issue of which standards apply when landing at airports in non-US locations whose standards are under the auspices of the ICAO. I'm no airline pilot but as an engineer I've worked on all manner of precision avionics systems, and to state that GPS "was declared inaccurate and outlawed in 2012" is beyond absurd, and whatever system requires a functional radar altimeter would only be able to rely on it below 2500 feet anyway. It's very clear that this is way more of a political than a technical statement, at the very least the person making this statement needs to specify which subsystems ON WHICH AIRCRAFT in which context required that functional radar altimeters be added to their basic architecture for correct operation, instead of making a blanket statement which cannot possibly stand. (And it's bad enough that the FCC managed to "hold AT&T and Verizon hostage for $78 billion ransom" in order for the FAA to wage this "C band" pissing contest against the FCC, we certainly should NOT allow our government three-letter agencies to hold auctions to raise money for questionable purposes only to waste it on internecine wars!) Jlawton11 (talk) 00:27, 25 January 2022 (UTC)