Talk:Monty Hall problem/Archive 33
| This is an archive of past discussions about Monty Hall problem. Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page. |
| Archive 30 | Archive 31 | Archive 32 | Archive 33 | Archive 34 | Archive 35 | → | Archive 39 |
Comments Welcome
I have been nominated for the Mediation Committee: Wikipedia:Mediation Committee/Nominations/Guy Macon. If anyone wishes to express an opinion, your input would be most welcome. Especially valuable would be criticisms or suggestions about how I could have done something better. Don't worry about possibly derailing the nomination; if there really is something I need to change I want to know it so that I can withdraw, spend six months or so showing that I have addressed the issue, and re-nominate myself. --Guy Macon (talk) 07:07, 28 October 2012 (UTC)
discuss on the nomination page or Guy's talkpage please. Inappropriate to discuss here
|
|---|
|
Conditional or Simple solutions for the Monty Hall problem?
- The following discussion is closed. Please do not modify it. Subsequent comments should be made in a new section.
Should the Monty Hall problem page be edited according to the 'Simple' or the 'Conditional' solutions? --Guy Macon (talk) 21:18, 6 September 2012 (UTC) The aim of this RfC is to resolve a longstanding and ongoing conflict involving multiple editors concerning the relative importance and prominence within the Monty Hall problem article of the 'simple' and the more complex 'conditional' solutions to the problem.
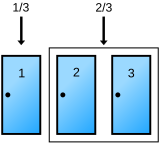
The 'simple' solutions do not consider which specific door the host opens to reveal a goat (see examples here and here). The 'conditional' solutions use conditional probability to solve the problem in the case that the host has opened a specific door to reveal a goat (see example here).
One group of editors considers that the 'simple' solutions are perfectly correct and easier to understand and that the more complex, 'conditional' solutions are an unimportant academic extension to the problem.
The other group believes that the 'simple' solutions are essentially incomplete or do not answer the question as posed and that the 'conditional' solutions are necessary to solve the problem. Both sides claim sources support their views.
That argument is unlikely to ever be resolved but two proposals have been made to resolve the dispute. Both proposals aim to give equal prominence and weight to the two types of solution.
One of the points of contention is whether either of the proposals below violates any Wikipedia policies and guidelines (in particular WP:NPOV, WP:NOR, WP:V, WP:WEIGHT, WP:EP, MOS:JARGON, WP:MOSINTRO, WP:MTAA and WP:OPINION). See the individual editor's comments below for arguments on both sides of this issue.
Proposal 1 is for the initial sections including 'Solution' and 'Aids to understanding' to be based exclusively on 'simple' solutions (with no disclaimers that they do not solve the right problem or are incomplete) then to follow that, for those interested, with a section at the same heading level giving a full and scholarly exposition of the 'conditional' solutions.
Proposal 2 is for the article to include in the initial 'Solution' section both one or more 'simple' solutions and an approachable 'conditional' solution (showing the conditional probability the car is behind Door 2 given the player picks Door 1 and the host opens Door 3 is 2/3) with neither presented as "more correct" than the other, and to include in some later section of the article a discussion of the criticism of the 'simple' solutions.
Extended content
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Proposal 1, Proposal 2, or Neither? (or Abstain.)Considering all Wikipedia policies and guidelines, should the Monty Hall problem page be edited according to Proposal 1, Proposal 2, or neither? Abstain is also an acceptable answer. Note: Because prior attempts to resolve this conflict have resulted in long discussions with many endless back and forth comments, please place any responses to other editor's comments in your own "Comments from user X" section and limit your comments to no more than 500 words. If you wish to have a threaded discussion, feel free to start a new section on this talk page but outside of this RfC or on your own talk page. Comments from Elen of the Roads(327 of 500 words) Note: I am assigning Neither to the comments below. If this is incorrect, please indicate "Proposal #1", "Proposal #2", or "Abstain". --Guy Macon (talk) 20:16, 20 September 2012 (UTC)
Commenting so there's no danger of ever being asked to close this, or PD a rerun Arbcom !! Seriously, the Monty Hall problem was originally presented as a parlour teaser for folks with a bit of mathematical knowledge who were familiar with game shows like Opportunity Knocks. The question was - should the contestant stick with his door or switch, and the utterly non-intuitive answer is that he should always switch, regardless of whether Monty knows where the goat is, whether Monty prefers the red door, or what Monty had for breakfast. The article has to present the puzzle and the answer in this light first. The conditional mathematicians contentions that the answer has the potential to be different if Monty has had his Weetabix must come separated, later in the article, for those who have an interest in such things. --Elen of the Roads (talk) 23:02, 6 September 2012 (UTC) @Guy Macon - I've always liked the ten goats explanation. Surely the actual, unspoken condition is that Monty always knows where the goats are. Everyone takes this as read, because they extrapolate from how real game shows work, and if he opened the door on the car, the show will end ten minutes early. All of the other potential conditions - whether Monty opens the door on the left first, or prefers the blue door, are not part of the original problem, and do not affect the solution to the original problem. --Elen of the Roads (talk) 15:29, 7 September 2012 (UTC) See section below Talk:Monty_Hall_problem#Does_this_version_work. Uses the approach taken in Zebra Puzzle, ie that it is the statement of the puzzle that is faulty, not the solution. Does this remove the divide? It is not true (for any given value of true) that "all the simple solutions are wrong" but it is true that Vos Savant's statement of the puzzle is incomplete, and anything claiming to be a solution to that version of the puzzle is incomplete if it does not highlight the missing assumption. --Elen of the Roads (talk) 14:18, 15 September 2012 (UTC) Comments from Glrx(63 of 500 words) Neither. I'll second Elen's comments. Unfortunately, this article has taken a mathematician's viewpoint much too seriously. For WP, it is an interesting puzzle and not a graduate level exercise in probability/statistics. The simple stuff must be first and the academic views much later. There should not be an overly precise description of the problem at the beginning. I'll explain the neither vote later. Glrx (talk) 23:40, 6 September 2012 (UTC) Comments from Ebe123(6 of 500 words) Neither. I echo Elen on this. ~~Ebe123~~ → report 00:50, 7 September 2012 (UTC) Comments from czarkoff(197 of 500 words) Proposal 1. Though I share the view by Elen of the Roads that the first things to present readers are the problem and the counter-intuitive solution, this is exactly the purpose of the lead section. I reject the notion that the math is taken too seriously in this article – it is the subject, not a side discussion, so it should be presented and explained in the article's body. By analogy with WP:WEIGHT I would present the material to the reader in order of complexity increase, so that the solutions involving less logical operations or iterations are placed on top of more complex material. That said, I would suggest to move the current lead section (I generally prefer the word "lede" over the phrase "lead section", but in this article it is indeed a magazine's lede, not a summary one would expect) into a first named section, which I would call "Background"; in the lead section I would overview the problem and state the solution in the first paragraph. In the second paragraph I would provide the brief descriptions of the solutions, as general as possible. The proposal 1 should be implemented in sections 2 and onward. — Dmitrij D. Czarkoff (talk•track) 01:48, 7 September 2012 (UTC) Comments from Noleander(187 of 500 words) Neither. Splitting the solutions into Simple and non-Simple seems like it would just perpetuate the underlying conflict for several more years. Is it not possible to simply enumerate the several different approaches to the problem? I suggest:
Bottom line: don't divide the approaches into two categories that could perpetuate the civil war. (Maybe this is Option 2?). --Noleander (talk) 02:28, 7 September 2012 (UTC) Comments from ChrisGualtieri(152 of 500 words) Neither - Clearly the problem and show's ORIGINAL problem diverge into a thought experiment along the way. First, go with the simple answer in no uncertain terms, with the most prevalent rules without behavior such as 'evil or angelic' Monty. The problem as classically postulated. Then get into the counters and thought process behind that. Once that is done, the 'complex' matter can be dealt with separately assuming X or X case, but by all means, each of these have to be explicit in their terms about the ideology (and not math) which goes into it. I'll end up doing it myself if this can't get resolved. Either way... this conflict is going to end shortly. ChrisGualtieri (talk) 02:31, 7 September 2012 (UTC)
Comments from Rick Block(468 of 500 words) Proposal 2 This is a POV dispute, plain and simple. POV 1) "Simple" solutions are the "right" way to solve the problem. POV 2) The "right" solution is to compute the conditional probabilities the car is behind Door 1 and Door 2, given the player has selected Door 1 and the host has opened Door 3. Proposal 1's "compromise" is to give "simple" solutions far greater WP:WEIGHT, and structurally endorse POV 1. Proposal 2 gives equal WEIGHT and endorses neither POV, remaining strictly NPOV. Regarding WEIGHT: many, many sources present "simple" solutions. But the vast majority of these are popular, not academic, sources and many of them uncritically parrot vos Savant's ("simple") solution. Within the field of probability, the textbook solution (literally and figuratively, meaning both appears in numerous textbooks and is completely standard) is to compute the conditional probabilities. This solution, presented by the preponderance of sources in the most relevant academic field, should have at least equal WEIGHT to any other. Regarding STRUCTURE: there is a controversial, but by no means fringe, POV expressed by numerous sources, e.g. [1] [2] [3] [4] [5] [6], criticizing "simple" solutions. To be NPOV the article must not endorse this POV (as it arguably did at one point, which is perhaps the actual source of much of the conflict). But it equally must not endorse the opposite view that "simple" solutions are universally accepted as "perfectly correct". Proposal 1 does exactly this, presenting "simple" solutions as "the solution" ("with no disclaimers that they do not solve the right problem or are incomplete") and relegating "conditional" solutions to a later section "for those interested". This creates a strong structural POV suggesting the "simple" solutions are true and undisputed, which (hardly coincidentally) exactly matches the POV of certain editors involved in this conflict.  The resolution here is simple. Follow Wikipedia's core content policy of NPOV. Include BOTH "simple" and approachable "conditional" solutions in an initial "Solution" section, presenting both as equally valid. Discuss the differences between these types of solutions in a later section "for those interested". I.e. Proposal 2. -- Rick Block (talk) 04:30, 7 September 2012 (UTC) Comments from Trovatore(209 of 500 words) Note: I am assigning Abstain to the comments below. If this is incorrect, please indicate "Proposal #1", "Proposal #2", or "Neither". --Guy Macon (talk) 20:16, 20 September 2012 (UTC) The problem with Elen's take is that there is no such thing as an answer independent of Monty. There are ("simple") answers that are based on certain assumptions of neutrality regarding Monty's strategy, assumptions that are arguably not unnatural, but are certainly not the way Monty in fact behaved. This is not "the mathematician's view"; this is simply the fact. That said, I think a mixture of Proposal 1 and Proposal 2 is probably appropriate. The bulk of the coverage has indeed been on the "simple" answers, with all their unexamined assumptions, and it should probably come first. However, to leave the qualification out of the lead paragraph is not reasonable. To fail to point out the hidden (and certainly inaccurate, compared to the real-life model) assumptions, is to be just plain incorrect. --Trovatore (talk) 09:32, 7 September 2012 (UTC)
Comments from Guy Macon(420 of 500 words) Neither. The article should start with a description of what the MHP is (using the Krauss and Wang version) and the "better to switch" question without (in the lead) saying what the answer is or why. Just present the problem in the lead and let the reader decide what the answer is. Next should be a history section, still not saying what the answer is but instead documenting what various letter writers to the American Statistician wrote in 1975, Marilyn vos Savant's answer, the answer of the 1,000 PhDs who disagreed with her, etc. The key here is not to say what the answer is, but rather to document (with citations) what various notable people say it is. Next should be a section on simulation starting with clear instructions on how to do the simulation yourself using plastic cups (better than playing cards; goats are indistinguishable). This has a huge advantage over the other "solutions" and "aids to understanding", which often end up with two people talking past each other, each convinced that they understand the problem and have the solution and that the other person isn't thinking clearly. Again, we shouldn't give the answer but rather should report (with citations) on the result of people running simulations. One big advantage of a physical simulation (or a computer simulation that you wrote yourself) is that Monty's behavior must be defined for it to work, and alternative Monty behaviors can be easily tested. Finally, after the Lead, History and Simulation sections, the other approaches should have a section or sections, with simple first followed by conditional. Here, for the first time, we should reveal what Wikipedia says the answer is, along with answers to different but related questions. I have gone through physical simulations many times (mostly with engineers and scientists, and with ten cups if they assert that there is no advantage to switching even if there are ten cups), and have found it to be a reliable way to convince even the most stubborn that switching is better, and to do so in a way that no amount of verbal argument can accomplish. Furthermore, watching "Monty" select which eight cups to turn over leads to understanding -- clearly "Monty" is choosing cups with goats and avoiding the car. This also makes it easy to understand variations like "random choice Monty", where sometimes he opens the door on the car and the player loses immediately without being given a choice to switch. --Guy Macon (talk) 19:04, 8 September 2012 (UTC) Comments from Martin Hogbin(381 of 500 words) I am the proposer of Proposal 1. Firstly let me say that I completely agree with Elen of the roads that, 'Monty Hall problem was originally presented as a parlour teaser for folks with a bit of mathematical knowledge who were familiar with game shows...', and I and many other editors have long argued that the article should concentrate on this aspect. However there are some who believe that the more esoteric mathematical aspects are important and who have pressed for what they see as the only 'correct' solutions' to dominate this article. That battle has raged for years with no sign of resolution and my proposal is a compromise which should be acceptable to all. My proposal makes no claim that any one solution is the 'correct' one and I am suggesting that we give both types of solution equal weight but: First, we treat the problem as a simple mathematical puzzle and give the 'simple' solutions to this puzzle. This is what 90% of our readers want. We need to concentrate on making the solutions convincing and the explanations understandable. There are two things that fool most people: that the answer is 2/3 and not 1/2, and that it matters that the host knows where the car is. Once we have fully resolved these two issues most readers will be satisfied. After we have done that, for the remaining 10% of readers and for mathematical completeness we should mention that some sources say that the simple solutions are defective in some way. We should then have a full and scholarly discussion of that claim, based on reliable sources.
Comments from Richard Gill(491 of 500 words.) Neither. The important distinction is between informal, heuristic, verbal solutions which anyone can understand, and formal solutions appropriate within some academic context. If there are simple verbal equivalents of solutions based on conditional probability then they can appear early in the article alongside other simple solutions. Marylin vos Savant's question was "should you switch?", not "what is the (this, that or another) probability?" What most readers need is to gain the intuition through being shown how to see the problem from another angle, that switching offers a huge advantage. MHP is carefully formulated so as to throw the newcomer off track. It's a trick question. It's fun. A classic brainteaser. Conditional probability is justs one of many ways to solve the problem, after just one of many possible formalizations of it has been chosen. Another important distiction for me is that between an argument being correct and incorrect. I see no need at all that the article should reproduce arguments which are logically wrong. With careful wording, we can stick to the Truth. Richard Gill (talk) 13:44, 27 September 2012 (UTC) Comments from Gerhard Valentin(486 of 500 words) Proposal 1. For the reader, it's easy to follow that "any group" of two doors has double chance to hide the prize, compared to one single door. The tricky story tells a brilliant honest puzzle. It is not so much important what is *the* original question and its "possible" ambiguity, but it is on the certainly *intended* paradox of a *confidential* host who observes *secrecy* regarding the car-hiding door in that one-time problem. — It is on helping people, *by modern reliable sources*, to decode and understand the puzzle.
The paradox can be decoded by careful evaluation, by game theory, principle of dominance and other approaches as per the sources, that all say that “staying” forever will diminish your probability to win the prize. The article first should show the common assumptions: All doors are initially equally likely to hide the car in this one-time problem.
And then in contrast, as an eye-opener, immediately followed by the inconsistent *strange scenario* of a forgetful host who is showing the car in 1/3 by just randomly opening one of his two doors, deleting the probability to win by switching in that 1/3, while in the remaining 2/3 ("goat:car" and "car:goat"), the chance of both still closed doors is 1/2:1/2 then, as per the most intuitive common appraisal. Conditional probability theory is not "needed" to decode the paradox. Show in later sections that the MHP is often used in textbooks and in teaching conditional probability theory, with adventuresome presumptions. What matters most is a clear structure of the article. Gerhardvalentin (talk) 14:26, 21 September 2012 (UTC) Comments from Tom Hulse(484 of 500 words) Proposal 2 I'll add Lambian to the long list of users who's comments are 100% irrelevant here and should not be considered, since he, like the others I mentioned, doesn't understand what this Rfc is about. He also thinks Position 2 is about about variations in the conditions of the problem (it's not at all). Boris Tsirelson misunderstands too, commenting about 'starting with the ideal case'. Both simple & conditional solutions start with the IDENTICAL PROBLEM. There is no variations in the conditions. Look more carefully. Ya'll are alsleep, lol! Condtional probability, not conditions in the problem. --Tom Hulse (talk) 07:55, 9 September 2012 (UTC) Comments from Salix alba(218 of 500) Proposal 1 My inclination is to stick with the status quo, this topic has been discussed to death. However I do fid the condition probability section has been poorly written and is confusing. Effort should go into fixing that. Condition probability can be explain better than it is.--Salix (talk): 17:59, 8 September 2012 (UTC) For all its flaws the Vos Savant explanation gives the gist of the problem and a simple means when the probabilities turn out to be. Before trying for a major overhall work need to be done on expanding the Decision tree section so that readers with only basic statistical background can undersand it. Its not made clear that the tree diagram really has conditional probabilites in it with each branch of the tree representing P(car at location 1 AND host opens door 2) = P(car at location) * P(host opens door 2 | car at location). The formal solution section is just a mass of symbols making it look more complicated than it really is. In has the effect of making the whole section incomprehensible to anyone who is not familier with Bayes theorem. Fix this before going on about the order of presentation.--Salix (talk): 16:19, 15 September 2012 (UTC) Oh the latest xkcd seems to capture some of the effect of these discussions.--Salix (talk): 16:24, 15 September 2012 (UTC) Comments from 203.171.197.35(48 of 500 words) Proposal 2 Comments from Boris Tsirelson(73 of 500 words) I replace my original comments; hope this does not violate the rules of RfC. Abstain. The first solution in the article should be the most simple (that is, accessible for the widest possible audience) among all available correct solutions. (Fortunately simple and correct solutions exist!) And I do not care, whether or not (and to what extent, and in which sense) this solution may be called "conditional", or "unconditional", or both, or neither. Boris Tsirelson (talk) 15:48, 13 September 2012 (UTC) Comments from Lambiam(302 of 500 words) Proposal 1. In the terminology of User:Martin Hogbin/Monty Hall History, I'm a card-carrying simplist. Let me repeat what I proposed on this talk page on 2 March 2008:
I'd like to add that I gave an "unconditional" mathematically solid simple proof on Richard Gill's talk page of a proposition he has dubbed "the Holy Grail of MHP studies", namely that the 2/3 chance of success on switching can't be beaten by any strategy, even if the player's initial choice and the host's choice are not necessarily random. This shows conclusively that the conditionalism is an unnecessary complication. --Lambiam 07:38, 9 September 2012 (UTC) Tom Hulse wrote: "Marilyn's answer was right but her math explanation to get there was wrong". Well, no, her answer was right and so was her explanation. The simple explanation is perfectly adequate, and we should not torture and confuse the reader with unnecessarily complications, or at least postpone their introduction as long as possible. --Lambiam 09:08, 9 September 2012 (UTC) Comments from Coffee2theorems(500 of 500 words) Proposal 2. I think an approachable conditional solution is doable, if care is taken not to dot every i and cross every t in sight, and maybe starting with a very short introduction to conditional probability and explanation of why it's relevant here (in the vein: if you want to guess a man's height, use statistics for men, not for all people). More sophisticated and rigorous discussion coming in a later section would be in line with WP:UPFRONT. The problem with the unconditional solutions is that they take considerable liberties with the problem. There are people who are just sophisticated enough to sense the holes in the argument and so fail to be convinced, yet are not sophisticated enough to see how the holes can be mended and the solutions salvaged by the symmetry proof. (concrete example: me when I was in high school) Those readers need the conditional solutions, and they need to be mentioned before some "aids to understanding section", or the readers will likely go away thinking that the article has no real solutions to offer. Incidentally, for all its simplicity, the symmetry proof is actually more sophisticated than the conditional one. It's the kind of shortcut you can take in a recipe once you know how to cook, not when you're struggling with the basic recipe ("what does it even mean that probabilities can change?!"). -- Coffee2theorems (talk) 10:57, 9 September 2012 (UTC) Boris: The "conditional proof" is a very straightforward application of the definition of conditional probability, so it can be understood with absolutely minimal prerequisites of probability theory, and the correspondence of the decision tree with the original problem is clear and explicit. It solves the "standard MHP" by directly computing the conditional probability which decision theory says you should compute, brooking no argument and being economical in the amount theory the reader needs to understand. It's also a very standard approach to such problems. The symmetry argument gives you another way of obtaining the conditional probability, by showing that it is equal to the unconditional probability here. It requires all the same concepts as the proof by direct computation, and more besides. The symmetry proof sections in the article use statistical independence at least. They are also even less clear than the conditional proof sections of the article, and I think the reasoning is fundamentally more sophisticated, and thereby fundamentally less accessible. The symmetry argument certainly should remain in the article. All I'm saying is that the conditional solution should be presented along with the unconditional solution, not much later in the article. The other proposal where no mention at all of conditional probabilities is made in the main "Solution" section would amount to presenting a lie to children as a full solution, which is clearly undesirable. Most of the "unconditionalists" don't want an "unconditional solution + symmetry argument", they want just the unconditional solution, with any mention of conditional probabilities ("unimportant academic extension") omitted, or as a "compromise" at least hidden as much out of sight as at all possible. -- Coffee2theorems (talk) 03:33, 10 September 2012 (UTC) Comments from User:Dicklyon(79 of 500 words) Proposal 1 – Rick Block's description of the 2 POVs is accurate enough, but his long-time insistence to putting so much weight on the minority POV 2 is what has kept this problem from being resolved. Readers would be better served by presenting the simple POV 1 solution first, without complications. Then, a later section can pay homage to those mathematicians who like to formalize the solution more carefully by appeal to conditional probabilities using conditions that don't matter. Dicklyon (talk) 18:50, 9 September 2012 (UTC) And of course, as others have noted, every time you invite comment on this article you'll be swamped by the noise by people who don't understand the basics of it and so can't even get close to the question at hand. Dicklyon (talk) 04:44, 11 September 2012 (UTC) Comments from Nijdam(331 of 500 words) Proposal 2, being, as Rick Block explained, in compliance with Wikipedia policy, as both the simple "solutions" and the conditional solution are widely sourced. I find it however very difficult, to accept the sources of the simple "solutions", being evidently mistaken, as reliable sources. I furthermore agree with Rick Block and Tom Hulse in their analysis of the situation. The latter also clearly shows where the problem lies. I would like to add to Proposal 2, at the point where the "conditional solution" is introduced, also the (well sourced) reason (need) for this solution. At this point the simple (vos Savant) solution, may be called an acceptable intuitive explanation. To Richard Gill I would say: Don't be naive, Vos Savant indeed asked: "Would you switch?" and the direct answer to this question would be: a yes or a no. In that way neither the simple nor the conditional solution is the answer. However, immediately following the answer "Yes, I'll switch" , will be the question "Why?". And it is this 'why' that is the core of the problem. And ... it will not surprise you, the answer is: because the conditional probability ...., etc. Or equivalently, because the odds are ...Nijdam (talk) 19:25, 9 September 2012 (UTC)
Comments from Linas(177 of 500 words) Note: I am assigning Proposal #1 to the comments below. If this is incorrect, please indicate "Proposal #2", "Neither", or "Abstain". --Guy Macon (talk) 20:16, 20 September 2012 (UTC) Both :-) Leaning to proposal 1. There is nothing 'mathematically' wrong with the 'simple' explanations, and they should come first. The Bayes Thm variant is a worthy exercise, but wow ... the current article presents it very badly, maximizing the total possible confusion. On first read, my knee-jerk reaction was that it was just flat out wrong; I fought off an urge to edit. I had to re-read the 'conditional' explanation a few times before I got it -- and I do math (& probability) for a living. After this stumbling block, I currently find it dubious that the Bayes variant is somehow 'more correct' -- mostly it just seems 'more difficult', and little else. First and foremost with math topics, explanations must be simple, easy, approachable. Don't confuse dense formulas with mathematical rigor. linas (talk) 16:01, 10 September 2012 (UTC) BTW: Appeal to authority: I edit little here on WP except for higher math articles. I recognize Trovatore, salix alba, Boris Tsirelson and Lambiam as other regulars in my edit circles, and I find it damning that they all lean to proposal 1. linas (talk) 16:10, 10 September 2012 (UTC) Joe Decker: Don't confuse counting arguments with frequentism. The 'simple' explanations here are counting arguments, not frequentist arguments. This has nothing to do with Bayesianism; there's no need to invoke 'priors' or 'ill-explicated pre-conditions': if something is 'ill-explicated', then turning it into a Bayesian prior doesn't magically make it 'well-explicated', nor any less 'hidden'. There is nothing wrong with using this problem to illustrate Bayesian-style reasoning, and indeed, the article already has an (opaque) section on this; none of the proposals are suggesting its removal. linas (talk) 18:25, 11 September 2012 (UTC) Comments from Joe Decker(113 of 500 words) Abstain (Previous material struck as I'd misunderstood the question the RfC was asking.) --j⚛e deckertalk 16:25, 15 September 2012 (UTC)
Comments from Ningauble(432 of 500 words) Neither proposal directly solves the problem which has plagued this article for years: attempting to give due weight to differing POVs has resulted in giving UNDUE weight to the dispute itself – a tempest in a teapot. Proposal 2 is "more worse" in this respect. Even the most strident and widely cited critic of vos Savant's "simple" solution, (Morgan et al. (1991), cited in the article) acknowledges in a rejoinder (printed in the same issue but not cited in the article) that if it is stipulated that Monty chooses goats uniformly at random (as is stipulated in most subsequent academic literature, and in this very article) then that is a legitimate basis for her "unconditional" solution, as he terms it. Taking their criticism out of this context is POV cherry picking. More fundamentally, there are different "frequentist" (statistical) and "Bayesian" (information theoretic) interpretations of probability. See §3 of Richard Gill's paper for Statistica Neerlandica,[7] which contrasts these perspectives as applied to MHP. Some who deny the validity of the "simple" solutions appear to be either unaware of this difference or to be dogmatic about only one being the "true" meaning of "probability". This epistemological distinction is probably too abstruse for the general readership of this article, and is seldom directly addressed in the literature on MHP. Presenting them as conflicting views rather than complementary approaches unduly makes a mountain out of a molehill. ~ Ningauble (talk) 00:41, 12 September 2012 (UTC)
Comments from User:Jouster(162 of 500 words) Note: I am assigning Abstain to the comments below. If this is incorrect, please indicate "Proposal #1", "Proposal #2", or "Neither". --Guy Macon (talk) 20:16, 20 September 2012 (UTC) Object Strongly to this Being an RfC—Wikipedia is not a democracy, principles of mathematics are not subject to being voted upon, and articles should be written in the way that best communicates the most correct information to the widest possible audience. If anyone does not support the implementation of these guidelines, they should discontinue editing the article. If there's a genuine desire to reach this, on the other hand, then a scientific approach is easiest adopted: find a trusted, neutral third party, have them run A/B comparisons between the two suggested complete articles, and then test for comprehension afterwards. Is this a terrible lot of effort? Of course! But so is me typing this. The reason I am typing it is because the readers' time, in aggregate, monstrously outweighs my own. Consequently, we owe it to the readers to spend more of our time making a better article from the readers' perspective(s), not from the perspective of a plurality of the editors. Jouster (whisper) 02:46, 12 September 2012 (UTC) Comments from User Albtal(413 of 500 words) Proposal 1 But surely start with the MvS version which caused the "furor" around the world, and state that the crucial rule there was missing, and clearly formulate this rule (K&W not needed), and then explain the solution based on: A strong argument for the simple solution - "strong" because it even holds for weaker conditions than those in the "standard problem": Forget The car and the goats were placed randomly, and forget he chooses one [uniformly] at random. The following holds: If the contestant has chosen door 1, he will win the car by switching in two of three cases: If the host opens door 2, he will choose door 3, and if the host opens door 3, he will choose door 2. So he will win the car, if it is behind door 2 or door 3. Therefore switching has a 2/3-chance of winning the car. We all know that we don't know the strategy of the host, neither in placing the car nor in choosing his door if he has a choice. So we have to decide without this knowledge. If now somebody says But it may be that the host does not choose symmetric strategies, we say Yes, it may be, but if so, we can't know; and therefore we have to decide without this knowledge. But if we don't know the strategies of the host, we cannot compute the conditional probabilities. May be, but we don't have to compute conditional probabilities to know that the contestant has a 2/3-chance with switching. Imagine you are the coach of the contestant, and (may be just before his final choice or earlier) he asks you: What shall I do? Do you say now: Sorry, I can't compute my conditional probabilities; I cannot help you? Or would you say, as another coach would do: Take the switch. Then you have a 2/3-chance of winning. (I think that these considerations belong to elementary game theory, and are as simple as the "game" Have I a coin in my hand?, which is even too simple to occur in elementary books there.) ...and in a separate section: Three doors, one car, two goats; two possible "Jokers": 1. The host must open a door with a goat before the contestant picks his door. 2. The contestant determines two doors of which the host has to open one with a goat. Then picking. Which Joker should he choose? --Albtal (talk) 07:39, 13 September 2012 (UTC) @JohnSRoberts99: The show never happened in the "MHP" mode. Monty Hall was free in his actions, and never offered a switch. And a show with the crucial MHP rule that the contestant has to determine two doors of which Monty has to open one with a goat is too boring not only for Monty Hall. And if taken place frequently results would be the same as if you throw a die counting "1 or 2" / "3, 4, 5, or 6".--Albtal (talk) 20:41, 14 September 2012 (UTC) Comments from JohnSRoberts99(33 of 500 words)
Does anyone have statistics from the show itself? That might be a bit more useful than trying to look at all the way people have calculated potential outcomes. I would back Proposal 2. JSR (talk) 19:33, 14 September 2012 (UTC) Looks like I was in favor of Proposal 2.JSR (talk) 20:46, 20 September 2012 (UTC) Comments from Wehwalt(50 of 500 words) Proposal 1 Agree with Elen. The game show host knows everything. That's part of the background assumption, along with the sun rising that morning, the end of the universe not yet having occurred, and the stagehands aren't leading the goat from door to door depending on what the contestant says.--Wehwalt (talk) 22:22, 20 September 2012 (UTC) Comments from CBM(106 of 500 words) I don't think I have commented yet. I prefer proposal 1, because I think it captures the spirit of the actual problem better. In general, Richard Gill's published analysis of the problem is very apt and I would be glad to see us follow it. It it matters, just to respond to something I saw on this page: I am an academic and I think the conditional probability is "a somewhat unimportant academic extension to the problem" - where "somewhat unimportant" means that it should be treated in later sections of the article and explicitly as an extension rather than something that addresses the original question. — Carl (CBM · talk) 23:03, 20 September 2012 (UTC) Comments from Mike409(28 of 500 words) I hate to do this, but I have to go with Proposal 1. Wikipedia is not meant to be first Mathematically rigorous (MTAA), unfortunate as that may be. Mike409 (talk) 04:40, 21 September 2012 (UTC) Comments from JonRichfield(439 of 500 words) Responding to this RFC is about as tricky as the MHP. If I am not doing it correctly, too bad. I certainly agree with Tom Hulse about re-thinking the RFC and probably with his reasons.
End of RfCPost-dated check to avoid archiving Glrx (talk) 23:35, 31 October 2012 (UTC) The Request for Comment has run for 30 days, and RFC Bot has cleared the rfc template. Responses to date are as follows:
– Tabulated by Ningauble (talk) 22:52, 6 October 2012 (UTC) We have passed the default 30 day duration for an RfC and it has been 2 weeks since anyone posted a comment. I am posting a closure request at Wikipedia:Administrators' noticeboard/Requests for closure --Guy Macon (talk) 15:02, 9 October 2012 (UTC)
Update: still under discussion by the closers. This is a Good Thing -- clearly they want to do it right rather than just posting a quick count. --Guy Macon (talk) 09:04, 24 October 2012 (UTC) |
Closing statements
- The following discussion is closed. Please do not modify it. Subsequent comments should be made in a new section.
The editors discussed the RFC summation after considering the proposal, entire debate, and previous threads on the issue, beyond the wording of the request summary at Wikipedia:Administrators'_noticeboard/Requests_for_closure/Archive 4#MontyHall and the wording of the RFC itself including the titles of the proposals, here. There was no off-wiki discussion.
Closing statement by Eraserhead1
- The following discussion is closed. Please do not modify it. Subsequent comments should be made in a new section.
To briefly summarise I find that there is a consensus in favour of proposal 1, and a consensus against proposal 2.
With regards to the arguments themselves I find the arguments in favour of proposal 1 to be more compelling. Covering topics in the simplest way we can while still going into appropriate detail later on is my experience of Mathematics articles in general, as well as explicitly with Derivative a GA. This is also the underlying point made by the guideline WP:TECHNICAL.
WIth regards to the NPOV concerns and WP:WEIGHT issues, unless the matter is extremely clear it is nigh on impossible to get the weight between two sides exactly right (especially as different editors will have different ideas about what "exactly right" means, the best we can hope for is to get it roughly within an acceptable range. It is far more damaging to the project to have disputes that go on, and on, and on, and on, than for in one's individual view the neutrality of the article to be slightly out of kilter with the article's content. I don't see any compelling evidence that there are significant neutrality issues with proposal 1. Certainly proposal 1 (and proposal 2) allow both solutions to be included in the article, and there is also agreement among almost all the RFC participants that the "simple" solution should be presented first.
With regards to the mathematical concerns raised I certainly think it is obvious that the host knows where the car is, that's the whole point of the problem.
Given the arguments in favour of proposal 1 are more compelling and they make up a majority of RFC participants I find a consensus in favour of proposal 1 and against proposal 2. There are also a minority of posters who favour neither option, but they seem to prefer something similar to proposal 1 either implicitly, or in the case of Elen of the Roads and others explicitly.
I think that there are legitimate concerns raised by a number of RFC participants around describing the "simple" solution as simple that are raised by a number of RFC participants, I think "solutions to the standard problem" or similar is a more appropriate way to cover it, and that comes across as a more neutral wording. I also think there are legitimate neutrality issues surrounding describing the probabilities for the standard problem in the lead, the lead is too long as it is, and simply describing that it is better to switch (which is true in all cases) satisfies WP:LEAD well.
WP:OWN and WP:AGF seem worth being very clear about, and given the length of the dispute editors should make sure they are following those policies as much as possible. -- Eraserhead1 <talk> 20:10, 29 October 2012 (UTC)
- The title of the RFC wasn't confusing, and all the arguments were looked at in detail. -- Eraserhead1 <talk> 18:46, 30 October 2012 (UTC)
Closing statement by I Jethrobot
The following discussion is closed. Please do not modify it. Subsequent comments should be made on the appropriate discussion page. No further edits should be made to this discussion.
I first want to make it very clear that there were many ideas brought up in this discussion that were outside the initial proposal (even if those ideas were intended to address similar concerns). While many of these ideas may be helpful, they were not the explicit subject of the proposal. I will comment on the ones that seem most related to the proposals, but explicit agreement of those ideas will be needed if they are to be implemented. I realize that the last thing this article needs is more RfCs, but my primary job here is to assess the proposals that were the subject of this RfC, not to "rule" on sidebars.
Proposal 1 had the most support among participants; it was also best supported by policies and editing guidelines. It is most sensible to present the lead and body of the article in a way that the more accessible approach should be made apparent first. This also is consistent with due weight, as present coverage of the problem in reliable sources is generally based off of vos Savant's approach.
Among those who rejected both proposals, some even made suggestions that would work with proposal 1, such as changing terms (e.g. from solutions to approaches and from simple solution to approach for the standard problem.). It also make sense from this proposal to represent conditional approaches in a later portion of the body. Given that these approaches are inherently more complex, it is reasonable to allow this section to be long, though editors should agree on only the most important components of these approaches to include in the article. In this way, problems with due weight can be avoided. The introduction to this conditional section should also be accessible for non-experts.
Proposal 2 was rejected for a number of reasons. First, it did not reach consensus. Second, some arguments supporting it were not based in policy, such as an assertion that readers would come to the article looking for "the most rigorous solution." There were other unsupported claims such as that the non-conditional solutions take liberties with problem parameters. Another editor said that the sources supporting vos Savant's approach were outside of academia and therefore less important or correct than academic sources.
I am not a mathematician, but the standard problem assumptions about Monty's knowledge of where the car is (he knows where it is) and that he chooses randomly are quite clear to me. Of course, I have been reading this article and its arguments over the last month, so perhaps I am biased. It's possible there are ways to make this clearer in the body, if this is needed to clarify the assumptions behind the problem.
The lead of the article was actually not a part of the proposals at all, but it was the topic of discussion among some editors. I have no particular comments to make since no specific suggestion was agreed upon, but it would make sense per WP:MOSLEAD to cover a solution in as accessible a way as possible. The Krauss & Wang (pg. 5) text in the diagram might be a good template to use to accomplish this goal.
Finally, per WP:FLAT, it is not the role of Wikipedia to "get the problem right," as this project is intended to reflect what has been reported in reliable sources, proportional to their weight. Therefore, suggestions that the first problem have an entire criticism section or that we include long discussions of how a limited number of sources have criticized vos Savant's approach seem unwarranted. This is especially true as one editor noted that much criticism of that approach has not been properly contextualized. I, Jethrobot drop me a line (note: not a bot!) 20:11, 1 November 2012 (UTC)
Closing statement by Churn and change
The following discussion is closed. Please do not modify it. Subsequent comments should be made on the appropriate discussion page. No further edits should be made to this discussion.
The rules
- Policies: WP:V, WP:NPOV, WP:OR
- Guidelines: WP:RS, WP:MOSINTRO, WP:LEAD, WP:UNDUE, WP:JARGON, WP:MTAA, WP:RFC
- Essays: WP:BETTER, WP:AESA, WP:UPFRONT, WP:ASTONISH
Debate summary
The central question of the RFC was whether it was better to present what was termed the "simple solutions" to the Monty Hall problem, starting with the one from vos Savant, or whether it was better to present what was called the "more complete" solutions, which included the simple solutions and qualifications and elaborations on it, first. However the discussion went well beyond this issue, with many respondents commenting the dichotomy presented excluded better options. The simple-solution proponents stated these solutions were comprehensible to, and precise enough for, lay people. The complex-solution proponents stated the vos Savant solution, in particular, was riddled with imprecision in formulation and inaccuracies in the analysis.
Terminology concerns
Some objected to the terminology of simple and complex, and, agreeing to that, I will refer to the two sets of solutions as "first set" and "second set." Where needed, I will refer to each solution (vos Savant, Krauss & Wang one and so on) separately. The solutions in the first set, referred to here, are: Krauss & Wang, vos Savant, Carlton, Adams/Devlin and the multi-door point of view. The Krauss & Wang solution was referred to deep in a tangled thread by one of the editors; the others are already present in the article.
The Lead
The lead should reflect the body text and should not contain something not in it. Hence presenting the first set in the lead and second set in the body text is not allowed. WP:LEADLENGTH specifies length of lead, and how much the body text should be compressed to generate the lead. The RFC has produced no consensus on what should be in the lead; however, considering the body text is under dispute, that doesn't seem a concern.
Presentation order of solutions
The RFC veers around to the view the first set should be presented before the second. While some arguments from a one-off psychological study were presented to show people had trouble with the solutions, the general feel is we need to go with our understanding of what lay people think like. Adding to that, I see the best order as Krauss & Wang, vos Savant, Carlton, Adams/Devlin and the multi-door point of view, followed by the solutions of the second set. The Krauss & Wang solution, on page 5 of their paper, does not use probability, and is a simple enumeration of all possible scenarios of the problem and the results from switching and not switching. The figures in that paper compactly cover the solution space. One can argue technically probabilities are implied, but that is no objection; the solution needs no background in math.
The RFC discussed objections to Savant's solution, and seemed to settle more on accepting it as good enough for the lay person. I note in these footnotes of the closers' original discussion that the criticism is mostly in journals catering to undergraduates or math teachers, and are written with them in mind. These are not refutations of correctness, they are more objections from a math pedagogical point of view. Lack of math precision and lack of generalizability seem the main objections, and neither matter for the average Wikipedia reader. The solution is accurate for the problem posed, as mentioned in greater detail here. As such, criticism of Savant's solution does not meet our neutral-point-of-view policy, since the context of WP is different from that of a journal intended for math pedagogy.
General wording of the problem
The weight of arguments in the RFC indicates we should avoid words such as random, uniform, unbiased and so on in the lead and the initial sections. People do not talk of tossing an unbiased coin in a random or uniform way. They just refer to a "coin-toss result." Math teachers do use such words for precision, but WP is not a math encyclopedia. In sections farther down, where the article discusses solutions of the second set, the more precise terminology should be used. Adding to the arguments in the RFC, I will point out the extensions to the vos Savant formulation (Monty Fall and Monty Crawl of Rosenthal an example) should not be treated in great length because: 1. The sources are actually primary, containing new analysis, and 2. In many cases, the sources are in journals without even an impact factor, indicating they, in this case Math Horizons, are meant for a non-research readership, typically math undergrads and teachers (see footnotes from closers' original discussion). Editors should not provide too much weight to extensions used by teachers to help students learn concepts. WP is not a textbook.
Total symmetry proof
The door numbers are irrelevant only before the beginning of the game. If one door has been chosen by the player then the number of this door is identified with the (content of the) specific door. A subsequent renumbering of the doors would imply another arrangement of the (content of the) doors themselves. If you think that the door numbers in a specific case are irrelevant to deciding whether to switch or stay, see the following example:
Assuming that the distribution of car and goats behind the doors is randomly but fixed, the player, who picks door No.1, picks the left door in common sense, and the host, who opens goat door No.3, opens the right door in common sense, basing on the permutation (1,2,3). Another permutation (3,1,2) would lead to the situation that the player picks the middle door No.1 and the host opens the left door No.3 which has a goat. With the car behind the middle door, switching in the first case would give the car, but switching in the second case the goat. So, on one side we have a contradiction referring to the chosen door (left vs. middle) and on the other side the Indicator random variable 'I' depends on which permutation has been realised. --213.102.98.78 (talk) 11:46, 22 October 2012 (UTC)
- Suppose the location of the car, the player's initial choice, and the choice of the host which door to open (when he has a choice) are all uniform at random. Full symmetry. Then the probability or conditional probability of any event is not changed by renumbering the doors. In particular, Prob(switching gives car | player chose door x and host opened door y) does not depend on x and y. Therefore, the values of the numbers x and y are irrelevant for making the choice whether or not to switch. Whether or not the remaining closed door hides the car is independent of the actual numbers on the door chosen by the player and the door opened by the host. Richard Gill (talk) 17:06, 22 October 2012 (UTC)
- Please read what the article says:"Now, however we renumber the doors, whether or not switching gives the car does not change, 'I' is invariant." This is not true for any permutation. --213.102.99.174 (talk) 17:30, 22 October 2012 (UTC)
- The article says that the event that switching gives the car does not change on renumbering the doors. Notation. Let (1,1,2) denote the outcome (omega, in probability theory language) car is at door 1, player chooses 1, host opens 2; let (1,2) denote car is at door 1, player dhooses 2 ( host necessarily opens 3). The event "switching would give car" consists of the outcomes (1,2), (1,3), (2,1), (2,3), (3,1), (3,2). Replace in that set the numbers 1,2,3 by any permuatation thereof, and the set remains the same.
- At the point when the player is offered the choice of stay or switch, the three doors each have a different manifest (visible) role: door chosen by player, door opened by host, remaining door left closed by host. Two of those three doors also have a hidden role: which of the two hides the car. That's one part of the problem. The three doors also have numbers (1, 2, 3: as viewed from left to right by the audience). With the probability assumptions giving total symmetry in problem description (except for the specific naming "say, Door1, say, Door 3"), ie first three choices completely random as far as the game rules allow -- location of car, door of player, door opened by host -- the relationship between manifest and hidden roles of the three doors is statistically independent of the numbering of the doors (ie which door as identified by roles is which door as identified by number). Thus to decide whether to switch or stay, the numbers are irrelevant. As Kraus and Wang (psychologists) emphasize, it's the specific numbering of doors which builds the visual picture of the problem which traps people into giving the wrong answer. Under the motto "less is more" they point out that a succesful strategy in problem-solving in general consists in realizing what is irrelevant and discarding it, thereby facilitating a new, better, mental picture. I think that many amateurs (people not trained in probability theory) instinctively can and do realise that the door numbers are irrelevant and hence - given this fact - intuitively know that the simple solution is perfectly adequate. My guess is that Vos Savant herself belongs to this category of people. A quick and flexible mind, but not formally trained as a mathematician. Time and time again, wikipedia editors come up spontaneously with the same informal solution. Such people can't be blamed for not knowing the professional mathematician's code words for describing a situation like this. Symmetry and invariance under a group of transformations which leave a problem invariant is one of the most elegant way a mathematician can reduce a problem to essentials, thereby making it easier to solve. Less is more! Personally, I like it that one of the mathematician's most powerful professional tools comes up here in this popular brain teaser as also being a general tool in problem solving, cognition. Richard Gill (talk) 10:36, 23 October 2012 (UTC)
- I hope you include change of goat revealed in your group of transformations which leave a problem invariant. Martin Hogbin (talk) 17:06, 23 October 2012 (UTC)
- The point is to simplify a problem by showing that certain features of the problem description are irrelevant. There is no point in adding superfluous detail only to thereafter to come up with a good reason why these extra details are not important. Anyone who wants to simulate MHP starts by choosing a door number for the car, choosing a door number for the player, and so on. It's a nontrivial fact that they could have done the following: decide with probabilities 2/3 and 1/3 whether the other closed door hides the car; then, independently of this, assign door numbers (1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2) or (3,2,1) to (door chosen by player, door left closed, door opened by host) each with probability 1/6. However, if you are aware of this fact, it means that the door numbers of any specific case are irrelevant to someone who has to decide whether to switch or stay. Martin: your intuitive understanding of MHP is splendid, but you seem unable to discriminate between what is given in advance and what can be / has to be derived from what is given, I take it that you "buy" the usual K&W assumptions. The irrelevance of door numbers is now a fact which can be deduced. And which needs to be deduced if you want to show, not only that "always switching" is smart, but also that there is nothing better. Richard Gill (talk) 17:50, 23 October 2012 (UTC)
- I have no idea where you get, 'Anyone who wants to simulate MHP starts by choosing a door number...', from, or what its relevance to my point is.
- The point is to simplify a problem by showing that certain features of the problem description are irrelevant. There is no point in adding superfluous detail only to thereafter to come up with a good reason why these extra details are not important. Anyone who wants to simulate MHP starts by choosing a door number for the car, choosing a door number for the player, and so on. It's a nontrivial fact that they could have done the following: decide with probabilities 2/3 and 1/3 whether the other closed door hides the car; then, independently of this, assign door numbers (1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2) or (3,2,1) to (door chosen by player, door left closed, door opened by host) each with probability 1/6. However, if you are aware of this fact, it means that the door numbers of any specific case are irrelevant to someone who has to decide whether to switch or stay. Martin: your intuitive understanding of MHP is splendid, but you seem unable to discriminate between what is given in advance and what can be / has to be derived from what is given, I take it that you "buy" the usual K&W assumptions. The irrelevance of door numbers is now a fact which can be deduced. And which needs to be deduced if you want to show, not only that "always switching" is smart, but also that there is nothing better. Richard Gill (talk) 17:50, 23 October 2012 (UTC)
- I hope you include change of goat revealed in your group of transformations which leave a problem invariant. Martin Hogbin (talk) 17:06, 23 October 2012 (UTC)
- At the point when the player is offered the choice of stay or switch, the three doors each have a different manifest (visible) role: door chosen by player, door opened by host, remaining door left closed by host. Two of those three doors also have a hidden role: which of the two hides the car. That's one part of the problem. The three doors also have numbers (1, 2, 3: as viewed from left to right by the audience). With the probability assumptions giving total symmetry in problem description (except for the specific naming "say, Door1, say, Door 3"), ie first three choices completely random as far as the game rules allow -- location of car, door of player, door opened by host -- the relationship between manifest and hidden roles of the three doors is statistically independent of the numbering of the doors (ie which door as identified by roles is which door as identified by number). Thus to decide whether to switch or stay, the numbers are irrelevant. As Kraus and Wang (psychologists) emphasize, it's the specific numbering of doors which builds the visual picture of the problem which traps people into giving the wrong answer. Under the motto "less is more" they point out that a succesful strategy in problem-solving in general consists in realizing what is irrelevant and discarding it, thereby facilitating a new, better, mental picture. I think that many amateurs (people not trained in probability theory) instinctively can and do realise that the door numbers are irrelevant and hence - given this fact - intuitively know that the simple solution is perfectly adequate. My guess is that Vos Savant herself belongs to this category of people. A quick and flexible mind, but not formally trained as a mathematician. Time and time again, wikipedia editors come up spontaneously with the same informal solution. Such people can't be blamed for not knowing the professional mathematician's code words for describing a situation like this. Symmetry and invariance under a group of transformations which leave a problem invariant is one of the most elegant way a mathematician can reduce a problem to essentials, thereby making it easier to solve. Less is more! Personally, I like it that one of the mathematician's most powerful professional tools comes up here in this popular brain teaser as also being a general tool in problem solving, cognition. Richard Gill (talk) 10:36, 23 October 2012 (UTC)
- You say above, 'I think that many amateurs (people not trained in probability theory) instinctively can and do realise that the door numbers are irrelevant...'. If I wanted to be as patronising as you I could say, 'It seems that you instinctively realise that the goat revealed is irrelevant...'.
- By the way, I think it would be better to continue this discussion in my user space as you started to. Martin Hogbin (talk) 23:56, 23 October 2012 (UTC)
- I am not trying to be patronizing. I want the article to be based on intuition and common sense, Reduce dogmatism and formalism. Keep MHP fun. I do not want the article deformed by the way so-called professionals think about probability problems. Who have become so accustomed to one particular formalusm that they can't even communicate with ordinary folk any more. Richard Gill (talk) 08:15, 24 October 2012 (UTC)
- I am with you there. Common sense tells us that the door numbers (and goat ID) are unimportant. It was also the clear intention of vos Savant that we should completely disregard these things. So let us do that and be done with it. The simple solutions (ones that do not consider door numbers, such as that opened by the host) are complete, correct, and answer the question exactly as asked. Nothing more is needed, no K&W, no symmetry argument, no special assumptions. That is what I, and many others, have been saying for years.
- The problem is you seem to be suggesting that 'mathematicians' are, in some way, not satisfied with the simple solutions, possibly for reasons that mere mortals do not understand. That seems to be where we disagree. If so, I would be happy to discuss that with you elsewhere. Martin Hogbin (talk) 09:11, 24 October 2012 (UTC)
- I would prefer not to see a side discussion in userspace. It is hard enough to keep up with the ever-growing wall of text as it is. BTW, in my opinion Dr. Gill is on the right track here. --Guy Macon (talk) 09:15, 24 October 2012 (UTC)
- Guy, I was only trying to stop clogging up this page with yet more discussion on the same subject. You were the one who complained about the quantity of text produced on this page. I am perfectly happy to keep all discussion here if you prefer. Martin Hogbin (talk) 17:59, 25 October 2012 (UTC)
- I would prefer not to see a side discussion in userspace. It is hard enough to keep up with the ever-growing wall of text as it is. BTW, in my opinion Dr. Gill is on the right track here. --Guy Macon (talk) 09:15, 24 October 2012 (UTC)
- Martin I am not trying to suggest that mathematicans collectively are not satisfied with simple solutions. There are several categories of mathematicians. There is the pedantic formalist type who only knows one way to solve MHP and thinks everything else us wrong. There is a more imaginative type who sees value in informal popular solutions and moreover sees that they correspond to other more creative mathematicians' solutions. Solutions based on fundamental structural insights, rather than on blind calculation by first principles (within the conventional formalism - which ordinary people don't know anything about). Richard Gill (talk) 10:21, 24 October 2012 (UTC)
- I agree with that exactly. The only question I have therefore is why have you supported pandering to the 'pedantic formalist type who only knows one way to solve MHP and thinks everything else us wrong' rather than the 'simplist' view which appeals to both the general reader and the 'more imaginative type who sees value in informal popular solutions and moreover sees that they correspond to other more creative mathematicians' solutions'? As I have said right from the start, the simple solutions are most easily understandable by the general reader and perfectly correct (or at least defensible) to experts.
- What are we doing complicating the puzzle with the so called 'conditional' solutions? These are an academic, and eventually rather pointless sideshow. Martin Hogbin (talk) 17:59, 25 October 2012 (UTC)
- The important thing is whether a solution is intuitive and accessible. There are solutions which are intuitive and accessible, whiche help the reader gain insight, while at the same time being mathematically/academically equivalent to a conditional probability solution. EG: Devlin combining doors argument fixed. Initially the odds on your door hiding the car are 2:1 against. The host opens a door (you don't know which) revealing a boy goat with blue eyes and a pink ribbon around its neck. The odds on your door hiding the car remain 2:1 against because he was going to open a door and reveal a goat anyway. The specific infirmation about the colour/sex/age/religion... of the goat is irrelevant. Finally you are told that the door that was opened was door 3. The odds on your door hiding the car are stilll 2:1 against since whether or not the car is behind your door, it's equally likely for you that door 2 or 3 gets opened.
- Why do you want to withhold this solution from the wikipedia reader? Already the discussants of Morgan et al. pointed out that symmetry means the difference between simple and conditional solutions is essentially a matter of taste.
- Do you agree that the chance of winning by switching is 2/3, whatever door the player picks and whichever door the host opens? Do you agree that it is not difficult to explain why this is the case? Why do you want to keep this fact hidden from the reader of wikipedia? There is nothing academic or formalistic about saying "the chance of winning by switching is 2/3, whatever door the player picks and whichever door the host opens". Solutions which deliver this, in particular which add the "whatever", come to a more powerful conclusion than solutions which don't deliver this extra. Some readers will appreciate the extra mileage. Others can ignore it. A matter of taste. See Bell's discussion of Morgan et al. Richard Gill (talk) 14:32, 26 October 2012 (UTC)
- What are we doing complicating the puzzle with the so called 'conditional' solutions? These are an academic, and eventually rather pointless sideshow. Martin Hogbin (talk) 17:59, 25 October 2012 (UTC)
Intuitive, accessible and convincing are the most important points of the initial solutions that we give to our readers. Nearly everyone finds it quite obvious that the door numbers and the goat ID are irrelevant. What many people do not find so easy to accept is that the odds of winning by swapping are 2/3 and that this is only true if the host knows where the car is. That is what the puzzle is all about and clearly was intended to be the point of both W/vS and Selvin's problems. If we start to discuss irrelevant facts too early readers may get the impression that the door numbers are the key to understanding why the player gains by switching.
I am not trying to hide anything but there is no record of any one of the thousands of replies that vS had mentioning anything about door numbers but, for the few readers who are interested, I have no problem in discussing all the things that you mention above but only after readers have grasped the intended point of the puzzle.
In some cases the average person's intuition turns out to be correct (that the door numbers do not matter) in other cases their intuition leads then astray (that swapping has no advantage}. It is the case where intuition goes wrong that we need to concentrate on. Martin Hogbin (talk) 15:36, 26 October 2012 (UTC)
- Martin, you didn't answer my question. Do you seriously think that the (fixed) Devlin combining doors solution is too difficult for the early part of the Wikipedia article? You even tried to write iit out yourself, a few months ago (your wording was a little careless, but easily corrected)! Richard Gill (talk) 13:45, 27 October 2012 (UTC)
- I am not against doing that. What exactly is the problem that you want to fix and how would you word the fix. Martin Hogbin (talk) 22:09, 27 October 2012 (UTC)
Okay, what has been proven is: If the rules are independent of the door numbers and the progress of the game is symmetric (the location of the car, the player's initial choice, and the choice of the host which door to open (when he has a choice) are all uniform at random) then the results are independent of the door numbers and symmetric. But does this need a proof, isn't it trivial (symmetry implies symmetry)? AND, the players initial choice is not uniform at random, his choice is optional in the 'standard' problem.
So, the "total symmetry proof" is fully superflouos, and it's only purpose is to propagandize a certain understanding of the standard problem, changing the problem's content by introducing additional assumptions. It is the same trick used again and again to reduce critics to silence, in this case to silence the editors who insist on the necessity of using conditional probability for problem solving. --213.102.98.191 (talk) 10:57, 29 October 2012 (UTC)
- Indeed it is trivial that symmetry implies symmetry! By symmetry, the specific door numbers in a particular case are irrelevant to the decision whether you should stay or switch. It is easier to talk about symmetry when the player's initial choice is also thought of as random, as a large number of sources do (Selvin, Grinstead and Snell) and as K&W acknowledge is common. Then the symmetry in question is that of all six permutations of (1,2,3). But if you don't like this you can use just the symmetry of permutations of 2 and 3. Moreover it is an approach which is out there in the published literature on MHP. A standard German introductory probability text by a respected matheamtician, I forget who just at the moment, sorry, starts by numbering the doors according to their roles: Door 1 is the door hiding the car. The original door numbers are explicitly "forgotten" because they are "obviously" irrelevant. Symmetry is used by William Bell, one of the discussants of Morgan et al., to bridge the gap between conditional and unconditional solutions.
- Your remark, 213.102,98.191 (how about getting yourself a name?), about how obvious this all is, is important. Bell too said that the symmetry is so obvious that it seems a matter of taste whether one is explicit about conditional versus unconditional. You say that it is necessary to use conditional probability for problem solving. You are welcome to your opinion. But not everyone has the same opinion. In particular, many sources on MHP don't have this opinion. My personal opinion is that it depends on the audience, on the context. For some readers this is an important distinction, for others it isn't. The challenge is to write the article so that both kinds of readers will be happy with it.
- By symmetry between doors 2 and 3, given that you chose door 1, whether or not you should switch is independent of whether the host opened door 2 or door 3. The chance of winning by switching is 2/3. By independence, the chance of winning by switching given the host opened door 3 is 2/3. That's all. Richard Gill (talk) 12:51, 29 October 2012 (UTC)
- You wrote:"The challenge is to write the article so that both kinds of readers will be happy with it." Okay, my proposal for the construction of the article:
- 1. Vos Savant's simple solution
- 2. The standard problem (Krauss and Wang)
- 3. The 'normal' answer for the 'normal' reader using conditional probability which is easy to understand
- 4. The 'smart' answer for the 'smart' reader using strategic thinking etc.
- 5. Variants of the problem
- 6. etc.
- This would be a clear set-up in my opinion. --213.102.96.132 (talk) 16:20, 29 October 2012 (UTC)
- I would be happy with that. As long as part 3 really is accessible to ordinary people, and the whole thing is not composed in a dogmatic style with suggestions of insufficiency of some solutions and superiority of others. But in a neutral, positive, way. Richard Gill (talk) 07:57, 31 October 2012 (UTC)
- You wrote:"The challenge is to write the article so that both kinds of readers will be happy with it." Okay, my proposal for the construction of the article:
- Doubling vos Savant's table it can be distinguished between six cases, all equally likey, with the left door chosen by the player. In three cases the right goat door, in other three cases the middle goat door is opened. In two of the respective three cases the player wins the car by switching. IMO this solution is easily to understand and fits to the K&W assumptions perfectly.
- Moreover the table's benefit is that from now on the reader is able to see the symmetry between doors 2 and 3, given that door 1 was chosen. Without such a picture symmetry is a very abstract mathematical concept unintelligible to ordinary people. So, why not go to meet the 'normal' reader at his decision situation in the game? --TotalClearance (talk) 10:59, 1 November 2012 (UTC)
Proposed text for the initial solution section, take 3
I started a new section, as the previous one is getting very long. The following is a new version of the previous proposal, trying to take into account various concerns raised. It's not minimalist anymore, and I'm very unsure which is better, the previous version or this one. I'm putting it up because I simply cannot know what others think without asking. If it's worse, then we can scratch this and build on the previous one.
Proposed text for the initial solution section, take 3
|
|---|
Resolving the paradoxThe player should switch. Switching doubles the chances of winning. [many citations] OutlineMost people initially imagine door 3 as already open, leaving only two possibilities: the car is either behind door 1 or door 2. This usually leads to the incorrect conclusion that the two possibilities are equally likely, and that switching is no better than staying. The problem is actually easier if one does not focus on the two closed doors in this way. It is not necessary to know the chances of the car being behind either closed door to solve the problem. (Krauss and Wang, 2003; Gill 2011; Morgan et al. 1991) The first subsection below covers explanations that take a step back and solve the problem by showing that the best strategy is to ignore the door opened by the host and switch no matter what. The second subsection below focuses on the two closed doors, explaining why the car is not equally likely to be behind either one. The explanations may be understood as analyzes of what happens on average to a simulated player in a sufficiently long simulation. It is not implied in any way that the actual show needs to be repeated multiple times. The optimal strategyIf the player is resolved to stay with their initial choice no matter what, they might as well not be offered the option to switch at all. Staying wins when the player initially picks the car door, which happens 1/3 of the time. Staying loses the other 2/3 of the time. A switcher wins where a stayer loses, so switching must win 2/3 of the time. (Adams 1990, Carlton 2005). This may be easier to grasp if the doors are grouped into player's doors (door 1) and host's doors (doors 2 and 3), as illustrated below. The player is basically given the choice of keeping what's behind their door, or taking everything behind the host's two doors. The host is saying in effect: "You can keep your one door or you can have the other two doors, one of which (a goat door) I'll open for you." No matter what the host does, a player who is determined to switch gets all cars behind the host's two doors. (Adams 1990) The situation can also be analyzed by cases, as illustrated below: Switching wins in two of three equally likely cases. A player who switches no matter what wins 2/3 of the time. (vos Savant 1990b; Krauss and Wang, 2003) Many people find the situation intuitively easier to understand by considering the same problem with a million doors instead of just three. In this case there are 999,999 doors with goats behind them, and the player's chances of picking the car door are one in a million. The host goes down the line of doors, opening each one to show 999,998 goats in total, skipping over only the player's door and one other door. The host then offers the player the chance to switch to the only other unopened door. On average, in 999,999 out of 1,000,000 times (i.e. the times the player initially picked a goat) the other door will contain the prize. (vos Savant 1990; Krauss and Wang, 2003) It is crucial that the host knows where the car is and is not allowed to reveal it. If he doesn't know, then switching and staying are equally good strategies. Staying still wins 1/3 of the time. However, switching also wins only 1/3 of the time. The reason is that switching wins only when the car is behind one of the host's doors (2/3 of the time) and the host nevertheless happens to open a goat door. That occurs 2/3×1/2 = 1/3 of the time when the host has no idea where the car is. (Devlin 2005) It is not actually necessary to assume that the car is initially equally likely to be anywhere, or that the host is equally likely to pick any allowed door. If the player makes their initial choice completely randomly e.g. by using a fair die, then the car is guaranteed to be behind the initial door 1/3 of the time, and behind the other two doors 2/3 of the time. The player's choice is still between taking one door or taking two doors, so the chances of winning by switching are still 2/3. However, with so few assumptions the chances of the car being behind any particular door are completely unknown. What is known is only the probability of winning if the strategy is followed, and that no other strategy has a better guarantee. (Gill 2011) A further look at the two closed doorsOnce door 3 is open, the probabilities of the car being behind each of the three doors have changed. The probability of the car being behind door 3 has dropped to zero, even though initially it was 1/3. Likewise, the probability of the car being behind door 2 has risen to 2/3. It is only the probability of the car being behind door 1 that is still 1/3. One way to see why this is so is to again group the doors into player's doors (door 1) and host's doors (doors 2 and 3), and argue as follows: Initially, the chances of the car being behind the player's door are 1/3, and the chances of it being behind the host's doors are 2/3. Imagine for a moment that the player notices only that the host opened one of his doors to show a goat, but not which door. As the host is certain to open a goat door no matter what, the information that he did so cannot change the chances of the car being behind the player's door. The chances of the car being behind the host's doors also must remain 2/3. As the car is not behind the opened door, the chances of it being behind the remaining door must be 2/3. Further knowing the opened door number cannot change these probabilities, because if it did, the answer would depend on the arbitrary numbering scheme used for the doors. The same argument does not apply when the host is ignorant of the car's location, because then it is not certain that the host will open a goat door. (Devlin 2003, Gill 2011) Another way is to consider what happens on average to players in a simulation, as illustrated below: The above illustration shows everything that can happen to players who pick door 1. On average, three in six end up in the situation where door 3 is open (shown to the left of the thick line). Two of the three win and one loses by switching; therefore the chances that switching wins in that situation are 2/3. (Chun 1991; Grinstead and Snell 2006; Morgan et al. 1991) One may also reason as follows. There are only two possible scenarios that match the observations (the same ones shown to the left of the thick line):
The first scenario is twice as likely as the second, so the car is twice as likely to be behind door 2. (Lucas et al. 2009) The effect of the host's random choice is visualized in the illustration by the thick line. |
Comments on the proposed text, take 3
Some of the concerns (many gleaned from general discussions as there weren't many comments on the previous proposal) I was trying to fix:
- Ningauble and Martin had concerns with section names, so I changed them.
- Elen and Martin (at least) wished for the ignorant host case to be covered, so I added it.
- Ningauble preferred the reference to actual simulations to be elided, so I elided it.
- Ningauble wanted the common confusion to be described before all explanations, so I moved it there.
- Ningauble was concerned with the text appearing to take a frequentist stance, so I explicitly stated that the averages and suchlike are about simulations, which are used both by Bayesians and frequentists, and hence are completely neutral.
- Gerhardvalentin was concerned about any appearance of the text to imply the existence of multiple repetitions of the show, so I added a clarification that it is not implied in any way.
- Martin was concerned that the text would appear to claim that the unconditional solutions do not solve the problem, so I added an explicit claim there that they do solve it.
- There appears to be some aversion to the word "always" in the air, so I replaced them with "no matter what", which are the words used by Krauss & Wang. Incidentally, they make much of getting people to ignore the host's behavior when he has a choice by using wordings like that ("[it] turns out to be a crucial building block of an intuitive solution").
- Richard apparently liked the unconditional/conditional split and Krauss & Wang's explanation of what is difficult for people, so I made the text more explicit about it. Hopefully this is also clearer to the reader and other editors. It is rather nice that the same splitline is significant both cognitively and mathematically.
- Richard likes a solution with objective probabilities and few assumptions and nobody has objected to it, so I added an explanation of it. Perhaps that also makes it clearer that the probabilities of the car being behind the two closed doors are not necessary for solving the problem, which also ought to help with Martin's concerns that those probabilities are portrayed as necessary for solving the problem.
- Martin was afraid that the conditional solution section would be incomprehensible to some readers, so I added two other explanations there, one from Devlin/Gill and another from Lucas et al.
- Ningauble was concerned that cases with unequal weights would require some explanation. Lucas et al.'s explanation does that. I also tried to tie it in with the pre-existing illustration.
- Nijdam was concerned that Devlin's explanation is completely bogus, so I used Gill's version of it.
- Martin was concerned that Devlin's explanation appears to give the wrong result for the ignorant host case. Gill's version is not as misleading, but I added an extra sentence explicitly saying how it fails for the ignorant host case.
- My concerns: I tried to clarify the text in various ways, cover the essential approaches, keep it nicely organized and also correct. I also more or less agree with the other concerns listed above.
Comments? -- Coffee2theorems (talk) 16:02, 16 October 2012 (UTC)
Comment from Richard Gill
I like it! Relaxed style, yet at the same time precise; covers different ways people have looked at the problem in a balanced and unprejudiced way. Richard Gill (talk) 10:06, 23 October 2012 (UTC)
In my opinion, Coffee2Theorems has recently made an excellent proposal for the start of the article. In my opinion it is well-written, encyclopedic, neutral, accessible to a broad (non specialist) audience. Why is no one commenting on his proposal? Richard Gill (talk) Richard Gill (talk) 17:11, 24 October 2012 (UTC)
Comment from Gerhardvalentin
+ Agree Gerhardvalentin (talk) 12:14, 25 October 2012 (UTC)
Comment from Nijdam
I comment step by step.
- I'm not happy with the sentence in the outline: The problem is actually easier if one does not focus on the two closed doors in this way. It is not necessary to know the chances of the car being behind either closed door to solve the problem. As you said, most people focus on door 3 opened, after door 1 has been chosen. And so they should. The solution should make clear the odds are 1:2 instead of 1:1. That's helpful. Nijdam (talk) 13:49, 25 October 2012 (UTC)
- And Kraus and Wang explain why the important step which newcomers have to make in understanding that their initial intuition is wrong, is abandoning their fixation on door number. Less is more! The problem is resolved by forgetting the door numbers. Richard Gill (talk) 14:22, 26 October 2012 (UTC)
- Well, if the train to Amsterdam is delayed, you can always take the train to Utrecht to arrive in time. Nijdam (talk) 15:24, 26 October 2012 (UTC)
- Depends where you come from. Not everyone has the same starting point. (Nijdam is being sarcastic, thinking of people like himself whose train journey to Amsterdam must start with taking a train to Utrecht)Richard Gill (talk) 13:38, 27 October 2012 (UTC)
- Well, if the train to Amsterdam is delayed, you can always take the train to Utrecht to arrive in time. Nijdam (talk) 15:24, 26 October 2012 (UTC)
- And Kraus and Wang explain why the important step which newcomers have to make in understanding that their initial intuition is wrong, is abandoning their fixation on door number. Less is more! The problem is resolved by forgetting the door numbers. Richard Gill (talk) 14:22, 26 October 2012 (UTC)
Comments from TotalClearance
- Coffee2theorems writes:"If the player makes their initial choice using a fair die, then the car is guaranteed to be behind the initial door 1/3 of the time, and behind the other two doors 2/3 of the time." You must not assume that the player is allowed to use a fair die in the show. And it is not self-evident for the reader that the player would use such a die and chose a door uniform at random. The article should avoid additional assumptions. --213.102.96.55 (talk) 13:50, 25 October 2012 (UTC)
- Supporting this comment. The problem does not mention a die, there is no reason to believe that the player has a die, why mention a die. Should just say "ifthe player makes their initial choice at random, then etc etc" --Elen of the Roads (talk) 14:32, 25 October 2012 (UTC)
- Instead of "If the player makes their initial choice using a fair die ..." IMO better: "As the distribution of the three objects behind the doors is unknown to the player, ..." --Gerhardvalentin (talk) 16:05, 25 October 2012 (UTC)
- My impression is that the whole passage from "It is not actually necessary to assume..." until "...no other strategy has a better guarantee." is basing on a die used by the player. Why not remove this section? --213.102.97.40 (talk) 17:22, 25 October 2012 (UTC)
- (edit conflict) The two alternatives in Gerhard's comment precisely identify the very crux of the difference between frequentist and Bayesian interpretations of probability. IMHO, the issue of deciding which it better is best mooted by striving for a way to express this that is agnostic about interpretations of probability. Elen's suggestion is better in this regard. ~ Ningauble (talk) 19:06, 25 October 2012 (UTC)
- My impression is that the whole passage from "It is not actually necessary to assume..." until "...no other strategy has a better guarantee." is basing on a die used by the player. Why not remove this section? --213.102.97.40 (talk) 17:22, 25 October 2012 (UTC)
- If I am the player and if '1' is my lucky number then I would chose the left door surely. Why should I be forced to chose a door randomly? "Suppose you're on a game show, and you're given the choice of three doors." (vos Savant). I have my choice!
- On the other hand, if I know the rules ahead in time and understand their consequences then I would avoid the left door and chose another door first. --213.102.98.151 (talk) 10:15, 26 October 2012 (UTC)
- How about we consult the sources here, rather than presenting our personal opinions? A whole lot of authoritative writers present solutions which start by supposing that the player chooses a door completely at random. The position of the car is considered as fixed (but unknown), what the host will do if he has a choice is fixed (but unknown). The only probability ingredient is the player's choice. And a player who chooses at random and thereafter switches wins the car with probability 2/3. Von Neumann's minimax theorem shows that this is the best the player can hope for. Conditional probabilities given which door was chosen, which was opened, and whether it was a boy goat or a girl goat are irrelevant, from the strategic point of view. Which, I repeated, is a common point of view in the literature, both popular and academic.The distinguished mathematical economist Barry Nalebuff popularized MHP in the ecomoics/game theory literature before Vos Savant made it famous world-wide. Richard Gill (talk) 14:11, 26 October 2012 (UTC)
- PS the smart player knows the rules in advance and therefore does *not* choose his lucky number. If he has any idea where the car is, he should choose the door where it's least likely to be. If he has no idea, he *should* pick a door at random, so that he does not have emotional capital invested in his initial choice. The smart player has read the piterature, knows game theory, and realizes that the optimal strategy is pick at random and switch. Richard Gill (talk) 14:16, 26 October 2012 (UTC)
- Consulting the article:"The car and the goats were placed randomly behind the doors before the show." and "If both remaining doors have goats behind them, he [Monty Hall] chooses one [uniformly] at random."(Krauss and Wang). No words about the player's way of choice.--213.102.96.162 (talk) 15:35, 26 October 2012 (UTC)
- AND, it is not true, that a whole lot of authoritative writers present solutions which start by supposing that the player chooses a door completely at random. On the contrary, many sources present solutions which start by supposing that the car and the goats were placed randomly behind the doors before the show. --213.102.97.241 (talk) 17:21, 26 October 2012 (UTC)
- Sorry, even Kraus and Wang also point out the solution which goes by thinking of the player's choice as random! Also, there is the popular article in The Economist. There are recent publications by A.V. Gnedin on the decision theoretic approach, which were spolighted in "Die Zeit", major German weekly magazine. Sure there are lots of articles taking the objective Bayesian approach and solving the problem using subjective probabiliies determined by symmetry. I'm not denying that. This is the common approach in the academic probability and statistics literature. The popular literature is more diffuse. There is also a decision theory literature. From time to time new wikipedia editors spontaneously bring up a solution of this type. Quite a few of the prob-stat crowd, by the way, also treat the player's choice as completely random. See for instance Selvin's first solution. Anyway, K&W do not say that you have to make the "usual" K&W assumptions. They just say that a majority of people make these assumptions intuituvely. Richard Gill (talk) 13:06, 27 October 2012 (UTC)
- Krauss and Wang make use of the supposition "You now randomly chose a door, say, number 1" only in one of the inquiry forms in the experimental section at the end of their paper. Previously in the mathematical solution section their only one explicitly specified supposition is:"The car and the goats were placed randomly behind the doors before the show."
- Gnedin 'The Doors', 2011 wrote:"It is commonly assumed, often implicitly, that the prize is hidden “uniformly at random”, meaning that it is equally likely to be behind each of the doors."
- I am not denying that in decision theorie it could be an efficient strategy for the player to chose a door randomly at first. But this is another approach and should be discussed later in the article. --213.102.97.179 (talk) 18:07, 27 October 2012 (UTC)
- OK, I clarified that a die is only an example in the text. It doesn't really matter though, as the text explicitly says that the explanations can be taken as analyzes of simulations. Obviously there is no need to use a die on a real show just because you used one in a simulation, any more than you need to bring along shells and a pea if you used those in a vos Savant -style simulation before going on an actual show. You just need some way of generating a random integer from U[1, 3]. -- Coffee2theorems (talk) 22:56, 26 October 2012 (UTC)
- Coffee2theorems writes:
- 1. "The explanations may be understood as analyzes of what happens on average to a simulated player in a sufficiently long simulation. It is not implied in any way that the actual show needs to be repeated multiple times." and later
- 2. "It is not actually necessary to assume...that the host is equally likely to pick any allowed door. If the player makes their initial choice completely randomly...so the chances of winning by switching are still 2/3."
The question is not about the average probability of winning the car by switching concerning a simulated multiple-player. The question is about a certain situation in which a certain player has chosen one door, say the left door, and the host has opened another door with a goat, say the right door. If the player has chosen randomly the left door and if the host, who has a bias torwards the right door to open, has opened the right door with a goat then the chances of winning by switching are not 2/3. --213.102.96.102 (talk) 15:39, 27 October 2012 (UTC)
- 213.102.96.102 said "The question is not about the average probability for winning the car ... if the host, who has a bias forward the right door to open ...". Monotonous and boring. So I repeat it once again and again and again: Millions of words, and binders full of "But what if the host is biased?" – Binders! We are discussing here the first part of the article, based on sources. Not the very later section about quite other scenarios. Gerhardvalentin (talk) 00:51, 28 October 2012 (UTC)
- Are you not aware of the problematic nature of the assertion 2? The 'simple' solution as described in the proposal requires the assumption that the host chooses one door uniformly at random if both remaining doors have goats behind them. For that reason the assertion 2 is wrong. --213.102.98.239 (talk) 10:24, 28 October 2012 (UTC)
- Assertion 2 is not problematic, it is fully correct, please read the sources. Millions of words. We finally should know at last what we are talking about. We are to clearly keep apart two quite different aspects that we must stop to mingle. There are sources on the paradox, and there are sources on teaching and learning conditional probability theory. Both aspects are to be considered, but never to be mingled. Working on this article requires knowledge of both kinds of sources. We have to distinguish
- the "paradox" (whatever door numbers involved, switching from the door first selected to the second remaining still closed door wins the car 2/3 of the time, period)
- and teaching and learning conditional probability theory.
- The paradox in three trials: "2/3, 2/3, 2/3".
By adding additional assumptions on given actual knowledge available to you regarding the car hiding door, e.g. if you assume transparent see-through doors, then those three trials will give "1, 0, 1" (in every possible permutation).
Or if you assume to have "knowledge (!)" that the host is extremely biased, and the direction of his bias as well, then the three trials will give
"1, 1/2, 1/2" (in every possible permutation).But don't forget the question is on a one-time game show with an unknown host. So Krauss and Wang say that you impossibly can get additional information on any host's bias, and Norbert Henze says the same with the words "the host is observing strict secrecy regarding the car-hiding door". – Btw, besides it is on a one time game show with an unknown host. it is absurd to assume a host who gives additional hints regarding the car-hiding door. Giving away hints on the actual location of the car is completely contrary to his focus of interest, it therefore has nothing to do with the actual question "is it to your advantage". This never is subject of the paradox, but this is only subject matters in schools teaching conditional probability. And Falk says that you can consider any host's bias only if it is given that the host "IS biased" and that you "KNOW" about this bias. So please read the sources. The biased host is not a matter of the paradox, but of school stuff in learning conditional probability theory.
And "If the host got two goats, then he chooses uniformly at random which door to open" resp. "The host is to observe strict secrecy regarding the car hiding door" are just only precautionary to keep the reader from being caught in the "host's bias" trap, to erroneously infer that door numbers could involve additional information regarding the car hiding door and therefore eventually "could" influence the odds of staying:switching. In effect, they never can. Within the paradox, all you ever will know is that the chance to win by switching will be 2/3 in each and every case. Read the sources that also refer to the law of total probability. Having been enabled to get that point, one can see that modern sources are correct in even saying that "the host is most welcome to be biased as much as he wants to", because we give a damn about and never need care. Krauss and Wang, Norbert Henze and other authorities just keep newcomers from erroneous futile side walks and false conclusions. No more deliberate confusion in the article. Gerhardvalentin (talk) 12:42, 28 October 2012 (UTC)
- Assertion 2 is not problematic, it is fully correct, please read the sources. Millions of words. We finally should know at last what we are talking about. We are to clearly keep apart two quite different aspects that we must stop to mingle. There are sources on the paradox, and there are sources on teaching and learning conditional probability theory. Both aspects are to be considered, but never to be mingled. Working on this article requires knowledge of both kinds of sources. We have to distinguish
- IMO it is obvious that the assumptions about the rules of the game including the host's behaviour are always asumptions about the player's knowledge. Otherwise they don't make sense because it is the player who wishes to compute his chances of winning the car.
- The "paradox" may be the result of solving the problem, but we need a solution firstly. And instead of "switching...wins the car 2/3 of the time", the answer for the one-time-player Conny can be solely "she should switch (or not) because her probability of winning by switching is...". --213.102.98.191 (talk) 20:08, 28 October 2012 (UTC)
- Yes, the question is what to do in a certain situation. There are many ways to answer it. One way is to argue that the average probability of winning the car is 2/3 when you follow the strategy "pick a door randomly, then switch", and no strategy has a better guarantee, so you should therefore follow this strategy. If you assume that the car is placed uniformly at random, then the strategy "pick door 1, then switch" also has 2/3 probability of winning, and no strategy has a better guarantee. With that assumption, you know that you should switch if you picked door 1, no matter how it was picked.
- Either way, 2/3 is the average probability of winning. It is not the probability of winning in a particular situation, but then again, you don't need to know that probability. If you want to know it nevertheless, it is computed in the "A further look [...]" subsection, which makes use of the extra assumption that the host picks uniformly at random among allowed choices (it is necessary for computing that probability, but unnecessary for showing that switching is better). -- Coffee2theorems (talk) 16:28, 29 October 2012 (UTC)
- The situation is: left door chosen, right goat door opened. In this moment you cannot argue with a strategy which has to be followed previously from the beginning of the game. The 'normal' reader is understanding his first choice as a search for the car, not as a choice to avoid it. We should keep such elaborated arguments (strategy, total symmetry etc.) for the section for the 'smart' reader. We all know that the conditional solution is fully correct and easy to understand with the aid of an illustration. So, why not give this chance of comprehension to the reader also? And why insist on the additional assumption about the player's first choice uniformly at random, if it isn't necessary? In this case: less is more! --TotalClearance (talk) 17:45, 31 October 2012 (UTC)
- Before discussing possible answers it should be clarified what the question is. At the moment the sole fully unambiguous, mathematically explicit version of the standard problem in the article is the statement from Krauss and Wang, with the contestant knowing all about the rules including the host's (symmetric) behaviour. This formulation should be referred to by the possible solutions and any additional assumptions should be avoided. --213.102.98.191 (talk) 20:08, 28 October 2012 (UTC)
- The question is what the player should do. And our task is not to answer that question ourselves, but to survey the literature, which provides one answer, switch, but many motivations. The reader first needs to understand that the usual immediate intuition "it doesn't matter, so I'll stay" is wrong. Simple solutions do just that. Kraus and Wang did not define the one and only way to mathematically formalize MHP. They merely attempted to write down what they observed that many subjects are explicitly or implictly prepared to assume. Richard Gill (talk) 09:30, 29 October 2012 (UTC)
- The question is what the player should do under specific circumstances, and the question should define the circumstances clear, complete and unambiguous before giving an answer. --213.102.98.191 (talk) 11:10, 29 October 2012 (UTC)
- Yes, it is on the specific circumstances, it is on the context. MvS told a tricky story of an imaginary one-time game show with an imaginary unknown one-time host. The story evolves in steps, and the paradox finally arises at the end of that story.
At first, you only know that three closed doors do hide only 1 car and 2 goats. – In that one-time event, the distribution of the objects behind the doors is known to the imaginary one-time host. For the player, the three doors have chances on the prize of 1/3 + 1/3 + 1/3 = 1.
The player selects one door, and by that he irrevocably divided the entity of those three doors into two parts: his door selected with a 1 in 3 chance on the car, and the group of two unselected doors, having together (as "any" group of two doors likewise) a 2 in 3 chance on the car, although they must contain one goat "at least". The unknown one-time host in this imaginary one-time show got either two goats in 1 out of 3, or he got one goat and the car in 2 out of 3. He has to open one of his two doors in order to show a goat, and he has to ask the guest if he wants to swap to the host's second door that he still left closed.
Such imaginary one-time host is out of position to show any bias in favour of a special door if he got two goats to show. So, whichever of his two doors the host did open, that does not change the 1 in 3 chance of the door selected by the player. Such unknown imaginary one-time host is unable to give away any additional "hint" regarding which door actually is hiding the car nor which door actually is hiding the second goat. Even if he would like to do so, in this context he is unable to show any of such additional hint. Besides, giving away hints on the actual location of the car is completely contrary to his focus of interest.In this context, the unknown imaginary host is not able to give away any of such additional "hint": Devlin's host is right in saying to the player, after having opened a door in order to show a goat behind, "I did NOT change the chance of your selected door". Norbert Henze says that the host "does observe secrecy regarding the car-hiding door", and Krauss and Wang call it "the host chooses uniformly at random which door to open if he got two goats to show". See the sources. So the core of the paradox is that the host's opening of one unselected door, in intentionally showing a goat, cannot change the chance of the door that the guest has first selected.
That means for the paradox that, irrespective of which door the guest did select, and irrespective of which of his two doors the host has opened to show a goat, the chance on the car of the guest's first selected door did not change but did remain 1 in 3. And the still closed host's door now has a chance of 2 in 3. So the guest should switch to the door offered. The probability to win by switching, considering all you know, is 2/3 in this special imaginary one-time game show, and you never will know better. Using conditional probability you get exactly the same result, it shows that switching gives the car with probability 2/3, whatever door is chosen by the player and whatever door is opened by the host. But more important: There are quite a range of other methods of approach that all are telling you the same result also, exactly the same solution: Staying is definitely excluded and switching is imperative.
The circumstances are clear, complete and unambiguous before giving an answer, so the only "solution" of the paradox is the correct answer: SWITCH here and now.
But please note that, for the purpose of teaching and learning conditional probability theory, there is a bulk of textbooks that use the MHP in various variants. Without impact on the famous paradox. Regards, Gerhardvalentin (talk) 10:21, 30 October 2012 (UTC)
- Yes, it is on the specific circumstances, it is on the context. MvS told a tricky story of an imaginary one-time game show with an imaginary unknown one-time host. The story evolves in steps, and the paradox finally arises at the end of that story.
- The question is what the player should do under specific circumstances, and the question should define the circumstances clear, complete and unambiguous before giving an answer. --213.102.98.191 (talk) 11:10, 29 October 2012 (UTC)
- Imagine that you have to give these explanations in the article to the reader who wishes to understand the core of the paradox. You would need at least 30 lines, and you cannot be sure that ordinary people is able to follow your arguments. Compared to that, a conditional solution table is short and a good picture to visualize what happens in the game.
- You said:"Norbert Henze says that the host "does observe secrecy regarding the car-hiding door"." This is a very artificial argument not helpful for the solution. If the host is unknown then you must not suppose that he does observe secrecy regarding the car-hiding door. --TotalClearance (talk) 18:24, 1 November 2012 (UTC)
- ??? Please read, not misconstrue. Morgan et al. say for example that the host e.g. could be "known" to prefer to open one of his two doors, say door #3, and to avoid to open door #2, if ever possible. Whenever such host opens his preferred door #3, then he can do that in only 2 out of 3 situations:
(1) if he got two goats but NO CAR, and switching will loose the car, and
(2) if he got the CAR behind door #2 and a goat behind door #3 and switching will win the car. In this "worst case scenario" of opening his preferred door #3, such biased host could be signalizing that sctually the chance to win by switching will be 1/2 only.
(3) But if such host got one goat and the car, and the CAR being behind his preferred door #3, he would be forced to open his avoided door #2 to show a goat, and in opening his avoided door #2 such biased host could signalize that switching actually will win the car for sure (best-case scenario): supposed asymmetry.Falk however says that for such considerations the host MUST in effect be biased and you have to KNOW about such bias. Not applicable to an imaginary one-time game show with an unknown imaginary one-time host. So the context says that this unknown imaginary one-time host in one imaginary one-time game show is out of position to give any of such "additional hint" on the actual location of the car by his actual opening of a loosing door, be it door #2, or be it door #3. No observer can expect any benefit in "utilizing any ungiven asymmetrical host's bias" for opening either door #2 or door #3, if he has a choice, to get any "additional hint" on the actual location of the car. For the "view of any observer" it makes no difference at all whether the host opens door #3 or door #2: Symmetry, no additional hint on the actual location of the car. Krauss and Wang call it "If the host has a choice between two goats, you have to take him to choose the door he opens uniformly at random": No additional hint, but symmetry. And Norbert Heinze calls it "take the host to be observing secrecy regarding the door that hides the car." – Very helpful to avoid aberrancy. In plain English: symmetry. The door first selected by the player had a chance to win the car of 1/3, and it remains 1/3, whether the host opens door #2 or door #3. This cannot and does not change the odds of the door first chosen by the player. Gerhardvalentin (talk) 21:32, 1 November 2012 (UTC)
- ??? Please read, not misconstrue. Morgan et al. say for example that the host e.g. could be "known" to prefer to open one of his two doors, say door #3, and to avoid to open door #2, if ever possible. Whenever such host opens his preferred door #3, then he can do that in only 2 out of 3 situations:
- The host who is forced to open an unchosen goat door thereby is forced to give a hint on the position of the car. The hint leads to the car being more likely behind the remaining door than behind the firstly chosen door. So, with the host's help you have additional information about the car's position namely the probability of the remaining door hiding the car is 2/3, not 1/2. In other words, a host who is observing secrecy referring to the position of the car has to take care that the odds for both the closed doors would be the same.
- If the host is complete unknown then you don't know why he has opened the goat door 3. If you don't know why he has opened door 3 then vos Savant's solution table is incomplete and you have to consider more alternatives all equally likely. From the fact "the host opened goat door 3" cannot be deduced the assumption "the host had to open an unchosen goat door". --TotalClearance (talk) 13:03, 2 November 2012 (UTC)
Comment from Reidme
Re: First stmt in Outline: "Most people initially imagine door 3 as already open..." My intuition is that this may be unimportant, even if true. Because I think that if MPH virgins had this presented in such a way that they only get information when they need to know it, that the outcome would be similar.
Test:
- Host: I play this game a lot. Here, pick one of these door - there is a prize behind one and nothing of value behind the others. Waiting... OK now that you have made your choice, I will let you know that I always open one of the remaining doors and it always is a loser. Here goes. OK, now that you see it isn't behind door X, would you like to stay or switch?
Is there any available evidence to suggest that people in such a test case are likely to process this problem differently and therefore get a different outcome? If not, the conclusion is not supported that the weak choice is because of people imagining door 3 to be open. i have not presented the above test, yet I have had no problem getting people to agree that the initial choice is 1/3 probability and go on to insist that with the open door it is now 1/2. But I am not familiar with the literature and also perhaps I don't understand what problem you are addressing. Reidme (talk) 03:34, 27 October 2012 (UTC)
- Read the article by Kraus and Wang. Online, free. The authors are psychologists / cognitive scientists. Who even carried out a lot of experiments to find out how people think and how ways the problem is posed influence their solutions. Richard Gill (talk) 13:33, 27 October 2012 (UTC)
Proposal to add a link to the External Links section
I propose allowing the following to be added to the External Links section:
→ Three Doors Probability Problem (Simulator to go through 100 simulations in a couple of minutes) ←
I have twice introduced the link and had my edits undone. I believe the link has strong merit because of its utility and is relevant to anyone who is struggling with, and studying, the Monty Hall problem. I link it as a valuable resource of functionality at a level that is not duplicated in the other links already there.
Though I did create the content on the pages (over a decade ago), I think it stands on its own merit and its self-evident utility in facilitating learning through experience. I have looked at the other simulators and I don't see why anyone would see the NYT version as even being equal, let alone providing an experience superior to the one my simulator offers. What the web application I have linked to does is allow people to quickly go through a bunch of Monty Hall problem-like games in real time while stats are kept for them. 100 games. They can switch or stay or change for every round. No waiting for the next game to load, since all 100 are loaded and visible at the onset.
I am currently in a Model Thinking class on coursera.org where more than a few people did not get the logic that is so obvious to you and me. Graphs mean nothing. Logic means nothing. If you have known this problem a long time then you know what I mean. They have to smash their heads against something that doesn't allow them to hold onto their erroneous constructs. And it has to be accessible enough to keep them engaged.
According to my calculations, if you run through the problem for 100 games, there is a 95% chance you will wind up with more than 57 wins if you switch every time. And a 99.7% chance that you will get 53 or more out of 100. But with 10 games, there is about 32% chance that you will get 5 or less wins by switching every time. That is based on my recent learning of standard deviations, so you can correct me if I am incorrect here. If it is correct, that means that if someone goes the NYT version for 10 tries (I found it to be very slow), they may well find it is 50/50, based on their limited experience, and be burned out from the transaction time. Simply put, the feedback from my simulation is instantanous with no waiting for a new game to load.
So why not allow the link above to be added to the External Links Section? Anyone in favor of this, please respond. And anyone opposed, please articulate why.
Thank you,
Reidme (talk) 18:59, 22 October 2012 (UTC)
- In favour. NYT uses flash, doesn't work on iPad. Wolfram is dull. This one is good. Richard Gill (talk) 06:48, 23 October 2012 (UTC)
- PS The probability an always-switcher wins 59 or more of 100 games is 95.66%. The probability he wins 53 or more of 100 is 99.83%. the probability he wins 5 or less of 10 games is 21.31%. (Binomial probabilities computed with "R"). Why report approximations, when you can easily report the exact probabilities? There are webpages which compute exact binomial probabilities for you, as well as state of the art free statistical software. Richard Gill (talk) 17:48, 24 October 2012 (UTC)
- Richard, Excellent! Will correct my simulator page accordingly and include links to two binomial probability calculator pages. Reidme (talk) 02:10, 26 October 2012 (UTC)
- Thank you, Richard. I posted the standard-deviation based binomial probabilities for this on the wiki page for the Model Thinking at coursera.org. The SD work I did changed my understanding of what we are dealing with when people don't quickly get it. Do you think we should inject this information into the immediate Article page? Reidme (talk) 17:35, 23 October 2012 (UTC)
- By SD based I suppose you mean that you used the mean n p and the standard deviation sqrt ( n p (1-p)) of the binomial distribution, and the Gaussian (normal) approximation, to compute tail probabilities approximately. I agree with you that just playing 10 times isn't enough, but 100 times is. So your webpage is a lot better in several respects than that of NY Times. Also better than Wolfram's (more interactive, accessible,.... ). Richard Gill (talk) 17:59, 23 October 2012 (UTC)
- Thank you, Richard. I posted the standard-deviation based binomial probabilities for this on the wiki page for the Model Thinking at coursera.org. The SD work I did changed my understanding of what we are dealing with when people don't quickly get it. Do you think we should inject this information into the immediate Article page? Reidme (talk) 17:35, 23 October 2012 (UTC)
- @Reid: I should however change it in such a way as to comply with the problem. I.e. the simulation should only count cases with the same chosen and opened doors. Nijdam (talk) 18:38, 23 October 2012 (UTC)
- @Nijdam, The first indented paragraph in the Article ends by posing the question, "Is it to your advantage to switch your choice?" So by my reckoning, that is what the simulator should be addressing. Nonetheless, it does count all cases and infers the advantage/disadvantage for every completed game if one had switched every time, even if they didn't. Reidme (talk) 20:45, 23 October 2012 (UTC)
- Richard, Yes, that is what I mean by SD. But I think I will leave it to anyone else who may want to get the underlying point across if they wish. Thank you for your support! Reidme (talk) 20:45, 23 October 2012 (UTC)
- @Reidme, Nijdam thinks your simulation does not address the question at all. He thinks that the question is, should you switch on those occasions when you chose Door 1 and the host opened Door 3. Supposing the website visitor makes the possible initial choices equally often, only one sixth of your simulation are relevant, according to his point if view. He would like six times as many trials and separate statistics on six different cases.
- @Nijdam, a simulation in which the player always chooses Door 1 and the host always opens Door 3 is highly artificial. It would require "throwing away" all the times when the host wants to open Door 2. And the player would be forbidden to make other choices himself. You could ask for separate statistics for each of the six cases "door chosen by player, door opened by host". But then the experiment should be a whole lot larger to ensure reilable statistics for all 6 cases. I don't think this will result in a popular or useful website. If you don't believe me, why don't you design one yourself? At last, a popular visual interactive introduction to the conditional approach? Richard Gill (talk) 07:55, 24 October 2012 (UTC)
- I know this all, but it should be made clear what situation the simulation simulates. And till now my experience is that most people think such simple simulation are correct simulations of the (standard) MHP. And, Reid, the question is not whether switching in general is advantageous, but whether it is in YOUR advantage to switch, referring to the player who is addressed. And they know which door they have chosen and which door is showing a goat. Nijdam (talk) 10:26, 24 October 2012 (UTC)
-
- Nijdam, the simulation allows you to select whatever door you like. No matter which door you selected, and no matter what door has been opened by the host, the result will always be identical. No matter what door you did select and no matter what door the host opened. You never are able to say that – for any "actual game" – the chance to win by switching definitely "IS" below 2/3.
- you select door 1 and host opens door 2 showing a goat: staying wins in 1 out of 3 whereas switching wins in 2 out of 3
- you select door 1 and host opens door 3 showing a goat: staying wins in 1 out of 3 whereas switching wins in 2 out of 3
- you select door 2 and host opens door 1 showing a goat: staying wins in 1 out of 3 whereas switching wins in 2 out of 3
- you select door 2 and host opens door 3 showing a goat: staying wins in 1 out of 3 whereas switching wins in 2 out of 3
- you select door 3 and host opens door 1 showing a goat: staying wins in 1 out of 3 whereas switching wins in 2 out of 3
- you select door 3 and host opens door 2 showing a goat: staying wins in 1 out of 3 whereas switching wins in 2 out of 3
- You can descry this without any "additional reasoning". And remember: It is just on ONE game show, so no need for unfounded assumptions on uncertain unknown empirical values. It is an illusion that "one still could know better" for the actual game, and it's insincere to pretend "one still could know better" for the actual game, by means of maths. You never can nor will know better.
Let us stop chasing after "before and after the host opened a door" in that one-time game show, although knowing that sources say that the number of the door opened does not give you any "new" information. Millions of words and binders full of "but what if the host ...", in just disliking the literature. Let us stop confounding the famous "paradox" with school class textbooks on teaching and learning conditional probability theory. Gerhardvalentin (talk) 12:09, 24 October 2012 (UTC)
- Gerhard, Nijdam knows that the chance of winning by switching is 2/3 in all six situations. His point is that Reidme's simulation does not demonstrate this. Nijdam thinks that the only correct way to solve MHP is to mathematically prove this fact. And that a simulation of MHP has to demonstrate this too. Not everyone agrees. Fortunately, what you or I or Nijdam think is irrelevant. What's important is what is found in the literature. Wikipedia is an encyclopedia of generally accepted facts, not an oracle containing only The Truth. If Nijdam wants to promote an idiosyncratic understanding of MHP, he had better publish articles about it in the academic literature, and get journalists to report his breakthrough in popular literature as well. After about 10 years, when every popular writer writes about MHP in Nijdam's fashion, wikipedia will be able to follow.
- I think that distinctions which are important in a university probability class, are not necessarily of much interest to an amateur. The first thing to get across to newcomers to MHP is that switching is advantageous. The simple solutions do that. The rest can be considered an academic refinement. Important for experts. Important in a probability class. In the article, this distinction can be discussed later.
- However, fortunately there are simple ways to present what is in effect a conditional solution. So the reader can be presented with a range of different solutions, making different assumptions, getting correspondingly weaker or stronger conclusions. The general reader will find for themselves what solution most appeals to them (a matter of taste). Most importantly, they will learn that there is not One And Only One correct way to think about MHP. An informal verbal question about an imaginary game show can be converted into a formal logical or mathematical problem in many different ways. The literature reflects this fact of life. The wikipedia article has to reflect the literature.Richard Gill (talk) 17:41, 24 October 2012 (UTC)
- Nijdam, the simulation allows you to select whatever door you like. No matter which door you selected, and no matter what door has been opened by the host, the result will always be identical. No matter what door you did select and no matter what door the host opened. You never are able to say that – for any "actual game" – the chance to win by switching definitely "IS" below 2/3.
- The first thing to get across to newcomers is that the odds for the chosen and the remaining closed door are not equal, as they are inclined to think. And for this the simple switching idea is not sufficient. Nijdam (talk) 07:41, 28 October 2012 (UTC)
- The simple switching idea shows that the odds for the chosen and the remaining closed door cannot be equal. If they were equal, whatever the door numbers involved, then switching would win the car half the time, not two thirds of the time. Richard Gill (talk) 11:15, 28 October 2012 (UTC)
- Maybe you changed again from opinion about the simple switching idea? Nijdam (talk) 11:41, 28 October 2012 (UTC)
- No. My advice to the player is to pick a door at random and switch regardless of which door is opened. The player is then sure of a 2/3 chance of winning the car. This is the best that can be done. Worrying about subjective conditional probabilities based on subjective appraisal of prior odds of this and that is a waste of time.
- Sasha Gnedin, in the first original contribution to MHP since it was invented, pointed out that for every player strategy (how to pick and whether or not to switch) you can think of, there is a strategy of always switching which is at least as good in every single circumstance (of where the car is, what the host does). So we're going to switch, anyway. The only thing left to decide is how to pick a door initially. Richard Gill (talk) 15:49, 28 October 2012 (UTC)
- Pity for you, but the player has already chosen door 1. Of course what you say is in itself right, but so is 1+1=2. Nijdam (talk) 21:26, 28 October 2012 (UTC)
- Maybe you changed again from opinion about the simple switching idea? Nijdam (talk) 11:41, 28 October 2012 (UTC)
- The simple switching idea shows that the odds for the chosen and the remaining closed door cannot be equal. If they were equal, whatever the door numbers involved, then switching would win the car half the time, not two thirds of the time. Richard Gill (talk) 11:15, 28 October 2012 (UTC)
- The first thing to get across to newcomers is that the odds for the chosen and the remaining closed door are not equal, as they are inclined to think. And for this the simple switching idea is not sufficient. Nijdam (talk) 07:41, 28 October 2012 (UTC)
- I would like to assume that the player did some thinking before the show. I suppose (a) that the player knows the rules in advance and (b) the player is smart. So he decided in advance to use the optimal strategy. He happened to choose door 1 by chance. The car is already hidden behind one of the doors, the host has already opened door 3. The chance the car is behind door 2 is 1 if is behind door 1, zero if not. The smart player is going to switch because he had already planned to. I think he has good reasons to switch, don't you?
- But the question is not whether or not this is a good answer, the question is whether or not this answer is given by reliable sources, On this page we should discuss editorial issues: how to present an overview of the literature on MHP in a balanced, informative, and hopefully appealing way. Readers first need to understand that their initial intuition is wrong. Simple solutions do this, very effectively indeed. We don't have to discuss whether some solutions are right, others are wrong (in my opinion, this is a matter of taste, an uninteresting diversion). We discuss the literature on MHP. Which consists of (a) popular literature (newspaper and magazine articles, the Vos Savant story, popular brain teasers), (b) academic probability and statistics literature, (c) academic decision and games theoretic literature, (d) psychology and cognition literature. Even the academic probabiilty and statistics literature is not agreed that there is One and Only One Correct Solution. Sorry. The most striking feature of the literature on MHP is the diversity of solutions. Selvin, the originator, published two completely different solutions using different sets of assumptions, without even mentioning the difference. There was a whole published discussion of Morgan et al in which many authorities gave interesting criticism of Morgan et al's approach. So that is what the article has to be about. The role of a mathematician in these discussions should be to build bridges between solutions, to clarify how more or less assumptions lead to stronger or weaker conclusions. The "consumer" can choose for themselves. Richard Gill (talk) 09:11, 29 October 2012 (UTC)
Richard Gill said:"I would like to assume that the player did some thinking before the show. I suppose (a) that the player knows the rules in advance and (b) the player is smart. So he decided in advance to use the optimal strategy. He happened to choose door 1 by chance." No, you must not assume that the normal reader, who is the player in person ("Suppose you're on a game show...") is smart (in mathematics) in this way that he is able to use a (optimal) strategy in advance. The normal reader is confronted with the situation given in the problem statement and his considerations must relate to this certain situation. It is not only a one-time-game but also a one-time-reading of the text. To read the wording 50 times doesn't mean to play the game 50 times, it is one and the same game ever. So, the reader has no possibility to assume that he has chosen door 1 by chance. --213.102.99.129 (talk) 13:25, 29 October 2012 (UTC)
- You are welcome to your opinion! The sources are divided on this. Richard Gill (talk) 08:00, 31 October 2012 (UTC)
Fixed Devlin
I was asked above by Richard if I objected to a fixed version of Devlin's 'combining doors' solution appearing near the start of the article. I said that I did not object to this but I wanted to make sure that we agree on what the problems are with that solution and how we would fix them. Martin Hogbin (talk) 09:28, 29 October 2012 (UTC)
- There was a missing step in Devlin's combining doors solution. He admitted that, and in effect withdrew it, endorsing instead a formal computation of conditional probability, because at least you would get the right answer as long as you were careful, even though the solution is no longer simple, intuitive. Instead he could have rewritten his combining doors argument as follows. Initially, the odds are 2:1 against your door, door 1, hiding the car. (Here I am using probability in its subjective - information -sense, and using symmetry in the door numbers / irrelevance of the door numbers, as far as the car's location is concerned). The host opens a door (identity temporatily kept secret) revealing a goat. The odds remain 2:1 against your door hiding the car, since he is going to do this anyway. Finally, you are informed that it was door 3 which he opened. The odds remain 2:1 against your door, door 1, hiding the car, since whether or not there is a car behind it, the chance is 50% that he'll open door 3. (Here again I use symmetry / irrelevance / absence of information, now also with respect to which door the host will open if he has a choice).
- Isn't that both a simple solution and a solution which tells us that the chance door 2 hides the car, given the player chose 1 and the host opened 3, is 2/3? Jeff Rosenthal gives this solution. So does RD Gill. It uses explicitly both K&W assumptions. It's based on ordinary people's understanding of probability (from symmetry in prior knowledge to equally likely). It is actually an application of Bayes' rule, "posterior odds equals prior odds times likelihood ratio" which means that it is of enormous pedagogical value. So many misunderstandings of probability and statistics, so many miscarriages of justice, can be traced back to failure to apply Bayes rule! — Preceding unsigned comment added by [[User:Richard Gill|Richard Gill]] ([[User talk:Richard Gill|talk]] • [[Special:Contributions/Richard Gill|contribs]])
- Fine with me, as long as you don't call it 'combining doors" or refer to Devlin, because it has nothing to do with Devlin's misleading idea of combining doors. Nijdam (talk) 10:01, 29 October 2012 (UTC)
- Strange. I read Devlin, saw his missing step, and fixed it. The odds on door 1 hiding the car is by definition the chance the car is behind door 1 divided by the chance it is behind the other two doors combined. But you can call it Rosenthal solution if you prefer. Richard Gill (talk) 10:10, 29 October 2012 (UTC)
- And here is Devlin's explanation "[Monty Hall in effect is saying] I'll help you by using my knowledge of where the prize is to open one of those two doors to show you that it does not hide the prize. You can now take advantage of this additional information. Your choice of door A has a chance of 1 in 3 of being the winner. I have not changed that. But by eliminating door C, I have shown you that the probability that door B hides the prize is 2 in 3." The problem here is that Devlin did not explain why opening the particular door in the case at hand, namely Door C, does not change the chance of Door A being the winner. It's true that the host is essentially offering the player Door A versus Door B+DoorC. But he does a bit more than that: he opens either Door B or Door C. One should explain why this particular piece of information doesn't change the chance for Door A to hide the car. The explanation I just gave you uses more than just the fact/assumption that initially the car is equally likely behind any of the three doors. It also uses the fact/assumption that the host is equally likely to open either door if he has a choice.
- It's an elementary mathematical fact that the chance of winning by switching is 2/3 whatever door is initially chosen, if and only if the car is initially equally likely behind each of the three doors. It's an elementary mathematical fact that the chance of winning by switching is 2/3 whatever door was initially chosen and whichever door was opened by the host, if and only if the car is equally likely behind each of the three doors and either door is equally likely opened if the host has a choice. Sources disagree about whether MHP is "solved" by making the first observation or by making the second observation (or in yet another way, e.g. "The Economist" 's decision theoretic solution). So editors have a problem on how to organize this material. But the mathematical facts are out of our control! Richard Gill (talk) 12:05, 29 October 2012 (UTC)
- I think you are both barking up the wrong tree. Let me start with something we all, I think, agree on. The missing step in Devlin's solutions is that assumption that the probability that the player has a car behind his originally chosen door remains at its initial value of 1/3 after the host has revealed a goat. Perhaps you could both confirm that we are agreed here.
- Disagree. That step was correct and complete. The missing step was why this probability doesn't change after we are also told which door was opened. Richard Gill (talk) 15:28, 31 October 2012 (UTC)
- Sorry there was a misunderstanding here. In the W/vS statement we are told the host reveals a goat by opening door 3 so I was assuming that the door number was revealed. I guess I should have said, 'door 3 is opened to reveal a goat'.Martin Hogbin (talk) 13:32, 1 November 2012 (UTC)
- Disagree. That step was correct and complete. The missing step was why this probability doesn't change after we are also told which door was opened. Richard Gill (talk) 15:28, 31 October 2012 (UTC)
- Now we need to ask ourselves how the probability that the originally chosen door hides the car might be changed by the revealing of a goat by the host. In fact Devlin does make this point, he says, 'Your choice of door A has a chance of 1 in 3 of being the winner. I have not changed that' , (my emphasis), but still it might be argued that he has not explained why. There two ways the probability might be changed, one which is trivial, and irrelevant to the basic puzzle, and one which is central to the MHP. Let us start with the trivial case.
- I think you are both barking up the wrong tree. Let me start with something we all, I think, agree on. The missing step in Devlin's solutions is that assumption that the probability that the player has a car behind his originally chosen door remains at its initial value of 1/3 after the host has revealed a goat. Perhaps you could both confirm that we are agreed here.
Which door opened by the host
Here the argument is that the specific door opened by the host might give us information about the likelihood that the car is behind the originally chosen door. But it clearly does not. Richard says, 'Here again I use symmetry / irrelevance / absence of information, now also with respect to which door the host will open if he has a choice'. This fact is obvious to most readers and to insist on mentioning it is selective pedantry, no more important that the sex of the goat that the host reveals.
- Possibly obvious and uninteresting to many readers, but important for some. And it's harmless! So why insist on omitting it! Moreover, without making Devlin's second step (originally missing) explicitly, we haven't explicitly used the second part of K&W assumptions (our ignorance of the host's choice strategy). So the solution is arguably incomplete without it.
- The comparison with the (also irrelevant) sex of the goat can't be taken seriously. The door numbers are named in the problem and help in the readers' mind the image of the problem which leads them intuitively to the wrong answer. It takes a flash of insight, or alternatively a logical deduction, to see that the door numbers are irrelevant. Once you have had the flash of insight it is obvious, but a priori it is not obvious. Read Kraus and Wang, the psychologists: seeing the irrelevance of the door numbers is part of the solution. Seeing the irrelevance of irrelevant information which we have not been given is ...? Richard Gill (talk) 12:22, 31 October 2012 (UTC)
- I do not think it is true that realising that the door numbers are unimportant is part of solving the problem. Most people do not even think that the door numbers might be important so bringing the numbers to their attention unnecessarily confuses the problem and forces them to go through the step of ignoring the door numbers intentionally rather than intuitively. Martin Hogbin (talk) 13:40, 31 October 2012 (UTC)
- Kraus and Wang disagree with you. They are psychologists and they thoroughly and empirically studied how "ordinary people" (=samples of psychology students) think about MHP. There is also literature by earlier researchers like themselves on this subject, which they took account of too. Secondly, it is vos Savant who in her written words brings the door numbers to your attention. Not so that you consciously think "wow these numbers are important", but so that a static picture of certain doors open and certain doors shut gets imprinted in your mind, and the story of how that situation arose becomes secondary. We process the visual information rapidly and instinctively. It tells us that it doesn't matter which closed door we choose. To get the right solution you have to look at the problem in a different way. Not in terms of a static still picture, but in terms of actions, in terms of a history. At least, this is what K&W's article is all about.
- Incidentally, about a formal written out mathematical solution using a calculation of conditional probability they say: this solves the problem at a formal level, but it does not give insight. Well, that depends on who you are of course: if you spend your life doing these conditional probability calculations then you will see beyond the calculations, and gain insight from doing them. But for most people, doing a calculation according to some formal rules does not give insight, it's like pressing a button and getting an answer, only more hard work.
- It's a long and difficult article and at first I hardly found it interesting, but the more I reread it nowadays, the more of value I find in it, precisely about the question how one should explain MHP to newcomers. Richard Gill (talk) 15:24, 31 October 2012 (UTC)
- I have read K&W and come to a different conclusion from you, but I will have another read. Martin Hogbin (talk) 15:33, 31 October 2012 (UTC)
- BTW once the visual picture has been created of left door closed, you standing beside it, right door open, goat, middle door closed, our spatial intuition says: two doors closed, one open. So it doesn't matter. Ie we use a false symmetry, a false indistinguishabiloty to get the wrong, but intuitive, initial answer. We have to understand that the doors need to be distinguished by their roles, their histories; not by their numbers. Distinguishing them by numbers makes us think the closed doors are exchangeable, equivalent. 1 and 2 are just two arbitrary numbers, right? Richard Gill (talk) 08:26, 1 November 2012 (UTC)
- Yes, I agree that people use a false symmetry to get the wrong answer. K&W is a good source which attempts to explain why so many people get this puzzle wrong, let me read it again. Martin Hogbin (talk) 13:38, 1 November 2012 (UTC)
- Here we go again by trying to deny the doors are numbered. Or labelled, or just distinguished by left, middle and right. The MHP is a brain teaser just because people picture the situation, with known doors. And the formulation also shows the doors are known, not just by their role, but by their numbers and which number plays which role. I've the impression this effort on the denial door numbers only serve the purpose to make the simple solution a correct explanation. Nijdam (talk) 14:02, 1 November 2012 (UTC)
- The simple solution is a correct argument to show that most people's initial intuition (that there is no point in switching) must be wrong. For many people that's enough. If you are interested in the difference between the chance of winning by switching when you chose Door 1, and the chance of winning by switching when you chose Door 1 and the host opened Door 3, then the answer is that there is no difference, by symmetry. Simple plus symmetry equals full. In other words, buy a simple solution, get a free upgrade to full conditional. A win-win solution for all parties. What an ado about nothing! Richard Gill (talk) 15:27, 1 November 2012 (UTC)
- Here we go again by trying to deny the doors are numbered. Or labelled, or just distinguished by left, middle and right. The MHP is a brain teaser just because people picture the situation, with known doors. And the formulation also shows the doors are known, not just by their role, but by their numbers and which number plays which role. I've the impression this effort on the denial door numbers only serve the purpose to make the simple solution a correct explanation. Nijdam (talk) 14:02, 1 November 2012 (UTC)
- Yes, I agree that people use a false symmetry to get the wrong answer. K&W is a good source which attempts to explain why so many people get this puzzle wrong, let me read it again. Martin Hogbin (talk) 13:38, 1 November 2012 (UTC)
- BTW once the visual picture has been created of left door closed, you standing beside it, right door open, goat, middle door closed, our spatial intuition says: two doors closed, one open. So it doesn't matter. Ie we use a false symmetry, a false indistinguishabiloty to get the wrong, but intuitive, initial answer. We have to understand that the doors need to be distinguished by their roles, their histories; not by their numbers. Distinguishing them by numbers makes us think the closed doors are exchangeable, equivalent. 1 and 2 are just two arbitrary numbers, right? Richard Gill (talk) 08:26, 1 November 2012 (UTC)
- I have read K&W and come to a different conclusion from you, but I will have another read. Martin Hogbin (talk) 15:33, 31 October 2012 (UTC)
- I do not think it is true that realising that the door numbers are unimportant is part of solving the problem. Most people do not even think that the door numbers might be important so bringing the numbers to their attention unnecessarily confuses the problem and forces them to go through the step of ignoring the door numbers intentionally rather than intuitively. Martin Hogbin (talk) 13:40, 31 October 2012 (UTC)
Devlin's first step is also wrong
Devlin says, 'Your choice of door A has a chance of 1 in 3 of being the winner. I have not changed that'. He is criticised for not explaining why the host's choice of door number does not 'change that' but he might equally well criticised for saying, 'Your choice of door A has a chance of 1 in 3 of being the winner'. Why does he not explain that, if you had chosen door B or door C, you would still have a 1 in 3 chance of being a winner? Because it is obvious of course, but how much more obvious is that fact than the fact that the door the host opens makes no difference either? Martin Hogbin (talk) 13:57, 1 November 2012 (UTC)
The fact the host know where the car is
The fact that the hosts know where the car is (or that he will reveal a goat with certainty) is central to the MHP and Devlin fails to make this point clearly. If, for example the host chooses a door randomly and it just happens to hide a goat then we are given information that allows us to revise our probability that the originally chosen door hides the car.
On the other hand, we know at the start, from the game rules, that the host will reveal a goat, so the revealing of a goat cannot possible give us information about the probability that the car is behind the originally chosen door.
So, I agree we should fix Devlin's solution but not by explaining the obvious fact that the door number makes no difference, but by showing how the fact the host knows where the car is is essential to probability that the car is behind the originally chosen door not being changed by the host's revealing of a goat. Martin Hogbin (talk) 16:50, 29 October 2012 (UTC)
- This fact is essential to the correctness of Devlin's first step: the fact the host opens a door (note emphasis) doesn't change the odds for Door 1. Because the host will certainly reveal a goat behind a different (as yet unspecified) door, whether or not there is a car behind Door 1. We know that he can and we know that he will do this, whether or not our first choice of door was correct. You may expand my text to emphasize this if you think it is so important (and if you think it was not obvious - I thought it was obvious, so not worth remarking on). If you expand the argument for step 1 while leaving step 2 short, you automatically put the emphasis on what you think is the main issue; the side issue is clearly a side issue. I think it is not a matter of pedantry. If you explicitly make two probability assumpions and use one of them but not the other, then you can't think straight. Richard Gill (talk) 08:04, 31 October 2012 (UTC)
- I think you still may be missing my point. It is far from obvious to most people that, if the host chooses an unchosen door randomly and just happens to reveal a goat, the answer is different from that if he must choose a goat-hiding door. This is a key part of the problem, and one that vS made clear at the start. It is a point that has puzzled many people here. So long as the host does reveal a goat, what does it matter how he comes to do this? The problem with the Devlin solution is that it can be applied to the ignorant host variant, where it gives the wrong answer. It is therefore incomplete in that it fails to say why the probability of the original door hiding the car does not change when the host reveals a goat; we know in slightly different circumstances it could change. Martin Hogbin (talk) 13:48, 31 October 2012 (UTC)
- Indeed I am missing your point, and I disagree with you that the Devlin (Devlin fixed) argument fails in the ignorant host variant. In the case that the host opens a different door at random and happens to reveal a goat, the probability that he opens a door and reveals a goat is 1/2 if your door hides the goat, while it is 1 if your door hides a car. He is twice as likely to reveal a goat if you happened to have chosen the car door, than if you didn't happen to have chosen the car door. His opening a door and revealing a goat is certainly very relevant to the question whether or not Door 1 hides the car. Your initial odds of 2:1 against get multiplied by 1:2 and the result is 1:1. After that we are told which door it was he opened. This is as before equally likely whether or not the car is behind door 1 so the odds don't change any more. Richard Gill (talk) 14:24, 31 October 2012 (UTC)
- Sorry I forgot something, it is not as bad as I thought. Devlin says (my emphasis), "I'll help you by using my knowledge of where the prize is to open one of those two doors to show you that it does not hide the prize". I do not give in completely though. It would not be immediately apparent to many people why if Devlin had said "I'll help you, I have opened one of the two doors at random and shown you that it does not hide the prize" the answer would be different. We need some more explanation.
- Indeed I am missing your point, and I disagree with you that the Devlin (Devlin fixed) argument fails in the ignorant host variant. In the case that the host opens a different door at random and happens to reveal a goat, the probability that he opens a door and reveals a goat is 1/2 if your door hides the goat, while it is 1 if your door hides a car. He is twice as likely to reveal a goat if you happened to have chosen the car door, than if you didn't happen to have chosen the car door. His opening a door and revealing a goat is certainly very relevant to the question whether or not Door 1 hides the car. Your initial odds of 2:1 against get multiplied by 1:2 and the result is 1:1. After that we are told which door it was he opened. This is as before equally likely whether or not the car is behind door 1 so the odds don't change any more. Richard Gill (talk) 14:24, 31 October 2012 (UTC)
- I think you still may be missing my point. It is far from obvious to most people that, if the host chooses an unchosen door randomly and just happens to reveal a goat, the answer is different from that if he must choose a goat-hiding door. This is a key part of the problem, and one that vS made clear at the start. It is a point that has puzzled many people here. So long as the host does reveal a goat, what does it matter how he comes to do this? The problem with the Devlin solution is that it can be applied to the ignorant host variant, where it gives the wrong answer. It is therefore incomplete in that it fails to say why the probability of the original door hiding the car does not change when the host reveals a goat; we know in slightly different circumstances it could change. Martin Hogbin (talk) 13:48, 31 October 2012 (UTC)
- On the other hand Devlin says (my emphasis), " Your choice of door A has a chance of 1 in 3 of being the winner. I have not changed that '. So it could be argued that he has fixed the door number problem, even if he does not explain fully how. 15:48, 31 October 2012 (UTC)
Question from Gerhard
Pardon for intruding with a question:
*Who* was ever assuming that Devlin *impossibly* can have been aware of the fact that he was talking about an "imaginary one time event with an unknown host"? – *Who* was it that ever said that Devlin, in citing the "imaginary one-time host", was not aware that such imaginary one-time host in a one-time event forever is absolutely unable (absolutely unable, even if he should want to, although it would be contrary to his strategy), yes absolutely incapable to reveal any additional hint concerning the car-hiding door? Being aware of this fact, for Devlin it was obvious to take his imaginary host, in saying "I have not changed the 1 in 3 chance of your door A of being the winner" to also be fully aware of his incapability to give away such additional hint, besides the fact that this would have been contrary to his strategy?
Who says that Devlin let his host say so, although he and his imaginary host "did not know" that such imaginary one-time host forever is absolutely unable to give "any" of such hint? IMO Devlin was aware of what he concluded, and of what he let his host knowingly say: "I have not changed that". for Devlin it was not necessary to add "because I am not able to, even if I wanted to". It was not necessary to let his one-time host say "I observed secrecy regarding the car-hiding door". It was enough to say "I did NOT change the chance of your selected door". Am I wrong? Gerhardvalentin (talk) 18:12, 29 October 2012 (UTC)
- Gerhard, am I right in assuming that your comments refer to the 'The door opened by the host' section above? Martin Hogbin (talk) 18:51, 29 October 2012 (UTC)
- Yes. In his todays 12:05h edit] Richard said
- The problem here is that Devlin did not explain why opening the particular door in the case at hand, namely Door C, does not change the chance of Door A being the winner. – and
It (the explanation) also uses the fact/assumption that the host is equally likely to open either door if he has a choice. – and later once more
... and either door is equally likely opened if the host has a choice.
My question refers to Devlin's omitting "equally likely to open either door if ..." – IMO such explicit addition – in the given context – is not necessary, if one "sees" that context. Devlin did not say "why" because the context allready tells why. Am I wrong? Gerhardvalentin (talk) 19:46, 29 October 2012 (UTC)- I think you are perfectly correct and, on a good day, so does Richard. Martin Hogbin (talk) 20:02, 29 October 2012 (UTC)
- Sorry, Devlin himself admitted that he had missed a step in his argument. And he didn't even see how to fix it quickly, himself. So to him it was not obvious. So it may be an obvious or superfluous step for Martin or Gerhard, but it wasn't for Devlin or Nijdam.
- For some people, some things are obvious from the context, for other people, not. Some people want to see a complete analysis which deals carefully with every single step of an argument, which takes care of every conceivable loop-hole. Others are happy to skip steps which seem obvious. The demands of how to treat MHP in a probability class-room are different from in a popular newspaper article. Somehow wikipedia has to satisfy legitimate demands of both kinds of readers. What I like about this "Devlin fixed" argument is that it shows that a conditional probability solution need not be complicated or technical. No need even to introduce the concept of conditional probability. All steps are intuitive, non-technical. It shows that a conditional probability solution can be built on top of a "simple solution" by a simple addition, a simple addition which some people even find superfluous, because - to them - obvious. It surely can't hurt them by making it explicit?
- I would like to see all notion of a conflict between simple solutions and conditional solutions to evaporate by realizing that conditional solutions can be very simple too, and that whether or not one goes the extra mileage is largely a matter of taste or, if you prefer, context. And simply be being careful with wording. For a large part of the article we will take K&W conditions for granted, like most people do instinctively (randomness is in the location of the car and the choice of door of the player and it is all uniform). The simple solutions show what they show, namely that switching gives the car with probability 2/3. The so-called conditional solutions show that switching gives the car with probability 2/3, whatever door is chosen by the player and whatever door is opened by the host. That's a stronger statement. Requires a tiny bit more work to establish. These are the facts. What's the big deal? Let's just report the facts and let the readers choose for themselves which of this information they find useful and interesting, which not. Richard Gill (talk) 13:09, 30 October 2012 (UTC)
- Great, thank you Richard. Yes – the article should be composed and reasoned in exactly that way. Gerhardvalentin (talk) 17:11, 30 October 2012 (UTC)
- I think you are perfectly correct and, on a good day, so does Richard. Martin Hogbin (talk) 20:02, 29 October 2012 (UTC)
- Richard Gill said:"For a large part of the article we will take K&W conditions for granted, like most people do instinctively (randomness is in the location of the car and the choice of door of the player and it is all uniform)." K&W conditions yes including the player's optional choice of door 1 , but no to the player's choice uniform at random. --213.102.96.77 (talk) 17:39, 30 October 2012 (UTC)
- Dear 213.102.96.77: (1) please get yourself a wikipedia user name; (2) many writers take the player's choice as random and everything else fixed. You might not like this solution, but apparently some writers on MHP do. The article can't be restricted to one editor's personal opinion of what MHP is about. I agree it is a less common approach than the approach based on subjective probability. Richard Gill (talk) 21:41, 30 October 2012 (UTC)
- Richard Gill said:"For a large part of the article we will take K&W conditions for granted, like most people do instinctively (randomness is in the location of the car and the choice of door of the player and it is all uniform)." K&W conditions yes including the player's optional choice of door 1 , but no to the player's choice uniform at random. --213.102.96.77 (talk) 17:39, 30 October 2012 (UTC)
- PS Here's another way to make a synthesis of simple and conditional, again, of course, under K&W symmetric subjective probability assumptions.
- * Switching gets the car with probability 2/3, because it succeeds if and only if your initial choice is a goat.
- * By symmetry, the specific door numbers chosen and opened are irrelevant.
- * So you get the car with probability 2/3 whatever initial door was chosen and whichever door was opened by the host.
- It seems to me that what we are arguing about is that some editors find the last two sentences irrelevant while others think they are the crux of the matter. No doubt, readers will be similarly divided. And obviously, sources are similarly divided. I would say that in a popular article the last two sentences are pretty irrelevant but on the other hand they are harmless (aren't they?) so why not "cover your base" and put them in. Later in the wikipedia article one can go into the "extra" in more depth, e.g., using formal probability theory language. As is appropriate e.g. In a probability class or probability text. In short: I don't see a conflict. Careful editing in which academics and "populists" collaborate ought to be able to resolve this to everyone's satisfaction, and more importantly, in accordance with the sources and in a way which best serves the readers. The academics need to develop their communication skills and develop empathy for how an ordinary intelligent person without any mathematical training reasons (correctly) with uncertainty. Otherwise they'll be eternally ignored. A dogmatic stance - "you have to do it my way" - is self-defeating.Richard Gill (talk) 07:47, 31 October 2012 (UTC)
- Why do we need a synthesis of simple and conditional solution? We need clear and intelligible answers without mixing up different concepts which could confuse the reader. --TotalClearance (talk) 16:49, 1 November 2012 (UTC)
- Why? Because Wikipedia is an encyclopedia. We have to. There are different solutions in the literature and even claims that some are wrong. Editors of wikipedia can't collectively determine the one and only one correct solution and disregard all the others. If we don't attempt synthesis we certainly will confuse the reader. Moreover: these "synthesis" solutions are also in the literature. I'm not proposing anything new. Just an editorial guideline to how to organise what is "out there". Richard Gill (talk) 07:57, 2 November 2012 (UTC)
You said:"Editors of wikipedia can't collectively determine the one and only one correct solution and disregard all the others." I didn'd say anything like that I want to disregard possible solutions! The reader has a legitimate interest not to be confronted, early in the article, with solutions mixing up very different concepts of problem solving, which certainly will confuse him. We have a non complex approach, easy to understand, with the conditional solution table which leads to the correct solution. And we should present it to the reader early in the article. The more complex solutions, combining different mathematical concepts, should be discussed later in the article. --TotalClearance (talk) 11:10, 2 November 2012 (UTC)
- Agree. Richard Gill (talk) 15:32, 2 November 2012 (UTC)
Win-win solution
The simple solution is a correct argument to show that most people's initial intuition (that there is no point in switching) must be wrong. For many people that's enough. If you are interested in the difference between the chance of winning by switching when you chose Door 1, and the chance of winning by switching when you chose Door 1 and the host opened Door 3, then the answer is that there is no difference, by symmetry (between Doors 2 and 3). Simple plus symmetry equals full. In other words, buy a simple solution, get a free upgrade to full conditional. A win-win solution for all parties. Richard Gill (talk) 15:35, 1 November 2012 (UTC)
- A win-win solution for all parties? Probably not for the 'normal' reader who may be overcharged by the concept of symmetry. The symmetry between Doors 2 and 3 arises by reason of the host's behaviour opening another goat door uniform at random. This is not obviously for ordinary people without additional explanations. Why not leave to the reader to observe this symmetry with the aid of a conditional solution table? --TotalClearance (talk) 16:33, 1 November 2012 (UTC)
- The symmetry is not by reason of the host's behaviour, about which we know nothing, but by reason precisely of our complete ignorance thereof!
- Both steps in the argument need further exposition, especially for the "new" reader (newcomer to MHP). The new reader is mostly interested in the first step. Why is sticking with your original choice *not* the right answer? The second step concerns what many readers and many editors and most importantly of all, many sources, think is at most a subtelty, at worst an "academic sideshow". My opinion is different, but that's not relevant.
- You think symmetry is tricky and needs argument. Other editors think it is so obvious it shouldn't even be brought up. I'm offering a way to structure solutions so that editors of different persuasion can collaborate instead of feud.
- My own opinion is that MHP has to be treated differently in a newspaper column from in an academic probability class, and wikipedia has to address needs of both kinds of readers, and survey the sources of both types. My own opinion moreover is that there need not be any conflict between approaches, instead there can be synergy, so we would make progress here by searching for it. Richard Gill (talk) 07:40, 2 November 2012 (UTC)
- You said:"The symmetry is not by reason of the host's behaviour, about which we know nothing, but by reason precisely of our complete ignorance thereof!" If the host is complete unknown then we don't know why he has opened goat door 3. Thus the only symmetry we are observing is the symmetry between door 1 and door 2, leading us to the conclusion that the odds are the same for both closed doors. So what? --TotalClearance (talk) 10:52, 2 November 2012 (UTC)
- We do know, of course,for sure, that the host will certainly open a different door to reveal a goat! What we don't know is how he chooses when he has a choice. This is symmetry between doors 2 and 3, in the situation that we initially picked door 1. Richard Gill (talk) 15:30, 2 November 2012 (UTC)
- You said:"The symmetry is not by reason of the host's behaviour, about which we know nothing, but by reason precisely of our complete ignorance thereof!" If the host is complete unknown then we don't know why he has opened goat door 3. Thus the only symmetry we are observing is the symmetry between door 1 and door 2, leading us to the conclusion that the odds are the same for both closed doors. So what? --TotalClearance (talk) 10:52, 2 November 2012 (UTC)
Moving Forward
OK, we have all seen the result of the RfC. The RfC was written by Martin and Rick, so I am expecting there to be no further dispute between the two of them.
That being said, there were a lot of comments with a lot of ideas not found in the RfC. How do we avoid spending another ten years and another million words arguing about those? Here is what I would like to see. I would like to see anybody who has a differing opinion write it up and insert it -- once -- into the article, and then follow WP:BRD. I would like any of you who see significant opposition to your edits and virtually no support to accept the consensus. And I would like you to follow Wikipedia:Dispute resolution for any content disputes that remain. We all need to give a little. We all need to accept that sometimes the article won't be what we want but will still be good enough. We all need to do something that no mathematician likes to do; jump on the bandwagon for "not the best but good enough" versions that are showing strong support. We need to compromise, quit fighting, and start cooperating. Can we all do that? Pretty please with sugar on top? --Guy Macon (talk) 16:46, 2 November 2012 (UTC)
- I for one, think this a great plan. It's time to start implementing changes as opposed to just keeping those ideas bottled up on the talk page. I, Jethrobot drop me a line (note: not a bot!) 22:32, 2 November 2012 (UTC)
Consensus for Proposal 1
Much to my surprise, it looks as though the result of the RfC is a consensus for proposal 1. I am therefore proposing to start organising the article according to that proposal.
Please note this is not an assertion that the simple solutions are 'correct' or better than the 'conditional' ones and it is not an attempt to hide any solutions, or anything else from our readers. All view shown in reliable sources can be represented in the article.
Proposal 1 was only to have the simple solutions first (without 'health warnings'), then a discussion of the two things that confuse most people, namely that the answer (probability of winning by switching) is 2/3 and that it matters that the host knows where the car is. After that, we can have as much or little discussion of deficiencies of the simple solutions and reasons why these may or may not matter as we wish.
There is still nothing to prevent us from presenting the 'simple' solutions in language that is acceptable to all parties wherever this can be done without it drawing attention to claimed deficiencies in the simple solutions. For example, we can say things like 'Players who switch win 2/3 of the time', rather than ' A player who chooses door 1 and sees door 3 opened will win 2/3 of the time' so long as this cannot be seen as an assertion that the second statement is false or deficient in some way.
I think it is very good news that we have a resolution of this longstanding dispute and I look forward to the resumption of cooperative editing. Martin Hogbin (talk) 18:24, 1 November 2012 (UTC)
- It's obvious to me that the closers (and many editors responding to the RFC) seriously misunderstood Proposal 2. Unless directly asked (on my talk page) I won't comment here again. -- Rick Block (talk) 00:09, 2 November 2012 (UTC)
- I welcome your explanation. I, Jethrobot drop me a line (note: not a bot!) 00:58, 2 November 2012 (UTC)
- Churn and change's characterization of the central question of the RFC as whether "it was better to present what was termed the "simple solutions" to the Monty Hall problem, starting with the one from vos Savant, or whether it was better to present what was called the "more complete" solutions, first" completely misses the mark. The proposals are asymmetrical (i.e. Proposal 2 is not the opposite of Proposal 1). Both proposals would have "simple" solutions presented first and any criticism of these solutions presented much later in the article (Proposal 2's suggestion to include criticism of the "simple" solutions in a later section was not meant to be a point of difference between the proposals, only to make it clear that there would be no criticism of "simple" solutions included in the initial sections of the article). The actual difference is whether the article is structured such that it endorses the POV that the so-called "simple" solutions are correct and complete (by not only presenting these solutions first but following them with several sections of explanation, clearly implying the "simple" solutions are universally understood to be correct and undisputed), or whether the article remains NPOV about the "simple" vs. "conditional" issue by including both "simple" and "conditional" solutions in an initial solution section (with "simple" solutions, of course, presented first - more or less like the drafts Coffee2theorems has suggested, which BTW have been supported by multiple respondents here including several claiming to support Proposal 1). The actual opposite of Proposal 1 would be to structure the article such that it endorses the POV that "simple" solutions are inadequate - by presenting "conditional" solutions first (with "simple" solutions perhaps presented in an "aids to understanding" section). This is not what Proposal 2 suggests. For the article to endorse either of these POVs is (at least to me) a clear violation of NPOV which is the most fundamental of Wikipedia policies. If this is the decision, so be it, but I cannot in good conscience participate in editing such an article. -- Rick Block (talk) 07:17, 2 November 2012 (UTC)
- I agree that Proposal 2 was not interpreted correctly there, but regardless, it still did not gain consensus. Also, if you want to interpret proposal 1 that way, I guess you can, but I don't agree with it. I disagree that proposal 1 violates NPOV. Just because something is presented first or that the two solutions are not presented together does not imply superiority of one approach over another. It does, however, imply weight, which solutions to the standard problem have more of over conditional approaches. Conditional solutions are still presented, but are presented later in the article for the reasons explained above. I, Jethrobot drop me a line (note: not a bot!) 07:35, 2 November 2012 (UTC)
- I think the neutrality argument is we include objections (seemingly largely to vos Savant's solution) to be neutral. Presenting the set 1 solutions initially with no qualification or inclusion of parts of set 2, as per Rick, gives the idea set 1 is correct and complete, and this violates NPOV since that conclusion is contested in the literature. The RFC consensus was that the criticism of vos Savant was from a pedagogy perspective. I dug into this a bit more since NPOV is a policy issue not subject to RFC consensus, and as mentioned in some detail on our RFC discussion page, agree with the consensus; the objections are in math journals meant for undergrads and math tutors, and hence have math pedagogy as their aim. None of the closers have disagreed with my opinion here. Churn and change (talk) 16:02, 2 November 2012 (UTC)
- I updated the summary of the RFC question. That is not very material, since the central issues that came out of the discussion were: 1. There was a consensus for proposal 1; 2. There wasn't for proposal 2; and 3. Criticism of vos Savant's solution was not to be included in any detail. As I mention later, yes, conditional solutions should be presented later, and the weight implied by the presentation order is determined by our appealing more to the general reader than to math tutors and students. That was the consensus of the RFC, and all three closers agreed that consensus was not from votes alone. The vos Savant solution, per the consensus in the RFC, is correct for the layperson's version of the problem; completeness depends on the scope of what you are looking at (whether it generalizes, largely). The consensus was the scope as seen by a lay person did not extend to all the myriad extensions which better clarify the math. Churn and change (talk) 15:35, 2 November 2012 (UTC)
- Do we have to have a consensus that there was a consensus now? This dispute has been running for years and we have a conclusion. Let us try to work together on the article now. Martin Hogbin (talk) 08:59, 2 November 2012 (UTC)
- @ Rick – As I read the closing statements this is not a matter of endorsing one POV or another: consensus is that "the 'simple' vs. 'conditional' issue" is not an NPOV issue. That "issue" is an artifact of how one interprets or generalizes the problem, and of the pedagogical purpose for which one examines it.
- @ Martin – I share your concern that it may be difficult to find a consensus in practice that there is a consensus in principle. Still, one can hope. ~ Ningauble (talk) 14:09, 2 November 2012 (UTC)
- Do we have to have a consensus that there was a consensus now? This dispute has been running for years and we have a conclusion. Let us try to work together on the article now. Martin Hogbin (talk) 08:59, 2 November 2012 (UTC)
- I agree that Proposal 2 was not interpreted correctly there, but regardless, it still did not gain consensus. Also, if you want to interpret proposal 1 that way, I guess you can, but I don't agree with it. I disagree that proposal 1 violates NPOV. Just because something is presented first or that the two solutions are not presented together does not imply superiority of one approach over another. It does, however, imply weight, which solutions to the standard problem have more of over conditional approaches. Conditional solutions are still presented, but are presented later in the article for the reasons explained above. I, Jethrobot drop me a line (note: not a bot!) 07:35, 2 November 2012 (UTC)
- Churn and change's characterization of the central question of the RFC as whether "it was better to present what was termed the "simple solutions" to the Monty Hall problem, starting with the one from vos Savant, or whether it was better to present what was called the "more complete" solutions, first" completely misses the mark. The proposals are asymmetrical (i.e. Proposal 2 is not the opposite of Proposal 1). Both proposals would have "simple" solutions presented first and any criticism of these solutions presented much later in the article (Proposal 2's suggestion to include criticism of the "simple" solutions in a later section was not meant to be a point of difference between the proposals, only to make it clear that there would be no criticism of "simple" solutions included in the initial sections of the article). The actual difference is whether the article is structured such that it endorses the POV that the so-called "simple" solutions are correct and complete (by not only presenting these solutions first but following them with several sections of explanation, clearly implying the "simple" solutions are universally understood to be correct and undisputed), or whether the article remains NPOV about the "simple" vs. "conditional" issue by including both "simple" and "conditional" solutions in an initial solution section (with "simple" solutions, of course, presented first - more or less like the drafts Coffee2theorems has suggested, which BTW have been supported by multiple respondents here including several claiming to support Proposal 1). The actual opposite of Proposal 1 would be to structure the article such that it endorses the POV that "simple" solutions are inadequate - by presenting "conditional" solutions first (with "simple" solutions perhaps presented in an "aids to understanding" section). This is not what Proposal 2 suggests. For the article to endorse either of these POVs is (at least to me) a clear violation of NPOV which is the most fundamental of Wikipedia policies. If this is the decision, so be it, but I cannot in good conscience participate in editing such an article. -- Rick Block (talk) 07:17, 2 November 2012 (UTC)
- I welcome your explanation. I, Jethrobot drop me a line (note: not a bot!) 00:58, 2 November 2012 (UTC)
How about we give it a try? I am not intending to try to impose my personal opinion (that the simple solutions are the best ones) on the article. I am just going to follow the consensus that we have the simple stuff, without health warnings, first then the more complicated stuff, as per the proposal. If I, or anyone else, start to add their own POV to the article then other editors are, of course, free to remove it.
I am going to make some structural changes shortly. This really is a genuine compromise that will allow all editors, whatever their views or interpretations of sources, to work together. Martin Hogbin (talk) 14:52, 2 November 2012 (UTC)
- Rick, one final thing: in the closing proposal, what we have suggested is to include Krauss&Wang initially as part of set 1. This was not one of the "simple solutions" of the RFC; I believe you pointed it out somewhere. I have further suggested the solution in K&W page 5 be the very first one, ahead of vos Savant. That positioning, however, is a personal suggestion, not an RFC or "closer" consensus (nobody commented on that specific suggestion). I will not defend that specific suggestion since I will not be editing here, but it seemed and seems a good idea. Churn and change (talk) 16:19, 2 November 2012 (UTC)
- I am very happy with Martin's conciliatory remark "There is still nothing to prevent us from presenting the 'simple' solutions in language that is acceptable to all parties wherever this can be done without it drawing attention to claimed deficiencies in the simple solutions." That is what editorial collaboration is all about. But then he goes on to say: "For example, we can say things like 'Players who switch win 2/3 of the time', rather than ' A player who chooses door 1 and sees door 3 opened will win 2/3 of the time' so long as this cannot be seen as an assertion that the second statement is false or deficient in some way." Martin seens to imply that the second statement might be false or deficient in some way. But the issue was not the correctness of the second statement, but the correctness of a "simple solution" as argument for the statement! And conversely, whether the first statement is considered an adequate answer to Vos Savant's question. The sources are not agreed. Richard Gill (talk) 16:48, 2 November 2012 (UTC)
- The consensus of the RFC, as pointed out in the closure summary, was that statements such as "players who switch win 2/3rd of the time," without the caveats of random initial picking of doors by contestant, and random picking of "non-car" doors by Monty, are good enough in the initial sections. The sources which disagree are largely articles in journals catering to math undergrads and tutors; journals with no impact factor, incidentally. We are not catering "equally" to the general reader and to the math undergrad/tutor type; the two groups are nowhere near equal in numbers, for one thing; Wikipedia is neither a math encyclopedia nor a math text, for another. RFCs are non-binding and you are free to dispute the results, but I want to clarify that you are not disputing just one editor's comments here. Rick's objection of NPOV is a different beast; that is policy, and RFC consensus cannot override that, and that is why I have responded at some length to the issue. Churn and change (talk) 01:33, 3 November 2012 (UTC)
Started change
I have started to move some things to make the article how most people want it. I have put the simple stuff at the top, followed by 'Sources of confusion' then 'Criticism of the simple solutions' which leads onto all the other solutions. Heading levels need to change and there needs to be some page reorganisation but nothing has been removed or added. Martin Hogbin (talk) 10:21, 3 November 2012 (UTC)
For what it's worth
As this whole discussion seems to get out of control, I want to copy what Richard Gill wrote on 22 February last year:
Of course the simple solution alone does not solve the "full problem". But I do not agree that you *have* to solve MHP with the "full problem". Simple solution plus symmetry, and symmetry plus simple solution, do solve the full problem. Actually, symmetry first tells you that you do not have to solve the full problem: you need not condition on stuff which is independent. From the mathematical point of view the full conditional solution is just one way of showing that the simple solution is optimal (in the sense of achieving the highest possible overall success-rate), as well as good. Mathematics does not have moral or legal authority. Mathematics can't ever tell you that you *must* act in a certain way. It can only tell you that it is wise to act in a certain way. The applied mathematician must explain to his client why it is wise. In the real world there are many other issues, and maybe it is wise not to be wise in some respects. Richard Gill (talk) 11:27, 22 February 2011 (UTC)
Especially note the first sentence, and remind that the full problem is the K&W-formulation. Nijdam (talk) 13:16, 2 November 2012 (UTC)
- Out of control? Nijdam, it is terminated. Note the conclusion of the RfC. But please also note my second sentence: 'I do not agree that you *have* to solve MHP with the "full problem" '.
- BTW, "full problem" is not meant to imply "correct problem". It is just a phrase I used to distinguish between whether or not you take account of the host's choice of door to open. (Equally likely, if he has a choice). Richard Gill (talk) 11:18, 3 November 2012 (UTC)
- You may write as you please, in our country we say: "paper is patient", but does it make sense? What does it mean to solve the Monty Hall problem with the full problem - matter of English language? Nijdam (talk) 21:25, 4 November 2012 (UTC)
Time to reactivate the Arguments page
Now that the way forward for the article is clear can I suggest that we reserve this page for comments directly relating to changes to the article.
There is a page (Talk:Monty Hall problem/Arguments) which can be used for wider discussion of the subject, but still ultimately aimed at improving the article. Martin Hogbin (talk) 22:33, 4 November 2012 (UTC)
Problem statement
Apart from the lead, there is currently no problem statement at the start of the article. Which statement should we have? Martin Hogbin (talk) 22:37, 4 November 2012 (UTC)
- The RFC was not about this. I've restored the K&W description. -- Rick Block (talk) 06:18, 5 November 2012 (UTC)
- Rick, I was not the one who removed it and I agree that we should have a problem statement at the start of the body of the article. I was asking which problem description is best to start with. I think there are only two contenders the Whitaker/vos Savant statement and the K&W. Which is best? Martin Hogbin (talk) 10:32, 5 November 2012 (UTC)
- I vote for Vos Savant plus minimal disambiguation: the host knows where the car is hidden, and is certainly going to open a different door from the player's door and reveal a goat and offer a switch.
- Everything else is part of the (a) solution. For instance, one can choose to attack the problem with subjective probabilities determined by ignorance: as far as we are concerned, the car is equally likely behind any of the doors and moreover either choice of door to open by the host is equally likely if he has a choice. It's not part of the problem specification that the car is hidden by choosing a door completely at random and that Monty chooses completely at random if he has a choice. We don't know anything about how it is done. The probabilities in the puzzle come from our ignorance, not from our knowledge. Richard Gill (talk) 16:22, 5 November 2012 (UTC)
- Richard - please speak from sources, not from your personal opinion. AFAICT, the majority of sources (including specifically the Barbeau book and paper, which are both literature surveys) fully disambiguate, consistent with the K&W problem statement, which K&W further suggest is how people interpret the problem whether the disambiguations are explicit or not. Solutions for less restrictive versions belong in the Variants section. -- Rick Block (talk) 17:35, 5 November 2012 (UTC)
- If we are going to present simple solutions first (i.e., first report on MHP in popular literature, not academic/maths pedagogical literature) then we need only write down the assumptions which those simple solutions use. Figuring out some sensible assumptions to make is part of the solution process. K&W don't deny that. They merely report some assumptions which it seems many people are happy to make.
- I don't think that a conventional list of formal mathematical assumptions from the mathematics - pedagogical literature belongs at the start of an overview of popular literature on a popular puzzle presented in ordinary words about an imaginary game-show. Richard Gill (talk) 18:07, 5 November 2012 (UTC)
- Richard - please speak from sources, not from your personal opinion. AFAICT, the majority of sources (including specifically the Barbeau book and paper, which are both literature surveys) fully disambiguate, consistent with the K&W problem statement, which K&W further suggest is how people interpret the problem whether the disambiguations are explicit or not. Solutions for less restrictive versions belong in the Variants section. -- Rick Block (talk) 17:35, 5 November 2012 (UTC)
- Rick, I was not the one who removed it and I agree that we should have a problem statement at the start of the body of the article. I was asking which problem description is best to start with. I think there are only two contenders the Whitaker/vos Savant statement and the K&W. Which is best? Martin Hogbin (talk) 10:32, 5 November 2012 (UTC)
- I agree with Richard here, I think that the Whitaker statement with the assumed standard rules would be the best place to start. I think the K&W statement should be included somewhere though. Martin Hogbin (talk) 19:50, 5 November 2012 (UTC)