Talk:Memristor/Archive 1

Archive 1

Archive 2

stop lurking Potatoswatter!

Stop going around deleting other people's comments. If you want to say something just say something but quit censoring the rest of us. How much is HP paying you to swat potatoes away from this article anyways? —Preceding unsigned comment added by 128.32.47.216 (talk) 15:29, 10 July 2008 (UTC)

Your issue was discussed when it had relevance to article development. Now it doesn't, and please follow the general guidelines I posted on top of the page. They apply equally across WP. Please get an account if you wish to comprehensively participate, or have an agenda. Please add new topics to the bottom of this page and read the existing discussion of your topic first—it's already here after all. Potatoswatter (talk) 20:42, 10 July 2008 (UTC)

Woot, now I'm a celebrity! :vD Potatoswatter (talk) 20:44, 10 July 2008 (UTC)

Anon guy: please search this page for "fourth element," "problems with sourcing," and "controversy." If you can make a positive contribution, please do. If you still feel the need to use this page as a soapbox because you feel Williams and Chua got an unfair publicity advantage, tough luck. At least add your text to the bottom of the page like everyone else. Potatoswatter (talk) 21:20, 10 July 2008 (UTC)

Whatever Dave. I'm glad you're a fan of bad science. Oh, and your last comment was right on the mark. I am just upset about how the "publicity advantage" is going to affect the awarding of this year's Ig Nobel Prizes.

If you have a link showing it's bad science, ie fraudulent claims, I'm all ears. New computer technologies, some promising, appear every year to about the same fanfare as this. Last time around it was chalcogenides, which IBM, Samsung, Intel, etc claim to have made advances with. Were their press releases and biased papers also "raping science"? As a EE grad student, I read lots of lame papers practically trumpeting their own bias. It's normal. When I noticed Williams' abysmal carrier mobility (I'm unfamiliar with ion conductors), it was disappointing but not mind-blowing.

Again, if you have a reference that Williams' device is not an ideal (or at least good) memristor, that does belong in the article. However many researchers unduly believe their research to be fundamental without ill effect to its quality, and everyone resigns to accept their self-opinion. They're hard workers and self promotion is part of the game. Ig Nobel on the other hand is for actual frauds, hoaxers, and jokes. Potatoswatter (talk) 01:21, 11 July 2008 (UTC)

Damn it Dave, I am not arguing that William's device isn't an ideal memristor,I'm arguing that the memristor is not a fundamental circuit element. I have no problem with Wiliamms' paper, I do however have a problem with Chua's papers. Williams is not guilty of bad science, Chua is. —Preceding unsigned comment added by 128.32.47.216 (talk) 01:24, 14 July 2008 (UTC)

negative resistance

Is this just a negative differential resistance? — Omegatron (talk) 20:02, 30 April 2008 (UTC)

No, A negative resistance still obeys Ohm's Law, but a memristor obeys a different law. Read the article text. A simple explanation is to think of a memristor as being a resistor whose value changes according to the amount of charge that has passed through it.192.55.12.36 (talk) 15:39, 8 May 2008 (UTC)

Is this a hoax? Andries (talk) 20:20, 30 April 2008 (UTC)

At least it is vague. Andries (talk) 20:21, 30 April 2008 (UTC)

I work at HP Labs and can get one of the authors to provide some technical details to flesh out this article. Would that be useful? If so, contact me at jamie.beckett@hp.com. Editgal (talk) 02:07, 6 May 2008 (UTC)

Constant negative resistance works as constant negative memristance, so presumably memristance may be negative. However, as mentioned in that article, it's no longer a passive component. Potatoswatter (talk) 04:12, 6 May 2008 (UTC)

Fourth element or just a reworking of resistance ?

Adding to the comments below - the differential equations in the article seem to imply that the units of "memresistance" are ohms as per normal resistance.

$M={\frac {d\phi }{dq}}$

$({\frac {1}{C}}={\frac {dV}{dq}})$ and inductance $(L={\frac {d\phi }{dI}})$.

$M={\frac {d\phi }{dq}}={\frac {1}{R}}{\frac {dV}{dq}}{\frac {d\phi }{dI}}$

This doesn't seem to support the claim that it is a fourth circuit element.

I can see how an infinite network of inductances and capacitors arranged as a "ladder" could look like a resistor and also exhibit memory charaterisitics. Is this what the article is actually referring to ?

As described here, there are four basic quantities, q, I, V, and Φ, and six ways to combine them:

• $dq=I\cdot dt$ (definition of current?)
• $d\Phi _{\mathrm {B} }=-V\cdot dt$ (Faraday's law of induction?)

• $dV=R\cdot di$ (resistance)
• $dq=C\cdot dv$ (capacitance)
• $d\Phi _{\mathrm {B} }=L\cdot di$ (inductance)
• $d\Phi _{\mathrm {B} }=M\cdot dq$ (memristance)

I'm not sure if this is really the right way to think about it, but it is apparently the way it's described in the paper. — Omegatron (talk) 14:12, 1 May 2008 (UTC)

I was the one who posted that at slashdot (but I said $d\phi =vdt$). It is not a complete description, but is rather the argument from symmetry for memristors being a fourth fundamental circuit element. The main missing element is that M is a function of the charge history of the element. Memristance does seem to be in units of resistance, because memristance instantaneously acts like a resistor. digfarenough (talk) 16:19, 1 May 2008 (UTC)

Hmmm.. If this is in the paper (I haven't gotten a chance to read it yet), then we should include it in the article, but I'm not yet convinced by this line of reasoning, especially if the inductor equation is about magnetic flux and the memristor equation is about electric flux. — Omegatron (talk) 17:41, 1 May 2008 (UTC)

Hmmm... "Electronic theorists have been using the wrong pair of variables all these years--voltage and charge. The missing part of electronic theory was that the fundamental pair of variables is flux and charge," said Chua.[1] — Omegatron (talk) 18:12, 1 May 2008 (UTC)

We might also note the lack of consistent dimensions for the definition of the "memristor" coefficient. If $M={\frac {d\Phi _{E}}{dq}}$ then the rearrangement into "$V=M(q(t))i(t)$" doesn't work dimensionally. It only works if the equation reads: $M={\frac {d\Phi _{B}}{dq}}$ then the chain rule completes the "symmetry" against inductance (magnetic flux derivatives) with resistors and capacitors (voltage derivatives). IMHO I think that the 4th component idea is overstated. It appears, on the surface, to be a hysteretic (if that is a word) device like a ferrite core. [See below] User:phy.tch 21:31, 1 May 2008 (UTC)

I'm looking at Chua's paper now, and it is magnetic flux after all, and his argument that it is the fourth basic circuit element is as described here ("Out of the six possible combinations of these four variables, five have led to well-known relationships"). — Omegatron (talk) 23:00, 1 May 2008 (UTC)

In the paper, the equations are

$v=R(w)i$

${\mathrm {d} w \over \mathrm {d} t}=i$

where w is a state variable and "The state variable is proportional to the charge q that passes through the device". Elsewhere, "The memristor is a 2-terminal circuit element defined by Um Rm (qm) fro, where Rm (qm) is a linear resistance whose value depends on the charge qm passing through its terminals." — Omegatron (talk) 02:14, 2 May 2008 (UTC)

-- I get the idea of exploring the various derivatives of a state variable in electrical systems (analogous to the exploration that one does in classical thermodynamics) but perhaps it should be pointed out that not all of these explorations yield fundamental values. Consider the resistor, it is possible (in fact, easy) to manufacture a device made from one material which exhibits a constant variation of voltage with a change in current. Similarly by placing two metal plates in close proximity we create a device that exhibits a constant change in voltage w.r.t. a change in charge. Wrap a wire in a coil and we get a device that maintains a constant change in flux w.r.t. a change in current. The proposed state system exploration here for the memristor doesn't produce such a "basic" device. In its purest form (ignoring the sign) it is has the same dimensions as resistance. A device that represents a constant in the change of flux w.r.t. charge is just a resistor. Negative resistance, incidentally, shouldn't be too big a surprise as this was a key feature of tunnel diodes. From the popular descriptions of this device it has all the appearance of another heterojunction device, not what might be referred to as a new "fundamental" device. It bears a close functional resemblance to a ferro-memory semiconductor device that was explored in late 80s. We shall see how all this plays out. User:phy.tch 11:58, 2 May 2008 (UTC)

Fourth element?

The article states that the memristor is the fourth fundamental circuit element, quoting verbatim a recent nontechnical news article about the subject. This claim has not been supported or verified by any technical source that I am aware of. The memristor does not seem to have any inherent properties that make it somehow more fundamental than other non-fundamental circuit elements like transistors or diodes. This claim should be either cited or removed, IMHO. 70.176.60.148 (talk) 23:28, 30 April 2008 (UTC)

It's a quote found in all of the citations on the page. But if the EETimes isn't "technical" enough, I'll link to the Nature article: "Electronics experts in California have finally succeeded in proving the existence of a fourth fundamental unit of electronic circuits: the 'memristor'."Michael Belisle (talk) 23:53, 30 April 2008 (UTC)

Researchers may claim many things.

This does not make them true.

Nor does reporting that simply runs with a 'fourth fundamental' circuit element, as a nice headline.

Hence I've removed the claim.

As I see it it can only reasonably be substantiated in several ways.

• It being in electronics textbooks published substantially after 1971 - when the paper was released - as a fourth fundamental component.
  • It's not in any - I just checked four major textbooks - Art of Electronics, Microectronics and integrated circuits, and a couple of others, and it's not mentioned at all.

• It actually being more fundamental than the analogous meminductor, memcapacitor, and for some reason being more fundamental than the ideal diode, transformer, ...
  • This is a very strong claim, that I don't see actually made anywhere other than the headlines.

• A diode is just a special case of a non-linear resistor.
• A transformer is not a two-terminal device, therefore not relevant here.
• A meminductor would be characterized by L=L(q); a memcapacitor by C=C(Φ). Although both may have physical realizations, they are not as fundamental as the memristor. This becomes apparent if you think in terms of state equations.

So the claims you memtion are actually legitimate.

Acasp (talk) 20:57, 3 May 2008 (UTC)

As of this date, 2020 hits on google occur for memristor, of these, half have been added in the last month. --Speedevil (talk) 00:19, 1 May 2008 (UTC)

It is referred to as a fundamental circuit element because it provides a relationship between two of the four fundamental circuit variables (voltage, current, charge, and flux), namely a function relating charge and flux. Charge is given as an integral of current. Flux is given as an integral of voltage. Resistors relate voltage and current. Capacitors relate charge and voltage. Inductors relate flux and current. The only missing relationship which could not be constructed as a passive device was the memristor which relates flux and charge. (confirmed by doublechecking Chua's original paper on the IEEE's site)69.108.213.131 (talk) 00:04, 1 May 2008 (UTC)

They've been added in the past month because the journal article was published today, which I just added a link to. I put it back, since there are multiple references in the issue of Nature that refer to the memristor on the same level as the other three passive components, not just the researchers. Diodes and transistors are not passive components. Michael Belisle (talk) 00:25, 1 May 2008 (UTC)

Diodes are not passive components? — Omegatron (talk) 23:41, 2 May 2008 (UTC)

No, they're active. They change their, um, resistance according to polarity and voltage. —Preceding unsigned comment added by 80.134.46.76 (talk) 15:08, 5 May 2008 (UTC)

Diodes are passive. They cannot add energy to the system. Actually according to passivity (engineering) transistors are passive as well, but a current source implemented using a transistor is active. The difference is when/whether you attach an "unlimited" energy source. Potatoswatter (talk) 21:13, 7 May 2008 (UTC)

I think the claim is supported because the behavior described is in a passive element (no active devices) and cannot be implemented with any other passive element and is not implemented by a combination of other passive elements (RLC).Skdvr369 (talk) 14:21, 1 May 2008 (UTC)

I've just read Chua's article, and made some modifications to the page that I hope will bring some light to the question. The confusion arises because it sound like the claim concerns linear circuits. It is not possible at all to complement the resistor, capacitor and inductor as the fundamental linear electronic components. Memristance can only be appreciated if we consider a non-linear memristor. A linear memristor is exactly a linear time-invariant conventional resistor. It is very easy to see that if we have a linear relation between the derivative of the current and of the voltage, then we obviously have a linear relationship between the original variables. Any knowledgeable electronics student should be able to deduce that. Chua's memristor is a non-linear relationship between the derivative of current and the derivative of voltage just as a non-linear resistor has a non-linear relationship between the current and the voltage. So, nothing changes for linear circuits, and basic linear electronics remains safe, sound and complete. It seems memristors can't be implemented with nonlinear RLCs, what is a very interesting result, but that seems to me something very difficult to grasp, and I would need to read about nonlinear circuits in general to fully admire that. I would like to ask: do the other nonlinear elements also can't be modeled with just the other three, for example? What about V-I correspondences?... (building L circuits with Cs, changing I for V) Final note: Chua's article brings a very interesting (linear) electronic circuit to simulate a memristor based on a nonlinear resistor, and anyone dying to have a memristor, even if active instead of passive, can build one of this. -- NIC1138 (talk) 02:25, 6 May 2008 (UTC)

What is the model for memristor?

Currently in the article:

The memristor is defined as an element in which the electric flux (φ) and the electric charge (q) are related by a time-independent function.

What is the actual math model describing the behavior of this component? The above isn't clear enough. -- KarlHallowell (talk) 00:38, 1 May 2008 (UTC)

At a glance, I'm guessing that an ideal memristor has a relation like flux is proportional to charge. The thing that puzzles me is how is it a regular ideal resistor isn't a memristor (or at least a special case). Since for a resistor, voltage is proportional to current, then one can integrate both sides with respect to time to get the equivalent of flux proportional to charge. Superficially, the relations for resistors seem to give the relations for certain memristors. I presume that's why the name memristor is so similar to resistor. -- KarlHallowell (talk) 00:55, 1 May 2008 (UTC)

As the article says, a linear memristor and a linear resistor are equivalent, for the reason you describe. However, a nonlinear memristor acts like a variable resistor, whose resistance is some function M(q) of the stored charge. Robert Southworth (talk) 01:26, 2 May 2008 (UTC)

Hmmm, that makes it unusual since the linear behavior of the other circuit elements is the underlying models of those components, even for nonlinear variations. Also, the very generic nature of the model (specifically the function "M(q)") still raises my hackles some. Is there a classification scheme in the literature for memresistors by characteristics of M(q)? It seems to me that different choices of M's might result in vastly different behavior. An analogy would be linear resistors versus diodes (the normal kind, not stranger ones like LEDs or varicaps) which since they can be specified mostly in terms of voltage and current, fit the model of a nonlinear resistor. -- KarlHallowell (talk) 18:57, 9 June 2008 (UTC)

Chua's IEEE paper gave the relation as M(q)=dφ(q)/dq for a charge controlled memristor, he refers to M as the "incremental memristance" and this allows you to write v(t)=M(q(t))i(t) which is basically restating Ohms law for a device whos resistance depends on the integral of the current which has already passed through it. Someone want to double check that I transcribed that correctly? Also note that this is from Chua's paper proposing the idea of an idea memristor. I do not know how closely this matches the recently constructed device.69.108.213.131 (talk) 01:12, 1 May 2008 (UTC)

While Chua's paper gives the relation as M(q)=dφ(q)/dq (so dφ(q(t))/dt = M(q(t))dq(t)/dt = M(q(t))i(t)), the question is whether the flux is the electric or the magnetic flux. If it is the magnetic flux then you are almost correct, except for a change in sign (the flow tries to counter the time rate of change in the magnetic flux). (Of course this would yield negative resistance, for positive memristance.) If it is the electric flux (as is the case with the HP device), then the relationship v(t)=M(q(t))i(t) (even with the opposite sign) doesn't hold (and even has the wrong units). -- DWHalliday (talk) 18:03, 1 May 2008 (UTC)

Is there a diagram of the flux and charge? Is there a graph of a V-I curve or anything? — Omegatron (talk) 12:51, 1 May 2008 (UTC)

From the Nature paper, "The i–v characteristic of such a nonlinear relation between q and phi for a sinusoidal input is generally a frequency-dependent Lissajous figure1, and no combination of nonlinear resistive, capacitive and inductive components can duplicate the circuit properties of a nonlinear memristor (although including active circuit elements such as amplifiers can do so)1." —Preceding unsigned comment added by Digfarenough (talk • contribs) 16:10, 1 May 2008 (UTC)

Wired news:[2]

"Indeed, Chua's original idea was that the resistance of a memristor would depend upon how much charge has gone through the device. In other words, you can flow the charge in one direction and the resistance will increase. If you push the charge in the opposite direction it will decrease. Put simply, the resistance of the devices at any point in time is a function of history of the device –- or how much charge went through it either forwards or backwards."

So I get the impression that if you apply a constant voltage, the current flowing through the device will increase over time, while if you apply a reverse constant voltage, the current flowing will decrease over time. (Exponential curve?) And if you apply 0 V for a while and then re-apply the voltage, the current will be the same as the last time you applied it, hence the memory function. Is this right?

Likewise for a constant current through the device creating a changing voltage. (linear curve over time?) Can we draw graphs of these relationships over time? Especially a graph with a break in it to demonstrate the storage property. So to measure the value currently in the device, I'm guessing you apply the voltage or current very briefly to measure it without affecting it?

So each device can really store an analog value and not just a 0 or 1? — Omegatron (talk) 13:27, 1 May 2008 (UTC)

It would likely also be possible to maintain the memristance by applying an AC voltage. During one half of the cycle charge would be lost, lowering the memristance, while on the other half of the cycle charge would be gained, raising the memristance. Assuming an equal amount of charge is lost and gained in each cycle, the memristance at the beginning and end of the cycle would be the same. RevEng (talk) 17:25, 1 May 2008 (UTC)

Yes, that's how they do it. — Omegatron (talk) 17:44, 1 May 2008 (UTC)

To simply go on saying that a memristor is a resistor that you can apply current to and "change its resistance" is saying almost nothing. This already happens in a non-linear resistor: a DC level changes the point of operation of the circuit, and the perceived resistance of an AC signal changes... The memristor dynamics is much more complicated. This low-frequency current can change this perceived resistance, and then come back to zero, keeping a desired perceived resistance for AC signals, and that is the main difference from a non-linear resistor... But I believe that a full understanding of what this element can do goes way beyond this AC/DC memory-building analysis. I am not quite sure a similar kind of memory could not be implemented only with non-linear RLC elements. Should this be possible, then this memory application would certainly not count as the most unique of the memristor characteristics. We must look for a behaviour only a memristor can have, and no circuit with passive non-linear RLCs can present!... That is not to say that a single memristor would not be a great element to build memories from.

One thing I still can't figure out is why it would be easy to disconnect a memristor from a source, as I've heard. This is something very difficult to do with an inductor. Why doesn't the memristor inherits this inductor characteristic?... -- NIC1138 (talk) 04:34, 6 May 2008 (UTC)

Possible edits

Thanks to whomever has access to the full IEEE article for posting the mathematical formula. Here are a couple of things I'd like to see, but I'll leave it for someone else to change if they see fit: Where it says that memristors can be combined to form transistors, that should probably be changed to "transistor-like devices known as crossbar latches". Also, I'd be curious to know if there is a unit of measurement of memristance, analagous to ohms, farads, or henries. John Mark Strain 02:10, 1 May 2008 (UTC)

---

The memristor would not be a fourth passive device but a 3rd passive hysteric device

i.e. passive devices Inductor, Resistor, capacitor. Passive hysteric devices: ferroelectrics, ferromagnetics such as ferrite, memristor. Passive hysteric device with retentivity: Electret, magnets, memristor?

Instead of mem they should use ferro as a prefix i.e. ferroresistor. Ferroelectrics do not have iron in them, they only use this prefix to represent the hysteresis effect.

1/5/2008

---

—Preceding unsigned comment added by 146.195.128.174 (talk) 07:27, 1 May 2008 (UTC)

What Chua should have called it is irrelevant. Its name is the memristor and it's 37 years too late to change it now!

Someone should add its other potential application: as an analogue device for use in building neural networks (see existing refs.) --84.9.67.105 (talk) 12:52, 1 May 2008 (UTC)

---

Reference 10 is not accurate. Passive components can amplify a signal, such as common L/C circuits designed to amplify signals from an antenna. It would be more accurate to state that a memristor is incapable of power gain because it's a passive component.

It is also possible to make an amplifier from only resistors and capacitors which work for a given frequency. Bob Pease at National Semiconductor way back in the '80s used this as an interview question. Imagine a multi-stage R/C low-pass filter that phase-shifts a particular frequency by 180 degrees. This circuit has only three terminals: in, out, and a common ground. Note that the voltage from out to in is an amplified version of the input signal. Simply relabel the terminals to turn it into an amplifier: in becomes ground, ground becomes in, and out remains out. Successive stages of this device can increase the gain to any desired level, though at an exponential cost in power.Smilindog2000 (talk) 18:51, 26 November 2008 (UTC)

Well, the main problem there is that it wasn't a reference at all, just an abuse of the reference tag to make an offhand footnote. In the context of digital logic, power amplification is the only kind that matters. Potatoswatter (talk) 19:07, 26 November 2008 (UTC)

Multitronic computing

Star Trek predicted (in the TNG tech manual) ultrasmall components that used multiple values, not just ones and zeros. This is the dawn of that era. --BlueNight (talk) 14:41, 1 May 2008 (UTC)

We could store analog values in a DRAM-like system, too, but we don't. — Omegatron (talk) 17:59, 1 May 2008 (UTC)

MLC (multi-level cell) NAND also store multiple bits per cell. 216.16.241.202 (talk) 15:53, 5 May 2008 (UTC)

It's probably not. Memristors are better at storing analog values than transistors, but transient currents will always cause them to drift in practice. Which may not be a problem for neural nets. The reason binary is popular is that a circuit only needs to "push hard up" or "push hard down". Finding somewhere in the middle is precise, and precision is laborious. Potatoswatter (talk) 02:15, 6 May 2008 (UTC)

Mechanical Equivalence

Would the property of memristance be equivalent to the mechanical property of viscocity of liquids? The more force that is applied to the liquid, one observes less resistance to flow. Isn't this the equivalent with electric flux as the "force" and current as the "flow" ? --192.251.13.62 (talk) 15:24, 1 May 2008 (UTC)

I'm just guessing here, but there appears to be a residual memory of the prior current passed through the device whereas your mechanical example is always a memory-less or context-free relationship. --76.111.49.144 (talk) 22:03, 1 May 2008 (UTC)

• It sounds like this would be more like shape memory alloy. This is probably a stretch but here's my thinking. A viscous fluid, whether shear-thickening, shear-thinning, or shear rate indifferent, only cares about the speed at which it is deformed right now. It doesn't care about last Saturday. Now a shape memory alloy does care about last Saturday (granted JUST Last Saturday) and depending on what you do it, it will revert to Last Saturday. I dunno, I think this is a stretch and probably not quite analogous. I would be interested in the true analog. (Inductor = Mass, Capacitor = Spring, Resistor = Damper, Memristor = ?) Also, what would this be in a bond graph? Dachande (talk) 12:35, 6 May 2008 (UTC)

A paper

Here is an old paper I've found that may (or may not, haven't gone through it myself yet) be helpful in understanding the concept: [3] (PDF, scanned). Maybe someone will make some sense out of it and fix the article. --87.99.27.160 (talk) 21:08, 1 May 2008 (UTC)

Actually it's several papers put together, including today's one from Nature. I've also found a paper seemingly explaining how to model a diode using memristor: [4]. --87.99.27.160 (talk) 21:40, 1 May 2008 (UTC)

Memristors are a very general concept describing how circuits change with DC current. That's a good application of the theory but it the memristance function they use for a highly accurate diode model isn't the same as the TiO2 switch. Potatoswatter (talk) 02:10, 6 May 2008 (UTC)

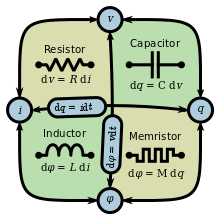
I made a graphic mimicking the ones in that PDF. Does anyone like it? Any suggestions or modifications? — Omegatron (talk) 02:04, 2 May 2008 (UTC)

The present media frenzy is making much use of the "missing link" aspect but that is too topical for an encyclopedia. Comparing with inductors etc is extremely confusing. Memristance is a theory more than memristors are a certain component. Potatoswatter (talk) 02:10, 6 May 2008 (UTC)

When I read them I thought the article needed those graphics. I'm not sure though to what extent the graphic must be different for us to be able to use it freely. Is it sufficient that the one we use is "home-made"? On another aspect, I think the simmetry which makes one think that memristance "must exist" is clearer if we use 1/C instead of C (Chua should have written 1/M...), although doing it maybe clutters the graphic... --euyyn (talk) 02:38, 2 May 2008 (UTC)

I'm not sure what you mean. Write $dv={1 \over C}dq$ and $dq={1 \over M}d\phi$? How does that make it clearer? — Omegatron (talk) 00:00, 3 May 2008 (UTC)

I'm very against putting the capacitor, resistor, inductor at the top of the memristor article. This article is only about memristors and shouldn't be cluttered with extraneous information which will distract layfolk (fascinating though it may be). Potatoswatter (talk) 02:10, 6 May 2008 (UTC)

Memristors were "invented" by extrapolating from R/L/C, so we absolutely have to mention that. Acasp (talk) 09:40, 6 May 2008 (UTC)

Yes but not in the lead. Potatoswatter (talk) 20:58, 6 May 2008 (UTC)

No, just $dv={1 \over C}dq$, so the four differential magnitudes in the graphic get alligned. --euyyn (talk) 00:29, 17 May 2008 (UTC)

Is it seriously also known as a flux capacitor? lol

P1415926535 23:27, 1 May 2008 (UTC)

I agree, that has to be a joke and minor, but humorous, incident of vandalism. the coincidence is just so unlikely. —Preceding unsigned comment added by 76.172.192.76 (talk) 03:15, 2 May 2008 (UTC)

There's been a rash of Back to the Future related vandalism on this article, due to the fact that much of the internet press is referring to this jokingly as a flux capacitor. I added a little sentence talking about how the internet is popularly referring to the memristor as a "flux capacitor". This is actual legitimate information regarding the popular press coverage on this subject and also a potential means of curbing vandalism; if the article already mentions Back to the Future, vandals may not deface the article with factually inaccurate references. --Logoskakou (talk) 15:57, 2 May 2008 (UTC)

This needs references. We don't put things like this in our articles until after they're used that way by other people. We don't create ideas; we just report on them. — Omegatron (talk) 23:43, 2 May 2008 (UTC)

Here's the text I removed: "Since news of the creation of a working memristor in April 2008, the memristor is popularly being referred to, accurately, as a flux capacitor due to memristance being a relation between charge and magnetic flux; this is a humorous reference to the flux capacitor from the Back to the Future trilogy."

Don't put it back without references. — Omegatron (talk) 23:54, 2 May 2008 (UTC)

The joke here is that it *is* correct to call a memristor a flux capacitor. It's a reasonably accurate description made interesting because it is so funny. However, no one in the mainstream media has called it a flux capacitor. And no scientist involved has called it a flux capacitor. So, if you want to see Flux Capacitor become a semi-official name for a memristor, encourage your local scientific community to write something describing why it is an accurate name and get it published somewhere. Kevin143 (talk) 23:37, 3 May 2008 (UTC)

Circuit analysis examples

Does anyone have any circuit analysis examples involving memristors they'd like to share, e.g. a memristor in series with a resistor, inductor, etc.?

Examples in the Laplace domain would also be interesting too. -Roger (talk) 23:56, 1 May 2008 (UTC)

I don't think you'll get anywhere with Laplace transforms since memristors are only interesting (that is, different from standard resistors) when they have a non-linear flux/charge relationship. As I recall, Laplace transforms are only useful in linear systems. —Preceding unsigned comment added by 142.244.81.32 (talk) 01:07, 2 May 2008 (UTC)

The memristor, like the other fundamental circuit components is a linear device, as if it does not obey the linear equation $M(q)={\frac {\mathrm {d} \Phi _{m}}{\mathrm {d} q}}$ then its not a memristor. 128.232.237.213 (talk) 19:50, 6 May 2008 (UTC)

charge that flows vs. charge accumulated

Omegatron, I really don't like the wording that M is a function of the charge that flows through the device, since that seems to imply the memristance could change if the charge "stops flowing". When we speak of capacitors we usually talk about charge accumulated in it (which of course is not "net" charge, but difference of charge between the terminals). You seem to dislike this wording for memristors. What do you think of "charge that has flowed through"? --euyyn (talk) 02:33, 2 May 2008 (UTC)

I changed it to "charge that has flowed through" because that's the wording used in the papers that describe it. I don't think the memristor accumulates charge at all. — Omegatron (talk) 23:38, 2 May 2008 (UTC)

Agreed, the memristor does not accumulate charge, not even in the sense that a capacitor does. Did you actually save your rewording ? The current version (209843059) still mentions "accumulated electric charge". Acasp (talk) 09:58, 3 May 2008 (UTC)

I've had a go at fixing this. I'm going by the IEEE Spectrum article, which says that the HP device shuffles oxygen dopant atoms around as current flows through it. Therefore it stores information about charge, not the charge itself. I was thinking of saying that it stores information about the integral of current over time, but I don't want to be guilty of OR. --Heron (talk) 18:20, 4 May 2008 (UTC)

Copyright vio needs rewrite

I deleted a paragraph that was taken verbatim from the News.com article. Its explanation of memristors' potential use in memories was valuable, and should be rewritten. Robert Southworth (talk) 16:51, 2 May 2008 (UTC)

Keep things separate

The device from HP seems to be quite different from the theoretical device that uses magnetic flux. I think we should keep the two separate in this article, and describe the HP device as one which emulates the properties of a memristor, or has similar salient characteristics or something. — Omegatron (talk) 00:01, 3 May 2008 (UTC)

• When defining a memristor, Chua actually didn't use the term "magnetic flux"; he called it "flux linkage", and defined it as just the integral of the voltage, in the same way that charge is the integral of current. He never said anything about magnetism. I've been unsure how to phrase the definition, since Wikipedia gives a definition for "flux linkage" that doesn't quite match either. - Robert Southworth (talk) 02:27, 3 May 2008 (UTC)

• He does speculate about magnetism later in the paper, but we simply know now it was a dead end. If we make any changes to Chua's formulation, it might just be best to replace flux-anything with an integral sign. "Flux linkage" is not a term that makes sense outside wire loops and "magnetic flux" doesn't make sense unless you're finding current through a loop. Potatoswatter (talk) 02:02, 6 May 2008 (UTC)

Agreed. Often the original formulation of a theory disappears after other scientists with a broader view reword it. See e.g. the Oster paper. Acasp (talk) 09:40, 6 May 2008 (UTC)

The article should not start with equations in differential form

To understand the difference between a resistor and a memristor, you need to start from equations between state variables, not from their differential forms.

From a purely mathematical point of view, a non-degenerate state equation $F(x,y)=0$ yields a local solution $y=f(x)$ (hence $dy/dx=f'(x)$), or $x=g(y)$ (hence $dx/dy=g'(y)$). And more generally (δF/δx)(x,y)dx + (δF/δy)(x,y)dy = 0.

Passive electronic devices link two state variables among the four (I,V,q,Φ). Therefore there are 4*3/2=6 types of state equations. Two of those (I=dq/dt, V=dΦ/dt) are actually definitions, and the remaining four are:

$Fr(I,V)=0$, which yields $dV/dI=R(I)$ (resistance)

$Fl(I,\phi )=0$, which yields $d\phi /dI=L(I)$ (inductance)

$Fc(q,V)=0$, which yields $dV/dq=1/C(q)$ (capacitance)

$Fm(q,\phi )=0$, which yields $d\phi /dq=M(q)$ and further $V/I=M(q)$ (memristance)

This explains why M is allowed to depend on q (or Φ), which in turn enables hysteresis, whereas even a non-linear R can only depend on I (or V).

Conversely, M cannot depend on I or V. Therefore a resistor is not just a special case of a memristor (i.e. there exists non-linear resistors that are not equivalent to any memristor).

Acasp (talk) 06:08, 3 May 2008 (UTC)

• This is the first post that begins to explain, at least to me, why a memristor is not a nonlinear resistor. Can you explain or point to a reference for the statement, "Passive electronic devices link two state variables among the four (I,V,q,Φ)."? In particular, why is it this particular set of 4 state variables that defines passive electronic devices, especially since two of them are time derivatives of the other two? What is it that guarantees there exists a function of each pair of these state variables that is equal to zero? In what sense are these equations the state equations? What should people read if they want to know more about this? Rdphair (talk) 03:13, 4 May 2008 (UTC)

• The choice of variables is like position/speed/acceleration in mechanics - maybe it is just how we model the world.
• Linking any two state variables among the four is the approach that led to inventing the memristor. I am not sure this was understood as a definition of fundamental passive electronic components before. It is quite reasonable though (you must connect at least two to get useful behaviour, and you can't connect three or more because of degrees of freedom).
• F(x,y) is the most general way to specify a relation between two variables. If you start from y=f(x) instead, you can rewrite it as F(x,y)=f(x)-y=0. Of course this does not say anything about whether there exists a corresponding simple physical device.
• Maybe Constitutive equation is a better wording than State equation.
• G. Oster and D. Auslander. The memristor: A new bond graph element. Trans. ASME on Dynamical Systems and Control. 94:249-252 (already mentionned here).

Acasp (talk) 09:48, 4 May 2008 (UTC)

Is R=DV/DI? 70.124.79.247 (talk) 17:49, 4 May 2008 (UTC)

It's formula is wrong. This device has nothing to do with magnetic flux. It should be the electric flux. —Preceding unsigned comment added by 69.253.87.22 (talk) 18:44, 4 May 2008 (UTC)

Agreed. Φ is just the time integral of V; it does not necessarily have a magnetic realization in actual devices. The reference to Faraday's law of induction should be deleted too. Acasp (talk) 22:51, 4 May 2008 (UTC)

I disagree. On one side, electric flux has nothing to do with the time integral of V. On the other, one must remember that the device done by HP and the theoretical device are only analogous, in a circuit analysis way. If one were to make an inductor which didn't use magnetism either, it would be fair to still call it an inductor. The theoretical device, which isn't but a bunch of equations, i.e., a model, was invented due to the simmetry of the equations of the other 3 circuit elements, which do use Φ as the magnetic flux (hence its name! there's no physical magnitude which equals the time integral of V, except for magnetic devices). If we want to present the simmetry discovered by Chao, we must use magnetic flux. --euyyn (talk) 01:23, 6 May 2008 (UTC)

Or we can realize that people named it "magnetic flux" because they first encountered it in the context of wire loops, and later found out that it also makes sense for modelling purposes to introduce new state variables which are the time integrals of other state variables. Similarly, the memristor also involves q (time integral of I), and we do not call it "stored charge", but rather "amount of charge that has passed through the device".Acasp (talk) 09:40, 6 May 2008 (UTC)

I don't think (correct me if I'm wrong) that it's used that way somewhere else; if it is, then ok. If it's not, I think we should present the abstraction here, not take it as granted. But what would be just erroneous would be to call it electric flux. --euyyn (talk) 00:38, 17 May 2008 (UTC)

This page is entirely about the idea, linear Memristor, the same as that for resistors. The ideal resistor is linear, and not a function of Current!! the resistance of a resistor is constant!! the resistance of a diode IS a function of current, giving a non-linear V-I graph. but for a resistor is a linear component. Other things can have resistance.. that have non linear V-I graphs, but these are not resistors, like diodes. The same is true for capacitors, inductors, and memristors which are all linear components. —Preceding unsigned comment added by 129.169.10.56 (talk) 11:55, 7 May 2008 (UTC)

If we restrict the page to linear memristors, then there will not be much to say, because there is no difference between a linear memristor and a linear resistor. To explain how the memristor concept relates to resistors, inductors and capacitors, we absolutely have to start from the most generic (i.e. nonlinear) version of the latter three. Acasp (talk) 20:53, 7 May 2008 (UTC)

Not well explained

Oh guys... I'm just a harmless physicist and not trained in the ways of electric engineers and higher circuit design thought, but finally I guess I've deciffered your explanations on what a "memristor" is supposed to be ... :-) It's confusing to talk about magnetig flux (1. equation). No magnetic flux needs to be involved, I guess (in analoy to an inductor) you denote by this the time integral of voltage. And for the 4 fundamental circuit elements, I guess people look at current and "charge" (integral of current) on one side and voltage and "flux" (integral of voltage) on the other side. Then they consider the 4 elements which give fixed functional relationships between these, e.g. V=f(I) ("resistor", if non-linear e.g. also diode) or V=f(Q) "capacitor". Memresistance then gives a relation between the time integrals (of I and V) (which, when linear, is simply again an ohmic resistance).

When it's this simple why not explain it that way? Problem is, I may not know enough electronics background and history to write it... arrogantly, yours :-) 212.171.245.23 (talk) 21:26, 3 May 2008 (UTC)

I've now added a brief explanation that here "magnetic flux" simply stands for the integral of voltage over time (in analogy to the law of induction for a coil). Everything could certainly be written better, but for the moment let's at least give people a change to understand.

Also it might be nice to have some rough qualitative description of the particular (non-linear) behaviour of the HP memristor. Is it symmetric (negative/positive voltage) or rather asymmetric (like a diode). Does memristance increase or decrease as we pass current through it (starting from some "equilibrium" point)? How permanent is the memory?

Also I don't think the remark is correct that we need the differential forms of the equations because things may be non-linear (and need to be for memristance to be any different from an ohmic resistance). Constructively (this time) :-) , yours 212.171.245.134 (talk) 10:51, 5 May 2008 (UTC)

Memristors are linear.. $M={\frac {\mathrm {d} \Phi _{m}}{\mathrm {d} q}}$ is a linear equation! Resistors, capacitors, inductors and memristors are all linear. 128.232.237.213 (talk) 20:08, 6 May 2008 (UTC)

What is this?

I am not even a physicist, I suppose I am what may be called an interested layman. As such, after reading this article, I have no idea what a memristor is, what it could be used for, why it is important that people have made one, or why its discovery is on the news section of the front page. I feel that the article as it is written currently doesn't explain memristors in terms that "ordinary people" could understand, yet clearly the topic is very important, so it probably should. Because I want to read this article and understand it, it sounds extremely interesting! Jdcooper (talk) 20:04, 4 May 2008 (UTC)

The link at he bottom of the page explains it quite nicely. Zazaban (talk) 05:03, 5 May 2008 (UTC)

The way I'm reading it, this is a component of a memory circuit with passing functional similarities to the magnetic core memory that was used back in the old days, though this is much more miniaturized. Afalbrig (talk) 10:54, 7 May 2008 (UTC)

Not a bad interpretation. That relied on storing power in a magnetic field, though. This is physically more like a current integrator controlling a variable resistor. Potatoswatter (talk) 11:53, 7 May 2008 (UTC)

Over a decade ago I took the first half of an electronics degee, sadly I have forgotten most of it so I straddle the fence between a layman and a trained physicists/EE. I don't think that a layman's description of it the topic under discussion would be possible in the sense that you are asking for. There are two issues for this in this case: a) A certain threshold knowledge of electronics, and to some degree math is required for appreciation of what is being present, although This does not mean to say that enrolement in one's local technical college is necessary, however. and b) VERY NEW: In any encyclopedia but wiki this wouldn't be around for 20-30 years. This esentially is a device of which a couple prototype models exist in the world, which seem to prove a somewhat contreversial interpretation of how certain basic electronic devices relate to each other in their opperation mathematically; based on a theoretical physics/electronics paper written 37 years ago with applications just now being discovered(possibly) due to modern materials/manufacturing science. The result of this is that, from what I can tell, even the experts have not decide whether the interpretation is accurate yet; a true layman's description will probably need to wait until the basic concept is no longer in a state of flux. Eoag (talk) 22:17, 4 May 2008 (UTC)

Well I know that a layman's description is possible, because subsequent to writing the above message i went and read this article from the BBC website, which cleared everything up for me, in layman's terms. Obviously the wikipedia article should include the formulae and technical physics, but it should also outline the topic in simple prose as in the BBC article. Jdcooper (talk) 14:08, 5 May 2008 (UTC)

The problem is that the article is inaccurate. They haven't been used to build transistors. A transistor is an amplification device and a memristor is a passive element which can only weaken a signal. Certain memristors can be used to implement memory, but at the same time the theory of memristance provides for different kinds of devices, all of which are under this article until they're fleshed out and given specific names. Potatoswatter (talk) 01:52, 6 May 2008 (UTC)

1. Transistors aren't "amplification devices"; they're valves.
2. Memristors haven't been into transistors, but they have been made into crossbar latches, which would likely take the place of transistors at this small scale. — Omegatron (talk) 04:28, 6 May 2008 (UTC)

Transistors are not "valves"!!!... They are nonlinear tripole electronic devices that can be exploited, among other things, to simulate transimpedance in small-signal approximations. Diodes, on the other hand, are nonlinear dipole electronic devices that can be exploited, among other things, as current "valves". -- NIC1138 (talk) 05:54, 6 May 2008 (UTC)

Nwerneck is right. Memristors are more like valves than transistors. Transistors regulate the current between A and B according to a stimulus (current or voltage) at C. ALL transistors are controlled current sources and if you think otherwise you need to go (back) to school. See my recent cleanup effort at diode logic. Potatoswatter (talk) 09:44, 7 May 2008 (UTC)

Transistors are most definitely not current sources. The math of a transistor is equivalent to a device with a controlled current source inside, but that doesn't mean they actually have a power source inside. They're current-regulating valves. They allow current to flow from a source to a load; they don't push charge through circuits. Transistors are not amplifiers; amplifiers are made out of transistors.

This is the kind of thinking you need to avoid if this article is going to be accessible to laymen. — Omegatron (talk) 21:39, 7 May 2008 (UTC)

This isn't the article and you know what I mean. Transistors can achieve amplification, unlike memristors, because they implement some sort of current source. You can't make a linear circuit with a transistor without a current source. In any case the notion of a "valve" is very ill defined. A valve on a firehose is an adjustable current source if you ask me. Potatoswatter (talk) 22:01, 7 May 2008 (UTC)

I'm afraid there is a misinterpretation of that what memristors really are !!!

The equation of memristance indicates an element, where the charge is a derivative of the magnetic flux. This leads to the fact, that a constant memristance has to store charge in case of an increasing magnetic flux and to release it in case of a decreasing magnetic flux (in form of a current). This is just a characteristic of an inductor and that what most inductors are used for. But memristance isn't equal to resistance nor inductance, it's really a totally own thing and the equation V(t) = M(q(t))I(t) isn't correct. (Please excuse my poor English - I'm a German) 92.193.127.227 (talk) 23:53, 4 May 2008 (UTC)

You probably mean that in a memristor, charge is a function of flux ("derivative" is a very poor choice of words in this context).

V=M(q)I (memristance) is completely different from I=LdV/dt (inductance), so please clarify why it is not correct and how you would change it.

Also, electronic components do not "store" charge - their overall electrical charge remains null. A capacitor stores energy in the form of an internal inhomogeneity of charge. Acasp (talk) 07:54, 5 May 2008 (UTC)

I mean memristance is the derivative of magnetic flux with respect to charge, as the equation of the memristance says. [[5]] A konstant memristance describes the fact, that the stored charge is changing proportional to magnetic flux. The equation V=M(q)I is wrong, because memristance is not resistance. The charge in a memristance isn't stored in form of separated charged particels but in form of changes of the magnetic field. 92.193.127.227 (talk) 23:25, 5 May 2008 (UTC)

M(q)=dΦ/dq=(dΦ/dt).(dt/dq)=V/I, as explained in the article. Nothing wrong.

Magnetic fields do not store charges. Besides, the flux in question is defined as the time integral of voltage (i.e. dΦ/dt=V), which reminds us of Faraday's law of induction, but this does not imply a magnetic phenomenon. In HP's memristor, when current and voltage are removed, there are no magnetic fields in the device, yet it retains its state.

Similarly, q is defined as the time integral of current (i.e. dq/dt=I), but this does not imply that the device works like a capacitor at the physical level. Acasp (talk) 01:12, 6 May 2008 (UTC)

I dont care where you are from, I love you and youre right, there is alot of misrepresentation here!! 128.232.237.213 (talk) 22:23, 6 May 2008 (UTC)

Lead

Please make the lead as accessible to a layman as possible. The way it stands, talking about time integrals and stuff from the first line itself is intimidating, if not downright scary. And it is too full of jargons to be of much use. Terms such as linear and non-linear functional relationships, and acronyms such as LTI and MOSFETs appear without any prior explanation. At least a half-a-line explanation provides enough context for readers to carry on the reading without having to read other articles just to comprehend one line. It makes for a much better reading experience. Layer the entire article (and the lead section in particular) according to complexity.

Why not start off with the layman's description sourced from the IEEE Spectrum article: A memristor is a circuit element the resistance between the two terminals of which vary according to the current flowing through it and which remembers the resistance when the circuit is switched off. (Note: May not be complete or correct; verify before using). Follow it up with a more formal definition using the functional relationships between V and I or Φ and q. That ends the first paragraph. In the second paragraph mention the history of discovering both the theoretical and practical existence. In the third paragraph, mention the proposed uses and the advantages over conventional methods.

Also, consider rewriting the definition section, focussing more on the difference from resistor rather than similarities to it. --soum ^talk 13:52, 5 May 2008 (UTC)

As memristors are being used as switches, I focused more on the difference from transistors in the last part of "definition". Switch memristsors (which are getting the media attention) are entirely different from resistors when DC current is applied and approximately like resistors when AC is applied. If you don't know the difference between DC and AC you should read those articles first, certainly not this advanced topic. Agreed definition needs a lot more expansion. Before I started reworking it yesterday/today, there was really no derivation at all. Potatoswatter (talk) 01:56, 6 May 2008 (UTC)

MOSFET might be quite enigmatic, but LTI is a crucial concept. High-school electronics is basically LTI systems, so we might just call it "basic electronics", I don't know...

I am very much against saying that we are somehow changing "resistance" as function of a current. That is a gross misunderstanding of what this stuff does. The fundamental definition of this element must be done just like it is done with resistors, capacitors and inductors: based on voltage and current (there is a physicist somhewere around here that said just that).

Resistors, capacitors and inductors are inherently more simple than memristors. and just like it's almost impossible to talk about capacitors without mentioning inductors, you can't talk about memristors without talking about the other three, so they stay there. The layman looking for information must learn that the stuff he is hearing in the news is an oversimplification, and that he can't possibly understand what it is without thinking about capacitors, inductors and resistors.

I also thing the "current switch" thing is an oversimplification of the first thought applications. What the heck is a "current switch"!?... We are talking about a complicated entity, and this must be clear in the introdution.

I am sorry if I am moving towards an edit wars!!... I will refrain from editing in the next few hours, and try to concentrate my discussion only to this topic... -- NIC1138 (talk) 05:11, 6 May 2008 (UTC)

I wasn't saying LTI need not be mentioned, I just said don't use an acronym without having used it in its expanded form before. Not everyone has electronics as their first language. :-) If the stuff being shown in the press is an oversimplification, then think of something more accurate. I still stand by my statement - we need a definition that is accessible to non-physicists: something that says what it does in plain english, without resorting to differential equations. Sometimes that is what people want. And that is why I said, increase the depth of technicality progressively - those who want more mathematical details can read more. --soum ^talk 13:15, 6 May 2008 (UTC)

The problem of LTI is difficult because many BSEEs forget what it is after leaving class. So we have to be very grammatically careful to write clearly for even a technical audience. Memristors are linear when solving a circuit at one point in time, which is an important bit of linearity. Essentially LTI theory developed to describe what Fourier/Laplace transforms and LCR circuits and can do. So it's surprising to an EE that a fundamental passive element would not work in that theory. But it's not important to a non EE. So we have to phrase it such that a non EE will gloss over but an EE stops and says, "what does that mean again?" Because as you can see on this talk page, a lot of people are getting confused on this particular point. Potatoswatter (talk) 09:37, 7 May 2008 (UTC)

MEMS

Is this memristor same as a MEMS device?Anwar (talk) 18:35, 5 May 2008 (UTC)

The simple answer is no, they are different concepts. The 'mem' in memristor stands for 'memory' while the 'MEM' in 'MEMS' stands for 'microelectronic mechanical'. The similarity is just a coincidence. However, I am sure someone will point out that the two technologies may overlap slightly, since some mechanical systems may display memristance (in its mechanical sense) and both types of device could be created using similar microelectronic or nanoelectric fabrication techniques, perhaps even with both technologies on the same chip. --Heron (talk) 19:05, 5 May 2008 (UTC)

MEMS are typically on the order of a few micrometers. The new memristors are on the order of a few nanometers. Potatoswatter (talk) 04:16, 6 May 2008 (UTC)

Please remove all references to 'magnetic'

Like the comment above in 'not well explained', I hereby urge you to remove all references to MAGNETIC flux.

Being a physicist myself, I have learned about electronics from textbooks that have been vetted by physicists. I was not even aware of the use of the word 'flux' (or even 'electric flux', which would be current density) in electronics books as the time integral of voltage.

What I'm writing here is of importance because people with knowledge of either electronics or physics (or both) are reading this, and the employed language should be compatible with both.

Voltage is a measure of energy when applied to a single electron. Integrating voltage over time does not make any sense. It just so happens that doing this for an inductor gives you a measure of magnetic flux, and therefore this 'flux' is used in a mathematical model of circuits. This is fine by me, as long as the proper definition is given, as it is right now in the article. There is an explanation, of course: an inductor stores energy in its magnetic field - that energy comes from the voltage across it. Integrating over time therefore makes perfect sense when building the mathematical model. But be aware that you are losing the link to physics, or a physical model. Ordinarily this problem does not arise because the only time a 'flux' is used mathematically, there is a magnetic flux present. The memristor is an exception and all references to MAGNETIC flux should be removed ASAP.

If there is consensus about this, I'd be happy to make the changes. If there is any further confusion over the terms 'flux' and 'magnetic flux', we should probably finish this discussion here on the talk page first before engaging in an 'edit war' or skirmish.

P.S. Of course memristors DO have magnetic fields - an electric current cannot exist without a magnetic field - but the values involved are ridiculously small, comparable to those of resistors. I think all electronics engineers will agree that the self-inductance of most resistors is negligible for practical purposes.

GilHamiltonTheArm (talk) 14:25, 6 May 2008 (UTC)

How, can you then define memristance? Memristance is defined as $M={\frac {\mathrm {d} \Phi _{m}}{\mathrm {d} q}}$ . Memristance have the same units as resistance.. but memristors are defined by having a constant ratio of magnetic flux change to charge change through the terminals. This ratio has units Ohms, but thats no reason for them to obey Ohms law. By analogy, would you want then to remove references to charge on the capacitance page? being an engineer, Im suprised you dont like magnetic fields :p. 128.232.237.213 (talk) 22:38, 6 May 2008 (UTC)

Yeah, it's a noble goal. We'll work on it :v) . It'll also help if someone reads Chua's section on magnetic fields to figure out what he thought about this. Too many people messing with what's already there and not enough new contribution... Potatoswatter (talk) 09:29, 7 May 2008 (UTC)

I read the blog article referenced below where they ask Chua what he thinks of this new invention, which he predicted in a way. In it, magnetic flux is not mentioned - instead, he is careful to refer consistently to "changes in voltage, or flux". (Just because "flux" scales with "magnetic flux" for an inductor, does not mean you can confuse the two.) So memristors are instead defined by having a constant ratio between "change in change in voltage" and "change in charge". I don't blame anyone for being confused by this.

GilHamiltonTheArm (talk) 13:53, 7 May 2008 (UTC)

Memristors are linear, and Memristance is not a function of charge!

$V(t)=\ M(q(t))I(t)$ is wrong.. the instantaneous value of the resistance of a memristor IS a function of the charge that has passed through it, but the memristance M is constant for a memristor and is not a function of anything (only in this simplified thory, for example resistance is a function of temperature.. but in simplified theory is is constant). You could make the claim that a capacitor has capacitance that is a function of charge, or current by looking at the differential equations that are accociated with it, but that is not the case.

The set of equations outlined here http://en.wikipedia.org/wiki/Image:Four_circuit_element_relationships.svg are all linear, and can therefore be manipulated usefully using Laplace and Fourier transforms, and in AC circuit analysis phasor notations can be used for memristors. Can anyone verify the claim that a memristor is a non-linear device? (like the other three basic circuit components?) .. not that I can do the analysis, but the bits that are wrong should be removed. 128.232.237.213 (talk) 20:31, 6 May 2008 (UTC)

What's the basis of your argument? Have you looked at the paper? v(t) = M(q(t))i(t) is Equation 1 in it. Potatoswatter (talk) 20:52, 6 May 2008 (UTC)

It depends entirely upon what context the equation was in.. you cant just pull an equation out of a document where you see it has memristance. In AC analysis, an inductor has impedance that is a function of frequency, which relates V and I, but a capacitor is a linear device, trust me. Its the same with inductors. The basis of my argument is that memristance is constant. Do you agree that the memristance of a memristor is contant? There is no such thing as a "memristance function". It does not obey the equation $M(q)={\frac {\mathrm {d} \Phi _{m}}{\mathrm {d} q}}$ by adjusting its memristance, it obeys the equation $M={\frac {\mathrm {d} \Phi _{m}}{\mathrm {d} q}}$ keeping constant memristance and adjusting its ${\mathrm {d} \Phi _{m}}$ assuming constant change in charge (constant ${\mathrm {d} q}$) or adjusting its ${\mathrm {d} q}$ assuming constant ${\mathrm {d} \Phi _{m}}$ . Infact keeping either of these constant does not matter, the only important thing it that their ratio of change is constant. This is what makes it a fundamental circuit element! just the same way that an inductor does not have an "inductance function".. an inductor keeps the ratio of current change to flux change constant.. the constant of proportionality being its inductance, a capacitor keeps the ratio for [any change in charge flow through one terminal] to the [voltage change across its plates] constant, the constant of proportionality being its capacitance. It is the same for memristamce, and hence how it was realised that they should exist because of this missing derivative ratio of electomagnetic parameters. A diode is a nonlinear device, and doesnt link into these fundamental relations (in a linear manner), and hence why its not the fifth fundamental element of a circuit. This page was correct as of about a week ago I see.. and god knows whats happened in the meantime.. all the media attention has not done this page any good it seems. 128.232.237.213 (talk) 21:26, 6 May 2008 (UTC)

Please read the whole discussion page; all your misunderstandings have already been adressed here. Differentials equations can be misleading because they contain unwritten, implicit variables and dependencies. Read #The_article_should_not_start_with_equations_in_differential_form.

dΦ/dq is always equal to dV/dI. The defining feature of the memristor is that this ratio is allowed to depend on q, whereas for (nonlinear) resistors it can only depend on I. Acasp (talk) 09:19, 7 May 2008 (UTC)

Id just like to point out that the equation $M={\frac {\mathrm {d} \Phi _{m}}{\mathrm {d} q}}$ was on here and was changed with no explanation to $M(q)={\frac {\mathrm {d} \Phi _{m}}{\mathrm {d} q}}$, and has lead to alot of confusion it seems, and a lot of .. wrong information.. (to put it lightly) has been entered. 128.232.237.213 (talk) 21:47, 6 May 2008 (UTC)

Ok, the equation $V(t)=\ M(q(t))I(t)$ is correct, but M is NOT the memristance, it is the instantaneous value or resistance attributed to the memristor, and in this way it is strictly NOT resistance. It is purely the ratio of intantaneous current to instantaneous voltage, hence instantaneous resistance. This is similar, but different to resistance. Resistance is the ratio of current to voltage for all time under any operation conditions. The same could be said for inductors.. the instantaneous value of capacitance for an inductor would be the ratio of the instantaneous change of charge passing though it to the instantaneous change of voltage across its terminals. (thats why 1/C has the same units as L like R has the same units as M... the 1/C as opposed to just C comes from convention, and the ratio should have been defined "the other way up" for consistency, but they were unaware of this inconsistency) Its probably best to keep the mathematical detail of a week ago.. 128.232.237.213 (talk) 22:20, 6 May 2008 (UTC)

You know, it would be a lot easier for me if you'd erase unwanted mathematical arguments rather than retracting them. There is a reason the articles use the symbol M(q(t)): because memristance is a function from charge to resistance, and charge as ∫Idt depends on time. M is specified as a function, unlike R, C, or L, because the device retains a linear I-V graph despite having a functional specification. There are also function-specified resistors, capacitors, and inductors, but they do not have linear I-V graphs. The voltage across a memristor is always proportional to the current by the memristance function. Finding C=Q/V for a resistor will yield a function depending on time... I don't really know where you're going with that. Also, please get an account if you plan to be a serious contributor. Potatoswatter (talk) 22:47, 6 May 2008 (UTC)

I know I should fix the article, but thered be so much chage that I dont think anyone would accept it.. Im just trying to convince people before I change it. Memristance is not a function. The same way that resistance if not a function. . con (unlike elsewhere on this discussion page that states it is a function of current?!) Memristance is constant for any given memristor. However the equation that links its instantaneous voltage to its instantaneous current is confusing people, because this is not what defines memristance. Memriatance is the constant ratio between the change of net magnetic flux held by the memristor to the change of net charge that has passed through it. This may go on to mean that it has a V-I graph that is potentially not a straight line and dependent upon the "charge history", but that does not mean it is non-linear just that this graph is depant upon charge history.. take the V-I graph for an inductor, which would be dependent upon time since (e.g.) a step voltage was applied. There is no such thing as a function specified resistor.. these devices would have instantaneous values of resistance that chance upon other given parameters.. would you say that a diode was a resistor? (a diodes resistance is a function of its current). I haven't found that Q = C/V for a resistor.. there are alot of simple differential equations that you can pull out of electromagnetic theory, but without knowledge of their physical interpretation, they can be misused. The truth is that these differential equations are infact partial derivatives, and so cannot be simply split up and manipulated with other equations.. otherwise you can rearrange equations to show that M=R.. Also is has been said that "flux is the time integral of voltage" which is especially vague. More correct is that the EMF (voltage) produced when a single coil passes through a magnetic field is equal to the rate of change of net flux through the coil with time .. or emf = d(phi)/d(t) where this is strictly a partial differential. which could be rearranged and errenously applied in other systems. basically trying to look at its V-I characteristics is as helpful as looking at the Q-V characteristics for an inductor, and because it is called a memristor, is leading people to believe that its a resistor but with memory having resistance related to the charge that has flown through it, so a V-I charachteristic makes most sense. I could say that a capacitor is an inductor with memory, as is has effective inductance (as explained before) that is related to the net current that has flown into the capacitor. Capacitors exhibit a similar form of memory.. a current memory, readable by the voltage across its terminals.. but this doesn't mean its a non-linear inductor where its inductance is a function of current. it is a capacitor with constant capacitance, and a function that relates its instantaneous value of inductance as a function of current, the same way that a memristor has an instantaneous value of resistance that is a function of the net charge that has passed through it, but this is perhaps the most confusing way to describe a capacitor, and memristor. 129.169.10.56 (talk) 12:34, 7 May 2008 (UTC)

I agree. There are two confusing issues muddying the waters here:

• referring to "flux" as "magnetic flux", essentially semantics but confusing to a physicist
• two conflicting definitions of memristance, $V(t)=\ M(q(t))I(t)$ and $M={\frac {\mathrm {d} \Phi _{m}}{\mathrm {d} q}}$ are confusing people. The first is, as outlined above, just instantaneous resistance. This is a pretty useless concept, unless you intend to use a second order model for e.g. a resistor to account for (small) nonlinearities, or you are modeling something else entirely like a transistor. Just because you can divide the current through a component by the voltage across it, and get a value in Ohms, does not mean that you've measured a resistance. You can do the same thing for a capacitor, or an inductor, or indeed a memristor. (And indeed, in AC circuit analysis this is just what is done, using the impedance (in Ohms) of Z=R for a resistor, Z=jwL for an inductor and Z=1/jwC for a capacitor.) The second definition is the memristance. It is indeed a constant, unless, similar to above, one intends to assemble a second order model of a memristor.

Oh yes, and please, do get an account, your input is very much appreciated but we'll need at least a nickname to address our comments to.

GilHamiltonTheArm (talk) 13:53, 7 May 2008 (UTC)

NPOV TO DO

Given all the news coverage, we should probably investigate sources besides Chua and Williams.

• Chua acknowledges Prof. P. Penfield, Jr. "for research activities on memristors at MIT over the last ten years." Penfield modelling varactors and superconductors. (Since all diodes are varactors, memristor diode models essentially preceded the memristor?)
• Samsung patented various bilayer oxide films, looking for an effect like memristance for some time. Potatoswatter (talk) 00:09, 7 May 2008 (UTC)

Some other sources of "nanoionics-based resistive switching memories" can be found in the Nature review article by Rainer Waser and Masakazu Aono [Nature Materials, vol. 6, p. 833 (2007)], which suggests that these "memristor" devices have been studied elsewhere besides HP and well before it was "discovered" in April 2008. Ahijado (talk) 16 May 2008. —Preceding comment was added at 19:17, 16 May 2008 (UTC)

Also see the Wikipedia page on Resistive Random Access Memory for other sources outside HP which have also been developing the so-called "memristor." Ahijado (talk) 29 May 2008. —Preceding comment was added at 23:31, 29 May 2008 (UTC)

But, remember that this article is only about HP's characterization of their device as an ideal memristor. Even if that's independent of practical value. Memristance occurs in the region between the "on" and "off" states. Although I haven't read all those other articles, most RRAM research exclusively focuses on the ability of a device to switch, regardless of specific behavior in between. So until other groups take it upon themselves characterize their devices in the "intermediate" regime, no memristors are reported outside HP. Potatoswatter (talk) 04:00, 30 May 2008 (UTC)

can anyone explain how memrister can have nonlinear VI relationship using M=\frac{\mathrm d\Phi_m}{\mathrm dq} ? I go threw the original IEEE article but didn't get concept of nonlinear resistance or charge variable resistance? —Preceding unsigned comment added by 117.199.208.11 (talk) 15:01, 17 May 2008 (UTC)

news (?) that reads like phony history

Today is only May 7, so it reads very strangely, when we hear that the memristor was invented on April 30, 2008, at HP and then "However, as of yet, none have been reported outside HP."

This also reads as if somebody (in the HP PR dept?) is taking up a phony perspective about 50 years in the future: "However, it would be 37 years until April 30, 2008, when a team at HP Labs ..." JamesD'Alexander (talk) 11:40, 7 May 2008 (UTC)

Yes it's news. Very big, recent news. I'm trying to take care to introduce that disclaimer and others. See talk section above this one. I WISH someone at HP were helping with this article. Potatoswatter (talk) 11:53, 7 May 2008 (UTC)

Major problems with the source of this article

I have read the original article by Chua. I have not found a peer-reviewed article by R. Stanley Williams. There may not be an actual memristor in existence today, though the photographs do seem to suggest so.

In Chua's article, I notice four things:

• the formula $M={\frac {\mathrm {d} \Phi _{m}}{\mathrm {d} q}}$ does not occur anywhere in the article. Instead, the relation $M={\frac {\mathrm {\Phi } }{\mathrm {q} }}$ is implied in the wording of the text, though never explicitly mentioned. Apparently, this is because Chua thinks that a memristor with a linear $\mathrm {\Phi } -\mathrm {q}$ relation reduces to a linear time-invariant resistor. And it certainly does, in AC circuit analysis. (I spent an hour working out the laplace transformation of a two-port network with a single memristor in it - and ended up with simply R, the instantaneous resistance.) This is of course only valid in the small-signal approximation.

• What article did you read?? "M:=dφ(q)/dq" (with := standing for Chua's triple-bar defined-as equality symbol) is Equation 2. He uses a lowercase phi with no subscript m, which doesn't make so much difference. Potatoswatter (talk) 19:19, 7 May 2008 (UTC)

• there is a large chapter filled with conjecture about how an eventual physical device would probably need a direct link between the electric and magnetic fields, or rather $\nabla \times \mathbf {H_{1}} =\mathbf {J(E_{1})}$, but it is not clear whether the quasi-static expansion of Maxwell's equations he uses are actually applicable to this situation. The memristor that HP claims to have made is certainly not of this category.

• No, and Williams mentions that Chau was wrong. I haven't read that section to the point of understanding but it might help to summarize it. Potatoswatter (talk) 19:19, 7 May 2008 (UTC)

• Chua uses $\mathrm {\Phi }$ to refer to the time integral of voltage (name of flux-linkage) and not to the rate of change in the voltage, which is claimed in the article in Information Week. This would be the derivative of voltage with respect to time. My

apologies for not seeing this sooner. Of course, that still does emphatically not mean that there is a relation to the magnetic flux.

• You just said two opposite things. "Chua uses phi to refer to the time integral... This would be the derivative. Potatoswatter (talk) 19:19, 7 May 2008 (UTC)

• The formula $V(t)=\ M(q(t))I(t)$ is indeed found in the article, but explicitly for the special case of the small signal approximation in a "charge-controlled" memristor. It should not be included in the article as some kind of "conveniently written" form of the basic formula.

• NO IT IS NOT. QUOTE SOME TEXT TO BACK YOURSELF UP. The section "CIRCUIT-THEORETIC PROPERTIES OF MEMRISTORS" begins:

By definition a memristor is characterized by a relation

of the type g(phi, q)=O. It is said to be charge-controlled (flux-controlled) if this relation can be expressed as a single- valued function of the charge q (flux-linkage phi). The voltage across a charge-controlled memristor is given by $V(t)=\ M(q(t))I(t)$

That's all your context for you! Potatoswatter (talk) 19:19, 7 May 2008 (UTC)

So how do we proceed? Which part of this article can actually be sourced reliably? I guess only Chua's hypothesis of a physical memristor device belongs in an encyclopedia. Since his analysis appears flawed (considering only the small-signal approximation, and incorrectly conjecturing that a physical device would need some kind of E-H coupling) we might as well scrap the entire article. —Preceding unsigned comment added by GilHamiltonTheArm (talk • contribs) 16:54, 7 May 2008 (UTC)

You've gotta chill out. Williams isn't a hoaxer. Chua says nothing about small signal, ever. Potatoswatter (talk) 19:19, 7 May 2008 (UTC)

I'm chilling, I'm chilling... Man, this is a confusing topic.

But I think it is clear to me now. I've found all the links and data, so clearly there is no problem with sourcing the article. I've cleared up the question of what exactly the "flux" is that they are talking about, namely integrated voltage over time and not the time derivative of voltage. And I now understand why people think this must be magnetic flux: that's because Chua hypothesized that a physical device would have to use that. And it's clear now that an ideal memristor is just a resistor: that's why Chua used nonlinear resistors to simulate memristors, and that's why my simple (linear) formulas tell me there's no such thing as memristance.

I don't have any helpful advice at the moment about how to make the article clearer, because all of the above is already in it somewhere. Apart from the "magnetic flux" thing.

GilHamiltonTheArm (talk) 20:50, 7 May 2008 (UTC)

I'm glad to hear that you've chilled, Gil. I was on the same journey of confusion that you were on, and I think I've come to the same conclusion as you. I'm wondering whether some people are getting confused by the colourful 4-quadrant diagram in the article by Tour and in the letter by Strukov et al, both in Nature, where it says "dφ = M dq". If you rely on that equation and don't bother to read the caption, then you will indeed be confused, since "dφ = M dq" reduces to a mere linear resistance if M is constant. You need to read the caption and the text to find out that in a memristor M is actually M(w), where w is a hidden variable and w=q only in a subset of memristors like the HP Labs device. Furthermore, in the even more general class of 'memristive systems', M becomes M(w,i), a multi-valued function of w, which sounds pretty hairy. Anyway, thanks for airing your doubts on this page, because it's helped me to understand. --Heron (talk) 21:10, 7 May 2008 (UTC)

What Williams really painfully hides is that w is a function of q only some of the time. The graphs he presents are produced in that regime, but then hysteresis occurs when internal charges "run out". Think we'd all best stay away from systems for now :v) Potatoswatter (talk) 09:55, 8 May 2008 (UTC)

Let me back off of my claim that the "flux" is not the magnetic flux, as well: it refers to the magnetic flux through the entire closed loop, and not just in the device, which was not clear to me. In that case it makes sense, and the "flux" or "flux-linkage" is just the magnetic flux.

GilHamiltonTheArm (talk) 14:02, 8 May 2008 (UTC)

Hi. No, I still think that "magnetic flux" here is out of place. At least a remark that here by it we simply mean the integral over voltage would be good. (Well, at least I think things got clearer in the article since I first looked at it.) In a way we simply abstractly describe the relation between voltage and current (really V(t) and I(t)) on a device. Greetings, (sorry, no account...) 212.171.245.127 (talk) 09:27, 9 May 2008 (UTC)

Can Memristance be parasitic?

The basic elements of resistors, capacitors, and inductors show up everywhere. With any circuit having source and load (say, battery and light bulb) there is electric field (hence capacitance) between the wires. And there is magnetic field (inductance) around the wires. The wires have resistance as well. If memristance is truly a fourth passive element then it should appear as a parasitic, even if it's miniscule, in everyday circuits. Indeed, hysteresis may show up with changes in temperature or magnetic flux, but aren't these due to nonlinear or second-order effects? A good explanation of memristance should include a reference to how a very simple circuit contains one by chance. —Preceding unsigned comment added by 68.21.231.254 (talk) 18:39, 7 May 2008 (UTC)

Yes. It would be nice if you looked up & summarized the references for memristors used to model diodes. Potatoswatter (talk) 19:21, 7 May 2008 (UTC)

The Nature article includes a bunch of links to other articles where parasitic memristance was apparently observed, but not recognized. Apparently it is only the dominant effect for small size devices.

GilHamiltonTheArm (talk) 20:50, 7 May 2008 (UTC)

Yes parasitic memresistance does exist but its just hard to measure. Memresistance will occur anywhere in electronics where the positive charge carries (ie. atoms with a stipped electron) are able to move, not just the electrons themselves. The start up voltages needed for some gas tubes with metallic and other gases mixed together do show hysteresis beacuse both +ve and negetive+ charges are able to move, and you can make an extremely crude memrister out of them. Normally parasitic effects are almost non-existant and could only be one-shotted by phsyical deformation of most electronic components.--155.144.40.31 (talk) 06:11, 23 May 2008 (UTC)

Physical restrictions on M(q)

This section is a bit speculative:

• Do we have references for a cyclic M(q) ? I cannot see how this could prevent Φ from growing to infinity. Note that the device must remain passive, which implies M>0.

• No, I rather extended one of Chua's graphs. Φ will grow to infinity no matter what, but a cyclic function puts modulo arithmetic on your side.

• If you agree that a cyclic function does not prevent infinite Φ, then why mention it in the article ? Besides, your example M(q)=sin(q/Q) does have a nice bounded integral, but it does not describe a valid memristor Acasp (talk) 16:36, 8 May 2008 (UTC)

• Hmm... well in that case, Φ is bounded because of the negative resistance. (Actually I wonder if it's right to restrict memristors to passive devices. Negative resistors are still resistors, right? Hmm.) Anyway, Φ=∫Mdt so if M is positive cyclic as in sin² it goes away and Φ increases without bound again. (M<0 is forbidden for passive devices). Potatoswatter (talk) 16:49, 8 May 2008 (UTC)

• Note: we say in the first sentence that memristors are passive. Regarding sin2(q/Q), my understanding of your comments is that unbounded Φ and unbounded q are physically acceptable, as long as the amount of information stored is bounded; and with a cyclic M(q), the stored information maps to [0,Q], which is finite because of charge quantization. Fine with me. Acasp (talk) 17:35, 8 May 2008 (UTC)

• What does it mean to "enter hysteresis" ? Hysteresis is a behaviour, not a state.

• From that article, "A system with hysteresis can be summarised as a system that may be in any number of states." It gets to a point and stops, hence staying in a state. Most sources including use the word hysteresis to describe the thin film behavior.

• Either a system has hysteresis (i.e. memory) or it does not; it cannot acquire hysteresis during operation. Maybe you meant "the device becomes saturated" instead of "the device enters hysteresis" ? See also my scenario where M(q) becomes constant when q reaches a threshold, below. Note that this does not imply that "the device ceases to act as a memristor" - it only ceases to act as a nonlinear memristor. Acasp (talk) 10:33, 9 May 2008 (UTC)

• From my understanding of the definition of the word, hysteresis is saturation with memory. Saturation describes a kind of response to transient conditions, like a FET transistor. Saturation of any state variable can be called hysteresis? In any case, HP and other thin-film device researchers seem to see this as an important physical property. Potatoswatter (talk) 12:35, 9 May 2008 (UTC)

• I agree that hysteresis is fundamental here. Actually, all (nonlinear) memristors exhibit hysteresis (i.e. if you connect one to a signal generator, the V-I diagram will have multiple branches); that is precisely why I object to mentioning "enters hysteresis" alongside with "ceases to act as a memristor". Acasp (talk) 10:51, 11 May 2008 (UTC)

• Φ=∫Vdt, therefore merely assuming a constant applied voltage leads to infinite Φ. Acasp (talk) 08:35, 8 May 2008 (UTC)

• Yep. That presents the problem at hand. Potatoswatter (talk) 09:51, 8 May 2008 (UTC)

• Basically what I'm holding out for is a reference on what kinds of memristors are likely to be found. From the looks of it, most examples are hysteretic type. A counterexample I can just cook up would be a motor mechanically and electrically connected to a potentiometer consisting of a single disc. More current turns it faster; turning integrates Q=∫Idt. I'm sure someone's thought of that in the last thirty years. Potatoswatter (talk) 10:12, 8 May 2008 (UTC)

• More thoughts: I am not sure "∫M(q)dq remains bounded but continues changing at an ever-decreasing rate" prevents the infinite memory paradox. Why would M(q) become quantized as q goes to infinity ? You can average measurements of V/I for as long as you need to measure M(q) with arbitrary accuracy. I think the simplest way to prevent unbounded information is to enforce that M(q) remain constant when |q|>qmax, for some qmax. This is probably what happens in the HP device: after all oxygen vacancies have moved to the same layer, saturation occurs. Acasp (talk) 10:23, 9 May 2008 (UTC)

• Yes. Hence "Eventually, this would encounter some kind of quantization and unideal behavior." - is this unclear? Basically my thought is that such might be "put off" longer for a macroscopic device. HP's M(q) does not appear to change at an ever-decreasing rate so much... it's more like a sudden brick wall. Of course I didn't solve the infinite memory problem :v) . I just want to convey that the problem might be "postponed" such that an ideal memristor may implement infinite memory. In any case, it isn't the same as M(q)=Rmax, q>Qmax, because that still supposes that q must increase and decrease after reaching Qmax before M(q) "de-saturates" from Rmax. So that would be saturation with infinite memory rather than hysteresis with finite memory. Potatoswatter (talk) 12:35, 9 May 2008 (UTC)

• So you are saying that my M(q)=Rmax,q>Qmax has infinite memory because, even though measuring the instantaneous resistance M=Rmax does not recover stored information, one can still measure how much charge is needed to desaturate the device. Good point. Now I would tend to think that a cyclic M(q) is the only alternative that yields an ideal memristor with finite memory. Acasp (talk) 10:51, 11 May 2008 (UTC)

Lissajous figures may indicate the meaning of memristance more clearly

It may be a good idea to include some of these nice Lissajous figures in the article, and put them next to Lissajous figures of the resistor (a straight line) and the capacitor and the inductor (both circles). This helped me to understand, and it also serves to highlight a defining characteristic of the wider set of memristive systems: the lissajous figure always passes through the origin (though I think there is another condition to that: something about needing to start at a zero energy state. I have to look that up.)

GilHamiltonTheArm (talk) 14:02, 8 May 2008 (UTC)

If you feel it would be part of an easier explanation, you should write it up ;v) ... I wonder if it's a copyvio to use graphs from an article though. Potatoswatter (talk) 16:42, 8 May 2008 (UTC)

I've made some Lissajous figures that represent memristic behavior that Strukov claims is typical. (like figure 2b in his Nature article.) This brings to light a difference of interpretation with what is expressed in the Wikipedia memristor article: "The type of memristor described by Williams ceases to be ideal after switching over its entire resistance range and enters hysteresis, also called the "hard-switching regime." ". According to Strukov, hysteresis is essential to a memristor. (This is also why I've made the Lissajous figures.) When the device enters the "hard switching regime", then it no longer behaves as a normal (hysteretic) memristor, but rather as a memristive system: this is a more general class of systems for which the state variable no longer depends uniquely on the charge q.

Cool - thx. Can we see? Potatoswatter (talk) 08:13, 23 May 2008 (UTC)

Ordinarily, hysteresis is computed as the area inside the loop. (e.g. magnetic hysteresis in an E-H diagram, or energy produced in the Diesel cycle in a p-V diagram, or is it p-T?) Strukov also evaluates it this way, and says that the normal double-loop I-V hysteresis of a memristor typically disappears for high frequency, i.e. it collapses to a line (like a resistor). But there is something I don't understand: doesn't that mean that a capacitor and an inductor also exhibit hysteresis? At least hysteresis in their I-V diagram. I guess that makes sense, because the "instantaneous resistance" of a capacitor depends on its charge.

GilHamiltonTheArm (talk) 16:50, 9 May 2008 (UTC)

Capacitors have constant zero current on an I-V diagram and (ideal) inductors have constant zero voltage. The expected linear relationship appears with an AC stimulus. Hysteresis requires multiple steady states in a given environment while L's and C's have only one. (The word for that is saturation.) Potatoswatter (talk) 08:12, 23 May 2008 (UTC)

Warburg Impedance?

How is this different from the Warburg Impedance that shows up in electrochemical impedance spectroscopy? My under standing of that has been as a sort of half resistor half capacitor. My experience with elements that fit a warburg model is that they have a memory, and seem very similar to every description I've heard for this memristor. http://en.wikipedia.org/wiki/Randles_circuit has a bit of a description, or google for more information.

Seamusfp (talk) 21:43, 9 May 2008 (UTC)

Controversy section

Is the best citation that there is a dispute over whether or not it's a fourth element really a commenter on the Nature article? The link isn't clear which comment it's referring to, and for all we know it could just be a Wikipedia editor who clicked over to the Nature article and added their argument there (and hence, I removed this citation since it's not reliable).

The section reads like an argument that spilled over from the talk page to the article page. I'm still not convinced that this is a substantive controversy, so I peppered some some fact templates in the section. Hopefully the editor who wrote the section can cite their sources. (Or someone else can can the whole section.) Michael Belisle (talk) 02:18, 14 May 2008 (UTC)

I kinda gather that the thesis of the section is that the memristor isn't really that novel or practical. It sounds to me like a POV that would be taken by partisans of competing, related technologies, who might be jealous of the free publicity. And engineers who feel disillusioned or confused. After all most care more for practical applications than cool theory. However POV it may be, the points do need investigation/elaboration:

• Can other RRAM technologies also be modeled as memristors?
• Williams has not published a "real" paper and does little to address the speed of his team's devices. The low charge mobility is hidden in a diagram caption explaining why his time axis isn't in seconds.

Also, the theory section needs refs too! (As tagged.) Which really should be my responsibility... but... tired... Potatoswatter (talk) 02:41, 14 May 2008 (UTC)

To consider that three elements only are sufficient and the four relations proceed, please see http://commons.wikimedia.org/wiki/Image:Mem1a.PNG Myrtilus (talk) 06:32, 14 May 2008 (UTC)

Nobody's claiming that there's just one definition for "basic element." By Chua's own definition, the memristor fits with Chua's own picture. That's why the article introduces the fourth element concept as Chua's "belief." The article clearly states that a memristor with linear Q(phi) <-> constant M is a resistor. Therefore there's no controversy - you can accept the theory and reject the notion that it provides "symmetry." Potatoswatter (talk) 07:39, 14 May 2008 (UTC)

I think the "fourth element" point in the "controversy" section can be removed. The only controversy I can document is right here on this talk page, namely people who, like myself, misunderstood the claim Chua made. However, Chua's claim that a basic, classical circuit element is defined by a relationship between two of the four fundamental circuit variables (i, v, phi and q) can be traced to a text book by Shearer. (Shearer, J.L., Murphy, A.T., and Richardson, H.H., Introduction to systems dynamics, Addison-Wesley, Reading, Mass., 1967.) His claim that the memristor is fundamental (even though by necessity nonlinear) is therefore justified and documentable. Controversy should only be reported on this page if it is widespread, and a phenomenon all by itself.

I also think the "magnetic flux" section should be removed. It's too much oriented to teaching the subject, rather than describing it. If it should be kept at all, it belongs in an article on Faraday's law.

GilHamiltonTheArm (talk) 15:53, 22 May 2008 (UTC)

Symbol

Given the controversy over whether a theoretical memristor is just a resistor or not, it is ironic that the symbol chosen for it was originally the symbol for a resistor (the zig-zag symbol was originally a general impedance, not a pure resistor). SpinningSpark 21:16, 14 June 2008 (UTC)

There's no such controversy and the symbol is not a zig-zag. Potatoswatter (talk) 22:05, 14 June 2008 (UTC)

I have no idea whether or not there is controversy in the world at large, and did not mean to suggest that there was - I based that purely on comments further up this page - several people suggested that the formula just comes down to a resistance. On the symbol, you are not reading what I said carefully enough - I know the symbol is not a zig-zag. Originally a zig-zag was general impedance and the "square-wave" was a pure resistance. The square-wave symbol has subsequently been dropped in favour of the zig-zag for resistance. It is ironic that the square-wave symbol (which originally meant pure resistance) is now being proposed for an element that is anything but. Is that clear enough? SpinningSpark 22:43, 14 June 2008 (UTC)

I guess so. It's not "anything but" tho: resistors are degenerate memristors and memristors approach resistor behavior at high frequency. Since complex impedance implies an external field, which must couple somewhere, it's no wonder modeling with "floating" devices fell out of fashion. Potatoswatter (talk) 01:41, 15 June 2008 (UTC)

Another Rape of Science

Over the years Nature Publishing Group has garnered a reputation for occasionally raping science (as in the discipline, not the journal). This time around Nature got mixed up with HP's PR department and Leon Chua in a widely publicized gang rape of physics and engineering. It all started in 1971 with a paper published by Chua in which he claimed that the memristor is the fourth missing fundamental circuit element (the other three being the resistor, the capacitor, and the inductor). The paper didn't make much of a splash, and neither did Chua's 2003 follow up paper in which he revised his theory to include the memductor, the memacitor, and an infinite array of other "fundamental" circuit elements. This is nonsense.

Resistance, Capacitance and Inductance are regarded as fundamental because to each there corresponds a different picture of what is going on with the energy. Resistance refers to the loss of energy to Joule heating. Capacitance refers to storage of energy in the electric field. Inductance refers to storage of energy in the magnetic field.

If memristance is the "fourth fundamental" circuit element then memristors must do something with the energy they are imparted other than turn it into heat, or store it in electric or magnetic fields. So what do memristor supporters have to say about this? nothing. This is not surprising, since the concept of memristance stems from a purely mathematical argument bent on taming the current/voltage relationships of nonlinear circuit elements. The concept of memristance was invented out of convenience to avoid dealing with frequency-dependent (time-dependent) resistance, inductance, and capacitance. Thus the memeristor is not "fundamental", unless in your book fundamental is synonymous with convenient.

I think you make a lot of good points. I would just like to point out that one thing the memristor is doing is turning electricity into work, by moving charges. Also, it may be possible that memductors and memacitors are all variations of the same fundamental 4th element (for example, you can choose one of the mem types and create any other mem type with it and standard linear components). jay (talk) 07:29, 13 December 2008 (UTC)

Polymeric Memristor

I've quickly added this section for the reference to this precedence claim. The PDF is available at the linked page. And oh, I've no idea how to add dual authors to an URl cite web <ref></ref> thingo... -- —Preceding unsigned comment added by Meika (talk • contribs) 07:57, 10 July 2008 (UTC)

Memristors work by moving dopant ions, not by changes in charge or flux

The article repeats the claim that the HP Labs device represents a new and canonical passive electronic device. I would like to see the article be modified to clarify that the new device does not actually work this way.

I don't mind HP Labs postulating the existence of a fourth passive electronic component, after Leon Chua. The three components of impedance certainly omit one out of the four possible equations involving voltage and current and their time derivatives.

However, HP Labs reports that their device works by moving dopant ions in one direction or the other (depending on the polarity of the external voltage), and this has nothing to do with magnetic flux. Their device appears to be quite unique and highly useful, but it does not seem to belong to the same basic "charge and flux manipulation" family as capacitors and inductors. David (talk) 02:04, 12 July 2008 (UTC)

By relating the integrals of two variables, the memristor is certainly more abstract, and also probably unrealizable in a physically useful form (see other discussion here). Williams, the earlier polymer device, and Chua's "emulator" all have memristor and non-memristor regimes because dopants and indeed anything used to "store the integral" will be a finite resource. I don't think anyone sane and impartial would argue that the memristor is really on equal footing with LCR elements—c'mon, those are made of solid metal. However it clearly is a model for a passive device, apparently good for modeling chemical changes. As for flux, the memristor generates it the same way as a resistor, by decelerating electrons. If you would like to see the article modified, be WP:BOLD. Cut some text out, see if nobody reverts. Or be more careful, if you care more. Potatoswatter (talk) 05:20, 12 July 2008 (UTC)

Potatoswatter, thank you for your sensible comments. So much better than deleting my Talk entry! The reason I haven't edited the article is that I don't see an easy way to do it. The entire article (as with most of the articles about memristors on the Web) has a "tone of voice" that describes memristors as new fundamental passive components. I don't see how deleting some text is going to change the tone throughout. Some text needs to be added to combat this misinformation that was apparently generated by HP Labs to enhance their commercial marketing. I see this as a fairly important issue, one that needs to be dealt with in Wikipedia, if not in the blogs (most of which are uncritical of this misinformation). Unfortunately, I just don't see how to do it myself. David (talk) 13:11, 14 July 2008 (UTC)

You don't have to fix everything. Shortly after the announcement, a number of new editors parroted HP's line and even attempted to reproduce the original diagrams from the Nature synopsis. I did a certain amount of reversion then, which is one reason I'm sick of it now. (And I don't feel so good about removing others' contributions when my own make up much of the article.) In any case, WP grows best when lots of people make little edits rather than one person going on a mission. Driven individuals are vulnerable to accusations of bias, and rightly so. So do a half assed, incomplete job to remove only the most glaring instance(s) of promotion. In particular, the lead is waay too long and has no business discussing the inspirational origins of the theory in the first place—IMHO. Potatoswatter (talk) 04:15, 16 July 2008 (UTC)

Really lacking

I have a EE degree. Granted that it's been 10 years and I work in marketing, but I'm just pointing out that I'm not your average layperson reading this article. That said, this article REALLY needs a better explanation. Honestly about 3 pictures would be worth the whole article. Can I change the article to include these pictures? If this would be controversial at all then I just won't bother, I'm bad at pic editing so it would take me a few hours and I wouldn't want the stuff to get deleted. 71.231.179.83 (talk) 05:21, 5 September 2008 (UTC)

OK I tried to create the pictures and I am just not good enough with pbrush. Pic (1): a circuit consisting of in series a battery, a resistance R, a memristor M. Pic (2) Graph of V(t) over M and R, i.e. both components voltage drops over time. Pic (3) same circult but voltage source is a sine wave. Pic (4) same as Pic (2). Could anyone make these? These would be invaluable to add to the dense language of the article 71.231.179.83 (talk) 05:30, 5 September 2008 (UTC)

I wrote the theory part of the article. It is supposed to address questions from a technical audience about characteristics as compared to other devices. Many technical people are interested, but I wouldn't bother trying to explain to a layperson beyond "this kind of thing generates hype now and then." You say three pictures would be worth the article, but what is the article worth to you at all? The sinusoidal graph you ask for is in the Nature article. I didn't think it was very enlightening. An illustration of ionic drift current would be nice though. Potatoswatter (talk) 06:39, 5 September 2008 (UTC)

Funny, thats a hoax

like some IEEE articles published as a april fools joke, or the articles in the "Journal of irreproducible results" Propose to delete it, as it is not encyclopedic information. 70.137.179.88 (talk) 00:26, 10 October 2008 (UTC) 70.137.179.88 (talk) 00:26, 10 October 2008 (UTC)

No idea what you are talking about. I think you're on the wrong talk page. Viriditas (talk) 03:43, 10 October 2008 (UTC)

Chua's "memristor" is not a resistor at all, in its ideal form it actually has no resistance (i.e. no heat loss), so the name is an unfortunate misnomer, implying a variable resistor with memory. HP's alleged "memristor" is simply a type of fuse with growback, a fuse "remembers" the current passed through it ("burning") and the voltage applied to it ("growback") , which raises the question of how many cycles is it good for. 75.0.0.175 (talk) 18:59, 18 December 2008 (UTC)

That's completely incorrect. Funny what you can do with the word "actually" and no references or bare understanding. By the way, are you claiming that a fuse doesn't release heat? Potatoswatter (talk) 19:28, 18 December 2008 (UTC)

Archive 1

Archive 2

Rewrite request.

One more voice to the "inaccessible article" choir. If I hadn't read about memristors elsewhere I would not be able to make head or tails of the article and I am not nearly technically qualified enough to do the re-write myself. Viciouspiggy (talk) 14:33, 15 February 2012 (UTC)

Mouttet citation

One of the sources cited is simply a PDF on scribd. There is no indication I can see that this paper ever appeared in a reputable publication -- if I'm not missing something both it and the statement that references it should be removed.

The citation appears as: Mouttet, Blaise (28 January 2012), The memristor and the scientific method, retrieved 2012-03-07

--128.163.7.133 (talk) 17:50, 29 March 2012 (UTC)

The reference is related to a recent EETimes article I cited and seems relevant to the memristor definition which is why I included it. I also found a related New Scientist article covering it indicating to me that the issue is worthy of inclusion in the wikipedia page. (links below).

http://www.eetimes.com/electronics-news/4234678/Memristor-brouhaha-bubbles-under

http://www.newscientist.com/article/mg21328535.200-online-spat-over-who-joins-memristor-club.html

Blm19732008 (talk) 00:20, 31 March 2012 (UTC)

Memristor timeline

The timeline seems to me to be too crowded and not well focused on significant memristor developments. There are numerous important developments related to ReRAM prior to 2008 but since this page is dedicated to the memristor it seems like overkill to try including so many. I am removing the references that do not explicitly discuss memristors (or the more generic memristive systems). Blm19732008 (talk) 00:08, 8 August 2012 (UTC)

"perpetual motion machine of the second kind"?

This comment from the memristor criticism section does not appear supported by the cited arXiv article from Meuffels and Soni. Meuffels and Soni even suggests a minimum energy requirement as a fix to the Landauer Principle violation so it seems to me that it may be an overreaction to call generalized memristive systems equivalent to a perpetual motion machine of the second kind. Blm19732008 (talk) 23:30, 23 September 2012 (UTC)

This should be removed

"Batteries can be considered to have memristance, but they are not passive devices."

This is incorrect. Batteries are passive devices that store energy, very much like capacitors. Unlike ideal capacitors, of course, they are non-linear charge storage devices with complex loss mechanisms and memory effect. The latter, however, changes nothing about batteries being passive devices without internal voltage or current sources. — Preceding unsigned comment added by 76.126.52.72 (talk) 09:39, 11 January 2013 (UTC)

OK. Blm19732008 (talk) 02:39, 13 January 2013 (UTC)

How is battery "a passive device without internal voltage source"? A battery is a voltage source, therefore it is an active device. — Preceding unsigned comment added by 169.231.33.209 (talk) 07:24, 17 January 2013 (UTC)

I also usually think of a battery as an active device since it is a power source. Under one definition an active device has to add energy to a signal while a passive device requires energy transformation without adding energy. Another definition of an active device discusses the requirement for an external power source for operation. Perhaps since batteries don't require an external power source for operation this is the reason the original poster does not consider them active. In any case I have not seen any references discussing the memristance of batteries so the statement seems without support.Blm19732008 (talk) 18:41, 20 January 2013 (UTC)

It seems Memristors aren't exactly a new invention

According to the recent works of Gaurav Gandhi and Varun Aggarwal it seems the memristance effect was put to practical use over a hundred years ago. Coherers and Cat's-whisker detectors seem to represent the canonical implementation of the memristor.

http://spectrum.ieee.org/nanoclast/semiconductors/nanotechnology/the-memristors-fundamental-secrets-revealed — Preceding unsigned comment added by 2A02:120B:C3CF:6DC0:EC1C:CFAA:DDB6:6A1B (talk) 17:21, 9 June 2013 (UTC)

Simple series parallel examples for a Memristor?

The other three basic components (R,C, and I) have simple series and parallel examples that show their additive or inverse properties. Also they show current and voltage curves graphs for the other three basic components. Could the same be done for a Memristor? Septagram (talk) 05:48, 9 June 2014 (UTC)

A number of the references no longer exist

As I looked through this entry, I wanted to check on some of the statements by looking at the references. A number of the references are no longer functioning. The references should either be updated with valid links or the statements scrutinized closely, since they are not supported by entries that can be reviewed. Reference 79 contains a spelling mistake and the DOI is invalid.

— Preceding unsigned comment added by Cebess (talk • contribs) 22:35, 1 December 2014 (UTC) 

Rotistor - Entangled Rotating Memristors of various spins

Not a forum as per WP:TALK a13ean (talk) 20:27, 17 December 2014 (UTC)
The following discussion has been closed. Please do not modify it.
[various spins are controlled by a classic CPU, and theory of number based noise is used to select the optimum spin diffusion patterns] The "ROTISTOR" is a term introduced by PhD. professor Veiler Sword at July 14, 2014. It is a non atomic quantum processor. It is a series of entangled memristors, that rotate by switching on and of. Each rotating entangled memristor of the overall rotistor rotates at various rpms. We let the rotistor render data at varius rpm combination controlled by noise and hum numeric generators, for simple tasks we don't use hum/noise ordered spin but algorithms. (hum and noise here are not sounds but numeric diffraction/diffusion modes) Then we average the optimum solution (or solutions) by a classic CPU and an opperating number theory program. Why is it better that atomic quantum computers? It is cheep, it works at non-extreme temperatures, easier to built, you can entangle as many rotating components you wish, if you want more accuracy you can entangle rotating memristor components with more available rotational angles, it is cheep to maintain-does not easily break. we all know that quantum computers are atomic entangled spin apparatuses, but requier very low temperatures and that is not practical for massive productions. we know also that quantum computers are averaging data machines, so they run very vast and average the optimum option. we can build mechanical and electrical non atomic quantum computers that allow entangled spin rotations, and still we will have to average running the apparatus for 500msec to average many million probable solution to select the optimum. today we have the math and the know how. Also, we all know about low temperature hypermagnetic levitation. We can mimic that at normal temperatures, with to classic electromagnets, but in order the system does not fail at the sides we have to create a complex magnetic grid, that even inverses at some points the field polarization in order the system does not fail at one side. Well, in my lab I have mixed both. Quantum non atomic computing and rotational systems, but we can build rotistors, tiny electric parts like entangled memristors that rotate at different speeds - each component, we run the rotistor for 500 msec to average and extract the optimum solution. Of course the old rotistors are not so fast, so it might take 3 seconds to average the optimum solition, but a well build one is way faster. The Koch family can support that effort! We need practical solutions with tiny rotistors so billions of people can buy a cheep great quantum computer and not like today, that we have so few atomic quantum computers that allow a tiny only number of entangled rotating components. The more it costs a design, the sillier the builder, and the most boring the science behind. We need PRACTICAL applications available for EVERYONE and HUGE computational power to subserve everyday tasks and not theoretical only. The "correct" entangled answers allow more current, higher values, wider dynamic ranges.

"Like other two-terminal components, real-world devices are never purely memristors ("ideal memristor"), but also exhibit some amount of capacitance, resistance and inductance."

This appears misleading. For example, if an ideal resistor is a device which obeys Ohm's Law then most metals and good conductors would be considered ideal resistors. Capacitors and inductors aren't usually necessary when modeling the conductance/resistance of metal or conductive wires. Parasitic capacitances (or inductances) may exist between elements or junctions formed when formed in a circuit but the wire or conductor by itself is usually modeled pretty well by an ideal resistor unless under extreme operating conditions. Capacitors can also be constructed (e.g. parallel plate capacitor) which are fairly ideal in terms of a linear relationship between the charge and the voltage (again unless operating under extreme conditions).

Also, I can understand how capacitance and resistance would be necessary to model a memristor based on a metal-insulator-metal junction but I don't see why inductance would be necessary. A reference should be used to support this if true. 207.86.127.218 (talk) 14:45, 27 January 2015 (UTC)

"pinched hysteresis" Is this just a made up term?

The reference in the article links to Wiki "hysteresis" which has no reference to "pinched." My general google search just turns up memristor references. So where is the definition? Bubsir (talk) 18:16, 1 March 2015 (UTC)

Aren't all terms made up by someone? I know the concept appears as early as 1976 in the article "Memristive Systems and Devices" by Leon Chua and means a hysteresis curve which crosses itself when the current and voltage equals zero. — Preceding unsigned comment added by 68.224.94.126 (talk) 07:43, 8 March 2015 (UTC)

Patents in Timeline

I am currently deleting several patents claimed to be about memristors from the timeline. These appear to have been added for purposes of self-promotion rather than as legitimate notable patents related to the memristor.

A search in Google Patents on memristors, ReRAM, or similar technologies related to resistance switching devices indicates thousands of results. Unless a patent is recognized to be notable by an independent source I don't think it should be included in the timeline. This is particularly true for cases where the patent is pre-2008 and prior to HP's article in Nature that sparked interest in memristors. It seems misleading to claim a "memristor patent" prior to HP's work when the patent itself does not mention anything about Chua's memristor. Blm19732008 (talk) 02:30, 23 March 2015 (UTC)

Spintronic article in timeline

Moarteen-

Stop adding your spintronic article to the memristor timeline. Your article does not mention memristors or memristive systems and there is no indication that it is considered an important article relevant to memristors or memristive systems. There are also earlier articles discussing resistance switching of spin valves (e.g., Tang et al. "Spin-valve RAM Cell", IEEE Transaction on Magnetics, Vol 31, issue 6, Nov. 1995). Blm19732008 (talk) 04:33, 12 May 2015 (UTC)

Blm19732008

It is not scientific to cast aside an article about what are in effect memristors because it does not mention them by name. The earlier IEEE 1995 article you cite does not mention memristive systems either. This article regards resistance switching in metallic (!) spin valves, i.e. the obtention of 2 device states, i.e. GMR. The origin of this effect is a purely spintronic one. The APL 2006 work that I propose for the timeline is the first to combine both this spintronic response and an electroresistive response akin to that observed in TiOx or VOx systems (see e.g. Argall 1968 in the timeline; note: this work also doesn't mention memristors by name). To summarize, I agree with you GMR (i.e. metallic) systems can be termed memristive. In that case you may as well cite Baibich et al PRL 1988. The APL 2006 combines this research with that on dielectric-based memristors. It is the first robust demonstration of its kind. As a measure of respect for your curating efforts of this page, I will await your response (until mid-june) before reestablishing the timelime. I hope in fact to achieve agreement with you on the best way to represent this work on spintronic metallic memristive systems, dielectric memristive systems, and the combination that is represented by the APL 2006 work. You are right when you suggest that the APL 2006 work isn't considered important at present (14 citations). That is precisely what I am trying to remedy, 9 years after its publication. Please refrain from thinking circularly here (it's not cited and therefore not important). — Preceding unsigned comment added by Moarteen (talk • contribs) 12:55, 12 May 2015 (UTC)

Moarteen

Firstly, I never claimed that the earlier article I cited is important to memristors or memristive systems or that GMR systems can be termed memristive. The point of the timeline is to reflect events that are ALREADY acknowledged as significant rather than try to attract attention to a paper you personally believe to be important. For example, the significance of HP's 2008 paper on TiO2 memristors is verified by numerous 3rd party sources and they actually present memristor/memristive mathematical models based on Chua's 1971 and 1976 papers. Where is the associated spintronic memristor/memristive model from the paper you want to add? The paper does not even acknowledge the existence of memristors or provide a memristive model so it is not correct to claim that your article is the first to combine spintronic research with research on dielectric-based memristors. More is required then just a resistance switching material to qualify as important to the memristor timeline since there are numerous ReRAM/phase change memory/MRAM and other devices that would clutter the timeline if included. If you insist on including the paper please place it in the external references section or another section besides the timeline unless you can establish a 3rd party source verifying the significance of this paper. Trying to establish the significance of a paper is NOT the role of wikipedia. Blm19732008 (talk) 14:34, 12 May 2015 (UTC)

??

If it can be "inferred" that memristance is charge dependent resistance (because dFlux/dq = M), why not say resistance is "current dependent memristance"? That same logic says inductance depends on current (dv/di=L), and capacitance depends on charge (dq/dv = 1/c) It's not a "4th fundamental component" because it's not new, and it's not fundamental because it's simply taking a resistor and saying its resistance is a function of charge, which is no longer fundamental because it's not a constant LTI system parameter. Otherwise that equation defining memristance, dFlux = M * dq, if you use faraday's law, it is just saying that a loop of wire having a finite resistance M will produce a certain current I=dq/dt when a certain EMF=dFlux/dt is induced by flux. Resistance, not memristance. I'm confused... (it's also not the only other meaningful relationship, because it's not meaningful, it's redundant, just like saying we need to define dv/dq = X, because 1/c would equal X--now, d^2i/ddt^2 = X*v WOULD be something new) The graphic showing the "symmetries" makes no sense because while resistance and memristance are the same when you apply calculus, inductance and capacitance aren't equivalent. That's not symmetrical. — Preceding unsigned comment added by 216.165.152.226 (talk) 17:45, 11 November 2015 (UTC)

Formal equivalence of mechanical v. electrical systems

The article states "it is well known that the mechanical equivalent of an electrical inductor is mass". Actually (in the customary lumped-parameter model) capacitors correspond to masses, and inductors to springs. I don't know how to mark up math symbols to display properly, so I will use prime for derivative and tilde for integral taken over time.

In a mechanical system the "through" variable is force F, the "across" variable is velocity v (equal to the time derivative of displacement x, or to the time integral of acceleration a). (m = mass; k = spring constant in Hooke's Law) In electrical systems the "through" variable is current I, the "across" variable is voltage E. (L = inductance; C = capacitance)

For a mass F = ma = mv' while for a capacitor I = CE'

For a spring F = kx = k~v while for an inductor E = LI' whence I' = (1/L)E and I = (1/L)~E

And the respective energy-dissipating elements: a damper obeys F = bv while for a resistor I = (1/R)E

---

No, the article statement that the mechanical equivalent of an inductor is mass is correct. Usually this analogy comes about when studying differential equations and comparing the second order differential equation used for modeling an LRC (L=inductor, R=resistor, C=capacitor) series electrical circuit to the second order differential equation for an mbk (m=mass, b=damper, k=spring constant) system. Using the prime derivative notation

L(q')'+Rq'+(1/C)q = E for an LRC series electrical circuit where E=voltage and q=charge (q'=current)

m(x')'+bx'+kx = F for a damped spring where F=Force and x=displacement (x'=velocity)

Thus L is comparable to m, R is comparable to b, and 1/C is comparable to k.

Also see the wikipedia page Impedance analogy and read the section on inductance. Blm19732008 (talk) 04:56, 16 January 2016 (UTC)

tempest in a teapot

If it were not for the general market buzz surrounding the prospect of non-volatile RAM, it is questionable whether there would be any eponymous motivation to extend the meaning of the so-called "memristor". Contrived graphical representations aside, non-volatile memory is not, like resistance, inductance, capacitance, a fundamental or necessary physical property of electron circuit phenomena. The entire "memristor" concept is an eponymous land grab. If this element can't even be determined to require any specific physical mechanism (not simply the phenomenological behavior described by the formula), much less, a fundamental physical mechanism (as in, resistance, capacitance, inductance), then grandiose claims of it being "the fourth" fundamental circuit element are silly and grasping.Wikibearwithme (talk) 09:00, 28 January 2016 (UTC)

Timeline

The "Timeline" section of this article needs some work. Seems like it's just become a list of published papers in the field, and not all of them seem particularly notable to me. Maybe if it's a seminal paper, or a breakthrough discovery... but not every single paper. I'm not an expert in this field, so I don't feel qualified to judge each one's notoriety, but maybe someone more qualified can. 72.229.242.168 (talk) 23:04, 30 June 2016 (UTC)

I agree. I initially created the timeline in 2008 and have deleted new references occasionally to avoid clutter but have been reluctant in most cases. The number of memristor-related papers is almost 10,000 at this point (Google Scholar gave me 9,480 hits for "memristor"). Perhaps it is a good idea to clean the slate and have new entries (or restoration of deleted entries) (post HP's 2008 paper) justify themselves in this talk section. The most notable post-2008 development seems to me to be the mem-capacitor and mem-inductor paper from DiVentra, Pershin, and Chua since this is most fundamental to the basic memristor concept extending to other basic circuit elements (capacitor, inductor) so this seems to me worth keeping. Blm19732008 (talk) 05:22, 1 July 2016 (UTC)

Problems with addition to titanium dioxide memristor section

There was an addition to the Titanium dioxide memristor section which needs to be fixed (or removed). The addition is interesting but has two minor problems and one major problem.

1 - (minor problem) The cited equation is more relevant to memristor theory than titanium dioxide materials used for memristors so is more proper to the theory section.

2 - (minor problem) The cited equation appears too obscure to be useful to the wikipedia memristor article. I can't imagine other than advanced researchers in memristor theory being interested. A cite to the arXiv article would seem sufficient without including the matrix equation.

3 - (major problem) The cited equation is incomplete from the arXiv article. It appears to be based from equation 7 in the most recent version of the arXiv article (https://arxiv.org/pdf/1608.08651v3.pdf) which is different from the equation posted which is missing the alpha*W term and includes Ron which is not present in the most recent version).

Blm19732008 (talk) 07:09, 7 January 2017 (UTC)

Memristor is not basic component in electric circuit.

All passive devices are linear device. Memristor is nonlinear device. The unit of memristance is ohm. This is similar with impedence. Syd776 (talk) 23:34, 30 April 2017 (UTC)

V=L(dI/dt)+RI+Q/C

: inductance+resistance+capacitance

What is memristance? Φ=MQ? V=MI? Syd776 (talk) 23:45, 30 April 2017 (UTC)

All passive devices are not necessarily linear. A device is usually considered passive when (1) it does not introduce energy into a circuit or (2) does not require an external energy source (usually dc bias in an ac system) to operate. Non-linear resistors can be considered passive if they do not require a dc bias to operate. Sometimes diodes are considered passive (see link below) but can also be considered active if a dc bias is necessary to overcome a voltage threshold and turn the diode "on".

https://www.allaboutcircuits.com/textbook/semiconductors/chpt-1/active-versus-passive-devices/

In any case, the memristor of Chua (1971) was a theoretical non-linear circuit element from which passivity was derived as a property. Mathematically the defining equation is Φ=M(Q)-->dΦ/dt=dM(Q)/dQ dQ/dt-->V(t)=R(Q) i(t) where Φ is magnetic flux linkage, M is a non-linear continuous function, Q is charge, R(Q) is the derivative of f with respect to charge (memristance function having units of ohms), V(t) is voltage (derivative of magnetic flux Φ with respect to time) and i is current (derivative of charge Q with respect to time).

However, research on materials that exhibit resistance memory has indicated a "nanobattery" effect which is not in agreement with the passivity criterion (see link below).

https://www.nature.com/articles/ncomms2784

It may be more apt to conclude that materials that exhibit resistance memory and are not passive are not memristors (as originally defined by Chua), rather than that memristors are not passive.

Blm19732008 (talk) 05:55, 7 May 2017 (UTC)

Thank you for your answer. I agree with your answer on passive device. Unintentionally, I thought all passive devices would be linear. I was wrong.

But I have questions. What is the difference between memristance and nonlinear resistance? What is the difference between memristance and impedance? This concept is somewhat confusing and unclear.

I think the basic components such as L,R,C are important in electric circuit.

If memristance is the basic component, the voltage equation should be modified.

V=L(dI/dt)+RI+Q/C --> V=L(dI/dt)+RI+Q/C+M(???)

'M(???)' is voltage drop by memristor. It may be somewhat inaccurate, but it must be expressible in any way. What do you think?

[3 basic component (L,R,C) vs. 4 basic component (L,R,C,M)] — Preceding unsigned comment added by Youngdae (talk • contribs) 15:53, 11 June 2017 (UTC)

Answering the above questions:

What is the difference between memristance and nonlinear resistance?

Short answer--> Memristance has memory of past current or voltage while nonlinear resistance is only dependent on the present current or voltage (i.e., doesn't have memory).

Long answer--> Non-linear resistors are described by a non-linear function relating current and voltage. For example, if you had a circuit element in which the voltage (v) was proportional to the square of the current (i) (i.e., v=k*i^2 where k is a constant) it would be considered a non-linear resistor. In contrast, Memristors are described by a non-linear function relating charge (=time integral of charge) and magnetic flux (=time integral of voltage). For example, if you had a circuit element in which the magnetic flux (m) was proportional to the square of charge (q) (i.e., m=k*q^2 where k is a constant) it would be considered a memristor. Differentiating both sides of this equation with respect to time produces dm/dt=2k*q*dq/dt which can also be written as v= 2k*q*i which has a form v=R(q)*i analogous to ohm's law thus represents a charge dependent resistor. So when contrasting non-linear resistors and memristors, the non-linear resistors can be considered having a current (or voltage) dependency while memristors have a charge (or magnetic flux) dependency. Memristance is actually a more general concept from memristors and is based on a broader notion of state dependency. A simplified memristive form of ohm's law would be v=R(x)*i with x being expressed by a differential equation (i.e., dx/dt=function of i and x). Basically this introduces memory into the resistive system (which nonlinear resistors don't have).

What is the difference between memristance and impedance?

Short answer--> Memristance has memory of past current or voltage while impedance is only dependent on the present current or voltage (i.e., doesn't have memory).

Long answer--> Impedance is a generalized term covering the electrical effects of resistances, capacitances, and inductances in a circuit. For a linear capacitor (C) current (i) is related to voltage (v) by i=Cdv/dt. For a linear inductor (L) current (i) is related to voltage (v) by v=Ldi/dt. However, these equations do not apply to non-linear capacitors of inductors. A non-linear capacitor is defined by a non-linear relationship between charge and voltage while a non-linear inductor is defined by a non-linear relationship between current and magnetic flux. Neither capacitors or inductors (linear or non-linear) provide memory as in memristance. Hybrid circuit concepts such as memcapacitors and meminductors have been discussed in the literature combining impedance with memristance.

V=L(dI/dt)+RI+Q/C --> V=L(dI/dt)+RI+Q/C --> V=L(dI/dt)+RI+Q/C+M(???)

My understanding is that the left side of this equation is expressing a series combination (via Kirchoff's voltage law) of a LINEAR inductor (L), a LINEAR resistor (R), and a LINEAR capacitor (C). Note that memristors and memristances are NOT LINEAR circuit elements. However, for arguments sake suppose you added a memristor in series with the linear inductor, linear resistor and linear capacitor represented by this equation. The equation would be modified to be:

V=L(dI/dt)+RI+Q/C+M(Q)I = L(dI/dt)+(R+M(Q))I+Q/C

where M(Q) is a function of charge having units of ohms.

In the more general case of memristance the equation would be modified to be:

V=L(dI/dt)+RI+Q/C+M(x)I = L(dI/dt)+(R+M(x))I+Q/C

where dx/dt is a function of x and current and M(x) is a function having units of ohms.

Blm19732008 (talk) 09:29, 24 June 2017 (UTC)

Thank you for your answer, but I don't understand some of your answer.

In order to understand your answer, I need more information about memristance.

For example, I can add these questions. 'What is the difference between memristance and charge-dependent resistance?'

You may say that the memristor has memory.

But, anyway, I don't deny the memory concept in memristor theory.

What I want to say is that there is no difference between memristance and resistance.

To be precise, memristance should be included in the category of resistance.

Likewise, mem-inductance and mem-capacitance should be included in the category of inductance and capacitance.Youngdae (talk) 04:21, 2 July 2017 (UTC)

One more thing,

Complexity : resistor < variable resistor < Memory resistor

(Memrory resistor has variable characteristic but also non-volatile characteristic) Youngdae (talk) 04:48, 2 July 2017 (UTC)

I agree that memristance may be interpreted as a more generalized type of resistance and your complexity hierarchy (resistor < variable resistor < Memory resistor) is valid. I also agree that the three categories of resistance, capacitance, and inductance generalized to memristance, mem-capacitance, and mem-inductance is a more accurate view than the memristor as a fourth fundamental circuit element. For further information the article that introduced the mem-capacitor and mem-inductor may be of interest (if you haven't read it yet):

Circuit elements with memory: memristors, memcapacitors and meminductors https://arxiv.org/abs/0901.3682

Note: equations 3,4 of this paper provide the definition of a (current-controlled) memristive system while equation 5 provides the memristor (i.e., charge dependent resistor) definition which is a particular case of a memristive system. Blm19732008 (talk) 09:17, 2 July 2017 (UTC)

My paper on viXra

http://vixra.org/abs/1708.0178 Youngdae (talk) 03:50, 17 August 2017 (UTC)

Re: update tag alleging memristors are on the market?

I am deleting the following update tag which appears erroneous -"This article needs to be updated. In particular: Memristors are currently in production and on the market, but a significant portion of the article still treats them as hypothetical. Please update this article to reflect recent events or newly available information. (September 2017)"

According to some recent articles (see links below) memristors are not yet on the market in products or at least have not been reported as such. Some memristor devices or samples have been available from startup companies (e.g., Knowm, Crossbar) but have not had much market impact as far as I know. Regarding treating the memristor as "hypothetical" I think some of the theory aspects of the memristor (e.g., interpretation as a fourth fundamental circuit element) might still be considered hypothetical (and debatable). Successfully marketing a product does not prove a hypothesis.

https://www.theregister.co.uk/2016/06/28/memristor_moves_closer_to_death_row/

https://www.scientificamerican.com/article/hpe-debuts-its-next-gen-computer-sans-much-anticipated-memristors/

Blm19732008 (talk) 08:24, 27 September 2017 (UTC)

External links modified (January 2018)

Hello fellow Wikipedians,

I have just modified one external link on Memristor. Please take a moment to review my edit. If you have any questions, or need the bot to ignore the links, or the page altogether, please visit this simple FaQ for additional information. I made the following changes:

• Added archive https://web.archive.org/web/20120323215048/http://www.cospa.ntu.edu.tw/aappsbulletin/data/18-6/33spin.pdf to http://www.cospa.ntu.edu.tw/aappsbulletin/data/18-6/33spin.pdf
• Added {{dead link}} tag to https://capocaccia.ethz.ch/capo/Fraw-attachment/wiki/2010/memris10/Lehtonen_implic_Elett.pdf

When you have finished reviewing my changes, you may follow the instructions on the template below to fix any issues with the URLs.

This message was posted before February 2018. After February 2018, "External links modified" talk page sections are no longer generated or monitored by InternetArchiveBot. No special action is required regarding these talk page notices, other than regular verification using the archive tool instructions below. Editors have permission to delete these "External links modified" talk page sections if they want to de-clutter talk pages, but see the RfC before doing mass systematic removals. This message is updated dynamically through the template {{source check}} (last update: 5 June 2024).

• If you have discovered URLs which were erroneously considered dead by the bot, you can report them with this tool.
• If you found an error with any archives or the URLs themselves, you can fix them with this tool.

Cheers.—InternetArchiveBot (Report bug) 16:34, 25 January 2018 (UTC)

Invalid equations

The article contains invalid equations such as R = dV / dI, clearly labelling R as being resistance. The resistance by _definition_ is R = V / I. I've already fixed the invalid equations, but somebody undid my fix claiming that R = dV / dI is a "generalization". A generalization of something contains the original as a consistent subset, which this does not, so it is not a generalization either. The article on Electrical resistance makes it clear that R = V / I by definition. It also mentions that the related quantity, dV / dI is called _differential_ resistance, which is not the same thing as resistance. We have two choices to correct the article, replace dV / dI with V / I like I originally did, or replace the word "resistance" with "differential resistance". The same problem applies in the invalid equations for capacitance and inductance in the same table. Humanoid (talk) 11:46, 18 August 2014 (UTC)

For a linear resistor V=IR with R as a constant defining the resistance value. Differentiating both sides of this equation with respect to current (I) produces dV/dI = R. Thus this equation is not wrong and as you mention is most commonly associated with differential resistance. Since the table explicitly lists this column as referring to differential equations it makes no sense to replace the differential form with the non-differential form R=V/I. In any case this is part of the argument Leon Chua made in explaining the memristor so it is appropriate within the context of this wikipedia article. — Preceding unsigned comment added by 69.23.88.121 (talk) 16:11, 20 August 2014 (UTC)

If you want to talk about an ideal "linear" resistor, then the table will have to mention that this equation is only valid for the resistance of an _ideal_ resistor. Because it is certainly invalid for resistance in general. Humanoid (talk) 04:03, 7 September 2014 (UTC)

Hello. The differential forms (dV/dI, etc.) are commonly used for generalized non-linear circuit theory and for calculating ac resistance of non-linear circuit elements such as diodes so it is not correct to say that these forms are limited to the linear (or ideal) case. The mapping between differential forms of current, voltage, charge and magnetic flux was a primary reason why Chua originally proposed the idea of the memristor as a fourth circuit element. Blm19732008 (talk) 23:47, 7 September 2014 (UTC)

"Ohm's law" is a rule of thumb without mathematical evidence. I learned so in my university days from a physics teacher. As an engineer, I can not find any ideally liner resistors. They usually drifts. To design precise analog circuits, usually several registers need to be used both in parallel or in series. Typical engineer suffers from choice of capacitors and inductors because each type of them shows different characteristics. There is no ideally linear devices in the world.

• What is the proof of ohm law rule V=IR in a mathematical way?
• Discovery, invention, and development: Human creative thinking

Cafeduke (talk) 13:14, 21 March 2018 (UTC)

Ohm's Law is more about experimental evidence than a mathematical proof and is not just a definition of resistance. Out of historical interest there was a competing law called Barlow's Law around the time Georg Ohm published his paper in 1827. Experimental evidence eventually established Ohm to be correct and Barlow to be wrong. Over the past 191 years since Ohm first published his paper there has been considerable experimental tests verifying the linear relationship between current and voltage for metallic conductors under normal circumstances (e.g., other than extreme conditions such as very low temperatures where superconductive effects may come into play for some metals). It is true that non-metallic materials such as semiconductors do not obey Ohm's Law and instead demonstrate a non-linear relationship between current and voltage. For example, semiconductor diodes exhibit exponential relationship between current and voltage. See Shockley diode equation. It is also true that changes in environmental parameters such as temperature can change resistance which may explain the "drift" you observe as an engineer. However, to the extent that you are working with metallic wires under fixed environmental conditions the veracity of Ohm's Law has been fairly well established and metallic wires can be considered "ideal linear resistors".Blm19732008 (talk) 05:48, 24 March 2018 (UTC)

Bad Science?

In view of the recent work by Meuffels and Soni (http://arxiv.org/abs/1207.7319) and Di Ventra and Pershin (http://iopscience.iop.org/0957-4484/24/25/255201), it is necessary to discuss this question again. There are now strong indications that the “memristor” will remain a pure mathematical hypothesis, that is, it seems to be impossible to turn this kind of idea into physical reality as the concept of purely current- or voltage-controlled memristors is in conflict with fundamentals of non-equilibrium thermodynamics. This raises the question: What are the claimed experimental “memristor” implementations all about? Has the catchy “memristor” label been used to sell old wine, namely the well-known resistance switching effects, in new bottles? One should definitely consider whether the section “Implementations” should be moved to the WIKIPEDIA entry “Resistive random-access memory”. — Preceding unsigned comment added by Lost C'Mell (talk • contribs) 07:51, 4 April 2014 (UTC)

Another review on arXiv (http://arxiv.org/abs/1403.5801) from the ReRAM community (Rainer Waser's group) criticizes the lack of predictability of memristor models (at least in the simplified forms). The paper concludes:

4) If the basic equations do not reflect the actual device physics well, as we see for the basic memristor equations, with or without window functions, low-predictivity is given at all.

205.132.119.8 (talk) 15:08, 6 May 2014 (UTC)

Sascha Vongehr also describes why certain classes of memristors might prove impossible:

• http://www.science20.com/alpha_meme/purely_mechanical_memristors-156889
• http://www.science20.com/alpha_meme/the_science_is_not_settled_memristor_edition-135143
• http://www.nature.com/articles/srep11657
• http://vixra.org/pdf/1503.0204v1.pdf (unsure why this wasn't accepted into arXiv)

Thangalin (talk) 04:11, 16 January 2016 (UTC)

Unreliable sources throughout

Well, this whole article is basically waffling back and forth between the unpublished paper of Meuffels and Sohni (uploading on arXiv does not count as published in academia) and the HP marketing materials echoed in the IT press. Consequently I've added the {{unreliable sources}} tag. 86.121.137.150 (talk) 09:29, 16 December 2014 (UTC)

Also, I know of some other academics (Dimian and Andrei) who have published their opinion in a Springer book in support of the HP memristor announcement: https://books.google.com/books?id=ltC4BAAAQBAJ&pg=PA130. So it's not like the whole of academia thinks it's bunk as this wiki article would lead you to believe... 86.121.137.150 (talk) 09:42, 16 December 2014 (UTC)

Interestingly, a lot of papers which remain purely as e-prints on arXiv.org and are never published in a peer-reviewed journal are cited in papers which are published in peer-reviewed journals. It’s the scientific community which decides on the quality and reliability of papers on arXiv.org. To consider some scientific sources to be “unreliable” is thus nothing else but a personal opinion. — Preceding unsigned comment added by 80.187.111.190 (talk) 13:16, 18 December 2014 (UTC)

Well, there's also this new Nature article very much related to memristors: http://www.nature.com/articles/ncomms14736#f2 31.128.16.154 (talk) 11:51, 4 April 2017 (UTC)

Chua's general proof that the memristor is passive based on his memristor equations is invalid because the memristor equations do not provide a sufficient description of the physics of memristors. A relevant statistical thermodynamics is needed for the memristors however the memristor equations do not contain sufficient physics to deduce that.(from: Myth-Busting in Physics and Information Science, http://noise.ece.tamu.edu/research_files/mythbuster.html) — Preceding unsigned comment added by Lost C'Mell (talk • contribs) 14:31, 25 May 2018 (UTC)

A simple example for a software developer please (:

I'm trying to make sense of the article, but I don't know that much electronics. So I can't really figure out what this text is saying. I am good at software though, academically trained. What I want to know:

How do I set a value on a memristor, and how do I get a value out of a memristor. Is this this value a digital bit, or can I represent analogue values as well? — Preceding unsigned comment added by Guidocalvano (talk • contribs) 12:25, 26 January 2012 (UTC)

I would recommend doing a Google search of "memristor" and "spice model" which might help you find examples if you want to do software modeling of Chua's or HP's memristor. Blm19732008 (talk) 20:08, 1 April 2012 (UTC)

It's measured in ohms and set by voltage. 78.33.156.1 (talk) 19:32, 14 January 2014 (UTC)

http://sparkbangbuzz.com/memristor/memristor.htm http://www-isl.stanford.edu/~widrow/papers/t1960anadaptive.pdf (memistors, but may be of use to you) Both these links have information on building them and how to get values out of it. 2001:1970:56E8:7700:D0F7:8CF0:2203:C510 (talk) 19:17, 16 June 2018 (UTC)

Request to add new reference

Hi, I would like to add the new reference The case for rejecting the memristor as a fundamental circuit element. I think it fits in the section "Memristor definition and criticism', under the paragraph relating to Vongehr's paper. Guidance appreciated. Thank you. Isaacpabraham (talk) 20:47, 27 July 2018 (UTC)

is someone able to please guide me about how this can be done? The issue is that the requested ref is my own paper in the Nature/Scientific Reports; and would be a conflict of interest if I made the edit. Guidance appreciate. Isaacpabraham (talk) 03:26, 2 August 2018 (UTC)

I see that this has now been added. — Cheers, Steelpillow (Talk) 12:56, 4 January 2020 (UTC)

Memtransistor

similar, related, or perhaps even the exact same thing: [6] 2602:304:CFD0:6350:6804:BBCA:A006:B33F (talk) 03:01, 27 February 2018 (UTC)

See Memtransistor. — Cheers, Steelpillow (Talk) 12:58, 4 January 2020 (UTC)

Menductor?

The section on Theoretical memristor component includes a sentence which reads; "Notice that this is the exact equation for an ideal menductor..." but the term "menductor" occurs nowhere else on Wikipedia. In the given context, "memristor" would appear to make more immediate sense. Is this a typing error, or something technical from Chua's cited analysis? — Cheers, Steelpillow (Talk) 13:07, 6 January 2020 (UTC)

Probaly, it should read "memductor".Lost C'Mell (talk) 15:34, 6 January 2020 (UTC)

Neither term is present in the cited paper by Chua. Searching the Internet reveals no "menductor" at all and just one "memductor" in a paper with a very poor grasp of English. Looks like the article needs to explain itself. — Cheers, Steelpillow (Talk) 17:42, 6 January 2020 (UTC)

Is the memristor still considered hypothetical?

The memristor was first claimed to have been found by a team at HP Labs. However, in 2012, a team of researches at HRL Laboratories and the University of Michigan made a functioning memristor array on a CMOS chip. Is the memristor, then, still considered hypothetical?

Even though their work was merely related to ReRAM devices, the buzzword "memristor" was used by many groups to sell their papers, taking advantage of the "memristor" hype in those days. Y. V. Pershin and M. Di Ventra have recently presented a test how to check experimentally if a resistor with memory is a memristor (https://arxiv.org/abs/1806.07360). They remark in their publication: "At the moment, we are not aware of any experimental resistance switching device that can pass our test." That's why the "memristor" is still considered to be a hypothesis. — Preceding unsigned comment added by Lost C'Mell (talk • contribs) 16:07, 24 February 2019 (UTC)

That paper is about the "ideal memristor". But there exist things known as memristors. Should the article only be about the hypothetical ideal, or about what exists? Dicklyon (talk) 01:54, 9 March 2019 (UTC)

The “memristor” as proposed by L. Chua is physically defined by some unique state equations. Up to now, no device has been presented which physically works in accordance with these defining equations (see section “Memristor definition and criticism” in the main article). There are devices which are termed “memristors”, but in these devices the well-known resistance switching effects occur, i.e., one is dealing with ReRAM devices. To name such devices “memristors” should be regarded as incorrect - from a scientific point of view.Lost C'Mell (talk) 13:34, 12 March 2019 (UTC)

Both the ideal theoretical device and the compromised practical circuit (such as ReRAM) are widely referred to as "memristors". This article needs to cover both (although the finer details of say ReRAM can be left to that article). However it also needs to be clearer than it currently is about which it is talking about at any given moment. — Cheers, Steelpillow (Talk) 10:26, 3 January 2020 (UTC)

Superconducting example?

The section on Theoretical memristor component claims that a superconducting real ideally-functioning memristor component has been identified. Elsewhere the article states that any such ideal memristor component remains hypothetical. Which claim is correct, or is there a verifiable controversy over it? — Cheers, Steelpillow (Talk) 14:26, 4 January 2020 (UTC)

Good scientific practice requires that a scientific hypothesis has to be unambiguously tested by means of experiments.

An ideal “memristor” has to satisfy the following mathematical equation:

$V(t)=\ M(q(t))I(t)$

Recently, Pershin and Di Ventra (see reference [5] in the main article) have proposed an experimental test which can show whether an ideal memristor does actually exist or is a purely mathematical concept. In case it is claimed that a “superconducting real ideally-functioning memristor component” has been identified, it should be no problem to prove whether such a component would pass the experimental test.Lost C'Mell (talk) 13:55, 5 January 2020 (UTC)

Thank you. Your use of grammatical tense implies that no example has yet been unequivocally identified. That flatly contradicts the claim in the article that one has been. Is the claim contested or have I misunderstood you? — Cheers, Steelpillow (Talk) 14:10, 5 January 2020 (UTC)

A theoretical "superconducting memristor" was proposed by S. Peotta and M. Di Ventra in 2014 in their publication "Superconducting memristors" (see reference [11] in the main article). In 2018, Y. V. Pershin and M. Di Ventra published their paper "A simple test for ideal memristors" (see reference [5] in the main article). In ref. [5], Y. V. Pershin and M. Di Ventra make the statement: "An ideal memristor is defined as a resistor with memory that, when subjected to a time-dependent current, $I(t)$, its resistance $R_{M}(q)$ depends only on the charge $q$ that has flowed through it, so that its voltage response is $V(t)=R_{M}(q)I(t)$."

Interestingly, a "superconducting memristor" isn't mentioned in the publication "A simple test for ideal memristors". It's thus not clear, whether a theoretical "superconducting memristor" might pass the proposed test for an ideal "memristor". The statement "No physical memristor component has yet been demonstrated." in the intro is thus to my mind justified for the moment.Lost C'Mell (talk) 11:41, 6 January 2020 (UTC)

Thank you again. Perhaps I am being stupid, as I still struggle to place the apparent contradiction in context. Are you saying that the Josephson based analysis identifies the only known theoretical candidate for an ideal memristor component? That would clear things up, as I have been reading it as the only known identified physical memristor component. — Cheers, Steelpillow (Talk) 13:05, 6 January 2020 (UTC)

In a publication entiteld "Quantum Memristors with Superconducting Circuiits" ( Scientific Reports, volume 7, article number: 42044 (2017) ), J. Salmilehto, F. Deppe, M. Di Ventra, M. Sanz and E. Solano write in the abstract: "Memristors are resistive elements retaining information of their past dynamics. They have garnered substantial interest due to their potential for representing a paradigm change in electronics, information processing and unconventional computing. Given the advent of quantum technologies, a design for a quantum memristor with superconducting circuits may be envisaged." [bold by Lost C'Mell]. That's all what is known so far. Whether an envisaged "quantum memristor" may represent an "ideal memristor" isn't memtioned in the paper.Lost C'Mell (talk) 15:03, 6 January 2020 (UTC)

In a recent publiction entiteld "Comment on 'If it's pinched it's a memristor' by L. Chua [Semicond. Sci. Technol. 29, 104001 (2014)]“ (https://arxiv.org/abs/1905.02254 published 2019), Y. V. Pershin and M. Di Ventra write: "At the same time, the "ideal memristor" (in the sense of its original definition [3]) still remains an elusive/idealized concept, leading many researchers to raise serious concerns about its actual existence as a physically-realizable device [4, 5, 6, 7, 8]. In fact, it is doubtful that any experimental system would pass the memristor test we have recently proposed in Ref. [9], which would differentiate between an ideal memristor and the more general, and physically-valid concept of memristive element.“

And at the end of this publication one finds: "A lesson can be drawn from all this: over-reliance on mathematical definitions to describe physical phenomena can easily lead to the wrong conclusions and away from physical reality.“Lost C'Mell (talk) 15:32, 6 January 2020 (UTC)

Well, thanks, but I can find nothing in that which directly addresses my questions. — Cheers, Steelpillow (Talk) 17:43, 6 January 2020 (UTC)

I would approach this in a pragmatic way.

Pershin and Di Ventra in 2019: "At the same time, the "ideal memristor" (in the sense of its original definition [3]) still remains an elusive/idealized concept, leading many researchers to raise serious concerns about its actual existence as a physically-realizable device [4, 5, 6, 7, 8]. In fact, it is doubtful that any experimental system would pass the memristor test we have recently proposed in Ref. [9], which would differentiate between an ideal memristor and the more general, and physically-valid concept of memristive element.“ (in https://arxiv.org/abs/1905.02254)

I thus assume that they no longer consider a "superconducting memristor" (which was envisaged just by Di Ventra and Peotta in 2014 (reference [11] in the main article)) as an “ideal memristor”.Lost C'Mell (talk) 15:52, 10 January 2020 (UTC)

2020 developments

https://www.nature.com/articles/s41586-020-1942-4

New implementations. Zezen (talk) 11:08, 4 February 2020 (UTC)

Source worth referencing?

This reference was recently added to the article lead but deleted because the accompanying text was inappropriate:

Muthuswamy, B.; Jevtic, J.; Iu, H. H. C.; Subramaniam, C. K.; Ganesan, K.; Sankaranarayanan, V.; Sethupathi, K.; Kim, H.; Shah, M. Pd.; Chua, L. O. (2014). "Memristor modelling". 2014 IEEE International Symposium on Circuits and Systems (ISCAS). pp. 490–493. doi:10.1109/ISCAS.2014.6865179. ISBN 978-1-4799-3432-4.

A copy can be freely downloaded here.

The paper describes the use of a gas discharge tube to allow exploration of certain memristor characteristics and its authors are a pretty solid bunch. I feel that it would actually make quite a useful addition to the article, but I am not sure how it could be fitted in with the current article structure. Any ideas/suggestions?

— Cheers, Steelpillow (Talk) 09:45, 22 May 2020 (UTC)

"Bioinspired bio-voltage memristors"

Could you add some short information on this paper?
It would probably fit best under section "Potential applications" (on the described type of bio-voltage memristors) and/or "Implementations".

Here is what I added to 2020 in science:

• Researchers demonstrate a diffusive memristor fabricated from protein nanowires of the bacterium Geobacter sulfurreducens which functions at substantially lower voltages than previously described ones and may allow the construction of artificial neurons which function at voltages of biological action potentials. The nanowires have a range of advantages over silicon nanowires and the memristors may be used to directly process biosensing signals, for neuromorphic computing and/or direct communication with biological neurons.

--Prototyperspective (talk) 11:59, 24 May 2020 (UTC)

The authors are certainly describing their creations as "memristor devices" or just "memristors". But is that description justified, or are they really just memristor systems, i.e. fabrications offering memristor-like properties? — Cheers, Steelpillow (Talk) 12:50, 24 May 2020 (UTC)

article is a mess

the information in this article is unorganised and has excessive sections.

also not written in an encyclopedic fashion. if anyone is knowledgeable on the topic please help. — Preceding unsigned comment added by RJJ4y7 (talk • contribs) 19:16, 20 June 2022 (UTC)