Talk:Leap second/Archive 1
| This is an archive of past discussions about Leap second. Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page. |
| Archive 1 | Archive 2 |
Leap hours predetermined?
With the proposed leap hour methods, are the leap hours predetermined like leap days and unlike leap seconds? Unless they are, the arguments in favor of leap hours seem completely bogus: you would still need to consult a table for leap hours, and you can still not predict time far into the future (albeit you can on a much larger time frame).
- This is of course assuming that the human race hasn't destroyed itself by the time solar time and UTC differ by 3600s. Gee Eight 22 December 2005 21.12 UTC
Bias
Towards the end of the section titled "Proposal to redefine UTC and abolish leap seconds" there is a conclusion made that introduces a strong bias to the article, the purpose of the last part was to show firstly the cons of removing leap seconds and then the pros, but then an attempt is made to refute the pros in a manner of an argumentative piece which is not the purpose of an encyclopedia.
I propose removing the last part, as the same point is already made in the cons regardless.
- Didn't check which paragraph you're referring to, but I just read the paper: The Debate over UTC and Leap Seconds [1]; and I suspect that if the comments in the wiki article seem skewed against change, the WP editor likely just read this paper. Talk about having a POV!
- But, I've just updated the article with reference to the latest paper by the ITU-R and the current status as of 2011-10; so if you think any of this 2010 paper should be ref'd in the main, I'll leave it to you to add. Cheers, — Who R you? Talk 09:17, 24 October 2011 (UTC)
- ^ David, Finkleman (2 - 5 August 2010), "The Debate over UTC and Leap Seconds" (PDF), AIAA Guidance, Navigation, and Control Conference, Toronto, Ontario Canada, p. 22, retrieved 2011-10-24
{{citation}}: Check date values in:|date=(help); Unknown parameter|coauthors=ignored (|author=suggested) (help)CS1 maint: date and year (link)
Is there any practical considerations with regards to leap seconds?
Is there any practical considerations with regards to leap seconds? How does it affect anything? I suppose, for example, that the Unix epoch which counts seconds starting from January 1, 1970 would be about 22 (?) seconds out of sync with UTC, right? I think that discussions on such practical aspects needs to placed in the article. --seav 06:05, Jan 3, 2004 (UTC)
- I believe it has something to do with GPS systems, airline computers and the like.... but i'm just drawing that from my head, from an article I read about the latest spin correction... I don't have enough info to add to the entry. Lyellin 06:12, Jan 3, 2004 (UTC)
- Here someone asks a few relevant questions
- * http://www.mail-archive.com/leapsecs@rom.usno.navy.mil/msg00051.html
- and here is some related discussion, I think
- * http://www.metrology.asn.au/leapseconds.htm
- Essentially, there is a tension between our convention that a day is a fixed length, and our recording devices, because it isn't quite as we wish; I expect the tension will increase as the accuracy of our recording and measuring devices increase. However, I'm far from any kind of expert on the matter! :) Kyk 06:32, 3 Jan 2004 (UTC)
- The following page has a very useful explanation of leap seconds:
The only reason for leap seconds, in fact calendars vs timekeeping is to keep the Earth's surface position, and season timings in sync with the traditional points in the sky which mark the events. The reason for the gregorian calendar adjustment was to insert days into the mix to move easter back to occuring in it's traditional relation with the sky positions. (I don't recall these exactly and the details are not relevant to my point). The leap seconds are gradually realiging the earth's position back to day alignment as the leap year days adjust the calendar.
The earths nutation has caused the slipage and it was traditionally ignored, but there is still a significant amount to be accounted for, if I recall, it is a matter of inserting the adjustments to minimize other factors.
- "Roughly 50000 years in the future, one can expect to have a day of 86401 seconds if the definition of the SI second is not eventually changed."
I'm not sure, but I think in the year 4000 the Gregorian Calendar won't work as it does now a days... so this phrase would be irrelevant... could someone check it out? I'm busy... --Henriquevicente 01:12, Apr 26, 2005 (UTC)
- You may be falling into a (popular!) intellectual trap here, namely confusing the length of the day with the length of the year. The two are independent oscillations. Changing the leap-year rule near 4000 (no serious astronomer is confident to predict the exact length of the year that far into the future) would not affect the length of the day after that. --anon
- The purpose of Leap Years in the Gregorian Calendar is to keep the calendar synchronized with the seasons, nothing more. The 4000-Year Rule as proposed by astronomer John Herschel, among others, i.e., dropping a leap year every 4000 years, is still just a proposal. Let 'em start worring about it, say, around 3990 A.D.! --QuicksilverT @ 18:58, 16 November 2005 (UTC)
- It seems to me that if leap seconds are thought necessary because the earth's rotation slows slightly, it's the value of the second that requires adjustment, not the number of seconds in a particular minute. Smerdis of Tlön 21:04, 1 January 2006 (UTC)
- Not sure what you're actually suggesting, but it's impractical to change the value of the second. Many very precise measurements are based on a constant value of the second, and you could cause chaos by trying to change that value. FireWorks 21:24, 1 January 2006 (UTC)
- Well, I'm all for causing chaos; but it strikes me that some other unit of time with a different name needs to be adopted. The length of the day, the length of the year, and therefore the value of the second are not constants; they are astronomical facts beyond the reach of human standards. Smerdis of Tlön 23:29, 1 January 2006 (UTC)
- I think you'll probly find that there's two seconds: One of which is 1/24*60*60 of a day long, and one of which is precisely "the duration of 9 192 631 770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom", whatever that means. It's a convenient fiction that they're the same, when in reality they've never been the same (at least as long as the latter's been defined), thus quoth: [1]. Because it's easier to make international standards based on the second definition (apparently) our second count is based on that. I think it would've been better if the SI had've called the latter one the "newcomb" or some such. It's probably relevant that before 1972 the basis for civil time did use these variable-length seconds. —Felix the Cassowary 14:05, 2 January 2006 (UTC)
Frequency of changes
The article states that "Historically, leap seconds have been inserted about every 18 months". I did a quick check of the table and it looks like the interval has been 18 months only 5 times, while it has been 12 months 14 times. Might it be better to start that paragraph at "The Earth's rotation rate is unpredictable..."?
Looking at the frequency of updates and the fact that we have gone 7 years without one, the higher frequency up to 1998 would appear to be some sort of gradual 'catch up'. Would that be a correct interpretation?
82.43.52.87 16:16, 30 July 2005 (UTC)
- The frequency of about every 18 months is correct for all leap seconds between 1 January 1972 and 31 December 2005, including the initial 6 month interval and the final 84 month interval, because the mathematical average during that period was 17.7 months. A graph showing the relationship of UTC to UT1 can be found at [2], showing that there was no attempt to 'catch up'. Rather, Earth's rate of rotation actually sped up slightly during 1997. — Joe Kress 21:15, 30 July 2005 (UTC)
I quite liked this: http://www.post-gazette.com/pg/05210/545823.stm although I have no idea if it's suitable as an external link on the article.
- I also like it and I'll add it. — Joe Kress 03:54, 31 July 2005 (UTC)
Simple naming question
Shouldn't this be called a leap day? Like... a leap year has an extra day, a leap day has an extra second? :-P --67.172.99.160 23:51, 5 August 2005 (UTC)
- Interesting question. Unfortunately, "leap day" is already the name for the extra day in a leap year. There was no doubt some discussion in the years leading up to their adoption in 1972 concerning what to call them. We only know the result of the discussion—the ITU decided that they will be called leap seconds. — Joe Kress 03:31, 6 August 2005 (UTC)
- On that basis it would be more precise to call it a "leap minute" because the effect is to increase or decrease the length of the last minute in the day: 23:59:60 is the extra second added for a positive leap second, 23:59:59 would be skipped for a negative leap second. EdDavies 23:26, 2 January 2007 (UTC)
Removed incorrect information
The reason we need leap seconds is that the rotation of the Earth is slowing down. The solar day does gradually become longer by about 1.7 ms every century, mainly due to tidal acceleration from the Moon. The SI second that is counted by atomic time standards has been defined in such a way that its length did match the nominal second of 1/86400 of a mean solar day some time during the 19th century. Since that time the length of the solar day has been slowly increasing. Therefore the time as measured by the rotation of the Earth has been accumulating a delay with respect to atomic time standards. Whenever the accumulated delay approaches one second, a leap second is added to UTC.
This misconception weas contradicted in the paragraph that followed it. Ben Arnold 07:05, 8 August 2005 (UTC)
- The paragraph you removed is completely correct. So is the paragraph which follows it in its own way. What seems to be missing is an obvious linkage between the apparently slow rate at which Earth is slowing down (milliseconds per day per century) and the apparently much more rapid rate at which leap seconds are added (many seconds per century). That is immediately achieved by restating the rate at which Earth's rotation is slowing down, 1.7 milliseconds/day/century (actually 1.7 ms/(d·cy)), in square centuries. To do this we multiply by the number of days in a century, which is 36525 days per Julian century (to two significant digits, it does not matter what kind of century is used, but astronomical equations are always stated in terms of Julian centuries, never in terms of Gregorian centuries or mean tropical centuries). That yields a rate of 62 seconds/century², which is obviously the proper magnitude to yield many leap seconds per century. But the actual mathematical equations should be given, which requires integration. I am composing a rewrite. — Joe Kress 17:40, 8 August 2005 (UTC)
Actually, it is not correct that the reason we need leap seconds is because the Earth is slowing down. We need leap seconds because the SI (atomic) second is not exactly 1/86400 of a mean solar day. Even if the Earth's speed could be locked today, and never changed again, leap seconds would still be needed at about the same rate we're used to. It's the difference in the two units, not the rate of change that matters.
Besides, it's not really that we "need" them, so much as that we have decided to use them. When UTC was established in 1972, harmonizing the definition of the civil second and the atomic second, we chose to adjust for the inevitable differences between the rock-solid UTC and the highly variable UT1 (earth rotation time) in one-second jumps.
Prior to that, the adjustments were still being done, but it was done as a fractional disseminated-frequency offset from the atomic time definition. That is, an adjustment trim was applied to the disseminated GMT time and frequency standards in order to keep them in fairly close agreement to actual earth-rotation time.
Then, by '72, it was decided to scrap GMT, and quit trying to keep adjusting it for minor earth-rotation variations. UTC was established, the disseminated frequency offset was set to zero, and, since then, civil and atomic clocks have ticked in sync. Standards organizations stopped trying to adjust the time scales, and let them drift apart, but published the predicted and measured differences between UTC and UT1, for those interests that required earth-rotation time to a precision of less than one second. Only when the differences threatened to accumulate to more than 700 ms would an ajustment to UTC be scheduled. These are the familiar leap seconds, scheduled (or waived) six months in advance for 23:59:60 UTC on the last day of June or December. --Jeepien 05:03:27, 2005-08-09 (UTC)
- If we do not explain that the Earth is actually slowing down, then it appears as if the SI second was set at the wrong value to stay in sync with mean solar time. So it would appear as if we would forever be fudging our clocks with leap seconds because of an initial mistake; it would be then more sensible to re-define the SI second. However, this is is not feasible because the Earth WILL be getting out of sync with the SI second because it is actually slowing down irregularly. So this information is totally relevant when explaining why we have leap seconds. -- Tom Peters 10 August 11:20 UTC
In the very least, this section is confusing. I had to find other sources in order to decipher it. It should in essence read "The reason that leap seconds are needed is because the SI second is not exactly equal to a solar second. The reason for this difference is that the SI second was defined in the 19th century and due to the slow change in the earth's rotation the SI second now differs from the solar second by X. While, X is very small, we are talking about a second and when you consider that there are 86400 seconds in a day and 365 days in a year this small difference is multiplied many times and results in a whole second of difference in only a matter of years. Basically, the SI second is based on an absolute amount of time that corresponded to a an average second in the 19'th century but is now off by X."
I would also like to see some reason why this was adopted rather than some "Atomic Equation of Time" that one could use to translate between atomic and solar (or sidereal) time. Or at least the existence of such. Does such a method exist now, for something like astonomy? Syscore 20:32, 18 August 2007 (UTC)
At this point in time, Leap seconds are required because the atomic clock is not and has never been an exact multiple of Solar time. The Earth slowing down or speeding up will just change the rate of occurrence of the leap seconds. the leap seconds would still be needed if the Earth rotated at the same speed. Canol (talk) 23:50, 20 January 2009 (UTC)
The Earth is... umm... speeding up.
All of this discussion about how the earth is slowing down ignores one inconvenient fact. The earth is, at present, not slowing down. It is, in fact, speeding up, and has been doing so since 1972, coincidentally just around the time that UTC was introduced.
When the International Atomic Time (TAI) scale was zeroed to civil UT, on 1958-01-01, the mean solar day was about 1.4 ms too long (as compared to a standard SI day of 86 400 s). Over the succeeding 14 years, the equivalent of around 10 s of "leap" time was introduced between TAI and UT, but in those days the adjustments didn't "leap". They were done by slightly padding civil time using a flexible frequency offset from TAI, so the adjustment was made continually, on the fly. Furthermore, in those days, the earth actually was slowing down. Over the course of that same 14 years, rotation slowed until it reached more than +3.1 ms/day relative to the SI day.
On 1972-01-01, when UTC was adopted, and set to 10 s offset from TAI exactly, it proceeded to tick at the same rate as TAI, i.e., 1 UTC second = 1 SI second, exactly. Since then, 22 leap seconds have been added, with one planned for 2005-12-31, which will bring the total offset between UTC and TAI to (TAI - UTC) = 33 s.
However, for the last 33 years something else has been going on. The day has been getting shorter. For some reason, no doubt related to internal fluid mechanics, the Earth's crust has been accelerating. By the time the last leap second was introduced at the end of 1998, the day length had shrunk back to something like +1.3 ms/day. It is this continued acceleration that accounts for the fact that leap seconds, once a circannual phenomenon, have become relatively rare. This winter's leap second will be the first in seven years.
During that seven years the acceleration has continued. The difference between a mean solar day and an SI day has now essentially vanished. Over the most recent 48 solar days for which data is available, 22 of them have been shorter than an SI day! If this acceleration continues much longer, at some point in the future a negative leap-second may be needed.
So it is not correct to blame leap seconds on tidal deceleration. In the first place, ever since they were introduced, there hasn't been any. Or, more correctly, the small tidal deceleration that exists has been swamped by the much larger short-term earth-rotation variability. And this the rule, rather than the exception. The vertical plate movement responsible for the "Christmas Tsunami" of 2004 added measurably to the angular velocity of the Earth's crust. No doubt other geophysical events will have different effects.
Although the current period of acceleration probably can't be maintained for many more years, and while the +1.7 ms/cy tidal effects (which some sources suggest may really be closer to +1.4 ms/cy) will continue to slow the planet over geological time scales, these effects will aways be swallowed up in the "noise" of short-term variations on the order of a human lifespan. --Jeepien 07:19:41, 2005-08-11 (UTC)
- My analysis produces somewhat different results than yours. I used the annual change in ΔT, which is TT − UT1, where TT (Terrestrial Time) is TAI + 32.184 s, close to the average time during the nineteenth century, which defines the SI day. For the last three years (2003.0-2005.0) I calculated ΔT from various IERS bulletins B (ΔT = 32.184 s + (TAI − UTC) − (UT1 − UTC)). I find that ΔT increased by 3.3 ms/d for 1898-1919, 1.2 ms/d for 1920-1927, −0.1 ms/d for 1928-1939, 1.2 ms/d for 1940-1964, 2.6 ms/d for 1965-1984, 1.4 ms/d for 1985-1990, 2.1 ms/d for 1991-1998, and 0.6 ms/d for 1999-2005. Near 1972, Earth's rotation rate actually slowed even more than it had before! Only during the last seven years (and during 1928-1939) can it be said to have sped up. Of course, the rates did vary a little within each period and for years at the limits of each period.
- Although the SI second and day is usually stated to be based on and hence defined as the average day between 1750 and 1890, the average day for the period 1686-1823 was the SI day (with a change in ΔT of less than 0.01 ms/d), ΔT changed by −0.5 ms/d for 1824-1834, 0.1 ms/d for 1835-1861, −0.5 ms/d for 1862-1866, −1.0 ms/d for 1867-1874, and −0.1 ms/d for 1875-1897; or an average change of −0.08 ms/d for the entire period of 1686-1897 (over two centuries). Of course, the long term (over 2700 years) lengthening of the mean solar day is about (1.7 ms/d/cy)T, which produces a parabolic ΔT of about (31 s/cy²)T², so the mean solar day was actually lengthening slightly during the base period. What source places the rate closer to 1.4 ms/d/cy? — Joe Kress 18:23, August 12, 2005 (UTC)
- I don't dispute your figures, but I think if you look at the numbers graphically, it will leap out at you. Here's a graph of excess length of day (LOD) from around 1720 until 2003. Positive slopes correspond to periods of deceleration, negative slopes to acceleration. The values are measured directly in ms, and correspond to the difference between the observed day length and a standard (86 400 s) SI day.
- As you can see, the peak near 1972 is the highest (i.e., slowest) in a lifetime, and since then, but for backsliding during the 1990s, the general trend has been downward (faster). If the last two years were shown, a smoothed average would be very close to zero.
- As long as the LOD difference hovers around 0, leap seconds are rare, and if it manages to drop below zero for any length of time, negative leap seconds will be required. Nobody is predicting that it will, but then again, nobody is clear on what's causing this current period of acceleration, either. --Jeepien 00:00:35, 2005-08-13 (UTC)
Proposed change
I am proposing replacing the entire section on Reasons for leap seconds with the following. Note that this would remove the reference to Creationists. I don't understand what that issue is supposed to be, and it wouldn't belong here anyway. Sure the earth was going faster in the past, so what? Any comments on the following text would be appreciated. --Jeepien 21:35:17, 2005-08-11 (UTC)
For most of history, the measurement of time has been an exercise in astronomy. Traditionally, the second was defined as 1/86400 of the length of a mean solar day. Units of time depended on the Earth's speed of rotation on its axis and the properties of its orbit around the Sun. For any ordinary purposes, this was fine but, as clock-making technology improved, the problems with using Earth as the standard timepiece became more evident. With the invention of the quartz clock in the 1930s, the best available timepieces were becoming increasingly stable. The length of a solar day, even when averaged over a year, proved to be anything but. Factors such as winds, ocean currents, plate tectonics, glacial melting, and fluid currents within the Earth's interior all combine to add a complex set of wobbles to the Earth's rotation, speeding it up or slowing it down slightly in unpredictable ways, often for decades at a time. Over the long term, however, the Earth is slowing down. The tidal effects of gravity between the Earth and the Moon cause the mean solar day to get longer by approximately 0.0017 seconds each century, on average. Compared to the short-term speed fluctuations, this is a small effect, but it is constant and inexorable, and will become more significant over time. All of these factors make the Earth a sub-standard timepiece.
Whenever the tools of measurement become more precise than the standard of measurement, a new standard is needed. With the development of the caesium atomic clock in 1955, an extremely precise and stable time scale became available. On 1958-01-01 the International Atomic Time (TAI) scale was defined, and set to match the civil time scale on that date. At first, TAI was used primarily by scientists, but proved itself to be a superior tool for all timekeeping. In 1967, this new definition of the second, based upon the vibrations of caesium atoms, was adopted as the official SI unit of time. Planning was begun to change the civil time scales around the world from the old astronomical standard (commonly called GMT), to the atomic standard. The switch was officially made on 1972-01-01. However, TAI could not be used directly; since 1958, mean solar time, which was still tracking the wobbly Earth, had drifted about 10 seconds "slow" with respect to TAI. A new scale, Universal Coordinated Time (UTC) was created, and simply set equal to TAI - 10 s. The two scales would thereafter remain locked at the same rate. Still, it was clear that more adjustments would be needed to keep UTC and mean solar time from drifting apart again. It was decided that future adjustments would be made in precise one-second steps. These steps, called leap seconds, allow the time and duration of each second to remain locked to the atomic standard, while making sure that the average time that the Sun crosses the Greenwich meridian is still noon, give or take 0.9 s. No such adjustments are ever made to TAI.
Since the inception of UTC, there have been 22 leap second adjustments (see list), all of them "positive", i.e., adding an extra second to UTC as opposed to skipping one. Leap seconds are announced six months in advance, and occur simultaneously around the world during the last minute of June or December, at 23:59:60 UTC. In recent decades, the Earth has been in a period of acceleration, so fewer leap seconds have been needed. The one announced for 2005-12-31 will be the first in seven years, bringing the difference between TAI and UTC to 33 seconds. That is, UTC-TAI = -33 s as of 2006-01-01.
- My comments:
- somewhat too extensive: it is a (brief) account of the history of the second, which should be or already is described in other articles: use links.
- It is, I believe, shorter than what's there now, isn't it? I would also reduce the now-redundant info in the Announcing section, or move the relevant info there.
- tidal deceleration contributes +2.4 ms/cy to the l.o.d.; the number +1.7 is the observed average over the past 25 centuries. The difference is probably mainly due to so-called glacial rebound, which is another long-term process since the end of the ice age; see the article on Delta-T.
- Tidal effects should contribute that much in theory. This has never been observed.
- Only the total effect of all processes can be observed. The partial contribution of known mechanisms, like the tidal deceleration, can be accurately modeled; I can give you scientific literature references. They are consistent with the OBSERVED acceleration of the Moon. The laws of preservation of energy and angular momentum then allow to compute the effect on the rotation rate on the Earth of the tidal effect by itself. There is a long-term discrepancy of about 0.7 ms/cy with the observed change in rotation rate, which is due to other long-term mechanisms. Models of glacial rebound largely explain this effect. So IMNSHO it is totally OK to mention these facts.
- Tidal effects should contribute that much in theory. This has never been observed.
- Jeepien, on your previous comment: I begin to find the discussion meaningless. The reason that we need leap seconds is that the rotation of the Earth is irregular, but nonetheless for civil life we want to keep in sync with the solar day. There are a zillion mechanisms that influence the rotation rate on all time scales, but the tidal deceleration is the main and most persistent one. I don't understand why you and some others are so opposed to even mentioning it. In any case I object to giving so much attention to recent short-term irregularities.
- I don't recommend leaving it out, and in fact I include it and mention that by its inexorable nature it can't help but be significant in the long term. But the fact remains that short term effects are an order of magnitude more significant than tidal effects in any given century.
- The rotation rate of the Earth has the statistics of a random walk: sometimes it is accelerating, sometimes it is decelerating. There is a long-term trend, driven by tidal deceleration and probably glacial rebound. Seasonal effects (winds, ocean currents) work both ways but do not exceed a few ms (accumulated). There are some longer-term (decades) mechanisms that can have an accumulated effect that will require leap seconds, but these can work both ways too: redistribution of mass between poles and aequator (ice caps) and exchange of angular momentum between core and mantle.
- I don't recommend leaving it out, and in fact I include it and mention that by its inexorable nature it can't help but be significant in the long term. But the fact remains that short term effects are an order of magnitude more significant than tidal effects in any given century.
- I did not add the piece about creationists misinterpreting the reason for leap seconds, but apparently this is an issue and if it should be addressed, this is the proper place; possibly under its own sub-heading. I say we keep it.
- This one is a no-brainer. Creationism deserves no mention in any scientific article. If it's an issue, deal with it under Creationism where it belongs. It is certainly not an issue to the community of earth-rotation interests. But I would be grateful to anyone who could explain what that paragraph says. It seems to say that leap seconds should not be confused with amount that the earth has slowed, yet that's exactly what they are.
- As I explain on the page, the creationists are confusing rate (velocity) with time passed (distance traveled). So they believe that whenever a leap second is counted, that the length of day has increased by 1 second, e.g. that the solar day has increased from 86400 to 86401 seconds. Counting backwards that way, the Earth would have had a ridiculous fast rotation rate in the recent past; which they take as proof that scientific chronology is false and (non sequitur) that the biblical short chronology is true. In any case, this distinction apparently is so confusing that it is proper to explain it here, even without creationist discussion. The anonymous anti-creationist tried to explain the difference between rate and time passed with an example, I elaborated on the concepts. If this still appears unclear to you, please try explain yourself. Iterum censeo that iff there is a vocal party that tells nonsense about the topic (leap seconds) then the page dealing with that topic is the place to refute it.
- This one is a no-brainer. Creationism deserves no mention in any scientific article. If it's an issue, deal with it under Creationism where it belongs. It is certainly not an issue to the community of earth-rotation interests. But I would be grateful to anyone who could explain what that paragraph says. It seems to say that leap seconds should not be confused with amount that the earth has slowed, yet that's exactly what they are.
-- Tom Peters 20050812T10:15 UT
- --Jeepien 07:58:46, 2005-08-14 (UTC)
- -- Tom Peters 20050814T08:43
- --Jeepien 07:58:46, 2005-08-14 (UTC)
- It's this kind of thing that shows people just how much credibility we really lack. Why is it necessary to attack the beliefs of creationists in this article? What did the article have to do with the beliefs of creationists in the first place? Also, the page dealing with a particular topic of issue is not the place to refute it, but rather, that article's corresponding Talk page. In closing, I believe a rewording of all parts of the paragraph, in addition to the removal of any reference to creationists (which separates the wrong and right interpretations of the need for leap seconds, making it that much harder to understand), and possibly merging it with the paragraph immediately following, would make the article easier to understand for most people (including myself).--JEmfinger 04:49, 23 December 2005 (UTC)
- Nice attempt, but too many words. I agree the slowing (or speeding) of the Earth's rotatation has almost nothing to do (~< 0.003%) with the leap second, and the current artile is not correct to imply that it does. The simple message should be that leap seconds are added to synchronise the measured length used in today's clocks (based on the SI definition) to the observed length of the day. While the Earth's rotation does contribute to the difference of the two, the effect is negligable. Commentary on the history of measurment should be left for another article. --Supcmd (talk) 04:01, 30 December 2008 (UTC)
Leap seconds on 31 December?
Am I the only one who has noticed that the introduction of a leap second at 23.59'60" UTC on 31 December is a bit unwitting, as that is the moment when quite a lot of people will be counting down official UTC seconds to the new year? Why and how will I, being British and therefore a UTC timezone resident, still be able to count down from 10 at 23.59'50" with Big Ben next Saturday despite the impending 2005 leap second threatening to make me miscount? Can someone please tell me where my logic has failed (preferably before the 31st) as this is really confusing me! Gee Eight, 22 December 2005 21.01 (unless they've added the leap second early) UTC
- Your logic hasn't failed, but unfortunately, there's no way of getting around this problem as far as I can tell. The only thing I can really advise is that, when there's 10 seconds remaining, start counting down from 11! --JEmfinger 05:31, 23 December 2005 (UTC)
Or they could just start the countdown at 23.59'51". I'll synchronise my watch with UTC later today and see. (Interesting point: the man responsible for keeping Big Ben on UTC has within the last 36 hours been given an MBE...is something going on here?) Gee Eight, 31 December 2005 15.12 UTC
Or, to be more accurate (as I understand it) with the idea of a repeating second (at least in some timescales), they could countdown "10...9...8...7...6...5...4...3...2...1...1...'Happy New Year!'". Of course, I guess it matters which timescale you're using, and I think UTC inserts a second rather than repeating one, so just adjusting the start time of your countdown would probably be more correct for the typical human-used timescale. OK...this didn't really add much to the discussion, but seemed slightly humorous, so I figured I would add it. Igjeff 16:59, 31 December 2005 (UTC)
- What the BBC actually did on their countdown on News 24 that night was to repeat the 2 second count, so it went 10...9...8...7...6...5...4...3...2...2...1...0. It's viewable on YouTube, though apparently the countdown projected on Canary Wharf, shown in the -40s, had already been adjusted. -- Arwel (talk) 19:49, 14 January 2007 (UTC)
- I think it is humour from timekeepers on their consumers - 1 January 0:00:00 is a totally arbitrary time and really means nothing if you follow the history of the calendar. There have been so many changes in the last 2000 years, that the joke is on all the NYE participants. Though I guess it is the same time most people in the world turn over a new page ... plus or minus 12 hours.--Supcmd (talk) 04:12, 30 December 2008 (UTC)
i think i spotted a vandal
someone who knows the truth check the edit by (17:00, 1 December 2005 70.23.27.61) where he/she changed a single date from 1890 to 1892. The edit is in the sentance: "The SI second that is counted by atomic time standards has been defined in such a way that its length matched the nominal second of 1/86400 of a mean solar day between 1750 and 1892." It is in the "Reason for..." category. There was no reason given why the date was changed in the first place. I've noticed that vandals try to change dates like this because they are hard to spot. 71.131.52.62 06:28, 26 December 2005 (UTC)
- The change is appropriate. 1890 is a rounded version for 1892. F. R. Stephenson, IIRC, used the range 1750-1890 when he selected 1820 as the vertex of his parabolic representation of Delta T, whereas the actual observations used by Simon Newcomb, on which he based his tables, which form the basis of Ephemeris Time, end in 1892, not 1890. — Joe Kress 07:54, 26 December 2005 (UTC)
Spelling errors
Corrected spelling errors in article. (IchBin 05:46, 1 January 2006 (UTC))
BTW, did you notice...
That 2005-12-31 T 23:59:60 Z was the first leap second observed since the founding of Wikipedia? -- Denelson83 08:21, 1 January 2006 (UTC)
Example
After exactly 500 rotations, your counter will register 43,200,001 seconds. Since 86400 × 500 is 43,200,000 seconds, you will calculate that the date is 12:00:01AM on May 16, 1971 (exactly 500 days after January 1, 1970) as measured in atomic time (UTC), while it is only 12:00:00AM on May 16, 1971 in solar time (UT1). If you had added a leap second on December 31, 1970 to your counter, then the counter would have a value of 43,200,001 seconds at midnight on May 16, 1971 and allow you to calculate the correct date. The actual system involving leap seconds was set up to allow TAI and UT1 to have an offset of 0 seconds on January 1, 1958.
This is exceedingly confusing. Could someone who understands it please reword it? It says that your counter will read 43,200,001 on May 16, but if you add a leap second, then you get 43,200,001 on May 16 and can calculate the actual date. The impression that that sentence gives is that you'll get 43,200,002 on your counter, and then you just have to fudge everything up to get the real date. Obviously this wasn't the intent of the writer... FireWorks 21:40, 1 January 2006 (UTC)
- I was just noticing that too, very long winded, and using UNIX epoch as an example is a little ironic, considering how poorly defined computer time is wrt leap seconds. I might take a crack at it, I think one clear sentence can replace that rambling paragraph. DonPMitchell (talk) 17:03, 7 August 2009 (UTC)
crazy approach
i'm just a guy who likes math, and knows nothing about leap second. what i do know is that the problem happens because there's one count of the time from Earth's translation movement and another one counting atoms. so that makes a difference of 1 second almost every 6 months between them.
as long as we are made of atoms, and we are moving around the Sun, i think a better approach would possibily measure another kind of frequency. once again, i'm no expert in those measurements details, but i do know that, logically, it makes more sense for us, as humans, measure frequencies closer to us, and that could potentially avoid any kind of "leap", not only in 6 months, but even in centuries.
my suggestion would be looking for something around carbon 12. either diamonds or maybe plain old coal. maybe, just maybe, a carbohidrate. the simpliest the better. now, that may sound pretty stupid for most specialists, but try to get the big picture. why did we started to use any of the ways we do today? because it was experienced they're stable at our home, some parts of earth's surface. it's already proved even that's untrue, on time dilation. so, why bother trying to find something that's whatever ns more precise? better if we can find a way to precisely measure things that walk in time in same "speed" than we do. that way it will keep changing over time, but it will be same than human.
maybe measuring the eletrons moving in water molecule. maybe measuring light (or photons) going across a carbohidrate. i'm really not sure which methods could be used, but i'm sure it's not impossible to find a one, and i believe it would be the more appropriate the closer it gets to our form of life.
--Caue (T | C) ![]() 13:36, Thursday March 30 2006 (UTC)
13:36, Thursday March 30 2006 (UTC)
Er I don't think you quite understand the issues here. Trying reading Atomic clock and Delta T and perhaps a bit more on time. If we really want to measure solar time, sundials are your best bet... Using the frequencies of other atoms is going to give the same result (albeit less accurately if at all possible) It's nothing to do with time dilation. We are moving in TAI (atomic time/realtime) more or less. Solar time simply depends on how fast we're going round the sound (more or less). A second is a second. It wouldn't be particularly smart if the length of second varies. Solar time is important but it isn't the end all. Nil Einne 17:00, 5 November 2006 (UTC)
Its not an issue of accuracy, it's one of standards. The "atoms" did walk in time the same way we did in the 19th century. However we are just a tad slower now and since the SI second is still defined as the same fixed number of oscillations the SI second is a bit faster now. Multiply that error in the second by 86400 seconds in a day and 365 days in a year and you get a whopping one second error in only a few years. What would seem to make sense to me is that you do the math ahead of time and publish real solar seconds. There will always be leap seconds (or math) involved since you are comparing a fixed time reference (atoms) to a changing time reference (the earth). SI seconds are needed because they are an absolute reference and when I say that some phenomena occurs in X seconds I mean X SI seconds regardless of when I said it. They are problematic though when trying to match them to what we think of in terms of calendar seconds, days and years.Syscore 20:52, 18 August 2007 (UTC)
merge with Coordinated Universal Time
Leap seconds are solely a feature of UTC, and UTC cannot be defined without discussion of leap seconds. They form a single topic, so it is silly for them to have separate articles. 81.168.80.170 12:10, 29 April 2006 (UTC)
- Both of these are fairly long articles. They seem to stand well on their own, connected by links. And after all, leap seconds are a relatively small part of UTC, so either information would be lost doing the merger or leap seconds would get a disproportionate amount of space in the combined article. I favor leaving them the way they are.
- --Rbraunwa 21:28, 28 May 2006 (UTC)
I agree with Rbraunwa. I know nothing (well, a little now) about UTC, I found this article looking for information on leap seconds. If they did get merged, make leap second a redirect but this article can stand alone. Rahulchandra 09:25, 8 June 2006 (UTC)
Encyclopedic tone
The encyclopedic tone of this article could be improved through the removal of personal phrasing, such as repeated use of the word "you" and phrases like "Take care not to confuse the difference between..." Robert K S 14:44, 18 May 2007 (UTC)
What would you write in place of these types of phrases? I to am in favor of encyclopedic tone but I guess I never thought engaging the reader was non-encyclopedic. Just curious. Maybe I should look this up.Syscore 20:55, 18 August 2007 (UTC)
collapsing table, a bit
Since there was no leap second from '99-'04, I'm going to shorten the table to have the box read:
1999(br)through/thru(br)2004|none . (Through is too wide). If 2008 doesn't get a leap second, that can be collapsed as well. It should have a span of at least four years, as the 'thru box' takes up three and hence takes up the same amount of space. I'm also shortening 1973 through 1979, as the results are the same. If anybody is against this and decides to revert it to the expanded version, please let me know that you will/did. The reason I'm against the expanded one is that it is getting lengthy as it's 37 rows long. A shortened version will have 31 rows if I add a "Year|June|December" box at the bottom so people won't have to go to the top if they do happen to forget which is June and which is December. Socby19 19:05, 29 October 2007 (UTC)
Passive voice
This article is suffering from an overload of passive voice. I came here specifically to find out what standards body announces the leap seconds, and I encountered an infuriating series of passive-voice statements that seem determined to keep this information secret:
- "...UTC is occasionally corrected by an intercalary adjustment..."
- "UTC ... is kept approximately in sync with UT1 (mean solar time) by introducing a leap second when necessary. This happens when the difference UT1−UTC approaches 0.9 seconds, and is typically scheduled either at the end of June 30 or December 31 though leap seconds can be applied at the end of any month."
- "The announcement to insert a leap second is usually issued whenever..."
Can someone who knows please change the article to say who adds the leap seconds? --Doradus (talk) 14:37, 21 November 2007 (UTC)
- It's in Leap second#Announcement of leap seconds. The International Earth Rotation and Reference Systems Service (IERS) announces leap seconds in IERS Bulletin C whenever they predict that the difference UT1−UTC might exceed 0.9 seconds at either the next January 1 or July 1, both with and without a leap second. Also see Earth Orientation Center and click on "leap second" at the upper left. I've added IERS to the introductory paragraph. — Joe Kress (talk) 22:25, 21 November 2007 (UTC)
US Law
The page currently has "Law of the United States indicates that the legal time of the US is based on mean solar time."
I believe that US legal time has now been legislated to be UTC-based. Perhaps an American can check and if appropriate edit the page.
82.163.24.100 (talk) 13:38, 23 November 2007 (UTC)
- Your are correct. I'm removing that sentence, which is no longer germane. — Joe Kress (talk) 21:26, 23 November 2007 (UTC)
Announcement of leap seconds
BIPM's most recent Bulletin, like many of its predecessors, states
"NO positive leap second will be introduced ..."
I point out that this wording leaves the introduction of a negative leap second completely undefined.
Perhaps there is a more rigorous French version?
82.163.24.100 (talk) 18:42, 24 December 2007 (UTC)
- No French version appears to exist. Even the French version of this Wikipedia article, Seconde intercalaire, only provides a link to the English Bulletin C. Of course, because the English version is provided by the French themselves, I trust their own translation. However, I did find a French article from l'Observatorie de Paris announcing the 2005 leap second: Une seconde de plus, including the variation from the long term trend of Earth's decreasing rate of rotation (the long term trend has been removed). Another graphic from the IERS shows that its rate of decrease has only slowed. Only if it increased would a negative leap second be needed. — Joe Kress (talk) 00:22, 25 December 2007 (UTC)
Source for real rate of change in solar (or is it earth?) day
The actual source for the 1.4 ms per day increase in day length is quite different from the one stated in the NASA web page (2.3 ms per day). As both may be considered trustworthy (although I would prefer NASA as a reference), we have to choose or seek other references to make this info accurate (I think it is somewhat essencial to the article). Preymond (talk) 15:56, 2 April 2008 (UTC)
- I'm not sure where the USNO got their figure of 1.4 ms/cy, but it disagrees with other sources. Some of this could be due to the period over which the rate applies. NASA's figure of 2.3 ms/cy is only one aspect. As stated in ΔT, the rate due to tidal friction alone is 2.3 ms/cy, but glacial rebound since the last ice age reduces that by 0.6 ms/cy to 1.7 ms/cy as the average rate over the last 27 centuries. All three of these figures come from Stephenson and Morrison as cited in ΔT, who personally studied the ancient eclipses. They note that the rate does fluctuate over periods of several centuries. — Joe Kress (talk) 16:40, 2 April 2008 (UTC)
cy
"cy" looks to me like "centiyear" (i.e. 3.6525 d or 315 576 s). Wouldn't "hy" (for both "hectoyear" and "hundred years") be better? 212.137.63.86 (talk) 09:51, 6 August 2008 (UTC)
- This was discussed at Talk:Tidal acceleration#"cy" is not a standard unit. I'll repeat that Wikipedia must use the abbreviation used in the references, which is "cy". — Joe Kress (talk) 20:04, 6 August 2008 (UTC)
Accumulated difference between UTC (without leap seconds) and UT1 ?
Currently, UTC is maintained within 0.9 s of UT1 by the addition of leap seconds. If we no longer add leap seconds, how long will it take for the difference to accumulate to an appreciable amount of time? It is my understanding that TT was formerly known as Ephemeris Time and that therefore the difference between TT and UTC (currently about 65 seconds) represents the leap seconds added in the last hundred years or so. If we had not added those seconds, our clocks would now be fast by that much. I would not consider that approximately one minute is significant to non-astronomers. We set our clocks as we are told to and live according to them. The apparent sun varies plus or minus 16 minutes or so because of the Equation of Time anyway. And few of us live exactly on a time zone meridian and so our clocks do not even show Local Mean Time in the first place. So, keeping our civil clocks in sync with the Sun is not an issue at present. How many years before it could become an issue in that 0 hrs on the civil clock, the beginning of the calendar day, would no longer be in the middle of the night? It would be inconvenient to begin a new calendar day during the daylight hours when most of us are already at work. As near as I can figure out, if we stopped adding leap seconds,it would take about a thousand years before UTC would be 30 minutes different from UT1.(thinking of UT1 by its old definition as Greenwich Mean Solar Time). Is this correct? If not, then how many years would it take? If it would take many thousands of years for the difference between civil time and apparent sun time to accumulate to four or five hours where it would be inconvenient for most of us then that fact should be made clear in the article when discussing the Pros and Cons of dispensing with leap seconds.
Alexselkirk1704 (talk) 22:17, 12 October 2008 (UTC)
- Although there are deviations on scales of days, years, decades, and millennia, in general, the long term time difference is TT−UT=ΔT. Several formulas have been proposed, but I like the simplist, ΔT = 31×((Year − 1820)/100)² seconds. Inverting yields Year = 1820 + 100×sqrt(ΔT/31). Thus the difference will reach one hour (3600 seconds) about 1000 years from now in the year 3000. But it is a square function, so the difference rapidly increases to 4 hours about the year 4000, and to 24 hours about the year 7000. — Joe Kress (talk) 03:11, 13 October 2008 (UTC)
- OK then. I had tried to calculate the accumulated difference from Length of Day = 86 400.002s + .0017 seconds per century. But, now having followed the links to [3] and on that page down to "Effects of disconnecting time from the sun",I see that my question is answered. What do you think, Joe Kress, would replacing UTC with TI, as suggested there, be a good idea seeing that it would take a very long time for most of us to have a problem with the absence of leap seconds? Alexselkirk1704 (talk) 18:45, 14 October 2008 (UTC)
- My opinion is irrelevant as is yours because neither belongs on this talk page (WP:TALK) nor in the article (WP:OR). This page is to be used only to improve the article, so only topics which are allowed in the article (editors' personal opinions are not) should be discussed here. Joe Kress (talk) 21:06, 15 October 2008 (UTC)
- I recommend looking at my plots [4] to get a better picture of the extrapolated offset and an idea for compromise using POSIX and zoneinfo, but my presentation is too political for wikipedia. Also see the latest publicly available presentation at CGSIC [5] Steven L Allen (talk) 18:40, 15 October 2008 (UTC)
- The debate over the elimination of the leap second is already part of the article. My question, here on the talk page, is how much difference would such elimination would make to most people. There are three groups of people who use time; (Three ways time is used by people.) those who design and use precision equipment, astronomers and the rest of us. The first two groups have their own times scales,TAI and UT1. UTC is for the rest of us. (The engineers don't necessarily use TAI, but they would make their work easier if they did.)The leap second is a feature of UTC only. How UTC should be modified is a question for the rest of us and the effects of such change are worthy of consideration for the article.
- As to opinions; there are only opinions and facts. There are no truths, not even in science. The Earth's spin velocity is slowing. Fact. Should UTC be modified with leap seconds, or not? Somebody's opinion will prevail on this question. I think that the fact that it will make a difference of only an hour or so in a thousand years (as if there were an extra hour of daylight savings time) is one fact that should be considered among the others. As far as avoiding political discussion; This affects the whole world society. How can politics possibly be avoided? This is all I have to say about this.Alexselkirk1704 (talk) 21:48, 19 October 2008 (UTC)
Lack of understanding
I may be missing the point or the article doesn't explain it very well. Since 1972 there has been 24 leap seconds (23 not counting one at the end of 2008), does that mean that the length of a day has increased by 24 seconds from 1972 to 2008? --HJKeats (talk) 13:29, 10 December 2008 (UTC)
- No. If you have counted correctly, in 1972 through 2008, there will have been 24 leap seconds and 10 leap years. So in a period of 37×365 + 10 = 13,515 days, it was necessary to add 10 leap seconds. This means the atomic seconds were faster than the mean solar seconds. If we evenly distribute the adjustment over the days, we find that on average, each day, measured in SI (atomic) seconds, was short by (24/13,515) or 8/4505 second, compared to a mean solar day. (Fixed and checked numbers per Spiffy sperry)
- This roughly agrees with the statement by the U.S. Naval Observatory that "the length of the mean solar day is at present [2008] about 86,400.002 seconds instead of exactly 86,400 seconds."--Gerry Ashton (talk) 19:14, 10 December 2008 (UTC)
- Should that be 24/13,515, or about 1/563 second? (37 years, not 36, between '72 and '08) Also, the article does explain that "The leap second adjustment (which is approximately 0.6 seconds per year) should not be confused with the difference between the length of the mean solar day and the SI day...." --Spiffy sperry (talk) 16:44, 10 December 2008 (UTC)
A Better Approach
For scientific purposes, the need is for a scale of pure SI seconds.
For civil purposes, the wish is for days of 24 hours of 60 minutes of 60 seconds, tracking mean solar time at Greenwich sufficiently closely, combined with local time zones and summer time.
These can both be provided, by
- 1) Distributing a scale of SI seconds, not grouped in minutes hours or days; a simple count of constant seconds, best labelled in binary.
- 2) Announcing by BIPM, instead of Leap Seconds, the rate of civil seconds in terms of SI seconds, for the following half-civil-year - that to be grouped into minutes hours days months in the usual manner. Since at present we have of the order of one leap second per 1E8 seconds, BIPM could announce the difference as an integer of nanoseconds or as an integer of 2^-32 seconds. That might be called Mean Greenwich Time - MGT.
Generating a frequency of exactly one count per 1E9+/-N nanoseconds, by reference to a signal at 1Hz or, say, 10MHz, is sufficiently easy; I have done that sort of thing myself.
82.163.24.100 (talk) 21:52, 27 December 2008 (UTC)
- What has this got to do with Wikipedia? -- Jao (talk) 21:09, 29 December 2008 (UTC)
Broadcast time
The meaning of the term broadcast standard time / broadcast time is not immediately obvious, at least not to me. Could someone elaborate? --TorArne (talk) 13:32, 29 December 2008 (UTC)
How does this effect global warming?
Any studies related to the earth's slowing rotation on how it effects global warming? —Preceding unsigned comment added by 71.117.211.23 (talk) 19:17, 30 December 2008 (UTC)
- As far as I can see (I'm no expert), such studies have pointed to global warming effecting the rotation speed rather than the other way around. Just googling "global warming" together with earth and rotation gives a lot of interesting results, which heavily contradict each other. I have no idea what the prevailing view is. -- Jao (talk) 20:19, 30 December 2008 (UTC)
Broadcasts?
What does this have to do with broadcasts? That is not explained at all. I suppose broadcasters are affected by this, but the intro suggests that they're the main reason and that sounds a bit odd. Isn't the main thing that there is a variation between atomic clock time, which is constant, and astronomical time, which varies because of variations in Earth's rotation? And shouldn't that then be in the intro? At the very least the broadcast thing should be explained better, because I don't get it. DirkvdM (talk) 19:03, 8 January 2009 (UTC)
- I've tried to clarify the article. "Broadcast" is meant to describe radio stations that exist only to provide time and frequency information; it is not meant to apply to ordinary radio stations that provide news and entertainment (although those stations may depend on UTC in less obvious ways). --Gerry Ashton (talk) 19:48, 8 January 2009 (UTC)
- Right. Melting polar ice should increase the moment of inertia, as the water redistributes throughout the oceans. You'd expect that to slightly slow the Earth. But we're talking about fractions of millisecond per century here. DonPMitchell (talk) 17:08, 7 August 2009 (UTC)
Observing the Sun
I agree that extra gallactic radio sources can be and are used for measuring the Earths rotation, but the Solar day can only ultimately be measured by observing the sun. By way of explanation, if the radio sources ever moved out of syncronisation with the rotation of the earth around the sun, ( an extremely unlikely but not impossible event) then we would have to rely on our observations of the Sun to give us our Solar day. The point I am trying to make is that apparant Solar time can be measured by nothing more complicated than a sundial. Canol (talk) 02:16, 21 January 2009 (UTC)
- It is mathematically impossible for an extra-galactic source to be out of synchronization with the Sun. Geometry requires that the number of sidereal days in any year (tropical or sidereal) be exactly one more than the number of solar days in that year (because a year is one revolution of the Sun) regardless of Earth's rate of rotation. This mathematical relationship is now used to convert an observed extra-galactic source into an 'observed' Sun. Furthermore, the extra-galactic source can be observed about a million times more precisely than the Sun can be observed. Thus, seconds are smaller than the precision with which the Sun can be observed in any one year, so the Sun can never be used to determine when leap seconds should be added on a timely basis. Indeed, the last time the Sun was observed to precisely determine time was about a hundred years ago. — Joe Kress (talk) 21:03, 21 January 2009 (UTC)
- There are three important terms: appparent solar time (observed with sun dial), mean solar time, and sidereal time (best determined by observing extra-gallactic radio sources). Both apparaent solar time and mean solar time are useful in daily life; apparent solar time is most useful for activities directly involving the Sun, such pointing moveable solar panels. Mean solar time is most useful for activities conducted according to clock time. Sidereal time is most useful when observing any celestial body other than the Sun. --Gerry Ashton (talk) 21:19, 21 January 2009 (UTC)
Hi Joe and Gerry
I'm not explaining myself very well here. Ignoring the maths for a moment, A solar day is based on the rotation of the earth relative to the sun, hence "Solar". Anything used to measure this that does not have a direct reference to the sun, has to be a secondary measurement, allbeit that it could be a very accurate one
One thing that bothers me though that needs inclusion somewhere in this article, perhaps you or someone could comment. I read somewhere, but can't now find the reference, that an experiment was conducted by taking one atomic clock to the North Pole and one to the Equator. After some time the clocks were brought together again and 'hey presto' they read different times due to the Equator clock moving faster relative to the Pole clock. This was due to Einsteins Theory of relativity as the periphery of the earth moves faster relative to the pole. How often would we need a leap second due to the Equator clock running slow? Canol (talk) 21:44, 21 January 2009 (UTC)
- I think we could say that all forms of solar time are motivated by the affect of sunlight on daily life, and that over the period of 25 to 100 years, observations of the sun are required to insure that our conversion of sidereal time to mean solar time is sufficiently accurate. On a day-to-day basis, observation of the sun is a poor way to measure time. I understand that Internatial Atomic Time does indeed include relativistic efects, but I don't know the details of the calculations. --Gerry Ashton (talk) 00:11, 22 January 2009 (UTC)
- We cannot state that the Sun is observed to determine time without some citation. I am not aware of any such program. All transit circles, which were used to observe the Sun during the 19th century, have now been retired or are in museums. Only telescopes designed to observe the Sun can be used because normal telescopes will be damaged by the intense heat of concentrated sunlight. Mean solar time is a ficticious time that cannot be observed directly, so an entire year of observations of the Sun's true time are needed to obtain a single crude average over a cycle of the equation of time. Even then, the result is about a million times worse than converting sidereal time. About AD 140 Ptolemy stated (Ptolemey's Almagest, tr. G. J. Toomer, III.9) that mean solar time was 360 time-degrees (a sidereal day) plus approximately 0;59 time-degrees (59/21600 sidereal day). The modern relationship between sidereal time and mean solar time (The new definition of Universal Time) has about ten more significant digits.
- Canol, you are probably refering to the Hafele–Keating experiment (1971) which flew four atomic clocks on regularly scheduled commercial aircraft around the world once east and once west. They did not describe the aircraft routes, except to thank Pan Am, TWA, and AA. Although latitude was used to predict the gain or loss of the travelling clocks, they explicitly stated that all clocks fixed to Earth's surface at average sea level, regardless of their latitude, keep the same time because the effect of the varying rotational velocity (the Sagnac effect) at different latitudes is exactly canceled by a corresponding difference in surface potential due to the oblate Earth, at least to the first order. However, all are proper times, meaning they only represent TAI at their locations on the geoid. A form of the Sagnac effect is applicable when comparing one such time with the time of another atomic clock elsewhere on the geoid ("News from the BIPM", Metrologia 17 (1981) 69-74). This experiment confirmed that atomic clocks run faster at high altitudes and run slower moving east (with Earth's rotation).
- The time of each fixed atomic clock must be corrected for the reduced potential (gravitational and centrifugal) at its altitude above mean sea level. The gravitational potential only depends on altitude, but the centrifugal potential depends on latitude. All times were corrected for the increased potential on the geoid at the beginning of 1977,[6] decreasing the frequencies of all atomic clocks and lengthening each SI second. This was formalized in 1980 by the statement "TAI is a coordinate time scale defined in a geocentric reference frame with the SI second as realized on the rotating geoid as the scale unit."(in above "News") Now each laboratory must steer the frequency of its atomic clocks to the value they would have if they were located on the rotating geoid (mean sea level). Recently, the required fractional frequency shift for the NIST-F1 atomic clock at Boulder, Colorado (1649 m above the geoid) was determined to be −1798.7×10−16,[7] about 1×10−13 per kilometer of height, which is several orders of magnitude smaller than the frequency shift used during 1968−1971 to steer TAI into UTC instead of using leap seconds (−300×10−8). Consequently, gravitational redshift changed the length of the SI second itself—the shift was much too small to warrant a leap second. — Joe Kress (talk) 03:48, 26 January 2009 (UTC)
- Joe referenced the Aoki et al. expression for UT1, which was published in 1982. In that work, "the new expression is based on the final values adopted for the position of the FK5 equinox". FK5 (meaning fundamental star catalog 5) is based on, among other things, "an analysis of absolute observations of the Sun, planets, and minor planets". Seidelmann describes an update in 2005, but I have not figured out if the update involves any new solar observations. --Gerry Ashton (talk) 22:29, 26 January 2009 (UTC)
- Thanks for the citations. A more fruitful search avenue might be literature associated with the national ephemerides such as JPL Solar System Dynamics and the Explanatory Supplement to the Astronomical Almanac. I remember reading that most of the sources used by JPL were various space missions, most of which they controlled. — Joe Kress (talk) 21:16, 27 January 2009 (UTC)
- Thanks for the suggeston about JPL. I'm afraid the Explanatory Supplement is rather out-of-date, but according to Seidelmann's home page he is working on a revision. --Gerry Ashton (talk) 21:45, 27 January 2009 (UTC)
- The limited view online version claims to be "completely revised and rewritten" (2005). However, all front matter, including its Abbreviated contents, Contents, List of figures, List of tables, Forward and Preface are identical to the 1992 edition, including all page numbers, so it is just a reprint. The blurb was apparently a reference by the publisher to the old Explanatory Supplement to the Astronomical Ephemeris and American Ephemeris (1961–1974). — Joe Kress (talk) 00:09, 28 January 2009 (UTC)
- The Explanatory Supplement stated that many transits of the Sun were observed (declination and time of day) by the USNO's six-inch and nine-inch meridian circles during 1911–1975 with a standard deviation of 1.0" which formed part of the observational data upon which the JPL ephemeris DE118 was based.(pp.290–1, p.301) However, it also stated that because the modern definition of UT1 is a function of its rotation angle in space (sidereal time), "UT1 deviates secularly from solar time; however, the divergence is extremely small."(p.51) Thus despite continued observations of the Sun, UT1 will continue to deviate by a very small amount from mean solar time. The defining equation for UT1 (p.50) is equation 13 in Aoki et al., relative to the precessing equinox, effective 1984 January 1:
- GMST1 of 0hUT1 = 24110.54841s + 8640184.812866sTu + 0.093104sTu2 − 6.2×10−6sTu3
- where Tu = Julian UT1 centuries since J2000.0.
- The equivalent definition for UT1 given in IERS Conventions (2003) 5.4.4 is the Earth Rotation Angle, relative to the Celestial Ephemeris Origin (a fixed or catalog equinox), effective 2003 January 1:
- θ(Tu) = 2π(0.7790572732640 + 1.00273781191135448Tu)
- where Tu is the number of UT1 days since J2000.0. Because the CEO does not move, no higher order terms are needed. Because the International Celestial Reference Frame is independent of Solar System dynamics, this definition is independent of observations of the Sun. — Joe Kress (talk) 06:13, 31 January 2009 (UTC)
- The Explanatory Supplement stated that many transits of the Sun were observed (declination and time of day) by the USNO's six-inch and nine-inch meridian circles during 1911–1975 with a standard deviation of 1.0" which formed part of the observational data upon which the JPL ephemeris DE118 was based.(pp.290–1, p.301) However, it also stated that because the modern definition of UT1 is a function of its rotation angle in space (sidereal time), "UT1 deviates secularly from solar time; however, the divergence is extremely small."(p.51) Thus despite continued observations of the Sun, UT1 will continue to deviate by a very small amount from mean solar time. The defining equation for UT1 (p.50) is equation 13 in Aoki et al., relative to the precessing equinox, effective 1984 January 1:
- The definition of UT1 is independent of observations of the Sun for now. The definition of UT1 has been changed a number of times during the 20th and 21st centuries; no doubt it will change again if any deviation between solar observations and the current definition makes the current definition inconvenient. --Gerry Ashton (talk) 13:39, 31 January 2009 (UTC)
- The group that wants to replace leap seconds with leap hours, which would displace UTC from UT1 by as much as half an hour, would argue that a much smaller disagreement between UT1 and mean solar time is of no concern. — Joe Kress (talk) 21:43, 31 January 2009 (UTC)
Thanks for taking the time and effort to answer me, I was aware of Hafele–Keating and the Pan Am aircraft experiments. If I have interpreted Joe Correctly, he is saying that there is a small time difference between the equator and the pole, but this is not due to the relative speeds at these locations, rather it is due to the earth not being a perfect sphere and so gravity at the pole is different from that at the equator.
I am in London next week and intend spending some spare time at the Greenwich observatory where I will put these questions to the historical experts there. If I learn, or can cite anything more, I'll report back here. Canol (talk) 23:55, 26 January 2009 (UTC)
- No. An atomic clock on the equator tries to 'tick' more slowly because it is moving rapidly, but it is also farther from Earth's center of mass so it tries to 'tick' faster. The two effects exactly cancel each other, so atomic clocks everywhere on the rotating geoid keep the same time regardless of their latitude. But atomic clocks above the rotating geoid, like that in Boulder, 'tick' faster because they are farther from Earth's center of mass than the geoid, but have the same speed as the rotating geoid so there is no cancelling slowdown. — Joe Kress (talk) 08:46, 27 January 2009 (UTC)
democratic process regarding proposals to abolish leap seconds
I have been advised to ask this question here rather than in the main article: Speaking as someone who thinks this is a bad proposal and wishes to lobby my appropriate representative if needed, how do I find out who represents me in the appropriate forum and what their position is? —Preceding unsigned comment added by 75.87.135.149 (talk) 05:44, 26 July 2010 (UTC)
- You should check this with ITU Working Party 7A (WP 7A) - Time signals and frequency standard emissions. As far as I can see from the 2009 meeting the situation is still inconclusive. --Muhandes (talk) 07:19, 26 July 2010 (UTC)
Leap Second Abolishment Progress Since 2008?
The section "Proposal to abolish leap seconds" appears to be written in 2008. As far as I can tell, there has been activity since then. However, as an outsider to the ITU I am not able to piece together the information well enough to update the page.
This 2011 ITU document is a second questionnaire on the issue. It says, in part:
From the responses to the Questionnaire sent by the Director of the Bureau it appeared that 8 Administrations were in favour of the revision of Recommendation ITU-R TF.460-6 while 3 were against it. Since no consensus could be reached at the SG 7 meeting in October 2010, SG 7 decided to send the Recommendation to the Radiocommunications Assembly, as well as sending a new circular letter reminding Administrations to respond to the questionnaire on this issue.
It requests responses before 19 September 2011, and refers to a 2012 Radiocommunication Assembly as the body that will receive the results of the questionnaire.
It's worth noting that 8 out of 11 (the apparent outcome of the earlier questionnaire) is 72%, exceeding the 70% threshold for abolition given in the current article text. --JeffEpler (talk) 20:46, 20 June 2011 (UTC)
Additional resources on abolishment timeline: Future of Leap Seconds - Recent Events Comission 32 Time --JeffEpler (talk) —Preceding undated comment added 01:28, 21 June 2011 (UTC).
Another graph showing leap seconds
The graph showing leap seconds as the difference between UT1 and UTC is fine, but it doesn't seem like it would be intuitive to the layperson. I have created a graph showing the number of seconds that have accumulated between the UTC, UT1 and the TAI atomic clock standard, established in 1959. One can clearly see the discontinuous nature of UTC through the addition of leap seconds, as well as the fact that it represents an approximation of UT1. It is also interesting to note that the international agencies had to issue corrections several times during a year prior to 1972, before deciding to use leap seconds. The data comes from the http://maia.usno.navy.mil/ser7/ website. On the other hand, perhaps this is one graph too many.
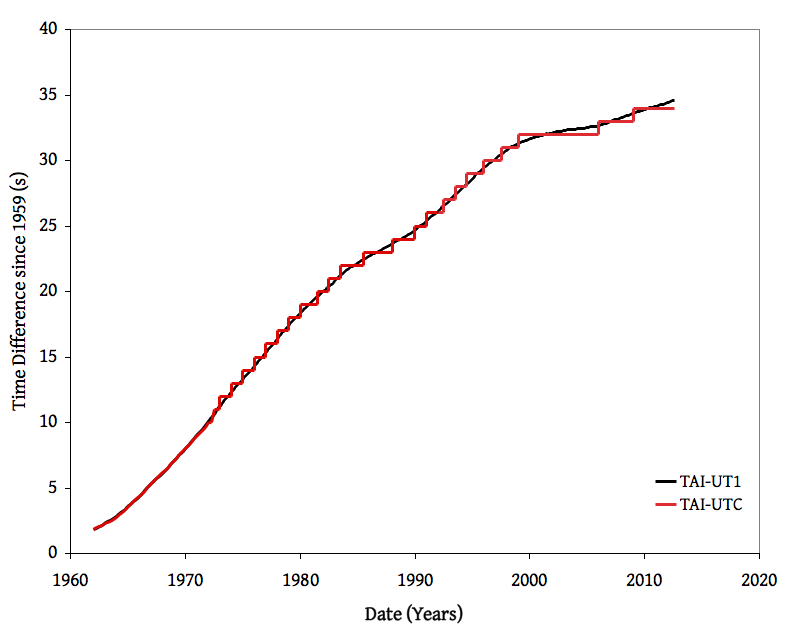 Jdlawlis (talk) 13:36, 16 August 2011 (UTC)
Jdlawlis (talk) 13:36, 16 August 2011 (UTC)
- The IERS provides a comparable figure from 1972 to 2009 [8]. Note that their figure shows a negative accumulation, that is, UTC−TAI and UT1−TAI, not TAI−UTC and TAI−UT1 (leap seconds and a slowing Earth cause specific UTC/UT1 times to be less than the equivalent TAI time). — Joe Kress (talk) 05:22, 17 August 2011 (UTC)
- Thanks for drawing that webpage to my attention, Joe. Jdlawlis (talk) 19:17, 18 August 2011 (UTC)
Clarification needed
At the bottom of the "Proposal to abolish leap seconds" section the article says:
- 2012: If 70% of member states agree, the Radiocommunication Assembly will approve the recommendation
- 2017: If 70% of member states have voted to abolish the leap second, application of leap seconds will stop and UTC will become a continuous time scale, otherwise they will stay the same.
Given that only 16 out of 192 member states responded, does this really mean "70% of member states" or does it mean "70% of member states who vote/agree"? -- Q Chris (talk) 12:00, 4 November 2011 (UTC)
Slowing of earth and leap seconds in Unix time
I've removed the statement and ref in the lead claiming that the earth's rate of rotation has not changed since 1700. The ref is a primary source and presents raw data which could be interpreted that way but the source itself does not state this as a conclusion. The other refs in the article clearly state that the earth is slowing. --Kvng (talk) 14:38, 6 May 2012 (UTC)
- I have reinstated the previous version. If you look at the next reference in the artcile, you will see that it incorporates the results quoted in the first reference exactly. I reverted the statement concerning UNIX because the article on UNIX supports the assertion that UNIX does not handle leap seconds. Martinvl (talk) 15:47, 6 May 2012 (UTC)
- The lead in Unix time is potentially misleading, "... the number of seconds elapsed since midnight Coordinated Universal Time (UTC), January 1, 1970, not counting leap seconds." Not counting leap seconds means that leap seconds are taken into account. The article body makes this clear. Feel free to rework the lead there to clarify. --Kvng (talk) 15:26, 7 May 2012 (UTC)
- Please add a quote to the citation that you think says that the earth is not slowing. Until I can see what you're seeing, I've marked what you've restored as unverified. --Kvng (talk) 15:26, 7 May 2012 (UTC)
- Hi Kvng,
- My reading of the the wording "not counting leap seconds" (backed up by almost every blog on the internet and heavily implied by the NASA site) is that UNIX time is 86400 seconds in length regardless of whether or nor that day has a leap second. It might be useful to remember that UNIX was first introduced in 1970, two years before the first leap second, so in order to maintain backward compatibility, UNIX time does not include leap seconds. There is of course nothing stoping you from writing a wrapper around the UNIX time-handling functions that takes into account leap seconds.
- I am about to reword the bit that I reinstateed. Sorry about the second reinstatement, I am being hounded by a banned editor, so that was nothing to do with you. Martinvl (talk) 16:39, 7 May 2012 (UTC)
- Be careful there. Yes, Unix time always moves forward exactly 86400 units per year. In years with a leap second it moves 86400 units in 86401 seconds. The last second of the day on which a leap second is scheduled is repeated. Unix time takes leap seconds into account because it knows when it needs to do this dance. This is what's described in Unix time. If you believe it works otherwise please only make the changes if you have reliable sources to back it up. --Kvng (talk) 20:26, 7 May 2012 (UTC)
- I appreciate that you've moved it from the lead but I have to insist that your assertion that the earth did not slow between 1735 to 1860 is original research. You've taken raw data from a primary source and drawn your own conclusion. This is not how we do things at WP and it is not good science. For any data set with enough of a random component I can select intervals that demonstrate any sort of trend I wish. --Kvng (talk) 20:26, 7 May 2012 (UTC)
- I do not believe what I have done to be OR. Last year I co-authored an essay Wikipedia:Using maps and similar sources in wikipedia articles on this topic and today I added a few comments based on this discussion. COul I invite you to contineu the discussion on the talk page of that essay. I have issued invitations to everybody else who contributed. Martinvl (talk) 07:14, 8 May 2012 (UTC)
- This might be a silly question, but how would they know if the earth slowed from 1735 to 1860. Weren't the most accurate clocks set/corrected by meridian circle, from the article "Prior to the invention of the atomic clock this was the most reliable source of accurate time". This means that by definition at these dates standard time would follow the rotation of the earth, so you are only saying "from 1735 to 1860 the rotation of the earth did not slow down compared to the otation of the earth", which is obviously true but meaningless. -- Q Chris (talk) 09:50, 8 May 2012 (UTC)
- This was back-calculated in about 1895 by checking records relating to movements of the planets, stars etc. If they could measure sunrise and sunset accurately to within say a second and relate an astronomical phenomena to that time, then this method is viable. Likewise, back-calculation to classical times was done from records relating to solar eclipses - eclipses that occurred in the "wrong" place could be explained by the slowing down of the earth. Does this help? Martinvl (talk) 10:09, 8 May 2012 (UTC)
- This might be a silly question, but how would they know if the earth slowed from 1735 to 1860. Weren't the most accurate clocks set/corrected by meridian circle, from the article "Prior to the invention of the atomic clock this was the most reliable source of accurate time". This means that by definition at these dates standard time would follow the rotation of the earth, so you are only saying "from 1735 to 1860 the rotation of the earth did not slow down compared to the otation of the earth", which is obviously true but meaningless. -- Q Chris (talk) 09:50, 8 May 2012 (UTC)
- I do not believe what I have done to be OR. Last year I co-authored an essay Wikipedia:Using maps and similar sources in wikipedia articles on this topic and today I added a few comments based on this discussion. COul I invite you to contineu the discussion on the talk page of that essay. I have issued invitations to everybody else who contributed. Martinvl (talk) 07:14, 8 May 2012 (UTC)
- Thanks, I understand now. What I am not sure about is how reliable the timing information would be at this time, if an expected time of an astronomical event happened a few seconds after the expected time would they have just put it down to their clocks being wrong rather than noting it? -- Q Chris (talk) 11:17, 8 May 2012 (UTC)
I can't answer Q Chris' question, but I can tell you where not to look. I found the various US Naval Observatory publications written by Simon Newcomb, who was deeply involved in this at the end of the 19th century. They are available in Google books. Those publications only show the result, not the calculations. Jc3s5h (talk) 11:47, 8 May 2012 (UTC)
- At risk of going off topic, I will respond to the last two questions:
- When the original readings were taken, they had not calculated the expected time - this was back-calculated a hunderd years later.
- The US Naval books catalogue formulae to calculate the time, but they do not say how they did it.
- I am a little ambivalent about Newcomb's calculations as they represent a discontinuity with eclipse observations. I can think of two reasons (both WP:OR, so I will not publish them in the article):
- Systematic error in Newcomb's calculations
- This corresponds with the Little Ice Age - so there could have been some phenomena which affected both the rate at which the earth slowed down and the climate.
- Martinvl (talk) 12:16, 8 May 2012 (UTC)
- Newcomb was barely aware that there might be variations in LOD. For purposes of calculations Newcomb, Brown, and others swept those into the so-called Great Empirical Term (GET, see plots in Newcomb (1909). The GET was shown to be due to LOD by Spencer Jones (1939) but its spectre persisted being discussed into the era when Ephemeris Time was being defined as seen in, e.g. Jackson (1952).Steven L Allen (talk) 19:22, 9 May 2012 (UTC)
Martinv, I read your essay and am unconvinced. I added some comments to Wikipedia talk:Using maps and similar sources in wikipedia articles. My original objection was that readers would walk away with the impression that the Earth is not slowing or that there is no scientific consensus that this is the general trend. That concern has been addressed. I think we can both expect diminishing returns by arguing this further. --Kvng (talk) 19:26, 8 May 2012 (UTC)
- I have to say that I agree. I am not an expert in this area, but it sounds to me like there are a lot of unknowns. I think this would be a really interesting PHD project for someone studying the history of Science/Astronomy, not just a conclusion that can be put in Wikipedia. -- Q Chris (talk) 20:12, 8 May 2012 (UTC)
Please do not use the data from the IERS page for conclusions. Those data came from Stephenson and Morrison (1984), very early in the effort to gather and process such observations. Much better is to find the data in Stephenson and Morrison(1995) and Morrison and Stephenson (2001). Before interpreting those it is good to read Stephenson (1997) and Morrison and Stephenson (2004).Steven L Allen (talk) 05:58, 9 May 2012 (UTC)
Martinv, your new Slowing down of the Earth section looks great. The issues I was concerned about have been addressed. The section is clear, informative and to the best of my knowledge, accurate. Kudos! --Kvng (talk) 15:10, 9 May 2012 (UTC)
- Thank you. Martinvl (talk) 15:39, 9 May 2012 (UTC)
- It seem odd not to mention the annual variation in LOD (which is hundreds of times larger than any earthquake might cause) and the decadal variations in LOD (which are thousands of times larger than any earthquake). Length of day variations correspond to weather in the atmosphere, oceans, and core.Steven L Allen (talk) 17:01, 9 May 2012 (UTC)
- Perhaps there is enough material concerning the existence, announcement, handling, and miss-handling of leap seconds in this article. So more extensive material on the mechanism of LOD variations could be placed at ΔT. Jc3s5h (talk) 17:11, 9 May 2012 (UTC)
- Agreed, but it remains odd that earthquakes merit mention when their effect has never been identified, whereas the LOD variation from a cold front that produces a newsworthy blizzard can be identified.Steven L Allen (talk) 17:22, 9 May 2012 (UTC)
- I have marked the section "Slowing down of the earth" as being a summary of the article ΔT. All that I need to do now is to ensure that the two articles align with each other and then see what needs doing in other articles that are of interst to me - Metric system, New SI definitions etc. Martinvl (talk) 19:21, 9 May 2012 (UTC)
- It is also odd to read that there was an acceleration in 1999 due to "unknown reasons" when
- the decadal variations have manifested as large fluctuations of LOD (both accelerations and decelerations) throughout observed history
- there exists the Special Bureau for the Core of the IERS Global Geophysical Fluids Centre whose main page shows plots of many papers which have good correlations between geomagnetic fluid measurements and LOD variations Steven L Allen (talk) 19:34, 9 May 2012 (UTC)
- It is also odd to read that there was an acceleration in 1999 due to "unknown reasons" when
- I have marked the section "Slowing down of the earth" as being a summary of the article ΔT. All that I need to do now is to ensure that the two articles align with each other and then see what needs doing in other articles that are of interst to me - Metric system, New SI definitions etc. Martinvl (talk) 19:21, 9 May 2012 (UTC)
- Agreed, but it remains odd that earthquakes merit mention when their effect has never been identified, whereas the LOD variation from a cold front that produces a newsworthy blizzard can be identified.Steven L Allen (talk) 17:22, 9 May 2012 (UTC)
- Perhaps there is enough material concerning the existence, announcement, handling, and miss-handling of leap seconds in this article. So more extensive material on the mechanism of LOD variations could be placed at ΔT. Jc3s5h (talk) 17:11, 9 May 2012 (UTC)
- It seem odd not to mention the annual variation in LOD (which is hundreds of times larger than any earthquake might cause) and the decadal variations in LOD (which are thousands of times larger than any earthquake). Length of day variations correspond to weather in the atmosphere, oceans, and core.Steven L Allen (talk) 17:01, 9 May 2012 (UTC)
Revocation of 23 May 2012
I removed the statement "The lengthening of the day length by about 1.7 microseconds per century is an increasing factor, but will only be responsible for 1 leap second in the next 3200 years" as it is technically incorrect - it is 1.7 milliseconds, not 1.7 microseconds - the two differ by a factor of 1000! Martinvl (talk) 16:22, 23 May 2012 (UTC)
Removed confusing example
- Moved the following comment from Talk:ΔT where it was inadvertently placed. — Joe Kress (talk) 21:23, 25 May 2012 (UTC)
I removed this example since it seemed to be more confusing than helpful:
- For example, suppose an atomic clock is used to count seconds from the Unix epoch of 00:00:00 on January 1, 1970. UTC and mean solar time (UT1) were almost identical at that time. After Earth makes one full rotation with respect to the mean Sun, the counter will register 86400.002 seconds (once again, the precise value will vary). Based on the counter, and assuming that a day is 24×60×60 = 86400 seconds long, the date will be calculated as 00:00:00.002 January 2, 1970. After 500 rotations, it will be 00:00:00 May 16, 1971 in solar time (UT1), but the counter will register 43,200,001 atomic seconds. Since 86400 × 500 is 43,200,000 seconds, the date will be calculated as 00:00:01 on May 16, 1971, as measured by atomic time. If a leap second had been added on December 31, 1970, then the date would be computed as 00:00:00 on May 16, 1971.
One problem with this example is that a leap second could not have been added in December 31, 1970 because they were invented in 1972, and also were not needed since (according to the article) at that time UTC was using the same solar "second" as UT1 rather than the Si second. To make sense, the example should be changed to some date after 1972. Also, the paragraphs should specify "SI second" or "solar second" rather than "second" or "atomic second"; and "UT1 date", "UTC date", "TAi date" rather than "date" or "atomic time". Also the term "mean Sun" is unknown to the target reader. --Jorge Stolfi (talk) 03:41, 24 May 2012 (UTC)
Mean solar day before year 1000?
Was anyone before year 1000 aware that the length of solar days varied? What units could they have used to determine this? Without being able to measure or even be aware of any variation, they would have no use for a concept such as a mean solar day, and no means or reason to calculate any average. --JimWae (talk) 23:23, 24 May 2012 (UTC)
- According to the solar time article, Babylonians knew that fact several centuries BCE, and computed the mean solar time from the position of stars instead of the Sun. Star measurements were accurate enough for that, it seems. Thus the concept of mean solar day was already very old when al-Biruni defined the second as 1/86400 of it. --Jorge Stolfi (talk) 02:15, 25 May 2012 (UTC)
- I don't know the details, but McCarthy & Seidelmann (2009, p. 9) state
Ancient astronomers were quite aware of the fact that measuring time using the daily motion of the Sun did not result in a uniform time scale. The solution of the problem goes back at least to the time of Ptolemy, who was looking for a uniform time to construct tables of the motion of the Sun.
- See the "Further reading" section of the article for the full citation to the book. Jc3s5h (talk) 02:17, 25 May 2012 (UTC)
- I have added citations to both Ptolemy and al-Biruni. Ptolemy was well aware of the variable length of the solar day (± 30 s) although he could not measure it, because he could measure its accumulation throughout the year (± 17 min), the equation of time, which he describes in detail. See the equation of time section of Harry van Gent's Almagest Ephemeris Calculator. Virtually all of Ptolemy's calculations use the mean solar day. He only uses the true solar day when he has to convert old observations to his uniform time scale, which uses the mean solar day as its basic unit. — Joe Kress (talk) 22:01, 25 May 2012 (UTC)
Early metric system
It seems that the CGS was not the first metric system, nor the first to incorporate the second as unit of time. According to the metric system article, the first official metric system (France, 1799) included the metre and the gram as basic units but no unit of time. The second was apparently first included in a 1861 British proposal. The CGS system was developed over the next few years by physicists who were mainly concerned with electromagnetic units. --Jorge Stolfi (talk) 03:10, 25 May 2012 (UTC)
- "CGS" does not merely refer to a system of units, it refers to a
coherentconsistent system of units. In a coherent system, one may write equations such as E = mc2 or P = VI without any conversion factors. CGS is the first coherent system I'm aware of. (In the equations, E is energy, m is mass, c is the speed of light, P is power, V is voltage, and I is current, where the units are chosen from any coherent system of units.) Jc3s5h (talk) 11:08, 25 May 2012 (UTC) Revised 2 July 00:45 UTC.
- not 100% sure but I think the English Engineering Units system has coeherence too, abet with a different choice of Orthogonality for it's base units, resulting in a different set of derived units.. ie see little reason why lbF.ft ,can't notate energy in the same as N.m and J can in metric? Surely J is mearly a Canonical form for it's system. True BTU's may get used in in EEU and need conversion factors, but can't BTU be simply a name for a derived unit with scaling, much similar to the conversion factor of 10^3 needed to convert m3 to litres. --82.47.140.47 (talk) 22:40, 1 July 2012 (UTC)
- I used the wrong word, I should have used "consistent system of units". English engineering units are not consistent because it uses both pound-mass and pound-force. I'm not convinced there are any official names for these English/British systems; the government measurement agencies, scientific societies, and engineering societies generally prefer all those old systems just go away and have no interest in clarifying terminology for what they view as old junk. Jc3s5h (talk) 00:49, 2 July 2012 (UTC)
- First, the discussion was supposed to be about the *early* metric system, whose motivation was to simplify commerce and basic engineering, not science. Thus its original scope was standardizing only units for weights, distances, areas, and volumes. Time was not even thought of at first: while the traditional timing system used base 60 rather than 10, it was the same everywhere and therefore needed no standardization. The extension of the metric system to electromagnetism came much later, and for a while was the concern of physicists rather than engineers.
Second, the choice of the basic units -- M of mass, L of length, T of time, and Q of charge -- is immaterial for the "consistency problem"; the latter arises when choosing the defining equations for non-basic units like energy and voltage. For any such choices, one can make an equally "consistent" system whether one starts from metres+kilograms or centimetres+grams. In particular, E = mc^2 and P = VI need no constant factors in the MKS system either, while P = VI will work in CGS (where the unit of power is erg/sec = 100 nanowatts) only if you measure voltage and current in its obscure units (1 statampere = 0.334 nanoamperes or 1 abvolt = 10 nanovolts) instead of volts and amperes. Third, some equations will need constant factors anyway. Having defined the unit of area as a square meter, the area of a square is just A = s^2 but that of a circle is A = Pi*r^2. If we had chosen "round meter" as the unit of area, instead of square meter, the area of a circle would be A = r^2 while that of the square would be A = s^2/Pi. So the "consistency problem" is actually deciding which of several competing equations is "more important" and thus deserves to get the unit constant factor. --Jorge Stolfi (talk) 22:18, 4 July 2012 (UTC)
- First, the discussion was supposed to be about the *early* metric system, whose motivation was to simplify commerce and basic engineering, not science. Thus its original scope was standardizing only units for weights, distances, areas, and volumes. Time was not even thought of at first: while the traditional timing system used base 60 rather than 10, it was the same everywhere and therefore needed no standardization. The extension of the metric system to electromagnetism came much later, and for a while was the concern of physicists rather than engineers.
2012 Leap second for June 30
On the table of past leap seconds, an entry for June 30 2012 appears. However, June 30 2012 has not yet come, and this confuses the reader because it has been previously mentioned that leap seconds are random and not predictable.
I believe that occurences that have not yet happened should not be included, especially when the table is of "leap seconds to date", and it has been previously mentioned that future leap seconds are not predictable. — Preceding unsigned comment added by 121.75.123.244 (talk) 05:01, 14 June 2012 (UTC)
- Although leap seconds are unpredictable several years in the future, the IERS typically announces leap seconds six months in advance. Note that the table is entitled "Announced leap seconds to date", not "leap seconds to date". The leap second at the end of June 30, 2012 was announced January 5, 2012 via IERS Bulletin C 43. — Joe Kress (talk) 05:50, 14 June 2012 (UTC)
I removed the "Citations needed" tag
I removed the citations needed tag, since the article seems to have plenty of citations, and no {{cn}}" annotations. If anybody has a specific fact they would like cited, then please do say. Thue (talk) 13:17, 29 June 2012 (UTC)
What about 60 cycle 120 vac power that runs wall clocks?
What about 60 cycle 120 vac power? That runs wall clocks and is kept very accurate so they do not drift. Do they adjust the cycles on the last 24 hours or what? Wall clocks can not change quickly like a digitalbut there must be a way to adjust. Garylcamp (talk) 22:03, 29 June 2012 (UTC)
