Talk:Chamberlin trimetric projection
| This article is rated Start-class on Wikipedia's content assessment scale. It is of interest to the following WikiProjects: | ||||||||||||||
| ||||||||||||||
which center?
[edit]"Unlike triangulation on a plane where three such compass circles will intersect at a unique point, the compass circles from a sphere do not intersect precisely at a point. A small triangle is generated from the intersections, and the center of this triangle is calculated as the mapped point."
A general triangle has multiple "centers"; which one? —Tamfang (talk) 23:04, 8 March 2011 (UTC)
- According to the paper by Bretterbauer here, Chamberlin did not specify, since it was originally done by hand and eye. (Nor are they proper triangles since the edges are arcs, not line segments) --Belg4mit (talk) 01:42, 6 August 2011 (UTC)
Use for Dymaxion map
[edit]Unless I'm misunderstanding something, this projection is the basis for the Dymaxion map - which divides the world into 20 equilateral triangles, and the Chamberlin trimetric is used to model each triangle (with the vertices as the three points of projection). Shouldn't this be mentioned in one or both places? 87.194.176.188 (talk) 17:19, 2 July 2011 (UTC)
- Nope, the patent cited on the dymaxion map page clearly states the facets of the polyhedron are gnomonic projections. Both date to 1964 as well, so it would have been difficult (but not impossible) for one to inform the other. --Belg4mit (talk) 01:29, 6 August 2011 (UTC)
- Although you could use it, since it would be an appropriate scale i.e; the dymaxion icosahedron splits Africa onto two facets versus the single map given as an example on this page. _-Belg4mit (talk) 01:49, 6 August 2011 (UTC)
- The Dymaxion map patent does mention that some polyhedral map projections use the gnomonic projection. It also mentions the Mercator projection.
- However, the projection used in the Dymaxion map is *not* a gnomonic projection.
- When a polyhedral map projection uses the gnomonic projection, along the edges of any triangle, a mile of distance near the corners of that triangle are stretched out *more* inches of paper than a mile of distance near the midpoint of that triangle.
- the Dymaxion map patent clearly indicates that, along the edges of any triangle of the Dymaxion map, a mile of distance near the corners of that triangle is forced to cover the *same* inches of paper as a mile of distance near the midpoint of that triangle.
- --DavidCary (talk) 17:19, 30 August 2022 (UTC)
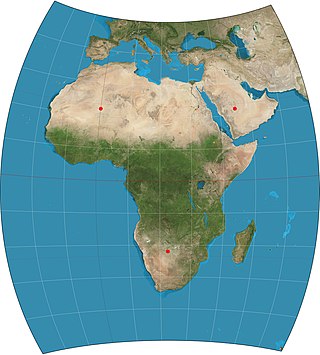
File:Chamberlin trimetric projection SW.jpg to appear as POTD soon
[edit]Hello! This is a note to let the editors of this article know that File:Chamberlin trimetric projection SW.jpg will be appearing as picture of the day on October 2, 2015. You can view and edit the POTD blurb at Template:POTD/2015-10-02. If this article needs any attention or maintenance, it would be preferable if that could be done before its appearance on the Main Page. Thanks! — Chris Woodrich (talk) 23:37, 14 September 2015 (UTC)
- Looks good to me, Chris Woodrich. Thanks! Strebe (talk) 08:17, 15 September 2015 (UTC)