Jump to content

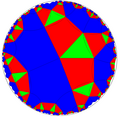
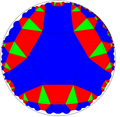
Quarter order-6 square tiling

Add links
From Wikipedia, the free encyclopedia
Quarter order-6 square tiling

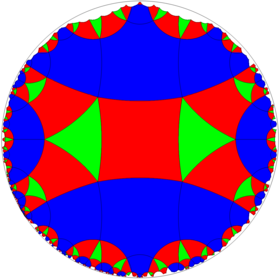Poincaré disk model of the hyperbolic plane
Type Hyperbolic uniform tiling
Vertex figure 3.4.6.6.4
Schläfli symbol q{4,6}
Coxeter diagram = = =
or or
or
Dual ?
Properties Vertex-transitive

In geometry, the quarter order-6 square tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of q{4,6}. It is constructed from *3232 orbifold notation, and can be seen as a half symmetry of *443 and *662, and quarter symmetry of *642.

Images

[edit]

Projections centered on a vertex, triangle and hexagon:

[edit]
Similar H2 tilings in *3232 symmetry
Coxeter
diagrams
Vertex
figure 		66 (3.4.3.4)2 3.4.6.6.4 6.4.6.4
Image
Dual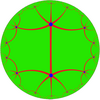
Uniform (4,4,3) tilings
Symmetry: [(4,4,3)] (*443) [(4,4,3)]+
(443) 		[(4,4,3+)]
(3*22) 		[(4,1+,4,3)]
(*3232)
h{6,4}
t0(4,4,3) 		h2{6,4}
t0,1(4,4,3) 		{4,6}1/2
t1(4,4,3) 		h2{6,4}
t1,2(4,4,3) 		h{6,4}
t2(4,4,3) 		r{6,4}1/2
t0,2(4,4,3) 		t{4,6}1/2
t0,1,2(4,4,3) 		s{4,6}1/2
s(4,4,3) 		hr{4,6}1/2
hr(4,3,4) 		h{4,6}1/2
h(4,3,4) 		q{4,6}
h1(4,3,4)
Uniform duals
V(3.4)4 V3.8.4.8 V(4.4)3 V3.8.4.8 V(3.4)4 V4.6.4.6 V6.8.8 V3.3.3.4.3.4 V(4.4.3)2 V66 V4.3.4.6.6

See also

[edit]

References

[edit]
  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
  • "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
[edit]
Retrieved from "https://en.wikipedia.org/w/index.php?title=Quarter_order-6_square_tiling&oldid=1189587281"