Girih tiles

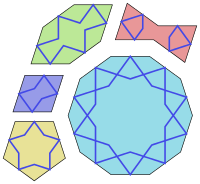
Girih tiles

Patterned Girih tiles

Construction lines are usually hidden: geometric tiles on left, girih pattern on right.

Girih tiles are a set of five tiles that were used in the creation of Islamic geometric patterns using strapwork (girih) for decoration of buildings in Islamic architecture. They have been used since about the year 1200 and their arrangements found significant improvement starting with the Darb-i Imam shrine in Isfahan in Iran built in 1453.

Five tiles

The five shapes of the tiles, and their Persian names, are:

Caption text

Name	Persian name	number of corners	convex	angle specifications
regular decagon	Tabl	10	yes	144°
elongated (irregular convex) hexagon	Shesh Band	6	yes	[ 72°, 144°, 144° ] ×2
bow tie (non-convex hexagon)	Sormeh Dan	6	no	[ 72°, 72°, 216° ] ×2
rhombus	Torange	4	yes	[ 72°, 108° ] ×2
regular pentagon	Pange	5	yes	108°

All sides of these figures have the same length, and all their angles are multiples of 36° (π/5 radians). All of them except the pentagon have bilateral (reflection) symmetry through two perpendicular lines. Some have additional symmetries. Specifically, the decagon has tenfold rotational symmetry (rotation by 36°); and the pentagon has fivefold rotational symmetry (rotation by 72°).

The emergence of girih tiles

By 11th century, the Islamic discovered a new way to construct the “tile mosaic” due to the development of arithmetic calculation and geometry—the girih tiles.

Girih

Main article: Girih

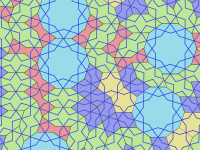
Girih are lines (strapwork) that decorate the tiles. The tiles are used to form girih patterns, from the Persian word گره, meaning "knot". In most cases, only the girih (and other minor decorations like flowers) are visible rather than the boundaries of the tiles themselves. The girih are piece-wise straight lines that cross the boundaries of the tiles at the center of an edge at 54° (3π/10 radians) to the edge. Two intersecting girih cross each edge of a tile. Most tiles have a unique pattern of girih inside the tile that are continuous and follow the symmetry of the tile. However, the decagon has two possible girih patterns one of which has only fivefold rather than tenfold rotational symmetry.

Mathematics of girih tilings

In 2007, the physicists Peter J. Lu and Paul J. Steinhardt suggested that girih tilings possess properties consistent with self-similar fractal quasicrystalline tilings such as Penrose tilings, predating them by five centuries.

This finding was supported both by analysis of patterns on surviving structures, and by examination of 15th-century Persian scrolls. There is no indication of how much more the architects may have known about the mathematics involved. It is generally believed that such designs were constructed by drafting zigzag outlines with only a straightedge and a compass. Templates found on scrolls such as the 97-foot (29.5 metres) long Topkapi Scroll may have been consulted. Found in the Topkapi Palace in Istanbul, the administrative center of the Ottoman Empire, and believed to date from the late 15th century, the scroll shows a succession of two- and three-dimensional geometric patterns. There is no text, but there is a grid pattern and color-coding used to highlight symmetries and distinguish three-dimensional projections. Drawings such as shown on this scroll would have served as pattern-books for the artisans who fabricated the tiles, and the shapes of the girih tiles dictated how they could be combined into large patterns. In this way, craftsmen could make highly complex designs without resorting to mathematics and without necessarily understanding their underlying principles.

This use of repeating patterns created from a limited number of geometric shapes available to craftsmen of the day is similar to the practice of contemporary European Gothic artisans. Designers of both styles were concerned with using their inventories of geometrical shapes to create the maximum diversity of forms. This demanded a skill and practice very different from mathematics.

Geometric construction of an interlocking decagram-polygon mosaic design

First, divide the right angle A into five parts of the same degree by creating four rays that start from A. Find an arbitrary point C on the second ray and drop perpendiculars from C to the sides of angle A counterclockwise. This step creates the rectangle ABCD along with four segments that each have an endpoint at A; other endpoints are the intersections of the four rays with the two sides of BC and DC of rectangle ABCD. Then, find the midpoint of the fourth segment created from the fourth ray point E. Construct an arc with center A and radius AE to intersect AB at point F and the second ray at point G. The second segment is now a part of the rectangle's diagonal. Make a line parallel to AD and passing through point G that intersects the first ray at point H and the third ray at point I. The line HF passes through point E and intersects the third ray at L and line AD at J. Construct a line passing through J that is parallel to the third ray. Also construct line EI and find M which is the intersection of this line with AD. From the point F make a parallel line to the third ray to meet the first ray at K. Construct segments GK, GL, and EM. Find the point N such that GI = IN by constructing a circle with center I and radius IG. Construct the line DN which is parallel to GK to intersect the line emanating from J, and find P to complete the regular pentagon EINPJ. Line DN meets the perpendicular bisector of AB at Q. From Q construct a line parallel to FK to intersect ray MI at R. As shown in the figure, using O which is the center of the rectangle ABCD as a center of rotation for 180°, one can make the fundamental region for the tiling.

An interlocking decagram-polygon mosaic design

An interlocking decagram-polygon mosaic design

An interlocking decagram-polygon mosaic design

An interlocking decagram-polygon mosaic design

Geometric construction of a tessellation from Mirza Akbar architectural scrolls

First, divide the right angle into five congruent angles. An arbitrary point P is selected on the first ray counterclockwise. For the radius of the circle inscribed in the decagram, one half of the segment created from the third ray, segment AM, is selected. The following figure illustrates a step-by-step compass-straightedge visual solution to the problem by the author. Note that the way to divide a right angle into five congruent angles is not a part of the instructions provided, because it is considered an elementary step for designers.

Step-by-step compass-straightedge construction of the tessellation

Examples

• Different patterns
• 
  Complex girih patterns with 16-, 10- and 8-point stars at different scales in ceiling of the Tomb of Hafez in Shiraz, 1935
• 
  A window of the crown prince's apartment in the Topkapı Palace, Istanbul, Turkey, with 6-point stars; the surrounds have floral arabesque tiling
• 
  Interior archway at the opening of the Sultan's Lodge in the Ottoman Green Mosque in Bursa, Turkey (1424), with 10-point stars and pentagons
• 
  Wooden screen from the Nishapur caravanserai

The girih has been widely applied on architecture. Girih on Persian geometric windows meet the requirements of Persian architecture. The specific types of embellishments utilized in orosi typically linked the windows to the patron's social and political eminence. The more ornate a window is, the higher social and economic status the owner is more likely to have. A good example of this is Azad Koliji, a Dowlatabad Garden in Iran . The girih patterns on its window successfully demonstrate multiple layers. The first layer would be the actual garden, of which people can have a glimpse when they open the window. Then there is the first girih pattern on the outside of the window, the carved pattern. Another artificial layer is represented by the colorful glass of the window, whose multicolored layers create the sense of a mass of flowers. This abstract layer forms a clear contradiction with the real layer outside the window, and gives the space for the imagination.

See also

• Aperiodic tiling
• Moorish architecture
• Penrose tiling
• Tadelakt
• Topkapı Scroll
• Zellij

External links

• Patterns in Arabic Architecture
• "Medieval Islamic architecture presages 20th century mathematics". Harvard University Gazette. 2007-02-22. Retrieved 2007-03-14.
• "Medieval Islamic tiling reveals mathematical savvy". New Scientist. 2007-02-22. Retrieved 2007-03-14.