Euler–Fokker genus

In music theory and tuning, an Euler–Fokker genus (plural: genera), named after Leonhard Euler and Adriaan Fokker,[1] is a musical scale in just intonation whose pitches can be expressed as products of some of the members of some multiset of generating prime factors. Powers of two are usually ignored, because of the way the human ear perceives octaves as equivalent.
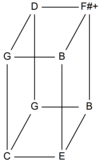
An x-dimensional tone-dimension contains x factors. "An Euler-Fokker genus with two dimensions may be represented in a two-dimensional (rectangular) tone-grid, one with three dimensions in a three-dimensional (block-shaped) tone-lattice. Euler-Fokker genera are characterized by a listing of the number of steps in each dimension. The number of steps is represented by a repeated mention of the dimension, so that there arise descriptions such as [3 3 5 5], [3 5 7], [3 3 5 5 7 7 11 11], etc."[1] For example, the multiset {3, 3, 7} yields the Euler–Fokker genus [3, 3, 7], which contains these pitches:
1
3 =3
7=7
3×3 =9
3×7=21
3×3×7=63
Normalized to fall within an octave, these become: 1/1, 9/8, 21/16, 3/2, 7/4, 63/32.
Euler genera are generated from the prime factors 3 and 5, whereas an Euler–Fokker genus can have factors of 7 or any higher prime number. The degree is the number of intervals which generate a genus. Alternatively [XXX...XYYY...Y], with x copies of X and y copies of Y, may also be notated [XxYy]. The degree is thus the sum of the exponents, and the number of pitches is obtained adding one to each exponent and then multiplying those ((x+1)×(y+1)=z).[2]
Adriaan Fokker wrote much of his music in Euler–Fokker genera expressed in 31-tone equal temperament. Alan Ridout also used Euler-Fokker genera.[2]
Complete contracted chord
[edit]The Euler–Fokker genus may also be called a complete contracted chord. Euler coined the term complete chord, while Fokker coined the entire term.[2]
A complete chord has two pitches, the fundamental and a guide tone, the guide tone being a multiple of the fundamental. In between are other pitches which can be seen either as multiples of the fundamental or as divisors of the guide tone (otonality and utonality). For example, given 1 as fundamental and choosing 15 as guide tone, one obtains: 1:3:5:15 (genus [35]). The quotient of the guide tone divided by the fundamental is the "tension number" or "exponens" (Euler: Exponens consonantiae).[2]
Erv Wilson created his own structures that overlap this territory called the "Combination Product sets" or CPS for short. These are formed by generating the products of a sets of factors which also including 1 as a member of the set as opposed to just a starting point. This led him to point out various uncentered structures like the Hexany, the Eikosany and the Hebdomekontany.
List of Euler genera
[edit]| Second degree | ||||||
|---|---|---|---|---|---|---|
| Genera | Notes | |||||
| 33 | 1/1 | 9/8 | 3/2 | |||
| 35 | 1/1 | 5/4 | 3/2 | 15/8 | ||
| 55 | 1/1 | 5/4 | 25/16 | |||
| Third degree | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Genera | Notes | |||||||||
| 333 | 1/1 | 9/8 | 3/2 | 27/16 | ||||||
| 335 | 1/1 | 9/8 | 5/4 | 45/32 | 3/2 | 15/8 | ||||
| 355 | 1/1 | 75/64 | 5/4 | 3/2 | 25/16 | 15/8 | ||||
| 555 | 1/1 | 5/4 | 25/16 | 125/64 | ||||||
| Fourth degree | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Genera | Notes | ||||||||||||||
| 3333 | 1/1 | 9/8 | 81/64 | 3/2 | 27/16 | ||||||||||
| 3335 | 1/1 | 135/128 | 9/8 | 5/4 | 45/32 | 3/2 | 27/16 | 15/8 | |||||||
| 3355 | 1/1 | 9/8 | 75/64 | 5/4 | 45/32 | 3/2 | 25/16 | 225/128 | 15/8 | ||||||
| 3555 | 1/1 | 75/64 | 5/4 | 375/256 | 3/2 | 25/16 | 15/8 | 125/64 | |||||||
| 5555 | 1/1 | 625/512 | 5/4 | 25/16 | 125/64 | ||||||||||
...
See also
[edit]References
[edit]- ^ a b Rasch, Rudolph (2000). Harry Partch, p.31-2. Dunn, David, ed. ISBN 978-90-5755-065-2.
- ^ a b c d "What is an Euler–Fokker genus?", Huygens-Fokker.org.
Further reading
[edit]- Franck Jedrzejewski (2006). Mathematical Theory of Music, p. 157. ISBN 978-2-7521-0023-8.