17 equal temperament
In music, 17 equal temperament is the tempered scale derived by dividing the octave into 17 equal steps (equal frequency ratios). Each step represents a frequency ratio of 17√2, or 70.6 cents.
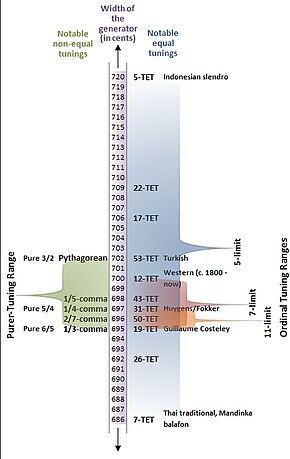
17-ET is the tuning of the regular diatonic tuning in which the tempered perfect fifth is equal to 705.88 cents, as shown in Figure 1 (look for the label "17-TET").
History and use
[edit]Alexander J. Ellis refers to a tuning of seventeen tones based on perfect fourths and fifths as the Arabic scale.[2] In the thirteenth century, Middle-Eastern musician Safi al-Din Urmawi developed a theoretical system of seventeen tones to describe Arabic and Persian music, although the tones were not equally spaced. This 17-tone system remained the primary theoretical system until the development of the quarter tone scale.[citation needed]
Notation
[edit]
Easley Blackwood Jr. created a notation system where sharps and flats raised/lowered 2 steps. This yields the chromatic scale:
- C, D♭, C♯, D, E♭, D♯, E, F, G♭, F♯, G, A♭, G♯, A, B♭, A♯, B, C
Quarter tone sharps and flats can also be used, yielding the following chromatic scale:
Interval size
[edit]Below are some intervals in 17 EDO compared to just.

| 17 EDO | |
| just | |
| 12 EDO |

interval name size
(steps)size
(cents)MIDI
audiojust
ratiojust
(cents)MIDI
audioerror octave 17 1200 2:1 1200 0 minor seventh 14 988.23 16:9 996.09 −7.77 harmonic seventh 14 988.23 7:4 968.83 +19.41 perfect fifth 10 705.88 3:2 701.96 +3.93 septimal tritone 8 564.71 7:5 582.51 −17.81 tridecimal narrow tritone 8 564.71 18:13 563.38 +1.32 undecimal super-fourth 8 564.71 11:8 551.32 +13.39 perfect fourth 7 494.12 4:3 498.04 −3.93 septimal major third 6 423.53 9:7 435.08 −11.55 undecimal major third 6 423.53 14:11 417.51 +6.02 major third 5 352.94 5:4 386.31 −33.37 tridecimal neutral third 5 352.94 16:13 359.47 −6.53 undecimal neutral third 5 352.94 11:9 347.41 +5.53 minor third 4 282.35 6:5 315.64 −33.29 tridecimal minor third 4 282.35 13:11 289.21 −6.86 septimal minor third 4 282.35 7:6 266.87 +15.48 septimal whole tone 3 211.76 8:7 231.17 −19.41 greater whole tone 3 211.76 9:8 203.91 +7.85 lesser whole tone 3 211.76 10:9 182.40 +29.36 neutral second, lesser undecimal 2 141.18 12:11 150.64 −9.46 greater tridecimal 2 / 3 -tone 2 141.18 13:12 138.57 +2.60 lesser tridecimal 2 / 3 -tone 2 141.18 14:13 128.30 +12.88 septimal diatonic semitone 2 141.18 15:14 119.44 +21.73 diatonic semitone 2 141.18 16:15 111.73 +29.45 septimal chromatic semitone 1 70.59 21:20 84.47 −13.88 chromatic semitone 1 70.59 25:24 70.67 −0.08
Relation to 34 EDO
[edit]17 EDO is where every other step in the 34 EDO scale is included, and the others are not accessible. Conversely 34 EDO is a subset of 17 EDO.
References
[edit]- ^ Milne, Sethares & Plamondon 2007, pp. 15–32.
- ^ Ellis, Alexander J. (1863). "On the Temperament of Musical Instruments with Fixed Tones", Proceedings of the Royal Society of London, vol. 13. (1863–1864), pp. 404–422.
- ^ Blackwood, Easley (Summer 1991). "Modes and Chord Progressions in Equal Tunings". Perspectives of New Music. 29 (2): 166–200 (175). doi:10.2307/833437. JSTOR 833437.
- ^ Milne, Sethares & Plamondon (2007), p. 29.
Sources
[edit]- Milne, Andrew; Sethares, William; Plamondon, James (Winter 2007). "Isomorphic controllers and dynamic tuning: Invariant fingering over a tuning continuum". Computer Music Journal. 31 (4): 15–32. doi:10.1162/comj.2007.31.4.15. S2CID 27906745 – via mitpressjournals.org.
External links
[edit]- "The 17-tone Puzzle — And the Neo-medieval Key that Unlocks It" by George Secor
- Libro y Programa Tonalismo, heptadecatonic system applications (in Spanish)
- Georg Hajdu's 1992 ICMC paper on the 17-tone piano project
- "Crocus", 17 equal temperament, 9 tone mode on YouTube, by Wongi Hwang

