Wikipedia talk:Requests for mediation/Monty Hall problem/Conditional probability solution
Problem
[edit][as in the article, i.e. with the quoted version from Parade and explanation that the usual analysis assumes the car is initially equally likely to be behind each door, that the host must open a door showing a goat, and that he must make the offer to switch - making a fully explicit version of the problem the K&W version]
Solutions
[edit]Simple solutions
[edit][as in the article, but we still need to talk about where "Aids to understanding" goes]
Conditional probability solution (draft 1)
[edit]The simple solutions show in various ways that a contestant who is going to switch will win the car with probability 2/3, and hence that switching is a winning strategy. Some sources, however, state that although the simple solutions give a correct numerical answer, they are incomplete or solve the wrong problem. These sources consider the question: given that the contestant has chosen Door 1 and given that the host has opened Door 3, revealing a goat, what is now the probability that the car is behind Door 2?
In particular, Morgan et al. (1991) state that many popular solutions are incomplete because they do not explicitly address their interpretation of vos Savant's rewording of Whitaker's original question (Seymann). The popular solutions correctly show that the probability of winning for a player who always switches is 2/3, but without additional reasoning this does not necessarily mean the probability of winning by switching is 2/3 given which door the player has chosen and which door the host opens. That probability is a conditional probability (Selvin 1975b; Morgan et al. 1991; Gillman 1992; Grinstead and Snell 2006:137; Gill 2009b). The difference is whether the analysis is of the average probability over all possible combinations of initial player choice and door the host opens, or of only one specific case—to be specific, the case where the player picks Door 1 and the host opens Door 3. Another way to express the difference is whether the player must decide to switch before the host opens a door, or is allowed to decide after seeing which door the host opens (Gillman 1992); either way, the player is interested in the probability of winning at the time they make their decision. Although the conditional and unconditional probabilities are both 2/3 for the problem statement with all details completely specified - in particular a completely random choice by the host of which door to open when he has a choice - the conditional probability may differ from the overall probability and the latter is not determined without a complete specification of the problem (Gill 2009b). However as long as the initial choice has probability 1/3 of being correct, it is never to the contestants' disadvantage to switch, as the conditional probability of winning by switching is always at least 1/2.
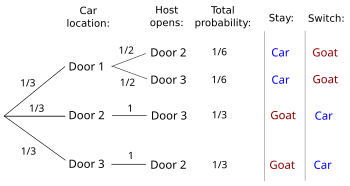
The conditional probability of winning by switching given which door the host opens can be determined referring to the expanded figure below, or to an equivalent decision tree as shown to the right (Chun 1991; Grinstead and Snell 2006:137-138), or formally derived as in the mathematical formulation section below. For example, the player wins if the host opens Door 3 and the player switches and the car is behind Door 2, and this has probability 1/3. The player loses if the host opens Door 3 and the player switches and the car is behind Door 1, and this has probability 1/6. These are the only possibilities given host opens Door 3 and player switches. The overall probability that the host opens Door 3 is their sum, and we convert the two probabilities just found to conditional probabilities by dividing them by their sum. Therefore, the conditional probability of winning by switching given the player picks Door 1 and the host opens Door 3 is (1/3)/(1/3 + 1/6), which is 2/3.
This analysis depends on the constraint in the explicit problem statement that the host chooses uniformly at random which door to open after the player has initially selected the car (1/6 = 1/2 * 1/3). If the host's choice to open Door 3 was made with probability q instead of probability 1/2, then the conditional probability of winning by switching becomes (1/3)/(1/3 + q * 1/3)). The extreme cases q=0, q=1 give conditional probabilities of 1 and 1/2 respectively; q=1/2 gives 2/3. If q is unknown then the conditional probability is unknown too, but still it is always at least 1/2 and on average, over the possible conditions, equal to the unconditional probability 2/3.
Mathematical formulation
[edit]The above solution may be formally proven using Bayes' theorem, similar to Gill, 2002, Henze, 1997, and many others. Different authors use different formal notations, but the one below may be regarded as typical. Consider the discrete random variables:
- : the number of the door hiding the Car,
- : the number of the door Selected by the player, and
- : the number of the door opened by the Host.
As the host's placement of the car is random, all values of C are equally likely. The initial (unconditional) probability of C is then
- , for every value of C.
Further, as the initial choice of the player is independent of the placement of the car, variables C and S are independent. Hence the conditional probability of C given S is
- , for every value of C and S.
The host's behavior is reflected by the values of the conditional probability of H given C and S:
-
if H = S, (the host cannot open the door picked by the player) if H = C, (the host cannot open a door with a car behind it) if S = C, (the two doors with no car are equally likely to be opened) if H C and S C, (there is only one door available to open)
The player can then use Bayes' rule to compute the probability of finding the car behind any door, after the initial selection and the host's opening of one. This is the conditional probability of C given H and S:
- ,
where the denominator is computed as the marginal probability
- .
Thus, if the player initially selects Door 1, and the host opens Door 3, the probability of winning by switching is
Notes
[edit]Discussion
[edit]Participants editing the section are requested to either: a) differentiate their edit through use of color font, or, b) propose the change in this section. Please use the "talking stick" approach to discussion. If you make a comment let other editors respond before commenting a second time. Keep comments brief and to the point. One of the mediators will moderate the discussion. Sunray (talk) 21:36, 7 October 2010 (UTC)
- I'll be moderating this discussion. I see that Glkanter, Gill110951, and Martin Hogbin have given substantive input. Are there any other views? Will Beback talk 07:11, 9 October 2010 (UTC)
- Are we "officially" focusing on this yet? I thought we were waiting a few more days for other input regarding what to focus on. -- Rick Block (talk) 21:01, 9 October 2010 (UTC)
Glkanter's comments
[edit]It's called the "Conditional solution section" in the MHP article. Anything that's not a solution to the MHP should be removed from this section. The 50/50 premise is listed as being part of The MHP at least 3 times in the article prior to this section. Any discussion of host behaviour when faced with 2 goats different than 50/50 is *not* the MHP and should be placed elsewhere in the article, perhaps in the 'Variants' section. This one issue comprises the entire section except for the paragraph supporting the decision tree.
This is what I propose, the decision tree and the narrative currently alongside of it. Nothing else seems pertinent.

The conditional probability of winning by switching given which door the host opens can be determined referring to the expanded figure below, or to an equivalent decision tree as shown to the right (Chun 1991; Grinstead and Snell 2006:137-138), or formally derived as in the mathematical formulation section below. For example, the player wins if the host opens Door 3 and the player switches and the car is behind Door 2, and this has probability 1/3. The player loses if the host opens Door 3 and the player switches and the car is behind Door 1, and this has probability 1/6. These are the only possibilities given host opens Door 3 and player switches. The overall probability that the host opens Door 3 is their sum, and we convert the two probabilities just found to conditional probabilities by dividing them by their sum. Therefore, the conditional probability of winning by switching given the player picks Door 1 and the host opens Door 3 is (1/3)/(1/3 + 1/6), which is 2/3.
Glkanter (talk) 21:52, 7 October 2010 (UTC)
Amazingly, that 2nd image with the images of 21 doors in this section was originally in the article as the visual aid for some OR paraphrasing of the simple solutions. It contains only the same 4 numeric values as the decision tree, and for various reasons is more of a distraction rather than any benefit. This is one of those times when 'less is more'. Glkanter (talk) 21:59, 7 October 2010 (UTC)
- Please revise the text above to make your proposal clear. You want to drop the formal mathematical section, right? And drop the expanded figure? Isn't Carlton a better reference for the decision tree, after all, his paper is available online.? And Grinstead and Snell give a different tree. Gill110951 (talk) 09:29, 8 October 2010 (UTC)
- I would like to see a reference to the argument by symmetry (Morgan et al, 1991b). Gill110951 (talk) 09:42, 8 October 2010 (UTC)
No, I haven't commented on the mathematical section. But if it relies on the 50/50 premise to come up with 2/3 and 1/3, I suppose Morgan's criticism would apply to it as well. I'm relatively agnostic about the decision tree. I'm much more focused on the unsupported/mis-attributed OR statements throughout the section. Here's the Morgan link you requested. Glkanter (talk) 10:03, 8 October 2010 (UTC)
- Thanks. Of course the formal mathematical computation uses 50/50 to get 2/3 and 1/3. It has to, as Morgan et al note, otherwise you don't get these numbers as the conditional probabilities. Gill110951 (talk) 16:58, 8 October 2010 (UTC)
Well, using the 50/50 premise, that the so-called "vos Savant scenario" did not make explicit, is why Morgan rejects the simple solutions, the decision tree, and by extension, the mathematical formulation as 'false'. It's peculiar that only the simple solutions are given the 'Morgan stigma' of being 'incomplete' (actually 'false'), in the Wikipedia article, despite Morgan's F6 solution explicitly being the decision tree, and the mathematical formulation having the exact same 'problem':
- "One must ask, however, how the probabilities for this sample space are determined. It turns out that this is a correct specification only if one assumes a certain strategy on the part of the host. We will show that the problem can be solved without any assumptions of this type, which is to say the problem can be solved."
Me, I see that inconsistent treatment of Morgan's criticisms as an NPOV violation. I guess others do not. Glkanter (talk) 17:17, 8 October 2010 (UTC)
I also see the 50/50 premise argument regarding Morgan's 'vos Savant scenario' as a moot point, given that the 50/50 premise is a part of the MHP presented in the Wikipedia article as best reflecting the reliable sources. Hence my argument that bringing the issue up in the Solutions sections is confusing, adds no value to the reader, and intentionally violates NPOV. Glkanter (talk) 17:23, 8 October 2010 (UTC)
Richard, do you like the way Morgan butchers Selvin's conversation with Monty in that link I just provided? It's consistent with the way they misquoted vos Savant's column in their original peer-reviewed paper, in order to improperly bolster their argument. Glkanter (talk) 17:30, 8 October 2010 (UTC)
Martin's comments
[edit]As this section makes some claim to present more 'correct' or rigorous solutions than are presented in the simple solutions section, it should start with:
- A clear and unambiguous statement of the problem it proposes to solve.
- A rationale for why this particular formulation of the MHP has been selected.
- A description of the philosophical approach to be used. Martin Hogbin (talk) 17:12, 8 October 2010 (UTC)
Rick's comments
[edit]Rather than simply delete the first two paragraphs (per Glkanter's suggestion) I think we should move most of this to a different section (not sure where yet) and craft a new paragraph introducing this section. To some extent, what I'd like this paragraph to say depends on how we resolve the placement of the "Aids to understanding" section. Assuming the "Conditional probability solution" comes immediately after the simple solutions (not separated by the lengthy "Aids to understanding" section) the point of the introductory paragraph would be to distinguish how a conditional probability solution differs from those that are presented immediately preceding. The content of the last paragraph (that introduces the variant where the host preference is a variable q rather than 1/2) is already covered in the "Variants" section. With these changes the "Conditional probability solution" section would look like this
Rick's suggestion
|
|---|
|
Conditional probability solution Another way to solve the problem is to treat it as a conditional probability problem (Selvin 1975b; Morgan et al. 1991; Gillman 1992; Carlton 2005; Grinstead and Snell 2006:137). With this approach the probability the car is behind any door can be analyzed both before and after the host opens a door. The probability the car is behind any one of the doors before the host opens a door is 1/3. Assuming the player picks Door 1 and the host then opens Door 3, the probability of winning by switching is the probability the car is behind Door 2 after the host opens Door 3. This is the conditional probability the car is behind Door 2 given the player initially picked Door 1 and the host opens Door 3, generally written:  This probability can be computed using Bayes' Theorem (see below), or directly from the figure below or a decision tree as shown to the right (Chun 1991; Grinstead and Snell 2006:137-138 presents an expanded tree showing all initial player picks). Referring to either the figure or the tree, in the cases the host opens Door 3, the car is behind Door 2 with probability 1/3 but is behind Door 1 with probability 1/6. The sum of these probabilities is 1/2, meaning the host opens Door 3 only 1/2 of the time. The conditional probability the car is behind Door 2 given the player has picked Door 1 and has seen the host open Door 3 is defined as the probability the car is behind Door 2 in the cases the host opens Door 3 (1/3) divided by the probability of all cases where the host opens Door 3 (1/2), therefore the conditional probability is (1/3)/(1/2)=2/3. The intuition behind this solution is that the host must always open Door 3 if the car is behind Door 2, but opens Door 3 only half the time the car is behind Door 1 - so a player who switches wins twice as often as a player who doesn't.
Mathematical formulation [as in the article] |
Some responses to comments from above:
- Why not use Carlton as a reference for the tree? Chun is the first source presenting a tree. Considerable effort has been spent on the sourcing of the article. One of the goals has been to use the first source making a particular point - hence, Chun (published in 1991), not Carlton (published in 2005).
- Why not drop the large figure? The figure is exactly equivalent to the tree diagram. Something like it was indeed originally introduced to illustrate the unconditional solution. The current version has many attributes that make it an effective illustration. In particular, the column widths within each row have the same proportion as their probability - so it is visually apparent that it is equally likely the host open door 2 or door 3, and that in each case it is twice as likely to win by switching vs. staying. I've changed the background in the cells that can't happen if the host opens door 3 to make it even more clear.
-- Rick Block (talk) 23:50, 9 October 2010 (UTC)
Kmhkmh's comment
[edit]Overall I'm ok with the current suggestion. I do however agree with one point that Martin has raised. We should avoid talking of a "correct solution of the MHP" without explicitly stating how the MHP is understood in this particular context. The same btw. applies to other chapters (like the simple solution) once we deal with them.--Kmhkmh (talk) 12:17, 10 October 2010 (UTC)
Richard's comment (Gill110951)
[edit]I too felt that the present text of this section was not bad at all. What was missing was a sound motivation for looking at the conditional probabilities. I would motivate that, by using the law of total probability to show that a player who only switches when the conditional probability that the car is behind the other door is at least 1/2 has the best overall success chance of all. I would next use symmetry to show that in the totally symmetric case, the door numbers don't give any new information, so always switching is the best you can do. I would then mention that if we don't know anything about host symmetry, but we do know there is symmetry in the location of the car, then one can still show using Bayes' theorem that always switching is the best one can do. Finally I would mention how MHP can be solved if you have no information at all: namely by making your initial choice completely at random and then switching. The text could look like this:
Richard's suggestion
|
|---|
|
Rick's comments on Richard's suggestion
[edit]Are you suggesting including this as an intro of sorts to the entire Solution section (before the Simple solutions), or in between the Simple solutions and Conditional probability solution sections, or maybe someplace else? If this were appropriately sourced, I think it (or something like it) might make a reasonable section following the Solution sections. But, before getting too far into exactly where, the first question is what source(s) would we use? -- Rick Block (talk) 00:28, 11 October 2010 (UTC)
- I realise there is a problem with reliably sourcing what I wrote there. In the long term I try to solve that problem by writing the reliable source myself. But I am looking for references, and I'll try to find good sources asap.
- Right now, I think the article should first present the simple solutions and then the more difficult conditional probability approach, in a clear and concise and neutral way. The general reader first has to be convinced that switching is smart. After that, some readers will be ready for a more sophisticated analysis. After both kinds have been presented it would make sense to give a discussion of pro's and con's preferably resulting in some kind of synthesis.
- The most simple solution of all, Monty Hall's, requires the least input: "initial choice has probability 1/3 of being right". And if you aren't prepared to take that premise on trust you can even force it to be true by your own action.
- If you want to know more, you must make more assumptions and do more work. We do need to give good motivation for studying conditional probabilities. For a subjectivist, all probabilities are conditional, they are conditional on all relevant information. (The circular definition of relevant is that information is relevant if it changes the probability in question!). But anyone should admit that the best decision to take might in principle depend on the specific doors chosen and opened. In order to investigate this, we do have to study the conditional probability that switching gives the car. In order to say something about it, we need to add further assumptions. In the standard MHP one learns what you might have already have guessed, namely that the specific door numbers are irrelevant. But the reader who has come so far is at last equipped to enjoy non-standard variants of MHP. Gill110951 (talk) 10:31, 11 October 2010 (UTC)
- I find your edit summary enlightening, Richard:
- "Richard agrees, this kind of stuff probably best later, and finding reliable sources still a problem"
- I interpret Wikipedia policy as 'starting with reliable sources is a requirement'. That's what the article are to represent, and that's what the talk pages are to sort out. It seems you have some other expectation of how to use the talk pages. I don't know why. Glkanter (talk) 11:07, 11 October 2010 (UTC)
- I find your edit summary enlightening, Richard:
- Finding reliable sources is a requirement on statements which otherwise could be disputed. Reliable sources are hardly needed as long as things are said which every reader (editor) finds completely obvious. That's what wikipedia guidelines say. If co-editors find what I say useful but feel reliable sources are needed, then they can help me look for them. If they don't find what I say useful or they don't understand, then I'm doing a bad job explaining or I should reconsider my opinions. I am looking for reliable sources myself, since I would like the article to reflect state-of-the-art understanding of MHP, so that it will have most value for most readers. I think this is especially important since looking at MHP from a higher level shows that the different points of view on MHP do not conflict with one another, at all. Gill110951 (talk) 12:32, 11 October 2010 (UTC)
Glkanter's response to Rick Block's Suggestion
[edit]I see a lot to like! I've read that the criticism of certain simple solutions is that they are indifferent to which door is open, rather than deciding before a door has been opened. Morgan says in their original paper:
- "Solution F5, like F1, is a true statement that answers a different problem. F5 is incorrect because it does not use the information in the number of the door shown."
and near the end of the article:
- "The unconditional problem is of interest too, for it evaluates the proportion of winners out of all games with the player following a switch strategy. It is instructive to express this as a mixture of the two conditional cases:
Then they give a formula reflecting door 2 being opened -or- door 3 being opened. Then in their rejoinder:
- "It could also have been mentioned that this means that which of the unchosen doors is shown is irrelevant, which is the basis for solving the unconditional problem as a response to the conditional one."
I still disagree strongly with using Selvin as a reference for why some sources sources say it is properly a conditional problem. Selvin made no such comment. He simply offered an alternative solution. I believe this is a full quote:
- "I have received a number of letters commenting on my "Letters to the Editor" in The American Statistician of February, 1975, entitled "A Problem in Probability." Several correspondents claim my answer is incorrect. The basis to my solution is that Monty Hall knows which box contains the keys and when he can open either of two boxes without exposing the keys, he chooses between them at random. An alternative solution to enumerating the mutually exclusive and equally likely outcomes is as follows:..."
That 2nd image is of dubious incremental value to the reader. I don't think the proportional column widths add that much clarity. Besides, in your words,:
- "The figure is exactly equivalent to the tree diagram".
Can you provide references for the explanations that follow the opening sentences in both paragraphs? Glkanter (talk) 17:26, 10 October 2010 (UTC)
Thinking about it, using Morgan to support the decision tree solution section in any way is inappropriate as well. They criticize the decision tree as false solution 6:
- "One must ask, however, how the probabilities for this sample space are determined. It turns out that this is a correct specification only if one assumes a certain strategy on the part of the host. We will show that the problem can be solved without any assumptions of this type, which is to say the problem can be solved."
Opting instead for:
- 2. CONCLUSIONS
- In general, we cannot answer the question "What is the probability of winning if I switch, given that I have been shown a goat behind door 3?" unless we either know the host's strategy or are Bayesians with a specified prior. Nevertheless, in the vos Savant scenario we can state that it is always better to switch. The fact that Pr(W | D3) >= 1/2, regardless of the host's strategy, is the key to the solution."
Which of course is all moot with the universally accepted 50/50 premise, anyways. Glkanter (talk) 19:06, 10 October 2010 (UTC)
- Some responses:
- re criticizing the simple solutions as being indifferent to which door is opened: I don't understand what your point is. The draft I've proposed doesn't say this, in fact doesn't criticize the simple solutions in any way (as far as I can tell). Are you suggesting this should be added?
- re citing Selvin: In the draft I've proposed, what is cited to Selvin is the sentence that says "Another way to solve the problem is to treat it as a conditional probability problem." This is nearly identical to Selvin's phrasing which you quote (and bold). I really don't see what the issue is.
- re the 2nd image: This is a matter of editorial preference. You want to delete it. I want to keep it. I suggest we have a focused discussion on this one subtopic if necessary. Is this necessary (i.e. are you insisting that it be deleted)?
- re references for the explanations that follow the opening sentences in each paragraph: The first paragraph is referenced to Selvin 1975b, Morgan et al. 1991, Gillman 1992, Carlton 2005, and Grinstead and Snell 2006. The second is referenced to Chun 1991 and Grinstead and Snell 2006. The wording in these paragraphs is not quotes from these sources by paraphrases what they say. Are you suggesting the wording misrepresents what these sources are saying? If so, what wording in particular are you objecting to?
- re using Morgan et al. to support the decision tree solution: This solution is in the second paragraph, which is not referenced to Morgan et al. I don't understand the issue.
I'm no expert on these things. It just seems that too few of the statements in your proposal are referenced. Then, the implication is that the sources given support the entire paragraph.
Morgan doesn't agree with the conditional solution you provide. I think its misleading to reference them at the start of the section, at least without their criticism ot the tree. Better to leave them out of this section.
I gave an example that contradicted the reference to [paraphrasing] 'before rather than after'. Glkanter (talk) 21:45, 10 October 2010 (UTC)
- Morgan doesn't agree with a conditional solution that assumes uniform random host choice between two goats to the "vos Savant scenario" (where the initial car placement is uniform and the host choice between two goats is unspecified). The "Problem" statement in the article makes it clear the problem the article is addressing is one where the host choice between two goats is specified to be random (thus, their objection doesn't pertain to this solution). Their objection to the unconditional solutions is entirely different, and still applies (per their rejoinder to vos Savant). Leaving this reference out of this section would be grossly negligent. It is one of the fundamental references to the MHP.
- By the "before rather than after" paraphrasing do you mean the sentence that says "With this approach the probability the car is behind any door can be analyzed both before and after the host opens a door."? This is talking about "conditional probability", which is linked in the previous sentence. Are you requesting a reference for this specific sentence? -- Rick Block (talk) 00:15, 11 October 2010 (UTC)
Rick, I'm gonna take a 'time out' on our discussion. Our versions seem *so* close. But the other editors are discussing much broader issues (that I thought had been resolved, or had never heard before.) Imma kick back and read what these other guys have to say for a little while, without my interference. Glkanter (talk) 00:41, 11 October 2010 (UTC)
Glkanter's response to Richard's suggestion.
[edit]I guess I have just 2 comments. Is that section sourced? Can it be sourced, or is that OR? Otherwise, how is such a lengthy discourse appropriate for a Wikipedia article's solution section for a simple, but confounding puzzle? Glkanter (talk) 20:02, 10 October 2010 (UTC)
- Comment: the total length of the coverage of the MHP need not be limited. The only concern is the relative amount of space devoted to individual sections and views. Per WP:NPOV, we should base decisions about weight on the amount of prominence in reliable secondary sources.
- Assuming sources are available, is the draft acceptable? How can it be improved? Will Beback talk 20:16, 10 October 2010 (UTC)
I am being polite when I refer to a 'lengthy discourse' The topics covered do not seem relevant to, or of an approriate level for the Wikipefia reader trying to find out if it's 50/50 or 2/3 & 1/3, and why, in a concise, readable manner. Glkanter (talk) 20:46, 10 October 2010 (UTC)
- What I wrote can be sourced. There's nothing original in it. It's all elementary commonplace statistical reasoning, you can find wikipedia articles supporting every step of the way. However since it seems to be above the head of the average wikipedia reader or editor this material doesn't belong "up front" in the article, if at all.
- Indeed, the average impatient and unsophisticated wikipedia reader wants to find out quickly and clearly whether it's 50:50 or 2/3, 1/3. But some wikipedia readers want to catch a glimpse of current professional and scientific activity on MHP. Some wikipedia readers will appreciate an attempt at synthesis. Some wikipedia readers are students following university courses on statistics and need a lot more depth and some intelligent discourse comparing the solutions, simple and complex.
- BTW, one of my "unpublished manuscript" was sollicited for, and is being published after peer review in, Springer's new encyclopedia of statistics. Another one will appear in the peer-reviewed journal Statistica Neerlandica; both can be found on arXiv.org, an eprint service which only accepts papers by accredited scientists. But though I use wikipedia to stimulate my OR, I don't use it to push my OR. Gill110951 (talk) 10:01, 12 October 2010 (UTC)
Mazel Tov, Richard! So, what are your thoughts specific to editing the Conditional solutions section? Glkanter (talk) 10:23, 12 October 2010 (UTC)
- Mazel Tov? Blood, sweat and tears, rather than good luck, I think. I think I gained a lot of understanding over the last year or so, participating in the fun here. Now I want to share what I learnt, with the world.
- Regarding the conditional section: I don't have strong feelings about it, one way or another. As long as it doesn't contain any nonsense I'm happy. In general I'm for "less is more", and keep it simple. I think the formal maths and the big picture with all the doors don't add to the decision tree and the little calculation. But if for some editors those items do help understanding, then they'll also help some readers. Gill110951 (talk) 13:09, 12 October 2010 (UTC)
More like 'Congratulations!' Glkanter (talk) 14:11, 12 October 2010 (UTC)
Weight
[edit]Could please editors comment on the length of this section? I count about 700 words, excluding the mathematical formulation (or about 1000 words with the formulas). By comparison, Rick's suggested text is about 360 words. The whole article is about 7100 words long, including the formulas. Will Beback talk 21:06, 10 October 2010 (UTC)
- Weight is a very tricky topic, and rather than get into it here I think it will be an entire topic of its own that we'll need to focus on at some point. As a preview, some other stats that are relevant are that the text related to the "simple" solutions is about 1500 words counting the existing "Aids to understanding" section or about 320 words counting only the text in the one subsection containing "simple" solutions proper. I think there are really two weight issues, i.e. weight of the presentation of the conditional solution(s) (as opposed to presentation of simple solutions) and weight of the criticisms of the simple solution. These are two different topics that are more or less combined in the current version of the article. My suggested text and Glkanter's suggestion both strip out the criticism from the section we're focusing on, leaving only the presentation of the conditional solution. With regard to this section, I think it's within our current focus to ask whether criticisms of simple solutions should be included in this section. -- Rick Block (talk) 23:43, 10 October 2010 (UTC)
- I think too much weight is given to this narrow academic approach to one formulation of the problem. It is of little interest to anyone except students of statistics, who have probably already come across this approach anyway. There is plenty more we can say about the MHP, as Richard has indicated. Martin Hogbin (talk)
- Let's please dispose of this canard right away. The "Conditional Probability" solution (sub)section as it is now discusses the problem at a level appropriate to high-school students exposed to a few formal introductory lesson on probability in much of the Western World - certainly in Italy, Canada and some parts of the USA. I know that for a fact because I have taught and written introductory material for students AND teachers at that level in all three countries. To say that it is a narrow academic approach which is of little interest to anyone except students of statistics strikes me as implying a rather demeaning opinion of the readers - as if it were Wikipedia's goal to be an encyclopedic reference for the unwashed masses only. glopk (talk) 15:29, 11 October 2010 (UTC)
- I think the whole article had got overweight. I disagree with Martin's suggestion that the conditional approach is "narrow" and "academic" and I hope we can present it so that it is crystal-clear and attractive. I like the compact texts proposed by several people now, I think they do the job pretty well. I hope we will also find ourselves able to write a sensible subsection on the situation that there is unknown host bias, building on the work done here. Not all sources, readers, or editors automatically use probability in the subjectivist sense, and probably for that reason, not all sources, readers, or editors find the conventional symmetry assumptions natural or implicit in vos Savant's question. After both simple and conditional solutions have been presented I would like to see a section which attempts a synthesis or comparison and which acknowledges the fact that different interpretations of probability have bearing on what assumptions are natural or not, and on what is the meaning of the conclusion. Jason Rosenhouse has a whole chapter on this. I recall that Martin once stated: anyone who thinks carefully about MHP is sooner or later forced to think about the meaning of probability. Gill110951 (talk) 15:25, 11 October 2010 (UTC)
- I think giving equal weight to both solutions (~300 words each not counting the "Aids to understanding" would be a good compromise), particularly as a unified solution section that would progress organically from one to the other. I'd move the "Aids" below this unified section, and the math formulation further below, as it was at the last FA. glopk (talk) 16:41, 11 October 2010 (UTC)
Martin's comments on suggestions
[edit]I understood the idea was to look a how we might edit the current 'Conditional' section rather than propose complete rewrites. For the current version and Rick's suggestion there can be no correct solution until we define the exact formulation that we are trying to solve and on what basis we are trying to solve it.
I would seem that both address the K & W formulation of the problem (or Selvin's final version). In this case we then need to say why we have taken the initial car placement, the player's initial door choice, and the host's goat-door choice to be uniform at random as Whitaker's question specifies none of this.
An alternative approach is given by Richard, who gives a more general discussion of ways in which the problem may be approached. Martin Hogbin (talk) 22:17, 10 October 2010 (UTC)
- Maybe the topic of 'why' those premises have become part of the 'MHP' belongs in the article somewhere, but not in any solutions section. Doesn't the intro already say something about vos Savant leaving a lot of loose ends?
- I don't agree that we need to delve into why the solutions differ in the solution sections. They all respond to the exact same problem (with the same premises), all get the same answer, all come from reliable sources. There's even some level of agreement that with the 50/50 premise, they're not a whole different. Each reader will find the solution that answers his interpretation (but not that the odds are 50/50). I see no problem addressing all the controversies subsequent to the solutions. Glkanter (talk) 22:32, 10 October 2010 (UTC)
- Isn't the exact formulation clear from context? It is what the "Problem" section says (uniform car placement and uniform host choice between two goats) and, under these assumptions, specifically P(car is behind Door 2|player picks Door 1 and host opens Door 3). The "Problem" section says what the usual interpretation is. Why this is the usual interpretation is not addressed. Are you aware of sources that address this point that we're overlooking? -- Rick Block (talk) 23:11, 10 October 2010 (UTC)
- To say that the he exact formulation should be clear from the context is not good enough for what claims to be a more correct solution, especially as the intro to the K&W formulation just states, 'A fully unambiguous...'. The conditional solution should make clear that it specifically addresses the K&W formulation given above, rather than Whitaker's question, which is also given above. In fact it might be a good idea to state that the conditional solution section specifically solves the problem of calculating P(car is behind Door 2|player picks Door 1 and host opens Door 3). This could save a lot of argument
- There are obviously no sources which tell us which problem formulation is addressed in a specific section of WP, it is up to us to make this clear. Martin Hogbin (talk) 10:13, 11 October 2010 (UTC)
- Martin says that if the conditional section is going to focus on the "standard problem", we need to say why *we* have taken the initial car placement, the player's initial door choice, and the host's goat-door choice all to be uniform at random. But the reason for us to do this on the wikipedia MHP page is easy: because many reliable sources do. Not many sources try to justify these assumptions by reference to the real world. Most sources either use the authority of other sources (who give no reasons) or say that the problem can't be solved without making such assumptions (which is manifestly untrue). A few sources say that the assumptions are already implicit in Whitaker/vos Savant's words. As I've said before, I think that these sources are using probability in a subjectivist sense. I think the article needs to discuss this question but separately from what can be done, given the assumptions.
- The sources are similarly very weak on *why* we should compute a conditional probability. Some people say Whitaker asks for one, but that is stretching my imagination. However, for a subjectivist all probabilities are conditional on all knowledge, which is the same by definition as conditional only on all relevant knowledge. For a subjectivist all probabilities are personal and can be determined by introspection. For the subjectivist there is one unique personal probability that switching will give him the car given all his information at the moment he must decide.
- But for an objectivist, probabilities are out there, and often they are not known. If the player doesn't know how the car is hidden before the show, and if he doesn't know how the host makes his choice, then he doesn't know the conditional probability. Fortunately, as Morgan et al. pointed out nearly 20 years ago, if you only know the car is hidden completely at random, then you do know that the conditional probabilities all support switching. If however you only know that you made your own choice completely at random then you can't say anything useful about the conditional probabilities. But you can still say that switching gives you the car with unconditional probability 2/3. You're not interested in the conditional probability since you don't know anything about it.
- It's amusing that the subjectivist knows the conditional probability is 2/3 for precisely the same reason that the objectivist can't say what it is: because they both know nothing.
- For most reliable sources, MHP is solution driven science. They have a solution method and they want to use it. For instance, they are teaching conditional probability and they want to use MHP to illustrate it. They can't use their favourite tool without adding to vos Savant's story. *Everyone* adds something. Carpenters everywhere see nails which need to be hammered in. On wikipedia we want to get an overview of the solutions out there. We can leave this diversity as it is, a mess, or we can try to develop some understanding of its origin. Why do some sources find certain assumptions implicit in vos Savant's words? Why do some sources find it obvious that Whitaker is asking for a conditional probability? I find these questions fascinating, and for my own research on MHP, and because I often talk about MHP both to specialists and to lay persons, I am daily confronted with them, and driven to study them. Gill110951 (talk) 13:19, 11 October 2010 (UTC)
- So how are we going to achieve consensus on this section? Are we closer? Will Beback talk 05:16, 13 October 2010 (UTC)
- I cannot see we are any closer to consensus at the moment, mainly because there seem to be different understandings of what we are trying to do. I understood that the plan was to collaboratively edit the current section but others seem to prefer complete rewrites or expanding the section to include wider approaches to the problem. What is your suggestion as to how we should approach the problem? Martin Hogbin (talk) 09:18, 13 October 2010 (UTC)
- I suggest that we find some text to which you and the editors can agree. Could you please draft a version that you think would be acceptable to all, even to the other side? Will Beback talk 09:24, 13 October 2010 (UTC)
- OK, I will start with Rick's suggestion as may people seem to like that. Martin Hogbin (talk) 10:13, 13 October 2010 (UTC)
- I suggest that we find some text to which you and the editors can agree. Could you please draft a version that you think would be acceptable to all, even to the other side? Will Beback talk 09:24, 13 October 2010 (UTC)
Martin's version of Rick's suggestion
[edit]Conditional probability solution
[edit]Another way to solve the problem is to treat it as a conditional probability problem Conditional probability can be used to solve the Monty hall problem (Selvin 1975b; Morgan et al. 1991; Gillman 1992; Carlton 2005; Grinstead and Snell 2006:137). Consider the mathematically explicit version of the problem given above . With this approach The probability the car is behind any door can be analyzed both before and after the host opens a door. The probability the car is behind any one of the doors before the host opens a door is 1/3. Assuming the player picks Door 1 and the host then opens Door 3, the probability of winning by switching is the probability the car is behind Door 2 after the host opens Door 3. This is the conditional probability the car is behind Door 2 given the player initially picked Door 1 and given the condition that the host opens Door 3, generally written:

This probability can be computed using Bayes' Theorem (see below), or directly from the figure below or a decision tree as shown to the right (Chun 1991; Grinstead and Snell 2006:137-138 presents an expanded tree showing all initial player picks). Referring to either the figure or the tree, in the cases the case that the host opens Door 3, and the car is behind Door 2 with has probability 1/3 but the case that the host opens Door 3, and the car is behind Door 1 with has probability 1/6. The sum of these probabilities is 1/2, meaning as the host opens Door 3 only 1/2 half of the time. The conditional probability the car is behind Door 2 given the player has picked Door 1 and has seen the host opens Door 3 is defined as the probability the car is behind Door 2 in the cases the host opens Door 3 (1/3) divided by the probability of all cases where the host opens Door 3 (1/2), therefore the conditional probability is (1/3)/(1/2)=2/3. The intuition behind this solution is that the host must always open Door 3 if the car is behind Door 2, but opens Door 3 only half the time the car is behind Door 1 - so a player who switches wins twice as often as a player who doesn't.
Richard proposes: The reason the relative probabilities that the car is behind Door 2 and Door 1 change on the host opening Door 3 and revealing a goat is because the chance that Door 3 is opened given the car is behind Door 2 is twice as large as the chance that Door 3 is opened given the car is behind Door 1. The initially equal odds of 1:1 for Door 2 versus Door 1 are shifted to unequal odds of 2:1, and Door 3 is excluded. We already saw in the section "Simple solutions" that the player who switches wins twice as often as the player who doesn't. The "conditional solution" shows that this is also true for any of the six particular cases of "door initially chosen, door open by host", for instance, Door 1 and Door 3 as named in Whitaker's question.
Glopk's comment
[edit]@Martin, can you please add a paragraph or two describing the rationale for this change w.r.t Rick Block's version? So far I can only see a shortening that hampers readability, see for example the first sentence: are you arguing that using conditional probability to solve the problem is not the same as treating the problem as a conditional probability one? glopk (talk) 22:53, 13 October 2010 (UTC)
- See my replies to Rick's questions. The first sentence seemed to me to say the same thing twice, there is no hidden message. Martin Hogbin (talk) 16:39, 14 October 2010 (UTC)
Rick's comments
[edit]I've added markup so the differences are apparent. Why delete references? Why destroy the parallel before/after wording that matches the description of what conditional probability can do? Why delete the sentence providing the intuition behind this solution? These all seem to make the wording less clear and less readable.
Adding a reference to the explicit problem definition seems fine, but I'd put it after the "can be analyzed" sentence. The other changes are simply mysterious to me. -- Rick Block (talk) 00:37, 14 October 2010 (UTC)
- Thanks for the markup.
- Two references are plenty, there is no need for any more, it fact it always makes it look more contentious to have a string of references. -- Martin
- Disagree, and this is a rather strange way to go about NPOV and giving due weight: "plenty"? "more contentious"? What are you talking about?glopk (talk) 19:39, 14 October 2010 (UTC)
- I am talking about writing an encyclopedia. We have agreed that the statement should be in the article, we need to provide support from a reliable source (or two) for the reader. Arguments here should not spill over onto the article. Martin Hogbin (talk) 09:00, 15 October 2010 (UTC)
- Disagree, and this is a rather strange way to go about NPOV and giving due weight: "plenty"? "more contentious"? What are you talking about?glopk (talk) 19:39, 14 October 2010 (UTC)
- As has been pointed out before, it is not whether the player decides before or after the door has been opened by the host that determines whether the problem is conditional. The player may know that the host will open a specific door before it is opened, on the other hand the player may not actually notice the door number after it has been opened. If the opening of door 3 is given as a condition in the problem statement (taken to be one) the the problem is conditional otherwise it is not. -- Martin
- Yes, "it" has been pointed out before, by yourself, and it has been refuted, by myself. What makes the problem conditional is that a probability value of winning by switching is computed for a particular initial door selection and host door selection, therefore after the host opens a door. Without these givens one can only computed marginal probabilities (as the simple solutions do), therefore not answering the actual problem. The two sentences above "The player may know that the host will open a specific door before it is opened, on the other hand the player may not actually notice the door number after it has been opened" are irrelevant, since we are talking within the K&W statement.glopk (talk) 19:39, 14 October 2010 (UTC)
- Hold it a moment, Glopk, it is a matter of opinion that "to answer the actual problem" requires computing a conditional probability. I admit that there are plenty of sources who state that this is the case, but there are plenty of others who disagree. I did not yet find a source who gave a good reason why you *must* compute the conditional probability (I know some good reasons, but I don't find them in any source, except ones written by me!). What makes the problem conditional is the choice to treat it as such. One can compute marginal probabilities at any time. Who says the player has to take notice of the door numbers? If the K&W conditions hold the smart player will realise in advance that the actual door numbers are irrelevant to making the best decision, by symmetry. Gill110951 (talk) 20:29, 14 October 2010 (UTC)
- OK, let's avoid drifting. Specifically let's table (for now) the issue of whether simple solutions address the actual problem. We are discussing about the first sentence of this section, and specifically whether Rick's text is preferable to the one revised by Martin. Do you agree that the cited sources treat the problem as a conditional probability one (because they choose to do so, to use your point)? (yes/no) If yes, do you agree that saying that is preferable to just saying, as Martin's version does, simply that cpnditional probability can be used to solve the problem? Next, can you please comment on which version is more readable? glopk (talk) 00:02, 15 October 2010 (UTC)
- English usage note. To 'table' a subject in UK English means to agree to discuss it now. In US English it means to agree not to discuss it now. I guess you are using it in the US sense. Martin Hogbin (talk) 09:05, 15 October 2010 (UTC)
- I suggest we use "park" (this does mean the same thing in both UK and US English, right?). -- Rick Block (talk) 14:23, 15 October 2010 (UTC)
- English usage note. To 'table' a subject in UK English means to agree to discuss it now. In US English it means to agree not to discuss it now. I guess you are using it in the US sense. Martin Hogbin (talk) 09:05, 15 October 2010 (UTC)
- Specifically, I thought we were talking about whether
- OK, let's avoid drifting. Specifically let's table (for now) the issue of whether simple solutions address the actual problem. We are discussing about the first sentence of this section, and specifically whether Rick's text is preferable to the one revised by Martin. Do you agree that the cited sources treat the problem as a conditional probability one (because they choose to do so, to use your point)? (yes/no) If yes, do you agree that saying that is preferable to just saying, as Martin's version does, simply that cpnditional probability can be used to solve the problem? Next, can you please comment on which version is more readable? glopk (talk) 00:02, 15 October 2010 (UTC)
- Assuming the player picks Door 1 and the host then opens Door 3, the probability of winning by switching is the probability the car is behind Door 2 after the host opens Door 3. This is the conditional probability the car is behind Door 2 given the player initially picked Door 1 and the host opens Door 3, generally written:
- or
- Assuming the player picks Door 1 and the host then opens Door 3, the probability of winning by switching is the probability the car is behind Door 2 given the condition that the host opens Door 3, generally written:
- is more readable. Since we're introducing this by saying conditional probability allows one to compute probabilities before and after the host opens a door, and that the probability of each door before the host opens a door is 1/3, it seems to me that switching to "given" terminology here without saying what this terminology means is likely to be confusing. Note that dropping "With this approach" only leaves it implied that conditional probability is what makes it possible to analyze both the before and after probabilities. Here as well, I think it's better to be explicit. Whatever argument you use, if you're talking about prior and conditional posterior probabilities (which is what you're doing if you're going to say the "probability" of the door the host opens is 0 and the probability of the door you're considering switching to is 2/3) you're using conditional probability. -- Rick Block (talk) 01:47, 15 October 2010 (UTC)
The intuition statement seems to me to be pure speculation, where did it come from? -- Martin
- Which intuition statement? Gill110951 (talk) 20:29, 14 October 2010 (UTC)
- My version is the odds form of the conditional argument and should probably have its own reference (like Rosenthal). -- Rick Block (talk) 01:47, 15 October 2010 (UTC)
Richard's comments
[edit]I think that one challenge to composing and to comprehending this passage is the difference in status between the two "given"s: player chose door 1, host opened door 3. The decision tree fixes the player's initial choice. The computed probability of one half is the probability the host will open door 3 given the player chose door 1. Sometimes "given player chose door 1" is written out explicitly, sometimes not. This always confuses me, reading all versions of this section. I somehow think this is more important than the issues of nuance and citation.
I do think there are good reasons that Martin deleted the last sentence on the intuition. It's a fact that the host would open door 3 with probability 1 if the car is behind door 2 but only with probability 1/2 if the car is behind door 1. That fact is the underlying reason why the probability the car is behind door 2 changes after seeing the host open door 3. From the odds form of Bayes' theorem we see it explicitly: even prior odds 1:1 are shifted to uneven posterior odds (equal to the ratio of the just mentioned probabilities) 1:1/2, i.e., 2:1.
The last part of the last sentence on intuition seems just to be repeating the unconditional solution, repeating something we already know. It doesn't add intuition why the conditional result should be the same as the unconditional result. The intuitive reason (and also the true underlying reason) is symmetry: the specific door numbers are irrelevant. The result of the conditional probability computation is that the chance a switcher wins is not influenced by the specific door-numbers of any particular case, provided we assume equal probabilities all over the place (symmetry). Maybe that should be made explicit. The final sentence could be:
- "Not only is it the case that overall, a switcher wins the car twice as often as a stayer, but this is also the case, on those occasions when the player chose door 1 and the host opened door 3".
Gill110951 (talk) 09:42, 14 October 2010 (UTC)
- Regarding the difference in status between the two givens, although some sources presenting conditional solutions present all 9 combinations of initial car location and player pick, I believe most don't (1 or 2 do, dozens don't). We could argue about which approach might be better, but I think the main goal here is to be faithful to the preponderance of sources. Since they omit discussion of this, I think most sources are thinking it's essentially obvious that P(car is behind Door 2) and P(car is behind Door 2|Player picks Door 1) are the same and that both are 1/3. These are indeed potentially different - but there isn't any source I know of that makes a big point out of this. To do so in the article would therefore be undue weight. -- Rick Block (talk) 02:26, 15 October 2010 (UTC)
- Yes, but that wasn't the point I was making. I was confused, while reading the draft, by the fact that sometimes the "given the player chose Door 1" is written out explicitly, as in the displayed mathematics formula, and sometimes not. For instance, the text said that the host opens Door 3 with probability 1/2. Well: given the player chose 1, this event has probability 1/2, but if the initial choice is not fixed (and if it is uniform random) then the probability that Door 3 is opened is 1/3. I would have helped me if the text said that the probability the host opens Door 3 given the player chose 1 is 1/2. Gill110951 (talk) 10:50, 15 October 2010 (UTC)
- Regarding the last sentence, perhaps a better wording might be "A more intuitive form of a conditional solution is that since the host must always open Door 3 if the car is behind Door 2, but opens Door 3 only half the time the car is behind Door 1, a player who switches wins twice as often as a player who doesn't [Rosenthal]." The symmetry intuition is something entirely different. I think it more properly belongs in the "simple" solution sections as a connection between the simple solution and the conditional problem that most people are no doubt thinking about (per wording I've suggested elsewhere - something like "assuming any specific case is like any other, this solution means a player who initially picks door 1 and sees the host open door 3 wins by switching with a probability 2/3"). I don't think this section needs to mention anything about symmetry. -- Rick Block (talk) 02:26, 15 October 2010 (UTC)
- No problem about moving symmetry. The symmetry business builds a bridge between conditional and simple solution, under the full "everything uniform random" assumptions. It doesn't matter where it is placed.
- Rick, I'd propose to replace your "a player who switches wins twice as often as a player who doesn't", which is the conclusion of the simple solution, which the reader already knows, with "a player who switches wins twice as often as a player who doesn't, whatever door was initially chosen by the player and whatever door was opened by the host". That's what the conditional argument gives us, and it gives us that, indeed, because of the ratio of the two conditional probabilities just mentioned. The simple argument already gave us 1/3 versus 2/3, unconditionally, essentially because you have the choice of Door 1 versus Door 2 + Door 3. The conditional argument gives us more!!! It tells us that "always switching" can't be beaten. Not only does "always switch" beat "always stay" (2/3 versus 1/3, overall), but 2/3 is the very best you can get. You can't do even better still by sometimes switching and sometimes not switching depending on the door numbers of your special case. This is where the conditional argument "beats" the unconditional argument. This is how we ought to be able to convince every reader that there is something to be gained, by spending a few moments thinking about conditional probabilities. Since we present the conditional solution after the simple solution we have an obligation to explain why we go to the trouble to do all this extra brain-challenging work. So far I have only seen arguments "by authority". They don't impress people who don't already think instincitively in terms of conditional probability. Gill110951 (talk) 10:50, 15 October 2010 (UTC)
I disagree that its our place to:
- "This is where the conditional argument "beats" the unconditional argument. This is how we ought to be able to convince every reader that there is something to be gained, by spending a few moments thinking about conditional probabilities."
That's a POV. Glkanter (talk) 11:51, 15 October 2010 (UTC)
It's a reliably sourced mathematical fact. But please distinguish between my proposed text, and my motivation for it. What's wrong with my proposal? That's a neutral observation, not a point of view. Gill110951 (talk) 13:31, 15 October 2010 (UTC)
- Not all reliable sources agree that one solution "beats" another, or that "there is something to be gained" by one solution over another. That is what I am referring to as a POV. Glkanter (talk) 15:10, 15 October 2010 (UTC)
- Your text is not what the sources presenting conditional solutions typically say, at least not that directly. They usually interpret the problem statement to be asking about the given example case, and provide a solution for this case. Since nothing in the analysis changes for any of the other 5 specific cases, it is perfectly true that the answer is the same regardless of which door the player picks and which door the host opens - but I think this is generally left as an unstated (but trivially obvious) fact. -- Rick Block (talk) 14:47, 15 October 2010 (UTC)
- + to Rick. Yes, regardless of which door she picks and which door the host opens. Gerhardvalentin (talk) 15:23, 15 October 2010 (UTC)
Gerhardvalentin's comments
[edit]Try to help new readers to understand what it's all about, separating the MHP from 'The MHP-example in teaching conditional probability theory'
Gerhardvalentin's suggestion
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Suggestion[edit]Try to help new readers to understand what it's all about, separating the MHP from 'The MHP-example in teaching conditional probability theory'

The host always can and will show a goat, and the question says that he just has shown a goat indeed and offered to switch to the second closed door.
We have no better evidence, and we are free to assume that, in showing a goat, the host will not give "better evidence" on the actual location of the car behind the two still closed doors: If the host (in 1/3) has got two goats to show, he will be opening each of his two doors uniformly at random, and by that we would have learned absolutely nothing to allow us to revise the odds on the door selected by the guest (Ruma Falk). But let's have a closer look on any possible relevant assumption that eventually could influence our actual point of knowledge for any single game. Only one permissible additional assumption should be mentioned here: variants of the procedural method of the host in showing a goat. Such variants have been discussed, considering that in any given game even better evidence on the actual location of the car behind the two still closed doors could be attained by the behaviour of the host in showing a goat. As said, by the procedural method of the host, who certainly cannot change the actual location of the car. Such variants never can advise however that in any single game "sticking" could ever be any better than to switch, because immutably on average Pws=2/3, and in every single game always varying around 2/3, from at least 1/2 (in 2/3 of games) to max. 1 (in 1/3 of games), as shown below per Falk. Namely, if the host in 1/3 has two goats to show, we admittedly could also take him to be biased to a certain extent, towards one special "preferred" door to open, and that we know about that bias (Falk). If we assume him to be extremely biased for example, he always will open only his preferred door whenever he can. The only time he would open his "unfavoured" and avoided door would be when in 1/3 the car was behind his preferred door. In that case it's still true that he always can and will show a goat. Yet, it is no more true that having opened "the door of his preference" in 2/3, "we've learned nothing to allow us to revise the odds on the door selected by the guest" (Falk). Considering that act, the probability that the car is hidden behind the door selected by the guest rises from l/3 to l/2 in that case (and never can be more), and the odds on the second still closed door now are 1/2 likewise (but never can be less). If however the host in 1/3 of games opens his unfavored door, we know for sure that the car is behind his preferred door (so actually Pws=1), and the probability that it is behind the door selected by the guest drops to zero (Falk):
Admittedly, although "logically correct", a host who eventually could give additional hints on the actual location of the car behind the two still closed doors is not provided for in the original question posed by Craig F. Whitaker, it's just a less important side aspect which of course anyone is free to ponder about, but we should pay regard to this variant because it shows that in each and every single game the actual Pws immutably has to be at least 1/2 or more, but never can be less, whatever door was opened by the host. And so it shows even more: that anyway nothing can ever be better than "always switching." Without using using Bayes, everyone - by a closer look - can plainly see that the immutable average Pws=2/3, whereas in each and every single game Pws will vary around 2/3, and (in max. 2/3) Pws can at worst be 1/2 , and never less (!), but (in the last 1/3) Pws "at worst" has to be 1. So in each and every single game – even assuming closest possible evidence on the actual situation concerning the present location of the car – Pws always is at least 1/2 or more. Whitaker's question "Is it to your advantage to switch your choice of doors?" asked for the decision whether you want to switch, and in any case the answer clearly has to be "yes". The question did not ask for any exact probability. Nevertheless the MHP is a favoured and useful example in teaching and learning conditional probability theory that just approves alike that nothing can ever be better than "always switching", and for that reason the answer to his question clearly should be "yes". Yes, conditional probability is really welcome in solving the MHP. It's qualified, easy and suitable and it can give us a lot of clear answers, too. On the other hand, no one could ever give real evidence that the "simple solution" - involving the evidently given obvious comprehension that Pws impossibly can ever be below 1/2, but in any single game has immutably to be at least 1/2 or greater, and also immutably 2/3 on average - that the simple solution was "out of position" to quote the fact that no other strategy ever can be better than always switching. Everyone can quote this fact, even without using Bayes. Gerhardvalentin Gerhardvalentin (talk) 15:52, 19 October 2010 (UTC) |
Discussion of Gerhardvalentin's suggestion
[edit]Gerhardvalentin, could you please describe how your version differs from the others, and why? In general, it'd be better if editors work towards a single draft rather than writing many individual ones. Will Beback talk 00:07, 15 October 2010 (UTC)
- Since this is basically an argument saying analyzing the problem using conditional probability is unnecessary and not a solution using conditional probability, I suggest we park discussion of it and consider its content for a later section. -- Rick Block (talk) 01:58, 15 October 2010 (UTC)
- Rick, why do you say so? You say "analyzing the problem using conditional probability is unnecessary and not a solution ..."? Who says so? Conditional probability is helpful, it's an easy aid to clearly show the result of the set parameters and implied underlying assumptions. So you should use it whenever it makes sense. But just not claim that it's the only correct way of "solving the MHP". Gerhardvalentin (talk) 20:13, 15 October 2010 (UTC)
- Thank you for your question, Will Beback. I just would be happy if the "unintuitive MHP" first could be presented in some manner that any new reader clearly can catch what it is all about, not just stumbling across the perceived conflict of dogma and authorities who claim their you have to agree, it is so because it is so-allegations. To avoid the article to present a textbook in conditional probability theory. And that, at least, reasonable underlying assumptions should clearly be shown when the dogma argues that the MHP cannot be solved but by conditional probability only, otherwise not. But presenting applied conditional probability as an easy aid to show the result of the set parameters and of the underlying assumption, and not anxiously hiding those implied assumptions and set parameters, arguing "because this is the only correct way to solve the MHP". Gerhardvalentin (talk) 19:57, 15 October 2010 (UTC)
The issues with Martin's version
[edit]The first sentence
[edit]- Another way to solve the problem is to treat it as a conditional probability problem.
- Conditional probability can be used to solve the Monty hall problem.
I believe that 2 is less dogmatic and more correct that 1. The difference to me is that 1 implies that the problem is one that can only be dealt with using conditional probability, I do not believe that it is ever possible to make such strong statements. Whatever the intended method of solving a problem it is always possible that there could be another way. Richard, for example, might argue that it is a game theory problem.
On the other hand,2 is undoubtedly true. Does anyone disagree with it? Does anyone feel the need to make a stronger point? Martin Hogbin (talk) 10:26, 15 October 2010 (UTC)
- I agree with both statements. I don't feel there is any hidden implication in 1 that the problem can only be dealt with this way. BTW I don't argue that MHP *is* a game theory problem. I only argue that game theory can be used to solve MHP. My own opinion is that the totality of different solutions gives much more insight than any one separately. Gill110951 (talk) 10:11, 15 October 2010 (UTC)
- Which wording do you prefer?
- My argument is that statements like, 'this is an geometry problem' are always wrong in mathematics. Better to say 'this is a problem that can be solved using geometry'.Martin Hogbin (talk) 10:26, 15 October 2010 (UTC)
- "Another way to way to solve the problem ..." in your mind means "The only way to solve the problem ..."? Seriously? I don't think #1 and #2 are semantically different and find it very curious that anyone thinks this is worth arguing about. -- Rick Block (talk) 13:56, 15 October 2010 (UTC)
- I guess it is a minor point. I am happy to go with the majority. Martin Hogbin (talk) 19:26, 15 October 2010 (UTC)
'After' vs 'given the condition'
[edit]- '...after the host opens Door 3. This is the conditional probability...'
- 'given the condition that the host opens Door 3'
I argue that 2 is technically more correct. The fact that the host has opened door 3 does not necessarily force this to be a condition of the problem. As Richard says, it is the choice of the person answering the question. Does anyone argue that 2 is incorrect? Martin Hogbin (talk) 10:26, 15 October 2010 (UTC)
- I would say that 2 is neutral, while 1 corresponds to the viewpoint of a Bayesian or subjectivist. They are both correct but they belong in slightly different contexts. The Bayesian thinks of the world as a continuously unrolling process as seen through his one pair of eyes, where all the time new information becomes available to the subject (observer), and all the time his probabilities (about unknown things, whether in the past or in the future) are updated according to the laws of probability, i.e., by Bayes' law. Initially he sees three closed doors and his information does not distinguish between them so he picks any one. *His* probability is 1/3 that the car is behind any of the three. Then the host opens a door revealing a goat and the player's personal probabilities change in order to take account of this new information. The player's subjective probability that the host would have opened the door he did if the car was behind the player's door is 1/2, but if it was behind the other door it's 1. The ratio 1/2:1 or 1:2 replaces the original odds of 1:1 between own door and other closed door. (Note that in this account, I nowhere mentioned the specific door numbers. I didn't, because they are irrelevant, but they can be added, but nothing changes). In conclusion: for a subjectivist, 1 is completely correct, since all probabilities are conditional on all presently available information and they change all the time as new information becomes available. 2 is more neutral: it does not presume a subjectivist understanding of probability. Gill110951 (talk) 11:15, 15 October 2010 (UTC)
- Distinguishing prior and posterior probabilities based on the occurrence of specific events is the entire point of conditional probability. The "given" terminology is specialized probability-jargon for "after" (actually not just "after" but "within the subset of possibilities that can exist after" - but I don't think we need to get overly technical here). The point of my original wording is to not necessarily assume the reader has any familiarity with the topic - it is basically defining the jargon word "given". #2 here uses this jargon word without giving any indication of what it means. All of the sources that are referenced in this section are interpreting "the probability" after the host has opened Door 3 to be the posterior (conditional) probability. #2 is not more neutral. It is simply less understandable to a non-specialist unfamiliar with the jargon. -- Rick Block (talk) 14:18, 15 October 2010 (UTC)
- "conditional on" and "given" are neutral technical terms for P(A | B) = P(A and B) / P(B) . The words "prior" and "posterior", with the implication of time ordering, and how your state of knowledge changes *after* getting new information, are specialist terms used inside Bayesian / subjectivist thinking. Bayesian theory is normative: it says how your SoK *must* be represented (with probability) and how it *must* be updated (with Bayes) on receipt of new info. But not everyone is a signed-up Bayesian. So I don't like "after". I prefer "on incorporating the information". Gill110951 (talk) 14:51, 15 October 2010 (UTC)
- As Richard says it is the revealing of information and the decision to incorporate it into the problem that makes a problem conditional not the time ordering of events. What is the objection to using a more neutral wording? Martin Hogbin (talk) 19:39, 15 October 2010 (UTC)
- I don't agree that it's more neutral - I think it's simply vague. Martin's wording changes (the change to the initial sentence, interjecting the reference to the problem statement before the sentence that talks about analyzing the probability before and after the host opens a door, dropping the "with this approach", and dropping the "after" terminology here) all serve to obscure the point, which is that conditional probability is precisely what enables you to analyze the difference between the situation before the host opens a door (at which point the probability is obviously 1/3) and the situation after the host opens a door (at which point the probabilities confusingly look to be 1/2, 1/2, and 0).
- Since you haven't objected to "the probability the car is behind any door can be analyzed both before and after the host opens a door" - I'm finding it odd that you're objecting to using "after" here. Can either of you suggest a wording in plain English without using jargon words? -- Rick Block (talk) 23:20, 15 October 2010 (UTC)
- The phrase "conditional on" is formal and technical, the word "given" is usually used as the plain language synonym. "What's the probability we'll still be at this a year from now, given we already spent so many years getting nowhere?" But I'm also happy with the time ordering picture as long as it is introduced properly. With a sentence like: "We study how the player's information about the location of the car is located changes, as he gains information from the host's actions". Gill110951 (talk) 07:15, 16 October 2010 (UTC)
- until now:
telepathy?No other evidence, at least. Regards, Gerhardvalentin (talk) 15:29, 16 October 2010 (UTC)
- until now:
- The phrase "conditional on" is formal and technical, the word "given" is usually used as the plain language synonym. "What's the probability we'll still be at this a year from now, given we already spent so many years getting nowhere?" But I'm also happy with the time ordering picture as long as it is introduced properly. With a sentence like: "We study how the player's information about the location of the car is located changes, as he gains information from the host's actions". Gill110951 (talk) 07:15, 16 October 2010 (UTC)
- Since you haven't objected to "the probability the car is behind any door can be analyzed both before and after the host opens a door" - I'm finding it odd that you're objecting to using "after" here. Can either of you suggest a wording in plain English without using jargon words? -- Rick Block (talk) 23:20, 15 October 2010 (UTC)
- I agree, 'given' is perfectly normal English word understandable to everybody in this context,as shown by Richard's example.
- I also like Richard's suggestion of explaining the situation more fully, although it is hard to make much of this in the standard case. There are two pieces of information potentially revealed when the host opens a door. The first is the obvious fact that the car is not behind the opened door. The second is the information potentially revealed about the probability the car is behind door 1. To talk about this here opens up the conflict that has been argued her for years, and I think is unlikely to be resolved now. It therefore seems to me that 'given' is the best way to go. Does anyone other than Rick have any objection to this? Martin Hogbin (talk) 10:12, 16 October 2010 (UTC)
- Pardon, don't jumble two different things: Finding the answer to Whitaker's question, and the technical terms in applying conditional probability theory.
The question can be solved and answered in many different ways, and only one narrow field is the use of conditional probability. It is okay to use it, but the problem discussed here does not address the answer to Whitaker's question, but only belongs to treating the problem using conditional probability. Gerhardvalentin (talk) 15:16, 16 October 2010 (UTC)
- Pardon, don't jumble two different things: Finding the answer to Whitaker's question, and the technical terms in applying conditional probability theory.
- I also like Richard's suggestion of explaining the situation more fully, although it is hard to make much of this in the standard case. There are two pieces of information potentially revealed when the host opens a door. The first is the obvious fact that the car is not behind the opened door. The second is the information potentially revealed about the probability the car is behind door 1. To talk about this here opens up the conflict that has been argued her for years, and I think is unlikely to be resolved now. It therefore seems to me that 'given' is the best way to go. Does anyone other than Rick have any objection to this? Martin Hogbin (talk) 10:12, 16 October 2010 (UTC)
- "Given", "prior", and "posterior" are ALL normal English words that have technical meanings (not coincidentally) related to their normal English meaning. I truly don't understand your objection is to saying in very plain English what the conditional probability corresponds to. Are you suggesting that the conditional probability is not modeling the temporal sequence (player picks, and then the host opens a door)? At least one source (Gillman) explicitly uses temporal wording to distinguish unconditional and conditional solutions: "This [vos Savant's solution] is an elegant proof, but it does not address the problem posed, in which the host has shown you a goat at #3. Instead it is still considering the possibility that the car is at #3-whence the host cannot have already opened that door (much less to reveal a goat). In this game-Game II-you have to announce before a door has been opened whether you plan to switch." [italics in the original]
- Since analyzing the differences in the situation before and after the host opens a door is the entire point or the problem, it seems to me using these words is the best way to go. Is there anyone other than Martin who objects to using the word "after"? -- Rick Block (talk) 15:37, 16 October 2010 (UTC)
- Before - After: What is it, besides a "technical aspect" in formulating conditional probability? This question has not been answered yet: "We study how the player's information about the odds on her door changes, as she gains information (?) from the host's actions". Without a clear answer to this question the article, including cited sources,
is worthlesshas a major shortcoming. Gerhardvalentin (talk) 16:07, 16 October 2010 (UTC)- Gerhard - are you disputing that the sources presenting conditional probability solutions are analyzing the probabilities in effect after the host has opened a door, specifically the case where the player initially picks door 1 and the host then opens door 3? I'm finding it very difficult to understand what your point is. -- Rick Block (talk) 16:41, 16 October 2010 (UTC)
- Before - After: What is it, besides a "technical aspect" in formulating conditional probability? This question has not been answered yet: "We study how the player's information about the odds on her door changes, as she gains information (?) from the host's actions". Without a clear answer to this question the article, including cited sources,
- Since analyzing the differences in the situation before and after the host opens a door is the entire point or the problem, it seems to me using these words is the best way to go. Is there anyone other than Martin who objects to using the word "after"? -- Rick Block (talk) 15:37, 16 October 2010 (UTC)
Yes, I have seen 'indifference to which door is opened' to explain the use of the simple solutions (but not the combining doors, that's apres door 3 has been opened). Which is equally likely to be the correct interpretation. Glkanter (talk) 15:52, 16 October 2010 (UTC)
- Glkanter - I have no idea what point you're making here. We're talking about the conditional solution section, not the simple solutions. Are you disputing that the conditional solution is analyzing the probabilities in effect after the host has opened a door? -- Rick Block (talk) 16:41, 16 October 2010 (UTC)
- 'After' is not a differentiator between simple and conditional per some sources. The phrasing 'this is the conditional problem' incorrectly makes it seem that it is. Glkanter (talk) 17:47, 16 October 2010 (UTC)
- Which sources? Are there any that in any way disagree that the probability the car is behind Door 2 after the host opens Door 3 is the conditional probability the car is behind Door 2 given the player initially picked Door 1 and the host opens Door 3, or conversely that the conditional probability is the probability after the host opens the door? Note that this doesn't say anything at all about what the simple solutions are or are not saying. We'll certainly talk about this eventually, but avoiding saying what the conditional probability is because it might make the simple solution look bad by comparison seems highly POV. -- Rick Block (talk) 20:39, 16 October 2010 (UTC)
- 'After' is not a differentiator between simple and conditional per some sources. The phrasing 'this is the conditional problem' incorrectly makes it seem that it is. Glkanter (talk) 17:47, 16 October 2010 (UTC)
- This section of the this talk page shows how Morgan phrases it. I disagree that avoiding saying [paraphrasing], 'before vs after differentiates the simple problem from the conditional problem' is a POV. I see the opposite case being POV. Glkanter (talk) 21:00, 16 October 2010 (UTC)
- I have also read, from Morgan and others that the only problem with the simple solutions is that Whitaker/vos Savant asked specifically about doors 1 and 3, and the only way to solve that particular (though not unique) pairing is with a conditional solution. I see a contradiction there in that doors 1 and 3 are not generally agreed premises of the MHP.
- Of course, even though they used quotation marks, Morgan distorted vos Savant's column by writing:
- ""...You pick door No. 1, and the host, who knows what's behind them, opens No. 3, which has a goat. He then asks if you want to pick No. 2. Should you switch?"" - Morgan's "quote" of Whitaker/vos Savant
- Instead of:
- "You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice?" - Whitaker/vos Savant
- The peer-reviewers didn't catch that either. Glkanter (talk) 21:10, 16 October 2010 (UTC)
- @Rick. The existence of a condition occurs when new information is revealed, which is not necessarily when a door is opened. If, after a door has been opened, we are told that 'a door has been opened to reveal a goat' there is no new information and thus no condition. If we are then told that it was door 3 that was opened, only then do we have a (potential) condition. Alternatively, if, before the door is opened, we are told that the host will open door 3 to reveal a goat, we have a condition before the door is opened. It is the revealing of information that creates a potential condition.
- Of course, it is not unreasonable to assume that the player becomes aware of the door number when the door is opened but this does not have to be the case. Why not give a correct description? Martin Hogbin (talk) 16:47, 16 October 2010 (UTC)
- It seems to me you are attempting to inject your own personal interpretation of the problem and objecting to using clear wording. The sources presenting conditional solutions are not in the least unclear about the situation they're addressing and none of them suggest the player is unaware of which specific door is opened or becomes aware of which door the host opens any way other than by seeing the host open the door. Are you saying the conditional solutions are NOT addressing the situation where the player has picked a known specific door at the point in time after the host has then opened some other known specific door? It seems you're trying very hard to obfuscate this. Why not make the situation that is being addressed clear? -- Rick Block (talk) 17:11, 16 October 2010 (UTC)
- Not correct. "Before vs. After" are vague and fuzzy weasel words in this respect. The word "after" is not the "general tenor" of the sources that characterize the difference between the simple solution and the conditional solution. The sources are very clear, specifying the difference as follows:
The simple solution, although aware of the door number the guest may have selected, say # 1, and although aware of the door number the host has opened showing a goat, say #3, does not pay regard to the specific door number the host has opened, in finding the answer whether to switch or not to switch. Followers of the simple solutions know it, but they see no motivation to "use this given information", and for that they are making no difference whether the host might have opened door #3 or door #2.
Whereas conditionalists (and that makes the difference) say that you mandatory have to use this given information (say door #3) to get the correct answer in applying conditional probability theorems.
So the words "before" and "after" may be the descriptive parlance of math teachers when teaching their students conditional probability theory, but they are not the tenor of the sources. We should avoid weasel words that just nebulize that difference:
Using this given information as a time-dependent sine qua non to correctly set a conditional probability calculation, or seeing all of that in a more general, uniform view, not needing the "special door numbers" of the actual game. However they are asking: "What makes the difference" with regard to the odds of the door selected by the guest? What's the secret specific effect, what's the real point? Gerhardvalentin (talk) 22:38, 16 October 2010 (UTC)
- Not correct. "Before vs. After" are vague and fuzzy weasel words in this respect. The word "after" is not the "general tenor" of the sources that characterize the difference between the simple solution and the conditional solution. The sources are very clear, specifying the difference as follows:
- Rick, the use of 'given' is not something that I have just made up. The article on Conditional probability starts, 'Conditional probability is the probability of some event A, given the occurrence of some other event B'.
- Reminder: We're not here to discuss the Monty Hall problem itself. The sole topic of this and other MHP talk pages is to work on drafting text for the Wikipedia article that will achieve consensus. Let's please keep the abstract mini-essays to a minimum and focus on the text instead. It is not necessary to provide one correct answer to this problem - we can have sections of appropriate length to cover different views. But we need to focus on finishing this section. Will Beback talk 23:17, 16 October 2010 (UTC)
- We are arguing here about whether the article should say:
- '...after the host opens Door 3. This is the conditional probability...' or
- 'given the condition that the host opens Door 3'
- From the comments above, I would say that there is a consensus to use 2. Would you agree Sunray? If not how should we proceed to resolve this issue? Martin Hogbin (talk) 09:43, 17 October 2010 (UTC)
- Does anyone disagree strongly with #2? If not, then we have consensus. Will Beback talk 21:51, 17 October 2010 (UTC)
- Yes, I disagree strongly with #2. And, we haven't heard from Nijdam or Kmhkmh or Glopk. -- Rick Block (talk) 23:59, 17 October 2010 (UTC)
My rationale for 2
[edit]I was asked to write a 'conditional' section that everyone could agree with. The facts as I see them are that:
- Some editors believe that the use of conditional probability is essential to solve the MHP 'properly'.
- Some editors believe that the use of conditional probability is an unnecessary complication.
- Some editors insist that there is a clear condition by virtue of the fact that player chooses whether to swap after the host has opened a door
- Some editors consider this fact to be irrelevant and that there is no significant condition.
- The sources do not clearly resolve this issue.
- All editors agree that conditional probability can be used to solve the MHP.
Saying 'given' a condition seems to me to be neutral wording with respect to the differing opinions here. It is technically correct and implies that if we accept that there is a condition we should work this way. It leaves open the question of whether there must be a condition or not. Martin Hogbin (talk) 10:09, 17 October 2010 (UTC)
Still on the first paragraph
[edit]So, back to the text, we're talking about the first paragraph. Martin has agreed to go with the majority regarding the first sentence, but apparently still prefers to reduce the number of references. I've agreed to adding a reference to the explicit version of the problem statement. So I think the two versions are now effectively:
- Another way to solve the problem is to treat it as a conditional probability problem (Selvin 1975b; Morgan et al. 1991; Gillman 1992; Carlton 2005; Grinstead and Snell 2006:137). With this approach the probability the car is behind any door can be analyzed both before and after the host opens a door. Consider the mathematically explicit version of the problem given above. The probability the car is behind any one of the doors before the host opens a door is 1/3. Assuming the player picks Door 1 and the host then opens Door 3, the probability of winning by switching is the probability the car is behind Door 2 after the host opens Door 3. This is the conditional probability the car is behind Door 2 given the player initially picked Door 1 and the host opens Door 3, generally written:
and
- Another way to solve the problem is to treat it as a conditional probability problem (Selvin 1975b; Morgan et al. 1991). Consider the mathematically explicit version of the problem given above. The probability the car is behind any door can be analyzed both before and after the host opens a door. The probability the car is behind any one of the doors before the host opens a door is 1/3. Assuming the player picks Door 1 and the host then opens Door 3, the probability of winning by switching is the probability the car is behind Door 2 given the condition that the host opens Door 3, generally written:
It is my contention that the first version better reflects the intent of the sources we're talking about here, and that they are indeed using conditional probability specifically to address the posterior probabilities in effect after the host has opened a (specific) door. This version says what the conditional probability means, using language easily understood by a non-expert reader. The other version confusingly brings up the ability to analyze "before" and "after" probabilities, says what the "before" probability is, but then doesn't specifically identify the conditional probability as applying to the "after" situation - which I think makes this version less readable, and harder for a non-expert to understand. -- Rick Block (talk) 00:05, 17 October 2010 (UTC)
- Rick you are still pushing your POV (supported by some sources) that after the door has been opened we must use conditional probability. Others (Glkanter, Gerhard, myself) believe that conditional probability is not required at all (and many sources solve the problem without its use). I am trying to form a neutral form of words that essentially says, if there is deemed to be a condition, we can/should use conditional probability. Martin Hogbin (talk) 12:49, 17 October 2010 (UTC)
- Martin - stop accusing me of pushing a POV - it's out of line and contrary to the ground rules. Perhaps you mean you find the first wording pushes the POV that after the door has been opened we must use conditional probability. How, exactly, is this POV being pushed? The first wording says "Another way to solve the problem ..." and "With this approach the probability the car is behind any door can be analyzed both before and after ...". You said before you thought "Another way to solve the problem ..." was implying that the problem can only be dealt with using conditional probability. Are you still reading these words as saying the opposite of what they actually say?
- The other difference is avoiding the "after" wording. Are you claiming it's POV pushing to explain that the sources presenting conditional solutions are saying "the probability of winning by switching is the probability the car is behind Door 2 after the host opens Door 3" and that they then proceed to compute this as "the conditional probability the car is behind Door 2 given the player initially picked Door 1 and the host opens Door 3"?
- Yes. I do think this does push the POV that the problem is inherently one of conditional probability. Although that position may be supported by some sources it is not universal. Many sources do not use conditional probability and some editors here think its use is unnecessary to solve the standard problem. We have been arguing about this for years and are no closer to agreement. The only way forwards I can see is for everyone to accept wording that may not be ideal for them but that is at least agreed to be correct. We all agree that CP can be used to solve the problem. I do not think that anyone could dispute that it should be used 'given a condition', especially bearing in mind that the article on Conditional probability starts with, 'Conditional probability is the probability of some event A, given the occurrence of some other event B'. There needs to be compromise on both sides. Martin Hogbin (talk) 17:16, 17 October 2010 (UTC)
- We need others who understand the conditional solutions to weigh in on this, but I think this wording is entirely accurate and neutral. It definitely doesn't say this is the only way to solve the problem. It seems you're reluctant to characterize the probability after the host opens door 3 as a conditional probability. Since it meets the definition of a conditional probability, I don't think saying this is in the least POV. On the contrary, NOT saying it strikes me as POV. -- Rick Block (talk) 16:11, 17 October 2010 (UTC)
- Rick, please consider that "before" and "after" for years have been the dazzling "fighting words" in the article discussion, taunting the simple solution (that just as well is aware of the door number opened but did not "need" this information to answer the question) as being "faulty, not answering the correct question." You feel the prickle? Gerhardvalentin (talk) 17:20, 17 October 2010 (UTC)
- We need others who understand the conditional solutions to weigh in on this, but I think this wording is entirely accurate and neutral. It definitely doesn't say this is the only way to solve the problem. It seems you're reluctant to characterize the probability after the host opens door 3 as a conditional probability. Since it meets the definition of a conditional probability, I don't think saying this is in the least POV. On the contrary, NOT saying it strikes me as POV. -- Rick Block (talk) 16:11, 17 October 2010 (UTC)
- We have had the views of Glkanter and Richard, who both seem to prefer 'given'. Martin Hogbin (talk) 17:16, 17 October 2010 (UTC)
- Do you mean Gerhard rather than Glkanter? I realize they're hard to distinguish :). -- Rick Block (talk) 04:04, 18 October 2010 (UTC)
- So there's no confusion, I, Glkanter, prefer #2. :) Glkanter (talk) 11:37, 18 October 2010 (UTC)
- I also prefer #2 as a clear presentation, but it's not up to me to decide, as this is the "conditional" section. Although I would appreciate if this section also could be pesented in a much clearer way, clearly presenting the underlying presumptions. Gerhardvalentin (talk) 12:17, 18 October 2010 (UTC)
- So there's no confusion, I, Glkanter, prefer #2. :) Glkanter (talk) 11:37, 18 October 2010 (UTC)
- How about "The probability the car is behind any one of the doors before the host opens a door is 1/3. Assuming the player picks Door 1 and the host then opens Door 3, the probability the car is behind Door 2 is now the conditional probability given the player initially picked Door 1 and the host opens Door 3, generally written"? Is this better, worse, or the same? -- Rick Block (talk) 04:04, 18 October 2010 (UTC)
- I like Rick's last proposed wording. And in general I think we're nitpicking: let's just settle on something which almost everyone finds more or less adequate, so we can move on and get to see how the whole article begins to shape up. The initial sentence of the paragraph we're fighting about said we are now going to look at a solution of MHP using conditional probability. People who don't like that can skip the whole paragraph. Everything that's written inside the paragraph is conditioned on taking this viewpoint. The idea of solving MHP with conditional probability is not just to use conditional probability, but to use it in a time-structured way, representing the way the totality of information available to the player modifies his state of uncertainty concerning the location of the car as he observes events around him taking place. This is a completely legitimate way of thinking. We assume that he does see the door numbers of the door he chose and the door opened by the host, so he does condition on this information, even if in retrospect it turns out to be irrelevant. Richard Gill (talk) 07:40, 18 October 2010 (UTC)
- Richard, I am surprised that you support 'Assuming the player picks Door 1 and the host then opens Door 3, the probability the car is behind Door 2 is now the conditional probability given the player initially picked Door 1 and the host opens Door 3' since you yourself have explained previously why this is not necessarily the case. This is the very claim that enrages the 'simplists' because it asserts that conditional probability must be used after the host has opened a door. Some here do not accept that claim.
- Sorry for being inconsistent. The conditionalists not only want to use conditional probability but also to compute probabilities from the point of view of a player who sees things happening in the outside world and who continuously adjusts his personal probabilities by conditioning on everything he has seen so far. At some point he sees the host open door 3 and reveal a goat so "his" probabilities - which reflect the totality of the information which has reached him - *must* be adjusted by conditioning on everything that he sees. He himself did choose initially door 1 and he saw the host open door 3 so he has to condition on these two pieces of information; not just that he chose "a" door and the host opened "an-other" door. The end result of his analysis is that he might as well have been blindfolded and ignored the door numbers altogether. But in advance he doesn't bother to think about that. It comes out in the wash, automatically (as it must).
- This is the Bayesian point of view, nothing wrong with it in itself. A Bayesian can always talk about "the" probability of anything: it is always that particular person's personal probability, and it is always conditional on the totality of information which that person has at any particular moment. Maybe the conditional solution section should be more explicit: its supporters want to adopt this philosophical view of what probability is about. According to this view, all probabilities are personal and all probabilities are conditional. Perhaps this section should be called "The Bayesian solution" not "The conditional solution". Richard Gill (talk) 20:28, 18 October 2010 (UTC)
- You have also written, 'let's just settle on something which almost everyone finds more or less adequate'. This is what I was asked to try to do and is exactly what I have proposed. Rick's wording asserts a particular POV. No one has claomed that my wording asserts anything that is not agreed by all. Martin Hogbin (talk) 19:57, 18 October 2010 (UTC)
- By the way, it is also fun to do the simple solution by conditional probability and time-structure. Imagine that the player is blind-folded. He chooses a door and doesn't know its number. The host opens another door and reveals a goat. The player hears the door opening and then a goat bleating so he knows the host has revealed a goat. He is asked if he would like to switch to the other closed door. Initially, all doors have for him probability 1/3 to hide the car. The host opens a door revealing a goat. The host had a choice of two doors if the player's initial choice was correct, the host had no choice if the player's initial choice was wrong. Therefore the probability the host opened the door he did, given the initial door hides the car, is 1/2; the probability the host opened the door he did, given the third door hides the car, is 1; the probability the host opened the door he did, given it itself hides the car, is zero. The probabilities of the information received, given the car is behind own door : other door: opened door are therefore 1/2 : 1 : 0. The initial odds were 1:1:1. The posterior odds are therefore 1/2 : 1 : 0 which is the same as 1 : 2 : 0.
- What I am saying is that the choice "conditional probability" or "not conditional probability" is not the essential choice which has to be made. The essential choice is "incorporate door numbers" or "don't incorporate door numbers" within the reasoning. You can actively choose to ignore the numbers at the outset. You get that the other closed door hides the car with probability 2/3. If you are wise you will ask yourself, if only briefly, if that conclusion should be modified, in the light of the actual door numbers (you chose 1 and host opened 3). You will convince yourself that by symmetry the numbers themselves are irrelevant. Therefore the other door hides the car with probability 2/3, also conditional on the specific door numbers involved so far. This extra information in one sense is irrelevant - it doesn't change the probability 2/3. In another sense it is rather important - it tells us that we couldn't have done even better, by sometimes switching and sometimes not switching, depending on the specific door numbers. IMHO a complete solution of MHP (under the standard conditions) does take account of the door numbers, either before or afterwards or during the argument. It's a matter of taste when. The question of whether one must use conditional probability or not is a red herring. Richard Gill (talk) 07:53, 18 October 2010 (UTC)
- I prefer Rick Block's latest version too. I have already said above that, IMHO, Martin Hogbin's wording is semantically equivalent but unnecessarily obscure for the readers lacking a mathematical education. Further, Martin hasn't offered any convincing argument in support of it (accusing another editor of "pushing" a POV, as well as negating the plain meaning of common English words is not convincing, in my book). All in all I think we'd be making a disservice to the users by preferring Martin's version to Rick's. Of the other editors who have commented, I find only Richard's notes to be relevant to the discussion, and he agrees with the latest by Rick Block's too. glopk (talk) 16:57, 18 October 2010 (UTC)
- Does your above finding of a lack of 'relevance' from the editors with whom you disagree:
- "Of the other editors who have commented, I find only Richard's notes to be relevant to the discussion, and he agrees with the latest by Rick Block's too. glopk (talk) 16:57, 18 October 2010 (UTC)"
- indicate a disinterest on your part in reaching a consensus with those editors? Glkanter (talk) 04:14, 19 October 2010 (UTC)
- Does your above finding of a lack of 'relevance' from the editors with whom you disagree:
- Please see my words above 17:20, 17 October 2010, and read this:
- F1: the player is offered to switch before she picks a door (as per Nijdam's talk page).
- F2: the player is asked to switch after the host opened a door
- Please pardon my wordings, but I find that just delusive.
- And even "Fx: the player is offered to switch after she picked a door, but before the host opened a door" would be delusive just as well. Fact: The host has already opened a door and, afterwards, has offered the player to switch then. That's exactly the starting point of the "simple solution" as well, that will be going to be criticized by conditionalists in the article. But instead of sticking to the facts and referring to the real difference between the "conditional solution" and the "simple solution", that for very good reason just does not need to discern "which one" of his two doors the host just has opened, to get the answer to the question "is it of advantage to switch", it is evident that an incorrect and sleazy characterization in dealing with the difference should be pushed by conditionalists. That's objectionable. We should refrain from further pursuing that everlasting strategy. The argument is not adequate to the real difference. Particularly because even the most exhaustive conditional solution never could confute the fact that nothing can be better than always to switch. So we at least should try to stick to the facts. Gerhardvalentin (talk) 18:44, 18 October 2010 (UTC)
- Gerhard: the unconditional argument shows that always switching is better than always staying. The conditional argument shows that nothing is better than always switching. That is a definitely stronger, better, conclusion. The unconditional argument says absolutely nothing about whether or not something else could be better than always switching, since it does not differentiate between the different possible situations the player could find themselves in at the last possible moment before they must commit themselves to a choice. I am sorry, but this is a definite advantage of the conditional solution. It adds to the unconditional solution by allowing one also to compare strategies in which the choice might depend on which door was chosen by the player, which door was opened by the host.
- Some people might find it intuitively obvious that nothing can beat 2/3 but a mathematician still likes to see a mathematical (logical) proof. Some people might prefer to use symmetry to extend the unconditional conclusion to the conditional conclusion: switching gives the car with probability 2/3, and by the symmetry of the problem, the conditional probability of getting the car by switching given any particular door chosen by the player and any particular door opened by the player is also equal to 2/3. Therefore any strategy of sometimes switching, sometimes not, depending on the door numbers in question (and if you like depending also on further randomization) is not as good as always switching. Because it results in a mixture of probabilities 2/3 for switching and 1/3 for not switching, hence in an overall probability of winning less than 2/3. Richard Gill (talk)l 20:07, 18 October 2010 (UTC)
- Thank you Richard for your riposte, but I do pay respect to a quite different fact, too, see above "Gerhardvalentin's comments" (show).
Without Bayes' help, everyone - by a closer look - can plainly see that the immutable average Pws=2/3, whereas in each and every single game Pws will vary around 2/3, and (in max. 2/3) Pws can at worst be 1/2 , and never less (!), but then (in the last 1/3) Pws "at worst" has to be 1. So in each and every single game - assuming to having closer evidence on the actual situation concerning the location of the car - Pws impossibly can ever be below 1/2. Repeat: Impossibly. And I repeat: It always will vary "around 2/3", and on average it will be 2/3, immutably. So you know "at one glance" that switching never can be worse (even without Bayes).
Yes, I really welcome the use of conditional probability also, in solving the MHP. It's qualified, easy and suitable and it can give us a lot of clear answers, too. But you conditionalists never could give evidence that the "simple solution" - involving the evidently given comprehension that Pws impossibly can ever be below 1/2, but in any single game has immutably to be at least 1/2 or greater, and also immutable on average 2/3 - that the simple solution was "out of position" to quote the fact that nothing can beat always switching. Everyone can quote this fact without using Bayes. Isn't it so? Why disclaiming the given facts? Gerhardvalentin (talk) 21:15, 18 October 2010 (UTC)- Dear Gerhard, I think we are saying the same thing in different ways. Everyone can see indeed without any help from Bayes that always switching gives Pws = prob win by switching = 2/3 and hence indeed the Pws in distinguishable subcases must vary around 2/3, because they must average out at 2/3. One can furthermore see in many ways that Pws can't ever fall below 1/2 (provided initially all doors were equally likely! Otherwise it certainly can fall below 1/2 in some individual cases). You can do this by Bayes, or you can argue a different way, just as you like. Bayes is part of elementary probability and elementary probability is just book-keeping. Arrange numbers in a spread-sheet, add over the rows and add the row totals gives the same grand total as adding over the columns and then adding column totals. Where I disagree with you, is when you say that you can see at a glance that the separate case probabilities can't fall below 1/2. But maybe I am missing something! It would not be the first time. Right now I think that you have to do some thinking or some calculating or both to do this. For me the easiest is Bayes in odds form, for some-one else another route might be preferable. Anyway: once you have done this we are indeed at the situation where we can extend our original "always switch" beats "always stay" to "always switch" beats everything. Richard Gill (talk) 18:34, 29 October 2010 (UTC)
- Thank you Richard for your riposte, but I do pay respect to a quite different fact, too, see above "Gerhardvalentin's comments" (show).
- Some people might find it intuitively obvious that nothing can beat 2/3 but a mathematician still likes to see a mathematical (logical) proof. Some people might prefer to use symmetry to extend the unconditional conclusion to the conditional conclusion: switching gives the car with probability 2/3, and by the symmetry of the problem, the conditional probability of getting the car by switching given any particular door chosen by the player and any particular door opened by the player is also equal to 2/3. Therefore any strategy of sometimes switching, sometimes not, depending on the door numbers in question (and if you like depending also on further randomization) is not as good as always switching. Because it results in a mixture of probabilities 2/3 for switching and 1/3 for not switching, hence in an overall probability of winning less than 2/3. Richard Gill (talk)l 20:07, 18 October 2010 (UTC)
Glkanter's Response
[edit]Nobody has explained why any of this paragraph is necessary. The decision tree is a reliably sourced solution. The paragraph next to the decision tree explains how it is used. The bulk of the paragraphs in both version sound like OR, and have no sources attributed to them. "Consider the mathematically explicit version of the problem given above." implies that it is the "*only* mathematically explicit version of the problem given above." Why say 'problem given above'? Is that different than the MHP the article has been about up until now? It seems to me that this is all a mechanism to promote the conditional solution as being better than the simple solutions in some way. My referenced comments on 'before or after' vs 'indifference' have not been discounted in any way. Heck, why even have separate Solution sections, anyways? Glkanter (talk) 00:25, 17 October 2010 (UTC)
If an introductory paragraph explaining the rationale for using a conditional solution is going to lead of the Conditional solution section, NPOV would require that there is a similar paragraph leading off the Simple solution section explaining why conditioning on door 3 being opened is not considered necessary by some reliable sources. Those sources are conditioning on the host revealing a goat behind a door, and are indifferent as to which door is opened, and some sources are indifferent as to which door the contestant selected (although the Combining Doors simple solution does show door 3 opened). But I think the article would be better if neither section had such a paragraph. Glkanter (talk) 10:20, 17 October 2010 (UTC)
- I've repeatedly suggested we include both types of solutions in a single solution section. I presume we'll be focusing on that sometime later (possibly next?). The paragraph we're talking about is not explaining the rationale for using a conditional solution, but rather explaining what a conditional solution is. When we talk about the simple solutions if you'd like to introduce a paragraph saying they are "conditioning on the host revealing a goat behind a door, and are indifferent as to which door is opened" we can talk about than then - although this would have to be sourced. Whether NPOV requires adding such a paragraph to the simple solutions is yet another topic - also not what we're currently focused on. -- Rick Block (talk) 16:11, 17 October 2010 (UTC)
Help!
[edit]I have tried to propose a reasonably neutral wording for the conditional section but have got nowhere. I have given a rationale for the proposed wording that no one seems to dispute but nevertheless I can get no agreement. Perhaps it is time for one of the mediators to step in. Martin Hogbin (talk) 21:29, 19 October 2010 (UTC)
- Again: yes, Martin's proposal using "given that" is technically okay and not so "bellicose", so we should use "given that". No need to controvert other solutions from the outset, that all base on this same state of knowledge. Gerhardvalentin (talk) 22:27, 19 October 2010 (UTC)
- Are editors making any progress towards consensus on any of the text here? Is there anything at all that folks here agree on? Do we need to restart this process from scratch, going back to first principles? Will Beback talk 22:51, 19 October 2010 (UTC)
- It seems clear to me fundamental Wikipedia principals regarding editing and editors are being disregarded. Glkanter (talk) 23:20, 19 October 2010 (UTC)
- Are there any sources that dispute that the conditional probability given the player has picked door 1 and the host has opened door 3 is the same as the probability the car is behind door 2 after the player has picked door 1 and the host has opened door 3? Or, is the objection to this wording only because some editors here do not agree that these are the same? -- Rick Block (talk) 23:51, 19 October 2010 (UTC)
- There are many sources that do not use conditional probability at all to solve the problem. Martin Hogbin (talk) 14:14, 20 October 2010 (UTC)
- No one disagrees about this. The issue here is whether we should or shouldn't clearly define what the conditional probability is. My question is whether there are any sources that say the conditional probability is anything other than the probability the car is behind door 2 after the host opens door 3 (assuming the player picked door 1). Sources that say nothing about conditional probability are not saying anything about this, so those sources are completely irrelevant to this question. -- Rick Block (talk) 15:53, 20 October 2010 (UTC)
- There are many sources that do not use conditional probability at all to solve the problem. Martin Hogbin (talk) 14:14, 20 October 2010 (UTC)
- Are there any sources that dispute that the conditional probability given the player has picked door 1 and the host has opened door 3 is the same as the probability the car is behind door 2 after the player has picked door 1 and the host has opened door 3? Or, is the objection to this wording only because some editors here do not agree that these are the same? -- Rick Block (talk) 23:51, 19 October 2010 (UTC)
Will, I do not think any progress is being made at all. There are still two sides, one side thinks that the conditional solution is the only correct solution and the other thinks that the conditional solution is an unnecessary complication that is not really needed at all.
My proposal was to give the conditional solution along with my 'given' wording which is essentially making the neutral statement that, 'if it is accepted that there is a condition then conditional probability should be used'. The 'given' wording is agreed to be correct by everyone but it does not assert that conditional probability must be used simple because the player chooses after the host has opened a door. On the other hand it does not push the point that conditional probability is unnecessary. This seems a reasonable and technically correct compromise to me. Martin Hogbin (talk) 14:15, 20 October 2010 (UTC)
- Then I must be on a 3rd side. I say all reliably sourced sourced solutions belong in a single solution section, without any narrative distinguishing them. That belongs later in the article. Glkanter (talk) 14:22, 20 October 2010 (UTC)
- Yes, in my opinion we should try to avoid even the misleading very "highlighting of alleged negative differences", as that has constantly been tried before. Gerhardvalentin (talk) 15:16, 20 October 2010 (UTC)
Maybe I am on my own then. My view of the MHP is that it is a simple problem that most people get wrong. That is the only reason that we have a WP article on it at all; there are plenty of complicated problems that people get wrong. The things that people get wrong and that have attracted the most interest from readers are firstly, why the answer is 2/3 and not 1/2, and why the fact than the host knows where the car is matters. These are, in my opinion, the most important things that the article should explain.
For those that find the basic MHP too easy (usually after they have been told the answer) there are plenty of extensions and variations that can be discussed to make things a little more complicated. In my opinion, the conditional solution, which is only relevant if the host is taken to choose a goat-door non-uniformly, is an academic extension of the MHP that should not be discussed at all until the basic problem has been fully explained. I did not think that I was the only one holding this view. Martin Hogbin (talk) 16:40, 20 October 2010 (UTC)
- I'm only talking about the single conditional decision tree solution. It answers the same (K & W) problem as the simple solutions. All the other stuff (variants), belongs later, if at all. Glkanter (talk) 16:45, 20 October 2010 (UTC)
- Is the assertion that the conditional solution is only relevant if the host is taken to choose a goat-door non-uniformly supported by any sources - or this is Martin's POV which is not published anywhere at all? -- Rick Block (talk) 16:56, 20 October 2010 (UTC)
- Additionally, is Martin's assertion above "The existence of a condition occurs when new information is revealed, which is not necessarily when a door is opened" backed by reputable MHP sources, or is this Martin's POV which is not published anywhere at all? glopk (talk) 21:02, 20 October 2010 (UTC)
- Glopk: "Is it of advantage to switch? Yes or no?" - Textbooks tell you that taking evident "nuts and trifles" as a "condition" can never and will never influence the result. So why using the "door opened" as a condition? Taking the "actual" hair color of the guest as a condition evidently is senseless. So you will never use it as a condition. And what about the "door opened? You did not tell why conditionalists like to use just the "door opened" as a condition. Taking the "door opened" as a condition would be senseless also, except you consider some "host's bias". And that you can assume to have "learned something ..." - otherwise that would make no sense at all. Only the specific procedural behavior of the host in showing a goat can be the reason to take the door opened as a condition. But sources also tell, even any "host's bias" given, there never can be a really "correct solution" saying that - for any single game - staying could ever be better than switching. You should tell that in the "conditional" section, too. Showing what result conditional probability theorems only can give: "No news". Or is there any reliable source that says that staying ever could be better than switching? And you should decide whether to switch of not. Please say in the article what the sources really say. Gerhardvalentin (talk) 23:27, 20 October 2010 (UTC)
- Gerhardvalentin, I am not aware of any MHP-related and reputable sources speaking about the guest's hair color. However, my and Rick block's questions to Martin are entirely about the existence of sources backing specific assertions made here by Martin himself. Do you have anything to add on this specific matter? I fail to see how your rather lenghty comment is in any way relevant. glopk (talk) 03:21, 21 October 2010 (UTC)
- Glopk: Thank you for your reply. Yes, it's on the "condition of the door opened", it's on assertions. And it's on this very condition treated by the sources, here. Martin did focus the asserted "condition" of the "conditional solution". Please read it, and then please "name" your relevant sources (source) saying that staying ever could be better than switching. And please consider that this lemma is on a required decision ("yes or no"), and it's just not on probabilities. But, back to Martin's point. Martin asked about your "condition" (the door opened) in the "conditional solution". So we focus on exactly this "condition". And yes, that matters the "conditional section", indeed. I am asking you: So please tell which source says that - even "conditioned" on the door opened - staying could ever be better than switching. This fact must be mentioned. Just not to leave people in the dark, just to not confuse the readers. Regards, Gerhardvalentin (talk) 19:10, 21 October 2010 (UTC)
- Gerhardvalentin, what part of my and Rick Block's questions to Martin do you not understand? Is there a language barrier between us? We asked for sources backing two specific assertions he made. The proper answer is to either provide the sources or retract the statements, but he is obviously doing neither. Please avoid pointless interjections. glopk (talk) 23:51, 21 October 2010 (UTC)
- Glopk: Thank you for your reply. Yes, it's on the "condition of the door opened", it's on assertions. And it's on this very condition treated by the sources, here. Martin did focus the asserted "condition" of the "conditional solution". Please read it, and then please "name" your relevant sources (source) saying that staying ever could be better than switching. And please consider that this lemma is on a required decision ("yes or no"), and it's just not on probabilities. But, back to Martin's point. Martin asked about your "condition" (the door opened) in the "conditional solution". So we focus on exactly this "condition". And yes, that matters the "conditional section", indeed. I am asking you: So please tell which source says that - even "conditioned" on the door opened - staying could ever be better than switching. This fact must be mentioned. Just not to leave people in the dark, just to not confuse the readers. Regards, Gerhardvalentin (talk) 19:10, 21 October 2010 (UTC)
- Gerhardvalentin, I am not aware of any MHP-related and reputable sources speaking about the guest's hair color. However, my and Rick block's questions to Martin are entirely about the existence of sources backing specific assertions made here by Martin himself. Do you have anything to add on this specific matter? I fail to see how your rather lenghty comment is in any way relevant. glopk (talk) 03:21, 21 October 2010 (UTC)
- Glopk: "Is it of advantage to switch? Yes or no?" - Textbooks tell you that taking evident "nuts and trifles" as a "condition" can never and will never influence the result. So why using the "door opened" as a condition? Taking the "actual" hair color of the guest as a condition evidently is senseless. So you will never use it as a condition. And what about the "door opened? You did not tell why conditionalists like to use just the "door opened" as a condition. Taking the "door opened" as a condition would be senseless also, except you consider some "host's bias". And that you can assume to have "learned something ..." - otherwise that would make no sense at all. Only the specific procedural behavior of the host in showing a goat can be the reason to take the door opened as a condition. But sources also tell, even any "host's bias" given, there never can be a really "correct solution" saying that - for any single game - staying could ever be better than switching. You should tell that in the "conditional" section, too. Showing what result conditional probability theorems only can give: "No news". Or is there any reliable source that says that staying ever could be better than switching? And you should decide whether to switch of not. Please say in the article what the sources really say. Gerhardvalentin (talk) 23:27, 20 October 2010 (UTC)
- Additionally, is Martin's assertion above "The existence of a condition occurs when new information is revealed, which is not necessarily when a door is opened" backed by reputable MHP sources, or is this Martin's POV which is not published anywhere at all? glopk (talk) 21:02, 20 October 2010 (UTC)
- According to a common understanding of what probability is (personal representation of your knowledge of the world) each individual person does always carry around in their head a collection of probabilities of everything they don't know about. IF that person is rational he/she does update your probabilities all the time according to *all* the information they have. From this point of view we can talk about THE PLAYER'S PROBABILITY and it does change in time and it is different before the door was opened and after. Moreover it does change by applying Bayes rule and the player must condition on everything he has observed. So he does condition on the specific door number opened by the host, even if this turns out to have been irrelevant. It is a fact that Prob(other door hides car| a door was opened showing goat, you chose 1) = Prob(door 2 hides car| door 3 was opened showing a goat, you chose 1), so the door numbers are not needed to follow the optimal strategy. I am sure you kind find academic sources presenting this normative view of probability.
- I like to argue for the conditional solution using a different point of view and with a completely neutral understanding of probability. In particular I don't have a normative point of view which says you *must* do this or that. I simply point out that the simple solution to MHP only compares the simple strategies "always switching" and "always staying". The former has overall succes probability 2/3 and the latter has overall success probability 1/3. The conditional solution tells us that switching beats staying, not only on average, but also for each configuration of door chosen by player door opened by host. This tells us that any mixed strategy of sometimes switching sometimes staying, depending on the door numbers, has a *lower* overall success probability than 2/3. Thus we learn that "always switching" beats *everything*. It cannot be denied that the conditional solution is a completion or extension or strengthening of the simple solution. It fills in the picture. It tells us something we didn't know before, and which is worth knowing. Now, it won't even occur to most readers that something in between always switching and always staying is worth thinking about. So for them this is an academic diversion. But it is a reliably sourced fact that mathematics shows that their intuition is correct. I think that's nice.
- Altogether, I don't see any conflict between the different solutions. Mathematics provides a spectrum of solutions. With weak assumptions and an easy argument you can get a weak conclusion: "always switching" beats "always staying". The conoisseurs will be interested that with stronger assumptions and a slightly more involved argument you can get a logically much stronger solution: "always switching" beats "anything". Actually if you derive the conditional solution using the unconditional solution and symmetry, the stronger result is quite within the intellectual reach of non-specialist readers. Richard Gill (talk) 08:29, 22 October 2010 (UTC)
Well, the question asked by both Selvin and Whitaker/vos Savant *is* whether switching is better than staying. As I read your narrative above, Richard, you agree that the various simple solutions offered by many sources are quite up to the task of answering that question. Negating the need for any qualifications or condemnations due to mathematical reasons in the solution sections. Conflicting sources can be addressed later, so as not to confuse or distract the reader who only came to the Wikipedia article, initially, for the answer to the question asked. Glkanter (talk) 11:53, 22 October 2010 (UTC)
- Yes Glkanter, and what the conditional solution reveals is that there are different senses in which that question can be answered. The simple solution shows that always switching beats always staying. The conditional solution shows that for each particular configuration of door chosen, door opened, staying beats switching. There is no conflict here. It just turns out that there is a simple interpretation of the question which has a simple answer, and a more subtle interpretation which has a more subtle answer.
- The assertion that the conditional solution is only relevant if the host is taken to choose a goat-door non-uniformly is Martin's POV only. The conditional solution is always stronger than the non-conditional solution, whether or not we assume host bias. Richard Gill (talk) 15:39, 22 October 2010 (UTC)
- More specifically, I thought we were discussing how to express what "the conditional probability" means, in particular (assuming the player initially picks door 1) is "the probability of winning after the host opens door 3" an accurate and NPOV way to explain to a general reader the meaning of "the conditional probability given the player picks door 1 and the host opens door 3"?
- Martin seems to think saying this implies conditional probability is the ONLY way to address the problem (?) and hence this wording is not NPOV. I, and I think Glopk and (based on the above) Richard, think the sources presenting conditional probability solutions mean the "after" probability when they are talking about the conditional probability "given" the host opens door 3. Furthermore, I think (and I believe Glopk and Richard agree) that this isn't a POV issue, i.e. there are NO sources that disagree with this and that it is simply elementary conditional probability. If anyone thinks there are sources that disagree, please say specifically which sources. -- Rick Block (talk) 16:14, 22 October 2010 (UTC)
My point is there is no need to describe the 'why' of the conditional solution. Just present the solution. Stating 'after' implies the simple solutions are not 'after'. Which is the same verbiage used when the simple solutions were called 'false' in the Solution section of an earlier version of the article. Which was a glaring NPOV violation, and not supported bythe sources at all. Otherwise, Morgan's paper calls the conditional solution 'false' as it relies on the non-existent (at least in Whitaker/vos Savant) 50/50 premise. If you're going to explain 'why' based on the sources (in the Solution section), you should also explain 'why not' (in the Solution section). The simple solutions don't have a 'why' paragraph, which is at it should be. Glkanter (talk) 17:52, 22 October 2010 (UTC)
- The simple solutions don't use any before or after concepts. However, the conditional solution can be thought of in a "before and after" way. The word "after" in this context is not verbiage. One may think of one's probabilities of things of interest developing in time, in response to observing events in the world around you. The word "after" is used in a specific, local, context, in which it is very meaningful and very useful. The simple solution stands on its own. The conditional solution stands on its own. Both exist. Neither need be seen as a criticism of the other. Both may be seen as enrichment, as complement, of the other. Please let's stop all this confrontational dogmatic manouvering. Wikipedia editors aren't supposed to be fighting to enforce their own POV on the world. If you want to do that, go and write some reliable sources or set up a political party or TV station or whatever. We just have to reflect what is out there. There is a spectrum of interesting solutions. Some will be more useful to more readers, others will only be understandable to a minority. None of them negate the others. Some of the authors of reliable sources have dogmatic positions. We may report such opinions if it seems useful to the readers but I think that's a waste of time. Richard Gill (talk) 19:21, 22 October 2010 (UTC)
- @Richard - Although you don't exactly say, I'm assuming you're thinking Glkanter is fighting to enforce his own POV here. I'm attempting to have the article clearly say what the conditional probability corresponds to, in this section that presents the conditional probability solution. The argument on the other side seems to be we shouldn't do that because it makes it too clear.
- Yes I suppport you here Rick. Richard Gill (talk) 12:29, 23 October 2010 (UTC)
- Glkanter has demonstrated via the reliable sources that 'after' is not a differentiator between the simple and the conditional solutions. An accurate way to portray that difference would be to explain that the conditional solution responds to door #3 being revealed, without any mumbo jumbo about 'additional information' being provided. Glkanter (talk) 12:45, 23 October 2010 (UTC)
- @Glkanter - We're not talking about the "why" of the conditional solution, but the "what". What it does (both as a mathematical fact and according to every source which talks about it) is compute the probability of winning at the point after the host has opened door 3 (assuming the player initially picked door 1). Whether you personally like this approach or not, it is what is going on in this sort of solution. My request (again) is if you think this point is arguable according to reliable sources then please tell us what source(s).
- @Will or Sunray - If Glkanter, or Martin, or Gerhard are unable to provide any such sources then I think it's high time for one of you to intervene. -- Rick Block (talk) 20:04, 22 October 2010 (UTC)
I've explained my view on the introductory paragraph and the Conditional solution section multiple times. I have included quotes and links to various relevant sources. I have explained how the verbiage favors a POV. That you disagree with and/or ignore my contributions, Rick, does not mean your opinions and thoughts on this subject are the definitive authority on editing the article. That would be an Ownership violation. Glkanter (talk) 20:20, 22 October 2010 (UTC)
Specific to 'after', Selvin gave a simple solution after describing a box being revealed to be empty. The combining door solution shows a door open. Carlton's simple solution says a door has been open. Some sources describe the simple solutions as 'indifferent' to which door is opened, and Morgan describes the conditional solution as the combination of two simple 'after' solutions, door 2 plus door 3. 'After' is not a differentiator between simple and complex as per many sources. Glkanter (talk) 23:31, 22 October 2010 (UTC)
- So the word "after" is quite neutral. The simple solution tells how the opinions of the player (who chose door 1) should change after (A) seeing a door being opened and revealing a goat: Answer (A): the other door now hides the car with probability 2/3. The complex solution tells how the opinions of the player (who chose 1) should change after (B)seeing Door 3 being opened and revealing a goat: Answer: (B) Door 2 now hides the car with probability 2/3 (under the usual symmetry assumptions) OR with probability at least 1/2 (under the condition only, that all doors initially are equally likely). Lots of people don't see any difference between these two statements. I think Glkanter is one. I have the impression that Gerhardvalentin and Martin Hogbin are two others. Because he (they) doesn't see any difference between questions A and B, nor between answers A and B, he doesn't see why you need a more complicated arguement to get the answer B to question B than the answer A to question A. Nijdam is someone who thinks that the only right question to be answered is B. Possibly Rick Block Glopk think the same. The previous fights about wikipedia MHP were between those who thought question A is the question being asked, and it's answer is answer A; and those who thought question B is beingh asked, and it's answer is answer B. As a mathematician all I can say is that from the point of view of mathematics, questions A and B are different questions, and A and B are different answers. I agree with Martin Hogbin that most readers of wikipedia will be perfectly happy with question A and answer A. The connoisseurs will appreciate question B and answer B. In my opinion, neither can dictate to the other what is the good question and the good answer, since reliable sources aplenty stand behind both. All this talk about whether "after" is enforcing a POV is (IMHO) pretty stupid. The conditional solution section is about the solution for those whose point of view is that this is how you should do it. It gives the argument which belongs with that (reliably sourced) POV. Those who don't hold to that POV should keep their mouths shut within this section. And vice versa. We won't make any progress till we admit to a multiplicity of reliably sourced POV's about how MHP should be solved. Please let's work towards some kind of peaceful coexistence. Richard Gill (talk) 12:29, 23 October 2010 (UTC)
- This all is a repetition of what has been discussed and repeated over and over. To be complete: Let F0 be the problem in which the player is offered to switch even before she has made her initial choice of a door. F1 the problem in which the player is offered to switch before a door with a goat has been opened, but after she has chosen a door. And F2 the problem in which the player is offered to switch after a door with a goat has been opened. The problem formulation clearly refers to F2!! F2 is also the only interesting formulation, as one is confronted with an opened door with a goat and a choice between two still closed doors. No one will convince me the MHP was ment to be otherwise. It is F0 to which the simple solution (S0) is a correct solution. Already for F1 there is the condition of the chosen door. Under the assumption of independence of choice and car placement, it is easy to understand that S0 also solves F1, but it needs this additional argument. Of course F2 is only solved by the "conditional solution" S2. My concern is that lots of people consider F2 as the MHP and S0 as a solution to it. Nijdam (talk) 15:35, 23 October 2010 (UTC)
- Every thread on this topic wonders over every possible issue of disagreement. This is reminiscent of a fight between an old married couple in which all of the same complaints keep being raised. I'm beginning to think that editors here are just here for the pleasure of arguing and are not actually interested in in finding consensus. I'm going to invoke my role as mediator and start structuring the discussions more so that we can stay focused. Any objections? Will Beback talk 23:48, 22 October 2010 (UTC)
- I think your taking a more active role here is the only way forward. Martin Hogbin (talk) 09:47, 23 October 2010 (UTC)
- I concur. Glkanter (talk) 12:45, 23 October 2010 (UTC)
- No objections from me. -- Rick Block (talk) 16:00, 23 October 2010 (UTC)
Nijdam's comment
[edit]As I already indicated, I'm not happy with the title, because a strong suggestion comes from it, that the correct solution, by calculating the conditional (or a posteriori) probability, is just some way of solving. Let's us call this section: Probabilistic solution. And then, I think the section with the simple solution is way too long. Let us just give one simple solution, and mention all the variants further on in the article. Thirdly: I like the mathematical formulation be more precise, as I've mentioned before. So for instance not P(C|S), but fully: P(C=1|S=2) or something alike. Nijdam (talk) 15:10, 18 October 2010 (UTC) It just crossed my mind, we may introduce a section "Criticism of the simple solution" after the "Simple solution" section, and before the Probabilistic one. Nijdam (talk) 15:14, 18 October 2010 (UTC)
- Conditional probability is just one way of solving the MHP. It is uncommon to find a mathematical problem that admits only one type of solution.
- I have no objection to making the conditional solution more rigorous. I suggest starting with including all the player's initial door choices. Martin Hogbin (talk) 20:00, 18 October 2010 (UTC)
- Nijdam, you say "the correct solution" by calculating the conditional (or a posteriori) probability. - Terms like "conditional - a posteriori" are of importance within the field of mathematical calculation of conditional probabilities, and just within that discipline these terms are of relevance. The world is not all mathematical theorems, and the question is: "of advantage?". In accordance with the sources we should have in view that switching never can be of disadvantage, based on all reasonable assumptions ever to be applied. Let's just both-way try to avoid discriminating other sources. Gerhardvalentin (talk) 15:49, 20 October 2010 (UTC)
Sources
[edit]- Adams, Cecil (1990)."On 'Let's Make a Deal,' you pick Door #1. Monty opens Door #2—no prize. Do you stay with Door #1 or switch to #3?", The Straight Dope, (November 2, 1990). Retrieved July 25, 2005.
- Bapeswara Rao, V. V. and Rao, M. Bhaskara (1992). "A three-door game show and some of its variants". The Mathematical Scientist 17(2): 89–94.
- Barbeau, Edward (1993). "Fallacies, Flaws, and Flimflam: The problem of the Car and Goats". The College Mathematics Journal 24(2): 149-154.
- Barbeau, Edward (2000). Mathematical Fallacies, Flaws and Flimflam. The Mathematical Association of America. ISBN 0-88385-529-1.
- Behrends, Ehrhard (2008). Five-Minute Mathematics. AMS Bookstore. p. 57. ISBN 9780821843482.
- Bloch, Andy (2008). "21 - The Movie (my review)". Retrieved 2008-05-05.
- Carlton, Matthew (2005). "Pedigrees, Prizes, and Prisoners: The Misuse of Conditional Probability". Journal of Statistics Education [online] 13 (2). Retrieved 2010-05-29.
- Chun, Young H. (1991). "Game Show Problem," OR/MS Today 18(3): 9.
- D'Ariano, G.M et al. (2002). "The Quantum Monty Hall Problem" (PDF). Los Alamos National Laboratory, (February 21, 2002). Retrieved January 15, 2007.
- Devlin, Keith (July – August 2003). "Devlin's Angle: Monty Hall". The Mathematical Association of America. Retrieved 2008-04-25.
- "The Monty Hall puzzle". The Economist (The Economist Newspaper) 350: p. 110. 1999.
- Falk, Ruma (1992). "A closer look at the probabilities of the notorious three prisoners," Cognition 43: 197–223.
- Flitney, Adrian P. and Abbott, Derek (2002). "Quantum version of the Monty Hall problem," Physical Review A, 65, Art. No. 062318, 2002.
- Fox, Craig R. and Levav, Jonathan (2004). "Partition-Edit-Count: Naive Extensional Reasoning in Judgment of Conditional Probability," Journal of Experimental Psychology: General 133(4): 626-642.
- Gardner, Martin (1959a). "Mathematical Games" column, Scientific American, October 1959, pp. 180–182. Reprinted in The Second Scientific American Book of Mathematical Puzzles and Diversions.
- Gardner, Martin (1959b). "Mathematical Games" column, Scientific American, November 1959, p. 188.
- Gill, Jeff (2002). Bayesian Methods, pp. 8–10. CRC Press. ISBN 1-58488-288-3, (restricted online copy at Google Books)
- Gill, Richard (2009a) Probabilistic and Game Theoretic Solutions to the Three Doors Problem, prepublication, http://www.math.leidenuniv.nl/~gill/threedoors.pdf.
- Gill, Richard (2009b) Supplement to Gill (2009a), prepublication, http://www.math.leidenuniv.nl/~gill/quizmaster2.pdf
- Gill, Richard (2010) Second supplement to Gill (2009a), prepublication, http://www.math.leidenuniv.nl/~gill/montyhall3.pdf
- Gillman, Leonard (1992). "The Car and the Goats," American Mathematical Monthly 99: 3–7.
- Granberg, Donald (1996). "To Switch or Not to Switch". Appendix to vos Savant, Marilyn, The Power of Logical Thinking. St. Martin's Press. ISBN 0-612-30463-3, (restricted online copy at Google Books).
- Granberg, Donald and Brown, Thad A. (1995). "The Monty Hall Dilemma," Personality and Social Psychology Bulletin 21(7): 711-729.
- Grinstead, Charles M. and Snell, J. Laurie (2006-07-04) (PDF). Grinstead and Snell’s Introduction to Probability. Retrieved 2008-04-02. Online version of Introduction to Probability, 2nd edition, published by the American Mathematical Society, Copyright (C) 2003 Charles M. Grinstead and J. Laurie Snell.
- Hall, Monty (1975). The Monty Hall Problem. LetsMakeADeal.com. Includes May 12, 1975 letter to Steve Selvin. Retrieved January 15, 2007.
- Henze, Norbert (1997). Stochastik für Einsteiger: Eine Einführung in die faszinierende Welt des Zufalls?, pp. 105, Vieweg Verlag, ISBN 3-8348-0091-0, (restricted online copy at Google Books)
- Herbranson, W. T. and Schroeder, J. (2010). "Are birds smarter than mathematicians? Pigeons (Columba livia) perform optimally on a version of the Monty Hall Dilemma." J. Comp. Psychol. 124(1): 1-13. Retrieved from http://www.ncbi.nlm.nih.gov/pubmed/20175592 March 1, 2010. http://people.whitman.edu/~herbrawt/HS_JCP_2010.pdf
- Krauss, Stefan and Wang, X. T. (2003). "The Psychology of the Monty Hall Problem: Discovering Psychological Mechanisms for Solving a Tenacious Brain Teaser," Journal of Experimental Psychology: General 132(1). Retrieved from http://www.usd.edu/~xtwang/Papers/MontyHallPaper.pdf March 30, 2008.
- Mack, Donald R. (1992). The Unofficial IEEE Brainbuster Gamebook. Wiley-IEEE. p. 76. ISBN 9780780304239.
- Magliozzi, Tom; Magliozzi, Ray (1998). Haircut in Horse Town: & Other Great Car Talk Puzzlers. Diane Pub Co.. ISBN 0-7567-6423-8.
- Martin, Phillip (1989). "The Monty Hall Trap", Bridge Today, May–June 1989. Reprinted in Granovetter, Pamela and Matthew, ed. (1993), For Experts Only, Granovetter Books.
- Martin, Robert M. (2002). There are two errors in the the title of this book (2nd ed.). Broadview Press. pp. 57–59. ISBN 9781551114934.
- Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991). "Let's make a deal: The player's dilemma," American Statistician 45: 284-287.
- Mueser, Peter R. and Granberg, Donald (May 1999). "The Monty Hall Dilemma Revisited: Understanding the Interaction of Problem Definition and Decision Making", University of Missouri Working Paper 99-06. Retrieved June 10, 2010.
- Nalebuff, Barry (1987). "Puzzles: Choose a Curtain, Duel-ity, Two Point Conversions, and More," Journal of Economic Perspectives 1(2): 157-163 (Autumn, 1987).
- Jason Rosenhouse: The Monty Hall Problem. Oxford University Press 2009, ISBN 978-0-19-536789-8 (online copy of the irst chapter, preprint)
- Rosenthal, Jeffrey S. (September 2008). "Monty Hall, Monty Fall, Monty Crawl". Math Horizons: 5–7.
- Selvin, Steve (1975a). "A problem in probability" (letter to the editor). American Statistician 29(1): 67 (February 1975).
- Selvin, Steve (1975b). "On the Monty Hall problem" (letter to the editor). American Statistician 29(3): 134 (August 1975).
- Seymann R. G. (1991). "Comment on Let's make a deal: The player's dilemma," American Statistician 45: 287-288.
- Stibel, Jeffrey, Dror, Itiel, & Ben-Zeev, Talia (2008). "The Collapsing Choice Theory: Dissociating Choice and Judgment in Decision Making," Theory and Decision. Full paper can be found at http://users.ecs.soton.ac.uk/id/TD%20choice%20and%20judgment.pdf.
- Tierney, John (1991). "Behind Monty Hall's Doors: Puzzle, Debate and Answer?", The New York Times, 1991-07-21. Retrieved on 2008-01-18.
- Tierney, John (2008). "And Behind Door No. 1, a Fatal Flaw", The New York Times, 2008-04-08. Retrieved on 2008-04-08.
- vos Savant, Marilyn (1990). "Ask Marilyn" column, Parade Magazine p. 16 (9 September 1990).
- vos Savant, Marilyn (1990b). "Ask Marilyn" column, Parade Magazine p. 25 (2 December 1990).
- vos Savant, Marilyn (1991). "Ask Marilyn" column, Parade Magazine p. 12 (17 February 1991).
- vos Savant, Marilyn (1996). The Power of Logical Thinking. St. Martin's Press. ISBN 0-312-15627-8.
- vos Savant, Marilyn (2006). "Ask Marilyn" column, Parade Magazine p. 6 (26 November 2006).
- Schwager, Jack D. (1994). The New Market Wizards. Harper Collins. p. 397. ISBN 9780887306679.
- Williams, Richard (2004). "Appendix D: The Monty Hall Controversy" (PDF). Course notes for Sociology Graduate Statistics I. Retrieved 2008-04-25.
- Wheeler, Ward C. (1991). "Congruence Among Data Sets: A Bayesian Approach". In Michael M. Miyamoto and Joel Cracraft. Phylogenetic analysis of DNA sequences. Oxford University Press US. p. 335. ISBN 9780195066982.
- Whitaker, Craig F. (1990). [Formulation by Marilyn vos Savant of question posed in a letter from Craig Whitaker]. "Ask Marilyn" column, Parade Magazine p. 16 (9 September 1990).
I've copied the existing bibliography and highlighted the references used for this section. Are these the most applicable sources for this material? Are any significant views omitted? Do we accurately summarize each source? A side issue: were the Gill papers ever published? Will Beback talk 00:42, 21 October 2010 (UTC)
- Carlton is relevant. Falk is definitely related. Krauss and Wang is relevant. The Rosenhouse book is relevant. Rosenthal is relevant.
- The "odds" form of the conditional solution (last sentence of my suggested wording) is not in Martin's version. I've suggested an alternate wording (revised again here), i.e. "A more intuitive form of a conditional solution is to reason that if the player picks Door 1 then the host must open Door 3 if the car is behind Door 2, but opens Door 3 only half the time the car is behind Door 1, so a player who initially picks Door 1 and sees the host open Door 3 wins twice as often by switching to Door 2 [Rosenthal]."
- Most of the versions we're talking about don't directly make the point Richard has suggested which is that the conditional solution can be used to show that with the standard assumptions always (unconditionally) switching results in the same probability as switching in any specific case - i.e. switching results in the same probability of winning regardless of which specific door the player chooses or the host opens. My comment to Richard about this above was that although I agree this is a mathematical fact, at least most of the sources we're talking about here don't directly make this point. They instead only show the probability in the one (presumably picked randomly) example case from the problem statement where the player picks door 1 and the host opens door 3.
- The view that IMO is expressed by Morgan et al., Gillman, Grinstead and Snell, Carlton, Falk, and Rosenthal (and others that are not currently referenced in the article) that the conditional solution is a better way or, more strongly, the only "correct" way to solve the problem is not in this section (in either Martin's or my wording). An applicable source we haven't included is Bar-Hillel's "How to Solve Probability Teasers" [1]. We're going to have to talk about how and where to represent this view eventually. I believe some editors think representing this view anywhere at all in the "Solution" section would be POV, although I think in some sense this section is the most natural place to include this.
- Another side issue we should talk about at some point is whether including the recent Gill references is a conflict of interest. Richard wrote these articles at least partly in response to discussions that occurred on the talk page and then added them as references. -- Rick Block (talk) 05:32, 21 October 2010 (UTC)
- A lot of that comment appears to be about issues besides sources. Let's stay focused. Will Beback talk 03:33, 22 October 2010 (UTC)
- These are the sources chosen by the recent editors of the article. They do not necessarily form a representative sample of all sources on the subject. There are many sources in addition to those listed here that give simple solutions without qualification or reservation. Martin Hogbin (talk) 08:21, 21 October 2010 (UTC)
- I believe we're talking about sources for the conditional probability solution section here, not the entire article. -- Rick Block (talk) 14:56, 21 October 2010 (UTC)
- Jeff Gill and Henze are relevant. In particular, the former is a source in support of using the "after the host opens" wording for the conditional probability: see here. Henze is a source for the three-variable formalization used in the Mathematical Formulation. glopk (talk) 00:02, 22 October 2010 (UTC)
- Regardless of their relevance, we can't use the Gill papers unless they've been published. The current entries say they're pre-publication versions. Will Beback talk 00:11, 22 October 2010 (UTC)
- Glopk is talking about the Jeff Gill reference (a published book), not the pre-publication Richard Gill references. -- Rick Block (talk) 02:03, 22 October 2010 (UTC)
- So, were the Richard Gill papers ever published? If not they shouldn't be used as sources. Will Beback talk 02:58, 22 October 2010 (UTC)
- I'm not sure - Richard (Gill110951) is commenting here. I've been expecting him to reply. Even if they have been published, I think we need to talk about whether Richard adding them as references to the article is a COI. -- Rick Block (talk) 03:24, 22 October 2010 (UTC)
- Let's leave the COI issue to other pages. Will Beback talk 03:33, 22 October 2010 (UTC)
- I have no COI since I don't have any opinion about whether my own (pre)-publications should be referenced on wikipedia MHP. If anyone wants to refer to anything, they should focus on two quite similar prepublications: [2] and [3] . The former was sollicited by the editors of a new Springer pubished encyclopaedia of statistics. It has been reviewed and enthusiasticly accepted. I don't know if it has come out yet. The second was submitted to Statistica Neerlandica, and refereed and enthusiastically accepted for publication. However I have been working on a complete re-write [4] with some new material, and I told everyone here about it, a few people sent me some useful comments. I'm going to be largely away from wikipedia for another two weeks from now, I'm sorry not to be able to participate for a while. Richard Gill (talk) 08:03, 22 October 2010 (UTC)
- Thanks for your reply. However Wikipedia policies require that we only use published sources. Once these papers are actually published they can be referenced. Until then we should remove the citations and any material that can't be sourced elsewhere. Will Beback talk 08:44, 22 October 2010 (UTC)
- I did not put those citations in the wikipedia MHP article. I only tell people about them here, on talk pages, because they might find some of the insights useful. I expound on my point of view and I refer to well-known and totally uncontroversial mathematical results, which can easily be reliably sourced by anyone who feels that is necessary. Richard Gill (talk) 15:48, 22 October 2010 (UTC)
- The only issue is whether they are published or not. If they are not then we can't use them as sources. Will Beback talk 23:41, 22 October 2010 (UTC)
- The Springer statistics encyclopedia preprint [5] and Statistica Neerlandica preprint [6] can't be cited on the MHP pages for a while yet, but I hope that some editors might find them useful bed-time reading matter right now. They were inspired by the discussions here, and they aim to contribute to the resolution of our present impasse, by giving a careful argument for the peaceful coexistence of the different solutions. The two papers explore the logical relations between the different solutions, their relationships to different philosophies of probability, and bring out the strengths and weaknesses of all. They contain nothing new and nothing controversial, and only elementary mathematics. I have communicated about their content with Morgan and his coauthors, with Jason Rosenhouse and Jeffrey Rosenthal, and with eminent probabilists and statisticians around the world. My analysis helps me to understand why each of the editors here is so strongly committed to their own point of view and unable to appreciate that of others. Mediators might find the analysis useful. But everyone is of course free to ignore their existence. Richard Gill (talk) 14:08, 23 October 2010 (UTC)
- Perhaps you could explain to me, 'why each of the editors here is so strongly committed to their own point of view and unable to appreciate that of others' some time, either privately or on an appropriate WP talk page. Martin Hogbin (talk) 09:43, 24 October 2010 (UTC)
- I would certainly like to try, Martin. This week I'm on vacation with almost no internet. Next week I'll make an attempt. First privately and then if it is useful on your or my talk page. Richard Gill (talk) 19:40, 27 October 2010 (UTC)
- Thanks, I look forward to hearing from you. Martin Hogbin (talk) 20:02, 27 October 2010 (UTC)
- The Springer | International Encyclopaedia of Statistical Science is due to be available from November (2010). I will get hold of volume number and page numbers of my article [7]. Richard Gill (talk) 17:19, 31 October 2010 (UTC)
- Thanks, I look forward to hearing from you. Martin Hogbin (talk) 20:02, 27 October 2010 (UTC)
- I would certainly like to try, Martin. This week I'm on vacation with almost no internet. Next week I'll make an attempt. First privately and then if it is useful on your or my talk page. Richard Gill (talk) 19:40, 27 October 2010 (UTC)
- Perhaps you could explain to me, 'why each of the editors here is so strongly committed to their own point of view and unable to appreciate that of others' some time, either privately or on an appropriate WP talk page. Martin Hogbin (talk) 09:43, 24 October 2010 (UTC)
- The Springer statistics encyclopedia preprint [5] and Statistica Neerlandica preprint [6] can't be cited on the MHP pages for a while yet, but I hope that some editors might find them useful bed-time reading matter right now. They were inspired by the discussions here, and they aim to contribute to the resolution of our present impasse, by giving a careful argument for the peaceful coexistence of the different solutions. The two papers explore the logical relations between the different solutions, their relationships to different philosophies of probability, and bring out the strengths and weaknesses of all. They contain nothing new and nothing controversial, and only elementary mathematics. I have communicated about their content with Morgan and his coauthors, with Jason Rosenhouse and Jeffrey Rosenthal, and with eminent probabilists and statisticians around the world. My analysis helps me to understand why each of the editors here is so strongly committed to their own point of view and unable to appreciate that of others. Mediators might find the analysis useful. But everyone is of course free to ignore their existence. Richard Gill (talk) 14:08, 23 October 2010 (UTC)
- The only issue is whether they are published or not. If they are not then we can't use them as sources. Will Beback talk 23:41, 22 October 2010 (UTC)
- I did not put those citations in the wikipedia MHP article. I only tell people about them here, on talk pages, because they might find some of the insights useful. I expound on my point of view and I refer to well-known and totally uncontroversial mathematical results, which can easily be reliably sourced by anyone who feels that is necessary. Richard Gill (talk) 15:48, 22 October 2010 (UTC)
- Thanks for your reply. However Wikipedia policies require that we only use published sources. Once these papers are actually published they can be referenced. Until then we should remove the citations and any material that can't be sourced elsewhere. Will Beback talk 08:44, 22 October 2010 (UTC)
- I have no COI since I don't have any opinion about whether my own (pre)-publications should be referenced on wikipedia MHP. If anyone wants to refer to anything, they should focus on two quite similar prepublications: [2] and [3] . The former was sollicited by the editors of a new Springer pubished encyclopaedia of statistics. It has been reviewed and enthusiasticly accepted. I don't know if it has come out yet. The second was submitted to Statistica Neerlandica, and refereed and enthusiastically accepted for publication. However I have been working on a complete re-write [4] with some new material, and I told everyone here about it, a few people sent me some useful comments. I'm going to be largely away from wikipedia for another two weeks from now, I'm sorry not to be able to participate for a while. Richard Gill (talk) 08:03, 22 October 2010 (UTC)
- Let's leave the COI issue to other pages. Will Beback talk 03:33, 22 October 2010 (UTC)
- Glopk is talking about the Jeff Gill reference (a published book), not the pre-publication Richard Gill references. -- Rick Block (talk) 02:03, 22 October 2010 (UTC)
- Regardless of their relevance, we can't use the Gill papers unless they've been published. The current entries say they're pre-publication versions. Will Beback talk 00:11, 22 October 2010 (UTC)
Planning
[edit]- Let's first remember that this is an encyclopedia article. It should be relatively short yet comprehensive, based mainly on secondary sources, and written with the reader in mind. It's OK to pitch it to a non-layman audience, but it should not presuppose any special knowledge of the issue.
- There are three core content policies which apply to every article on Wikipedia:
- It's usually best to combine sources to give a general view. However I think that has proven elusive with this topic. There are so many ways of framing the issue that it's hard to organize the article without favoring some assumptions over others.
- Instead of trying to create an integrated summary, I suggest that we go forward by summarizing the sources. We can give each major author a paragraph, with another paragraph for the minor authors. The format would be something like, "Paterson describes the problem as ..." "Gilpin presents it as a choice between ..." "Other views include Murphy, et al, who highlight some particular aspect, and Doe, who says that..." Every assertion is attributed and we simply summarize the sources, one by one.
- I realize this is a drastic step, but it has proven successful in other contentious articles I've dealt with. It makes the writing very concrete, we're just summarizing the sources, and eliminates the dilemma of preferring one view over another through article structure. It requires deciding which points by an author are most significant and how to summarize them, but those are simpler problems.
- Do editors think this approach might result in a comprehensive and stable article? (I have other ideas, but this is the best one.) Will Beback talk 10:46, 24 October 2010 (UTC)
- Will - It's been nearly a week. What are the next steps? -- Rick Block (talk) 13:57, 29 October 2010 (UTC)
Glkanter's Response
[edit]Whatever we've been doing isn't getting us anywhere. We asked for your increased participation, and this is your preferred approach. I'm certainly willing to give it a try. Glkanter (talk) 12:34, 24 October 2010 (UTC)
But if its gonna drag out like before, and I get called 'impatient', and we lose any 'momentum' whatsoever with the 'tag team' mediator approach, well... Glkanter (talk) 20:34, 26 October 2010 (UTC)
Martin's response
[edit]I have to say that I do not much like that approach and consider that it should be unnecessary, as you say above, 'It's usually best to combine sources to give a general view'. I believe that most editors are happy with nearly all of the article as it is now, and, bearing in mind that it is still an FA, starting from scratch and treating it more like a literature survey is not a good way to go in my opinion. Martin Hogbin (talk) 12:48, 24 October 2010 (UTC)
Rick's response
[edit]Regardless of whether we use these summaries as the basis for the article's structure, I think doing this would be very useful. As an example, I previously summarized Carlton's paper here. Rather than commit to a literature survey style now, I would prefer if we revisit the question of how to structure the article after we write a selection of these summaries. To be clear, your suggestion is not to collect verbatim quotes from sources but to concisely summarize entire sources. Is this correct? -- Rick Block (talk) 16:57, 24 October 2010 (UTC)
- I would be happy to go through the sources and discuss exactly what each one says, in fact I tried to set up such a discussion here. It is likely to lead to the same old arguments though. Martin Hogbin (talk) 16:47, 25 October 2010 (UTC)
Richard's response
[edit]I'm happy to try this. But I also have the opinion that the article is fairly decently organized right now. Sources can be separated into simple solutions and complicated ones, though some sources give both kinds of solutions.
It would be good to cut down the number of sources we talk about. There are a couple of historically important, primary sources. And there is a recent book which consolidates much of the earlier literature (Rosenhouse).Richard Gill (talk) 19:53, 27 October 2010 (UTC)
I think there is another way to get to a concensus. I believe that it is a red-herring that the distinction between the conditionalists and the unconditionalists is whether or how conditional probability should be used in solving MHP. Actually it is whether or not the individual door-numbers should be used in solving MHP.
When one converts a "real-world problem" (or realworld-like problem) into a problem which can be solved with logic or mathematics one reduces the verbiage and cuts down to the essentials. There is a pre-processing stage where we talk informally and use common sense, we arrive at a formal problem, we solve it with formal methods, then there sometimes follows some post-processing to get the answer. Whitaker wanted to know whether to stay or switch. The pre-processing results in a probability problem, some logic or probability calculus gives the answer, 2/3. The post-processing results in the advice "switch".
Now, does one decide right at the start that the door-numbers are irrelevant, only the actions? If so one can procede to solve the problem with a simple solution. If not one has to do some work during the formal stage. One could argue within the mathematical/logic stage that by symmetry the conditional probabilities do not depend on the specific doors hence are equal to the unconditional probability. Or one could just calculate away with the formal definition of conditional probability ... it comes out in the wash. Or one uses Bayes' theorem (odds formulation) to avoid calculation. Then one does the post-processing. Switch doors.
Possibly the simple solution lovers will say that there is no formal or mathematical arguing needed in solving MHP. But then I think they forget that initially everyone gives the wrong answer. So ordinary intuition gives the wrong answer, common sense logic can give the wrong answer. You have to think out of the box and look at the problem in a different way and only then do you suddenly "see" that switching is the right answer. But still, if you try to clear your mind and forget all the discussions, I think it still remains an amazing conclusion.
I have written a little essay on this on my talk page, at [8] Richard Gill (talk) 18:55, 29 October 2010 (UTC) Richard Gill (talk) 18:55, 29 October 2010 (UTC)
- Although I agree with what you write, I do not think that it is an approach that we can use to help us here as there are not many (any?) independent sources that propose your method of solution. I have suggested discussing what the sources say below. Do you think this is a good idea and, if so, would you like to suggest one? Martin Hogbin (talk) 17:11, 30 October 2010 (UTC)
- +1 to Martin, but: What Richard proposed above imo could really help us to get ahead in the actual situation/mediation. Yes, can really help. And I also agree to what you say below, in "Let us look at the sources", because that's exactly the point. We really should work on those advisable sources to be used, helping the reader to finally catch both, the "dilemma" (it's indicative for the existing dilemma that more than 90 % of intuitively given answers are completely wrong), as well as the "problem-problem" of controversy surrounding the fighting of those parochial and narrow-minded "only correct solutions". I therefore agree to you that treating it more like a literature survey is not a good way. And I hope Will could appreciate such proceeding to come to a mutually agreed welcome solution. Imo such proceeding could help to get to a really profitable outcome, at last. Gerhardvalentin (talk) 19:10, 30 October 2010 (UTC)
- Martin, I'm not proposing to rewrite the article on the lines of an approach which is not yet available in the sources, ;-) . I'm saying that in order to get out of the dead-lock between the editors one needs to somehow find some common ground. A higher point of view guided by "the truth" could be useful. The spectrum of opinions between the editors is similar to the spectrum of opinions in the sources. For some editors and sources, the distinction between the conditional formulation and the unconditional formulation is the distinction between the right problem formulation and the wrong problem formulation. For others it is an academic distraction and apparently to some (both editors and sources) the distinction is so subtle that they can hardly recognise it. What I'm saying is that if we think about the process of solving puzzles like this one, we will recognise that there is a process of deciding what is essential and what is ornamentation. It seems to me clear that this process is an art, not a science, and consequently that there is also room for differences of taste.
- Let me put it another way. The article is not about THE solution to THE MHP, it is about the rich history of different persons' solutions to different perceived interpretations of MHP.Richard Gill (talk) 13:09, 31 October 2010 (UTC)
Let us look at the sources
[edit]It has been suggested by the mediators that we look at what the sources say on the subject but is seems to me that most editors here do not want waste all the hard work put in to get this article to FA status. I therefore propose, that we agree to look at the sources and discuss what they do say about the MHP but that we do not attempt to rewrite the article as simply a literature review. If we can agree on what the sources do say we can then edit the article collaboratively to reflect their overall balanced view, if necessary.
If we agree on this perhaps someone would propose a source to discuss first. Martin Hogbin (talk) 17:05, 30 October 2010 (UTC)
- Will said above "I'm going to invoke my role as mediator and start structuring the discussions more so that we can stay focused", and (as I interpret his suggestion) has suggested we collaboratively write (as opposed to discuss) summaries by author (one section per major author and a paragraph each for minor authors). Here's the current TOC of the article:
Current TOC
|
|---|
* 1 Problem
* 2 Solutions
o 2.1 Simple solutions
o 2.2 Aids to understanding
+ 2.2.1 Why the probability is not 1/2
+ 2.2.2 Increasing the number of doors
+ 2.2.3 Simulation
o 2.3 Conditional probability solution
+ 2.3.1 Mathematical formulation
* 3 Sources of confusion
* 4 Variants – slightly modified problems
o 4.1 Other host behaviors
o 4.2 N doors
o 4.3 Quantum version
* 5 History of the problem
* 6 See also
o 6.1 Similar problems
* 7 References
* 8 External links
|
- I don't think there's much disagreement about anything other than the solution section, so rather than rewriting the article in literature survey style, another way to view this suggestion is as rewriting the solution section (which I think is ultimately what any resolution of this mediation will entail). Specifically, this would change the TOC to be something more like:
Proposed TOC
|
|---|
* 1 Problem
* 2 Solutions
o 2.1 vos Savant's solution
o 2.2 Devlin's solution
o 2.2 Grinstead and Snell's solution
o 2.2 Morgan et al.'s solution
o 2.3 Rosenthal's solution
o 2.3 Formal mathematical solution
* 3 Sources of confusion
* 4 Variants – slightly modified problems
o 4.1 Other host behaviors
o 4.2 N doors
o 4.3 Quantum version
* 5 History of the problem
* 6 See also
o 6.1 Similar problems
* 7 References
* 8 External links
|
- To write these sections we don't need to agree in the least which one is THE TRUTH - only that the words in each section accurately reflect what the author/source is saying. Given how cantankerous some of us seem to be, I don't expect that even this much will be easy - but I think it's definitely worth a try. I wouldn't consider him a "major author", but as I mentioned above I've written a summary like this for Carlton's solution.
Carlton's solution
|
|---|
|
Carlton's solution  Carlton (2005) presents a solution based on conditional probability using a decision tree showing all probabilities assuming the player initially selects Door 1 (as shown to the right). The probability the host opens Door 3 given the car is behind Door 1, Door 2, and Door 3 is 1/2, 1, and 0, respectively. The total probability the host opens Door 3 is therefore 1/3 x 1/2 + 1/3 x 1 + 1/3 x 0 = 1/2.
hence
In other words, a player who sees the host open Door 3 and switches has a 2/3 chance of winning the car. An intuitive explanation of this result is that switching loses if and only if the player initially picks the car, which happens with probability 1/3, so switching must win with probability 2/3. |
- I don't care whether we use this as one of the sections or not (it's already written, so in some sense why not?), but I think writing sections about of this length cited to a single source should be possible. -- Rick Block (talk) 18:16, 30 October 2010 (UTC)
- Rick, one of us has lost the plot here. I suggested that we discuss what the sources say not rewrite the article or even part of it literature-survey style. Nobody, including yourself, liked that idea much. Martin Hogbin (talk) 22:49, 30 October 2010 (UTC)
- I agreed we write sections summarizing sources as if we intended them to be included in the article - but suggested we defer the decision about exactly how to structure the article until after we do some. I've asked Will to comment. Are you willing to follow what he suggests? -- Rick Block (talk) 03:43, 31 October 2010 (UTC)
- Rick, do you really think that the article we be better with the a 'solutions' section written as a series of literature quotes? Why not discuss what the sources say and use the results of that discussion to guide (not control) our approach to improving the article. To rewrite sections of an FA just because of a minor but intractable disagreement between editors is madness. Martin Hogbin (talk) 10:34, 31 October 2010 (UTC)
- I agree with Martin here. Richard Gill (talk) 12:58, 31 October 2010 (UTC)
- Not literature quotes - summaries of sources. Are you saying no, you won't even consider trying this? -- Rick Block (talk) 16:28, 31 October 2010 (UTC)
- I think Martin and I are both happy to contribute to writing summaries of sources and to discuss same. But we are both bothered by your suggestion to actually structure the article as a sequence of various sources' solutions. I was also put off by the idea that there would be a section "formal mathematical solution". I suppose Rick you are thinking here of a formal mathematical version of the conditional solution. Yet it is perfectly easy (but probably a waste of time) to write a formal mathematical version of most of the simple solutions, too. The difference between conditional and simple is not a question of mathematical rigour, but a question of focus: what is the mathematical problem to be solved. Anyway, I believe the essential content and even the idea of the simplest proof (the proof by symmetry) of the conditional solution can be communicated to most lay-persons. So we don't have to give readers the idea that there is a simple solution for dumbo's which people with a PhD in maths will realize are wrong, and they and they only can read the formal mathematical proof... . I think it would be wonderful if we could present both the simple PROBLEM and the conditional PROBLEM and their solutions in such a way that readers can decide for themselves which problem they think is the right problem. After all, both the sources and the editors disagree on exactly this question. Our task is to present the spectrum of problems-with-solutions which are out there. Let each reader choose what suits them best. Richard Gill (talk) 17:13, 31 October 2010 (UTC)
- I think this is what the current solution ordering automatically does. Those who just want a simple explanation of why the answer is 2/3 will read the first part of the article. Those who want to consider the problem in more detail will read further. Is this not how most people approach a book or article on a new subject. If the first part gives them the answers that they want the just read that and then stop, if they think the first part is too simple for them, they skim through it and move on to the more complex bit. Martin Hogbin (talk) 22:24, 31 October 2010 (UTC)
- +to Richard, +to Martin (... the end of the tunnel). Rick, Will: Finally, a solution in sight Gerhardvalentin (talk) 14:54, 1 November 2010 (UTC)
- @Will, Rick. I agree with co-authoring source summaries for the solution section, and deferring to a later discussion whether they should become the text of the section itself, or simply inform it.
- @Martin. The current section ordering in the article is part of the issues under mediation (see structural POV). Repeating for the n-th time your explanation for why you think it is all well and good is not helpful at all. Will and Rick have proposed a way forward with the co-authoring of source summaries. This may be helpful, as past experience on the talk pages has shown repeated cases of editors speaking from ignorance (of the sources). And that includes editors involved in this mediation.
- @Richard. The formal mathematical solution is published in reputable sources (cited J.Gill, Henze, and many uncited others) - that it is perfectly easy [...] to write a formal mathematical version of most of the simple solutions, too is perfectly irrelevant at least until reputable sources doing so are produced (translation: either you do the legwork of finding them, or please avoid wasting WP's valuable disk space and our as-valuable time alleging they may exist somewhere).
- @All: There is a constructive proposal on the table that involves each of us editors doing actual work upon actual sources, as opposed to bitching to each others about how excellent our own understanding of the problem is, and how obviously good the readers will find it. Please please, let's move forward with it. glopk (talk) 15:21, 1 November 2010 (UTC)
- @Glopk. A formal mathematical solution corresponding to the simple solution is published in [9], an article by the mathematical statistician R.D. Gill appearing in the International Encyclopaedia of Statistical Science (sollicited by the editors, and peer reviewed), published by Springer, November 2010. The same scientist is currently working on a revision [10] of his paper [11] accepted by Statistica Neerlandica, and would probably be still able to add further details if that might be found useful by readers like you. Who knows, maybe that work might be useful to the wikipedia article in a few years time, after the dust has settled around the present fighting. Personally I wouldn't call those papers "own research". Whatever new they do contain, was learnt from coeditors here.
- I agree that wikipedia can't refer to unpublished work and that there is a possible conflict of interest, in that a scientist working on MHP is taking part of the present mediation on the MHP article. Wikipedia editors tend to like to work on articles about topics on which they are well informed! I am happy to withdraw from the mediation, if you fellow editors would prefer that.
- The important thing I want to say is that as long as the wikipedia article contains statements which, to many readers, are obviously nonsense, it will remain very unstable. An example is the notion that the simple solutions can't be made mathematically rigourous while the conditional solution can. They can both be made equally rigorous. Please try to appreciate that they are both correct solutions, but to different problems. The important question "what is the right problem to answer?" is a matter of dispute among editors, as it is among sources. Let's keep our sights on that and not waste time each pushing our own favourite solution with silly arguments. Precisely that tactic has been getting us nowhere for a long time. Richard Gill (talk) 09:51, 2 November 2010 (UTC)
- I think this is what the current solution ordering automatically does. Those who just want a simple explanation of why the answer is 2/3 will read the first part of the article. Those who want to consider the problem in more detail will read further. Is this not how most people approach a book or article on a new subject. If the first part gives them the answers that they want the just read that and then stop, if they think the first part is too simple for them, they skim through it and move on to the more complex bit. Martin Hogbin (talk) 22:24, 31 October 2010 (UTC)
- I think Martin and I are both happy to contribute to writing summaries of sources and to discuss same. But we are both bothered by your suggestion to actually structure the article as a sequence of various sources' solutions. I was also put off by the idea that there would be a section "formal mathematical solution". I suppose Rick you are thinking here of a formal mathematical version of the conditional solution. Yet it is perfectly easy (but probably a waste of time) to write a formal mathematical version of most of the simple solutions, too. The difference between conditional and simple is not a question of mathematical rigour, but a question of focus: what is the mathematical problem to be solved. Anyway, I believe the essential content and even the idea of the simplest proof (the proof by symmetry) of the conditional solution can be communicated to most lay-persons. So we don't have to give readers the idea that there is a simple solution for dumbo's which people with a PhD in maths will realize are wrong, and they and they only can read the formal mathematical proof... . I think it would be wonderful if we could present both the simple PROBLEM and the conditional PROBLEM and their solutions in such a way that readers can decide for themselves which problem they think is the right problem. After all, both the sources and the editors disagree on exactly this question. Our task is to present the spectrum of problems-with-solutions which are out there. Let each reader choose what suits them best. Richard Gill (talk) 17:13, 31 October 2010 (UTC)
Rick, why is Selvin excluded from the solutions? He offers a simple solution, the decision tree, and Monty Hall's simple solution. Carlton's simple solution is very similar to Hall's solution, which is enthusiastically endorsed by Selvin. Glkanter (talk) 14:06, 2 November 2010 (UTC)
- I haven't excluded anything. The proposed TOC above is merely exemplary. If we decide we want a section on Selvin's solution that's fine with me. -- Rick Block (talk) 15:10, 2 November 2010 (UTC)
Its just my long-standing, hard-earned lack of trust in some editors. I clearly recall the days when I was criticized and ostracized by most editors, including a so-called Wikipedia subject matter expert for arguing that the simple solutions were *not* flawed, which contradicted the overwhelming POV of the Wikipedia article at the time, and is still present today. Which no one seems all too interested in eliminating. Back then 'reliable sources' were deemed of no import, and/or were called 'lazy'. Rather, arguing about math, and card game simulations and 'because it fails for similar, but different problems' and other horrible crap took up the talk pages. While they have changed their arguments (they had to, Selvin had the 'equal got door constraint', Morgan threw in the towel, and "Suppose you're on a a game show..." is pretty unambiguous), none of those still-active editors have acknowledged their errors, and some keep demanding the article be edited with an emphasis that the simple solutions indeed, are wrong. Glkanter (talk) 17:43, 2 November 2010 (UTC)
Carlton
[edit]So let us discuss what Carlton says about the MHP here. Martin Hogbin (talk) 20:44, 1 November 2010 (UTC)
- See above. -- Rick Block (talk) 00:12, 2 November 2010 (UTC)
Richard's comment on the text above. I just read Carlton's paper carefully. The summary above looks fine to me, except that I would add the words "According to Carlton" before the final sentence "An intuitive explanation". I think it needs emphasis that Carlton thinks this is an intuitive explanation, the wikipedia editors don't necessarily subscribe to that opinion. It might also be added that Carlton makes all the usual "equal probability" assumptions without any attempt at motivation whatsoever. Richard Gill (talk) 14:05, 2 November 2010 (UTC)
It's like pulling teeth to get you guys to edit rather than argue. Here's the text (with Richard's suggested clarification re "intuitive explanation"). Please edit as if it were a section in the article. -- Rick Block (talk) 15:19, 2 November 2010 (UTC)
Carlton's solution
|
|---|
|
Carlton's solution  Carlton (2005) presents a solution based on conditional probability using a decision tree showing all probabilities assuming the player initially selects Door 1 (as shown to the right). The probability the host opens Door 3 given the car is behind Door 1, Door 2, and Door 3 is 1/2, 1, and 0, respectively. The total probability the host opens Door 3 is therefore 1/3 x 1/2 + 1/3 x 1 + 1/3 x 0 = 1/2.
hence
In other words, a player who sees the host open Door 3 and switches has a 2/3 chance of winning the car. Carlton also presents what he calls "an intuitive explanation" of this result, specifically that switching loses if and only if the player initially picks the car, which happens with probability 1/3, so switching must win with probability 2/3. |
Rick, I do not wish to edit this as though it were a section of the article because it is not one and most editors do not wish the article to have sections such as this. My suggestion was to discuss what salient points Carlton makes about the MHP. — Preceding unsigned comment added by Martin Hogbin (talk • contribs)
- I think all salient points are captured in the summary above. Is there anything you disagree with or would like to add? -- Rick Block (talk) 00:12, 3 November 2010 (UTC)
In other words, a player who sees the host open Door 3 and switches has a 2/3 chance of winning the car.
Carlton does not mentioning that the player, 'sees the host open Door 3'. Martin Hogbin (talk) 09:15, 3 November 2010 (UTC)
Carlton also presents what he calls "an intuitive explanation" of this result, specifically that switching loses if and only if the player initially picks the car, which happens with probability 1/3, so switching must win with probability 2/3.
Carlton does not state that this intuitive explanation is in any way incomplete or defective or that it answers the wrong question. Martin Hogbin (talk) 09:15, 3 November 2010 (UTC)
- Martin, I don't see what is wrong with "sees". According to the model which is described in the diagram, where initially all doors are equally likely to hide the car and where the host is equally likely to open either goat-door if the car is behind the player's initial choice, it is a fact that for a player who initially chose Door 1 and then saw the host open Door 3, the chance is 2/3 that Door 2 hides the car. Moreover, the simple solutions, including Carlton's intuitive solution, do not give us this information.
- *Because* this chance does not depend on which door numbers are involved, the player can safely ignore the numbers altogether. Though he "sees" the numbers, he doesn't need to make any use of them. In other words, it does not disadvantage him to be blindfolded. He could be told that the doors are coloured red, green and blue, but he can't see the colours, doesn't know the correspondence with position on the stage, and he chooses a colour by naming it. He next hears a door being opened and a goat bleating, and is asked if he would like to switch to the third door.
- All in all, it is pretty clear that Carlton's paper is written under the assumption that the right question is the conditional probability question, and that the "intuitive explanation" is only an intuitive explanation, not a solution. As we know, but Carlton doesn't say, the intuitive solution can be completed by taking account of the symmetry of the problem.
- The problem *we* have in this controversy is that the symmetry is so obvious and intuitive that people not accustomed to formal mathematical reasoning don't even realise that they are using it. The unconditional solution tells us that if you ignore the door numbers, you should switch. It does not tell us that the door numbers are irrelevant to your decision, though almost everyone will intuitively feel that. Carlton doesn't tell us *why* he thinks the conditional question is the right question to ask. He takes this for granted. He asks, given you chose Door 1 and the host opened Door 3, what is the best action to take? His answer: switch, because - under the supplementary assumptions - we know that the conditional probability is 2/3.
- His paper further contains a genetics example, and the prisoner's dilemma example. The prisoner's dilemma is just MHP in disguise. The genetics example is more involved. I guess that all the unconditionalists here would agree that the genetics example does need to be solved by Bayes. There is not a short cut to getting the right answer because the problem does not have the same symmetries as MHP. Richard Gill (talk) 11:47, 3 November 2010 (UTC)
Richard, this paragraph is unsupported by the reliable sources:
- " Martin, I don't see what is wrong with "sees". According to the model which is described in the diagram, where initially all doors are equally likely to hide the car and where the host is equally likely to open either goat-door if the car is behind the player's initial choice, it is a fact that for a player who initially chose Door 1 and then saw the host open Door 3, the chance is 2/3 that Door 2 hides the car. Moreover, the simple solutions, including Carlton's intuitive solution, do not give us this information."
Selvin's simple solution is in response to a empty box 'A' having been revealed. Monty Hall's simple solution (heartily endorsed by Selvin) is in response to empty box 'A' being revealed. vos Savant's simple solution is in response to a door being opened to reveal a goat. Devlin's (and others) Combining Doors simple solution shows Door 3 opened to reveal a goat.
Describing Carlton's 'intuitive explanation' as an 'intuitive explanation' is obviously a true statement. It just happens to be meaningless, and therefore does not support your personal interpretation of his paper. Glkanter (talk) 12:12, 3 November 2010 (UTC)
Carlton does include this statement "...Monty Hall must reveal the location of the other goat, and you switch to the remaining door - the car."
As for symmetry, I think the Wikipedia reader capable of dressing him or herself in the morning will understand the existence of the symmetry from "Suppose you're on a game show...". Don't you agree? Even if a solution does not explicitly spell it out. Besides, every symmetry is explained in the premises that precede the solution sections of the Wikipedia MHP article 3 times. Why should any solution have to make a federal case of it? Its no great secret available only to insiders. Glkanter (talk) 12:22, 3 November 2010 (UTC)
- Garry: My first sentence "according to the model which is described in the diagram, where initially all doors are equally likely to hide the car and where the host is equally likely to open either goat-door if the car is behind the player's initial choice, it is a fact that for a player who initially chose Door 1 and then saw the host open Door 3, the chance is 2/3 that Door 2 hides the car" is objectively reporting what Carlton does. My second sentence : "the simple solutions, including Carlton's intuitive solution, do not give us this information" is, I believe, also a matter of fact. But perhaps I should be more precise. The authors of those sources may think that they are giving us this information, but they don't do that explicitly, as you can see by studying their solutions. Explicitly, those solutions only lead to the fact that switching gives the car 2/3 of the time, overall. Selvin's two papers are quite a mess since he solves different mathematical questions in different ways and does not even comment on the fact that his solutions have different meanings to one another. Vos Savant's written reasoning and Monty Hall's written reasoning do not lead to this fact. The statement of Carlton "...Monty Hall must reveal the location of the other goat, and you switch to the remaining door - the car" is about the recommended action ("switch"), not about the reasoning behind it.
- We are talking about solving brain-teasers. If you use symmetry to solve a brain-teaser, you ought to say so. We are reporting the reasoning of those sources. We know they all claim to solve vos Savant's question, that is not in any doubt. By "solution" we don't mean the answer "2/3" or "switch" or whatever, but in the reasoning behind it. The logical reasoning behind it.
- I think that any wikipedia reader who is capable of getting dressed in the morning ought to be able to see the difference between the statements "2/3 of all the times, the car is behind the other door" and "2/3 of the times that Monty opened door 3, the car is behind the other door". It can't hurt the article to say a few words about this difference.
- By the way, not everyone assumes symmetry from the words "Suppose you're on a game show". Or rather, depending on how people understand *probability*, people will make use of the symmetry in different ways. If probabilities are in the real world, in the way the quiz team hides the car, and the way Monty Hall chooses a door to open, then the words "suppose you are on a game-show..." do not tell us anything about them at all. On the other hand, if probabilities are in your mind, then for the same reason, you will translate this lack of information into equal (personal, subjective) probabilities.
- But anyway, if actually every simple solution is using symmetry implicitly, then what's the harm in saying so? Are you saying that you agree that you *would* be interested in Prob(Door 2 hides car| you chose Door 1, host opened 3) *if* you had any reason to believe it would be different from Prob(Other door hides car)? But since you do *know* that it is not different, the simple solution is indeed complete?
- This would be a great step forwards! It would mean that we are simply quarelling about the use of the word "complete". You say the simple solution is complete because you have already thought about the matter and know there is no need to condition on the door numbers, whereas the conditionalists say the simple solution is incomplete because these thoughts are not written down explicitly. I think the mediation can now quickly draw to an end, if everyone will agree with this. Richard Gill (talk) 13:49, 3 November 2010 (UTC)
- I was using my analytic abilities to show the flaws in your arguments, above. For the article, and its editing, I rely solely on what the reliable sources say. The opinions and preferences of any editor, including myself, are of little interest. Glkanter (talk) 15:54, 3 November 2010 (UTC)
- Richard, what is wrong with 'sees' is simply that Carlton does not use that word and, in particular, does not give it as a reason for using conditional probability. It may well be that the player sees a door opened but that is not what Carlton actually says neither does he say that he considers what the player sees to be important. Martin Hogbin (talk) 13:52, 3 November 2010 (UTC)
- Here's Carlton's quote:
- Let C denote the event that the car is behind Door #2; the a priori probability of C is P(C) = 1/3. Let D denote the event that Monty opens Door #3; according to Figure 5.
- P(D | C) = 1 and P(D) = 1/3 x 1/2 + 1/3 x 1 + 1/3 x 0 = 1/2
- Hence, by Bayes' Rule,
- (equation showing P(C|D) omitted)
- Therefore, the car is hidden behind the remaining door two-thirds of the time. In other words, the contestant can double his chance of winning the car (from his initial 1-in-3 guess) by employing the strategy of switching when Monty Hall gives him the option.
- Rather than
- In other words, a player who sees the host open Door 3 and switches has a 2/3 chance of winning the car.
- would you be OK with
- In other words, a player who switches when given the option has a 2/3 chance of winning the car.
- We all know the option is not offered until after the host opens a particular door (door 3, in the example case) and that the player "sees the host open" this door - so this has the same meaning - but if you're going to refuse to summarize with comprehension of what the source is saying, IMO the revised wording is equivalent. -- Rick Block (talk) 14:40, 3 November 2010 (UTC)
- IMO this is getting silly. The word "sees" is irrelevant. Carlton shows with his decision tree that in 2/3 of those times that the player chose Door 1 and the host opened Door 3, the car is behind Door 2. That is a very different statement from the statement which corresponds to Carlton's intuitive solution: in 2/3 of those times that the player chose Door 1, the car is behind the other door than the door which the host opened. Of course, because the fraction 2/3 in both statements is the same, it turns out that "seeing" the number of the door opened by the host doesn't help you to decide whether to switch or stay. Of course, if you are smart, you can argue a priori that the door numbers don't give any information, so you might as well compute the unconditional chance. If you are not smart, you might not think about this issue at all.
- The whole point of MHP is that we must mistrust our "inborn" probabilistic intuition. Everyone's initial intuition is that you can stick with your original choice because the action of the host doesn't give any useful information. *We* all agree that that *this* initial intuition is wrong. The simple solution proves to us, that that initial intuition is wrong. Next, some annoying professors of statistics who publish in specialist journals say that this solution is not complete, because you are not taking account of *which* door was opened by the host. Explicit computation, this time, ... confirms initial intuition! So the intuitionists say to the academics "keep your cake-hole shut" (to quote Colonel Quarich in "Avatar"). The academics say, "oh yeah, Ranger Rick, are you going to shoot me?" and "Quarich retorts "Yeah, I could do that". Richard Gill (talk) 21:54, 3 November 2010 (UTC)
- You understand that saying the car is behind Door 2 2/3 of the times that the player chose Door 1 and the host opened Door 3 is a very different statement from the statement corresponding to Carlton's intuitive solution (i.e. that always switching wins 2/3 of the time) - but it seems that some editors here a) refuse to accept that these are different statements, b) refuse to accept that the "simple" solutions say the latter but not the former, c) refuse to believe that this is exactly what (at least some) sources say, and d) do not want the article to clearly say anything like this. If you're standing in front of two closed doors and an open door, judging that the probability the car is behind the open door is now 0 and thinking about the probabilities that the car is behind the other two doors (which intuitively seem to be 1/2 for each door) - what kind of probabilities are we talking about? Morgan et al., Gillman, Carlton, Grinstead and Snell, Eisenhauer, Rosenthal, etc. etc. are ALL saying these are conditional probabilities. You can clearly get the "switch" answer other ways, but if you want to say "the probability of winning by switching is 2/3 if you pick door 1 and the host opens door 3" (at which point the probability the car is behind door 3 is obviously 0) you have to be (you ARE) talking about conditional probabilities. What is silly is arguing that any sources contradict this point or that saying this has anything to do with POV. It's a plain mathematical fact undisputed by any sources, hence not in the least POV. -- Rick Block (talk) 05:34, 4 November 2010 (UTC)
Rick, many reliable sources solve the MHP where the contestant has selected door 1 and the host has revealed a goat behind door 3 with simple solutions. You don't need me to list them. That contradicts the conclusion of your posting, above. Glkanter (talk) 09:45, 4 November 2010 (UTC)
- Glkanter, there is no contradiction. Rick lists a set of sources clearly stating that the above-mentioned probability is conditional (indeed, plain mathematical fact). Are you saying that there are reputable sources disputing this fact - i.e. explicitly stating that it is not a conditional probability? glopk (talk) 15:11, 4 November 2010 (UTC)
Not that the question matters, but sure, any professional (Selvin, vos Savant- who did argue with the Morgan boys, Carlton, Devlin, Adams, etc...) that gives a simple solution says the problem does not need to be solved with a conditional solution. The false argument that an outright statement to that effect is a 'Wikipedia necessity' (what's the consequence, otherwise?) has long since been discredited on these talk pages. Those sources solve the exact same problem with the simple solution. They're reliably published sources. They continue to be published subsequent to and despite the papers that call it conditional. It's a popular POV, not universally shared. Exactly the same as the conditional solution. What else is needed? Glkanter (talk) 15:56, 4 November 2010 (UTC)
- I'm with Rick here. Sure, there are sources that say that the simple solution solves vos Savant's question. But that is not what this particular thread is about. We are talking about: what is in Carlton's paper? Carlton thinks that the simple solution does not solve the question that Carlton thinks needs to be answered. Carlton thinks that the question to be answered is: in what percentage of the time that you chose door 1 and the host opened 3, is the car behind door 2? He shows that the answer is 2/3. The simple solution only shows that in 2/3 of the time that you chose door 1, the car is behind the other door from the door opened by the host. It does not show that in 2/3 of the time that you chose door 1 and the host opened 3, the car is behind door 2. Richard Gill (talk) 22:55, 4 November 2010 (UTC)
Well, we're right back to the 'Bible Study' aspect of the sources' intent I had hoped we would avoid. 'Intuitive explanation' followed by a simple solution apparently is not up to certain editor's standards as wording for 'a solution'. It's similar to Monty Hall's solution that Selvin heartily endorsed, a little more explicit, actually. Glkanter (talk) 23:14, 4 November 2010 (UTC)
- I don't understand this interjection about "source intent"? Are you saying that Rick's summary above does not reflect what Carlton says in his own words? Please read the paper: it's Calton himself that uses the words "intuitive explanation". Do you agree that Rick's text above is an accurate and comprehensive summary of Carlton's paper (the part of it related to the MHP)? If not, which sentences of the summary do you disagree with, and how do you propose to change them? glopk (talk) 23:52, 4 November 2010 (UTC)
- Yes, I understand 'intuitive explanation' are Carlton's words, and they immediately precede a simple solution. My response was to Richard's response, not Rick's. And the mention of Hall/Selvin shows that Carlton is not the only source for this particular simple solution. Glkanter (talk) 00:08, 5 November 2010 (UTC)
As for presenting simple solutions first, let's let Carlton address that:
- "Before presenting a formal solution to the Monty Hall Problem to my students, I find that it helps to give an intuitive explanation for the 1/3 - 2/3 solution."
I presume that's true for Wikipedia readers, as well. Maybe more so. Glkanter (talk) 23:38, 4 November 2010 (UTC)
- The order in solutions in Rick's summary above follows the one in the source itself (Carlton's paper). Again, do you agree that Rick's text above is an accurate and comprehensive summary of Carlton's paper (the part of it related to the MHP, including its order of presentation)? If not, which sentences of the summary do you disagree with, and how do you propose to change them? glopk (talk) 23:52, 4 November 2010 (UTC)
- The inclusion of Carlton's comment about preceding the conditional solution with a simple solution for his probability (?) students was meant to show that, as Martin has explained extensively, putting simple solutions first is not an NPOV violation, as has been claimed by opposition editors. Its simply how things are commonly done, for very obvious reasons. Glkanter (talk) 00:08, 5 November 2010 (UTC)
- But we are only talking about summarizing Carlton's article right here and now. Summarizing the sources so we have consensus on what they actually say is a step requested by the mediator. The sooner we have consensus on these summaries, the sooner we can go back to shaping the article, and hopefully edit it from a sounder basis. So, do you agree that Rick's text above is an accurate and comprehensive summary of Carlton's paper (the part of it related to the MHP)? Yes or no? If not, which sentences of the summary do you disagree with, and how do you propose to change them? glopk (talk) 05:26, 5 November 2010 (UTC)
- Martin objects to the word "sees" in the phrase "In other words, a player who sees the host open Door 3 and switches has a 2/3 chance of winning the car". OK, then how about: "In other words, when the player has chosen Door 1 and the host opened Door 3, there is a 2/3 chance that the car is behind Door 2". The sentence is an honest attempt to summarize what comes out of Carlton's math in a small number of words. I don't think the wikipedia editor has to be limited to words in Carlton's vocabulary. I don't think that this summary of what Carlton is actually calculating can be considered by anyone to be an opinion rather than a fact.
- The simple solutions can be summarized with the words "The player who switches wins 2/3 of the time". They do not show "The player who switches wins 2/3 of the time, whatever door he initially first chose and whichever door was subsequently opened by the host".
- The fact that Carlton tries to make his students more comfortable with the initially surprising result of a few lines of computation by giving the simple solution does not in any way imply that he thinks that the simple solution directly addresses the problem which he thinks ought to be addressed.
- Of course, we know that an appeal to symmetry would close the gap, and indeed there are also reliable sources including Morgan et al. who say so.
- I think that Carlton's side remark about his pedagogical methods is pretty irrelevant to the job of summarizing what his main contribution was. Richard Gill (talk) 07:44, 5 November 2010 (UTC)
A better way to summarize Carlton is not by confusing the reader by bringing in his remarks on the intuitive solution, which he sees merely as a shock-reducing comfort-blanket, but the following:
- He certainly sees the 'intuitive explanation' aka 'simple solution' as 'correct', or he wouldn't include it in his book. 'Shock-reducing comfort-blanket'? That's simply your interpretation, isn't it? Those are not his words. In any way. Hopefully, at least one student in the lecture will be awake enough to ask, 'If that works, why is the complicated stuff required?'. To which it would be responded, 'Well, in this particular problem, its not really required, per se, but since this *is* a course on introductory probability...' Glkanter (talk) 12:27, 5 November 2010 (UTC)
When wondering where the car is, you shouldn't just use the hard information which you have in front of you, but also the likelihood that that information came to you under the different scenarios which concern you. You chose Door 1. The host is twice as likely to open Door 3 if the car is behind Door 2 than if the car is behind Door. 1. When the game is repeated many times, the car will be behind Door 2 twice as often as it is behind Door 1, within those occasions that you chose Door 1 and the host opened Door 3.
Forget about probability, forget about information. This is about very simple logic and very simple arithmetic. Richard Gill (talk) 08:03, 5 November 2010 (UTC)
How about the following:
Carlton's solution (according to Richard)
|
|---|
|
Carlton's solution  Carlton (2005) presents a solution based on conditional probability using a decision tree showing all probabilities assuming the player initially selects Door 1 (as shown to the right). The probability the host opens Door 3 given the car is behind Door 1, Door 2, and Door 3 is 1/2, 1, and 0, respectively. The total probability the host opens Door 3 is therefore 1/3 x 1/2 + 1/3 x 1 + 1/3 x 0 = 1/2.
hence
In other words, when the player has chosen Door 1 and the host opened Door 3, there is a 2/3 chance that the car is behind Door 2. The underlying reason for this is that the host is twice as likely to open Door 3 if the car is behind Door 2 than if the car is behind Door 1. When the game is repeated many times, then, on those occasions that the player chose Door 1 and the host opened Door 3, the car will be behind Door 2 twice as often as it is behind Door 1. |
Carlton also writes "Incorrect revision of probabilities also lies at the heart of the now-famous Monty Hall Problem". He means by this that the usual, WRONG, intuitive solution "50-50 because you did not get any new information from the host's action" is an example of incorrect updating of probability according to new information. He presents the conditional solution as the right way that that usual, wrong, intuitive solution needs to be adjusted. His whole paper is about right and wrong ways to solve conditional probability puzzles. His paper is nicely written and very accessible, it is freely available on internet, and it is published in a reputable journal on teaching very basic math. It's not a paper about rocket science for rocket scientists. Richard Gill (talk) 08:15, 5 November 2010 (UTC)
- I look forward to the Morgan discussions. They say there is no 50/50 host bias, the only 'correct answer' is that its >=1/2 at all times - so switch, all simple solutions are false, and the conditional decision tree is false. Although they later say 'its 2/3, period'. Using Richard's argument and logic that Carlton can't be used as a source for the simple solutions, Morgan is disqualified as a source for most things in the article. Glkanter (talk) 11:54, 5 November 2010 (UTC)
- I too look forward very much to the Morgan discussions.
- BTW, I do not say that Carlton can't be used as a source for simple solutions. His paper obviously does contain one. He can also be used as a source for probability trees, and you can use probability trees to formalize the simple solutions too, which of course also can be presented in terms of conditional probability. But his paper can't be used as a source for the claim that the intuitive solutions are solutions to (what Carlton considers to be) the MHP. Richard Gill (talk) 08:20, 6 November 2010 (UTC)
- I respectfully disagree with your personal interpretation (OR) of Carlton's paper, and how it may appropriately be referenced. Also could you please help me to understand the differences here?:
- "BTW, I do not say that Carlton can't be used as a source for simple solutions. His paper obviously does contain one."
- -and-
- "But his paper can't be used as a source for the claim that the intuitive solutions are solutions to (what Carlton considers to be) the MHP."
- Thank you. Glkanter (talk) 08:59, 6 November 2010 (UTC)
- I respectfully disagree with your personal interpretation (OR) of Carlton's paper, and how it may appropriately be referenced. Also could you please help me to understand the differences here?:
- I don't think my personal interpretation of Carlton's paper is OR. He is a mathematics educationalist and so am I. Yet my own POV on MHP is very different from Carlton's.
- Your question about my use of the words "solution": there is a POV that MHP is about finding a conditional probability given the player chose Door 1 and the host opened Door 3. There is a POV that MHP is about finding "the" probability that switching gives the car. Let's call them the intuitionalist and the conditionalist POV's. So we have two MHPs: intuitionalist-MHP and conditionalist-MHP. Carlton uses one of the "correct" solutions to intuitionalist-MHP in order to push his students to accept that intuitive reasoning about conditional probability does not always give the right answer to what he sees the right question. Thus he prepares them for going through the sweat and tears of computing the conditional probability according to the rule-book rather than by intuition. The intuitive solution which he gives is a correct solution to intuitionalist-MHP but not a correct solution to conditionalist-MHP. The intuitionalists don't realise that talking about "the" probability that switching gives the car, though plain English and part of the man in the street's thinking about the world, does not make certain distinctions which sometimes are rather important. (Failure to appreciate this distinction is the cause of many scandalous miscarriages of justice, for example). Now, in our particular case, the distinction is actually "harmless" in the sense that the right advice "switch" is also obtained when one only conditions on the probability-1 event: "host opens door revealing goat". And because many editors don't appreciate these subtle distinctions we will remain quarreling here till the sun goes out and the seas freeze over.
Not what Carlton actually says
[edit]Both Rick and Richard give their own understanding of what Carlton means in his article. Were we to be planning a critique of Carltons's work that would be fine, but we are not. We are trying to discuss what Carlton actually says about the MHP, in order to inform us in the writing of an WP article. For example, Richard talks about what would happen 'When the game is repeated many times' but Carlton says nothing about this at all. Please note that I am neither agreeing nor disagreeing with this statement just pointing out that it was not made by Carlton.
We need to discuss exactly what each source actually says about the issues under dispute here. Interpreting each source in our own way is simply going to reproduce out personal opinions on the subject. Martin Hogbin (talk) 09:31, 5 November 2010 (UTC)
- The summary I wrote is intended to be exactly what Carlton says, no more, no less. Is there anything other than your previous comment about "player sees" (that I've responded to above) that you think is different in any way than what Carlton says? -- Rick Block (talk) 06:01, 6 November 2010 (UTC)
- I tried to help summarize the content of Carlton's paper, emphasizing the main conclusion, in a few lines and avoiding using technical language. I proposed an alternative to Rick's "sees" - though I don't think his wording was wrong. I use some words and some imagery which Carlton does not use. I conclude the section with a little executive summary for the readers who are not at home with probability calculus and formal mathematics and who are put off by arithmetic and numbers. Carlton talks about a probability being 2/3. How do you explain that a probability, say P(A), is 2/3? You say "in two out of three times that what we are talking about is repeated, A happens". How do you explain that a so-called conditional probability [say P(A|B) ] is 2/3? You say "in 2 out of 3 times that B happens, A happens too". I hope that Martin and Garry agree that the executive summary is an absolutely uncontroversial summary of what Carlton is doing, even if he doesn't waste paper in his publication in a specialist journal by reminding the reader what conditional probability actually is. I believe I have seen both of them using wording like "two out of three times" instead of "the probability is 2/3".
- No I didn't take the task literally "write down what Carlton says", no instead, I understand our task as to "write down what Carlton's paper is saying". It is interesting that all the major miscarriages of justice (e.g., O J Simpson, Lucia de Berk, Sally Clarke, Kevin Sweeney ..) involving probability and statistics, are about the fact that lawyers medics and journalists and jurors are absolutely incapable of distinguishing between P(B|A), P(A|B), P(A). O J Simpson case: most battered wives who get murdered, get murdered by their husband. The defence argued that most husbands who go in for wive-battering, don't murder their wives, and O J Simpson got off the murder charge. Kevin Sweeney: most times you smoke in bed, you won't die in a housefire, yet most times someone dies in a house-fire, it was because they smoked in bed. Kevin was sentenced for murder though the fire his wife died in was caused by her smoking in bed, because the prosecution argued that smoking in bed usually doesn't result in a house-fire. Richard Gill (talk) 08:05, 6 November 2010 (UTC)
- Unlike the unfortunate Mr. Sweeney, we have restricted our discussion and article editing to reliably published sources. Glkanter (talk) 08:59, 6 November 2010 (UTC)
- Do you want a reliably published source to back up the claim that P(A|B)=2/3 means that 2/3 of the time that B happens, A happens too? If Carlton goes to all that trouble to compute P(A|B), and we think he's an important "reliable source", wouldn't it be useful for the wikipedia reader to know what all that rigmarole was about? Isn't it also useful to understand why he uses a simple solution to prepare the student's mind for the counter-intuitive conclusion that you should switch on seeing Door 3 opened after you chose Door 1, but he does not present it as a legitimate and full solution itself?
- I agree that I expressed myself with slight bias to a "frequentist" way of thinking. I'm thinking about events which might or might not happen in some situation (the quiz-show...) which one can imagine unrolling, developing, in different ways. Sometimes certain events would happen, sometimes they wouldn't.
- Would you prefer: P(A|B)=2/3 means that when B is true, it is rational to bet at odds 2:1 on A being true too? Now I'm using probability as a description of my state of knowledge concerning a single situation, about some aspect of that situation which can be true or false. That's more how a subjectivist might think about probability.
- Or do you want a reliably published source which explains all the problems ordinary people have with the notion of conditional probability? Carlton's paper is about explaining conditional probability to students, which he considers is well known to be a very difficult task, he even mentions that some educationalists believe it is totally impossible. I guess the MHP deadlock is proof of that. Time for the troops to go home. Richard Gill (talk)
Another try, my executive summary is now
- Behind all this is the given assumption that if the player chooses Door 1, the host is twice as likely to open Door 3 if the car is behind Door 2 than if the car is behind Door 1. Initially it is equally likely that the car is behind Door 2 and Door 1. But because the host's reaction to the player's choice is twice as likely in the first case than in the second, it follows that on those occasions that the player chooses Door 1 and the host opens Door 3, the car is twice as likely behind Door 2 than behind Door 1.
Richard Gill (talk) 08:45, 6 November 2010 (UTC)
Carlton's solution (according to Richard, bis)
|
|---|
|
Carlton's solution  Carlton (2005) presents a solution based on conditional probability using a decision tree showing all probabilities assuming the player initially selects Door 1 (as shown to the right). The probability the host opens Door 3 given the car is behind Door 1, Door 2, and Door 3 is 1/2, 1, and 0, respectively. The total probability the host opens Door 3 is therefore 1/3 x 1/2 + 1/3 x 1 + 1/3 x 0 = 1/2.
hence
In other words, when the player has chosen Door 1 and the host opened Door 3, there is a 2/3 chance that the car is behind Door 2. Behind all this is the given assumption that if the player chooses Door 1, the host is twice as likely to open Door 3 if the car is behind Door 2 than if the car is behind Door 1. Initially it is equally likely that the car is behind Door 2 and Door 1. But because the host's reaction to the player's choice is twice as likely in the first case than in the second, it follows that on those occasions that the player chooses Door 1 and the host opens Door 3, the car is twice as likely behind Door 2 than behind Door 1. |
How about P(A|B)=2/3 means that when B is true, it is twice as likely that A is true than that A is not true. Carlton shows with his decision tree that when the player initially chooses 1 and the host opens 3, the car will twice as likely turn out to be behind door 2 as behind door 1. Carlton shows with his intuitive argument that when the player initially chooses 1, the car will twice as likely turn out to be behind the door the host doesn't open as behind door 1. And he knows the difference, and he thinks that the former is what is needed to solve MHP. I am not saying you have to agree with him. I'm saying that this is a fair representation of his work, which apparently is thought of as a reliable source for present purposes.
What is the objection against writing in easy and plain English what Carlton's conditionalist solution tells every reader? Why obscure it by not making the translation to plain English?
Since the simple solution can be explained in a few lines, and since the symmetry argument which bridges the gap between the two can be explained in a few lines, both solutions can be easily explained to all readers of wikipedia without any long words or formulas, and then every reader can decide for themselves which solution they like better. And it's all reliably sourcable. Richard Gill (talk) 14:20, 6 November 2010 (UTC)
- Richard - you are, of course, completely correct. However, I think the first step here is to get Martin and Glkanter to agree with the unadorned summary. Rather than muddy the waters with an original "executive summary", can we keep the focus on what Carlton more or less literally says? The translation to understanding of the meaning is what seems to be contentious - if we focus on the literal rather than the meaning it seems like we should be able to make some progress. -- Rick Block (talk) 16:05, 6 November 2010 (UTC)
- OK Rick, then you give a rewrite of your version which (a) addresses the problem that Martin thinks you can't use the word "sees" because Carlton doesn't use exactly that word, and which (b) omits any "executive summary". I agree that the executive summary could be considered as something outside of the summary itself.
- But it is interesting to discover that Glkanter and possibly also Martin consider any attempt to write what the ordinary person is supposed to understand by "P(A|B)=2/3" as "own research". My reply would be: "RTFM". Wikipedia tells you what are commonly accepted interpretations, and I just make use of them.
- I think it is not only legitimate but also important to use plain English translation of technical terms when one summarizes, for the use of wikipedia editors, an article which was written by and for mathematics educationalists. Moreover, since the editors here are quarreling about whether we do or do not need a conditional probability solution to MHP, I think it is also useful, for our discussion here, to emphasize that part of Carlton's work which bears precisely on the discussion. I was trying to fairly represent Carlton's point of view. (I do not have the same point of view, I have a different POV from every editor here, though it is at least the POV of a small minority of reliable sources.)
- Glkanter, for one, does not question the appropriateness of including the reliably sourced conditional solutions in the WP MHP article. In fact, I have repeatedly promoted a single Solution section which would include the conditional solution tree. RTF-EDITS. Glkanter (talk) 16:07, 7 November 2010 (UTC)
- My apologies, Glkanter. Now, do you also agree with my translation of P(A) and P(A|B) into plain English? And do you also agree with my summary of Carlton's point and the point of difference in the mediation, below? Then it seems to me that we are nearly home. Richard Gill (talk) 16:50, 7 November 2010 (UTC)
- What's the point of this whole 'Carlton' exercise in the first place vis a vis editing the article? Glkanter (talk) 17:29, 7 November 2010 (UTC)
- Carlton says that people get the wrong answer to MHP "don't switch" because their "wrong" understanding of conditioning makes them think the conditional probabilities are 50:50. He thinks that doing the conditioning according to the rule book is a reliable way to get the right answer. He uses the intuitive approach to 2/3 as an aid to intuition. He says that he uses it as a pedagogical device to motivate the students for the concentrated brain work necessary to solve what he sees as MHP, by showing that alongside the intuitive reasoning that you needn't switch because the conditional probability that the car is behind door 1 or door 2 given it isn't behind door 3 is 50:50, there is an intuitive reasoning which says that switching gives the car 2/3 of the time while staying gives the car 1/3 of the time. Richard Gill (talk) 13:57, 7 November 2010 (UTC)
- Carlton's point is that
- Prob(car is behind door 2 | car isn't behind door 3)
- is something different, conceptually, and in this example numerically, from
- Prob(car is behind door 2 | host opens door 3)
- Carlton's point is that
- The quarrel between the intuitionists and the conditionalists is all because
- Prob(car is behind other closed door | host opens door 3)
- is different conceptually, but not numerically (under the standard conditions), from
- Prob(car is behind other closed door | host opens a door)
- The quarrel between the intuitionists and the conditionalists is all because
- Here, Prob( A | B ), read "conditional probability of A given B", can be understood as the probability that A is true if/when B is true.
- It is all so bloody simple, pardon my French. Richard Gill (talk) 14:11, 7 November 2010 (UTC)
What Carlton literally says
[edit]Are we all now agreeing that this is what Carlton (more or less literally) says - using his own words where there's any possible contention, e.g "switches when given the option" as opposed to "sees the host open Door 3"? -- Rick Block (talk) 18:33, 7 November 2010 (UTC)
Carlton's solution
|
|---|
|
Carlton's solution  Carlton (2005) presents a solution based on conditional probability using a decision tree showing all probabilities assuming the player initially selects Door 1 (as shown to the right). The probability the host opens Door 3 given the car is behind Door 1, Door 2, and Door 3 is 1/2, 1, and 0, respectively. The total probability the host opens Door 3 is therefore 1/3 x 1/2 + 1/3 x 1 + 1/3 x 0 = 1/2.
hence
In other words, a player who switches when given the option has a 2/3 chance of winning the car. Carlton also presents what he calls "an intuitive explanation" of this result, specifically that switching loses if and only if the player initially picks the car, which happens with probability 1/3, so switching must win with probability 2/3. |
Rick, thank you. For the reader it really is of importance to understand WHAT it's all about, and WHAT the sources really try to say in their specific context, and WHAT conclusions they are trying to express, WHAT conclusions they are trying to present. So YES, you not only need to "quote indistinct citations", you also can express exactle WHAT Carlton finally menant in his specific line of sight, in his specific context. You easily are able to do that, to help new readers to destinguish, to winnow what it's about, what the sources REALLY want to say and try to say, paying attention to their given context. Gerhardvalentin (talk) 21:24, 7 November 2010 (UTC)
Rick, I disagree with your executive summary
- "In other words, a player who switches when given the option has a 2/3 chance of winning the car."
A good executive summary is
- "In other words, a player who switches when given the option after he chose door 1 and the host opened door 3, has a 2/3 chance of winning the car."
Remember that the executive summary of the simple solutions is
- "A player who switches when given the option has a 2/3 chance of winning the car"
The conditionalists think that the player ought to worry about whether this chance might depend on the specific door numbers in the story so far. The intuitionalists don't worry about this, and of course, under the usual or standard conditions, fortunately for them, they didn't have to. Richard Gill (talk) 21:43, 7 November 2010 (UTC)
- Richard - the "executive summary" is simply a paraphrase of Carlton's text where he says "In other words, the contestant can double his chance of winning the car (from his initial 1-in-3 guess) by employing the strategy of switching when Monty Hall gives him the option." In context I think he clearly means "after the player chose door 1 and the host opened door 3", but he does not explicitly say this himself (we're being literal here). We can't, without some level of interpretation, tell whether his "in other words" pertains to the conditional probability equation immediately preceding or to the entire solution. If the former, then adding "after the player chose door 1 and the host opened door 3" is what is meant - but if the latter then we could add "given any initial selection of door and door the host opens since door 1 and door 3 were arbitrarily chosen and the analysis is the same in any specific case". The point here is not that I think you're interpreting what he's saying incorrectly, but that you are interpreting (you might think of it as "understanding"). If the summary is sufficiently literal, no interpretation (or understanding) is required. -- Rick Block (talk) 00:21, 8 November 2010 (UTC)
- I see your point. But this identical sentence could be taken as summary of every source which argues "switch because it's 2/3". I tried to expand it without any interpretation in a way which would differentiate it from the sources which only give a simple solution. Since that is the important thing everyone is fighting about, and that is what Carlton's paper is all about (IMHO). Richard Gill (talk) 13:06, 9 November 2010 (UTC)
- The point is this is not our summary, it's a summary directly taken from Carlton's paper. This entire section is cited to Carlton, in much the same way a direct quote would be. We could add "Carlton says ..." in front of every sentence in this section. It's like the clarification you wanted for the sentence about the "intuitive solution". If you think it's necessary, we could make it very clear this is Carlton's summary (rather than a summary by Wikipedia's editors) by prefacing this particular sentence with something like "Carlton summarizes this solution by saying a player who switches ...". Wikipedia's editors are not saying anything at all in this section, we're merely condensing what Carlton says to a paragraph (or two). -- Rick Block (talk) 19:01, 9 November 2010 (UTC)
- I see your point. But this identical sentence could be taken as summary of every source which argues "switch because it's 2/3". I tried to expand it without any interpretation in a way which would differentiate it from the sources which only give a simple solution. Since that is the important thing everyone is fighting about, and that is what Carlton's paper is all about (IMHO). Richard Gill (talk) 13:06, 9 November 2010 (UTC)
Something got me to thinking about this, this morning. Here's Carlton, including a simple solution in a rigorous-enough text book describing how he uses a simple solution in his classroom in a paper he wrote for the Journal of Statistics Education. He ain't writing about it, or using it in his classroom because its wrong, or deceptive, or anything but, in his opinion a valid and accessible way of understanding why its 2/3 & 1/3, and not 50/50. Somehow, that's not good enough for some editors. I just don't get it. There's an old saying, 'That guy knows the cost of everything, but the value of nothing'. I see similarities here. Glkanter (talk) 10:18, 8 November 2010 (UTC)
- Do you agree with the summary, or not? -- Rick Block (talk) 14:49, 8 November 2010 (UTC)
- Agree? What is its the function of the summary? Glkanter (talk) 16:22, 8 November 2010 (UTC)
- Carlton doesn't say it is a valid and accessible way of understanding why it's 2/3 and 1/3 not 50/50. He says very little. He implies that the "reasoning solution" shows his students that the simple (or intuitive) reasoning for 50/50 must be wrong, since it conflicts dramatically with another simple (or intuitive) reasoning. He spends a lot of time patiently explaining how the students should do it, as he thinks it ought to be done. Richard Gill (talk) 12:59, 9 November 2010 (UTC)
- Are you serious? You go off on multi-screen/endless-diff distillations of each perceived nuance of Carlton's paper, and I'm *wrong* to say he uses the simple solution in his classroom on probability and writes about it in a paper because he finds it 'valid and accessible'? I think you're applying a distorted double standard here. And I resent it. Glkanter (talk) 13:28, 9 November 2010 (UTC)
- You guys don't know me and I probably shouldn't be here since I'm not a party to this mediation, but somehow this page came to my attention and I've been watching the discussion with increasingly tensed jaw muscles, and I have a question. What publication of Carlton are you talking about? The only Carlton reference in the article is to a paper in J. Educational Statistics (or J. Statistical Education?-- at any rate the ASA publication for statistics educators whatever it's called) which includes only a short section on the Monty Hall problem and bears very little resemblance to this discussion as far as I can see. But now I see that the source you're discussing is described as a "rigorous-enough textbook" which makes me think maybe you all are discussing a completely different source than the one I'm reading. So what's the source, please, for those of us reading along in the background? Woonpton (talk) 16:52, 8 November 2010 (UTC)
My bad, I guess. I'm reading the same linked document as you. Glkanter (talk) 17:08, 8 November 2010 (UTC)
- Right, the Carlton source we're talking about is the paper (not book) currently referenced in the article, available online here. As far as the point of the summary, this is in response to Will's suggestion above (#Planning) that we consider restructuring the article to be summaries of sources rather than an integrated narrative. I wouldn't say there's consensus that we'll go ahead and restructure the article this way, but this would be the summary of Carlton. It would presumably fit into a revised TOC, as a section in the "Solution" section - perhaps like this (exact order TBD)
* 1 Problem
* 2 Solutions
o 2.1 vos Savant's solution
o 2.2 Devlin's solution
o 2.3 Grinstead and Snell's solution
o 2.4 Carlton's solution
o 2.5 Somebody else's solution
o 2.6 Yet another solution
* 3 Sources of confusion
* 4 Variants – slightly modified problems
o 4.1 Other host behaviors
o 4.2 N doors
o 4.3 Quantum version
* 5 History of the problem
* 6 See also
o 6.1 Similar problems
* 7 References
* 8 External links
- The question is whether you agree this summary captures all the relevant points from the Carlton paper, neutrally and without bias - and, if not, what you think is either missing or misrepresents something from the paper. -- Rick Block (talk) 01:03, 9 November 2010 (UTC)
Who's this "Will" you mentioned? Glkanter (talk) 03:03, 9 November 2010 (UTC)
- Will Beback ? Richard Gill (talk) 13:06, 9 November 2010 (UTC)
- Apparently not. Glkanter (talk) 19:49, 9 November 2010 (UTC)
- Glkanter - Do you understand the question? Is there some reason you're not replying? -- Rick Block (talk) 18:39, 9 November 2010 (UTC)
- I've expressed my discomfort with that approach previously, and choose not to encourage it. Glkanter (talk) 19:49, 9 November 2010 (UTC)
- Is it some other Glkanter who said "Whatever we've been doing isn't getting us anywhere. We asked for your increased participation, and this is your preferred approach. I'm certainly willing to give it a try."? -- Rick Block (talk) 20:59, 9 November 2010 (UTC)
I read the suggestion as a means of organizing our thoughts, not as a new format for the article. What do I know? Glkanter (talk) 21:27, 9 November 2010 (UTC)
A change of plan?
[edit]It is quite clear that mediation is not working here at the moment. There is no point in trying to blame the mediators or the belligerent regular editors, it just seems not to have worked.
There is only really one issue about which there is serious disagreement and this is the validity of the simple solutions. This disagreement manifests itself in two ways:
- What degree of 'health warning' is needed in the 'Simple solutions' section (and also the 'Conditional probability solution' section)?
- Should 'Aids to understanding' come before or after the 'Conditional probability solution' section?
Could we agree to limit the dispute to just items 1 and 2 above? After that I am sure that we could work cooperatively on most other issues. Martin Hogbin (talk) 10:48, 14 November 2010 (UTC)
- Okay, my suggestion is: the correct (conditional) solution first, Then, with an introductory sentence like: "Although some sources consider the following as incorrect, because not being complete, as a way of understanding, one may consider.....". Nijdam (talk) 15:04, 14 November 2010 (UTC)
- I was asking if we could just stick to the two points above. I guess your answer is 'no'. Martin Hogbin (talk) 23:15, 14 November 2010 (UTC)
- Martin - Rather than change directions yet again, I'd like to see if we can agree about the Carlton summary, or (popping the stack) agree about the rewrite of the Conditional solution section, or (popping the stack even further) agree about the rewording of the single sentence about Carlton's intuitive explanation that's in the "Simple solutions" section. I think for each of these we are extremely close to a consensus, and establishing that we CAN reach a consensus (about a single sentence, or a section of the article, or even a description of what a single source actually says) would be vastly preferable to changing topics again. -- Rick Block (talk) 23:03, 14 November 2010 (UTC)
- I guess it is a 'no' from you too. Martin Hogbin (talk) 23:15, 14 November 2010 (UTC)
- As for the Carlton summary, I have no idea what we hope to achieve with a summary of Carlton. What will we do with it when we have agreed? But if everyone else wants to do that let us do it. Martin Hogbin (talk) 23:15, 14 November 2010 (UTC)
- I have looked at your Carlton bit (it is not really a summary) and have no real objections to it. It seems to reasonably reflect what Carlton says. Now what? Martin Hogbin (talk) 23:20, 14 November 2010 (UTC)
- Now we ask others whether they agree it captures all the relevant points from the Carlton paper, neutrally and without bias. Richard? Glkanter? Kmhkmh? Nijdam? Glopk? If we all agree, then I think what Will had in mind is we'd proceed to another source and do the same thing. There wasn't any particularly good reason we started with Carlton, and although we'll have to do Morgan et al. and vos Savant and Rosenhouse's book eventually, I think it might be better to tackle an easier one next. I think it might be better to do these one subpage per source. I'd be happy for us to focus on any specific source (or author), so long as we're all focused on the same thing (what does this source or author actually say, in a paraphrased and condensed way that we could put into the article if we decided to restructure the article by source). Maybe these sections will be strung together in a new version of the article, but even if they won't doing these will give us practice collaboratively editing - focusing on what sources say rather than on our individual opinions. -- Rick Block (talk) 06:35, 15 November 2010 (UTC)
- I'm completely neutral whether we follow Martin's or Rick's proposal. Richard Gill (talk) 08:47, 15 November 2010 (UTC)
At the moment I'm just observing and have no (strong) opinion on how to proceed. As far as Carlton is concerned to be honest I don't understand the whole discussion. To me Carlton is just another a source for conditional solution (using the decision tree) of which we have already plenty, so there is no need to use him at all, though mentioning him is of course possible. It seems like a completely unnecessary distraction from the core conflict between martin and Rick/Nijdam. If that core conflict can't be resolved, this whole mediation becomes pointless and if the current conclusion is, that it can't be resolved, we might as well close the mediation.--Kmhkmh (talk) 09:53, 15 November 2010 (UTC)
- Kmhkmh - The discussion here was prompted by Will's suggestion above (#Planning) that we consider restructuring the article to be a summary of individual sources, rather than an integrated narrative - simplifying the task at hand to accurately and neutrally summarizing sources. I suggested starting with Carlton for no reason other than such a summary already existed. This approach presumably makes any conflict between editors moot - requiring only that we all agree on summaries of specific sources as opposed to any broader statements. We haven't agreed to restructure the article using this approach, with Martin expressing disfavor - although I hope if everyone else favored this approach Martin would not object. Whether we ultimately decide to restructure the article this way or not, I think the exercise of collaboratively editing summaries of individual sources will be worthwhile since it forces the focus to be on what specific sources say (as opposed to what we think). -- Rick Block (talk) 16:23, 15 November 2010 (UTC)
I think y'all are describing unicorns. There is no mediation occurring, there are no mediators participating, there is no consensus close to being reached (see Nijdam's recent comments). There is nothing but the same old NPOV violating Wikipedia MHP article. Glkanter (talk) 16:28, 15 November 2010 (UTC)
- I agree there is no mediation. I think that planning to rewrite a featured article from scratch as a literature survey is the worst possible way to resolve a comparatively minor disagreement. This is not the way WP articles should be written. Is there anyone at all who supports this idea? Martin Hogbin (talk) 16:56, 15 November 2010 (UTC)
- Part of the reason there may be little mediation occurring is that editors herein have shown time and again a surprising inability to stay focused on the specific issues under discussion, be concise, and comment always with a goal of producing consensus edits (as opposed to trying to convert the others to one's revealed truth). The mediators have shown patience and willingness to help, but I strongly suspect that mediating the MHP is not their full-time job, nor even part-time, and we have sorely tried their patience and goodwill. The rules that everyone here has allegedly accepted about focus and concision are there for a reason: given the large number of editors involved in this mediation, limiting the noise is not optional.
- Will's proposal to collaboratively produce sources' summaries is, I think, a de minimis request to see who in here is serious about working toward a compromise based on the things that matters most, namely the sources. If we don't have the discipline to summarize collaboratively a source every one-two days, and agree on their meaning, there's really no point in continuing - we have been talking over each other's heads for well over one year now. glopk (talk) 02:06, 16 November 2010 (UTC)
- I have no objection to discussing and recording what the sources say. In fact I made this same suggestion myself and set up this page for that very purpose some months ago. What I object to is rewriting the whole article from scratch as a literature survey. Do you support the idea or rewriting the article in that way? Martin Hogbin (talk) 09:25, 16 November 2010 (UTC)
- Martin - "rewriting the whole article from scratch as a literature survey" is not necessarily required. We could rewrite only the "Solution" section - which, as I've said, I think any resolution to this mediation will entail. Are you saying you're refusing to even consider this approach? -- Rick Block (talk) 14:55, 16 November 2010 (UTC)
- I've have no objection against that approach being tried. However I'm not really clear on the selection process there far more than 40 papers with solution in English alone. Which do we pick by what criteria? More directly addressing the current dissent - why do we pick Carlton? Also there is another potential problem coming up. If we use a rather close paraphrasing or literally quoting the articles own summaries extensively, then we are likely to create a potential copyright issue.--Kmhkmh (talk) 17:41, 16 November 2010 (UTC)
- Martin - "rewriting the whole article from scratch as a literature survey" is not necessarily required. We could rewrite only the "Solution" section - which, as I've said, I think any resolution to this mediation will entail. Are you saying you're refusing to even consider this approach? -- Rick Block (talk) 14:55, 16 November 2010 (UTC)
- I have no objection to discussing and recording what the sources say. In fact I made this same suggestion myself and set up this page for that very purpose some months ago. What I object to is rewriting the whole article from scratch as a literature survey. Do you support the idea or rewriting the article in that way? Martin Hogbin (talk) 09:25, 16 November 2010 (UTC)
- Yes I object strongly to rewriting the 'Solution' section as a literature survey. That is not how to write a encyclopedia article and I have seen it proposed in any WP policy. I would rather have a health warning in the simple section that wreck the article because of a minor disagreement. How is a literature survey a service to our readers? Who is it for? Most people will give up, or, quite rightly start to edit the article to bring into line with other, properly written, articles.
- All I am pushing for is to start with a simple section without that explains to the vast majority of our readers why the answer is 2/3 not 1/2, and why the fact that the host know where the car is matters. This is what most of our readers want to know. After that we can go into whatever detail you like. Martin Hogbin (talk) 18:32, 16 November 2010 (UTC)
- I have no objection against a simple section, as long as it is complete, and hence is more then what we in the sources refer to as the simple solutions. These simple solutions cannot be presented without the sourced criticism. Nijdam (talk) 22:23, 16 November 2010 (UTC)
- The simple sources are criticised later in the article. Martin Hogbin (talk) 22:48, 16 November 2010 (UTC)
- Well technically you could skip the criticism at that point as long as the simple solution restricts itself to solving what you call the simple problem, i.e. it specifies which interpretation of the MHP it is adressing rather than vaguely claiming to be a solution of "the" MHP.--Kmhkmh (talk) 22:50, 16 November 2010 (UTC)
- I have no objection against a simple section, as long as it is complete, and hence is more then what we in the sources refer to as the simple solutions. These simple solutions cannot be presented without the sourced criticism. Nijdam (talk) 22:23, 16 November 2010 (UTC)
- All I am pushing for is to start with a simple section without that explains to the vast majority of our readers why the answer is 2/3 not 1/2, and why the fact that the host know where the car is matters. This is what most of our readers want to know. After that we can go into whatever detail you like. Martin Hogbin (talk) 18:32, 16 November 2010 (UTC)
- Kmhkmh points out the way to go, I think. We should explain the "simple solutions" first, accurately and neutrally reporting what they achieve. Then we point out that some sources consider that what Whitaker really wants to know is something else and show how they get what they think Whitaker wants to know. It's a weakness of these "conditional" sources that they don't give very convincing arguments why Whitaker should be more interested in their solution than in the simple solution. Jeff Rosenthal ("Monty Hall, Monty Crawl, Monty Fall") actually does try hard to do this, but apparently does not succeed in convincing a large majority of editors here. (Other authors such as Morgan et al. just invoke their authority as professors of statistics, but give no arguments). I have given what I consider a good reason in my recent (pre)publications but that apparently does not convince a large majority of editors here either. I think that the presently active editors represent a quite representative cross-section of readers, conditional on the reader agreeing that the player ought to switch.
- So let's concentrate on fairly representing what the so-called reliable souces actually do. It goes without saying that each source thinks it "solves the MHP". The reader will discover for him/her self that the sources don't agree on what constitutes a solution. If the reader prefers to trust professors of psychology above professors of statistics that's up to them. If they don't understand the professors of statistics and if the professors of statistics don't have compeling arguments why their approach is the right one, that's the way it is; on wikipedia we can't do otherwise than report this fairly. On wikipedia the earth would stay flat and remain the centre of the whole universe till more or less everyone does not find this a problem anymore. But as long as only a few controversial scientists (Galileo, Copernicus, ...) think the world is not flat and not the centre of the universe, wikipedia will report their findings as a minority opinion. Richard Gill (talk) 23:25, 18 November 2010 (UTC)
- Well, the Wikipedia MHP article currently reflects the POV of the error-riddled Morgan paper. I'm can't imagine anything worse than that. Glkanter (talk) 02:14, 19 November 2010 (UTC)
Why should that minority POV of the reliable sources be required in the simple solution section? Glkanter (talk) 00:38, 17 November 2010 (UTC)
- Why not? Richard Gill (talk) 23:25, 18 November 2010 (UTC)
- Because it violates the Wikipedia NPOV requirement, and gives prominent Undo Weight to a minority (non-existent?) POV. Glkanter (talk) 02:14, 19 November 2010 (UTC)
- And how about having in the simple solution section the remark that from the simple solution, elementary logic gives us the conditional probability as well and thereby tells us that always switching is optimal (the simple solution only tells us always switching beats always staying)? Advantage: this defuses the controversy and renders much of the later complicated stuff in the conditional solution superfluous. By the way, the Morgan et al. paper is not error-ridden. It only contains one mistake and that concerns a side issue. It was historically significant but is not a good reference nowadays. Richard Gill (talk) 09:28, 19 November 2010 (UTC)
- I'll reserve comment on your simple solution proposal until the other editors share their comments. Martin has a talk page devoted to Morgan's errors, but how about substantial misquotes of Whitaker/vos Savant that serve to support their argument, lack of awareness of Selvin's paper - specifically the host's uniform 2 goat behavior, and the math error for starters? Glkanter (talk) 09:37, 19 November 2010 (UTC)
Martin's urn
[edit]On Richard Gill's discussion page Martin came up with the following urn problem.
Ten balls, numbered 0 - 9, are put in an urn. Successively three players draw a ball from the urn, without replacing it. The first player doesn't draw ball number 9, nor does the second player. He then asks: what is the probability the third player will draw ball number 9?
Strictly speaking the answer is 1/10, as he doesn't ask for the conditional probability. Martin himself however takes the answer 1/8 as the correct answer. And I think most people will. Of course it would be clear if the question was: what is now (or in this case) the probability the third player will draw ball number 9? Yet the phrasing of the problem leads one to the answer 1/8, the conditional probability.
I guess anyone will notice the similarity with the MHP. But in the MHP Martin doesn't want to calculate the conditional probability. Nijdam (talk) 10:39, 17 November 2010 (UTC)
- Nijdam, I am surprised that you have moved the discussion to this page, which was intended for discussion of a section of the MHP article.
- I'm happy with this discussion continuing on my talk page. Everyone is welcome. Richard Gill (talk) 18:57, 17 November 2010 (UTC)
- Moved. Nijdam (talk) 16:54, 18 November 2010 (UTC)