Wikipedia:Reference desk/Archives/Mathematics/2024 April 2

Welcome to the Wikipedia Mathematics Reference Desk Archives
The page you are currently viewing is a transcluded archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages.

April 2

Is a stretched circular arc similar to a circular arc of a different circle?

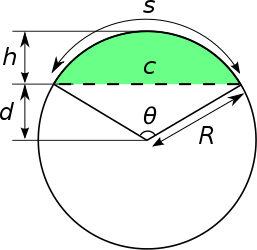
Consider a circular segment, such as the one bounded by circular arc S and chord C in the diagram below. Assume that θ is "small". If we stretch (scale) the circular segment horizontally, will the "stretched" circular arc still be (approximately?) similar to a circular arc on a circle with a different R? If that's the case, will the (approximate?) similarity get worse as the scaling factor increases? Is there a simple formula that can characterize how similar the stretched circular arc is to a true circular arc?

134.242.92.97 (talk) 03:26, 2 April 2024 (UTC)

By 'stretching', do you mean a non-uniform scaling, such that the size is enlarged along the chord while preserved along sagitta...? --CiaPan (talk) 14:48, 2 April 2024 (UTC)

Yes (scaling along the direction of the chord but not along the direction of the sagitta). --134.242.92.97 (talk) 16:25, 2 April 2024 (UTC)

When you scale a circle, the resulting figure is an ellipse. An elliptical segment is not similar to a circular one in geometric sense. Of course the elliptic segment can be approximated with a circular one, so in a common speech they can be called 'similar', but I suppose that's not an appropriate use of the word here, at math ref.desk. --CiaPan (talk) 17:36, 2 April 2024 (UTC)

Note that the question assumes θ is "small" and the "similarity" may be approximate. Is there a simple answer to the question in terms of some intuitive similarity metric? (A similarity metric can be defined, in different ways, in terms of the deviation of the stretched arc relative to the best-fitting circular arc.) --134.242.92.97 (talk) 19:06, 2 April 2024 (UTC)

The area between the two curves (the stretched circle and the circle approximating it) could be used as a measure of the error. If the stretching factor is $f_{s}$ the area of the stretched segment is

${\begin{aligned}A_{s}&={\frac {1}{2}}f_{s}(\theta R^{2}-dc)\\&=f_{s}\left(\arcsin \left({\frac {c}{2R}}\right)R^{2}-{\frac {(R-h)c}{2}}\right)\\&={\frac {f_{s}}{4}}\left(\arcsin \left({\frac {4h}{4h^{2}+c^{2}}}c\right)\left({\frac {4h^{2}+c^{2}}{4h}}\right)^{2}+{\frac {4h^{2}-c^{2}}{4h}}c\right)\end{aligned}}$

If the approximating circle is chosen to go through the end-points and the mid-point off the stretched arc, then its radius $R_{a}$ satisfies

$R_{a}^{2}=(R_{a}-h)^{2}+\left({\frac {f_{s}c}{2}}\right)^{2}$

so

$R_{a}={\frac {4h^{2}+f_{s}^{2}c^{2}}{8h}}$

and the area of the approximating segment is

${\begin{aligned}A_{a}&=\arcsin \left({\frac {f_{s}c}{2R_{a}}}\right)R_{a}^{2}-{\frac {(R_{a}-h)f_{s}c}{2}}\\&={\frac {1}{4}}\left(\arcsin \left({\frac {4h}{4h^{2}+f_{s}^{2}c^{2}}}f_{s}c\right)\left({\frac {4h^{2}+f_{s}^{2}c^{2}}{4h}}\right)^{2}+{\frac {4h^{2}-f_{s}^{2}c^{2}}{4h}}f_{s}c\right)\end{aligned}}$

and the area between the curves is

$A_{a}-A_{s}={\frac {1}{4}}\left(\arcsin \left({\frac {4h}{4h^{2}+f_{s}^{2}c^{2}}}f_{s}c\right)\left({\frac {4h^{2}+f_{s}^{2}c^{2}}{4h}}\right)^{2}-f_{s}\arcsin \left({\frac {4h}{4h^{2}+c^{2}}}c\right)\left({\frac {4h^{2}+c^{2}}{4h}}\right)^{2}-{\frac {c^{3}f_{s}(f_{s}^{2}-1)}{4h}}\right)$

or given that the angle is small, approximating $\arcsin(x)\approx x+{\frac {x^{3}}{6}}$

$A_{a}-A_{s}\approx {\frac {2c^{3}f_{s}h^{3}(f_{s}^{2}-1)}{3(4h^{2}+f_{s}^{2}c^{2})(4h^{2}+c^{2})}}={\frac {f_{s}c^{3}h(f_{s}^{2}-1)}{96RR_{a}}}$

(barring mistakes) catslash (talk) 00:01, 3 April 2024 (UTC)

Thanks for the reply. It seems that your formula is for the difference in area between the two segments, but not the area between the two curves. --134.242.92.97 (talk) 17:12, 3 April 2024 (UTC)

That is true, but the the two segments have the same lower boundary, namely the stretched arc, and so the difference in their areas is area between their upper boundaries, i.e. the area between the two curves. But in any case, Lambian's answer is better. catslash (talk) 22:30, 4 April 2024 (UTC)

A suitable measure for the dissimilarity of two curves is the Fréchet distance.  --Lambiam 21:04, 3 April 2024 (UTC)

Then if the approximating circle is again chosen to go through the end-points and the mid-point off the stretched arc

$F=f_{s}{\sqrt {R^{2}+{\frac {(f_{s}^{2}-1)(2R-h)^{2}}{4}}}}+{\frac {h(f_{s}^{2}-1)-2Rf_{s}^{2}}{2}}$

(this gives $\left.F\right|_{f_{s}=1}=0$ and $\left.F\right|_{f_{s}=0}=-{\frac {h}{2}}$ as expected, so could be correct). However, it is possible to get a smaller $F$ by choosing an approximation which passes above/below ($f_{s}\gtrless 1$)the mid-point of the stretched arc rather than through it. catslash (talk) 22:22, 4 April 2024 (UTC)

One way someone could define how noncircular a curve is, is by taking the minimum, over all possible circles and all positions and orientations of the curve, of the cumulative distance between curve and circle. At the same time, one doesn't need to specify the positions of both circle and curve; one can just assume the circle is centered at the origin, and use the curve's offset instead. Similarly, because of circular symmetry, one can assume that the curve is one specific orientation. This means that we can parametrize a circle purely on radius, and the curve on offset (in addition to whatever else is used to parametrize the curve.) We essentially want:

$\min _{(X,Y,R)\in \mathbb {R} ^{3}}\int _{{\mathcal {C}}(X,Y)}D(\mathbf {r} ,proj_{R}(\mathbf {r} ))ds$

Where we take the line integral over the curve ${\mathcal {C}}(X,Y)$ parametrized with offset $(x,y)$, of the distance between each point $\mathbf {r}$ and its projection $proj_{R}(\mathbf {r} )$ onto the circle of radius $R$.

Note that although $proj_{R}(\mathbf {r} )$ doesn't make sense at the origin, the distance to the circle still does. For all values of $\mathbf {r}$, it can be easily seen that the distance from $\mathbf {r}$ to the circle of radius $R$ is $|\|\mathbf {r} \|-R|$, so we can rewrite this as:

$\min _{(X,Y,R)\in \mathbb {R} ^{3}}\int _{{\mathcal {C}}(X,Y)}|\|\mathbf {r} \|-R|ds$

Now, ${\mathcal {C}}$ here is a stretched circle segment, so it can be further parametrized with angle $\theta$ and stretch factor $S$. We write $\mathbf {r} (t)=(\cos(t)+X,S\sin(t)+Y)$ for $t\in [-\theta /2,\theta /2]$. We now have our final formulation for the problem:

$\min _{(X,Y,R)\in \mathbb {R} ^{3}}\int _{-\theta /2}^{\theta /2}|{\sqrt {(\cos(t)+X)^{2}+(S\sin(t)+Y)^{2}}}-R|{\sqrt {\sin(t)^{2}+S^{2}\cos(t)^{2}}}dt$

Or, using nonnegativity to bring the last term into the absolute value:

$\min _{(X,Y,R)\in \mathbb {R} ^{3}}\int _{-\theta /2}^{\theta /2}|({\sqrt {(\cos(t)+X)^{2}+(S\sin(t)+Y)^{2}}}-R){\sqrt {\sin(t)^{2}+S^{2}\cos(t)^{2}}}|dt$

Although I have no idea how to solve this analytically, I imagine there's a way to solve it numerically, and also I suspect that for intuitive reasons the minimum $(X,Y,R)$ occurs with $Y=0$. If someone else could weigh in, that would be greatly appreciated. GalacticShoe (talk) 20:35, 10 April 2024 (UTC)

For which n, A269252(n) is -1?

[1] proves that A269254(110) and A269252(34) are both -1, and there is a sequence for the n such that A269254(n) = -1: A333859, but there seems to be no OEIS sequence for the n such that A269252(n) = -1, and A269254 and A269252 are similar sequence, so for which n, A269252(n) is -1? 118.170.19.90 (talk) 09:41, 2 April 2024 (UTC)

A269252(n) = -1 for n = 1, 2, 34, 53., but there may not be a sequence 1, 2, 34, 53, ... Bubba73 ^{You talkin' to me?} 20:04, 2 April 2024 (UTC)

Could you compute the terms <= 1000? Thanks. A333859 has the terms <= 1500. 49.217.123.95 (talk) 08:21, 9 April 2024 (UTC)