Mathematics desk
< October 4	<< Sep \| October \| Nov >>	Current desk >

Welcome to the Wikipedia Mathematics Reference Desk Archives
The page you are currently viewing is a transcluded archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages.

October 5

Regarding Brocard's Problem

I am nowadays trying to find a way to solve Brocard's problem. As the problem states, our task is to find $(n,m):n!+1=m^{2}$ . As we all know, $n!$ for $n>1$ is even, therefore $n!+1$ is odd, so if the condition has to be satisfied, $m$ must be odd. The given expression can be changed to $n!=m^{2}-1$ Since we can understand that $m$ is odd, let $m=2x+1$ for some $x$ . From here, we'll get that $n!=m^{2}-1=(2x+1)^{2}-1=4x(x+1)$ . From this, we get that any factorial that can be expressed as 4 times the product of two consecutive natural numbers is a solution for $n$ . From there, if we get a value for $x$ , we'll be able to calculate what value should $m$ take for that value of $n$ .

This proof seems OK but still it is a bit vague... I require some help to move further. Anything that I can do to work it out ?--Sam Ruben Abraham (talk) 06:24, 5 October 2020 (UTC)[reply]

An observation I had is that the values of $m$ that are currently found to solve the problem are primes, so maybe we may try narrowing our search to prime numbers, can't we ? -Sam Ruben Abraham (talk) 06:47, 5 October 2020 (UTC)[reply]

@Lambiam:, I have put up a question here which may sound like an opinion poll question, but please do help me... -Sam Ruben Abraham (talk) 08:11, 5 October 2020 (UTC)[reply]

If Erdős' conjecture is correct, there are only three solutions, and then it is hard to tell whether it is a coincidence that for all three the value of

m

is a prime. What is not a coincidence is that both

m-1

and

m+1

are rich in factors; for example,

70=2\cdot 5\cdot 7

and

72=2^{3}\cdot 3^{2}

. For small numbers this is more likely for primes, but 65, for example, is not prime yet has factor-rich neighbours.

The statement that solutions can be expressed in the form

n!=4x(x+1)

is entirely correct, and the proof is satisfactory. For the three known solutions:

4!=4\cdot ~~2\cdot ~~3=~~~~24,

5!=4\cdot ~~5\cdot ~~6=~~120,

7!=4\cdot 35\cdot 36=5040.

I don't see how I can help you further. If you hope to find a fourth solution by searching, it is much better to compute factorials and try whether

x=\mathrm {isqrt} (n!/4)

gives a solution, where

\mathrm {isqrt}

denotes the integer square root function, since the factorials are much sparser than numbers of the form

4x(x+1)

. It is known that if there are any further solutions, they are for

n>10^{9}

,^[1] so a simple brute-force search does not appear to be a promising approach. I have no ideas to offer, though, for something more sophisticated. There are various interesting observations one can make. Since the gcd of

m-1

and

m+1

divides

2

, a given odd prime raised to some power in the factorization of

n!

is found in the factorization of precisely one of the two neighbours of

m.

I don't see, though, how this can be used to narrow the search. --Lambiam 11:47, 5 October 2020 (UTC)[reply]

@Lambiam: Why can't Erdős be wrong ? What if the probability of finding such numbers in a given range is very low ? Our own imagination has limits, and we can't exceed that limit. Also, this limit varies from person to person, right ? So probably, Erdős should be wrong, I feel -Sam Ruben Abraham (talk) 16:17, 5 October 2020 (UTC)[reply]

Erdős did not claim these were the only solutions, that's why we write "conjectured" and not "claimed". But do you have a plan of attack? Try

(10^{9}+1)!

, then

(10^{9}+2)!

, until you hit the hidden pot with gold? If I have to choose between betting on a hunch of Erdős Pál or one of Sam Ruben Abraham, then I'm putting my money on Erdős. --Lambiam 22:17, 5 October 2020 (UTC)[reply]

The equation n! - 1 = m² is much simpler. Maybe you should start with that. If you can't find all solutions and prove that they're the only ones, then I don't see much hope that you can make progress in the more difficult problem. --RDBury (talk) 18:08, 5 October 2020 (UTC)[reply]

@Lambiam: , great , but I'm not into bets. What I meant to say is that there could be a way we get hold of any other possible solution.Yesterday night, as I slept, I was thinking of using geometrical figures to work out the problem (especially a square - that would work just fine but we end up in the same expression Brocard suggested, which means things are going kind of nuts). My thoughts concentrated on the square more than any other figure. But that was of no use. But there is something that is still making things harder... -Sam Ruben Abraham (talk) 03:15, 6 October 2020 (UTC)[reply]

@Lambiam: : I think we can try proving the existence of more Brown numbers (or those number fulfilling the conditions of Brocard's problem) geometrically. I felt so because Sir Andrew Wiles had to use a bit of graphing to prove Fermat's Last Theorem from Taniyama-Shimura-Weil conjecture (something I don't know actually). -Sam Ruben Abraham (talk) 17:44, 6 October 2020 (UTC)[reply]

I took the liberty of altering one of your solutions to what I think you meant. —Tamfang (talk) 01:24, 9 October 2020 (UTC)[reply]

@Lambiam:: I have ended up in a wonderful conclusion ! I'll share it with you when I get some time.. -Sam Ruben Abraham (talk) 14:29, 11 October 2020 (UTC)[reply]

Circumference of circles in elliptic and hyperbolic geometries

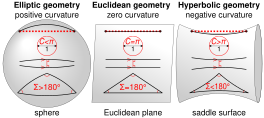
While drawing this diagram, I was unsure whether the circumference of the circles in elliptic and hyperbolic geometries should be less or greater than $π$ : http://pinterest.com/pin/415034921909206347 and http://pinterest.com/pin/405816616395536891 have opposite signs.

Hyperbolic geometry#Circles_and_disks states, "In hyperbolic geometry, the circumference of a circle of radius r is greater than 2 $π$ r." Elliptic geometry doesn't make any claim.

Can someone knowledgeable please confirm?

Thanks,
cmɢʟee⎆τaʟκ 20:01, 5 October 2020 (UTC)[reply]

It is indeed the case that in an elliptic geometry the circumference of a circle with radius

r

is less than

2\pi r

. See e.g. here, Exercise 2. --Lambiam 22:06, 5 October 2020 (UTC)[reply]

Thanks for confirming, Lambiam. Much appreciated, cmɢʟee⎆τaʟκ 00:48, 6 October 2020 (UTC)[reply]

Elliptic geometries have positive curvature, hyperbolic negative, not vice versa as in the diagram to the right.John Z (talk) 19:13, 6 October 2020 (UTC)[reply]

Since corrected; figure now shows the correct polarity. --Lambiam 21:25, 6 October 2020 (UTC)[reply]