Mathematics desk
< March 18	<< Feb \| March \| Apr >>	March 20 >

Welcome to the Wikipedia Mathematics Reference Desk Archives
The page you are currently viewing is an archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages.

March 19

Fractions

I was reading a math book and it said that if ${\frac {a}{b}}={\frac {c}{d}}$ , then ${\frac {a}{b}}={\frac {a+c}{b+d}}$ . Is this true? If so, why? --70.250.214.164 (talk) 01:29, 19 March 2010 (UTC)[reply]

It's true. I'm not sure this is the simplest way, but it works:

{\frac {a}{c}}={\frac {b}{d}}

If you multiply both sides of this equality by cd, you get

ad=bc.\,

Then, dividing both sides by ab, you get

{\frac {d}{b}}={\frac {c}{a}}

and let us call this number k. Thus we have

{\frac {d}{b}}={\frac {c}{a}}=k,

so c = ak and d = bk. Then

{\frac {a+c}{b+d}}={\frac {a+ak}{b+bk}}={\frac {a(1+k)}{b(1+k)}}={\frac {a}{b}}.

Michael Hardy (talk) 02:16, 19 March 2010 (UTC)[reply]

I think this is probably one of the cases where a proof doesn't really capture the intuition. Here's a visual way to understand it:

Think about these numbers as lengths of line segments. The assumption is that the ratio of a to b is the same as that of c to d, which is to say, that d can be obtained by stretching/shrinking c by the same factor that b can be obtained from a. Visualize that, and visualize joining the line segments a and c together (this new line segment will have length a+b), and the line segments b and d together (length c+d). Do you see why these joined segments also have to have the same ratio? If it helps, draw some line segments.

That demonstrates it for positive real numbers. --COVIZAPIBETEFOKY (talk) 02:54, 19 March 2010 (UTC)[reply]

Well, I consider the Michael's explanation is pretty intuitive—possibly it's a matter of what intuition each of us has. See the image below, it's presents in graphical form what Michael wrote in algebraic form. The 'k' coefficient is a proportion ratio between the green and red triangle.

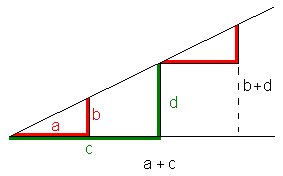
Generally we can say, if we add proportional values we get proportional sums. --CiaPan (talk) 08:32, 19 March 2010 (UTC)[reply]

Short proof: a/b=(a+c)/(b+d)⇔ a(b+d)=b(a+c) ⇔ ab+ad=ba+bc ⇔ ad=bc ⇔ a/b=c/d. Bo Jacoby (talk) 15:33, 19 March 2010 (UTC).[reply]

This, of course, is all true only after you add the prerequisite that b+d, b and d all be nonzero. --COVIZAPIBETEFOKY (talk) 18:28, 19 March 2010 (UTC)[reply]

That is pretty obvious for everybody who knows what division is, I suppose. If they were zero (any of them), some or all the fractions would not make sense, so there were no numbers to make equal in proportions. This is simply out of scope of the question (so called domain). --CiaPan (talk) 08:41, 21 March 2010 (UTC)[reply]

"Half" of the real numbers

Resolved

Is there a set $X\subseteq \mathbb {R}$ such that $\textstyle m(X\cap I)={\frac {1}{2}}m(I)$ for every interval $I\subseteq \mathbb {R}$ , where m is Lebesgue measure? If so, is there a nice construction for it? —Bkell (talk) 02:43, 19 March 2010 (UTC)[reply]

I don't think there is, but I'm pretty rusty at this. Michael Hardy (talk) 03:12, 19 March 2010 (UTC)[reply]

Suppose such an X exists. Its compliment, Y, has the same property. For any ε > 0 there's an open set S with X ⊂ S and m(S - X) < ε. Since S - X = S ∩ Y and S is the disjoint union of countable open intervals, m(S - X) = m(S ∩ Y) = m(S)/2 so m(S) < 2ε. Then m(X) = 0, which leads to a contradiction. Rckrone (talk) 05:16, 19 March 2010 (UTC)[reply]

Wonderful --pm a 06:42, 19 March 2010 (UTC)[reply]

Also, by assumption all points of X have density 1/2, so m(X)=0 as a.e. point of X has density 1; for the same reason m(X^c)=0, a contradiction.--pm a 06:42, 19 March 2010 (UTC)[reply]

Ah, I see. Very nice arguments. Thank you. —Bkell (talk) 07:27, 19 March 2010 (UTC)[reply]

sum of fractional differences

When a sequence whose nth term is the form:
${\frac {1}{n+a}}-{\frac {1}{n+b}}$
What is the sum to n terms?
Thanks, --Wikinv (talk) 05:21, 19 March 2010 (UTC)[reply]

Assuming the sum starts at 1 and goes to n, we're adding up terms from 1/(1+a) to 1/(n+a) and subtracting terms from 1/(1+b) to 1/(n+b). Consider which terms are in common and therefore cancel out, and which terms are left over. Rckrone (talk) 05:30, 19 March 2010 (UTC)[reply]

Hmm... doing that leaves a few terms remaining at the beginning of the sequence. That would give me the sum to infinity, but when doing the sum to n terms there are a few terms at the end of the sequence that remain uncancelled, and I'm don't know how to get them in terms of n. Is there a formula for the sum to n terms given a and b?--Wikinv (talk) 05:50, 19 March 2010 (UTC)[reply]

Yeah, that's right. You'll have some terms left at the beginning and also some terms at the end. Let's assume for now that a < b. Then the ones at the beginning are all the terms from 1/(1+a) up to 1/b. The terms at the end are all the ones from -1/(n+a+1) up to -1/(n+b). That first set we can write as

\sum _{i=a+1}^{b}{\frac {1}{i}}.

See if you can formulate a similar sum for the negative terms at the end. Rckrone (talk) 06:05, 19 March 2010 (UTC)[reply]

\sum _{i=n+a+1}^{n+b}{\frac {-1}{i}}

? =

-\sum _{i=n+a+1}^{n+b}{\frac {1}{i}}

In which case $\sum _{x=1}^{n}{({\frac {1}{x+a}}-{\frac {1}{x+b}})}=\sum _{i=a+1}^{b}{\frac {1}{i}}-\sum _{i=n+a+1}^{n+b}{\frac {1}{i}}$

--Wikinv (talk) 06:26, 19 March 2010 (UTC)[reply]

That's correct. If you want, you can also simplify a bit more by phrasing it as

\sum _{i=a+1}^{b}{\frac {1}{i}}-\sum _{i=a+1}^{b}{\frac {1}{i+n}},

since then we can combine the two sums to get

\sum _{i=a+1}^{b}{\left({\frac {1}{i}}-{\frac {1}{i+n}}\right)}=\sum _{i=a+1}^{b}{\frac {n}{i(i+n)}}.

Rckrone (talk) 06:43, 19 March 2010 (UTC)[reply]

Is this also true?:

\sum _{x=1}^{n}{\left(f(x+a)-f(x+b)\right)}=\sum _{i=a+1}^{b}{\left(f(i)-f(i+n)\right)}

--Wikinv (talk) 07:14, 19 March 2010 (UTC)[reply]

Yeah, you can generalize the same argument used here for 1/x to any function f(x). Rckrone (talk) 07:58, 19 March 2010 (UTC)[reply]

Quickly glancing at this discussion, I don't see any links to telescoping series yet. Michael Hardy (talk) 18:39, 19 March 2010 (UTC)[reply]

Alternative notations for exponentiation

It stuck me that the standard way we write exponentiation (and particularly scientific notation) uses an ordering and typography that de-emphasises what (at least from a scientific if not mathematical perspective) seems to be the most important parts. If, for example, we take the Avogadro constant of roughly 6.022 × 10²³ we're writing things in the order sign;significand;base;signOfExponent;exponent, and writing both the exponent and its sign in small letters - even though (again from a scientific perspective) they're much more important than the significand. If the Avogadro constant was 7.022 × 10²³ instead, that wouldn't make that much difference; if it was 6.022 × 10²⁴ that would make a huge difference. Our exponentiation#History of the notation section is pretty thin, but it seems to show that things have always been denoted this way (since people cared about writing down the mathematical concept of exponentiation formally). One might think it would smarter, at least for scientific uses, to write the same number down in a way that emphasises the exponent, say [23]6.022 or 23_E6.022 . I appreciate that we're stuck with the notation we have, and that mathematicians (and particularly number theorists) won't necessarily agree that the exponent is necessarily the most "important" bit, but has any serious mathematician or scientist used or proposed another, more exponent-emphatic, notation? -- Finlay McWalter • Talk 13:47, 19 March 2010 (UTC)[reply]

How about this: _{6.022 × 10}23 ? StuRat (talk) 14:12, 19 March 2010 (UTC)[reply]

A good source for mathematical notations that have been used in the past is Florian Cajori's work A history of mathematical notations. I'm sure he has a section on exponentiation in there. But it dates from the 1920s, I believe, so you won't get information about proposed replacements for standard exponential notation since then. —Bkell (talk) 14:14, 19 March 2010 (UTC)[reply]

That looks just the ticket, thanks. It does indeed have a section on exponentiation (para 481) but unfortunately the Google Books preview omits that. I'll see if the library has it. -- Finlay McWalter • Talk 16:57, 19 March 2010 (UTC)[reply]

Not only ordering and typography, but also pronounciation, de-emphasises the important parts. Some people use a logarithmic unit for big or small positive numbers to emphasise the important parts. Avogadros number indicate that a mole is 238 dB greater than a molecule. Bo Jacoby (talk) 15:54, 19 March 2010 (UTC).[reply]

Yes, that occurred to me, and I'd presume that an exponent-first notation might encourage people to say it differently, like "23 raises 6.022". But that left->right reading order isn't universal, and was pondering whether the de-emphasis of the exponent might not be felt so much in a r->l language. Our mathematics in medieval Islam article doesn't go into this sufficiently, and I note that Abū al-Hasan ibn Alī al-Qalasādī#Symbolic algebra presents a polynomial written in l->r order; so I don't know if medieval arab mathematicians still wrote algebra in l->r despite writing text r->l (which would seem incongruous). -- Finlay McWalter • Talk 16:50, 19 March 2010 (UTC)[reply]

Automorphisms of the Riemann sphere

Why is complex conjugation not an automorphism of the extended complex plane? It's an automorphism of the complex plane, and if we define the conjugate of the point at infinity to be itself, I don't see why this isn't an isomorphism from the extended complex plane to itself. Isn't this just a reflection of the Riemann sphere in the great circle which the real axis is mapped to? Thanks, Icthyos (talk) 14:01, 19 March 2010 (UTC)[reply]

An automorphism is a structure preserving permutation. Thus, whether something is or is not an automorphism is very sensitive to the choice of the structure, it's not just a property of the domain as a set. What structure do you impose on the Riemann sphere and on the complex plane, respectively?—Emil J. 14:10, 19 March 2010 (UTC)[reply]

Ah, so complex conjugation is an automorphism of the complex numbers as a field, but not of the Riemann sphere because it is not a holomorphic function, and the Riemann sphere is a Riemann surface, so any automorphism must be biholomorphic? Thanks! Icthyos (talk) 15:18, 19 March 2010 (UTC)[reply]

Yeah, an automorphism is an isomorphism from one space to itself; so it is necessarily bijective. I think that conformal mappings of the Riemann Sphere are, or at least were, what people are most interested in. For example, the extended complex plane is conformally equivalent to a sphere (hence the Riemann Sphere as an analogue of the extended complex plane). A map of the extended complex plane onto itself is conformal if and only if it is a Möbius Transformation. •• Fly by Night (talk) 15:30, 19 March 2010 (UTC) Actually, I just found this: Riemann_sphere#Automorphisms. •• Fly by Night (talk) 15:42, 19 March 2010 (UTC)[reply]

To see the Möbius Transformations in action the take a look at this. •• Fly by Night (talk) 15:47, 19 March 2010 (UTC)[reply]

...although complex conjugation is an antiholomorphic function, as is the composition of complex conjugation with a Möbius transformation, such as inversion in a circle - these mappings preserve the magnitude of angles but reverse their sense. 86.136.246.229 (talk) 12:53, 20 March 2010 (UTC)[reply]

q test not for idiots ... (a q test table for a 99.9999% confidence level?)

I don't know why I can't find a statistical basis for the tables presented for the Q test. Just what function /distributions are the Q tests describing? I'm trying to look up the function because I can't find any tables for a 99.9999% confidence level. John Riemann Soong (talk) 15:24, 19 March 2010 (UTC)[reply]

The Dean and Dixon paper cited in the Q test article says "In this paper all conclusions are based on a normally distributed population." Of course, most "normal" distributions in the real world are only approximately normal, so doing anything at the 99.9999% confidence level is tricky. See for example kurtosis risk. 66.127.52.47 (talk) 23:14, 19 March 2010 (UTC)[reply]

Or Black swan theory for a more colourful version. Dmcq (talk) 10:19, 20 March 2010 (UTC)[reply]

Can I ask why you need such a high confidence level? At that confidence, there is a significant chance of accepting an outlier when you shouldn't - a Type II error. Zain Ebrahim (talk) 10:18, 20 March 2010 (UTC)[reply]

I think the whole idea of rejecting outliers is a bad one and the statistics I've seen supports normally keeping them. It's the sort of thing that kept the ozone hole hidden. Dmcq (talk) 10:25, 20 March 2010 (UTC)[reply]

Because the Q-value I'm getting is so high that the confidence level I will get should be high as well. John Riemann Soong (talk) 17:42, 20 March 2010 (UTC)[reply]

I think you're looking for a p value then, not the confidence level (which is independent of the data). Usually people just say the p-value was less than some significantly small level (i.e. you could just say p < 0.00001) to indicate the result of the test was significant. Zain Ebrahim (talk) 19:07, 20 March 2010 (UTC)[reply]

rack

calculate how to make a pinion size to a rack. like if i have a rack with a tooth spacing of .050 , how would i calculate the dia of the pionion and teeth to match the rack.i am a retired die maker and i have no use for this but i can't figure this out.i would like a nice simple explanation.i have a ford shop theory book , but i can't figure out which formula i should use. any help would be appreciated , or where i could go to ask.thanks , and have a nice day.---------ted----email removed by User:Coneslayer to prevent spam —Preceding unsigned comment added by 64.131.46.188 (talk) 16:43, 19 March 2010 (UTC)[reply]

The complication is that, unlike the rack, the teeth on the pinion don't all point in the same direction, as they are mounted on a circle. But as a first approximation, a pinion of diameter d will have a circumference πd which can accommodate πd/0.050 teeth. If you want the diameter d for a given number of teeth n, it will be d = 0.050n/π. For any other tooth spacing, just replace the 0.050 figure.→86.155.185.122 (talk) 20:38, 19 March 2010 (UTC)[reply]