User talk:Alfredr

Hi, wellcome to Wikipedia.

Danko Georgiev MD 05:19, 1 June 2006 (UTC)

Dear Alfred, you can modify your user page any way you like, you can upload pictures in wikipedia at this adress:

http://en.wikipedia.org/wiki/Special:Upload

Of course the images should be not copyrighted by someone else.

How to insert your picture in some of your Wikiposts you can find here:

http://en.wikipedia.org/wiki/Wikipedia:Picture_tutorial

In order to put signiture after your posts you can just type 4 tilde at the end of your message.

You also can input mathematical formulas in LaTex format they are automatically converted into equations when you view the web page.

I hope these comments are helpful in editing Wikipedia and making your posts more informative. Danko Georgiev MD 08:01, 2 June 2006 (UTC)

Afshar experiment

Hi Alfredr, I read your comments on the Afshar experiment talk page. My conclusions were that the results are as expected from QM; and that the experiment doesn't rule out any interpretations of QM, or the principle of complementarity. You can map Afshar's experiment onto a simpler one with polarizers: pass a photon through a polarizer (replaces Afshar's pinholes); then pass it through a second polarizer with the same orientation (the "non-destructive measurement," replaces Afshar's wire grid); and finally, measure the polarization at 45 degrees. --Reuben 00:27, 4 June 2006 (UTC)

Dear Reuben I agree with you.Burt Pr Afshar used the analogy of "plane with wings/ plane without wings", so I beleive it is important to discuss *exactly* his experiment, not just similar ones, to see exactly what goes on. My point is that everything is due to Huygens principle: absorption causes necessarily diffraction, and even if diffracted amplitude from pinhole 2 cannot be actually seen because its only effect is to *destroy* diffracted amplitude from pinhole one, then precisely the effect of this destruction (restauting 100% instead of 94%) does come from pinhole 2 and this experiment is not a pure unambiguous "welcher weg" one. And this is the solution to the paradox! Alfredr 23:04, 10 June 2006 (UTC)

The following discusion does not belong to the Afshar experiment talk page, and has been moved to your user page as per the agreed upon statement at the top of the Afshar experiment talk page. You are more than welcome to continue your discussion here, but I will not waste my time responding to Danko Georgiev for reasons discussed before, and well-known to Wiki administrators.Afshar

Maybe I did not make myself clear

Rereading what I wrote, maybe it is not so clear that, though I entirely agree that Pr. Afshar's experimental results are correct, this does not mean that I believe that it proves that the photon actually went through one pinhole rather than the other (unless you follow Bohm, but then it is a different question altogether: nonlocality is in the "guiding" wave). Indeed, whether you believe Everett (many-worlds) or Wigner (consciousness causes reduction) the split/reduction is *not* retroactive. Consider a simpler mind-experiement (easy to realize, in fact). For the sake of convenience assume the photon moves vertically. First it goes through a polarizer oriented North-South. Then it hits a two-way analyser at 45 degrees. A beam would be split along polarisations NW-SE or NE-SW. But we do not have a beam but one photon at a time. If the photon is "understood" by the analyser as being NW-SE it goes one way and a red lamp lights up, if it NE-SW a green lamp lights up. Now I assume we wait for a few dozen photons, that arrive well separated, one at a time. So one photon goes through and a green lamp goes up. Does it mean that the photon was always NE-SW? I claim it does not say that. It only says that *after* going through the analyzer, it is so. Before that it was N-S.

And indeed, suppose I do the experiement again but adding a E-W polarizer between the N-S one and the two-way analyzer. If the fact that the green lamp goes on means a photon has *always* been NE-SW, then some of these photons (one half, on the average) should be "lucky" and go through the E-W polarizer. So the green lamp should light up once in a while, half as often as in the first case; as half the NE-SW photons are stopped, but half go through. That should be the case if a green light meant indeed the photon was NE-SW *retroactively*. But this is not the case! The crossed polarizers, N-S first, E-W then stop *all* the photons. I never see anything! If the fact that I do not see anything bothers you, assume that instead of being exactly perpendicular, the two polarizers make an angle of 89 degrees or so. Once in a while a photon will go through, and thus once in a while a green lamp will light up. But if the photon that activates it had *always* been NE-SW, retroactively, then why are they so few of them? They should cross the first polarizer with a 1/2 probability, then the second one with a 1/2 probability, and thus the count rate shoud be 1/4 of what one gets without polarizers. But it is not so! The count rate is considerably less. So the "final" NE-SW polarisation happens only "after" the photon goes through the two-way analyzer, not retroactively: otherwise it would have a fifty-fifty chance of crossing the E-W polariser, which is not the case: it will never (or only very rarely) be able to go across it. After the N-S polarizer it was N-S, not NE-SW or NW-SE, which is waht it appears to be after going through the tw--way anayser and lghting up one lamp or the other. A similar reasoning in Afshar's experiment means that the photon gos through both pinholes, has an interference pattern, passes the grid without seeing it and only *after that* either splits the world, for Everett, or is "collapsed" by the consciouness for Wigner, to "choose" between one lens or the other. Alfredr 10:12, 30 May 2006 (UTC)

It seems I missed what people were discussing about

• Reading in more details, I see that the question is not so much whether Pr. Afshars *experimental results* are correct (only one person suggested they were falsified, and quite unjustly so) but whether they disprove some interpretations of QM. What I claim is that, quite clearly, they do not. Again all interpretations of QM agree with these results. The misunderstanding is here: people believe that Afshar's experiment is an *unambiguous* "welcher weg" one. But it is not so! The fact that photons can arrive *only* at the images of the pinholes when the grid is there and both pinholes open does *not*, and I insist, does *not* meant that a photon arriving at the image of one pinhole necessarily went through that pinhole. Assume that only *one* pinhole is open. Then there is no interference pattern, and some amount of light *is* diffracted by the grid. Since the grid is periodic, that light cannot go anywhere but only in selected positions, including the image of the *other* pinhole, because of the grid spacing. So when the grid is present, photons from one pinhole can reach the image of the other one! Which is to say, when the grid is there but both pinholes are open, arrival of a photon at one image is perfectly compatible (with a small but not negligible probability of 3%, half of the 6% intercepted by the grid) with its going through the other one. So the experiment is not an "unambiguous welcher weg". What obscures this fact is that indeed it is "mostly welcher weg". But note that with only one pinhole, its image gets anyway 94% of the light. The interference pattern only increases the visibility to 100%% from 94%, not from 50%. This is obtained by a small weakening of the "welcher weg" which was perfect and becomes 94%. So complementarity is preserved, and every interpretation of QM is compatible with this experiment. Alfredr 22:39, 31 May 2006 (UTC)

• Dear Alfred, I will suggest you more careful reading of Afshar's results before you try to calculate possibilities. If you dig deeper you will see that the experiment is not superficial as it seems. The fact that I was misunderstood several times is the super-ego of the physicists who rely on their professional background, and suppose that a non-physicist cannot point out their mistake. So, your calculations are totally flawed! As you read carefully the wires absorb 6% of the light in the "mixed state" experiment where only one pinhole is open at a time. The "mixture" comes from the fact that you should take statistical average of two different experiments. When both pinholes are open there is absorbtion of light by the grid <0.1%, so this proves that there is interference! The wires are as if placed in completely dark region. This is just Reininger negative measurement experiment and at this point you collapse the wavefunction in momentum basis [you measure the wavelength!]. Of course Afshar does not claim that you will not absorb 6% of the light everywhere in space, but he says that the wires should be adjusted to fit in the interference minima. This is possible - just take and compute the interference picture behind the double slit and you will be able to predict, where the wires with the given spacing should be placed to absorb minimal number of photons. In the Afshar's case with grid and two pinholes open the chance of photon to get to A or B is 50% [minus half of 0.1% loss] and the photon passes through both pinholes at the same time. This is the MW interpretation. In Bohmian picture the photon passes through pinhole A or pinhole B, but then the trajectory may end surpizingly in the opposite detector with 50% chance. Since I am not Bohmian follower, I prefer to attribute real status of the superposition because its is mathematical fact. So in this case there is "pure state" density matrix where the off-diagonal elements are not zeroes. In such case you cannot say that there is any "which way" information. You make serious error to say that the grid reflects 3% of the light into the wrong detector. There is no logical reason to suppose that the light that is absorbed by the grid in the "mixed state" single pinhole experiment, now in the "pure state" double slit should be reflected to the wrong detector. Regards, Danko Georgiev MD 09:36, 1 June 2006 (UTC)

• In order to see sketch of the probability distributions of the wavefunctions in "mixed state" and "pure state" experiments see Wiki-post There is nothing special in putting a grid or not. The difference of probability distributions comes from purely mathematical reasons and mirrors the difference you compute probabilities in mixed and in pure state. Danko Georgiev MD 09:43, 1 June 2006 (UTC)

• Predictions - Dear Alfred, consider the fact that putting polarization filters on the pinholes will immediately restore the 6% photon absorbtion by the wires. This proves that the loss of coherence and loss of interference that now change the environment of the wires and they are not in dark region but on the path of the light beam see the suggested probability distribution pictures. If in both cases the probability distribution is the same "which way" then the ammount of light coming to the wires will not change, and I AM CURIOUS to understand why the wire in one case chooses to absorb, but in other case chooses to reflect like a mirror towards the wrong detector?! Danko Georgiev MD 09:58, 1 June 2006 (UTC)

• Dear Danko, You misunderstood me. When both pinholes are open, *all* interpretations, whether MW, WIgner's consciouness causes reduction, and Bohm's (whether youu like that interpretaion or not) predict the SAME result: interference IS present, and the gird is not seen (or only at the 0.1% level, not 6% level). So Afshar's result are OK for QM whatever interpretation you favor. Where I disagree with Afshar's conclusion is not on the *experimental result* which is obviously correct, nor in the fact that, for instance, the transactional interpretation gives the correct result, but in the claim that *other* interpretations would not agree. I claim ALL interpretations do agree. My argument in the case where the grid is present but only one pinhole is open is in accordance with Huygens principle: if the grid intercepts (absorbs) 6% of the light, it removes *twice as much* from the main beam and diffracts the other 6%. Some amount of this diffracted light reaches the image of the other hole. This does not mean that it happens when both pinholes are open: when this is thaz case the grid is in the dark bands and is not seen. I only bring this as an argument against the incorrect "unambiguous welcher weg" argument: when the grid is present there is a (small) ambiguity: arival of a photon in one place is only 94% indication or so that it went through the pinhole one thinks it came from. There is a 6% possibility it came from the other pinhole. This is again in agreement with QM predictions and is true for *every interpretation*.

• Dear Alfred, You say that in the case of "mixed state" experiment the grid is "visible" so it absorbs 6% od the light, but then you say that in "pure state" experiment the grid is in the interference minima. This is it (!) - the first state is which way setup, the second setup is no which way one. BUT THEN you make wrong comment that in the "which way" experiment with "mixed state" actually the state contains 3% probability that the photon comes from the other pinhole. This is wrong because the wires either "absorbs" these 6%, or "diffracts them in space outside the detector". So in both cases these 6% DO NOT ARRIVE at detector AT ALL. If you realize this fact, you will see that the experiment remains purely "which way" or if there is diffraction from the grid to the wrong detector, this diffraction will be negligible to the 6% loss. The main point is that the possible "cross-talk between the two channels A and B" should be "negligible" because the wires diffract light everywhere in space, and in most cases this light does not arrive at detector [6%] and the smaller percent [possibly << 0.1%] of diffracted light will arrive at wrong detector. Why? Because the diffraction can occur everywhere in space, and the volume of space occupied by the detector say 2-3 m away is relatively small. Well, actually the above error of yours has nothing to do with the discussion of the "no which way" information in the "pure state" experiment with both slits open. The main point is that if you have coherent light and interference you cannot say that the "images" are providing which way information. I investigate case in which THERE IS NO WIRE GRID and I say that there is "no which way" information in that case also. The fact that in both cases you will have almost similar two pinhole image at the image plane in case [i] using coherent light, and case [ii] using polarization filters procuding "mixed state" setup, does NOT mean that in both cases you have "which way" information at the image plane. This is a fundamental error to suppose that the image at the "image plane of the lens" always provides which way information independent on the density matrix of the photons in the setup. This error is done by everybody [for example Drezet in this forum] and including Anton Zeilinger [in journal publications] - the case [ii] produces "almost the same" image but not "identical" to case [i]. The case [i] is purely "no which way" experiment with off-diagonal elements non zeroes, while in case [ii] has zero off-diagonal elements. But my argument is even stronger - EVEN IF the two images were completely identical then this still does not mean that the same image at the image plane is indicator for "which way" information. I say that the probability distribution functions are 3 dimensional, so in order to say what kind of distribution you have, you should know how the function varies in the 3D space and having only 2D slice of such a function YOU CAN NEVER say what is the distribution. By clever arrangement you can produce any kind of 2D distribution by both coherent or incoherent light, but for the expense of differences in the P distribution outside this 2D plane. Now I think I am more than clear. Regards, Danko Georgiev MD 08:12, 2 June 2006 (UTC)

The action of the wire grid

If the density matrices are different [in the double slit compared to the mixed single slit setup] then the number of photons arriving to the wire grid will be different, and the explanation of Afshar experiment will be result of the different density matrices, so nothing special in the presence of the grid!

If one suspects that the grid has some special function to "change the density matrix" one should start from identical density matrices in the double slit and the mixed single slit setups, and then should try to explain the magic function of the grid to transform itself from absorber into reflector. This is fundamentally flawed idea [see the above post of Alfredr]. Danko Georgiev MD 10:10, 1 June 2006 (UTC)

I repeat: there is nothing magic in the grid diffracting as much light as it absorbs (and extracts therefore twice each amount from the main beam). This is just Huygens principle. There is nothing flawed here, it has been confirmed again and again.

If the beams are polarized at the exit of each pinhole, some part of the energy is lost (because there are no interferences and the grid is seen), but if you check, you'll see that the light reaching each receptor is not 100% , so with only one pinhole open (or with polarisers in front of the pinholes) 6% is absorbed and another 6% diffracted. If 6% is the total loss with a grid intercepting really 3% of the spacing, then it will be 98,5% versus 1.5%. And before anyone challenges me on Huygens principle: it stands to reason that the doubling is *only* valid for *small* absorption: an absorbing obstacle representing 6% of the area is small enough that it will diffract *almost* 6% more (for 3% absorption it is even better), but 40% of absorbing area will certainly not diffract another 40%, but significantly less than that! Do not oppose to me that with Huygens principle 50% of absorbing area would remove all the energy of the beam! I know perfectly well that it is not the case! In fact the exact expression is quite simple. If x is the fraction occupied by absorbers, the forward beam is reduced by a factor T=(1-x)^2, so the attenuation is 1-T=2x-x^2, out of which the absorption is of course x and the remainder, x-x^2=x(1-x) is diffracted. In fact Huygens principle says that the diffraction is the same when the absorbing area is x or (1-x). The approximation diffracted energy = absorbed energy is only valid when x is small. Alfredr 16:53, 1 June 2006 (UTC)

Dear Alfred, please read my reply in the preceding section. Possible clearing of the mess with the 6% should be done - these 6% is light not arriving at any of the detectors. So these 6% are both result from absorption by the wires plus diffraction in the space outside each of the two detectors Danko Georgiev MD 02:38, 2 June 2006 (UTC)

Dear Danko Let us not get into all the fine details but stay on the main problem. It seems now that you agree that Afshar's experimental results are correct, i.e., 6% loss for a single pinhole, ot polarised pinholes, and negligible loss when both pinholes are open. So we agree on that. Now what do we disagree on? Do you find this result expected, as I do, or bizarre? If the former, than let us not disagree when in fact we agree! 87.88.114.80 23:28, 3 June 2006 (UTC)

Do you mean that the density matrix is fine detail? I think that it is the main problem. Complementarity is simply mathematically formulated as that - [i] mixed state density matrix -> which way information; [ii] pure state density matrix -> no which way information. A mini-Wiki-lecture on this topic written by me using 4 slit setup is here four-slit. Now comes my question: TO HAVE BOTH TYPES of which way + no which way information what kind of density matrix you need??? A new mathematics??? What I disagree is on Afshar's anti-scientific speculations. Also if you read my previous post you will see also that there is a predictable effect on Airy disc pattern that Afshar has erased by apodization in order to have experimental evidence of the "false prediction" of identical images at the image plane both in mixed state and in pure state setups. I don't see how to be more clear on that - or maybe you don't care about my arguments but just post replies to keep the discussion going? best, Danko Georgiev MD 11:44, 4 June 2006 (UTC)

No "which way"

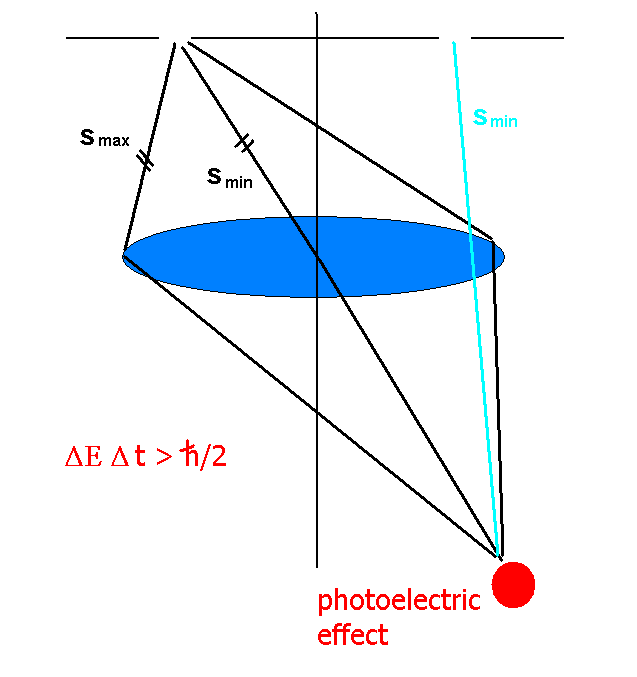
Let me put my point more clearly; I entirely agree with the experimental result of Pr. Afshar. Apodisation is irrelevant. No fraud is conceivable here. On the other hand, if Afshar wants to use his result to disporve QM, or any interprtation of it, he is mistaken. When the grid is present, the experiment is NOT a "welcher weg" one. The fact that in a *single* experiment one has both wave and particle aspect is usual. Any Young slit experiement using one photon at a time with photon detectors on dark and bright lines which do detect a photon, once in a while one bright lines and never on dark ones, exhibitds both wave-like character early in the experiment (existence of bright/dark bands) and particle-like later (effective arrival of photons one by one on detectors). So this in itself is NOT in contradiction with anything. Now what happens here is the same. One has wave-like behavior early (interferences) and particle-like later (detection). What obscures the matter is that one has the feeling that is is an unaambiguous "welcher weg" experiement. It is NOT. Some amount of *amplitude* is diffracted by the grid towards the image of the wrong pinhole (and yes, contrary to what Danko says, the amplitude diffracted by a *grid* is not in all directiosn in space, but more or les focalised at specific positions, so the amount that reaches the "wrong" image is small but not negligible). Now this amount is small, but not so small. ANd it is in *phase* with the main amplitude and when taking the square, the main extra contribution is not the square of the small contribution but the double product.

In a usual Young slit, the intensity at the center of a bright line is not twice, but 4 times what one has with a single pinhole. One for each pinhole plus two more for the double product. Because each contribution ia already unity, the 2 extra coming from the double product does not surprise anyone. Here what is surprising is that the amount that reaches the wrong image, if measured, is very small. I now doubt very much that one can measure the de-polarisation due to this effect if both pinholes are followed by polariser. If only one pinhole is open, one might measure a non-zero amount of light there, but not 3%! 3% is the amplitude, the intensity should be 0.09%. Still measurable, probably, but very small. The whole point if that if both pinholes are open and not polarized, this 3% amplitude interferes constructively with the 97% coming from the "right" pinhole. So the recovery of 100% is not so much that one does not know which pinhole the photon went, but whether it when through the right one (97% square, so about 94%,) from BOTH at the same time, causing a positive interference of 2*3%*97% so about 6%. This is a purely wave-like effect, where coherence is essential (so a pure state density matrix effect, which disappears in mixed-state, for instance polarised pinholes). What obscures this is that people are used to this double product when both the squares are obviously present (1^2+1^2+2*1*1=4 in usual bright lines of Young experiments) but here, because one of the terms is so small that its square is easy to forget (the small amount that the grid refracts to the image of the wrong pinhole) one has a tendency to think it is absent. By itself (i. e. when measured directly, which means taking its square) it is so hard to see that one just assumes there is nothing there. But it is there, it is exactly what is predicted by QM, it is exactly what reconstructs the 100% (or nealry so) visibility, and it is explained by every interpretation of QM. There is no paradox, because this extra 6% is precisely what shows that this is not an unambiguous "welcher weg" experiment: 94 percent from one pinhole, 6% from constructive interference of a photon going through "both pinholes" at the same time. The fact that it is a 94%-"welcher weg" obscures the crucial 6% "non-welcher weg" in the mind of the people who look at the problem, while when both pinholes contirbute equally (usual Young slits) nobody is surprised by the extra 2 coming from positive interference. And nobody is shoked that this wave-like phenomenon, interference fringes, is measured, photon by photon, by a detector, through a particle-like behaviour. 87.88.114.80 22:52, 4 June 2006 (UTC) Forgot to log in again. That was me also above. Alfredr 22:54, 4 June 2006 (UTC)

• Dear Alfred, the experiment is exactly 100% "no which way", and this means that in 100% the photons pass through both pinholes. You make big mistake to consider a classical situation in the fashion of Afshar suggesting that the detection of photon at detector A, means that the photon necessarily passes ONLY trough pinhole A' but not though both pinholes A' and B'. Below I make clear exposition with writing the state of the photons.

• Case [i] "mixed state" experiment in which you either close pinhole A' or B'. In this case the photon detected at A necessarily passes through A' and only through A'. The density matric of such a state is $1/2|A><A|+1/2|B><B|$ But this is a statistical mixture so the real state vector of a photon in the setup is either |A> or |B>, and this is crucial. Such a photon if being in state |A> can only end at detector A, and if being in a state |B> can only end at B. No magic - this is the essence of the which way information - you are 100% sure where the photon will be detected IF you could knew its state vector.

• Case [ii] Afshar's lens "pure state" setup. The photon's state vector reaching the lens is exactly ${\frac {1}{\sqrt {2}}}(|A>+|B>)$, so this means that EVERY PHOTON has 50% - 50% chance to be refracted towards detector A or B, but this is superposed state, so actually it is refracted at both places AT ONCE. This is the same as having the interference picture at a screen - the photon is presented everywhere at the screen, but only the measurement "collapses" it as a point somewhere on the screen. So it is the non-linear "collapse" that localizes the photon at only one of the detectors, but before the collapse the photon actually were at both detectors. This is simple description based on non-linear collapse [this is needed because QM is not relativistically correct] and actually if ordinary QM were true then everything would be reversible. This is not the case, so some non-linear process does the job.

• WHAT IS THE CONCEPTUAL and practical difference of this discussion? Well, if you try to capture the photons at the detectors in an optical cable, instead of "absorbing them" on a photo film, you will see the difference. If you cross the beams of "mixed state" photons as in case [i] you will not observe interference picture. But if you cross the beams of photons of Afshar's case [ii] you will see interference. This PROVES that the photons in Afshar's setup are in pure state ${\frac {1}{\sqrt {2}}}(|A>+|B>)$ so there IS NO which way information. And this DOES NOT depend on the presense of a wire grid or not. Simply you cannot apply classical optics in quantum experiment.

• Therefore dear Alfred, what do you think about Afshar's setup without any grid. Is it "which way"? You will understand that it is 100% no which way, if you try to understand the "realness" of the quantum superposition. This is not just mathematical non-zero off-diagonal elements, this is real phenomenon. The experimental implication is that if you believe that in Afshar's setup without wire grid there is "which way" information then you SHOULD predict NO interference of two beams [1] captured in optical cable photons arriving at A and [2] captured in optical cable photons arriving at B. But I suspect you will predict like me that there will be interference, and if so, then NO which way information is present. Think in density matrices and you will avoid confusion about complementarity - it is just labeling of the density matrices - "mixed state" ones being "which way", pure state ones being "no which way". Note: this is valid if you have at least two slits, for a single slit it is meaningless as well as the whole original idea to use such kind of misleading labels. But this is what happens if you want to do popular science. Danko Georgiev MD 12:02, 8 June 2006 (UTC)

I keep saying this is not an "unambiguous which way" setting.

But the which-way/no which way quality of a setting depends on the whole setting. Certainly I predict, like you, that if at arrival points A and B there are optical cables, which are then reconnected, there will be interferences! But if you put "destructive" detectors, then obviously there is a "partial which way". I drop square roots of 2 and I begin kets with / , I don't know how to type verticals If only pinhole A' one starts with /A'>

• Without * grid it goes through the lens to A: the ket is then /A>!

Pure which way. Similarly /B'>goes to /B> STILL if both pinpoints are open, start from /A'>+/B'>, still no grid. - a setting with destructive detectors at A and B will tell unambiguously which pinhole the photon went through, pure "which way" - the setting you suggest with optical cables will show interferences, "zero which way". The difference is in the final setting, as *always* the case in QM: depending on what you measure, you get a different information.

Now add the grid. In the "zero which way" setting with optical cables, you get interferences, grid or no grid. But this is a "zero which way" setting! In the "destructive detectors" setting, of course there is "partial which way". This is precisely what makes the whole thing confusing, and why people keep arguing. If *only* pinhole A' is open. Begin with /A'>, one has at the end /A>+/A diffraction> The effect of the /A diffraction> term is - you get a small amount of light in various places, including B - it interferes *destructively* with /A> so that you get only 94% flux there (and Huygens principle says that this negative interference reduces the full intensity both to take account of absorption *and* diffraction! This is where the 2 in (1-b)^2=1+b^2-2*b plays a crucial role!) So it is possible for a photon coming through A' to reach B, but this probability is very small, typically 3% of 3%. In that sense, the setting is certainly "mostly which way", but not fully.

If *only* pinhole B' is open, one has at the end /B>+/B diffraction>

Now let us start with both pinholes open /A'>+/B'> Because the grid is situated where it is, at interference minima /A diffraction>+/B diffraction>is exactly zero: you cannot see the diffraction. But there does not mean that /B diffraction> does not exist! It does exist and its role it to destroy /A diffraction> that would be visible if /B diffraction> were absent.

And one recovers full intensity because (/A>+/A diffraction>)+(/B>+/B diffraction>) is the same as /A>+/B> because /A diffraction>+/B diffraction>=0

But remember the two roles of /A diffraction>: - send light at various places - interfere negatively with /A>

The effect of /B diffraction> has the opposite sign, so it destroys the amplitude (hence the square amplitude, hence the amount of light) that would go to many other places in the case where A' only is open and grid is present.

• AND* it has constructive interference with /A> restauring full flux.

But saying that a photon actually "irreversibly measured" in A (whether you understand this as the Copenhague way, of the Wigner way, or Bohm's way - in Everett's view, both detectors detect) is a 50-50 cahnce of its coming from either pinholes is clearly wrong. It is a 94% coming from A', a very small amounr (0,09%) coming from B' and 6% constructive interference from going throug hboth at the samre time.

Now that should suprise noone. Take a completely usual standard Young slits experiment. At the center of a bright line you have not twice but four times as many photons if both slits are open than if only one is. Why four? One from one slit, plus one from the other slit, plus two from positive interferecne (and in the center of a dark line you get zero, one plus one minus two). So having photons here rather than there because of constructive or destructive interference is something that everybody that deal with QM accepts implicitely.

What is confusing here is that the *square amplitude* of a photon reaching A coming from B' is so small (0.09%) that one tends to forget it is even there. But hte *amplitude* itself is not so small, 3% and therefore its constructive interference is far from being negligible: doubled by the famous (a+b)^2=a^2+b^2 + 2 ab it gives the famous recovered 6%

So it is still a "mostly" (94%) which way, and this is just what makes people think it is a "full which way". People have a tendency to ignore very small quantities, such as 0.09% reaching A when *only* B' is open. But in QM amplitudes can play a role by there interferences and so an amplitude of 3% is not negligible if it ca nonterfere with amost 100%, even where it is alone it is almost invisible because the square is so small. Alfredr 01:27, 9 June 2006 (UTC)

Dear Alfred, thank you very much for your exhaustive reply. Actually I fully agree that squaring a small amplitude will produce observable close to zero, while negative interference of this small amplitude with greater positive one, will result in big decrease of observable, compared in case in which there were only the big positive amplitude. This is simple mathematics so nothing frustrating about this, you raise important precaution.

My point, however is totally different. There is a modern definition of which way information as presented in lectures by prof. Bob Eisenstein [1]. It is unambiguously linked with the density matrix of the quantum state, so to say that a pure state density matrix of double slit setup at the image plane of lens gives you "which way" information is WRONG.

You of course use a kind of intuitive or popular view of the which way information. However such kind of view is inherently illogical and inconsistent. I like to use gedanken experiments due to so-called principle of Counterfactual definiteness, according to which you can imagine experiment and predict its outcome even if you haven't performed it. So do not directly tell me that my capturing of photons with optical cables changes fundamentally the experiment. It is not so. I DO NOT CHANGE the density matrix, of the photons so they remain in pure state if they were in pure state, and they will remain in mixed state if they were in mixed state [i.e. polarized ones].

Imagine first case with different polarization filters. You have mixed state so actually the probability distribution is as in case 1. This has photon "trajectories" being more or less straight lines, therefore this is really close to what you classically understand as "which way" - you have well defined photon traces behind, so if you put obstacles on the trajectory, you will be able to stop the photons.

Now come the pure state Afshar's setup as seen in case 2. In this situation even without the grid the probability distribution in space does not follow classical trajectory but has many interferences minima and maxima. The fact that at the image plane the function resolves the two pinholes is of not special significance because outside the image plane the probability distribution is significantly different.

SO, where comes the Counterfactual definiteness - well, imagine that you have imaginary physical situation in which there are tiny black holes in the place of the wires. You can adjust their mass and Swartzchild radius to be exactly such to fall in the interference minima of Afshar's setup. Then you could possibly assume that there will be not diffraction/reflection in space, but only absorption if the photon falls in the black hole. In this case I can still explain Afshar's experiment, where your logic with diffraction will almost certainly fail.

Now, comes the obvious QUESTION: what is the purpose to call your popular view of "which way" information as being "truelly which way". Since the photons state is pure state even without any wires, any blackholes, etc. their mathematical probability distribution DOES NOT FOLLOW straight trajectories! Why you call this "which way" setup? IF you decide to CAPTURE a photon you should put for greater efficiency the absorbing wires, or black holes not in the straight lines as seen in case 1 but better strategy is to put exactly in the center an obstacle that will be at 4 times greater probability peak, due to interference as you already have shown in your post. So think now about inverse experiment in which you want to capture light. In this case you will not assume that your wires diffract to the wrong detector, but for OPTIMIZATION of your captiring, you should better put in the central maximum. So the interference distribution PRECEDES your choice to capture the photons, and does NOT follow it. So you cannot call probability/intensity distribution of photons that DO NOT have straight "trajectories" with the name or label "which way". It is NOT impossible, but is inherently paradoxical, and is the source of Afshar's error. He has disproved the popular notion of "which way" that layman have, but has not disproved complementarity as defined in modern terms as just labeling or putting another name on the types of the density matrices. Actually it is labeling whose purpose is to avoid confusions in the popular explanations of complementarity to laymen. Danko Georgiev MD 09:48, 9 June 2006 (UTC)

An INVERTED Afshar's setup (updated!)

Here I present a setup that shows that Alfred's critique is flawed, otherwise Alfred's logic should be applicable to a setup which I call "inverted Afshar's setup" (note: error in the previous post is removed).

Suppose Afshar first puts a wire on the axis centered between the two slits. Now he performs measurement in a mixed setup in which he first closes the slit A', then closes slit B' and takes the statistical mixture of those two experiments. Of course the same thing can be achieved by simply putting different polarization filters on the slits. With suitably chosen width of the wire the result will be 2.2 % loss of light transmission. See the case 1 on the next figure.

Now consider case of both pinholes open (and no polarization filters put) - since the wire is located at the same place that now falls in the central interference maximum it will absorb 8.8 % of light, not 2.2 %. Now it should be clear that this 4 times increased loss of light is proving undoubtedly that there is interference.

Now comes the obvious QUESTION: If Alfred's critique were correct then what happens with the presence of the single wire in the case where there are no polarization filters? Does it has the "magic power" to attract the light in order to absorb it? Surely not, it absorbs light and diffracts light only because of the fact that it is put in the central interference maximum. But this means that the central interference maximum is pre-existent even before the single wire was put in it. To defend the thesis that this maximum is produced by the presence of the single wire and is not pre-existent means that you argue for some magic power of the wire to "attract the light" which is not very good idea. Therefore I conclude the inverted Afshar's setup is good argument that there is no which way information even if there is no wire at all in the case when the light through both pinholes remains coherent (indistinguishable). So the "inverted Afshar's setup" shows that the density matrices of the photons are pre-existent and do not depend on the presense of wire or not! Since the non-zero off-diagonal elements of the density matrix of the photons SHOW EXISTENT INTERFERENCE therefore the interference or not is also pre-existent and does not depend on the presence or not of the wire! Therefore putting wire, or not putting it does not change the density matrix of the photons, and this means that putting wire or not, cannot per se change the nature of the setup from "which way" into "no which way", or mixture of "which way plus no-which way". (p.s. the computer simulations in the above figures were performed for the case of Afshar's experiment with photon wavelength of 650 nm and lens put 4.2 m behind the double slit; and a technical comment a purely "which way" experiment should have mixed state density matrix with zero off diagonal elements, "mixture of which way plus no which way" will have also mixed state density matrix but with non zero off-diagonal elements, and finally "pure state" density matrix of purely no which way setup will have density matrix $\rho$ with non-zero off-diagonal elements such that $\rho =\rho ^{2}$). Danko Georgiev MD 05:25, 12 June 2006 (UTC)

The density matrix of purely no which way setup is given by the 2x2 matrix ${\begin{bmatrix}1/2&1/2\\1/2&1/2\end{bmatrix}}$

The density matrix of purely which way setup is given by the 2x2 matrix ${\begin{bmatrix}1/2&0\\0&1/2\end{bmatrix}}$

The density matrix of mixed 6% no which way and 94% which way setup is given by the 2x2 matrix ${\begin{bmatrix}1/2&3/100\\3/100&1/2\end{bmatrix}}$

This last setup can be obtained as statistical mixture if you run 94% of the time the experiment with polarization filters and in 6% of the time you remove the filters. You see that if the setup was actually as you suggest then the diffracted light would not be almost zero, but there would be about 5.64% loss.

Since the density matrix cannot be changed by the presence or not of the wire grid, the suggestion that in Afshar's setup there is 94% which way information and 6% no which way is clearly wrong, because it essentially leads to prediction of 5.64% loss which is not the case. Danko Georgiev MD 06:19, 12 June 2006 (UTC)

When did I ever say that the pattern does not exist unless the wire is present? Easy to prove I am wrong if you attribute me ridiculmous claims! Of course there will be 8,8% attenuation in this case (well, 8,8 out of 200, really, quadrupling the amount out of the beam certainly, but the total intensity is doubled). Also, half is absorption and half is scattering (but that was alsos the case of the 2,2% if only one pinhole is open). I never claimed anything to the contrary;

You misunderstand what I mean by 94% "which way" I am speaking of a *pure state* density matrix, not at all a partial mixed state. The point is that though it is pure state, it still does not treat both holes equally.

What I keep saying over and over is that in Afshar's experiement arrival of a photon at the image of a pinhole does not mean that it came from that pinhole. The *vector* describing the "in-flight" photon is, as you say, ${\begin{bmatrix}1/{\sqrt {2}}&\\1/{\sqrt {2}}&\end{bmatrix}}$

I agree with you on that point. But the probabilty of arrival of a photon on the image of a pinhole is skewed. Afshar claims it is 100% that it came from the correct pinhole and that would violate complementarity. So it is not 100%. But still the probability *amplitude* of arrival at the image of a pinhole is 97% from the right one and 3% from the wrong one, when both pinhomes are open, and these amplitude are positively correlated (with polarisers, they would not be), so the sum is really one, so the 100% recovery is there.

The matrix I have in mind is ${\begin{bmatrix}0.9409&0.0291\\0.0291&0.0009\end{bmatrix}}$ but this is not a density matrix. Rather, it is the efficiency matrix, which you have to "sandwich" between the vector describing the photon and its dual. This tells what probability the photon described by the above vector has to reach one pinhole. The answer is 1/2, globally (no absorption and no visible diffraction either, when bot pinholes are open, all the light reaches the image of one pinhole or the other). But you can break it down into "coming from one pinhole", "coming from the other one", "positive interference"

Afshar would have it that this efficiency matrix is ${\begin{bmatrix}1&0\\0&0\end{bmatrix}}$ arrivla of a photon at one image means it comes from the correct pinhole

What is your analysis, here? Alfredr 03:45, 13 June 2006 (UTC)

Dear Alfred, I am glad that we reached actually concrete mathematics, so you have clearly formulated what you mean, or at least you have pointed out what kind of math object [in this case matrix] should describe your concepts. The problem is that I don't understand at all your concepts of "which way" that has also interference? As I understand the logic of your previous post, then possibly you mean that in pure state say 1/4 there is "which way" contribution from one pinhole, 1/4 from the other one, and 1/2 from positive interference? But all this is totally confused way to think about complementarity. WHY? Because this is NOT EQUIVALENT to closing one slit 1/4 of the time, then closing the other one 1/4 of the time, and letting both slits open in 1/2 of the time. Therefore it is not logically, philosophically, or mathematically justified to "break down the pure state" into "which way" components and "contributions from interference". Once you understand that your approach is inherently paradoxical then you will see that the density matrix of the photon is all that matters in QM, and it is the density matrix that solely determines the "which way" or not of the setup. Once you make this modern step (that is not mine creation) you will see that the "which way"/"no which way" controversy is JUST language confusion. Now please understand me in correct way - I do not say that your definitions of the which way/no which way are wrong. It is fully possible to start from your definition, so that finally we will agree what you want to say. But my argument is that you introduce artifical naming of things with wrong names. This is the same if I make definition that when I say "white" you should understand "blue". Finally the meaning will not be lost, but this is unnecessary confusion and nobody will try to speak this new language of mine. The same holds for your view of "which way" definitions.

Below I provide the basic guideline: If one says "which way" he must be 100% percent sure that nothing else could have happened but the photon must have passed only and really only through one of the pinholes. So any time you imagine experiment in which you say there is x % "which way" information, you should be sure that this experiment can be performed as a statistical mixture of different setups in which you use x % single slit experiment in which you are really sure of the "which way" info. By the way - if I follow your suggestion then it will follow that there is no purely "no which way" experiment, because in every coherent state you will be allowed by your procedure to break it into "interference components" and "which way" components. I hope we have basicly understood each other. The fact is however that my density matrix oriented approach is simpler and more easier for intuitive grasp. Of course it accepts the ontological reality of superposition and is close to the Many Worlds Interpretation of the QM, but actually I never defended MWI. I think that QM is wrong in its current form, and it surely is so, because it is not relativistic. In a relativistic QM version surely there will be non-linearity and superposed states will be unstable - so there will be half-time for decay of the superposed state into a single space-time geometry. This is proposed by Penrose and Diosi. Danko Georgiev MD 02:03, 13 June 2006 (UTC)

Defining "which way"

OK, I agree that I am using the expression "which way" in a different meaning than you, so that accounts for a lot of the confusion. So let us agree on something (and I won't use the phrase "which way") When, in a simple minded Young experiement, at the center of a bright fringe I get four times the intensity that would get there it is because there is one square plus one square plus two times one times one , the latter being positive interference, yes or no?

In that case both holes play the same role and since when a photon arrives we have no idea where it comes from, we all agree that this is clearly a "no-which way" situation. Agreed? Alfredr 03:45, 13 June 2006 (UTC)

Dear Alfred, of course that I agree that when both pinholes are coherent there is positive interference. The main logic for linking the density matrices with the terms "which way" and "no which way" has been derived in a web posted pdf by me from basic logical gates. Think about:

case [1] mixture of 2 single-slit setups. In this case you know absolutely sure that A XOR B. In this case you have zero off-diagonal elements, so no interference. This is "which way" because you at one hundred percent know this "A XOR B".

case [2] coherent double slit. In this case you know NOT (A XOR B), which is exactly the logical gate "A AND B". It is then seen that do detect a photon behind the double slit in such setup the photon MUST always pass through both pinholes simultaneously. This is exactly revealed by the presence of the non-zero off diagonal terms. The logic is simple in order to have the interference term, you need at hundred percent passage through both pinholes. Whether you have observed this interference or not, does not matter because it is part of the photon's density matrix. So whether you might in some intutitve sense think that there is "single slit contributions" plus "interference contribution" actually this is inherently paradoxical, since the logic starts from the basic fact "NOT (A AND B) -> NOT interference term" and by modus tollens you have "interference term -> A AND B".

Now I hope you see how the interference term is linked with the classical logical gates XOR and AND. This is not just pure coincidence, its actually what our intutive vision about "which way" is - namely it is intutively - XOR case, while "no which way" is the XNOR case, which is the AND gate. Now you see how the superposition is born from logical negation.

p.s. 1: By the way, here "interference term" means interference from slits A and B. So the which way is relative - there is no which way information from which part of the single slit the light comes, because there is single slit interference [producing the Airy disc]. So "which way" is a relative concept - consider the 4-slit setup discussed in Wikipedia by me. You might have 4-slit intereference [global no which way] or you may put L-filter at the slits A and B, and R-filter at slits C and D. In this case you will have (A & B) XOR (C & D) "which way" info, but you will have A & B "no which way" info since you might be sure it came from A & B, but you cannot tell from where exactly. Actually the AND logical gate implies that the photon really came from "all possible points of the A & B", and this is NOT just "lack of knowledge" from where it came.

p.s. 2: I would like to point out this FUNDAMENTAL difference - the AND gate implies really A & B, and this is NOT equivalent to "lack of knowledge" whether it was A or it was B. This is the "magic" of QM Danko Georgiev MD 06:56, 13 June 2006 (UTC)

OK so far we agree. Note that I *always* consider pure state (unless I specify: when using polarisers, that is mixed state), which in your terminology would mean "no which way". However you'd agree that if a *single* pinhole is open and there is NO grid, then this is a pure state, not a mixed state. But the photon always gets to the same place, and when a photon gets there, you know where it comes from. So in that sense it is a *pure* (not *mixed*) situation, thus "no which way" but you know exactly where the photon comes from and where it gets.Of course there being a sigle beam there are no interferences! This is what in my "uncontrolled" terminology I would have called a "which way" situation but I'll avoid to do it to avoid confusion.

Now if a single pinpoit is open *and* there is a grid, Huygens principle says the following: If a completely opaque grid occupies, say 3% of the surface it will absorb this 3%. Whether black holes or black paint there is no difference. Then an additional 3% (well, 2,91% really, 3% of 97%) will be extracted from the main beam and diffracted away. This amount does *not* come from the same 3% of the beam (and that is why your argument on black holes is irrelevant). It is extracted from the beam *near* the obstacle. It is a purely wave phenomenon. The principle is exactly the same that causes the "Airy fringes" in the shadow of an opaque object. You know that the shadow is never sharp, there is some amount of light that seeps into it, in the form of an Airy function. That would be diffraction at a finite distance- in our case since we use a lens to form an image, at finite distance, of what would otherwise go to infinity, we have "diffraction at infinity" visible on the image plane. But the principle is the same. Light that obiously went in the open part, not through the opaque part, ends up where one does not expect it, *because* there is an absorber neaby. That is Huygens principle and believe me it has been tested over and over again.

So I have one pinpoint open and a grid. For convenience assume the grid is perfect and infinite. Where does the diffracted light go? Because the diffractor is a grid, not a single wire, the diffracted light must go to the dual grid. Now because the wire separation of the grid is just tuned to the two pinholes (one of which is closed for now, but we know where it is and the grid has been positioned accordingly), therefore the dual grid has just the separation of the images of the two pinholes. The light goes to the part ot the grid which is in the diffraction cone of a wire. Since width of the wire is 1/30 of the separation, the diffractio cone is roughly 30 times a wide as the separation of the dual grid. So there are roughly 30 dual grid points in the cone (note that the cone is not sharply defined, it is just the measure of the width where the intensity is still not too small). So 3% is absorbe, 94 % goes to the image and 3% is distributed over dozens of points on the dual grid. In particular, 0.09% reaches the image of the other pinhole (though it is still closed).

You can try it, it will work exactly as I say. Still, most (94%) of the light goes to the correct image, and moreover the amount in the wrong image is quite tiny, just 0,09%. Ths is because what you measure is intensity, not amplitude. Amplitude is 3%. So far this is not even QM, just standart wave propagation.

Do you believe me or not?

Alfredr 10:02, 13 June 2006 (UTC)

After reading several times your reply, I am now asking - "So what?". Does the wire absorb in the double slit setup also 3% of the coming amplitude? It should be, but because the 99.99% of the light goes to the images, then the amplitude being at the wire grid is ZERO. Zero is due to negative interference from the two pinholes. So as well the diffracted amplitude to the other image will be ZERO. If there were amplitude to be difrfacted, then there would be percent of it that should be absrobed. I still do not understand the obvious assymetry that you are trying to defend - it is impossible in one case 3% of the incoming amplitude to be absorbed, 3% diffracted to the other image, and on the other occasion stil 3% to be diffracted, but 0% to be absorbed. To explain 0% absorption, you should consider that there is 3% absorbtion of 0% amplitude coming, but the same will hold for the diffracted light. Danko Georgiev MD 04:51, 14 June 2006 (UTC)

Dear Danko, This is precisely where the whole solution to the paradox is!!!! Remember we are in a PURE STATE, situation, adding AMPLITUDE, not SQUARED AMPLITUDE. SO the grid diffracts 3% aofthe amplitude coming from one pinhole (and also absorbs another 3%) If only yhis pinhole is open,you lose 6% in the forward direction. Now opne the second pinhole. Also 3% of the amplitude will be absorbed, BUT AT THE WIRE THE AMPLITUDE HAS OPPOSITE SIGN! So the amplitude coming from the second pinhole absorbed will CANCEL the amplitude absorbed that comes from the other pinhole (one way to say this is saying that the total amplitude is zero at the wire, but I can look at it and say that there are two quazntities ,thatr happen to cancel. Also the diffracted amplitude coming from the second hole is not zero, it is 3% but these 3% cancel exactly the amplitude cominf from the foirst pinhole which is cancelled. But this is VERY IMPORTANT: because when only one pinhole is open, you get 94% only because the FORWARD-DIFFRACTED amplitude interferes destructively with the main beam (and here we go back to my pet Huygens Principle) It is the 3% FORWARD-DIFFRACTED amplitude coming from pinhole one that porduces the loss. Now, whne you opne the second pinhole, the amplitude diffracted (not forward, in that case, that would be at ITS image, but at the next point of the dual grid, that happens to be the location of the imagre of the other point, the amplitude is again 3%, but it has the opposite sign from the FORWARD-DIFFRACTED amplitude from the first hole. Thus it interferes CONSTRUCTIVELY. So in one sense yes, there is no diffraction at all. But htis is a "non QM" view of things. There is diffraction, from each hole, one that causes negative interference (from the "right" pinhole) and one, cancelling thare first one, that recovers 100% by causing constructive interference. ANfd for that reason the diffraction of light coming from the second pinhole is important.

The "so what" is just Afshar's mistake: because MOST of the light that reaches one image comes from one pinhole, he forgets the other component. Just as, in what I wrote above, you'll say that if one pinhole has an absorber that reduces the light to 1/100 onre would tend to say that only one hole is eally open and it looks like a "which way" setting. But you still get up to 20% interference,up and down! Here it is exactly hte same thing. Alfredr 07:12, 15 June 2006 (UTC)

Dear Alfred,

After this last post, I see you agree that the wire is in the interference minimum so it actually diffracts 0%. But you cannot interprete that the wire absorbs 3% with wave A negative amplitude, and 3% wave B with positive amplitude, and this is why actual photon detection is almost zero. This not consistent interpretation because you should consider what happens further at the image plane and the normalization says the $\Psi '$ for the waves A and B is ${\frac {1}{\sqrt {2}}}=0.70$. So if you have absorbed 3% of each amplitude A and B at the detector you will have amplitude of 0.68 and squared you will have 4% loss of intensity for each image A and B, which is 8% total loss. So I think the only valid interpretation is that due to negative interference the wires DO NOT absorb any quantum amplitude because 3% absorbtion from zero amplitude at the wire, is just zero. Danko Georgiev MD 05:03, 15 June 2006 (UTC)

Dear Danko We are in a pure state situation. So when amplitudes are opposite the net effect *is* zero. There is zero *net* absorption (because the amount of the absorption is the square of the sum of the amplitudes ,not the sum of the squares, and amplitudes add up to zero), but as far as Huygens principle is concerned, it is the amplitude that counts, and this causes diffraction for each of the two beams. Of course these amplitudes also cancel each other. *Net* diffraction is also zero! BUT that the TOTAL diffraciton is zero (sum of two opposite amplitudes) does NOT mean that amplitude does not come from pinhole 2. It kills the diffracted amplitude from pinhole 1. So you cannot see it, it adds up to zero everywhere. But in so doing by removing the destructive forward-diffracted amplitude of pinhole 1, it acts as a constructive interference.

And yes, I do insist that I claim this amplitude is "real",

Consider a simple minded Young slit experiment. Take a point near the center of a dark fringe, but not quite the center. There is a small amount of light there. Where does it come from? Answer: from both holes, with almost total negative interference. But the amplitude coming from each pinhole is not any smaller there. It always have the same modulus. It is just that the relative phase is almost pi. So by continuity when you reach the dead center of the dark fringe, you MUST interpret it as two amplitudes reaching there, but exactly opposite. Saying "nothing reaches there" is a conceptual mistake. When thinking quantum-mechanically these distinctions are conceptually important. Afshar's error is just to ignore that pinhole 2 DOES affect the amount of light reaching the image of pinhole 1! Afshar's error is not experiemental (apodisation has NOTHING to d owith the result) nor mathematical (what he computes he should get is quite correct, and he does get it) but PHILOSOPHICAL. His experiment is OK, but the conclusion he wants to make are erroneous. His experiemtn proves QM is perfectly right, and not the contrary. And the crux of the solution to the paradox is that an amplitude that cancels another amplitude is STILL real. Saying 3oh, but it adds up to nothing, so it is as if it were not there, nor is its counterpart there" is a severe conceptual error. Both are there, and if they add up to zero, so be it. Alfredr 07:12, 15 June 2006 (UTC)

Dear Alfred, you are "beating about the bush" as I see from your post. Afshar makes this simple contradiction - [1] the image at the image plane carries "which way information", [2] there is interference, therefore complementarity is violated.

Suppose there is NO wire grid, there still be interference at the place where the grid is missing now, and if you continue to claim that at the image plane there is which way info, the same controversy will be there if there is NO wire grid at all. The problem is that there is "no which way" information at all at the image plane, and I don't see why your ideas about diffraction at all contribute anything positive towards the discussion. The explanation of Afshar's error is not in the fact that the grid is there, the error is that he forgets that the photons are in pure state. I think that here we are sharing the same position. I don't understand why you continue to focus on the difrfaction, since the main problem is the pure state of the photons.

Concerning the apodization, you still do not understand what I am talking about. Having one pinhole open has smaller uncertainty in x - i.e. 250 microns is the pinhole aperture, than having both pinholes open - 1 milimeter is the distance between pinholes. So in the first case of one pinhole open the uncertainty in the wavelength is bigger, while in the second case the wavelength uncertainty is very small. If you have superposition of wavelengths the Airy disc pattern will be sifferent from the Airy disc pattern of exactly monochromatic light. This is important difference that is masked by apodization. If you let it be manifested then you should have to explain why this difference exists, and you will not be able to claim that you have disproved complementarity.

By the way, I don't see anything positive from our discussion. The ideas in science are not "mine" or "yours", they are judged only by the value of their semantical content. Whether you will at all consider what is happening without apodization and whether you will see potential "massage of experimental data" is of no interest for me. After communication with Afshar you will see that he is quite ignorant in physics, but this is result of the bad educational system in Universities. If the examinators did their job correctly, such persons would never be able to pass the final exams. Danko Georgiev MD 09:41, 15 June 2006 (UTC)

Unbalanced pinholes

Dear Alfred, I have just read your e-mail on unbalanced pinholes in 100 to 1 fashion. You say wrongly that in pure state 100 of the photons go through pinhole A and only one through B, but you don't know when exactly this photon will pass thorugh B. This is totally wrong because the logical structure of the above sentence is "100/101 A XOR 1/101 x B". But this is the mixed setup when you close at random 100 time pinhole B, and only 1 time pinhole A.

In the balnaced setup actually you have quite different knowledge - every single photon passes through both pinholes simultaneously in unbalanced fashion, so that 100/101 of its amplitude goes through A and only 1/101 goes through B. And yes, this absolutely "no which way" information, in sense that the photon COMPULSORY goes THROUGH BOTH pinholes in unbalnaced fashion.

It is Russel, and later Wittgenstein who pointed out that most philosophical problems are nothing but "language confusion". Actually you make not only "language error" because the logical structure of your thesis is "A XOR B", but I suspect that you believe that this is somehow semantically correct. Alas, as I proved above you cannot say that you lack of knowledge whether in this unbalanced setup the photon goes through A or B, because it goes at the same time through both. Actually you may imagine a kind of Bohmian picture, but I am not sure at all that Bohmian idea of defined "trajectory" is consistent at all, since you cannot think of pure state setup within the terms of mixed state one. Danko Georgiev MD 12:58, 15 June 2006 (UTC)

APODIZATION !!!

Dear Alfred, actually it is my fault that so far I speak without providing images. They can be easily created within Wolfram's Mathematica software, so here is the vizualization of what I am talking about.

Case [i] Afshar double slit open - the images of the pinholes will have sharp Airy Disc pattern because the interference of photons provides exact value for their wavelength being $\lambda =650nm$. So there will be sharp dark negative interference rings around the central Airy maximum. In this case with exact wavelength, the uncertainty of the position is huge because the photons actually pass trough both pinholes, hence span region of 1.5 mm [250 micrometer aperture plus 1 mm inter-pinhole distance].

Case [ii] Single slit "mixed setup". In this case the position of the photon is defined within range of 250 micrometers only. So there will be uncertainty of the photon's wavelength. In this case the Airy disc pattern will be as if produced with photons spanning wide and continuous region of wavelengths. In the graph below I have calculated graph for $\lambda$ varying from 600 nm to 700 nm. The main effect is that the dark negative interference minima become BRIGHT! I.e. due to wavelength uncertainty there is non-zero probability for the photon to fall in the interference minimum of the monochromatic case of wavelength of 650 nm. Also this "shift" of intensity comes from decrease of the higher order Airy maxima.

Now what will you say about this??? Is it a QM prediction? IF so, isn't it a fraud in order to massage the date to fit Afshar's to his interpretation. If he did not use apodization, people will immediately see this difference in the Airy disc pattern and will say - "Hey, Afshar, the two images differ, how will you explain that?". But in the current situation this is not visible, because of the apodization, and Afshar says that the images in case [i] and case [ii] are identical. So I do not believe that Afshar if he is professor, as he says, will not know of this effect. If he knows about it, however emerges the question why he "masked it". Is it aimed manipulation of data? Danko Georgiev MD 02:30, 16 June 2006 (UTC)

Dear Danko In *principle* what you say is true and is QM predictable. But your orders of magnitude are wrong by a very large factor (by 30, really). Say the wavelength is 650 nanometers. The pinhole has diameter 250 micrometres. This is about 400 times as much. So the relative spread in wavelenght will be 1/400, or just more than 1,5 nanometers. Do the same curve with the interval 648,5 to 651,5 nanometers instead of 600 to 700!. You won't be able to tell the difference with monochromatic light, unless you take a magnifier (and assuming your laser printer has a fantastic definition! No experiment, however "non-apodised" will see such a small effect. Moreover, the case of two pinhles is not so different. You say the spread should be six times smaller, but this is not so simple. Two 250 micrometres at 1 mm distance is not at all the same thing as a single 1,5 mm hole! So there *will* be a difference (QM calculable, yes, but rather hard to compute and probably not as devastating as you think), but it will apply on a such a small effect (1,5 nm spread, not 50) that it will be totally impossible to see it.

You really do not understand my point. Don't you see that I keep saying that photons go through both pinholes at the same time? I keep repeating that the 6% recovery is precisely due to positive interference of photons going AT THE SAME TIME through pinhole 1, straight ahead, and from pinhole 2, diffracting on the grid. How can one be more convinced that a photon does go through both pinholes? So my thinking is as QM as they come. But saying that the photon does go through both holes does not mean either that it goes to the same places. Afshar has it that in his images photons from each pinhole only reach the image of that pinhole. This is false and would lead to paradoxes. The truth is, some light from pinhole 2 play a role. But you seem to argue that light from both pinholes reach *equally* both images. What would you say of the case where NO GRID at all is present. Do you argue that in that case *also* light from one pinhole reaches the image of the other, because we are in a pure state and each photon goes through both pinholes? This is a misapprehension. I don't know how to explain it to you, but you do not think "dually" enough. You do not grasp the fact that, even in a pure state, the photons, AT THE SAME TIME, go through both pinholes at the same time AND go through one OR the other, DEPENDING on what QUESTION is asked to them. This is real QM dual thinking. If there is no grid at all, of course what Afshar says is correct: each photon gets to the image of the pinhole it went through, IF there is a destructive measuring device. If at the image of the pinholes, there are light guides which later are recombined, then each photon goes through both pinholes. Yes, it is so. The point is, the grid explores only *part* of the interference pattern, only the very center of dark lines. So its effect is what it is: destroying the guarantee that each photon reaches the image of the pinhole it went through, but only weakly: up to 6%. Alfredr 18:19, 16 June 2006 (UTC)

I don't claim that I have actually estimated the exact value of the effect, I just wanted to manifestedly show you what I am talking about. By the way, one should start from Heisenberg's relations, and I cannot say anything on the topic before I do the exact calculations. Danko Georgiev MD 04:07, 17 June 2006 (UTC)

Non-apodization and effect on wavelength uncertainty

Dear Alfred, I just have computed the actual effect on photon's wavelength in case where there is no apodization, and I obtain really very very small effect, so it maybe should be not visible experimentally. So possibly apodization is ok from experimental point of view as you say. Below is the exact computation which you did not perform, and you also hugely overestimated it in the 1.5 nm prediction.

Haisenberg's uncertainty relation is: $\Delta x\Delta p>{\frac {h}{4\pi }}$. Start with single pinhole case: $\Delta x=2.5x10^{-4}$ m. Photon's momentum is $p={\frac {h}{\lambda }}$. In Afshar's setup he uses laser with photons at $\lambda _{ave}$ = 650 nm. Let $\Delta \lambda =2k$, where k > 0.

$\Delta x({\frac {h}{\lambda -k}}-{\frac {h}{\lambda +k}})>{\frac {h}{4\pi }}$

$\Delta x{\frac {2k}{\lambda ^{2}-k^{2}}}>{\frac {1}{4\pi }}$

k = 0.067 nm

So the uncertainty in photon's wavelength $\Delta \lambda$ is only 0.134 nm in single slit setup.

For the case where both pinholes are open $\Delta x=1.5x10^{-3}$ m the uncertainty in photon's wavelength $\Delta \lambda$ is 0.022 nm. These calculations are done by me to close this issue, it seems that apodization effect is negligible, despite of the fact that it is theoretically there, and is evidence that his setup is NOT "which way". Danko Georgiev MD 14:18, 18 June 2006 (UTC)

How to compute contributions in QM

OK, a question for you. Assume the pinholes are of different diameters. What do you see at their images, if there is NO GRID AT ALL?

And what do you expect with a grid, when the pinholes are of different diameters? Alfredr 18:19, 16 June 2006 (UTC)

Dear Alfred, If you have read my previous message above on unbalanced pinholes you should not waste your time in asking me the same question several times. My logic is clear, and only your logic suffers from inherent inconsistency. So have pure state with

[i] two pinholes with equal diameter. So actually you have to take the normalization in mind, and you will see that for the photon arriving at one of the images, its quantum state is |$\Psi$> = 0.70 |A> + 0.70 |B>, and here you do not put 1/2 immediately on amplitudes. One of the ways to say how much intensity comes from the pinhole A is to take the amplitude passing thorugh A which is |$\Psi _{A}$> = 0.70 |A> and then to take the square of the inner product $|<\Psi _{A}||\Psi >|^{2}$, and you only now see 1/2 intensity comes from A, and you will have 1/2 coming from B also. But this CANNOT be said to be 1/2 A XOR 1/2 B, because this is MATHEMATICALLY WRONG! The correct statement is 1/2 A AND 1/2 B. The small difference is seen immediately when you consider a single photon experiment. The quantum logic still holds, and you should say about this single photon coming from both pinholes, nor A XOR B.

[ii] have now two pinholes with different diameter so that pinhole B is 3 time bigger than pinhole A. The state of photons coming at the images is |$\Phi$> = 0.50 |A> + 0.87 |B> and in order to check how much intensity comes to the image of a pinhole from slit A is to take $|<\Psi _{A}||\Psi >|^{2}$= 1/4, and similar computation will show that coming intensity from B is 3/4. NOTE THAT THIS IS TRUE FOR BOTH IMAGES OF THE LENS BECAUSE THE QUANTUM STATE OF THE PHOTONS AT EACH IMAGE A OR B ARE SUPERPOSED STATES.

Conclusion: you cannot think that one amplitude is refracted towards A and other amplitude is refracted towards B. This is completely wrong intutive confusion. The photon arriving at the lens is superposed photon, so it do not have momentum vector whose direction is only towards A or only towards B, but his momentum vector is superposed to both images at the same time, so this is DIFFERENT STATE, NOT REDUCIBLE TO THE OTHER TWO CLASSICAL STATES. So in this case each photon arrives to both images. Above I have presented the basic theory how to compute how much light comes from slit A or slit B to given image of the lens. Since the state is superposed you see you get SURPRIZINGLY the same result for unbalanced setup. Despite of the fact that slit B is 3 times bigger that the slit A, the image of the slit B contains 3/4 intensity from B and 1/4 intensity from A, and despite of the fact that the image of A is 1/3 of the image of B, its light is also 3/4 intensity from B and only 1/4 from A. Amazing isn't it !!!! If you don't think in classical terms but use the inner product, which is the correct way to find how much intensity from the pinholes comes to the images, then you might see that the image B not only has 3 times more photons but it seems to has "swallowed" some A-pinhole photons from the image of A (this is based on your terminolgy of "which way"), where the image of A has only 1/4 photons coming from A. Of course it is the pinhole B that provides 3/4 light intensity to the image of A, so it "compensates" the swallowed by the B image A-pinhole photons from the A image (again based on your terminology for correspondence of slits and images). Do you see that quantum mathematics is totally different from your previous and wrong posts. Actually the classical correspondence is totally wrong, and I have showed that there is no such correspondence at all. So if there is interference there is no which information. And this does not depend on the ballanced or unbalanced pinhole diameters.

I hope now you will see your errors, and if you want to collaborate with me on this issue I will be glad to continue our discussion.

post scriputm: By the way putting of wire grid does not change the density matrix of photons hence no effect on the final intensity ratio contributions to the images. And you said that you completely agree that photons in Afshar's setup are in superposed state 0.70 |A> + 0.70 |B>. If so do by yourself the computation with the use of Born's probability rule to say how much light gets to image A from slit A, or B respectively. Are you surprized to find 1/2 to 1/2? Forget about your classical thinking and welcome in the quantum reality that speaks in matrices Danko Georgiev MD 04:03, 17 June 2006 (UTC)

Sorry, Danko, but this is completely false. If there is no grid, photons from A go only to the image of A and conversely. Your way of thinking is totally incorrect. Even though it is a pure state, (and if your setup involves interferences -a simple Young fringe setup, of a wave guide at the images with subsequent recombination- you will see interferences effects) , if your setup is with destructive detectors, your thinking is wrong. The argument is : if only A is open you don't get anything in B' so < B'|A>=0 (bra is arrival , ket is departure) So even if the ket is pure state .7(|A>+|B >) what arrives in B' comes *only* from B. And that's it! The bra < B'| acting on this ket has nonzero product *only* with the |B > part. Your QM thinking is confused, I see it now much more clearly than I realised before. Alfredr 22:24, 17 June 2006 (UTC)

Dear Alfred, your last post is totally incorrect. You are "confused" by classical thinking. Your error is "transparent" from quantum point of view. First I will give you example with the lens action, and then I will make my claim even stronger!

Case [i] you have "mixed state" in which you close slit A or slit B in random fashion. The lens in this case acts on photons that have non-superposed momentum direction (note: momentum is vector with magnitude and direction). So the lens easily recognizes the "direction" of momentum and "separates" uniquely all photons from slit A to image A, and all photons from slit B to image B.

Case [ii] you have "pure" double slit state. Then the photons have superposed direction at the moment they touch the lens. So having "superposed direction of motion" the lens cannot recognize the photon correctly as in the case of superposed photons the lens refracts the photon towards the two images at once! The photon is superposed state at two images so if you write down the photon's state in basis of detecors |D1>, |D2> then you will see that the photon is in state ${\frac {1}{\sqrt {2}}}|D1>+{\frac {1}{\sqrt {2}}}|D2>$. What you forget is that at the image A the photon is not in state |A> or |D1>, but it remains in superposed state being simultaneously at the image B.

Clearing of possible confusions

[1] The fact that the photon is in state ${\frac {1}{\sqrt {2}}}|A>+{\frac {1}{\sqrt {2}}}|B>$ at any of the images makes the amazing trick that it is at image A but "comes also by 1/2 from slit B". See the previous usage of inner products! The lens does not change the density matrix of photons but forwards them to one of the two images being in the superposed state of A and B. If you compute a pure state ${\frac {1}{\sqrt {2}}}|A>+{\frac {1}{\sqrt {2}}}|B>$ photon has exactly 1/2 chance to reach image A, as 1/2 chance to reach image B, with the difference that it reaches them both at the same time, and only after this arrival to the image plane, a measurement can collapse the superposition.

[2] The fact that you make measurement of photon in basis state |D1>, |D2> does not collapse the photon in basis state |A>, |B>. MOST IMPORTANT NOTE! Only in case where there is "entanglement" between the detector and slit there is collapse in |A>, |B> basis also. This can be achieved when the photons are polarized. But in this case there will be no interference of the two slits.

[3] Afshar's makes the error to think that measuring in basis |D1>, |D2> measures also the "which way" which is the |A>, |B> basis. This is based on wrong usage of photon momentum that has momentum vector with precisely determined direction of motion. In quantum world the photon may have "superposition" of paths, hence superposition of "momentum vector direction".

[4] Consider now the case of photon arriving at photofilm forming a Fraunhofer diffraction. At the moment of arrival the photon is "everywhere at the photofilm", so this is superposed state, and you cannot think that it is only at a certain point of the photofilm. Only AFTER measurement takes place, this is non-linear "collapse" of the quantum amplitude being now 1 at the place where the photon was actually detected. This localization of quantum amplitude being 1 only at given place is non-linear process that violates the linear Schroedinger equation but occurs after the arrival of the photon to the photographic film. The situation is the same with the lens images - do not forget that the photon at the moment of arrival at the lens images is in superposition, so this is real state being at two places at once. Only after "measurement" in basis |D1>, |D2> you find the photon being classically at only one detector, but in order to say that you have "which way" information, you must be sure that there is entaglement between the |D1> state and the |A> state. This can be done by polarization of the photon, yet you will lose the interference.

I hope my comments help. Danko Georgiev MD 15:07, 18 June 2006 (UTC)

Direct disproof of your supposed counter example. The fact that the photon at the image plane is in state ${\frac {1}{\sqrt {2}}}|A>+{\frac {1}{\sqrt {2}}}|B>$ gives him 1/2 intensity from A and 1/2 intensity from B (the state is the same at image A, or at image B, exactly as is the superposition of the Frauhofer diffraction pattern, do not forget that only after measurement you collapse this state). The case will be completely different if you can prove that the image at A contains photons that are in state |A>. Then I will immediately agree that there is zero contribution from B. The fact that inner product of |A> and |B> is zero is NOT PROOF that image A in double slit contains |A> photons. To say that at the image A the photon is in state |A> is equivalent to say that at the same time it is not coherent with the photon's wavefunction at B. Do you see the problem? If it is not coherent with the photon's wavefunction at B, then there is something that prevents the coherense [like polarization, etc.]. If the photon at A is coherent with the image B photons, then you cannot say that it is in state |A> because it immediately will follow that it is in state ${\frac {1}{\sqrt {2}}}|A>+{\frac {1}{\sqrt {2}}}|B>$. So there is no way to preserve your wrong position. The coherence/superposition is very "sticky" and only logical errors lead you into delusion to believe in which way info. Danko Georgiev MD 15:30, 18 June 2006 (UTC)

Your counterexample contains elementary error!

Dear Alfred you say "So even if the ket is pure state .7(|A>+|B >) what arrives in B' comes *only* from B. "

Really!? If this ket arrives at B' then do the check <A|.7(|A>+|B >) and you will see that there arrives an amazing 1/2 intensity at B from A. How did you calculate this *only* in the quotation above? Danko Georgiev MD 15:41, 18 June 2006 (UTC)

Actually if you read the classical paper from Heisenberg on quantum logic, you will see that "photon being at image A" does NOT imply quantum state |Image A>. Superposed state 0.7 |Image A> + 0.7 |Image B> satisfies the premise "photon being at image A", so you certainly make huge error thinking that "photon being at image A" implies |Image A>. This is wrong, and you will see this conclusion in every introductory textbook of QM. Reference: Werner Heisenberg (1973) Development of concepts in the history of quantum theory. In: Jagdish Mehra, ed. The physicist's conception of nature. Dordrecht: D.Reidel. pages 264-274.

Sorry, Danko, but you malke a huge mistake here. Since <A|B >=0 <A|.7(|A>+|B >) =<A|.7(|A> and this exactly means that the photon arrives from A *only* Which "inner product" are yoy referring to? Afshar's error is much more subtle thant you think. He is wrong, indeed, whent there IS a grid. Without grid, his analysis is correct. His mistake is to neglect the grid. If B only is open, there is some small amout of light at the image of A and thus <A|B > is small but not zero. Ignoring this small contribution is Afshar's error. Not realising that when the gird is absent <A|B >=0 implies a photon arriving is A' came though A is a worse error!

Dear Alfred, your post for second time is wrong. The superposed state has contributions both from A and from B. The born probabilty rule is

$P=|<\Phi ||\Psi >|^{2}$

If the photon's state at the image A is superposed state $|\Psi >=0.7|A>+0.7|B>$ then the probability to come from slit A is

$P=|<A||\Psi >|^{2}$

$P=|<A|0.7|A>+<A|0.7|B>|^{2}=1/2$

For the same photon at the image A the probability to come from slit B is:

$P=|<B||\Psi >|^{2}$

$P=|<B|0.7|A>+<B|0.7|B>|^{2}=1/2$

This is the root of your error as I said above, being at image A, the photon is still in superposed state $|\Psi >=0.7|A>+0.7|B>$, because there is no implication

"being at image A" -> $|\Psi >=|A>$.

Danko Georgiev MD 06:20, 19 June 2006 (UTC)

Look, Danko, I am giving up. No way to make you see your error , and the worse is that your error obfuscates Afshar's error. It is easy for him to reject your opinion, so there is no way to show his exact error, which is much more subtle than you think. What is depressing is that, both for you and for Afshar, there is no difference whether the grid is present or not.

You say, since we are in a pure state, arrival of a photon in one image has no correlation with the pinhole it went through, which is of course absurd and allows Afshar to reject your thesis.

He says, whether the grid is present or not, there is 100% correlation. Without grid, he is of course corrrect because < B' |A>=0. Yes, he is correct! Danko, I am sorry but you are wrong and in the absence of grid, Afshar is right.

But when the grid is present he is wrong. There is a strong correlation but not perfect. I keep repeating again and again and again, the global diffraction is zero, but there is diffraction from both pinholes that add up to zero. And this is not the same thing.

If a supporter of Prof Afshar (or he himself) reads this, the following argument is not against Danko but against Afshar: once more, in an ordinary Young slits interference experiment, near the center of a dark fringe, the small amount of light that gets there, where does it come from? From amplitudes of both pinholes, with the same amplitude as everywhere else, and phases almost opposite. So by continuity at the exact center one cannot say that nothing reaches there. The amplitude coming from each pinhole is as large as everywhere else, but the phases are exactly opposite and cancellation is perfect. But one cannot say that nothing gets there! In Afshar's experiment it is exactly the same situation: no net diffraction, but yes, there is diffraction from both A and B, which cancel each other. But one cannot say that B does not contribute. It is wrong and the solution of the paradox is there. Now if one does only the maths, there is n difference, but also no paradox. The paradox comes only if one reasons beyond the maths. And this reasoning must be consistent. The paradox comes from an inconsistent reasoning. What makes Afshar's error harder to see is that the correlation is very large, 94%. And while everybody agrees that near, or at the dead center of a dark fringe, amplitude from both holes contribute, people tend to ignore the small contribution from B, all the more so that it is cancelled by an opposite contribution from A. But it is there, oh, yes, it is there and therefore there is NO paradox. QM is fully vindicated. Alfredr 18:35, 20 June 2006 (UTC)

Dear Alfred, you are playing with the symbols! You say $<B'|A>=0$, but WHAT IS $B'$? DEFINE IT! If it is the image in the "mixed state" experiment - YES, this is true, but the Afshar setup is not mixed state one, so this is NOT valid math relation in this second case. Danko Georgiev MD 03:56, 21 June 2006 (UTC)

Do NOT play with symbols!

Suggestion for definition [I use asterisks to avoid any further confusion with previous posts]:

[i] let the wavefunctions of photons in the single slit mixed setup at the image plane be as follows: at the image A you have wavefunction $A*$, and at image B you have $B*$.

[ii] let in the double slit pure state setup you have at the image plane: at image A you have wavefunction $A**$, and at image B you have wavefunction $B**$.

Please write down now the wavefunctions of $A*$, $B*$, $A**$, $B**$ as a function of the wavefunctions through slit A denoted just as A, and through slit B denoted just as B. Now you have 6 different symbols, and you cannot play anymore with their meaning.

The argument now is clear, yes in mixed single slit setup you know A XOR B, so YES:

|A*> = |A> and |B*> = |B >

$|<A|B*>|^{2}=0$

$|<B|A*>|^{2}=0$

But in the double slit coherent setup you have completely different picture, you know A XNOR B:

|A**> = 0.7 |A> + 0.7 |B> and |B**> = 0.7 |A> + 0.7 |B>

$|<A|B**>|^{2}=1/2$

$|<B|A**>|^{2}=1/2$

Best, Danko Georgiev MD 03:56, 21 June 2006 (UTC)

OK so let us be clear with the symbols. All refer to pure states. in mixed state, there is no vectorial wavefunction at all (no ket!) at all, the only thing that makes sense is density matrix, which is not of rank one and thus not the tensor product of a ket with its associated bra (the "ket-bra" which is a 2*2 matrix, not the braket which is a scalar), so denoting a mixed state as A*, B* is meaningless.

Without grid |A0> is photon trough pinhole A. the *same* wavefunction, but described on the plane of the lens (where it is spread all over the lesn) is denoted |A1> It is the same wavefunction but described at a different position |A2> still the same object but on the image plane. |A0>|A1>|A2> are the same objetc but described at different places. So the notation assumes that one takes into account evolution and when writing a braket, the index 0,1,2 can be omitted, as the Hamiltonian bringing the bra and the ket at hte same position is implied. OK? < A**| is the bra that describes arrival of a photon at the image of pinhole A.

Without the grid we really have

< A**| =< A2| , so < A**| A>=1, < A**| B>=0

In the pure state with both slits open, the photon wavevector | F>= 0.7 |A> + 0.7 |B > , true of course at all positions 0,1 and 2. So

$|<A**|F>|^{2}=1/2$

$|<B**|F>|^{2}=1/2$

However it always remain true that

$|<A**|B>|^{2}=0$

The wavevector |F> is a combination of |A> and |B>, but this does not change the meaning of the objects |A> and |B> themselves. The kets are orthogonal, the braket of one with the other is always zero. Do not mix the photon wavefunction | F> which is a superposition, with the objects that enter the superposition , these objects themselves do not depend on anything. They are the building blocks. They are determined by the evolution throgh the system, not by the fact that one pinhoe or the other is open. Openig one or the other or both means you take one or the other or a linear combiantion of |A> and |B>, it changes what | F> is, it does not affect the objects |A> and |B> themselves. By the way the mixed case does nor have a wavefunction at all, its density matrix is

0.5|A><A| + 0.5 |B >< B|

What makes things more complicated when the gris IS present is that the evolution of |A> from |A0> describing the photon going through pinhole is more complicated. When it arrives at the image plane, |A2> is not just what you think. The bra <A**| describing arrival of a photon at the image of pinhole A is the same (the detector at pinhole A is the same) but when the grid is present the ket |A2> which is the evolution of |A0> though the grid is now much more complicated and is NOT the associated ket to the bra <A**| !

With grid

<A**| A2>=0.97

and

< B**| A2> is not zero anymore, but -0.03.

When only one pinhole is opne this is visible because diffraction is indeed present.

OK so far?

If you do not see that opening one or the other pinholes determines what the photon wavevector | F> is in terms of | A> and | B > but has no effect on the building blocks | A> and | B > themselves, then there is no point dicussing anymore. Alfredr 07:30, 23 June 2006 (UTC)

Dear Alfred,

THIS IS EXACTLY MY ESSENTIAL POINT OF VIEW: the pinhole building blocks |A> and |B> are not changed, but the wavefunction at the image A is exactly the same as the wavefunction at image B and both images have photons with wavefunction 0.7 |A> + 0.7 |B>. What MORE CLEAR statement than that??? If you measure photon in basis |D1>, |D2> (which in words is to ask question: "image A" or "image B"?) at any one of the images the probability for the photon to come from each of the pinholes is 1/2 regardless of the fact at which image you measure the photon! This is the essential fact - "no which way" information, no correspondence between the images and the pinholes. And knowing that photon is detected at image A does not say that it came only from slit A. However you obtain 1/2 contribution also for coming from slit B! To have which way information you need entanglement between basis |A>, |B>, and basis |D1>, |D2>. For example if you use polarized photons you may have this "which way" entanglement $|\Psi _{ww}>=0.7|A>|D1>+0.7|B>|D2>$ and now you see that detection of photon at D1 has "zero" contribution from B, not because of the lens action, since $<B||B>$ gives you still 1.0, but because this is multiplied once again by the orthogonal |D2> that makes it zero.

Actually you are the one who makes big error. I suspect at the very moment of seeing this reply that you do not try to analyze what I say just becuase your ego has already decided that I am wrong. BUT YOU ARE THE ONE WHO MAKES ANOTHER ELEMENTARY ERROR. Yes, the global "mixed state" has NO wavefunction, and I KNOW that, but this does not imply that each photon does not have wavefunction. INDEED YOU KNOW that the wavefunction of photon is 1.0 |A> XOR 1.0 |B>. Do you see the amplitude normalized to 1.0?

Now go back to the double slit without grid. Whatever you do, you cannot get probability for photon at image A to arrive from slit A with probability 1.0, simply because in this double slit case its amplitude is normalized in different way and is now 0.7.

My advice - don't be frustrated to accept that all that you post is wrong. For a newcommer it is normal - in the beggining when I started to study QM for first time, I was confused exactly like you. But maybe you will move forwards faster, if you have 30 minutes and try to understand my last two posts. Regards, Danko Georgiev MD 03:19, 24 June 2006 (UTC)

Why < A**| =/= < A2|

Dear Alfred, you say "Without the grid we really have $<A**|=<A2|$ ", and this is exactly the moment of your confusion. I have stated clearly that this is classical error, done by lot of people. You still make confusion between the evolution of "wavefunction of photon" and "wavefunction of slit". This is not acceptable huge error.

[1] Suppose a point where the two wavefunctions interfere, so you have contributions from both wavefunctions. Still $<A||B>=0$ buth this is NOT relevant to "photon's wavefunction" at this point! The photon CAN arrive at this point of interference as accessed by Born's rule by "photon's wavefunction" and "wavefunction of the slit of interest".

[2] So at the image plane at image A you should use "photon's wavefunction at image A" which is superposed one. You make huge error here!

[3] Maybe you are not convinced so far? Consider the usual interference pattern at a screen, and take arbitrary point $x_{i}$. What is the photon's wavefunction at point $x_{i}$. Is it $a_{i}|x_{i}>$? No, the photon is not is this state, but in superposition $|\Psi >=a_{1}|x_{1}>+a_{2}|x_{2}>+...+a_{i}|x_{i}>$. So the "photon's wavefunction" does not depend ONLY on the AMPLITUDE $a_{i}$ at $x_{i}$. DO YOU REALIZE THIS? Now go ahead and you will see that the "photon's wavefunction" at image A DOES NOT depend ONLY at the quantum amplitude at image A, but depends on the distribution of all quantum amplitudes in the image plane.

[4] So what? The Afshar's error as well as the error of yours and others, is that you should take the inner product of "photon's wavefunction" and "slit of interest" in order to understand what is the contribution of the slit of interest to the "photon's existence at the point of interest".

[5] What you do instead?? You take "slit's wavefunction" at certain point, and take inner product of say "slit A wavefunction" with "slit B wavefunction". OF COURSE you will get zero, but this shows what you already know that two slits have orthogonal wavefunction. DID YOU PROVE SOMETHING MORE?

Conclusion: The error of you, Afshar, etc. is very severe, and is simply a LOGICAL FALLACY. You speak about "slits wavefunction" and then ATTRIBUTE the result to the "photon's wavefucntion". If you want to speak about slit, speak about slit, if you want to speak about photon, speak about photon. This is logical fallacy, and is so simple that you cstill do not believe that it is there. There is nothing deep and nothing mysterious about Afshar's fallacy. It is very simple, and you have just done it again. Danko Georgiev MD 05:16, 24 June 2006 (UTC)

Addition: You naively believe that if at a point x the amplitude from slit A is say 0.3 and the amplitude from slit B is 0.1 there is 3 or 9 times more A "which way" information than B "which way" information. In previous post I have shown that the "which way" is exactly ZERO, because each photon passes through both pinholes in unbalanced fashion. ROOTS OF YOUR NAIVE BELIEVE are in the naive presumption that the amplitudes are real numbers. THIS IS WRONG! AMPLITUDES are COMPLEX NUMBERS!!! So in such a naive interpretation how you will interprete contribution by: Note: before reading consider that possibly there are some other slits C, D, E, which contribute amplitudes in a way so that the normalization is perfect up to 1. For the naive thinking that you seem to defend these other slits existence should be not relevant for the next discussion.

[case 1] (easy one) 0.3 A + 0.1 B

[case 2] (little harder) 0.3 A + 0.1 i B

[case 3] (hard one) (0.3 - 0.1 i) A + (- 0.1 + 0.3 i) B

[case 4] (not solvable!) (0.7 - 0.2 i) A + (-0.5 + 0.9 i) B

Well, how did you solve by the naively wrong thinking for "which way" the case 4? Answer: IMPOSSIBLE to reply by consistent logic.

My thesis clearly shows that such intuitive logic does not work, and what really matters is photon's wavefunction. Only knowing the photon's wavefunction, you can estimate how much intensity contributes a slit to given image. The examples are given in previous posts of mine with unbalanced pinholes. Danko Georgiev MD 05:39, 24 June 2006 (UTC)

Photon wave function vs photon wavefunction somewhere

Dear Danko

You are deeply in error. I'm quoting you

[3] Maybe you are not convinced so far? Consider the usual interference pattern at a screen, and take arbitrary point $x_{i}$. What is the photon's wavefunction at point $x_{i}$. Is it $a_{i}|x_{i}>$? No, the photon is not is this state, but in superposition $|\Psi >=a_{1}|x_{1}>+a_{2}|x_{2}>+...+a_{i}|x_{i}>$. So the "photon's wavefunction" does not depend ONLY on the AMPLITUDE $a_{i}$ at $x_{i}$. DO YOU REALIZE THIS? Now go ahead and you will see that the "photon's wavefunction" at image A DOES NOT depend ONLY at the quantum amplitude at image A, but depends on the distribution of all quantum amplitudes in the image plane.

$|\Psi >=a_{1}|x_{1}>+a_{2}|x_{2}>+...+a_{i}|x_{i}>$

Yes the wavefunction of the photon is indeed the sum of all these.

But if each $|x_{i}>$ is a localised wavefunction, the full one means that the amplitude (and thus, the probability) of finding the photon at each of the positions is nonzero, it remains that the amplitude (the square of which is the probability) of finding it specifiaclly at one place, say at place i is just $a_{i}$. The other part of the wavefunction tells you the amplitude (the square of which is the probability) of finding it elsewhere Of course if the elementary objects are themselves nonlocalised, as happens for instance in the plane of the lens, where the wavefunction from each pinhole is spread over the whole lens, then you have to add the amplitude at a given point before taking the sqaure to get the probability. But when you are not in the lens plane but either the pinhole plane or the image plane, each elementary object, |A> or | B > is localised and the only think that counts when measuring at the image of A is the amplitude that is localised in A, namely that of |A> . Without grid, |B> has a contribution on the image plane only at the image of B, not at the image of A! And do not argue that in that case one could never see interferences: in the plane of the lens both |A> and | B > contribute all over the plane and there, indeed one has to sum their amplitudes at each given point (with the effect that they sometimes add, sometiimes subtract, and of course, they are complex numbers so that both real part and imaginary part have to be considered, I never claim otherwise - it is just that on the plane of the images, the phases being opposite, it turns out that real numbers, but of either sign, suffice to describe what happens, I never calimed amplitude cannot be complex in principle)

Dear Alfred, your post is wrong again, but at least you formulate some statements, that are really the root of your error, and now I can show them clearly to you.

[i] Yes, if you consider the probability for measuring the photon locally at $|x_{i}>$ you usually take $a_{i}a_{i}*$ where $a_{i}*$ is the complex conjugate of $a_{i}$. But you make measurement in basis $|x_{1}>,|x_{2}>,...,|x_{i}>$, where all these vectors $|x_{1}>$ through $|x_{i}>$ are ORTHOGONAL! In this case you measure the probability of finding the photon at $x_{i}$. BUT!!! see in section [iii] how this actually happens!

[ii] If you want to know the contribution of slit A or B to the state at $x_{i}$ YOU TAKE the squared inner product of the whole wavefunction, and the wavefunction through the slit. For example despite of the fact that the point $x_{i}$ might be closer to slit A, compared to slit B, you DO NOT say that slit A has greater contribution than slit B at that point. The distribution at every point remains ALWAYS 1/2 from both slits.

[iii] Is some contradiction with case [i]? NO! In case [i] you also use the whole photon wavefunction, but this is not explicitely stated because of the orthogonal basis. So obviously you do not know how to use the Born rule for calculating probabilities, and you make elementary error considering a kind of naive your own way to calculate contributions in quantum events. Once you realize the invarinace of the wavefunction of photon at every point of coherent setup, you will understand what means the reality of superposition. The local probabilties for finding a photon really depend on squaring the local amplitude, simply BECAUSE you use "position orthogonal basis". What can be shortly described by $a_{i}a_{i}*$, which looks like as only local dependence, is indeed shorthand for writing the TRUE squared inner product which is $|<x_{i}|(a_{1}|x_{1}>+a_{2}|x_{2}>+...+a_{i}|x_{i}>)|^{2}$. Since $<x_{i}||x_{i}>=1$ finally what remains is exactly $|a_{i}|^{2}$ which is $a_{i}a_{i}*$. In this case you also use the whole wavefunction in the inner product, but you have hidden assumption that is understood by default that you perform measurement in basis $|x_{1}>,|x_{2}>,...,|x_{i}>$, where all these vectors $|x_{1}>$ through $|x_{i}>$ are ORTHOGONAL! Part of the effect that the you DO NOT have local dependence ONLY, is the fact that the normalization of the "local amplitude" is done in global way. Here is where the global coherence is "hidden" but it is there! Simply you cannot normalize the wavefunction at image A, as being 1.0 |A> what you want to do. Since the photon is coherently at image B also, then its wavefunction is normalized as 0.7 |A> + 0.7 |B>, and the fact that you misunderstand the difference between photon's wavefunction, local amplitude, and the certain fact that ALWAYS when you take inner products you take THE WHOLE WAVEFUNCTION is your own problem.

[iv] And last, but not least there is NO contraposition "Photon wave function vs photon wavefunction somewhere" BECAUSE THE WAVEFUNCTION OF A PHOTON AT GIVEN POINT IN COHERENT SETUP IS THE SAME AS THE GLOBAL WAVEFUNCTION FOR THE SETUP. Once you realize that the wavefunction is invariant, you will see that only the "local quantum amplitude" at the given point is variable, but the wavefunction is invariant. Synonymous correct mathematical formulation is to point out the difference between "function at given point" and "value of function at given point". The "function" at everypoint DOES NOT CHANGE itself, what changes is "the value of the function" at different points. The "value of the function at point" is the "quantum amplitude at that point" but the "wavefunction at the point" is the same as the wavefunction at every other point. What you always square in the inner product is the "wavefunction" not the "value of the wavefunction at the point". ONLY in the special case where you make position measurement in the orthogonal basis as described above you have squared inner product of the "wavefunction (itself)" and "the position basis at that point". Therefore appears an pseudo-effect as if there is only local dependence because of orthogonality of the other position basis vectors. Danko Georgiev MD 10:31, 25 June 2006 (UTC)

Dear Danko Sorry but this is nonsense:

[iv] And last, but not least there is NO contraposition "Photon wave function vs photon wavefunction somewhere" BECAUSE THE WAVEFUNCTION OF A PHOTON AT GIVEN POINT IN COHERENT SETUP IS THE SAME AS THE GLOBAL WAVEFUNCTION FOR THE SETUP. Once you realize that the wavefunction is invariant, you will see that only the "local quantum amplitude" at the given point is variable, but the wavefunction is invariant. Synonymous correct mathematical formulation is to point out the difference between "function at given point" and "value of function at given point". The "function" at everypoint DOES NOT CHANGE itself, what changes is "the value of the function" at different points. The "value of the function at point" is the "quantum amplitude at that point" but the "wavefunction at the point" is the same as the wavefunction at every other point. What you always square in the inner product is the "wavefunction" not the "value of the wavefunction at the point". ONLY in the special case where you make position measurement in the orthogonal basis as described above you have squared inner product of the "wavefunction (itself)" and "the position basis at that point". Therefore appears an pseudo-effect as if there is only local dependence because of orthogonality of the other position basis vectors.

If I measure the arrival of a photon at the image of A, then I take the inner product of the (full, of course) wavefunction of the photon with just the bra describing its arrival at the image of A. Therefore any contribution in the wavefunction that does not contribute to the amplitude at that point does not contribute to the inner product. Without the grid, the amplitude coming through B does NOT get to A, whatever your claims to the contrary are. You are mistaken and should really think about what linearity means: if when B alone is open there is no light at the image of A, then when both pinholes are open STILL B does not contribute at the image of A; this is linearity. Anything else is nonsense. --Alfredr 21:41, 25 June 2006 (UTC)

Clarifying the Born's rule

Dear Alfred, let us stop insulting each other for a while. Only in that case we can clarify the issue. My knowledge in maths is certainly quite good, so below I try to clarify consistently your and mine views. I start with your usage of the Born's rule to show you that I understand what you try to defend, but the logical consequences lead to total change of "terminology" and semantical meaning of words. Then I again discuss the fact that the whole wavefunction at the image A is superposed one 0.7 |A> + 0.7 |B> because the image at B coherently co-exists with the image of A. This is non-local effect and the presence of image at B nonlocally affects the image at A, so local thinking is not applicable and necessarily will lead into delusion. Linearity is NOT THE PROBLEM, what make me have different conclusions is the nonlocality, so you should properly localize the problem, not to attribute it to "possible misunderstanding of mine of linearity".

The fact that you are blind for this nonlocal influence is based on misunderstanding of the mathematical meaning of "function" and "value of function at a point". Lets have the function $y(x)=x^{2}+5$. The function y(x) is the "law that gives you the value y of the function at any given point x". The function y(x) however is the same at all points x, because the law that you used to compute y is the same, what is variable is the position x and the actual value of y at the point.

function = the correspondence law between two sets Y and X

value of function at point x = the member y that is corresponding to the member x

So what you use to calculate probabilities is the "wavefunction" f(x) itself, not the value y of the function at the point. Your understanding of linearity is based on taking the local value of the wavefunction in the inner product which is wrong.

Example: always you can find a point $x_{1}$ behind a double slit where the amplitude from A is say 0.3 and amplitude from slit B is 0.1. Also you can always find another point such that the amplitude from A is say 0.2 and amplitude from slit B is 0.4. Comment: The fact that the amplitudes are not normalized to 1 is possible for local case at a point because there is also amplitude spread outside the point $x_{1}$ that squared adds to 1.

[i] Inner product with the "local value of the wavefunction" gives you the following

For point $x_{1}$

$|<A|(0.3|A>+0.1|B>)|^{2}=0.09$ - "contribution from A"

$|<B|(0.3|A>+0.1|B>)|^{2}=0.01$ - "contribution from B"

$|0.4|^{2}=0.16$ - local intensity of light. Appears a paradoxical situation in which 0.06 more intensity is observed at the point $x_{1}$. Of course you can say by degenerative ad hoc adjustment that this 0.06 intensity is "contribution from interference"

For point $x_{2}$

$|<A|(0.2|A>+0.4|B>)|^{2}=0.04$ - "contribution from A"

$|<B|(0.2|A>+0.4|B>)|^{2}=0.16$ - "contribution from B"

$|0.6|^{2}=0.36$ - local intensity of light. In the ad hoc "local version of complementarity" there should be 0.16 intensity more than expected coming from interference at $x_{2}$

Questions, problems and consequences

It is obvious that in this case the slits A and B have different contributions to points $x_{1}$ and $x_{2}$.

It is obvious that the "contribution from interference" is different at points $x_{1}$ and $x_{2}$.

It follows that interference at one point DOES NOT IMPLY similar interference at another point, or interference at all. SO IF THIS IS THE COMPLEMENTARITY PRINCIPLE - YES, AFSHAR PROVES THAT IN THE SAME SETUP THERE IS INTERFERENCE AT ONE POINT AND ZERO INTERFERENCE AT ANOTHER POINT.

Arises the question is this the right formulation of complementarity, and DOES THE BORN RULE require you to use in the inner product the local value of the wavefunction. Answer is: NO!

[ii] Modern understanding based on CFD principle and reality of superposition - you should always use in the inner product the wavefunction itself, NOT the local value of the wavefunction. So at both points $x_{1}$ and $x_{2}$ the wavefunction is the same $|\Psi >=0.7|A>+0.7|B>$. Use now the Born probability rule in its true formulation

$|<A|(|\Psi >=0.7|A>+0.7|B>)|^{2}=1/2$ "contribution from A".

$|<B|(|\Psi >=0.7|A>+0.7|B>)|^{2}=1/2$ "contribution from B".

In this case you have always "invariant" contribution from the two slits at any point behind the double slit, distant enough so that the two waves have interfered. After the interaction this interference CANNOT BE UNDONE this is the essence of nonlocality. What you need is say "entanglement" between detector (in the future) and the slit (in the past) for example by polarization of photons, to prevent the interference/coherence at first place.

Questions, problems, and consequences

Is there some problems here - No, this is what quantum mechanics is all about, the reality of superposition/coherent states. In "mixed" single slit setup you know A XOR B, so you get 100% sure knowledge that photon passed through A comes from A. In coherent double slit you NOT (A XOR B) = A AND B, so your knowledge is that photon always passes 50-50 through both slits. So this knowledge is "invariant" and does not depend on the "local value y of the wavefunction" but depends ONLY on the "wavefunction f(x) itself". THIS INVARIANT KNOWLEDGE IS INCONSISTENT WITH THE WRONG INTERPRETATION OF THE BORN'S RULE IN CASE [i]!

As a consequence, this fundamental meaning of complementarity NEVER can be violated, without at the same time you destruct the QM mathematical formalism itself. Complementarity is tightly linked to the "wavefunction" of the photon, not to the "local values of the wavefunction".

Outline:

One should understand the difference between "mathematical function" (as correspondence law!) and "the value of the math fucntion at a point" (as a number)

One should be careful about the meaning of the Born's rule. Whether you put the "wavefunction" or the "local value of the wavefunction"

One should think about CFD, and possible "invariant" knowledge that is there, but not as a "consequence" BUT AS A BASIS from which we build up the wavefunction itself! Actually you start from the knowledge A XOR B or A XNOR B (A AND B) in order to write the global wavefunction $\Psi (x)$, therefore if your mathematical reasoning is correct you can never get at contradiction, since the Born's rule in case [ii] that I defend is just MANIFEST of this basic knowledge XOR or AND that I use to write the wavefunction at first place.

I hope the fact that have shown you that I understand your position, will at least make you the effort to study my position as well, because we are arqueing about the DEFINITION OF THE BORN'S RULE - DOES IT TAKE THE WHOLEWAVEFUNCTION OR DOES IT TAKE THE LOCAL VALUE OF THE WAVEFUNCTION. At one place you agreed that you should take the "whole wavefunction" f(x), but intuitively you still continue to use the inner products with the local value of it. Please make the effort to clarify properly this issue. Best, Danko Georgiev MD 04:37, 26 June 2006 (UTC)

Dear Danko

In principle I agree with your distinction between a function and the value of a function at some point.

However what you seem to refuse to see is that, the actual probability of measuring the arrival of a particle at some point of space is nothing but the square of the modulus of the value of the wavefunction at this particular point. My lack of distinction of the 2 notions in my previous posts was not due to my not seeing the difference of the two notions but to my jumping ahead to the fact that as far as probability of arrival of the photon, only the value at that particular point counts.

Without grid, the wavefunction of a photon that went through pinhole B is concentrated at the image of B (contrary to the situation on the plane of the lens, where this wavefunction is spread all over the lens). Therefore though it does contribute to the wavefunction as a whole, the contribution to the value of the wavefunction at the image of A is zero. Therefore it does not contribute ot the probability of arrival of a photon at the image of A, because this probability depends only on the value at the position of the image of A. So though I agree on the difference of the notions I stand by my point that in that particular measurement, only the value at this particular point, namely the image of A, plays a role.

And this is where I differ with Afshar!

Because when the grid is present, because of diffraction, the contribution of the photon through pinhole B at the image of pinhole 1 is not zero! The value of the wavefunction at the image of A is not the same when one pinhole only is open (it is 0,97) and when both are open (it is 1/sqrt 2 and not .97/sqrt 2) because there is a contribution (+0.03/sqrt 2) coming from pinhole B.

Do you see my point more clearly now? --Alfredr 05:33, 26 June 2006 (UTC)

Dear Alfred, I don't want to comment on other issues before we are clear about the Born's rule. You say " as far as probability of arrival of the photon, only the value at that particular point counts". This is AMBIGUOUS! You MUST BE specific whether you ALWAYS use in the Born's rule [i] the local value of the wavefunction, or contrary [ii] you use the wavefunction as a "math function" (law). Why I insist on clearly stating your position - simply because if [ii] is the case in your example of local probability for photon you also have

$|<x_{i}|(a_{1}|x_{1}>+a_{2}|x_{2}>+...+a_{i}|x_{i}>)|^{2}=|a_{i}|^{2}=a_{i}a_{i}*$

However ALL other predictions DO DIFFER FUNDAMENTALLY. So I do not understand what you mean by your comment - you believe in [i] or you believe in [ii]? So, please do not use such ambiguous comment "in case of arrival of photon" because this seems to imply measurement in basis $|x_{1}>$ through $|x_{i}>$. To avoid further confusion state clearly - what type of Born's rule you believe in - true is Born's rule given by me as case [i], or true is Born's rule given by me as case [ii]. The Born's rule is a basic physical law in QM, so we must agree what participates in the squared inner product - [i] ALWAYS the local value of the wavefunction or [ii] ALWAYS the whole wavefunction as a function. Let by default we accept that ALWAYS this is the ket part in the Born's rule, while the bra part will be different and reflect the "question you ask" to the quantum system (flipping the places of the bra and the ket have no effect on the final squared value). Thus refined my question to you is: "what always is the ket in the Born's rule - the local value of the wavefunction or the wavefunction as a math function (whole)?" Danko Georgiev MD 14:07, 26 June 2006 (UTC)

Dear Danko

To answer your question

the ket is always the whole wavefunction.

The question is, what is the bra? That depends on what is the question asked.

For arrival of a photon at a given point, the bra is a delta function at that point.

Therefore, though the ket does contains information everywhere (it is a function!) if I want to know the probability of arrival at point $x_{i}$, only the value of this function at $x_{i}$ is relevant. So, if the question is , what is the probability of the photon arriving at some point only the local value matters. If the question is different, the information to be extracted is different, and knowledge of the full function is needed. But here what we want is probability of arrival at the image of A! So in that particular case, though in principle it is your rule [ii] that applies, when thequestion is "what is the probability of finding a photon at $x_{i}$ since the relevant bra is $<x_{i}|$ i.e. a delta function at $x_{i}$, rule [ii] which is the correct one in general, turns out to reduce to rule [i] in that particular case.

Does this answer your question? --Alfredr 16:50, 26 June 2006 (UTC)

Effects of change of basis and applications to Afshar's experiment

Dear Alfred, YES you answered my question perfectly, clearly and without any ambiguity. So I keep firm now to your explanation above, which is one to one explanation of my previous post. Therefore from now on I will speak only in mathematical terms, because you will understand what my thesis is indeed. I speak for arbitrary double slit and lens, not necessarily with balanced pinholes.

Wavefunction $|\Psi >=\alpha _{1}|A>+\alpha _{2}|B>$

The same wavefunction in another basis $|\Psi >=\beta _{1}|x_{1}>+\beta _{2}|x_{2}>+...+\beta _{i}|x_{i}>$

Ask QUESTION at any point $x_{i}$: "what is the contribution of slit A to $x_{i}$?"

$|<A|(\alpha _{1}|A>+\alpha _{2}|B>)|^{2}=|\alpha _{1}|^{2}=\alpha _{1}\alpha _{1}*$

Ask QUESTION "what is the contribution of slit B to $x_{i}$?"

$|<B|(\alpha _{1}|A>+\alpha _{2}|B>)|^{2}=|\alpha _{2}|^{2}=\alpha _{2}\alpha _{2}*$

Ask QUESTION "what is the probability to detect photon at point $x_{i}$?"

$|<x_{i}|(\beta _{1}|x_{1}>+\beta _{2}|x_{2}>+...+\beta _{i}|x_{i}>)|^{2}=|\beta _{i}|^{2}=\beta _{i}\beta _{i}*$

Several observations:

when you change the question, you need to change the basis!

when you change the basis the quantum amplitudes change!

Answers do NOT depend directly on quantum amplitudes of $|\Psi >$ that appear in basis DIFFERENT from the basis in which the question is asked.

What does mean in direct text - well, the contribution of slit A at point $x_{i}$ depends ONLY on $\alpha _{1}$ but not on $\beta _{i}$. The inverse however is true, see further in text - $\alpha$'s are constants, while $\beta$'s are functions depending on $\alpha$'s.

$\alpha _{k}$ describes how much intensity contributes given slit K to $x_{i}$.

$\alpha _{k}$ is invariant proportion that depends only on the area of the slit K via normalization. If there are k-slits the amplitude $\alpha _{k}={\sqrt {s_{k}/\sum _{k=1}^{k}s_{k}}}$, where $s_{k}$ denotes the surface area of the k-th slit.

$\alpha _{k}$ is the coefficient that tells you what proportion of the coming amplitude at $x_{i}$ from slit K you should take - that is you multiply f(K) by $\alpha _{k}$ to get "part of" $\beta _{i}$ (see below). Therefore $\alpha _{k}$ does not depend on the actual value of the amplitude that comes from the slit, it is the opposite - it enters as coefficient in its determination.

$\beta _{i}=\sum _{k=1}^{k}\alpha _{k}f(K)$ describes the ACTUAL value of the amplitude at $x_{i}$

$\beta _{i}$ is dependent on the geometry (shape) of the slit as well as on the location of the point $x_{i}$ behind the double slit.

In the Afshar's double slit we have $\beta _{i}=\alpha _{1}f(A)+\alpha _{2}f(B)$, where f(A) and f(B) are functions for amplitude contributions by slits A and B to points beahind the double slit.

Comment: f(A) and f(B) depend on the actual geometry of the slits! Just for completeness I want to define the function f(K) for each slit. Now $f(K)={\sqrt {I_{0}}}g(K)$, where $I_{0}$ is the total intensity that passes behind the k-slit. Let us denote the plane of the slit as xy-plane, and z is the distance from the xy-plane. The function g(K) is a function of x, y, and z, specific for the slit K describing the amplitude distribution behind the slit K. For each parralel plane located at a distance z from the xy-plane, g(K) satisfies the condition $\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }g(K)\,dxdy=1$. Now you see that since f(K) depends on ${\sqrt {I_{0}}}$ the coefficients $\alpha$ appearing in the expression for each $\beta$ are result of the normalization of the intensity contributions by each slit. If this is basic knowledge (constant) involved in the description of the whole QM setup, then you cannot apply any logic that "makes the $\alpha$ variable". In any case however when you integrate $\Psi$ for a whole plane parralel to the xy-plane located behind the double slit and after squaring, you should always get $I_{0}$.

Conclusion: in QM you cannot make valid inference about questions in basis with $\alpha$ amplitudes, based on logic that takes into account the results obtain in basis with $\beta$ amplitudes.

Going back to Afshar's setup. It seem that you infer "only the local amplitude$\beta _{i}$ determines the intensity at $x_{i}$", "$\beta _{i}$ seems to be sum 0.7 x 1.0 (from slit A) + 0.7 0.0 (from slit B)", therefore the answer to question "how much intensity contributed slit A and slit B" should be "slit A = 1", "slit B = 0".

WHERE IS THE ERROR: you make invalid inference because the question is another basis, where the proportions "$\alpha _{1}=\alpha _{2}=0.7$" give you the answer. You forget that when you change the question, you change the basis, therefore the relevant amplitudes do change also. Do you agree with my analisis? I think so, because the mathematics is not ambiguous. Therefore you may conclude - thinking in classical way, leads easily into delusion. The Born's rule, as well as change of basis dependence seems bizzare, and controversial, but this is the QM logic. The answers differ fundamentally. Are you convinced now? Regards, Danko Georgiev MD 04:05, 27 June 2006 (UTC)

Dear Danko

I am certainly not convinced!!! You write

Ask QUESTION at any point $x_{i}$: "what is the contribution of slit A to $x_{i}$?"

$|<A|(\alpha _{1}|A>+\alpha _{2}|B>)|^{2}=|\alpha _{1}|^{2}=\alpha _{1}\alpha _{1}*$

Ask QUESTION "what is the contribution of slit B to $x_{i}$?"

$|<B|(\alpha _{1}|A>+\alpha _{2}|B>)|^{2}=|\alpha _{2}|^{2}=\alpha _{2}\alpha _{2}*$

Where does $x_{i}$ enter the question? The question you ask here is, what is the global contribution of A. The question you ask does not depend on the postion of $x_{i}$ at all!!! Globally I never denied that A and B contribute half and half. But the two questions you ask here does not depend at all on a particular position $x_{i}$!

Now $|\Psi >=\alpha _{1}|A>+\alpha _{2}|B>=\beta _{1}|x_{1}>+\beta _{2}|x_{2}>+...+\beta _{i}|x_{i}>$

You agree that

Ask QUESTION "what is the probability to detect photon at point $x_{i}$?"

$|<x_{i}|(\beta _{1}|x_{1}>+\beta _{2}|x_{2}>+...+\beta _{i}|x_{i}>)|^{2}=|\beta _{i}|^{2}=\beta _{i}\beta _{i}*$

But this is the modulus square of

$<x_{i}|(\beta _{1}|x_{1}>+\beta _{2}|x_{2}>+...+\beta _{i}|x_{i}>)$

=$<x_{i}|\Psi >$

=$<x_{i}|(\alpha _{1}|A>+\alpha _{2}|B>)$

But on the plane of the images, |B > has zero contribution on the image of A. Therefore the only contribution comes from |A> at that particular point. This is of course independent on the basis. No result can depend on the basis you use. It is just, you have to ask the quesion correcty in each basis. The first two questions you ask do not depend on a specific point!!!!! --87.88.114.80 06:30, 27 June 2006 (UTC)

Dear Alfred, please define what you understand by $<x_{i}||A>$ because the first vector is defined in different vector space. The vector $x_{i}$ is defined in i-dimensional complex space W while the vector |A> is defined in 2-dimensional complex space V. I have concerns about the meaning of $<x_{i}||A>$ and $<x_{i}||B>$ so please define them. At least for now this looks like nonsense! For now I don't see why you are allowed to multiply vectors from two different vector spaces. It does not seem to be mathematically correct, or please specify what you mean Danko Georgiev MD 07:37, 27 June 2006 (UTC)

Dear Danko

There is only one vector space.

There may be different bases to expand this vector space; but even if one vector is expressed in one basis and another in a differnet basis, one can make the inner product, provided one puts the appropriate matrix in between to bring both to the same basis. This is automatically understood, writing this matrix is redudent.

One basis is the description of the function on the plane of the images of the pinholes, as a function of the position $x$ This is indeed a full basis, as the $x$ span the entire line.

In the other representation, the one in the plane of the pinholes, I don't give the full basis, since I am not interested in describing all possible incident wavefubnctions, but only the two I am interested in namely |A> and |B >, the rest of the basis is left vague. I just assume it can be completed to a basis, but I do not care exactly how. This is certainly not a two-dimensional space. All kind of initial values are conceptually possible, nobody forces me to have only two pinholes! I could add more pinholes, or more sources on this plane. That I choose to restrict myself to just two dimensions in that space, because it is the only two I am interested in, does not decrease the intrinsic size of this space, which is just as infinite dimensional as the space in the plane of the images!

Now without the grid what I keep repeating is that what is |A> in the plane of the pinholes becomes, in the plane of the images, a localised object, ideally a delta function. Well, it has a size, of course, related first to the size of the original pinhole augmented by the diffraction of the lens, with or without apodisation but all in all it is a very localised bump near the image of A and zero everywhere else. So by $<x_{i}||A>$ I mean the amplitude of the wavevector at the point $x_{i}$ if only pinhole A is open. This is a function of $x_{i}$ which peaks round the position of the image of pinhole A and is zero everywhere else.

Certainly this a well-defined mathematical operation! --Alfredr 11:40, 27 June 2006 (UTC)

Dear Alfred, did you checked for consistensy what you say? I guess no! This is impossible. You say: "So by $<x_{i}||A>$ I mean the amplitude of the wavevector at the point $x_{i}$ if only pinhole A is open." I also consider that analogous definition holds for $<x_{i}||B>$.

Suppose that $x_{i}$ is a point that has 0.3 contribution from slit A and 0.1 contribution from slit B. In this case $\beta _{i}=0.4$. Let however check what happens:

Born's probability rule when you use the expression for the wavefunction in the position basis gives you $|<x_{i}|(\beta _{1}|x_{1}>+\beta _{2}|x_{2}>+...+0.4|x_{i}>)|^{2}=0.16$

Now let we use the wrong thesis that you suggest $|\Psi >=0.7|A>+0.7|B>=\beta _{1}|x_{1}>+\beta _{2}|x_{2}>+...+0.4|x_{i}>$ , so we can write down the wrong formula that you propose $|<x_{i}|(0.7|A>+0.7|B>)|^{2}$ and we get $|0.7(<x_{i}|A>+<x_{i}|B>)|^{2}$ where I consider that your formulation holds and $<x_{i}|A>$ is the amplitude when only slit A is open. After substituion analogously for $<x_{i}|B>$ we get $|0.7(0.3+0.1)|^{2}=0.08$ . Obviously this leads to different result from the already obtained 0.16, SO YOUR THESIS IS WRONG. PLEASE EXPLAIN WHY THE BORN'S RULE DOES NOT WORK NOW AFTER THE SUGGESTED BY YOU SUBSTITUTION? What you suggest is wrong application of results from the single slit setup into the double slit setup. Your definition for the inner product is wrong, or please clarify why the Born's rule does not work. Danko Georgiev MD 16:06, 27 June 2006 (UTC)

Dear Danko

I really don't see what the difficulty is. Let slit A only be open, and take a point $x_{i}$ - say, on the plane of the lens, because on the plane of the images, you never have amplitude both from A and from B without grid (and even with grid, diffracted amplitude from one is small where direct amplitude from the other is large).

So say at this point, when A only is open amplitude is for instance, $|\Psi >(x_{i})=|A>(x_{i})$=0.3(cos 32°+i sin 32°). The integral of $|\Psi >|^{2}$ is normalized to one, by definition, not to the actual power that comes through, do we agree? We count probability of arrival, not total energy. If only B is open you would have there $|\Psi >(x_{i})=|B>(x_{i})$=0.3(cos 32°-i sin 32°).

If both A and B are open, one has to be careful: the wavefunction is still normalized to 1, so now $|\Psi >=0.7|A>+0.7|B>$ Though the total power is double we count probability, not total flux. Born rule, right?

So now the amplitude is $|\Psi >(x_{i})$=1.4*0.3 cos 32°

In order to normalise correctly, the contribution each of the slits is reduces by square root of 2. You can easily see that the integral of $|\Psi >|^{2}$ will still be one.

Your argument "contribution from A is 0.3", "contribution from B is 0.1" has to be qualified. From A when A only is open? Or from A when both A and B are open? There is a noramlisation factor that shoud enter, divide by square root of 2.

Now if you do not think in terms of probability, but of *power* then opening both holes doubles the power. The integral of $|\Psi >|^{2}$ is not one but the energy, say, five watts when only A is open, five watts when only B is open, but 10 watts when both are open. Then the contibution when bot hare open is reallyt the summ, without dividing by square root of two, there is still an interference pattern but the power per unit surface element in the center of a bright line is four times, not just twice, the power per unit surface element when only one pinhole is open and the total power (averaged in bright and dark zones) is twice the power from each pinhole. But if you normalize to probability, not power, then the inverse of square root of 2 is needed, the probability density at hte center of a bright line is just doubles and the total probability is one. Born rule is quite straightforward. I really don't see what your difficulty is!

87.88.114.80 17:03, 27 June 2006 (UTC) Ooops! Forgot to log in again That was me, Alfred

Comment: message repaired and moved below (Danko Georgiev)

Dear Danko

I am giving up. You refuse to see the obvious. You say I am mixing symbols, when I am just describing, in a unique vector space, two situations, one with one slit open and one with both slits open. Nothing else changes, neither the definition of A, B nor that of $x_{i}$. The only difference is whether $\Psi$ is |A>, |B> or 0.7|A>+0.7|B>. That what a vector space is for, describing in a unified way several intial conditions. If whenever the initial conditions are changed you call that a different vector space with different inner products, one is getting nowhere.

Now I obviously cannot make you see that you are completely wrong and I am spending all my energy showing you to what extent Afshar is right instead of having this energy left to show exactly on what very subtle but still fundamental point Afshar is wrong.

Anyway nobody is reacting to the latter point. So the whole point of this discussion page is moot, and I think I will stop visiting it.

Bye Alfred

Dear Alfred, it seems that you use:

$<x_{imageA}|A>={\sqrt {1}}$

$<x_{imageA}|B>={\sqrt {0}}$

where A and B are the wavefunctions thorugh the single slit, and $x_{imageA}$ is the point at the image A. For arbitrary point $x_{i}$:

$<x_{i}|A>={\sqrt {p_{A}}}$

$<x_{i}|B>={\sqrt {p_{B}}}$

where $p_{A}$ and $p_{B}$ are the probabilities of finding a photon when only one of the slits A or B is open. OK, so far I agree with you.

Then you seem to defend the idea that asking about slit contribution at point $x_{i}$ should be done by the procedure:

$|<x_{imageA}|\Psi >=<x_{imageA}|0.7(|A>+|B>)|^{2}=|0.7x1+0.7x0|^{2}=1/2$

HOWEVER HOW DID YOU ESTIMATE THE SLIT CONTRIBUTIONS - YOU JUST SCAN BY EYES WHAT IS GOING ON IN BRACKETS, SO YOU DO NOT ACTUALLY USE THE BORN'S RULE! The question sits in the bra part of the Bron's rule.

YOU USE A MODIFIED RULE - CONTRIBUTIONS BY SLITS IN DOUBLE SLIT IS ESTIMATED ON THE BASE OF $<x_{imageA}|A>={\sqrt {1}}$ and $<x_{imageA}|B>={\sqrt {0}}$. This is NOT the Born's rule, but some kind of new invented rule! But what is exactly the formulation of this new rule for answering "contribution" questions?

Candidate rule [1]: "The contribution of slit A at $x_{i}$ in the double slit is the amplitude that slit A contributes at point $x_{i}$ in the single slit experiment when slit A is open"

In this case the contribution of slit A at $x_{i}$ in percents should be calculated as the percent from the total amplitude at $x_{i}$. Therefore at different points the amplitude contribution from slit A will vary in percents. Obviously if this is the criterion of "which way" then Afshar proves that in the same setup "which way" is both present and absent! NO PROBLEM! You have assumed as a rule [varying "which way" slit contribution at various points] as what you want to prove.

Candidate rule [2]: "The contribution of slit A at $x_{i}$ in the double slit is the probability to detect a photon that slit A contributes at point $x_{i}$ in the single slit experiment when slit A is open"

In this case you have the following result - you have "contribution from slit A", contribution from slit B", and residual contribution from interference". In this case the "interference" is variable at various points, so there is no problem for Afshar to prove that "slit contributions of 1" and "interference" are both there in the same setup but at different space point. This again consequence of your own definition of the "which way" as "slit contribution of probability in the single slit case". So in this case Afshar is again right.

Where is the problem - You do not use Born's rule to answer the question what is the slit contribution to the point $x_{i}$, so obviously you invent a new QM rule, where you introduce new definition of interference and "which way". IN THIS NEW INTERPRETATION YOU HAVE POSSIBILITY FOR BOTH "WHICH WAY" AND "INTERFERENCE" SO THEY ARE NOT EXCLUSIVE NOW, BUT SIMULTANEOUSLY POSSIBLE AT DIFFERENT POINTS OF THE SAME SETUP!!!

Born's rule

step 1: Use the whole wavefunction in the ket

step 2: ask question with bra

step 3: square the inner product and what you get is the answer

Modified pseudo-Born rule (that you do)

step 1: use the whole wavefunction as a ket

step 2: ask something with bra

step 3: additional info aside from the main question asked with the bra, can be obtained by some other instructions

step 4: the final value of the squared inner product tells you nothing about the info that you have extracted by other means

Well, I hope you agree that you "look what happens" in the brackets before squaring in order to determine the slit contributions. So the logic should be explicitely state as a rule by which you got your conclusion. It is NOT obvious, it is some kind of rule that you should invent that is different from Born's rule to ask questions. Otherwise the question $|<x_{i}|\Psi >|^{2}$ gives you the answer for probability to detect a photon at $x_{i}$. The answer is given as the "end" of the whole computation, you are NOT allowed to extract information from the intermediate steps before the compuitation of the result is obtained. If you extract such information, you should provide rule, how you may extract information from "Born's rule under progress" which is obviously new QM formulation. Danko Georgiev MD 06:16, 28 June 2006 (UTC)

"Pseudo" Born rule

Dear Danko

OK, you have a point here, but this is precisely where the whole problem hinges about.

If one looks only at the Born rule there is nothing to discuss about. There is only mathematical expressions and that is it. There is no paradox because no paradox can even occur.

What I keep saying, and, for instance you will see that Unruh holds the same attitude, is that it is still' meaningful to give extra information by "reading off things.

Look at this website http://www.theory.physics.ubc.ca/rebel.html

Consider figures 1 and 1a: Path 4 is open.

Since when path 2 is blocked everything gets in 5, when path 1 is blocked it gets to 6 one can infer that when both paths are open what gets to 5 comes from 1, what gets to 6 comes from 2. This is extra information, beyond Born's rule. But everyone does it, it does not perturb anyone and even Afshar agrees to that.

Closing path 4 does not change the results (Born rule is invariant, because nothing goes through 4 anyway) but destroys the inference.

But Afshar denies that his experiment is essentially equaivalent to that. He uses the argument "plane with wings/plane without wings " to dismiss it. But this is wriong, Unruh's (Gedanken)experiment and Afshar's (real) one are deeply equivalent even if that does not appear so clearly.

Now your argument would say that the inferences that Unruh makes are wrong. Welll, in a sense they are beyond Born's rule. But in the case of Unruh almost eveyone but you would admit the inferences are valid. Denying their validity would weaken Unruh's point. I say one should

a) support Unruh's point : he is 100% correct

b) show in detail why this also applies to Afshar's experiment, and that the "plane with wings/plane without wings " argument is invalid. In this, Unruh was perhaps insufficently pedagogical. The equivalenc e between his case and Afshar, though absolutely correct, is not vey obvious without further explanations, and this is what left room for the (incorrect, but plausible to the unaideded eye) "plane with wings/plane without wings " argument.

But spending so much energy to defend my point of view, which is also the one that Unruh takes, against your attack is counterproductive. Everyone agrees with Unruh's inferences, beyond Born's rule

Please read Unruh's paper and tell me if you agree with hilm (forgetting, for the time being, whether there is or not a connection with Afshar) --Alfredr 11:33, 28 June 2006 (UTC)

Dear Alfred, actually in 2004 I did a correspondence with Unruh, where I dismissed his reasoning. He uses a rule beyond Born's rule to detect "which way". My position is clear, and I am acquainted with Unruh's point. The idea is that when the two slits are open now $<x_{i}|A>$ and $<x_{i}|B>$ become questions beyond the Born rule, because now A and B are part of the whole superposed wavefunction of the double slit. My statement is "accepting new rules beyond the Born's rule" will lead you to possibility to have "which way" information and "interference" in one setup but at different points! So there is no actual problem with your point:

possibility [i] : accepting the new pseudo-Born rule, will give you possibility to have in the same setup both "which way" and "interference" but in different points. This follows from the definition of the new pseudo-Born rule, that makes the "which way" VARIABLE during the intercourse of the photon propagation! In this case Afshar is right, simply he shows what the pseudo-Born rule gives you theoretically - $V^{2}+K^{2}=2$. Do you see why? simply at the Fourirer plane if the lens you have point with double positive contribution both by A and B, while at the end point at the image plane you have point with relative amplitude from A being 100%, while relative amplitude by B being zero %.

possibility [ii] : deny the "variability of the which way during the whole setup"! This is the original formulation of complementarity. So in this case all extractions of additional info is "not acceptible" and therefore for every point beyond the slit $|<x_{i}|\Psi >|^{2}$ is question giving you the probability to detect photon at that point, and $|<slit|\Psi >|^{2}$ gives you the contribution of the given slit at every point behind the slit. This is true because the whole wavefunction is the same for every point, so it is meaningless to object that I should specify for which point I measure the contribution of the slit. The whole function is the same, so for every point the contribution of the slit will be the same. In this case however you have different relation being $V^{2}+K^{2}=1$.

possibility [iii] Aurelien Drezet believes in the pseudo-Born rule but he is arguing that $V^{2}+K^{2}=1$ is true if you are not allowed to speak about the whole setup, but only plane by plane, hence Afshar's error is measuring the photons at two different planes in the same setup. Yes, this is true also - the pseudo-Born rule keeps the $V^{2}+K^{2}=1$ ONLY for given plane parralel to the xy plane of the slits. So in a certain sense Drezet's point is that you are not allowed to consider the whole setup, but you should think in plane by plane.

Actually if we do not start from the same mathematical rules, all results derived by different basic postulates could be true! So nobody makes error, in this sense. In another sense if someone starts from new mathematical principles that are not accepted, although his reasoning might be true, he makes "error" in accepting the "wrong math rules" at first place.

My conclusion is that there are 3 different formulations that are equally consistent, the "semantics of the words" however differs dramatically. Finally we agreed on existence of such alternative formulations, that use different mathematical rules to answer QM questions, and my main point against your diffraction explanation is - ALL DEPENDS ON THE DEFINITION OF THE ADDITIONAL PSEUDO-BORN RULE [TRUE/FALSE], AND ON THE CONSENSUS WHETHER YOU SHOULD APPLY $V^{2}+K^{2}=1$ FOR THE WHOLE SETUP, OR PLANE BY PLANE. Therefore once you have consensus of the theory, the whole problem will be settled by clarification of the definitions, and nothing else will come by eventual considering of diffraction. By the way your diffraction idea is flawed, because the grid is put at a distance from the lens x << f, where f is the focal distance of the lens. This fact implies that the diffracted light will be dispersed in space and not concentrated at the images A or B. This is true since the light diffracted by the grid will be emitted at a distance x << f, and the image of this light is "virtual image" being on the side opposite of the side with the images of the pinholes A and B. I hope you will now stop on insisting that there is something important coming from diffraction of light to the wrong image. The possibility is negligible. Let us focus on the QM basics and the formulation of complementarity - what is this ? - is it a single concept, or everybody understands by complementarity whatever he wants. Best, Danko Georgiev MD 14:06, 28 June 2006 (UTC)

Dear Danko To summarize:

if one refuses to look beyond the Born rule (i.e. if you disagree with the entire principle of Unruh's thinking) then there is no paradox. QM probabiliies are given by Born's rule at that is all there is to it.

Now if one accepts Unruh's inferences, then that means that QM practtitioners have lived for many decades with the fact that you can have inferences (not experimental proofs) of "which way" information in situations where there are interferences. Unruh's point was just that: except for you and people like you who just refuse these inferences, and keep strictly with Born's rule, people have lived with that for decades without being shocked.

Now the point is, what is the difference between Afshar's experiment and Unruh's one?

Afshar says there is one. Unruh says there is none. Who is right?

Unruh.

But why? Superficially, it looks like there is a difference: in Unruh's case, when 4 is open and a photon arrives at 5, one can infer it went through 1. If 4 is blocked this inference is lost. But this is easy to follow logically (unless one rejects all inferences beyonf Born's rule, as you do).

Now superficially it would seem that in Afshar's case, the inference is not lost. That would make it very different from Unruh's case which is something people have long made their peace with.

But this is not so! Inference is partially lost. One can infer that a photon getting to the image of A did go through A, with probability 94%.

But, crucially, the 6% recovery correspond to 6% uncertainty about where the photon went through.

And, yes, I insist, it is because of diffraction. What you forget is that you do not have diffraction by a single wire but by a grid. A grid does not diffract anywhere, but only towards its dual grid. Yes, this is so. Therefore, the amount diffracted towards the image of the other pinhole (which is the next point in the dual grid) is small but not negligeably so (in fact, the grid itself diffracts beams each made of rays, that appear to come from the dual grid, formed of equidistant points in the plane of the pinholes. Because the grid is precisely the one corresponding to interferences of A and B, it follows that one of the diffracted beam from each pinhole seem to come from the image of the other, and many more points in a periodic pattern with distance AB. Then the lens concentrates these beams to images of points equally spaced in the image plane, including the images of A and B). Yes, it is of the order of 3% in amplitude. That is far from negligible. As far as intensity is concerned this is indeed negligible (3% square... ) . But because it is phase-linked with the main beanm, it produces a 6% constructive interference. This is exactly the recovered intensity.

Now whether you believe me or not, I can't do anything about. But it is so.

The fact that the diffraction from B is 3% at A can easily be seen.

Why is there only 94% of the expected power when the gris is presenr and only A is open? The amplitude is 97%. It is reduced by 3%. This 3% (with minus sign) is destructive, forward diffracted amplitude from A itself.

Now as Afshar keeps saying, since the grid is at the dark fringes, there can be no diffraction. If you think in mathematical terms only, he is right. But then there is no paradox. Paradox comes from thinking beyong maths, beyond Born's rule. But if you reason that way one must think like that: diffraction from A is as in the previous case. There is still a 3% destructive forward diffractio nfrom A. But since hte NET diffractio is zero (and yes, it is zero ,of course) that means that there is 3% constructive diffraction from B!

If you disagree with Unruh ,you won't ever agree with me. But what can I do about it?

My point against Afshar is that he is wrong to dismiss Unruh's reasoning in his case. You do not, but most people agree that Unruh is right as far as his Gedankenexperiment is concerned, and that people have learned to live with that for decades. Apparently, Afshar agrees with that too, but claims his case is different because the inferences that first exist but then are lost in Unruh's case are not lost in his case. What I keep saying is that Afshar is wrong because the inference is partially lost, 94% preserved and 6% lost, and the source of the loss is diffraction.

Now if you don't want to enter into Unruh's reasoning I can't do anything about it.

But you seem to think that if one accepts Unruh's point of view, one must accept Afshar's too.

I am claiming that it is not so. Unruh is right and Afshar is wrong and the difference is that because of diffraction Afshar's case is essentially identical to Unruh's one.

--Alfredr 06:47, 29 June 2006 (UTC)

Where diffracts the grid

Dear Alfred, please clarify your position, because you speak without sufficient argument. The grid is a distance x < f from the lens. The grid acts as "source of secondary emission" as the Huygens principle implies. These light rays emited however have virtual image on the same side where is the grid itself [2], therefore on the other side of the lens where are the detectors this diffracted light is dispersed in space and not concentrated at the images.

So, please provide exact mathematics that explains why ALL diffracted quantum amplitude comes to the images A and B, and is not dispersed as the laws of optics imply?? Danko Georgiev MD 12:28, 29 June 2006 (UTC)

Dear Danko

I never said all diffracted amplitude comes only to images of A and B if only one pinhole is open. I am saying it appears to come from the dual grid.

Assume just pinhole A is open.

The light from pinhole A reaches the grid. The phase on each wire is precisely determined because it all emanates from pinhole A;

Now the width of the wire is very small compared to the distance between wires.

So in first approximation let us say that is is extremely small, and the phase is uniform on each wire.

Diffracted light predicted by Huygens principle will appear to come from any point such that the phase would be just the value it has. That means, it would appear to come from A (forward diffraction, in the same direction as the main beam, and causing destructive interference) and all points such that the phase difference between two wires is the same as from A, plus any integer number times 2pi. This includes B, because remember where the grid is: at places where the phase difference between A and B is the same for all wires (it is an ODD number times pi, so that there is a global sign between the beam that comes from A and the one that seem to come from B), but there is indeed a beam that seem to come from B. But not only A and B, all the other points on the same line with the same distance interval.

Now the wire is not infinitely narrow, so it has a finite diffraction cone (this is the dispersion yo uare referring to) the width of which is roughly in inverse proportion, compared to the AB distance, as to the inter-wire distance to the wire width. So if the wire width is 1/30 of the wire distance, the cone will roughly cover 3 dozen points, not just A and B. This is not strict, the cone is not a yes-no business, points near the center are brighter than points near the sides and the sides are not sharp.

However I am saying : near the center we have amplitude 3% thus intensity 3 %of 3%= 0.09%, on each apparent source. Total absorbed intensity being 3% implies total diffracted is 3% (or, more precisely, 3% of 97 % according to Huygens rule) so since even the points nearest the center have 0.09% you need at least 3 dozen.

Now all these points are apparent sources of diffracted amplitude. And yes, they spread over a rather large region, dozens of times the interval AB, but each of them is a quasi-point source, about the size of the pinhole that illuminates the grid.

Since all these apparent sources are in the plane of the pinholes, the lens will converge the light that seems to come from them to images on the plane of the images of A and B, three dozen or so images with the same interval between them as A and B. On all of them EXCEPT A amplitude is 3%, intensity 0.09% (near the center, decreasing when you go out, total intensity 2,91% when summed over all thes 3 dozen or so points),

Now in A itself what happens is that the forward diffracted amplitude is 3% but interferes destructivley with the main beam. So we get just 97% amplitude (one way to look at it is to say that, indeed, the surface area that is effective is only 97%- but the correct way is to think that the reduction by 3% is the negative forward diffracted amplitude).

Note that since the amplitude in A is just 97%, the intensity is 94,09%. Add the 2,91 % diffracted everywhere else plus 3% absorbed by the grid, you get the correct total.

Now open the other pinhole.

You get just the same thing but with opposite sign, because the grid is where A and B have odd number of pi difference.

Consquence: the intensity in all the beams except A and B cancel out. No light seems to come from any of them. One way to describe things is to say, as Afsahr says, no light hits the grid so none can be diffracted? Yes, it is true, mathematically. If you do just Born rule, no difference? But if yo uwant to think beyond, you have to say: A and B both diffract, but the amplitudes are opposite.

Now what about the beams that seem to come from A and B themselves?

I say there are 3 contribution to each.

- Main beam

- forward diffracted amplitude from the correct pinhole (desteuctive)

- diffracted amplitude from the other pinhole

(now, if we speak of power, one just adds the contribution and powers of both pinholes add up, if we consider probabilities, on has a one over square root of 2 factor to normlize the probability to unity)

Now the sum of the last two contribution is zero. So they cancel. So the total amplitude mathematically is just the unperturbed main beam. For you who only admit Born's rule and refuse to think outside, there is no difference at all. But I want to reason in terms of Unruh and Afshar. So please follow my argument even if you dismiss it as a matter of principle.

Conceptually I claim (and this is in the logic of Unruh, except that he did not point it out explicitely, but I am sure he would agree with me) that one is not allowed to ignore the fact that the amplitude from B is needed to cancel the destructve amplitude from A.

Either one takes Born rule as the ultimate rule, as you do and there is no paradox. Fine!

Or one wants to go beyond, as Afsahr, Unruh and mself are ready to do. But then one has to do it consistently. One cannot retreat behind pure math to say ``Oh, well, since these amplitudes cancel let us forget about them`` This is what Afshar does, and it is inconsistent. One must admit that what comes from B really comes from B and that it just cancels the destructive contribution of A is no ground to dismiss its existence.

And that means that the experiment is not a pure which way one, and that Unruh's argument applies here, too, contrary to Afshar "plane without wing" argument.

Now all of this runs against your point of view. Just look at it in the logic of Unruh. You'll see that this solves the paradox.

I am not asking whether you agree with me, I know you do not. But do you agree that in the logic of Unruh it is just diffraction that does the trick? --Alfredr 15:38, 29 June 2006 (UTC)

Dear Alfred, sorry again, but your logic seems to be not very clear. I do agree that at the place of the grid wires the two waves come in exactly the opposite phase so they do destructive interfere. However I don't see why the diffracted amplitude from A should also exactly interfere with the diffracted amplitude from B. Please provide a geometrical sketch.

I don't see why the diffracted amplitude from A should exactly interfere with the diffracted amplitude from B. They come from two different directions so the plane is which the amplitude A is diffracted, forms the same angle with the plane where amplitude B is diffracted, as the angle between the two rays coming from A and B, so the two diffracted images cannot overlap and destructively interfere. See [3] in order to understand what I am talking about. Danko Georgiev MD 07:23, 30 June 2006 (UTC)

Dear Danko You show diffraction from a single wire We are talking diffraction by a whole grid Of course the central blob, the one where most of the light goes is not the same for A and B! But that contains not only the forward diffracted light, but principally the non-diffracted light. That will of course differ for A and B. What I am referring to is all the other discrete places where diffracted light from the grid ends up. These points ,once again form the dual grid, and are a large array of equidistant points , several dozens of each. Of course if A only is open the array is symmetrical around the image of A, while it is symmetrical around the image of B if only B is open. But because there are several dozens such points, the intensity of which vary quite slowly when one moves out of the respective center of symmetry, I am saying that, yes, except for the images of A and B themselves where the main beam reaches, the amplitude coming from A and B at each of these points are almost opposite. And of course it has to be so: when both holes are open, the wire are in the dark zone, so very little light gets there, so the net diffraction is almost zero! Afshar claims there is NO diffraction. Logically you should claim the same (you only look at Born's rule and refuse to think beyond. But I (following Unruh's logic) claim that diffraction from A and diffraction from B exist, event though their amplitudes cancel each other. At all the points of the dual grid but the images of A and B, this cancellation gives zero (or almost zero) intensity. At the images of A and B, the cancellation restores full intensity: forward diffraction from A interferes destructively with the main beam, diffracted amplitude from B (at a small angle, just one unit of the elementary angle off the forward direction, knowing that the cone spans dozens of such elementary angles) causes constructive interference that brings us back to the unperturbed amplitude thus full intensity.

Now why do we have almost cancellation and not perfect cancellation: the wire has finite width. At the center of a dark fringe, the intensity of light is like sin^2(x). If we the width of the wire is 1/30 of the interwire distance this means the largest value of x at the edge of the grid is pi/60, giving a very small value if the intensity indeed, but not exactly zero. This non quite zero value would correspond to the fact that the amplitude diffracted by A and B at the same point of the dual grid, but at slightly different angles from the center of each pattern, are very close to be opposite but not exactly so. Still I say that seing the dual grid when only open pinhole is open should be easy, (intensity 0.09% of the main beam), but when both pinholes are open one loses an additional factor of order 1/3*(pi/60)^2 (1/3 from the average of x^2 from zero to some maximal value), 1000 times less, I doubt this can be seen. at all. But this extremely small amount correspond to the fact that the pattern of diffraction from A and B respectively are centered around different points and thus, there is a small variation, at given point, of what comes from one pattern with respect with the other since the distance from the center of symmetry is nor the same. But one unit of angle for a pattern of several dozens, the relative difference in amplitude would be of the order of 1/30, and when squared we recover the order of magnitude of a further 1/000th.

IS it clear now why diffraction from A and B alost cancle each other? Alfred --134.157.252.131 11:11, 30 June 2006 (UTC)

I see I have been a bit ambiguous about symmetric around A vs B. The points themselves are totally independent on whether A alone, B alone or both are open. The points are just , formally, the infinite array of points on the straight line through image of A- image of B, at the same interval as the two images.

What changes when A vs B is open in the distrubution of light on these points. Mostly, the main beam gets to the corresponding image. Second ,the repartition of light is symmetrical around the correct point. But since the effective width of the array is large, several dozen of points effectively visible, with slowly decreasing amplitude outward, with a global minus sign when it is A vs B) the off-shift by one unit from the respective centers makes only a very small residual contribution. This is compatible with the fact that sin^2(x) is only strictly zero at a point, not in the full interval (-p1/60; pi/60) but is very very small there. It is the same factor that enters in both calculations, and it has to be! This is just the amount of power which is taken out of the main beam when both A and B are open: considerably smaller, but not rigourously zero, computed in two differnet ways:

- as residual effect of the grid in the dark but not completely zero (sin^2(x)) intensity zone, - as residual diffraction in all the other points

In both case, down by a factor of 1/1000th or so.

Alfred --134.157.252.131 12:24, 30 June 2006 (UTC)

Dear Alfred, sorry to ask a simple question, but it is important for me. Does the secondary emission by the grid starts with exactly $\pi$ phase difference compared to the phase of the incoming ray. If so, I start to see your logic that seem to hold. Please answer whether my guess is indeed what the Huygens principle implies.

Well, if you can help me to figure out what exactly is the definition of "which way" I might agree partially with your interpretation.

Danko Georgiev MD 09:34, 1 July 2006 (UTC)

Dear Danko To answer you:

yes, secondary emission from the grid in the forward direction is indeed with $\pi$ phase difference compared to the phase of the incoming ray. It has to reduce the overall amplitude compared to the value in the absence of grid! 

I am not sure I follow your x and y. When both pinholes are open there is a $1/{\sqrt {2}}$ normalisation factor, but let us forget it for the time being. We look at what reaches the image of A

main beam (through A) is 1 forward diffraction from A is -y (of the order of 3%) and yes, the phase difference is $\pi$ diffraction from B is +y (or almost that; in fact there may be a very small difference, of order maybe y/30 but let us ignore second order corrections related to the finite width of the wire which necessarily is wider than the infinitely narrow "strictly zero intensity" interference fringe)

So total from A : 1-y

contribution from B : y

Total : we recover 1-y+y=1 (with maybe a small discrepancy, but much smaller than y) BUT

from A is (1-y)^2 of the order of 94% : this is "which way", we can infer that it indeed went through A along Unruh's philosophy which I personally follow 100%; because that is just what gets there when pinhome A onyy is open.

from B alone is a very small contribution y^2, negligible

and finally there is a 2y(1-y) positive interference bertween A and B; being interference from two pinholes "at the same time" this is most definitely "not which way"

Afsahr's mistake is to claim that the full value 1-y+y= 1 can actually be attributed to pinhole A;

Born rule sees only the total, but then one does not attribute anything to A or B; this is your poitn of view and there is no paradox by defintion. But this is not an answer to Afshar's specific mistake, it would refute Unruh's point of view in his own Gedankenexperiment just as much.

I claim that Unruh's approach beyond Born does make sense, and moreover that when applied consistently to Afsahr's experiment it solves the paradox ,which only appears because Afshar uses incorrectly an approach which you see as fundamentally flawed but which Unruh and I consider as valid provided it is followed precisely and consistently which is not the way Afshar does it.

Note that in Unruh's experiment, when channel 4 is blocked and which-way information is lost, and you compute carefully the contibution, you'll find that what reaches either 5 or 6 is half the total intensity. But referring to the cases where 4 and also either 1 or 2 is blocked, you'd get only 1/8; thne if 1 and 2 both are one, you get 1/8 from 1, 1/8 from 2 but the total is 1/2, not 1/4. So the other 1/4 is again constructive interference of 1 and 2. I entirely agree with Unruh approach both his calculations and his interpretations, but pedagogically I find his explanations wanting. He does not stress sufficiently, in my opinion, some subtle but important aspects of his own Gedankenexperiment.

I hope I at least convinced you of the relative consistency of my vierw of Afshar's experiemtn and Unruh's view of his own Gedankenexperiment, and how much diffraction is indeed crucial for this relative consistency.

I again forgot to sign in but that was me, Alfred 87.88.114.80 22:25, 1 July 2006 (UTC)

Is there difference between the interpretations?

Dear Alfread, I agree that your approach within a reasonable approximation is valid. Yes, the diffracted amplitude from the pinhole B seems to come to the image A when there is grid, and it should be well approximated by 0.09% intensity that is the square of 3% amplitude. BUT, something that is very important you use the following rule:

at point x with complex amplitude A + B the information is as follows:

which way from $A=|A|^{2}=AA*$

which way from $B=|B|^{2}=BB*$

interference = $A*B+B*A$

But in my resembling to Many Worlds interpretation the "which way" is estimated solely by Born's rule. I take a very classical approach and apply it extremely rigorously - when you say "which way from slit A" you should know "coming from A and only from A at 100%". Thus in extreme case mixed state density matrix with zero off-diagonals is purely which way, while a pure state density matrix is purely no which way.

Now emerge questions is these two interpretations different BECAUSE ACTUALLY WE ESTIMATE BY DIFFERENT MATHEMATICAL RULES THE "WHICH WAY"!?So I think these are experimentally falsifiable - i.e. can be distinguished.

Suppose that we have a modified Afshar's setup with size of pinholes 0.2 micrometers separated at distance of 1 millimeter, and the wavelength of the source is $\lambda$ = 750 nm. Then according to my interpretation ALL photons pass through both pinholes despite of the fact that they are detected at image A or image B.

Heisenberg's uncertainty makes the estimate

single slit / mixed single slit $\Delta x=2\times 10^{-7}$ m, $\Delta \lambda =2\times 109$ nm

double slit lens $\Delta x=10^{-3}$ m, $\Delta \lambda =2\times 0.02$ nm

for formulas see my above entry on the apodization vs. no apodization

Now you see that the effect on the Airy disc WILL BE PERFECTLY VISIBLE. The two interpretations however make different predictions for the actuall strength of the effect.

Born's rule - ALL photons are superposed in the double slit through both pinholes, will predict that ALL photons should be governed by a single Airy Disc distribution, with sharp completely dark Airy Disc minima.

Unruh's/Ramani's rule - 94% of 1/2 photons will have passed through A only, therefore they will have definite position [since you know the slit] but because each photon might have every possible wavelength from the uncertainty interval then the wavelength of the Airy disc will not be sharp and completely dark Airy minimum but exactly the opposite you will expect bright Airy minimum [see my previous images for the illustration of the effect], and ONLY approximately 6% of 1/2 of the photon's will have sharp Airy disc minimum (comment: negligible amount of photons 0.09 % will come only from slit B therefore they will have also bright Airy minima).

Do you agree that now the two interpretations are distinguishable - I say that the effect on the Airy disc is complete = 100%of strength, but you will say that the effect is very small and only about 6% of the strength that I predict. Since the final intensity of light in the Airy minima will differ by quantity, the two interpretations seem not to be equivalent! Do you agree? Danko Georgiev MD 06:25, 2 July 2006 (UTC)

--129.78.208.4 00:30, 7 July 2006 (UTC)== Duality equation, which way and Heisenberg's uncertainty ==

Dear Alfred,

I was able to investigate the duality equation by Englert et al. so below I provide some cricial facts. Surprisingly I came to very interesting conclusion - your analysis shows that Afshar does NOT violate the duality relation, while my finding is that the duality realtion is NOT criterion for "which way" at first place. Please tell me whether you can download the next references.

Duality relation

$D^{2}+V^{2}=1$

D - distinguishability - physical interpretation/significance controversial??? (Englert, 1996 interprets it as "which way" information - see the dependence on the intensity in the single slit setup)

$D={\frac {|A|^{2}-|B|^{2}}{|A|^{2}+|B|^{2}}}$

V - visibility - physical interpretation/significance controversial??? (Englert, 1996 interprets it as "no which way" - see dependence on the interference term)

$V={\frac {2|A||B|}{|A|^{2}+|B|^{2}}}$

ref: see Drezet, 2005

The duality relation is NOT dependent on Heisenberg's relations

ref: see Englert in Phys Rev Lett 1996; 77: 2154-2157

My comment here is that this is a serious problem when you start to think about V and D in terms of "which way". In the case "which way" means that you have knowledge part of photons passed only through given slit. But in this case you have direct claim on the UNCERTAINTY of $\Delta x$ ! Since V and D do not depend on the Heisenberg's relations by general reasons it follows that you should NOT interprete them in such a way that attributes them "knowledge that affects the uncertainty of any variable"! Of course you might argue that if V and D are correct to describe "which way" or "no which way" then they will have to be experimentally tested towards the Born's rule as single rule to determine "which way". Actually both interpretations of "which way" are NOT interpretations, but MATHEMATICALLY AND EXPERIMENTALLY DISTINGUISHABLE THEORY, therefore I conclude that only 1 of them is the true one!

Now summarizing on the importance of your scenario with the grid diffraction towards the opposite image. YES, you have contributed something positive to the discussion, you have proved that Afshar DOES NOT violate the duality relation, while my argument is aimed at showing [i] the duality relation is NOT linked with the idea of "which way", and [ii] the whole setup of Afshar does not violate "which way" complementarity as based on Born's rule and density matrix formalism. I am interested to have your comments. Regards, Danko Georgiev MD 04:14, 3 July 2006 (UTC)

Dear Danko

I said from the beginning that Afshar's experiment does not violate complementarity. The crucial point is to interpret complementarity correctly. The problem is not so much interpretation of the results, but of what exacly it is that one calls, and one expects, by complementarity. The entire pseudo-paradox comes from an inadequate understanding of the very notion of complementarity. The point is that your position, to refuse to see anything beyond pure Born's rule is intrinsically consistent, but evacuates the whole discussion. But people do discuss, so it is important to enter into their arguments to refute them from the inside. Besides I do agree with Unruh's attitude. And the crucial point is to show that from Unruh's point of view, Afsahar is wrong to believe his case is specail, his case is perfectly equivalent (even if it does not meet the eye) to Unruh's case.

Now as for the measure of the non-apodised minima, that won't give an answer. There are several ways to formulate the reasons, one being that measures will be according to Born's rule and everybody agrees to it. One different way to look at it is, Heisenberg inequality is just that, an inequality, not an equality. If $\Delta x$ is small this implies a minimal value to $\Delta p$, but a much larger $\Delta x$ can still cause a large $\Delta p$ if the situation is not optimal. And two very small but distant pinholes is a highly suboptimal situation. In fact the corresponding $\Delta p$ will essentially be the one determined by the pinhole size, not their distance. In that case $\Delta x\times \Delta p$ will be much much larger than the minimal value, but this is in no way a contradiction. And this is just what will come out of calculations, since the calculations are the same for everybody.

More some other day, I have to run now

--Alfredr 11:42, 4 July 2006 (UTC)

Dear Alfred, your comment is irrelevant - even if $\Delta x\Delta p>{\frac {\hbar }{2}}$ then you still should predict bright Airy disc minima if you believe in the duality relation as "which way" criterion, while I still predict dark Airy minima because I believe the Born's rule is the correct criterion to estimate the "which way". The problem is purely mathematical, and the fact that the duality relation is a kind of mathematical triviality [so called inequality of triangle] if you interprete it in wrong way such that you make claim on the uncertainty of x, then you will violate the QM formalism, or at least you will make wrong experimental prediction.

p.s. Actually it is me who can claim that the inequality does not imply well-defined wavelength, so in case that I make wrong prediction of dark minima, it is me who can go out "dry from the water". So please reply something logical and do not try to post just something to keep the discussion alife, I will appreciate if you try to understand the power of my argument which is far from easy to solve if you believe in Englert's duality interpretation.

I don't understand why you are not interested at all at this important remark, or at that point when I agreed with your diffraction idea, you already think that everything is settled?

p.s. 2 When you interprete "photon at image A comes only from slit A" you make durect claim on $\Delta x$. This is INEVITABLE otherwise "which way" is converted into parody of its original classical sense. The point is interesting when you consider the passage through both slits simultaneously [as I believe follows from Born's rule] therefore you may ask me why I think in very well defined wavelength with small uncertainty. My argument is that the source is laser, so the coherent emmission should be at a single optimal frequency, therefore the large position uncertainty reveals this exact wavelength of the photons emitted by the laser to be measured. Hence I predict image of A with dark Airy minima, as if the photon comes from both pinholes. So I believe that the large $\Delta x$ allows for the small $\Delta \lambda$ to be revealed. Danko Georgiev MD 08:55, 5 July 2006 (UTC)

Dear Danko

I am not home now, I won't for quite a time and my access to the web is sketchy at best. So I cannot get into all details. So just one thing: photon through A cones through slit A is indeed a small $\Delta x$ claim, this is not the point I am discussing. What I do discuss is, two small pinholes even if they are far apart, are essentially as strong a small $\Delta x$ claim. It is not at all the same thing to say that the photon had to go through either of two small pinholes, even far apart, and to say that its $\Delta x$ is large and compatible with a small $\Delta p$. The $\Delta p$ is essentially determined by the size of the pinholes, not their distance. This can be ascertained by computing the exact shape of the Airy mimima by Born's rule and what you'll find is the same shape whether one or two pinholes are open. You do not get a smaller $\Delta p$. Definitely not. This is provable by calculating the arrival of a photon near a minimum of the Airy profile, and you'll find the same shape with one or two pinholes. The apparent large $\Delta x$ due to the pinhole separation is totally irrelevant to the Airy shape.

Alfred (forgot to log in again --129.78.208.4 00:33, 7 July 2006 (UTC)

Please define $\Delta x$

Dear Alfred, as I see everything depend on how you calculate $\Delta x$, but I think that this is defined only by the minimal and maximal values of the interval, and it is completely irrelevant whether the values of x in this interval are continuous or discrete. Please give me definition of $\Delta x$ and the way you compute it. Danko Georgiev MD 07:35, 7 July 2006 (UTC)

Dear Danko

Heisenberg relation is an inequality

It says that it is impossible to have a small $\Delta x$ at the same time as a small $\Delta p$, essentially because (up to hbar) the x and p are Fourier transforms.

But the Fourier transform of the set of two very small intervals even widely separated needs as much information in the Fourier variable as a single interval. So it is not that I have a different definition of $\Delta x$ but that I claim that we are in a situation where Heisenberg relation is way way underoptimal. In no way does Heisenberg relastion give an upper bound, it only gives a lower bound. Any situation that has at the same time a wide separation and small scale details will cause the same problem: the $\Delta p$ will be determined by the smallest details. Conversely the fact that the $\Delta x$ is large will cause fine details in the p distribution. In the present case (two small pinholes widely separared) the p distribution will be wide (because of the smalll pinholes) and consist of a beat (rapidly oscillating mins and max) with a typical narrow separation determined by the large separation of the pinholes. So small details in p come from large $\Delta x$, but overall $\Delta p$ determined by small details in x (size of the pinholes) Only when there are no details smaller tham $\Delta x$, bell shaped shape, can one expect Heisenberg inequality to be optimally satisfied i.e., almost equality.

Otherwise the $\Delta x$$\Delta p$ product cqn be as high as the situation demands, there is no upper bound

To be explicit:

the Fourier transform of the interval (-1,+1) is sin(2pi*x)/x (up to normalisations)

The central lobe has width roughly unity

Consider two intervals (-n-1,-n+1) together with (n-1,n+1)

You get

FT=cos(2pi*n*p) (sin(2pi*p)/p

If n is very large, the overall width of the central lobe is unchanged!

What happens is, instead of a unique lobe, you have very many very narrow peaks, but they are all below an envelope which is exactly the same as with a single interval: the size of the envelope (about unity) is fixed by the size of the intervals, the width of the small details (all the different peaks under the envelope) is fixed by the distance of the intervals. So in this case $\Delta x$$\Delta p$ is of the order of 2n and highly un-optimal if n is very large.

And do not argue that with my reasoning I miss the case of double interval. I repeat: if n is very large the shape of the envelope is the same whether there are many small peaks under it or if it is a single lump (one interval only). If n is exactly one, then the two intervals merge, to an interval of double size. But look at the fourier transform: you get just (elementary trigonometry)

cos(2pi*p) (sin(2pi*p)/p =(sin(4pi*p)/2p

and the width is indeed halved!

The central oscillation combines with the envelope to divide the latter's width by two. Here, in an optimal situation doubling $\Delta x$ did result in halving $\Delta p$ But this effect happens only for n=1. For very large n, there are many many oscillations under the envelope and this has negligible effect on its width. You cannot argue that the $\Delta p$ is the size of one peak under the envelope. Only for n=1 does the shape of the envelope and the size of the central peak smoothly combine (by trigonometrical identity) to a twice-narrower curve. In general, for very large n, it is not so.

Again I do not change the definition of $\Delta x$ (it is the full separation, not the size of the holes), nor are you allowed to change the definition of $\Delta p$. What happens is, it is a non-optimal situation and Heisenberg inequality is very very far from its optimal value. But this is allowed. Heisenberg never said that $\Delta x$$\Delta p$ should have some value, only it cannot be smaller than some value. If the situation is not optimal it can be much much larger!

Alfred

129.78.64.106 10:25, 8 July 2006 (UTC)

Dear Alfred, I don't understand why should I take the Fourier transform of x and p at first place? I calculate $\Delta x$ as the difference between the maximal and minimal value of the position coordinate of the superposed state $\Delta x=x_{max}-x_{min}$. For a single pinhole $\Delta x=2\times 10^{-7}$ m, while in the double pinhole case we have $\Delta x\simeq \times 10^{-3}$. Sorry for my simple question but if you don't change the definition of $\Delta x=x_{max}-x_{min}$ I don't understand why something is fundamentally changed. Please explain more concretely what you mean? Best, Danko Georgiev MD 07:18, 9 July 2006 (UTC)

p.s. By the way please provide the formulas and exact computation of $\Delta x$ and $\Delta p$ in suggested by me example. Yes, I used the equality in my calculations, but I don't see something to forbid that the equality is satisfied? Please prove me wrong by concrete calculation. Danko Georgiev MD 07:27, 9 July 2006 (UTC)

Dear Danko

I just gave you a concrete calculation! $\Delta x$ is indeed as large as you say, but that does not necessary mean that $\Delta p$ is small. Heisenberg inequality does not say both cannot be large at the same time.

The whole idea of the Heisenberg inequality is that the distribution of p is (up to multiplication by hbar) the Fourier transform of the function of x. This is a basic fact of QM. So because the narrower a function of x is, the wider its Fourier transformmust be, Heisenberg inequality follows. But if a function with a wide separation (large $\Delta x$ ) but with small details, just like I chose, a combination of two narrow (width 2) slits at a very large distance 2n has a Fourier transform of overall width related to the details of the x distribution, the width of the slits (namelyly, the sin(2pi*p)/p Fourier transform of a slit) and the wide 2n separation is reflected in the multiplicative factor cos(2pi*n*p), very rapidly varying, defining details in p space of order 1/n, very detailed, but since there are many many such small narow oscillations, this does not reduce the $\Delta p$.

SO I just wrote for you explicitely this situation where you have a large $\Delta x$ which has consequences in very fine details in the p distribution (oscilations on a 1/n range) but without decreasing the overall $\Delta p$ which in turn is related to the fine details of the x distribution. I computed for you the product $\Delta x$ $\Delta p$ in this case and found that it exceeds the optimal value by a factor of n. Still you can see the calculations are correct because if n is exactly one, and the two intervals (-n-1,-n+1), (n-1,n+1) become contiguous, and one recovers the double length interval (-2,2), then the cos has just the right value, multiplying the sin, to give the sin of the double argument and in this case indeed the $\Delta p$ is halved when you double the $\Delta x$. Because a single slit is nearly an optimal situation and of course the result is the same when you look at a single slit of length 4 or two adjacent slits of length 2. But when n is very large, i.e. the slits are separated by a distance very large compared to their width, a lot of very narrow oscillations muntiplying the sin(2pi*p)/p function will not reduce the value of $\Delta p$ and Heisenberg inequality is satisfied very very far from its optimum. So the width of cos(2pi*p) (sin(2pi*p)/p =(sin(4pi*p)/2p

in indeed half of that of (sin(2pi*p)/p

But for very large n the width of cos(2pi*n*p) (sin(2pi*p)/p

is essentially the same as that of (sin(2pi*p)/p, there are fine details in p, very narrow oscillations but that does not make the full distribution narrower!

And yes, the Fourier transform is exactly what you should look at, since it is the basis of Heisenberg inequalty. One cannot have a narrow function with a narrow Fourier transform, there is an intrinsic limitation which, experessed in x and p, is just Heisenberg inequality. But a wide (with fine details) function can easily have a wide (width determined by the fine details in x) but also with fine details, (on a small scale related to the overall width of the x function) Fourier tranform and Heisenberg inequality is far far from optimum.

I gave you explicitely the calculation, $\Delta x$ is just what you say it is, $\Delta p$ is a measure of the width of

cos(2pi*n*p) (sin(2pi*p)/p

but I think youd qgree thqt - if n=1, one recovers exactly (sin(4pi*p)/2p so the widht is half taht of (sin(2pi*p)/p

but whne n is very large, a lot of very narrow oscillations in an envelope (sin(2pi*p)/p have essentially the same width as the envelope, whatever definition you care to use for the width (last time the half maximum is reached, for instance - clearly the first time the half maximum is reached, which is indeed in 1/n, is not a valid definition of the width if the value recovers almost maximum value for many, many occurences when one moves out). What decreases with n is the width on one elementary oscilllation under the envelope, but not the overall width of the distribution.

Is it clear now? Of course if you do not agree that the Fourier distribution is the whole point of Heisenberg inequality, you'll inssit that you can satisfy the inequality close to its optimal value for two widely separated narrow slits, but if you follow my calculations you can see it is not so.

Alfred--203.5.70.1 10:47, 9 July 2006 (UTC)

Dear Alfred, usually where there is some technical problem I need some time to study the theory. I am not specialist in QM and this means that I will need some time. One thing however is certain and this is the mathematical reasons that back up my thesis:

Duality relation is NOT dependent on Heisenberg's relations, but you interprete it in such a way that you attribute directly value of $\Delta x$ - this is the "which way claim".

Therefore at some experimental case this INCONSISTENCY WILL BE MANIFESTED!

I don't understand why you do not comment on my main thesis that is extremely important, instead you deviate the discussion in things that are irrelevant to the main problem "is the duality relation true way to estimate which way info?". If you actually were interested in some constructive discussion you will see that it MUST BE possible to find experimental inconsistency from wrong predictions of this wrong interpretation, and I am amazed why you did not do that? What about having 50 slits in located in assymetrical fashion?? Will this make the function enough complex so that $\Delta$ p be decreased enough to be experimentally detected? Having these 50 slits will change nothing in the duality relation interpretation at the image plane - each image has amplitude contributions only from the corresponding slit, so finally there will be difference. Of course I am not sure right now exactly how the setup should be modified in order this inconsistency to be vizualized, but this MUST be possible, due to mathematical reasons. Danko Georgiev MD 03:38, 10 July 2006 (UTC)

Dear Danko

My whole point is precisely that there can be no experimental proof of what you call a wrong interpretation!

All interpretations perforce agree with all experimental results of QM. Now some mistaken interpretations can make some paradoxes seem to appear, namely Afshar's reading of his own experiment, while Unruh's reading makes the paradox disappear. But do not try to find an experimental proof that your vision is correct over that of Unruh. Such a proof cannot exist. Your point of view has some validity, I can see why you would not agree with the way Unruh and I are ready to give meanings to things beyond Born's rule. But don't try to put this point of view in contradiction wiht experimental data. This is impossible by definition.

Alfred--128.250.69.246 23:18, 10 July 2006 (UTC)

Spectral decomposition of photons by a prism

Dear Alfred, there is possibility for such a contradiction and this is simply formulated by me. You cannot interprete facts with attributing them meaning of NEW MATHEMATICS. As I say if the duality relation is independent mathematically from Heisenberg's relation, you cannot derive from it claim on uncertainty of $\Delta x$. Simply there will be some such wrong attribution of "small x" where you will necessarily have "large p", while contrary to that I suspect that in such case I can be able to predict the "small p". The fact that you don't understand this simply formulated mathematics is your own problem. It is pitty but I am engaged in many other projects so I usually do not decide by myself where I will have time to do the precise calculations or study the necessary theory. One thing is better to take as advice from me - there is HUGE difference between different interpretation and different mathematical modeling. Please do not say that "interpreting of duality relation" is which way "interpretation only". This is plain wrong - In case where I predict "enourmous x" you predict "well defined x" and do not tell me that this should be always hidden for experimental testing. One of the best things in the Born's rule is that I am not the one who has to prove something, nor I am confused by all your derogatory remarks. You are the one who must from now on prove that your wrong mathematics will eventually remain hidden for experimental testing. So please prove it, and let us start with well defined coherent laser source of photons with well defined wavelength $\lambda$ and energy. And please this simple but very bad fact for you

"which way" attributes small $\Delta x$ to photons but this implies not only large $\Delta p$ but also large $\Delta E$!

the laser will emit photons in certain energies also as defined by the orbitals of electrons. Therefore if you know E then you know its wavelength precisely $E={\frac {hc}{\lambda }}$.

Now I predict that if you "wrongly interprete" the duality relation as "which way" you will wrongly predict that photons at the image A since they come from slit A will have large uncertainty in their energies that is $\Delta E$ is high, and if you capture these photons in optic cable you should be able to decompose them in a rainbow when passing them through prism! Alas, I do not reach to such a wrong prediction, and I predict that $\Delta E$ is small and remains well defined by the energy levels between the atom orbitals in the atoms of the laser. So I do not predict such a spectral decomposition of photons captured at image A.

So take a careful look on these two dependences on the photons wavelength:

$p={\frac {h}{\lambda }}$

$E={\frac {hc}{\lambda }}$

Don't think that "you will get dry from the water". Duality relation affects E, and you should predict spectral decomposition of photons caputured at the image A. I predict that only if you capture photons direcly behind the slit this spectral decomposition will be possible, but capturing them at the image A will not produce a spectral decomposition when passed through a prism, because the photons at image A has passed through slit B also. Kind regards, Danko Georgiev MD 08:10, 11 July 2006 (UTC)

Dear Danko Since everything is time independent , $\Delta E$ is not only small, it is strictly zero What we are discussing here is not a variation of the modulus of p (which being E/c, is strictly conserved), but the orientation, i.e. the $\Delta p_{x}$, $\Delta p_{y}$ $\Delta p_{z}$ which in all cases conspire to a stricly constant modulus of p and a striclty conserved energy. There is no spectral decomposition, but the effect of a change in the directions (variation of each component of the p) can be measured. Still, you won't ever see any effect of Unruh's predictions violated by Born's rule results because Unruh's interpretation is just that, an interpretation and will always agree with all experimental results.

And yes, your 'enormous' $\Delta x$ being the result of two small pinholes widely separated will create very fine details in the p (transverse) distribution, but not reduce the overall wide shape. And all this with strictly zero $\Delta E$.

The only thing that could change E would be if the wole setting was vibrating (and pretty rapidly, too, if you want a measurable effect....)

With your argument, with a single very small pinhole there would be spectral decomposition???? This is provably wrong! Only the direction of p changes, even with a single pinhole! Try as you can, you'll never find a situation where Unruh's reasoning will lead to a measurable experimemtal prdiction in contradiction with actual experimental results

Alfred--203.5.70.1 11:43, 11 July 2006 (UTC)

Dear Danko

From now on and for several weeks I will have only sketchy, if any at all, access to the web. So I suggest we continue this discussion in August. Warmly Alfred

RAMANI-UNRUH interpretation vs. Born's rule

Dear Alfred I agreed with your comments above that my examples were not good to show testable effect. Yet this doesnot mean that I have give up the idea that duality relation should not be interpreted in such a way that makes direct claim on uncertainty of photon's parameters. Now I will use the energy/time uncertainty to suggest a new setup that in my view can distinguish between your interpretation as opposed to Born's rule. The magnification of lens is given by:

$M=-{\frac {s_{2}}{s_{1}}}={\frac {f}{f-s_{1}}}$

where $s_{1}$ is the distance from the lens to the object, f is the focus distance, and $s_{2}$ is the distance from the lens to the image.

Distance between points in the plane is given by the analytic expression:

$d={\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}}$

Now let D be the diameter of the lens, $s_{1}$ be the distance between the lens and the double slit, $s_{2}$ be the distance between the lens and the image plane, and the interslit distance be $2\alpha$.

The incertainty of the time travel of photon $\Delta t$ from the source to the detector is

$\Delta t={\frac {\Delta S}{c}}$

where $\Delta S$ is the uncertainty in the legth of the photon path.

Now consider the Ramani-Unruh interpretation - it says that the photon at $D_{1}$ comes from slit 1. This immediately makes claim on the uncertainty of the $\Delta S$ being the length of the longest path through refracted trajectory passing at the end of the lens diameter minus the shortest path through the lens center.

$\Delta S_{RAMANI}={\sqrt {(\alpha +{\frac {D}{2}})^{2}+s_{1}^{2}}}+{\sqrt {({\frac {D}{2}}+{\frac {\alpha s_{2}}{s_{1}}})^{2}+s_{2}^{2}}}-{\sqrt {({\frac {\alpha (s_{1}+s_{2})}{s_{1}}})^{2}+(s_{1}+s_{2})^{2}}}$

Then we have the interpretation by Georgiev (and maybe others) that the photon at $D_{1}$ comes from both slits as inferred by the application of the Born's rule. In this statement however the shortest photon trajectory comes from the opposite pinhole as indicated on the figure, and the path uncertainty is

$\Delta S_{GEORGIEV}={\sqrt {(\alpha +{\frac {D}{2}})^{2}+s_{1}^{2}}}+{\sqrt {({\frac {D}{2}}+{\frac {\alpha s_{2}}{s_{1}}})^{2}+s_{2}^{2}}}-{\sqrt {({\frac {\alpha (s_{1}-s_{2})}{s_{1}}})^{2}+(s_{1}+s_{2})^{2}}}$

Now can we distinguish the two interpretations?

Yes, under proper arrangement of the setup, and taking f=0.999... with $\alpha$ being slightly shorter that ${\frac {D}{2}}$ but closely approacing it, one gets:

$\Delta S_{GEORGIEV}=2\times \Delta S_{RAMANI}$

This so far is purely classical calculation being just geometry! Yet when we consider the Heisenberg's uncertainty and quantum mechanics we obtain that in the Georgiev case when we emit light from laser source, and put a detector catching photons by photoelectric effect adjusted exactly to the emitted photon energies by the laser, one will detect almost 50% of the photons at the image of the pinhole. Yet in Ramani interpretation the knowledge of the time travel is 2 times sharper, and this will cause twofold increase in the uncertainty of the photon energies. Part of the photons will have energy less than the threshold one for the photoelectric effect and thus reduction in the detected photons < 50% is to be expected.

Conclusion: as Georgiev has argued if the duality relation IS NOT consequence of Heisenberg's relations, INTERPRETATION SHOULD NOT GIVE IT MEANING THAT ALLOWS ONE TO MAKE PREDICTIONS ON THE UNCERTAINTY OF THE PHYSICAL PARAMETERS OF THE SETUP. Therefore the interpretations by Ramani-Unruh and georgiev should not be equivalent, and be subject to experimental testing.

Dear Danko Your calculation of the uncertainty on the arrival time is totally irrelevant. One does NOT know at what time the photon left the source with any accuracy at all. The source has to be weak so there is only one photon at a time in the apparatus. So the uncertainty on the Poisson probability of photon emission is huge in time and corresponds to an extemely small /delta E. The uncertainty on the flight time is totally neglibible in comparison with　the uｎcertainty on th　emission time. And if you try to reduce this uncertainty by hqving a strong source but opening the apparatus for a short time, that THAT would be th sourc of a large /delta E, not any uncertainty on flight time. This is duality for you AlfredAlfredr 14:11, 19 October 2006 (UTC)

Dear Alfred, please don't think in lab dimensions only. I am interested in the general principle, and you can think in the framework of bigger distances as realized within the solar system with space aircrafts, etc. Remember the FELIX experiment proposed by Penrose (see Towards quantum superpositions of a mirror, William Marshall, Christoph Simon, Roger Penrose, Dik Bouwmeester [4]). So I am interested IF in principle my experiment can work, not necessarily resembling Afshar's setup in the lab. It could well be big lens in the cosmic space, with laser emission from space aircraft, and detected by detector. All this might seem impossible practically, but I think not impossible theoretically, and this is all that matters. Let us first settle the issue is the experiment proposed here theoretically doing the job I think it does, or it is theoretically flawed. Addendum: part of the construction is that s_1 / s_2 ratio can (should) be very very small, thus basicly the lens position should be near the laser, and the image detection is distant. But all this is calculable, and in the proposed experiment the detector might be in flight already as a "target" and the emission by the laser [with associated double slit and lens] could be strong. Then the $\Delta S_{GEORGIEV}=2\times \Delta S_{RAMANI}$ is satisfied, and can be adjusted in the needed way. The "check" of the result is to have mechanism to "get the target back" and see how good was our shot. I expect you reply in not hostile way (you can investigate the functions written by me with appropriate software, I used Wolfram's Mathematica), and hope that only some conceptual problem will be objected, not replies of the sort that it is technically not possible, etc. Danko Georgiev MD 14:31, 19 October 2006 (UTC)

p.s. I don't need single-photon experiment, for bosons the single particle experiment is equivalent to experiment performed with a bunch of particles together. :-))) Danko Georgiev MD 14:44, 19 October 2006 (UTC)

Dear Danko The whole idea of what you suggest is completely flawed. The certainty or uncertainty on the lenght of the path of a photon from emission to receptor has absolutely nothing to do with the \delta E. Consider a very simple setting, just a source, a narrow diaphragm, near the source, and a narrow diaphragm, near the receptor. So the trajectory is very well defined and the uncertainty on the time of flight is as small as you want. (note again that the small diaphragm may modify the individual *components* of the wavevector, but will preserve the energy and thus the modulus of the wavevector) STILL if the source has a very small \delta E which means that it emits photons at very uncertain intervals, say atoms in a mesastable state with energy very precisely defined because the half-life of the metastable state is very long, then the absence of an uncertainty on the time of flight (or the presence of an extremely small uncertainty) is totally irrelevant: the \delta E at arrival is small because the half life on the source is large. Certainly it has nothing to do with the precise or unprecise knowledge of the time-of-flight. Also you keep using Heisenberg' INEQUALITY as if it were an equality. If things are not done is exactly the right way a very large \delta T is compatible with a very large \delta E, just as a large \delta p is compatible with a large \delta x. It is only when one is SMALL that the other must be at least large enough to satisfy Heisenberg's INEQUALITY. A large value does not necessarily mean that the conjugate value is small UNLESS one is careful about it, for instance choose a SINGLE metastable state of large half-life, with a large \delta T and corresponding small \delta E. Using a MIXTURE of several metastable states, each having a large \delta T, will still leave a large \delta T but if the states are chosen with widely different energies, the \delta E can be as huge as one wants!!!!! So any argument of the kind you can prove you are right by comparing the \delta E (or \delta p) which will be smaller in your interpretation than in the correct one that I share with Unruh will be experimentally inconclusive: the \delta E or \delta p will be the larger one, compatible with Heisenberg' INEQUALITY with the smaller \delta t (respectively \delta x) and presumably considerably larger because the optimal situation where the inequaliry is almost an equality is extremely hard to attain. None of your ideas will ever cause the \delta E or \delta p to become smalller, leading to a contradiction. Just like I explained in the case of two narrow, widely separated pinholes; where the \delta p is not related to the large separation but their small size (and thus is large). The only effect of the large separation is to cause small scale details in p-space, of scale indeed very small if the separation is large, but that do not affect the overall width. A similar situation will happen in all the schemes you suggest. You cannot force Heisenberg's INEQUALITY to be near the equality if it does not want to. It will end up as far as a near equality as it wants to be. Alfredr 06:57, 24 October 2006 (UTC)

Dear Danko Lest you argue that my previous argument was based on a large \delta T because of a very precise enrgy of some metastable state, I can show you an even more devastating argument in the case of a wide \delta E; Suppose I have a diaphragm that I keep completly closed and open only for a very SHORT time \delta t1. By Heisenberg's inequality the energy uncertainty is at least h/\delta t1. Now this short-time-opening diaphragm is at the entrance of your proposed experiment. Now the total uncertainty on arrival time of the photon is \delta t1 PLUS the uncertainty in the time of flight. I do not dispute that this lattter uncertainty has different values along your interpretation than mine. So since \delta t1 is supposed extremely small compared to either of the estimates in the time of flight (which only differ by a factor of 2) the final uncertainty in time is, in any case, considerably larger than \delta t1. But will this large uncertainty reduce \delta E? CERTAINLY NOT. The large value of \delat E has been caused from the start, by the vey small \delta t1, and no further uncertainty on arrival time will REDUCE it!!!! So in that case the Heisneberg inequality will be extremely far from the opimum quasi equality, with a very large \delta E (of ordre h/\delta t1) and a considerably larger \delta T on arrival time. The fact that the latter varies by a factor 2 between the interpretations just changes how badly the inequality ia away from the near equality, but in NO WAY does it reduce the large initial \delta E. Alfredr 07:38, 24 October 2006 (UTC)

Dear Alfred, did I have wrong idea of time uncertainty or you fail to see my argument? I can control the $\Delta t_{flight}$ >> compared to $\Delta t_{emission}$ by controling the photon's path length $\Delta S$. That is why I suggested experiment in the cosmic space IF NEEDED, not just because I like sci fiction, but because I was clearly aimed at making $\Delta t_{flight}$ >> $\Delta t_{emission}$ thus invalidating all reasoning of yours about uncertainty of time emission. By the way, IF you consider Wheeler delayed choice but NOT Cramer's version, instead this version seen here [5], you will see that Heisenberg's uncertainty controls retrocausally the emission time to shift it forth and back. YET IN CASE OF VERY SHORT OPENING OF THE DIAPHRAGM, you will see that shifting of time emission will be impossible because the diaphragm is classically closed. So in this case ONLY a failure in the detector registering (by the suggested photoeffect) is going to be EXPECTED! Does this help to clarify my idea? Danko Georgiev MD 11:56, 24 October 2006 (UTC)

Dear Danko No, this does not clarify it at all. If $\Delta t_{flight}$ >> $\Delta t_{emission}$ then $\Delta E$ will be entirely determined by $\Delta t_{emission}$ and thus be rather large. The large uncertainty in $\Delta t_{flight}$ will in no way reduce $\Delta E$ This will lead to a Heisenberg inequality very far from the equality. What if the source is a very unprecise frequency one (thermal source). How could all a large uncertainty in $\Delta t_{flight}$ turn this into a near monochromatic one? Your insistance on the Heisenberg relation being an equality instead of an unequality leads you to absurd reasonings. Alfredr 12:41, 24 October 2006 (UTC)

Dear Alfred, I have not argued that from large $\Delta t_{flight}$ follows small $\Delta E$, which leads to the absurd conclusion done by you for converting thermal emission into monochromatic one. I have argued exactly the opposite : decrease in $\Delta t_{flight}$ converts the emission into polychromatic one. The inequality can be interpreted only in one direction. Danko Georgiev MD 07:29, 25 October 2006 (UTC)

Dear Danko But if $\Delta t_{flight}$ >> $\Delta t_{emission}$ which is what you say is the situation you want, you have already a $\Delta E$ of the order of $h/\Delta t_{emission}$ which is much much larger thant $h/\Delta t_{flight}$! So what do you expect to measure? Alfred

Dear Alfred, thanks for your comment. I have just noted that the pinhole 2, does not only provide the shortest path to D1, but also the longest path. Thus the $\Delta t_{flight}$ will be even bigger that 2 times the $\Delta t_{flight}$ in your interpretation. Well, I have understood your question, so I decided to modify a little the setup. I will collect photons at the detector D1 for time interval. Thus I will have a shorter time interval of flight for photons in your interpretation, and you will expect that that when you perform the single slit experiment you will collect all emitted photons for open time of detector D1 being say $\Delta t_{D}$. When you open both pinholes you expect that for open time of detector D1 being also $\Delta t_{D}$ you will collect the same number of photons. Yet, if I am correct and the photons at D1 come from both pinholes at once, then the open time for detector D1 in the case of double slit vs. single slit, should be open for 2 times more the time $\Delta t_{D}$ (or even more but I have to recalculate now the largest trajectory through pinhole 2). I am not sure now now big will be the loss of photons that will not be captured due to too early, or too late arrival according to your interpretation. I would like to hear your comment. Danko Georgiev MD 08:38, 26 October 2006 (UTC)

Dear Alfred, this note is just to express my gratitude for your comments. Basicly I have to conclude that your approach towards the explanation of Afshar's data is correct, so I will support any of your edits on that topic in Wikipedia. Basicly a suggestion is that you start editing on Unruh's experiment and describe briefly the mirror setups of Unruh. Then you can add your Huygens based explanation with diffraction into the opposite image with in-phase, and diffraction in the correct image out-of-phase. Danko Georgiev MD 07:53, 28 October 2006 (UTC)

Dear Danko

Thanks for your support. But somehow I understand that Wikipedia rules says that the discussion on the Afshar's experiment article should discuss only the structure of the article itself, not a general discussion on the validity of the experiment. Though this does not make much sense to me, because what is the point of discussing the structure of an article if one does not discuss the fundamentals on which the article is based, my comments have been censured once already. So anyone who want to know my opinion on the correct interpretation of Afshar's experliment must read my explantions here, on my personal page, not there. I was a bit upset by this censure, but what can I do? Warmly Alfredr 18:23, 29 October 2006 (UTC)

Something could be done :-)

Dear Alfred, you asked "what can I do?" above. There is a possibility to edit/create the article Unruh's experiment where to be decribed the set of experiments proposed by Unruh. Then, as a second part one can say that they are proposed in connection with Afshar's setup, and then will follow your explanation with the Huygen's principle. However please explain me in your analogy what happens if you put a wire in the arm with destructive interference in Unruh's setup. I think that if your approach works in Afshar's setup, will be applicable in Unruh's also. Once the Unruh's experiment article is created and equipped with suitable set of formulas, etc., we might hope that it will override the Afshar's article, and further Afshar's entry will be repaired accordingly. Danko Georgiev MD 05:46, 30 October 2006 (UTC)

Dear Danko Yes, that is a good idea! Since it is on a new topic, Unruh's experiement, I can write what I want and make the connection with Afshar. I'l do it as soon as I can. I am just back from a trip abroad, I had some access to the net then, but not much. Now I am back so I have more time. I have to think about your question on a wire in Unruh's setting, I am not sure just what you mean. More soon.

Alfredr 19:26, 2 November 2006 (UTC)

Wikipedia procedures

Dear Alfredr, I will discuss your views via e-mail, but allow me to inform you as a new contributor to Wikipedia that there are procedures that must be followed. After a contentious period of disputes etc. which had turned the Wiki article and talk pages into a blog, the decision was made to: Please limit discussions to topics directly concerning the content and structure of the article Afshar experiment. This page is not the place to have general discussions on quantum mechanics or its interpretation, nor to debate the correctness of Afshar's findings and conclusions. (linas 15:49, 20 January 2006 (UTC))

You can join the debate by submitting a paper to quant-ph (or other arxiv groups) and your name may be included in the list of critics in the article. Of course, I would suggest that you wait for my response to your e-mail prior to doing so, as there are major errors in your argument. Meanwhile you can do whatever you like in your user page, as the rules for user pages are much more relaxed. Thank you for your patience. Prof Afshar 00:20, 11 June 2006 (UTC)

I agree to wait. However there is absolutely no error in my argument. Mathematically, this is exactly what QM predicts. And as I pointed out on your page, an amplitude that cancels another one is still "there" in the sense that the cancelling is a measurable, if negative, effect. Arrival of aphoton on one detector does not mean that it went through the pinpoint you think is did. It deos so with a 94% probability, and the other 6% is positive interference of both pinholes at the same time. Just like in a simple minded Young slit interference pattern, the rare but possible event of arrival of a photon near, but not exactly at, the center of a dark fringe is due to its coming from both slits at the same time, but with almost but not quite opposite amplitudes. Alfredr 05:05, 11 June 2006 (UTC)