User:Unitfreak

http://commons.wikimedia.org/wiki/User:Unitfreak

The following table will be used in my new Bully Row Timestamp project.

Bully Row Timestamp			Era Description
5C2A	6600	0000	Eoarchean
			The Eoarchean is the first era of the Archean Eon. The beginning of the Eoarchean is characterized by heavy asteroid bombardment within the Inner Solar System: the Late Heavy Bombardment. At that time, the atmosphere was without oxygen and the pressure values ranged from 10 to 100 bar (around 10 to 100 times the atmospheric pressure today). The beginnings of life on Earth have been dated to this era and evidence of archaea and cyanobacteria date to 3500 Mya, comparatively shortly after the Eoarchean. The largest Eoarchean rock formation is the Isua Greenstone Belt on the south-west coast of Greenland, which dates from 3.8 billion years. The Acasta Gneiss within the Canadian Shield have been dated to be 4,031 Ma and are therefore the oldest preserved rock formations. In 2008, another rock formation was discovered in the Nuvvuagittuq Greenstone Belt in northern Québec, Canada which has been dated to be 4,280 million years ago.
6036	FA00	0000	Paleoarchean
			The Paleoarchean name derives from Greek "Palaios" ancient. The earliest confirmed evidence of life comes from this era, and Vaalbara, one of Earth's earliest supercontinents, may have formed during this era. There are only two locations in the world containing rock formations that are intact enough to preserve evidence of early life: the Kaapvaal Craton in Southern Africa and the Pilbara Craton in Western Australia. The Dresser Formation is located in the Pilbara Craton, and includes a great variety of structures caused by ancient life including stromatolites and MISS once formed by microbial mats. Such microbial mats belong to the oldest ascertained life form and may include fossilized bacteria. The Barberton Greenstone Belt, located in the Kaapvaal Craton, also contains evidence of life. It was created around 3.26 Ga when a large asteroid, about 37 to 58 kilometres (23–36 mi) wide, collided with the Earth.
63F8	FF00	0000	Mesoarchean
			Microbial life with diverse metabolisms expanded during the Mesoarchean era and produced gases that influenced early Earth's atmospheric composition. Cyanobacteria produced oxygen gas, but oxygen did not begin to accumulate in the atmosphere until later in the Archean. However, small oases of relatively oxygenated water did exist in some nearshore shallow marine environments by this era. Analysis of oxygen isotopes in Mesoarchean cherts has led researchers to draw an estimate of an oceanic temperature around 55-85°C, while other studies of weathering rates postulate average temperatures below 50°C. The Mesoarchean era is thought to be the birthplace of modern-style plate subduction.
67BB	0400	0000	Neoarchean
			The Neoarchean (/ˌniːoʊ.ɑːrˈkiːən/ NEE-oh-ar-KEE-ən; also spelled Neoarchaean) is marked by major developments in complex life and continental formation. During this era, the supercontinent Kenorland is proposed to have formed about 2.7 billion years ago. Kenorland is of particular interest due to it containing deposits of volcanic-hosted massive sulphide, gold, and uranium found in the Canadian Shield. The growth of juvenile continental crust as well as the onset of plate tectonics in the Archean allowed for the colonization of a larger variety of niches by microorganisms through increasing the number of rock types present and thereby increasing the surface's chemical diversity. The environmental changes that occurred in the Neoarchean such as its developing atmospheric and soil compositions drastically differentiated the era from others in its encouragement of microbial metabolisms to evolve and diversify.
6A8C	8800	0000

Another table for my Bully Row Timestamp project.

Bully Row Timestamp			Era Description
5720	9200	0000	Hadean
			The Earth is formed out of debris around the solar protoplanetary disk. There is no life. Temperatures are extremely hot, with frequent volcanic activity and hellish-looking environments (hence the eon's name, which comes from Hades). The atmosphere is nebular. Possible early oceans or bodies of liquid water. The Moon is formed around this time probably due to a protoplanet's collision into Earth.
5C2A	6600	0000	Archean
			Prokaryote life, the first form of life, emerges at the very beginning of this eon, in a process known as abiogenesis. The continents of Ur, Vaalbara and Kenorland may have existed around this time. The atmosphere is composed of volcanic and greenhouse gases.
6A8C	8800	0000	Proterozoic
			The name of this eon means "early life". Eukaryotes, a more complex form of life, emerge, including some forms of multicellular organisms. Bacteria begin producing oxygen, shaping the third and current of Earth's atmospheres. Plants, later animals and possibly earlier forms of fungi form around this time. The early and late phases of this eon may have undergone "Snowball Earth" periods, in which all of the planet suffered below-zero temperatures. The early continents of Columbia, Rodinia and Pannotia, in that order, may have existed in this eon.
7CF9	5000	0000	Phanerozoic
			Complex life, including vertebrates, begin to dominate the Earth's ocean in a process known as the Cambrian explosion. Pangaea forms and later dissolves into Laurasia and Gondwana, which in turn dissolve into the current continents. Gradually, life expands to land and familiar forms of plants, animals and fungi begin appearing, including annelids, insects and reptiles, hence the eon's name, which means "visible life". Several mass extinctions occur, among which birds, the descendants of non-avian dinosaurs, and more recently mammals emerge. Modern animals—including humans—evolve at the most recent phases of this eon.
8209	2900	0000

Bully Row Time System

Here is a table from my latest project. It doesn't render well in cell phones and needs work.

Announced leap seconds to date

Year	30 Jun	31 Dec	Bully Row Timestamp	International Atomic Time (TAI)	Coordinated Universal Time (UTC)
1972	+1	+1	8209 28E5 DFFB 8209 28E5 DFFC 8209 28E5 F44F 8209 28E5 F450	1972-06-30 23:34:45 TAI 1972-07-01 00:25:40 TAI 1972-12-31 23:45:05 TAI 1973-01-01 00:36:00 TAI	1972-06-30 23:34:35 UTC 1972-07-01 00:25:29 UTC 1972-12-31 23:44:54 UTC 1973-01-01 00:35:48 UTC
1973	0	+1	8209 28E6 1CA2 8209 28E6 1CA3	1973-12-31 23:57:50 TAI 1974-01-01 00:48:45 TAI	1973-12-31 23:57:38 UTC 1974-01-01 00:48:32 UTC
1974	0	+1	8209 28E6 44F4 8209 28E6 44F5	1974-12-31 23:19:40 TAI 1975-01-01 00:10:35 TAI	1974-12-31 23:19:27 UTC 1975-01-01 00:10:21 UTC
1975	0	+1	8209 28E6 6D47 8209 28E6 6D48	1975-12-31 23:32:25 TAI 1976-01-01 00:23:20 TAI	1975-12-31 23:32:11 UTC 1976-01-01 00:23:05 UTC
1976	0	+1	8209 28E6 95B6 8209 28E6 95B7	1976-12-31 23:30:50 TAI 1977-01-01 00:21:45 TAI	1976-12-31 23:30:35 UTC 1977-01-01 00:21:29 UTC
1977	0	+1	8209 28E6 BE09 8209 28E6 BE0A	1977-12-31 23:43:35 TAI 1978-01-01 00:34:30 TAI	1977-12-31 23:43:19 UTC 1978-01-01 00:34:13 UTC
1978	0	+1	8209 28E6 E65C 8209 28E6 E65D	1978-12-31 23:56:20 TAI 1979-01-01 00:47:15 TAI	1978-12-31 23:56:03 UTC 1979-01-01 00:46:57 UTC
1979	0	+1	8209 28E7 0EAE 8209 28E7 0EB0	1979-12-31 23:18:10 TAI 1980-01-01 01:00:00 TAI	1979-12-31 23:17:52 UTC 1980-01-01 00:59:41 UTC
1981	+1	0	8209 28E7 4B1C 8209 28E7 4B1D	1981-06-30 23:19:00 TAI 1981-07-01 00:09:55 TAI	1981-06-30 23:18:41 UTC 1981-07-01 00:09:35 UTC
1982	+1	0	8209 28E7 736F 8209 28E7 7370	1982-06-30 23:31:45 TAI 1982-07-01 00:22:40 TAI	1982-06-30 23:31:25 UTC 1982-07-01 00:22:19 UTC
1983	+1	0	8209 28E7 9BC2 8209 28E7 9BC3	1983-06-30 23:44:30 TAI 1983-07-01 00:35:25 TAI	1983-06-30 23:44:09 UTC 1983-07-01 00:35:03 UTC
1985	+1	0	8209 28E7 EC84 8209 28E7 EC85	1985-06-30 23:55:40 TAI 1985-07-01 00:46:35 TAI	1985-06-30 23:55:18 UTC 1985-07-01 00:46:12 UTC
1987	0	+1	8209 28E8 517D 8209 28E8 517F	1987-12-31 23:40:35 TAI 1988-01-01 01:22:25 TAI	1987-12-31 23:40:12 UTC 1988-01-01 01:22:01 UTC
1989	0	+1	8209 28E8 A23F 8209 28E8 A240	1989-12-31 23:51:45 TAI 1990-01-01 00:42:40 TAI	1989-12-31 23:51:21 UTC 1990-01-01 00:42:15 UTC
1990	0	+1	8209 28E8 CA91 8209 28E8 CA92	1990-12-31 23:13:35 TAI 1991-01-01 00:04:30 TAI	1990-12-31 23:13:10 UTC 1991-01-01 00:04:04 UTC
1992	+1	0	8209 28E9 06FF 8209 28E9 0700	1992-06-30 23:14:25 TAI 1992-07-01 00:05:20 TAI	1992-06-30 23:13:59 UTC 1992-07-01 00:04:53 UTC
1993	+1	0	8209 28E9 2F52 8209 28E9 2F53	1993-06-30 23:27:10 TAI 1993-07-01 00:18:05 TAI	1993-06-30 23:26:43 UTC 1993-07-01 00:17:37 UTC
1994	+1	0	8209 28E9 57A5 8209 28E9 57A6	1994-06-30 23:39:55 TAI 1994-07-01 00:30:50 TAI	1994-06-30 23:39:27 UTC 1994-07-01 00:30:21 UTC
1995	0	+1	8209 28E9 944B 8209 28E9 944C	1995-12-31 23:12:05 TAI 1996-01-01 00:03:00 TAI	1995-12-31 23:11:36 UTC 1996-01-01 00:02:30 UTC
1997	+1	0	8209 28E9 D0B9 8209 28E9 D0BA	1997-06-30 23:12:55 TAI 1997-07-01 00:03:50 TAI	1997-06-30 23:12:25 UTC 1997-07-01 00:03:19 UTC
1998	0	+1	8209 28EA 0D60 8209 28EA 0D61	1998-12-31 23:36:00 TAI 1999-01-01 00:26:55 TAI	1998-12-31 23:35:29 UTC 1999-01-01 00:26:23 UTC
2005	0	+1	8209 28EB 27DC 8209 28EB 27DD	2005-12-31 23:45:40 TAI 2006-01-01 00:36:35 TAI	2005-12-31 23:45:08 UTC 2006-01-01 00:36:02 UTC
2008	0	+1	8209 28EB A0F0 8209 28EB A0F1	2008-12-31 23:18:40 TAI 2009-01-01 00:09:35 TAI	2008-12-31 23:18:07 UTC 2009-01-01 00:09:01 UTC
2012	+1	0	8209 28EC 2E04 8209 28EC 2E05	2012-06-30 23:45:00 TAI 2012-07-01 00:35:55 TAI	2012-06-30 23:44:26 UTC 2012-07-01 00:35:20 UTC
2015	+1	0	8209 28EC A6FC 8209 28EC A6FD	2015-06-30 23:32:20 TAI 2015-07-01 00:23:15 TAI	2015-06-30 23:31:45 UTC 2015-07-01 00:22:39 UTC
2016	0	+1	8209 28EC E3BF 8209 28EC E3C0	2016-12-31 23:41:05 TAI 2017-01-01 00:32:00 TAI	2016-12-31 23:40:29 UTC 2017-01-01 00:31:23 UTC

https://bullyrow.eeyabo.net/index.php/Main_Page

Txt Planck epoch Grand unification epoch
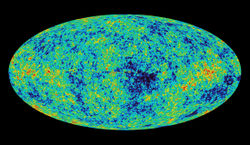
Txt Inflationary epoch	Gravitational waves are hypothesized to arise from cosmic inflation just after the Big Bang.
Txt Electroweak epoch
Txt electroweak symmetry breaking	The diagram depicts the crucial role of the Higgs boson in electroweak symmetry breaking, and shows how the properties of the various particles differ in the (high-energy) symmetric phase (top) and the (low-energy) broken-symmetry phase (bottom).
Txt Quark epoch Hadron epoch Lepton epoch Photon epoch
Txt recombination	An image, created using data from the WMAP satellite telescope, of the radiation emitted no more than a few hundred thousand years after the Big Bang.
Txt Dark Ages
Txt	The Hubble eXtreme Deep Field (HXDF) taken in 2012

Work in progress

The following images and accompanying text were initially designed for the Wikipedia mass article. However, this piece of writing has exceeded the scope of the article for which it was originally intended; therefore, I have decided to continue development offline in my own user page. These images and accompanying text are hereby made available to be placed in any appropriate Wikipedia article at the discretion of any Wikipedia editor. Unitfreak (talk) 01:08, 26 September 2009 (UTC)

Aristotelian gravity

Main article: Aristotelian physics

Aristotle believed that every object and every substance has a natural place in the universe, and every object would try to achieve that position.

One issue that had puzzled scientists and philosophers was the relationship between an object’s weight and its free fall velocity. The Greek philosopher, Aristotle, had reasoned that every substance and every object has a natural place in the universe, and every object will try to achieve that position. Aristotle had reasoned that there were four terrestrial elements: earth, water, air, and fire (or heat). In Aristotle’s worldview, when a rock is released in a lake it sinks to the bottom because earth belongs at the bottom, beneath water, air, and fire. Rain falls from the sky because water belongs beneath air. Air bubbles rise to the surface of water because air belongs above water. And heat from a fire rises heavenward because heat belongs above earth, water, and air. Aristotle supposed that the heavens were composed of a special "fifth element" called aether which was unlike the other elements.

According to Aristotle, forces result when an object is taken out of its natural position. When an earthly object (one composed of earth) is lifted, one feels a force of weight from the object trying to return to the earth, and upon being released the object returns to its natural position. In Aristotle’s worldview, objects are not compelled to move by an external force such as gravity, but rather, they move according to their own independent need to be in their natural positions. Aristotle reasoned that a freely moving object would move at a constant speed, and the speed would be proportional to its weight but inversely proportional to the density of the medium through which the object was passing. For example, Aristotle believed that a rock would fall quickly through air but slowly through water, because water is denser than air, and a heavy rock would fall quicker than a light one. Aristotle’s beliefs about heavenly motion were different from his concepts of terrestrial motion. Aristotle believed that terrestrial objects would eventually come to their natural position and then stop moving, whereas heavenly objects, such as stars, planets, and the moon, continue to move forever and never come to rest.

For falling objects: ${\frac {Distance}{Time}}\propto {\frac {Weight_{object}}{Density_{medium}}}$

The observational limitations which prevented Aristotle from accurately describing free fall motion were related to those which had prevented Aristotle and other early astronomers from accurately describing the solar system. Early astronomers were limited by their inability to measure large distances. They could accurately measure the periods of time required for a planet to complete a cycle, but they couldn’t measure the distances and paths followed to complete these orbits. Ironically, early scientist and philosophers were similarly restrained. They could accurately measure the distance traveled when an object was dropped a short length, but they couldn’t accurately measure the short time periods involved in free fall motion. So early astronomers had failed to accurately characterize the solar system and early scientist and philosophers had failed to accurately characterize earth's gravity. To overcome this limitation, Aristotle appears to have relied upon experiments with solid objects falling in water. However, water being dense and viscous had complicated the experimental results, thus confusing Aristotle’s comprehension of physical law.

History

Johannes Kepler was the first to give an accurate description of planetary motion, and doing so allowed the standard gravitational parameter of the Sun to be calculated. Kepler determined that the planets follow elliptical orbits under the Sun’s influence, and in 1609, he published three rules known as Kepler's laws of planetary motion. The standard gravitational parameter is an immediate consequence of Kepler's third law of planetary motion. To understand how Kepler arrived at the final form of his third law, it may be helpful to review the history of the underlying values used in this calculation, and the role that the first and second laws played in the development of the third law.

Orbital periods of the planets

Main article: Orbital period

$\mu ={\frac {4\pi ^{2}a^{3}}{\color {Red}T^{2}}}\$

The Divine Planets
English Name	Babylonian deity	Hindu Navagraha	Chinese Wu Xing	Sidereal orbital period
Mercury	Nabu	Budha	Black Tortoise	0.240 842 sidereal year
Venus	Ishtar	Shukra	White Tiger	0.615 187 sidereal year
Mars	Nergal	Mangala	Vermilion Bird	1.880 816 sidereal year
Jupiter	Marduk	Brihaspati	Azure Dragon	11.861 776 sidereal year
Saturn	Ninurta	Shani	Yellow Dragon	29.456 626 sidereal year

The periods of the planets were discovered at a very early stage of human prehistory, and played a significant role in many early religions and cultures. The word planet comes from the Greek verb πλανώμαι planōmai which means to wander around. The planets appear to move through the night sky and are thus distinguished from the stars, which appear to maintain a fixed position with respect to each other . This ability to move freely may have given the planets the appearance of self-determination. Many early cultures either directly worshipped the planets as deities or at least associated them with divinity. The modern English names for the planets were all derived from their names as Roman gods.

Zodiac in a 6th century synagogue at Beit Alpha, Israel.

As the Earth orbits the Sun, to an observer on Earth the Sun appears to move with respect to the background stars. A sidereal year is the time required for the Earth to complete one orbit around the Sun, or equivalently, the time required for the Sun to appear to complete one orbit and to return to the same relative position with respect to the stars. In the western zodiac, as depicted in the image to the right, the ecliptic is divided into twelve equal zones of celestial longitude. Ancient Europeans used the zodiac to track the Earth’s orbit, and were thus aware of the duration of the sidereal year. Recording the periods of other planets in sidereal years allows a direct comparison to the Earth’s orbital period.

Stone carving of Chinese zodiac

A stone carving of the Chinese zodiac is depicted in the image to the left. Chinese astronomers built this system (know as the Earthly Branches) from observations of the orbit of Jupiter (歳星 Suìxīng, the Year Star), which has an 11.86 yr period. Chinese astronomers divided the celestial circle into 12 sections to follow the orbit of Jupiter, and assigned an animal to each year. These Earthly Branches were cyclically paired with celestial stems, a base ten numeral system, to produce a 60 year Sexagenary cycle, and each year was assigned a Tai Sui deity to be worshipped, or at least respected during that year .

The sun stone also called the Aztec calendar on display at the National Museum of Anthropology in Mexico City.

A stone carving of the Aztec calendar is depicted in the image to the right. This astronomical system, used by some early Americans, has surprising similarities with the Asian system. The Asians obtained their 60 year Sexagenary cycle by cyclically pairing the base ten celestial stems with the base twelve Earthly Branches, the least common multiple of 10 and 12 being 60. The Americans obtained a 260 day tonalpohualli (Mayan Tzolkin) cycle by pairing their base twenty numeral system with a base thirteen trecena cycle, the least common multiple of 20 and 13 being 260 . The exact origin of the Mayan calendar is uncertain, but some scholars speculate that it may have been derived form the orbit of Venus, which held special significance within Mayan culture.

Early astronomers were successful in accurately measuring the duration of time required for each planet to complete its cycle, but they didn’t have the means to accurately measure the distances and path traveled by each planet during an orbit. Therefore, these early astronomers all failed to accurately describe planetary motion. Many envisioned the planets as following circular paths around the Earth. Although drawn from geographically distinct cultures, the above images all use a similar circular motif to represent the passage of time.

Orbital distances

Kepler's Platonic solid model of the Solar system from Mysterium Cosmographicum (1600)

$\mu ={\frac {4\pi ^{2}{\color {Red}a^{3}}}{T^{2}}}\$

Kepler’s first attempt to describe planetary orbits was similar to the Wu Xing philosophy employed previously by the Chinese. The Chinese had reasoned that there are five directions on a compass, five stages in a process (each with an associated element), and five planets visible to the naked eye. The Chinese therefore associated each planet with a particular direction and element. In a similar fashion, Greek philosophers approximately two thousands years prior to Kepler had proven that there were exactly five Platonic solids. The Greek philosophers had reasoned that each solid must be associated with a specific element, and Kepler further reasoned that perhaps the distances between the planetary orbits could be determined by placing Platonic solids inside of concentric spheres. This theory was somewhat successful, but didn’t agree with available astronomical data to the level of precision that Kepler desired.

After abandoning his Platonic solids model, Kepler began working with an array of traditional astronomical methods. In 1600 AD, Kepler sought employment with Tycho Brahe and consequently gained access to astronomical data of a higher precision than any previously available. Using Brahe’s precise observations of the planet Mars, Kepler proved that the traditional astronomical methods were inaccurate in their predictions, and he spent the next five years developing his own method for characterizing planetary motion.

Orbital paths

Main article: Kepler's_laws_of_planetary_motion

The factor of four pi squared in kepler’s third law of planetary motion is a consequence of the orbital paths that the planets follow as defined in Kepler’s first and second laws of planetary motion.

$\mu ={\frac {{\color {Red}4\pi ^{2}}a^{3}}{T^{2}}}\$

Kepler's first law

The orbit of every planet is an ellipse with the Sun at one of the two foci.

An ellipse characterized by its angular eccentricity.

In Kepler’s planetary model, he described planetary orbits as following elliptical paths with the sun at a focal point of the ellipse. The image to the right illustrates one method for characterizing ellipses. Four significant points, A, B, C, and F are identified on the illustration. Point C is located at the center of the ellipse. The line running from point C to point A is called a semi-major axis of the ellipse (meaning that it is half of the longest diameter). The line running from point C to point B is called a semi-minor axis (meaning that it is half of the shortest diameter). With a proper choice of coordinate system, an ellipse can be described as the set of all points (x,y) of the Cartesian plane that satisfy the implicit equation:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$

where a and b are respectively the length of the semi-major and semi-minor axes.

Point F in the illustration is a focal point of the ellipse. A point is a focal point if and only if it is located on a semi-major axis and its distance from point B is equal to the length of the semi-major axis. The angular eccentricity of an ellipse is the angle between the line running from point B to point C, and the line running from point B to point F. Given that points B, C, and F form a right triangle with hypotenuse of length a, it is an immediate trigonometric consequence that the length of the semi-minor axis is equal to the length of the semi-major axis multiplied by the cosine of the angular eccentricity. Hence, the above implicit equation can be rewritten in terms of angular eccentricity as follows:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{a^{2}\cos ^{2}\alpha }}=1$.

This equation can be expressed parametrically as the path of a point (x(E),y(E)), where

$x(E)=a\,\cos E$

$y(E)=a\,\sin E\cos \alpha$

The parameter E in this representation is called the eccentric anomaly.

Kepler's second law

A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.

The Kepler equation can be solved by adding the area of a triangle to the area of an elliptical arc

Kepler lived in an era when there was no clear distinction between astronomy and astrology, and when these fields of study, together with geometry, were viewed as intrinsically divine. Kepler was motivated by religious convictions and incorporated religious arguments and reasoning in his work. Kepler reasoned that the sun was representative of the monotheistic God of Christianity, that the sun sat in the center of the solar system and controlled the motions of all other objects in the solar system. Kepler further reasoned that since the sun was the source of motion, then an object’s motion should be inversely proportional to its distance from the sun . In other words, the closer an object gets to the sun the faster it moves. Kepler later refined this to state that an orbit sweeps out equal areas in equal times.

Kepler’s second law was especially difficult mathematically, since no one had previously developed equations to describe the area swept out by a line joining an ellipse to one of its focal points, and Kepler lived prior to the invention of calculus, so he would have to solve this problem using geometry. The image to the left illustrates one possible solution to Kepler’s problem. In this solution, the sun is located at focal point F while a planet orbits from point A to point P along an elliptical path. The total area swept out by the planet can be obtained as the sum of two distinct areas. The points P, C, and F define a triangle (marked in green on the illustration). The points P, C, and A, together with the elliptical path, define an elliptical arc (marked in brown on the illustration).

The Kepler equation can be solved by subtracting the area of a triangle from the area of an elliptical arc

The image to the right illustrates a second solution to Kepler’s problem. In this solution, the sun is located at focal point F while a planet orbits from point A to point P along an elliptical path. The difference between this solution and the previous solution is that in this solution the focal point F is located between the center point C and point A, whereas in the previous solution F was located opposite A. In this solution, the area swept out by the planet (marked in yellow on the illustration) is obtained by taking the difference of two distinct areas. The points P, C, and F define a triangle (marked in green on the illustration). The points P, C, and A, together with the elliptical path, define an elliptical arc.

The area of a triangle is always equal to half of its base multiplied by its height.

$A_{triangle}={\frac {1}{2}}\,base\times height$

The two green triangles, one in the illustration above and the other in the illustration to the right, are dissimilar. However, these triangles have the same base lengths and the same heights, so the magnitudes of their areas are identical. The base of each green triangle is the length from the center point C to the focal point F, which for an ellipse is equal to the length of the semi-major axis multiplied by the sine of the angular eccentricity. The height of each green triangle is equal to y(E) as given in the above parametric equations:

$base=a\,\sin \alpha$

$height=a\,\sin E\,\cos \alpha$

Hence, the area of each green triangle is:

$A_{triangle}={\frac {1}{2}}\,a^{2}\,\sin E\,\cos \alpha \,\sin \alpha$

The area swept out by an elliptical arc is equal to half of the angle multiplied by the lengths of the semi-minor and semi-major axes:

$A_{arc}={\frac {\theta }{2}}ab$

In terms of angular eccentricity:

$\theta =E$

$b=a\,\cos \alpha$

The area of the arc thus becomes:

$A_{arc}={\frac {1}{2}}\,a^{2}E\,\cos \alpha$

Two solutions to kepler’s equation can now be written out, one by adding the area of the green triangle to the area of the elliptical arc, and a second by subtracting the area of the green triangle from the area of the elliptical arc:

Solution 1: ${\frac {1}{2}}\,a^{2}E\,\cos \alpha +{\frac {1}{2}}\,a^{2}\,\sin E\,\cos \alpha \,\sin \alpha$

Solution 2: ${\frac {1}{2}}\,a^{2}E\,\cos \alpha -{\frac {1}{2}}\,a^{2}\,\sin E\,\cos \alpha \,\sin \alpha$

A quick review of trigonometric identities reveals that these two solutions are in fact the same solution (one representing positive angular eccentricities and the other representing negative angular eccentricities). These solutions to Kepler’s equation give the area swept out by a planet as it orbits around a central mass. Kepler’s second law states that the elapsed time will be proportional to this area, hence:

$t(E)\propto {\frac {1}{2}}\,a^{2}E\,\cos \alpha -{\frac {1}{2}}\,a^{2}\,\sin E\,\cos \alpha \,\sin \alpha ={\frac {1}{2}}\,a^{2}\,\cos \alpha \left(E-\sin E\,\sin \alpha \right)$

To get an equality it is necessary to divide both sides by some exact value, we will use T, the duration of one full orbit:

${\frac {t(E)}{T}}={\frac {t(E)}{t({\color {Red}2\pi })}}={\frac {{\frac {1}{2}}\,a^{2}\,\cos \alpha \left(E-\sin E\,\sin \alpha \right)}{{\frac {1}{2}}\,a^{2}\,\cos \alpha \left({\color {Red}2\pi }-\sin {\color {Red}2\pi }\,\sin \alpha \right)}}={\frac {E-\sin E\,\sin \alpha }{{\color {Red}2\pi }-\sin {\color {Red}2\pi }\,\sin \alpha }}={\frac {E-\sin E\,\sin \alpha }{\color {Red}2\pi }}$

Multiplying both sides by the duration of one full orbit, we obtain:

$t(E)={\frac {T}{\color {Red}2\pi }}\left(E-\sin E\,\sin \alpha \right)$

From Kepler’s first and second laws, Kepler now had a complete set of parametric equations for describing orbital paths:

$x(E)=a\,\cos E$

$y(E)=a\,\sin E\cos \alpha$

$t(E)={\frac {T}{\color {Red}2\pi }}\left(E-\sin E\,\sin \alpha \right)$

The only remaining task was to determine the relationship between the semi-major axis, a, and the orbital period T.

Kepler's third law

The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.

$\left({\frac {T}{\color {red}2\pi }}\right)^{2}\propto {a}^{3}\$

Or equivalently, the ratio of these values is constant for all planets in the solar system, a value known as the standard gravitational parameter.

$\mu ={\frac {{\color {red}4\pi ^{2}}a^{3}}{T^{2}}}\$

constants table

My original table was moved to the conventional electrical units article and a significantly altered version now resides in the natural units article. I really like this table, so I will make a copy here as backup in case someone deletes the other.

Quantity / Symbol	Planck	Stoney	Schrödinger	Atomic	Electronic	Conventional Electrical Units
speed of light in vacuum $c\,$	$1\,$	$1\,$	${\frac {1}{\alpha }}\$	${\frac {1}{\alpha }}\$	$1\,$	$299792458\$
Planck's constant $h\,$	$2\pi \,$	${\frac {2\pi }{\alpha }}\$	$2\pi \,$	$2\pi \,$	${\frac {2\pi }{\alpha }}\$	${\frac {4\times 10^{-18}}{(25812.807)(483597.9)^{2}}}\$
reduced Planck's constant $\hbar ={\frac {h}{2\pi }}$	$1\,$	${\frac {1}{\alpha }}\$	$1\,$	$1\,$	${\frac {1}{\alpha }}\$	${\frac {2\times 10^{-18}}{\pi (25812.807)(483597.9)^{2}}}\$
elementary charge $e\,$	${\sqrt {\alpha }}\,$	$1\,$	$1\,$	$1\,$	$1\,$	${\frac {2\times 10^{-9}}{(25812.807)(483597.9)}}\$
Josephson constant $K_{J}={\frac {2e}{h}}\,$	${\frac {\sqrt {\alpha }}{\pi }}\,$	${\frac {\alpha }{\pi }}\,$	${\frac {1}{\pi }}\,$	${\frac {1}{\pi }}\,$	${\frac {\alpha }{\pi }}\,$	$483597.9\times 10^{9}\,$
von Klitzing constant $R_{K}={\frac {h}{e^{2}}}\,$	${\frac {2\pi }{\alpha }}\,$	${\frac {2\pi }{\alpha }}\,$	$2\pi \,$	$2\pi \,$	${\frac {2\pi }{\alpha }}\,$	$25812.807\,$
characteristic impedance of vacuum $Z_{0}=2\alpha R_{K}={\frac {\hbar }{e^{2}}}{\frac {(g_{1})^{2}}{g}}$	$4\pi \,$	$4\pi \,$	$4\pi \alpha \,$	$4\pi \alpha \,$	$4\pi \,$	$2\alpha (25812.807)\,$
electric constant (vacuum permittivity) $\varepsilon _{0}={\frac {1}{Z_{0}c}}\,$	${\frac {1}{4\pi }}\,$	${\frac {1}{4\pi }}\,$	${\frac {1}{4\pi }}\,$	${\frac {1}{4\pi }}\,$	${\frac {1}{4\pi }}\,$	${\frac {1}{2\alpha (25812.807)(299792458)}}\$
magnetic constant (vacuum permeability) $\mu _{0}={\frac {Z_{0}}{c}}\,$	$4\pi \,$	$4\pi \,$	$4\pi \alpha ^{2}\,$	$4\pi \alpha ^{2}\,$	$4\pi \,$	${\frac {2\alpha (25812.807)}{299792458}}\$
Newtonian constant of gravitation $G\,$	$1\,$	$1\,$	$1\,$	$-\,$	$-\,$	$-\,$
electron mass $m_{e}\,$	$-\,$	$-\,$	$-\,$	$1\,$	$1\,$	$-\,$
Hartree energy $E_{h}=\alpha ^{2}m_{e}c^{2}\,$	$-\,$	$-\,$	$-\,$	$1\,$	$\alpha ^{2}\,$	$-\,$
Rydberg constant $R_{\infty }={\frac {E_{h}}{2hc}}\,$	$-\,$	$-\,$	$-\,$	${\frac {\alpha }{4\pi }}\,$	${\frac {\alpha ^{3}}{4\pi }}\,$	$-\,$
caesium ground state hyperfine transition frequency	$-\,$	$-\,$	$-\,$	$-\,$	$-\,$	$9\ 192\ 631\ 770\,$

Relativistic Mass

The energy and momentum of an object with invariant mass m (also called rest mass in the case of a single particle), moving with velocity v with respect to a given frame of reference, are given by

${\begin{array}{r l}E&=\gamma mc^{2}\\\mathbf {p} &=\gamma m\mathbf {v} \end{array}}$

respectively, where γ (the Lorentz factor) is given by

$\gamma ={\frac {1}{\sqrt {1-(v/c)^{2}}}}.$

Quantum Mass

The Compton wavelength, λ, of a particle is given by

$\lambda ={\frac {h}{mc}}\$

where h is the Planck constant, m is the particle's rest mass, and c is the speed of light. The significance of this formula is shown in the derivation of the Compton shift formula.

The de Broglie equations relate the wavelength $~\lambda ~$ and frequency $~f~$ to the momentum $~p~$ and energy $~E~$, respectively, as

$\lambda ={\frac {h}{p}}$ and $f={\frac {E}{h}}$

where $~h~$ is Planck's constant.

{{Quantum Variables}}

prefixes

SI prefixes

Prefix		Base 10	Decimal	Adoption
Name	Symbol
quetta	Q	1030	1000000000000000000000000000000	2022
ronna	R	1027	1000000000000000000000000000
yotta	Y	1024	1000000000000000000000000	1991
zetta	Z	1021	1000000000000000000000
exa	E	1018	1000000000000000000	1975
peta	P	1015	1000000000000000
tera	T	1012	1000000000000	1960
giga	G	109	1000000000
mega	M	106	1000000	1873
kilo	k	103	1000	1795
hecto	h	102	100
deca	da	101	10
—	—	100	1	—
deci	d	10−1	0.1	1795
centi	c	10−2	0.01
milli	m	10−3	0.001
micro	μ	10−6	0.000001	1873
nano	n	10−9	0.000000001	1960
pico	p	10−12	0.000000000001
femto	f	10−15	0.000000000000001	1964
atto	a	10−18	0.000000000000000001
zepto	z	10−21	0.000000000000000000001	1991
yocto	y	10−24	0.000000000000000000000001
ronto	r	10−27	0.000000000000000000000000001	2022
quecto	q	10−30	0.000000000000000000000000000001
Notes