User:Tomruen/Polytile

In geometry, a polytile is an equilateral polygon defines with specific angles. An n-tile is a polygon defined by an edge-to-edge cycle of regular n-gons. The vertices of the n-tile are positioned at the center of the n-gons.

A polytiling is a tessellation made from one or more polytiles from the set defined by the angles of a regular n-gon.

Polytile definition

A polytile or p-tile as an equilateral polygon notated by a set of integers representing vertex angles. The p is an even whole number 4 or greater. The polytile angles representing multiples of a 360°/p degree turns. Angles are measured as turn angles, zero for straight (colinear edges), positive for counterclockwise turns, and negative for clockwise turns. For example: #Tetratiles, #Hexatiles, #Octatiles, #Decatiles, and #Dodecatiles have turn angles that are integer multiples of 90°, 60°, 45°, 36° and 30° turns respectively.

A p-tile notational is: p:a₁.a₂…a_m^n. (A square is 4:1^4 as four quarter turns, 90°.)
Each turn angle a_i' index is an integer less than p/2. (Indices ±p/2 are half turns, 180°.)
A ^n exponent repeats sequence n times. A chiral pair is mirrored as ^-n, including ^-1.
The turning number is computed by: t=n(a₁+a₂+…+a_m)/p. If |t|=1, it is a simple polytile (convex or concave), otherwise, a star polytile.
If the “p:” is not given, we assume simple (t=1), and compute p=n(a₁+a₂+…+a_m).
Turn angles a_i may be allowed outside (-p/2,p/2), but to correctly compute the turning number, they need be given within the signed range modulo p.
A p-tile can be up-scaled: p:a₁.a₂..a_m^n to kp:ka₁.ka₂..ka_m^n, for any whole number k. In reverse, any kp-tile, with all indices as multiples of k, can be down-scale to a p-tile.
A polytile expression that does not close as cycle is called a polychain.

A regular n-gon tile is represented by n 1's. The sum of these numbers equal n. For example 111111 or 1.1.1.1.1.1 or 1⁶ is a regular hexagon, with 6 60° angles. Odd-sided regular polygons can only be generated by even, 2n-tiles. For example a triangle is 222 or 2.2.2 or 2³, with 3 120° angles.

Zero indices can be given for collinear edges, and negative indices allow for concave, self-contacting and self-intersecting tiles. For example 1111 or 11² or 1⁴ is a square, while a 2:1 rectangle is 110110 or 110².

An exponent is always at the end, and applies to the full string of indices. A negative exponent can imply a reverse order for a chiral pair. For example 4321 = 1234^-1.

A regular n-gon has r2n symmetry. For example a square is r8 symmetry.

Odd (2n+1)-tiles are only a subset of 2(2n+1)-tiles and are geometrically and notionally identical. For example, a hexagon is both 1⁶ as a cycle of 6 hexagons, and 1⁶ as a cycle of 6 triangles in alternating orientations.

Geometric interpretation

Polytiles have a helpful geometric interpretation where each p-tile can be described by a cyclic path of regular p-gons connected edge-to-edge. The p-tile is constructed with its vertices centered on each regular p-gon of the cycle, with equal edges defined between adjacent p-gons.

Classifying and naming

A p-tile can be called a t-turn m-adic n-gram, with 3 parameters n, m, t:

A polygram or n-gram, like monogram, digram, trigram, tetragram, pentagram, hexagram, etc. is any equilateral polygon with n-fold rotational symmetry.
A polyad or m-ad, like monad, dyad, triad, tetrad, pentad, hexad, etc. as the number of vertices with its symmetry of a polygram.
t-turn is the turning number. Crossed polygons, like a regular polygon with two vertices flipping places, can be a 0-turn which may be called counterturn. If we are interested in clockwise polygons, we can call them contra-t-turn.

An m-adic n-gram is an equilateral nm-gon. If m is 1, that qualifier can be suppressed.

Covers and compounds

A 4th parameter can be extracted, c-cover. If p:a₁.a₂…a_m^n is a valid polytile, then p:a₁.a₂…a_m^nc is a degenerate c-cover of it, repeating the same vertices and edges c times.

Multicovered polygons are degenerate and can’t be seen, but have a topological existence.

An ordinary interpretation of a c-cover regular polygon {ca/cb} factors out as c{a/b}, and draws it as a c-compound, adding rotated copies, giving ac-fold cyclic symmetry. This can be generalized for any polytile. A c-cover polytile, p:a₁.a₂…a_m^nc, is written as a c-compound c*p:a₁.a₂…a_m^n, interpreted as c rotated copies of p:a₁.a₂…a_m^n. A c-compound m-adic nc-gram has mnc vertices.

Shorter names for regular polygons (-are suffix)

Regular polygons (monadic, m=1) have no general specific names, except for the square. I propose we use the square as a guide, and use -are suffix for all regulars. An equilateral triangle becomes a trigram-are or triare for short. Regular polygons become: triare, tetrare, pentare, hexare, heptare, octare, etc.

Regular star polygons apply as well. A pentagram {5/2}, 2-turn monadic pentagram, becomes a 2-turn pentare. Generally, a regular {p/q} star polygon, p:q^p becomes a q-turn p-are.

Shorter names for isotoxal polygons (-us suffix)

An isotoxal or edge-transitive polygon (dyadic, m=2) has one edge type, 2 vertices within its symmetry. Polytile notation is: p:a.b^n. The smallest class are rhombi: p:a.b^2. Using the name rhombus as a standard, I propose a -us suffix. Then a rhombus is a digramus, or di-us for short. And in sequence: dius, trius, tetrus, pentus, etc.

Here we also find a new quality, convexity. The concave form will have one negative index, like p:-a.b^n (a, b positive). I differentiate as stella- prefix if concave and (optional) arch- prefix if convex, and lineo- if colinear edges. A concave isotoxal decagon can be called a stellapentus.

Shorter names for m-adic polygons

An m-adic n-gram can also be written as one word as n-gram-m-ad. An m-gon with no symmetry, a m-adic monogram, can be called a monogram-m-ad and mono-m-ad for short. An equilateral pentagon with no cyclic symmetry, a pentadic monogram, can be called a monogram-pentad and monopentad.

Number of convex tiles

A full set of convex polytiles represent all solutions for a given polygon. The numbers of forms are given below, chiral column counting chiral pairs. The number of tiles by sides are also given, with bold 1 given for regular polygon solutions.

Odd family polytiles, (2k+1)-tiles, are given for completeness. They are a subset of 2(2k-1)-tiles, identified with all odd-turn angle multipliers. The smallest odd solution is one triatile, with 6 triangles around a point, making a regular hexagon, and same as 6 hexagons for the first hexatile.

Number of convex tiles
2n	Unique tiles	With chirals	Counts
2n	Unique tiles	With chirals	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
4	1	1	0	1+3
6	3	3	1	1	0	1+1
3	1	1		0		1
8	4	4	0	1+1	0	1	0	1
10	7	7	0	2	1	2	0	1	0	1
5	2	2		0		1		0		1
12	16	17	1	1+2	1	1+3	1	3	1	1	0	1
14	17	19	0	3	0	4	1	4	0	3	0	1	0	1
7	4	4		0		2		0		1		0		1
16	28	34	0	1+3	0	5	0	1+7	0	5	0	4	0	1	0	1
18	70	92	1	4	1	1+8	4	12	1+5	12	4	9	1	4	1	1	0	1
9	10	11		0		1+3		0		3		1		1		0		1
20	85	115	0	1+4	1	8	1	16	2	1+16	2	16	1	8	1	5	0	1	0	1
22	125	187	0	5	0	10	0	20	0	26	1	26	0	20	0	10	0	5	0	1	0	1
11	15	18		0		4		0		5		0		4		0		1		0		1
24	392	616	1	6	2	15	8	33	20	50	27	1+65	27	50	20	33	8	15	2	6	1	1	0	1
26	379	631	0	6	0	14	0	35	0	57	0	76	1	76	0	57	0	35	0	14	0	6	0	1	0	1
13	30	40		0		5		0		10		0		8		0		5		0		1		0		1
28	704	1201	0	7	0	16	1	47	1	79	3	126	4	1+133	4	126	3	79	1	47	1	16	0	7	0	1	0	1
30	3359	3359	1	7	1+2	1+23	17	71	60	1+172	145	329	249	442	1+314	442	249	329	145	173	60	71	17	24	3	7	1	1	0	1
15	82	116		0		9		0		1+17		5		21		3		15		2		6		1		1		0		1

Tetratiles

A tetratile only has turn angles of 90°. There is only one convex tetratile, the square itself. The only tiling is the square tiling.

Hexatiles

Convex Hexatiles
"Hexare" 1⁶, r12	Rhombus 21², d4	"Triare" 2³, r6

A hexatile uses turn angles of 60° and 120°. With 3 tiles, it is the smallest nontrivial set. The 3 tiles are: the regular hexagon 111111 or 1⁶, the equilateral triangle 222 or 2³, and 60 degree rhombus 1212 or (12)². These are related to the rhombille tiling, and trihexagonal tiling.

Examples

Triatiles

Triatiles
Hexagon 1⁶, r12

There is only 1 convex triatile, repeated as odd-only-indices from the hexatiles.

Convex Triatiles

Octatiles

Convex Octatiles
"Octare" 1⁸, r16	Hexagon 121², i4
Square 2⁴, r8	Rhombus 31², d4

An octatile has turn angles of 45°, 90° and 135°. There are 4 convex octatiles: the "octare" (11111111) or (1⁸), Flatted hexagon (311211) or (311)³, and square (2222) or 2⁴, and rhombus (4131) or (31)³.

The tiles are related to the Ammann-Beenker tiling which includes the square and rhombus. The chamfered square tiling is a simple tiling with the right hexagon.

Examples
Square tiling	Truncated square tiling	Ammann-Beenker tiling	Chamfered square tiling

Decatiles

Convex Decatiles
"Decare" 1¹⁰, r20	Octagon 2111², d4	Tall hexagon 212², i4	"Pentare" 2⁵, r10
Flat hexagon 131², i4	Rhombus 32², d4	Rhombus 41², d4

A decatile has turn angles of 36°, 72°, 108°, and 144°. There are 7 convex decatiles: the regular decagon 11111111 or 1¹⁰, octagon 21112111 or 2111², tall hexagon 221221 or 221², and regular pentagon 22222 or 2⁵, flat hexagon 113113 or 113², wide rhombus 3232, or 32², and thin rhombus, 4141 or 41².

The penrose tiling contains the wide and narrow rhombus.

Penrose tiling	Rhombille tiling	decagon-octagon-rhomb	pentagon-octagon-rhomb

Pentatiles

Convex Pentatiles
Decagon 1¹⁰, r20	Flat hexagon 131², i4

There are 2 convex pentatiles, repeated as odd-only-indices from the dodecatiles.

Dodecatiles

Convex Dodecatiles
"Dodecare" 1¹², r24	Decagon 11211², i4	Enneagon 121³, i6	Tall octagon 1221², p4	Octagon 21⁴, d4
"Hexare" 2⁶, r12	Octagon 3111², d4	Heptagon 2131131, i2	Hexagon 321² (a), g2	Hexagon 312² (b), g2
"Trius" 31³, d6	Square 3⁴, r8	Flat hexagon 141², i4	Right pentagon 41331, i2	Wide rhombus 42², d4
"Triare" 4³, r6	Thin rhombus 51², d4

A dodecatile has turn angles of 30°, 60°, 120°, and 150°.

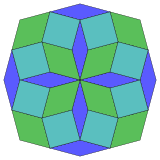
There are 16 convex dodecatiles. The dodecatiles are used in pattern blocks, triangle, wide and narrow rhombs, square, and hexagon.

Pattern blocks		Dissections of convex dodecatiles

Examples
222²	111⁴ and 444	222² and 444	444	141²

Truncated square tiling variations
3⁴ and 21⁴	3⁴ and 1122²	3⁴ and 1122²

Tetradecatiles

Convex Tetradecatiles
Tetradecagon 1¹⁴, r28	Dodecagon 211111², d4	Decagon 21112², i4	Decagon 21212², i4	Octagon 2221², d4
Heptagon 2⁷, r14	Decagon 11311², i4	Decagon 3211² (a), g2	Octagon 3112² (b), g2	Octagon 3121², d4
Hexagon 313², i4	Hexagon 232², i4	Octagon 4111², d4	Hexagon 412² (a), g2	Hexagon 421² (b), g2
Rhombus 43², d4	Hexagon 511², i4	Rhombus 52², d4	Rhombus 61², d4

There are 17 convex tetradecatiles, 19 with chiral pairs.

Heptatiles

Convex Heptatiles
Tetradecagon 1¹⁴, r28	Decagon 11311², i4	Hexagon 313², i4	Hexagon 151², i4

There are 4 convex heptatiles, repeated as odd-only-indices from the tetradecatiles.

Hexadecatiles

Convex Hexadecatiles
Hexadecagon, r32 1^16	Tetradecagon, i4 2111111^2	Dodecagon, i4 221111^2	Dodecagon, p4 211121^2	Dodecagon, i8 211^4
Decagon, i4 22112^2	Decagon, g2 21212^2	Octagon, r16 2^8	Dodecagon, d4 113111^2	Decagon, g2 32111^2 (a)
Decagon, g2 32111^2 (b)	Decagon, g2 31121^2 (a)	Decagon, g2 31211^2 (b)	Octagon, p4 1331^2	Octagon, g2 1223^2
Octagon, d8 13^4	Octagon, d4 1232^2	Octagon, d4 1322^2	Hexagon, i4 323^2	Decagon, i4 11411^2
Octagon, g2 1124^2 (a)	Octagon, g2 1142^2 (b)	Octagon, d4 1214^2	Hexagon, g2 143^2 (a)	Hexagon, g2 134^2 (b)
Hexagon, g2 242^2	Square, r8 4444	Octagon, d4 5111^2	Hexagon, g2 125^2 (a)	Hexagon, g2 152^2 (b)
Rhombus, d4 53^2	Hexagon, i4 161^2	Rhombus, d4 62^2	Rhombus, d4 71^2

There are 28 convex hexadecatiles, 34 with chiral pairs.

Octadecatiles

Convex Octadecatiles
Octadecagon, r36 1^18	Hexadecagon, d4 11111112^2	Tetradecagon, i4 1113111^2	Tetradecagon, i4 1111122^2	Dodecagon, d4 111114^2	Pentadecagon, i6 11211^3
Tetradecagon, i4 1121211^2	Tridecagon, i2 1111221121113 (a)	Tridecagon 3111211221111 (b)	Dodecagon 112311^2 (a)	Dodecagon 113211^2 (b)	Hendecagon 11114112114
Decagon 11511^2	Tetradecagon 2111211^2	Dodecagon 312111^2 (a)	Dodecagon 312111^2 (b)	Dodecagon 222111^2	Hendecagon 11122221114
Decagon 42111^2 (a)	Decagon 42111^2 (b)	Dodecagon 3111^3	Hendecagon 11131221123 (a)	Hendecagon 32112213111 (b)	Decagon 33111^2
Decagon 1114113114	Enneagon 111422115 (a)	Enneagon 511224111 (b)	Octagon 1116^2	Dodecagon 112113^2	Dodecagon 112122^2 (a)
Dodecagon 221211^2 (b)	Decagon 11214^2 (a)	Decagon 41211^2 (b)	Dodecagon 1122^3	Hendecagon 11222113113	Decagon 1122222114
Decagon 11223^2 (a)	Decagon 32211^2 (b)	Decagon 11232^2	Enneagon 112411314 (a)	Enneagon 421141311 (b)	Octagon 1125^2 (a)
Octagon 5211^2 (b)	Decagon 11313^2	Enneagon 113222214 (a)	Enneagon 412222311 (b)	Octagon 1134^2 (a)	Octagon 4311^2 (b)
Enneagon 411^3	Octagon 11414115	Octagon 11422224	Heptagon 1144116	Heptagon 1152225	Hexagon 711^2
Dodecagon 21^6	Decagon 31212^2 (a)	Decagon 32121^2 (b)	Octagon 5121^2	Decagon 31221^2	Decagon 22221^2
Octagon 4122^2 (a)	Octagon 4221^2 (b)	Enneagon 312^3 (a)	Enneagon 321^3 (b)	Octagon 3312^2 (a)	Octagon 3321^2 (b)
Octagon 4212^2	Heptagon 1242315 (a)	Heptagon 5132421 (b)	Hexagon 612^2 (a)	Hexagon 621^2 (b)	Octagon 4131^2
Octagon 3132^2	Hexagon 513^2 (a)	Hexagon 531^2 (b)	Heptagon 1414224	Hexagon 441^2	"Trius" 51^3
Pentagon 15426 (a)	Pentagon 62451 (b)	Rhombic 81^2	Enneagon 2^9	Octagon 3222^2	Hexagon 522^2
Hexagon 423^2 (a)	Hexagon 432^2 (b)	"Trius" 42^3	Rhombic 72^2	Hexagon 3^6	Rhombic 63^2
Rhombic 54^2	"Triare" 6^3

There are 70 convex octadecatiles, 92 with chiral pairs.

Enneatiles

Convex Enneatiles
Octadecagon, r16 1^18	Tetradecagon, i4 3111111^2	Decagon, i4 51111^2	Dodecagon, d6 3111^3
Decagon, i4 33111^2	Decagon, i4 31131^2	Hexagon, i4 711^2	Hexagon, g2 513^2 (a)
Hexagon, g2 531^2 (b)	"Trius", d6 51^3	Hexagon, r12 3^6

There are 10 convex enneatiles, 11 with chiral pairs, identical to the subset of octadecatile with only odd turn angle multiplers.

Icosatiles

Convex Icosatiles
Icosagon 1^20	Octadecagon 211111111^2	Hexadecagon 31111111^2	Hexadecagon 22111111^2	Tetradecagon 4111111^2	Hexadecagon 21211111^2
Tetradecagon 2311111^2 (a)	Tetradecagon 3211111^2 (b)	Dodecagon 511111^2	Hexadecagon 21111211^2	Tetradecagon 2131111^2 (a)	Tetradecagon 3121111^2 (b)
Tetradecagon 2221111^2	Dodecagon 241111^2 (a)	Dodecagon 421111^2 (b)	Dodecagon 331111^2	Decagon 61111^2	Hexadecagon 2111^4
Tetradecagon 3111211^2 (a)	Tetradecagon 3112111^2 (b)	Tetradecagon 2211121^2 (a)	Tetradecagon 2212111^2 (b)	Dodecagon 411121^2 (a)	Dodecagon 412111^2 (b)
Dodecagon 311122^2 (a)	Dodecagon 322111^2 (b)	Dodecagon 321112^2	Decagon 25111^2 (a)	Decagon 52111^2 (b)	Dodecagon 311131^2
Decagon 41113^2 (a)	Decagon 43111^2 (b)	Octagon 7111^2	Pentadecagon 211^5	Tetradecagon 2211211^2	Tridecagon 1121131211213
Dodecagon 411211^2	Tetradecagon 2112121^2	Dodecagon 311212^2 (a)	Dodecagon 321211^2 (b)	Dodecagon 321121^2 (a)	Dodecagon 312112^2 (b)
Hendecagon 11214121133	Decagon 51121^2 (a)	Decagon 51211^2 (b)	Dodecagon 311221^2 (a)	Dodecagon 312211^2 (b)	Dodecagon 222211^2
Decagon 41122^2 (a)	Decagon 42211^2 (b)	Decagon 33112^2 (a)	Decagon 33211^2 (b)	Decagon 42112^2	Octagon 6112^2 (a)
Octagon 6211^2 (b)	Dodecagon 311^4	Hendecagon 11313121313	Decagon 41131^2 (a)	Decagon 41311^2 (b)	Decagon 31132^2
Enneagon 113412143	Octagon 5113^2 (a)	Octagon 5311^2 (b)	Octagon 4411^2	Hexagon 811^2	Dodecagon 312121^2
Dodecagon 222121^2	Decagon 41212^2 (a)	Decagon 42121^2 (b)	Decagon 33121^2	Octagon 6121^2	Dodecagon 221^4
Decagon 41221^2	Decagon 31222^2 (a)	Decagon 32221^2 (b)	Decagon 32122^2 (a)	Decagon 32212^2 (b)	Octagon 5122^2 (a)
Octagon 5221^2 (b)	Decagon 31231^2 (a)	Decagon 32131^2 (b)	Octagon 4123^2 (a)	Octagon 4321^2 (b)	Octagon 4312^2 (a)
Octagon 4213^2 (b)	Octagon 5212^2	Hexagon 712^2 (a)	Hexagon 721^2 (b)	Decagon 31^5	Enneagon 131331314
Octagon 5131^2	Octagon 4132^2 (a)	Octagon 4231^2 (b)	Octagon 3331^2	Heptagon 1343144	Hexagon 613^2 (a)
Hexagon 631^2 (b)	Octagon 41^4	Hexagon 514^2 (a)	Hexagon 541^2 (b)	Tetragon 91^2	Decagon 2^10
Octagon 4222^2	Octagon 3322^2	Hexagon 622^2	Octagon 32^4	Hexagon 523^2 (a)	Hexagon 532^2 (b)
Hexagon 442^2	Tetragon 82^2	Hexagon 433^2	Tetragon 73^2	Pentagon 4^5	Tetragon 64^2
Tetragon 5^4

There are 85 icosatiles, 115 including chiral pairs.

Icosiditiles

There are 125 convex icosiditiles, 187 with chiral pairs.

Hendecatiles

Hendecatiles
Hendecagon 1²²	Octadecagon 111131111²	Tetradecagon 1115111²	Tetradecagon 1111133²	Tetradecagon 1111313²	Decagon 11117²
Tetradecagon 1113113²	Decagon 11135² (a)	Decagon 15311² (b)	Decagon 13151² (a)	Decagon 15131² (b)	Decagon 13331²
Hexagon 191²	Decagon 31313²	Hexagon 137² (a)	Hexagon 731² (b)	Hexagon 515²	Hexagon 335²

Icosihexatiles

There are 379 convex icosihexatiles, 631 with chiral pairs.

Tridecatiles

Hendecatiles
Icosihexagon 1¹³	Icosidigon 31111111111²	Octadecagon 511111111²	Octadecagon 331111111²	Octadecagon 313111111²	Tetradecagon 7111111²
Octadecagon 311311111²	Tetradecagon 3511111² (a)	Tetradecagon 5311111² (b)	Octadecagon 311113111²	Tetradecagon 5111131² (a)	Tetradecagon 5131111² (b)
Tetradecagon 3331111²	Decagon 91111²	Tetradecagon 5111311² (a)	Tetradecagon 5113111² (b)	Tetradecagon 3311131² (a)	Tetradecagon 3313111² (b)
Decagon 71113² (a)	Decagon 73111² (b)	Decagon 55111²	Tetradecagon 3311311²	Tetradecagon 3113131²	Decagon 71131² (a)
Decagon 71311² (b)	Decagon 51133² (a)	Decagon 53311² (b)	Decagon 53113²	Decagon 51511²	Hexagon 1.1.11²
Decagon 51313² (a)	Decagon 53131² (b)	Decagon 51331²	Decagon 33331²	Hexagon 913² (a)	Hexagon 931² (b)
Hexagon 715² (a)	Hexagon 751² (b)	Hexagon 7337²	Hexagon 553²

There are 30 tridecatiles, 40 with chiral pairs. They represent a subset of icosihexatiles with only odd turn angle multipliers.

Triacontatiles

There are 3359 convex triacontatiles, 3359 with chiral pairs.

Pentadecatiles

Pentadecatiles
"Triacontare" 1³⁰	Icosihexagon 1111111111113²	Icosidigon 11111111115²	Icosidigon 11111111133²	Icosidigon 11111111313²	Octadecagon 111111117²
Icositetragon 11111113³	Icosidigon 11111113113²	Icosagon 11111113311113111115 (a)	Icosagon 51111131111331111111 (b)	Octadecagon 111111135² (a)	Octadecagon 531111111² (b)
Icosidigon 11111131113²	Octadecagon 111111315² (a)	Octadecagon 513111111² (b)	Octadecagon 111111333²	Tetradecagon 1111119²	Icosidigon 111113⁴
Octadecagon 111113115² (a)	Octadecagon 511311111² (b)	Octadecagon 111113133² (a)	Octadecagon 331311111² (b)	Hexadecagon 1111133133111117	Tetradecagon 1111137² (a)
Tetradecagon 7311111² (b)	Octadecagon 111115³	Hexadecagon 1111151133111135 (a)	Hexadecagon 5311113311511111 (b)	Tetradecagon 1111155²	Octadecagon 111131115² (a)
Octadecagon 511131111² (b)	Octadecagon 111131133²	Octadecagon 331131111² (b)	Octadecagon 111131313²	Tetradecagon 1111317² (a)	Tetradecagon 7131111² (b)
Octadecagon 111133³	Hexadecagon 1111333111151115	Tetradecagon 1111335² (a)	Tetradecagon 5331111² (b)	Tetradecagon 1111353²	Tetradecagon 1111515²
Decagon 1.1.1.1.11²	Icosagon 1113⁵	Octadecagon 111311133²	Octadecagon 111311313² (a)	Octadecagon 313113111² (b)	Tetradecagon 1113117² (a)
Tetradecagon 7113111² (b)	Octadecagon 111313³	Tetradecagon 11131333131117	Tetradecagon 1113135² (a)	Tetradecagon 5313111² (b)	Tetradecagon 1113153²
Tetradecagon 5131113² (b)	Tetradecagon 1113315² (a)	Tetradecagon 5133111² (b)	Tetradecagon 1113333²	Decagon 11139² (a)	Decagon 93111² (b)
Tetradecagon 1115115²	Dodecagon 111531333117 (a)	Dodecagon 711333135111 (b)	Decagon 11157² (a)	Decagon 75111² (b)	Dodecagon 1117³
Decagon 1117331337	Octadecagon 113⁶	Tetradecagon 1131135² (a)	Tetradecagon 5311311² (b)	Tetradecagon 1131315² (a)	Tetradecagon 5131311² (b)
Tetradecagon 1131333² (a)	Tetradecagon 3331311² (b)	Tetradecagon 1131513²	Decagon 11319² (a)	Decagon 91311² (b)	Tetradecagon 113311²
Tetradecagon 1133133²	Decagon 11337² (a)	Decagon 73311² (b)	Dodecagon 1135³ (a)	Dodecagon 5311³ (b)	Decagon 11355² (a)
Decagon 55311² (b)	Decagon 11373²	Decagon 11517² (a)	Decagon 71511² (b)	Decagon 11535²	Hexagon 1.1.13²
Tetradecagon 1313133²	Decagon 13137² (a)	Decagon 73131² (b)	Dodecagon 1315³	Decagon 13155²	Decagon 13317²
Dodecagon 1333³	Decagon 13335² (a)	Decagon 53331² (b)	Decagon 13353² (a)	Decagon 5331353313 (b)	Decagon 13515² (a)
Decagon 53151² (b)	Hexagon 1.3.11² (a)	Hexagon 11.3.1² (b)	Decagon 15⁵	Hexagon 159² (a)	Hexagon 951² (b)
Hexagon 177²	"Trius" 19³	Decagon 3¹⁰	Hexagon 339²	Hexagon 357² (a)	Hexagon 753² (b)
"Trius" 37³	Hexagon 5⁶

There are 82 convex pentadecatiles, 116 including chiral pairs. They represent a subset of tricontatiles with only odd turn angle multipliers.

Examples

Regular tiles

Each set of n-tiles has regular p-gon tiles for whole number divisors of n, 3 or larger.

Example regular tiles
a^b	Tetratile 4	Hexatile 3,6	Octatile 4,8	Decatiles 5,10	Dodecatiles 3,4,6,12	Tetradecatiles 7,14	Hexadecatiles 4,8,16	Octadecatiles 3,6,9,18	Icosatiles 4,5,10,20
1^b	1⁴	1⁶	1⁸	1¹⁰	1¹²	1¹⁴	1¹⁶	1¹⁸	1²⁰
2^b		2³	2⁴	2⁵	2⁶	2⁷	2⁸	2⁹	2¹⁰
3^b					3⁴			3⁶
4^b					4³		4⁴		4⁵
5^b									5⁴
6^b								6³

Rhombic tiles

Rhombi are named as ab², where a and b are positive integers, making a 2(a+b)-tile. A rhombus has d4 symmetry.

Example rhombi
ab²	Tetratile	Hexatile	Octatile	Decatiles	Dodecatiles	Tetradecatiles	Hexadecatiles	Octadecatiles	Icosatiles
a1²	11²	21²	31²	41²	51²	61²	71²	81²	91²
a2²			22²	32²	42²	52²	62²	72²	82²
a3²					33²	43²	53²	63²	73²
a4²							44²	54²	64²

Elongated rhombic tiles

An elongated rhombus (hexagon) is named by aabaab or aba², where a and b are positive integers, making a 2(2a+b)-tile. If a>b, it makes a short hexagon, and b>a makes a tall hexagon. An elongated rhombus has i4 symmetry.