User:Tomruen/Metatron's Cube
Metatron's Cube research
Article copy
[edit]
Metatron's Cube is a sacred geometric figure composed of 13 equal circles with lines from the center of each circle extending out to the centers of the other 12 circles, also described as a variant of the Flower of Life.
Description
[edit]
The name of Metatron's Cube makes reference to Metatron, an angel mentioned in apocryphal texts including the Second Book of Enoch and the Book of the Palaces.[2] These texts rank Metatron second only to the God in the hierarchy of being.[citation needed] The derivation of Metatron's Cube from the Flower of Life, which Jewish texts states, was excluded from human experience during the exile from Eden.[citation needed] This has led some scholars including Johann Andreas Eisenmenger to portray Metatron as the means by which humanity was given knowledge of YHVH.
The image below relates how the platonic solids can be projected in two dimensions as hexagonally-symmetric figures within the framework of the Metatron cube.
The Platonic solids drawn as projections with the framework of Metatron's cube, including a star tetrahedron (stellated octahedron)
Metatron's Cube in 3-dimensions
[edit]The 13 circles of the Metatron's cube can be seen as a diagonal axis projection of a 3-dimensional cube, as 8 corner spheres and 6 face-centered spheres. Two spheres are projected into the center from a 3-fold symmetry axis. The face-centered points represent an octahedron. Combined these 14 points represent the face-centered cubic lattice cell.
|
|
|
|
| Metatron's cube | Stellated octahedron | Cube and octahedron | Face-centered cubic lattice cell |
|---|
See also
[edit]References
[edit]- ^ Melchizedek, Drunvalo (1999), p.160 Figure 6-12.
- ^ A. Orlov, The Enoch-Metatron Tradition (Tuebingen: Mohr-Siebeck, 2005) 148-208; http://www.scribd.com/doc/2024701/Hebrew-book-of-3-Enoch.
- Sacred Geometry Design Sourcebook: Universal Dimensional Patterns Bruce Rawles. pp. 94–95
- Melchizedek, Drunvalo (1999). The Ancient Secret of the Flower of Life. Vol. 1. Light Technology Publishing. p.194-198
External links
[edit]
Geometry notes
[edit]Platonic solids in 2D orthogonal projection
[edit]I made some images showing each figure in a Flower of Life (geometry) pattern of circles, and made cube vertices green, octahedron vertices blue, and intermediate vertices purple.
| Stellated octahedron {3,3} + {3,3}    +
|
Cube and octahedron {4,3} + {3,4}  +
|
Dodecahedron and cube {5,3} + {3,5}  +
|
|---|---|---|
|
|
|
Here's the vertices projected onto Metatron's cube, in dual polyhedron configurations (red and green edges), sharing the same outer hexagon vertices.
3D presentation
[edit]Cube and octahedron |
Face-centered cubic lattice cell |
As spheres |
 As tangent cubic spheres |
Here's another representation, visualized as an actual cube, viewed on the diagonal, with 8 corners of the cube as transparent blue spheres, and 6 transparent red spheres on the centers of the 6 faces. The projection center has 2 cube corners, so there are (8+6) 14 spheres in 3D space of this cube. A second one has larger spheres/circles which might be harder to see.
So the 3D presentation the connection to the cube and octahedron are apparent. The cube vertices are the 8 blue spheres, and the octahedron vertices are the cube face centers. You can also see a relation to the face-centered cubic lattice cell.
Related 5-dimensional figure
[edit]Metatron's Cube 13 vertices |
 birectified 5-simplex A5 Coxeter plane (doubled vertices in orange) |
 birectified 5-simplex A4 Coxeter plane 20 vertices visible |
| ||
The 5-dimensional birectified 5-simplex seen in projection of the A5 Coxeter plane has its vertices match this geometry exactly, although it is missing some of the edges.
It has 20 vertices rather than 13, but the center and first ring have double-vertices, coinciding within the projection.
It has a very symmetric Coxeter diagram: 
. It has 90 edges, 120 triangular faces, made of 30 tetrahedra, and 30 octahedra.
It also represents the intersection of 2 5-simplices (like the 3D tetrahedron as a 3-simplex), in dual configurations (
+ 
), like the hexagon center of a hexagram in 2D, and the octahedron () center of a tetrahedron star in 3D (
+ 
).
Also interestingly the birectified 5-simplex has a 10-fold symmetry 2D projection in the A4 Coxeter plane.
I wonder if that means anything helpful to the Metatron cube? I've not seen any evidence anyone else has noticed this similarity, but I'll look around.
Related 6-dimensional figure
[edit]Incidentally, the 5-dimensional birectified 5-simplex is the vertex figure for the 6-dimensional 122 polytope, with symmetric Coxeter diagram: . It also has a hexagonal projection, although more of a seed of life, containing total 72 vertices, but overlapping with 2,3,6 multipliers (red, orange, yellow), into 19 vertices. It also represents the root vectors of the simple Lie group E6. It is most symmetrically seen in the E6 Coxeter plane with order 12 symmetry.
 A5 coxeter plane |
 A4 coxeter plane |
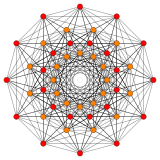 E6 coxeter plane |