User:Tomruen/Composite polytope

A composite polytope is a polytope that can can be decomposed into orthogonal elements. Examples include prisms, duoprisms, pyramids, bipyramids, duopyramids.

Four operators

There are four classes that can be expressed as product operators on f-vectors.

The join, with descending wedge symbol ∨, include both f_-1, and f_n. The rhombic sum only includes f_-1, and its dual rectangular product only includes f_n. The meet includes neither and only applies to flat elements.

For instance a triangle has f-vector (3,3), with 3 vertices (f₀) and 3 edges (f₁). Extended with the nullitope (f_-1) gives f=(1,3,3), extending with the (polygonal interior) body (f₂) gives f=(3,3,1), while extending both is f=(1,3,3,1).

The rhombic sum and rectangular product are dual operators, with f-vectors reversed. The join and rhombic sums shares vertex counts, summing vertices in elements. The rectangular and meet products also share vertex counts, being the product of the element vertex counts.

The meet product, with wedge symbol ∧, is the same as Cartesian product if elements are infinite. Meets are not connected unless polytopes are polygons or higher.

An n-polytope existing in a space higher than n-dimensions, it can be categorized as skew. It does not have a well-defined interior.

Four product operators on polytopes

Operator names	Symbols	Powers	f-vector	Polytope names
Join Pyramid product	A ∨ B A ⋈ B A ×1,1 B	n ⋅ A n ⋅ ( )	(1,fA,1)*(1,1) (1,fA,1)*(1,2,1) (1,fA,1)*(1,fB,1) (1,fA,1)*(1,fB,1)*(1,fC,1) (1,fA,1)n (1,1)n	A ∨ ( ) = Pyramid A ∨ { } = Wedge A ∨ B = Duowedge A ∨ B ∨ C = Tri-wedge n ⋅ A = A-topal n-wedge (n+1) ⋅ ( ) = n-simplex, αn
"Rhombic sum" Direct sum Tegum product	A + B A ⊕ B A ×1,0 B	n A n { }	(1,fA)*(1,2) (1,fA)*(1,fB) (1,fA)*(1,fB)*(1,fC) (1,fA)n (1,p,p)n (1,2)n	A + { } = Fusil or bipyramid A + B = Duofusil or duopyramid A + B + C = Tri-fusil n A = A-topal n-fusil n { } = n-fusil, n-orthoplex, βn n {p} = p-gonal n-fusil
Rectangular product Cartesian product Prism product	A×B A ×0,1 B	An { }n	(fA,1)*(2,1) (fA,1)*(fB,1) (fA,1)*(fB,1)*(fC,1) (fA,1)n (2,1)n (p,p,1)n	A×{ } = Prism A×B = Duoprism, duoprism A×B×C = Tri-prism An = A-topal n-prism { }n = n-prism, n-cube, γn {p}n = p-gonal n-prism
Meet Topological product Honeycomb Comb product Torus product	A ∧ B A □ B A ×0,0 B	A(n) { }(n)	(fA)*(2) = (2fA) (fA)*(fB) = (fA*fB) (fA)*(fB)*(fC) = (fA*fB*fC) (fA)n = (fAn) (p,p)n = p(1,1)n (∞,∞)n = ∞(1,1)n (2)n = (2n)	A ∧ { } = Skew meet A ∧ B = Skew duomeet A ∧ B ∧ C = Skew tri-meet A(n) = Skew A-topal n-meet {p}(n) = Reg. skew p-gonal n-meet {∞}(n) = cubic n-comb, δn+1 { }(n) = Skew dionic n-meet

Hybrid product operators on polytopes

Operator names	Symbols	Powers	f-vector	Polytope names
Prism-meet	A ⋋ B A ⋌ B		(fA,1)*(2) (2,1)*(fA) (fA,1)*(fB)	A ⋋ { } = Semi-prism { } ⋋ A = Open-prism A ⋋ B = Semi-duoprism

Examples

Four product operators on polytopes

Operator names	Symbols f-vector	Rank	Polytope names	Examples
Join Join product Pyramid product	A ∨ B A ⋈ B A ×1,1 B (1,fA,1) * (1,fB,1)	Rank(A) + Rank(B)+1	A ∨ ( ) = pyramid A ∨ { } = wedge A ∨ B = duowedge A ∨ B ∨ C = tri-wedge	3D polyhedron { } ∨ { } or {3,3} [2,1] or [4,2+] Dionic wedge (1,2,1)*(1,2,1) = (1,4,6,4,1)	4D skew polyhedron 3{ } ∨ { } [3,2,1] Trionic wedge (1,3,1)*(1,2,1) = (1,5,8,5,1)	4D polychoron {3} ∨ { } or {3,3,3} [3,2,1] Triangular wedge (1,3,3,1)*(1,2,1) =(1,5,10,10,5,1)	5D polyteron {3,3} ∨ { } or {3,3,3,3} [3,3,2,1] Tetrahedral wedge (1,4,6,4,1)*(1,2,1) =(1,6,15,20,15,6,1)	5D skew polyhedron 3{ } ∨ 3{ } [3,2,3,1] or [[3,2,3],1] Trionic duowedge (1,3,1)*(1,3,1) = (1,6,11,6,1)	5D skew polychoron {3} ∨ 3{ } [3,2,3,1] Triangle-trion duowedge (1,3,3,1)*(1,3,1) =(1,6,13,13,6,1)	5D polyteron {3} ∨ {3} = 2⋅{3} or {3,3,3,3} [3,2,3,1] or [[3,2,3],1] Triangular duowedge 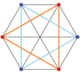(1,3,3,1)*(1,3,3,1) =(1,6,15,20,15,6,1)	6D polypeton {3,3} ∨ {3} or {3,3,3,3,3} [3,3,2,3,1] Tetrahedron-triangle duowedge (1,4,6,4,1)*(1,3,3,1) =(1,7,21,35,35,21,7,1)	7D polyexon {3,3} ∨ {3,3} = 2⋅{3,3} or {3,3,3,3,3,3} [3,3,2,3,3,1] Tetrahedral duowedge (1,4,6,4,1)*(1,4,6,4,1) =(1,8,28,56,70,56,28,8,1)
"Rhombic sum" Direct sum Tegum product	A + B A ⊕ B A ×1,0 B (1,fA) * (1,fB)	Rank(A) + Rank(B)	A + { } = fusil or bipyramid A + B = duofusil or duopyramid A + B + C = tri-fusil	2D polygon { } + { } = 2{ } or {4} [ ]2 = [2] or [4] Dionic fusil (1,2)*(1,2) = (1,4,4)	3D skew polygon 3{ } + { } [3,2] Trionic fusil (1,3)*(1,2) = (1,5,6)	3D polyhedron {3} + { } [3,2] Triangular fusil (1,3,3)*(1,2) = (1,5,9,6)	4D polychoron {3,3} + { } [3,3,2] Tetrahedral fusil (1,4,6,4)*(1,2) = (1,6,14,16,8)	4D skew polygon 3{ } + 3{ } = 23{ } [3,2,3] or [[3,2,3]] Trionic duofusil (1,3)*(1,3) = (1,6,9)	4D skew polyhedron {3} + 3{ } [3,2,3] Triangle-trion duofusil (1,3,3)*(1,3) = (1,6,12,9)	4D polychoron {3} + {3} or 2{3} [3,2,3] or [[3,2,3]] Triangular duofusil (1,3,3)*(1,3,3) = (1,6,15,18,9)	5D polyteron {3,3} + {3} [3,3,2,3] Tetrahedron-triangle duofusil (1,4,6,4)*(1,3,3) = (1,7,21,34,30,12)	6D polypeton {3,3} + {3,3} = 2{3,3} [3,3,2,3,3] Tetrahedral duofusil (1,4,6,4)*(1,4,6,4) = (1,8,28,56,68,48,16)
Rectangular product Cartesian product Prism product	A × B A ×0,1 B (fA,1) * (fB,1)	Rank(A) + Rank(B)	A × { } = prism A × B = duoprism A × B × C = tri-prism	2D polygon { } × { } = { }2 or {4} [ ]2 = [2] or [4] Dionic prism (2,1)*(2,1) = (4,4,1)	3D skew polygon 3{ } × { } [3,2] Trionic prism (3,1)*(2,1) = (6,5,1)	3D polyhedron {3} × { } [3,2] Triangular prism (3,3,1)*(2,1) = (6,9,5,1)	4D polychoron {3,3} × { } [3,3,2] Tetrahedral prism (4,6,4,1)*(2,1) = (8,16,14,6,1)	4D skew polygon 3{ } × 3{ } = 3{ }2 [3,2,3] or [[3,2,3]] Trionic duoprism (3,1)*(3,1) = (9,6,1)	4D skew polyhedron {3} × 3{ } [3,2,3] Triangle-trion duoprism (3,3,1)*(3,1) = (9,12,6,1)	4D polychoron {3} × {3} or {3}2 [3,2,3] or [[3,2,3]] Triangular duoprism (3,3,1)*(3,3,1) = (9,18,15,6,1)	5D polyteron {3,3} × {3} [3,3,2,3] Tetrahedron-triangle duoprism (4,6,4,1)*(3,3,1) = (12,30,34,21,7,1)	6D polychoron {3,3} × {3,3} = {3,3}2 [3,3,2,3,3] Tetrahedral duoprism (4,6,4,1)*(4,6,4,1) = (16,48,68,56,28,8,1)
Meet Topological product Honeycomb Comb product Torus product Skew product	A ∧ B A □ B A ×0,0 B fA * fB	Rank(A) + Rank(B)-1	A ∧ { } = meet A ∧ B = duomeet A ∧ B ∧ C = tri-meet	2D skew 1-polytope { } ∧ { } = 2,2{ } or 4{ } [ ]2 = [2] or [4] Dionic meet (2)*(2) = (4)	3D skew 1-polytope 3{ } ∧ { } = 3,2{ } [3,2] Trionic meet (3)*(2) = (6)	3D skew polygon {3} ∧ { } [3,2] Triangular meet (3,3)*(2) = (6,6)	4D skew polyhedron {3,3} ∧ { } [3,3,2] Tetrahedral meet (4,6,4)*(2) = (8,12,8)	4D skew 1-polytope 3{ } ∧ 3{ } = 3,3{ } = 3{ }(2) [3,2,3] or [[3,2,3]] Trionic duomeet (3)*(3) = (9)	4D skew polygon {3} ∧ 3{ } [3,2,3] Triangle-trion duomeet (3,3)*(3) = (9,9)	4D skew polyhedron {3} ∧ {3} = {4,4|3} [3,2,3] or [[3,2,3]] Triangular duomeet (3,3)*(3,3) = (9,18,9)	5D skew polychoron {3,3} ∧ {3} [3,3,2,3] Tetrahedron-triangle duomeet (4,6,4)*(3,3) = (12,30,30,12)	6D skew polyteron {3,3} ∧ {3,3} = {3,3}(2) [3,3,2,3,3] Tetrahedral duomeet (4,6,4)*(4,6,4) = (16,48,68,48,16)

A product A*B, with f-vectors f_A and f_B, f_A∨B=f_A*f_B is computed like a polynomial multiplication polynomial coefficients.

For example for join of a triangle and dion, {3} ∨ { }:

f_A(x) = (1,3,3,1) = 1 + 3x + 3x² + x³ (triangle)

f_B(x) = (1,2,1) = 1 + 2x + x² (dion)

f_A∨B(x) = f_A(x) * f_B(x)

= (1 + 3x + 3x² + x³) * (1 + 2x + x²)

= 1 + 5x + 10x² + 10x³ + 5x⁴ + x⁵

= (1,5,10,10,5,1) (triangle ∨ dion = 5-cell)

Examples

Examples

Names Symbols f-vectors Examples Description f-vectors Images Join / wedge sum Join product Pyramid product A ∨ B A ⋈ B A ×1,1 B (1,fA,1) * (1,fB,1) { }∨{ } (3D) disphenoid (1,2,1)*(1,2,1) = (1,4,6,4,1) {3}∨{ } triangular wedge (4D) 5-cell (1,3,3,1)*(1,2,1) = (1,5,10,10,5,1) {3}∨{3} triangle duowedge (5D) 5-simplex (1,3,3,1)*(1,3,3,1) = (1,6,15,20,15,6,1) ({4}∨( ))∨{ } square pyramid wedge (5D) (1,5,10,5,1)*(1,2,1) = (1,7,21,30,21,7,1) ({3}+{ })∨{ } triangular bipyramid wedge (5D) (1,5,9,6,1)*(1,2,1) = (1,7,20,29,22,8,1) {3}×{ }∨{ } triangular prism wedge (5D) (1,6,9,5,1)*(1,2,1) = (1,8,22,29,20,7,1) {3,3}∨{ } tetrahedral wedge (5D) 5-simplex (1,4,6,4,1)*(1,2,1) = (1,6,15,20,15,6,1) {3,3}∨{3} tetrahedral-triangle duowedge (6D) 6-simplex (1,4,6,4,1)*(1,3,3,1) = (1,7,21,35,35,21,7,1) {4,3}∨{4} cubic-square duowedge (6D) (1,8,12,6,1)*(1,4,4,1) = (1,12,48,87,81,40,10,1) {3,4}∨{4} octahedron-square duowedge (6D) (1,6,12,8,1)*(1,4,4,1) = (1,10,40,81,87,48,12,1) {3,3}∨{3,3} tetrahedral duowedge (7D) 7-simplex (1,4,6,4,1)*(1,4,6,4,1) = (1,8,28,56,70,56,28,8,1) "Rhombic sum" Direct sum Tegum product A + B A ⊕ B A ×1,0 B (1,fA) * (1,fB) { }+{ } (2D) rhombus (1,2)*(1,2) = (1,4,4) {3}+{ } triangular fusil (3D) triangular bipyramid (1,3,3)*(1,2) = (1,5,9,6) {3}+{3} triangular duofusil (4D) 3-3 duopyramid (1,3,3)*(1,3,3) = (1,6,15,18,9) ({4}∨( ))+{ } square pyramid fusil (4D) (1,5,10,5)*(1,2) = (1,7,20,25,10) ({3}+{ })+{ } triangular bipyramid fusil (4D) (1,5,9,6)*(1,2) = (1,7,19,24,12) {3}×{ }+{ } triangular prism fusil (4D) (1,6,9,5)*(1,2) = (1,8,28,21,23,10) {3,3}+{ } tetrahedral fusil (4D) tetrahedral bipyramid (1,4,6,4)*(1,2) = (1,6,14,16,8) {3,3}+{3} tetrahedron-triangle duofusil (5D) tetrahedron-triangle duopyramid (1,4,6,4)*(1,3,3) = (1,7,21,34,30,12) {4,3}+{4} cube-square duofusil (5D) Cubic-square duopyramid (1,8,12,6)*(1,4,4) = (1,12,48,86,72,24) {3,4}+{4} octahedron-square duofusil (5D) Octahedral-square duopyramid (1,6,12,8)*(1,4,4) = (1,10,40,80,80,32) {3,3}+{3,3} tetrahedral duofusil (5D) tetrahedral duopyramid (1,4,6,4)*(1,4,6,4) = (1,8,28,56,68,48,16)

Names Symbols f-vectors Examples Description f-vectors Images Rectangular product Cartesian product Prism product A × B A ×0,1 B (fA,1) * (fB,1) { }×{ } (2D) rectangle (2,1)*(2,1) = (4,4,1) {3}×{ } triangular prism (3D) trip (3,3,1)*(2,1) = (6,9,5,1) {3}×{3} triangular duoprism (4D) 3-3 duoprism triddip (3,3,1)*(3,3,1) = (9,18,15,6,1) ({4}∨( ))×{ } square pyramid prism (4D) tisdip (5,10,5,1)*(2,1) = (10,25,20,7,1) ({3}+{ })×{ } triangular bipyramid prism (4D) (5,9,6,1)*(2,1) = (10,23,21,8,1) {3}×{ }×{ } triangular prism prism (4D) 3-4 duoprism (6,9,5,1)*(2,1) = (12,24,19,7,1) {3,3}×{ } tetrahedral prism (4D) tepe (4,6,4,1)*(2,1) = (8,16,14,6,1) {3,3}×{3} tetrahedron-triangle duoprism (5D) tratet (4,6,4,1)*(3,3,1) = (12,30,34,21,7,1) {3,4}×{3} octahedron-triangle duoprism (5D) troct (6,12,8,1)*(3,3,1) = (18,54,66,39,11,1) {4,3}×{3} cube-triangle duoprism (5D) trahex (8,12,6,1)*(3,3,1) = (24,60,62,33,9,1) {3,4}×{4} octahedron-square duoprism (5D) squahex (6,12,8,1)*(4,4,1) = (24,72,86,48,12,1) {4,3}×{4} cube-square duoprism (5D) 5-cube pent (8,12,6,1)*(4,4,1) = (32,80,80,40,10,1) {3,3}×{3,3} tetrahedral duoprism (6D) tetdip (4,6,4,1)*(4,6,4,1) = (16,48,68,56,28,8,1) Meet product Topological product Honeycomb product A ∧ B A □ B A ×0,0 B fA * fB { }∧{ } = 4{ } dion meet (1D/2D) regular skew tetron (2)*(2) = (4) {3}∧{ } triangle meet (2D/3D) regular skew hexagon (3,3)*(2) = (6,6) {3}∧{3} = triangular duomeet (3D/4D) {4,4|3} = {4,4}3,0 (3,3)*(3,3) = (9,18,9) ({4}∨( ))∧{ } square pyramid meet (3D/4D) (5,10,5)*(2) = (10,20,10) ({3}+{ })∧{ } triangular bipyramid meet (3D/4D) (5,9,6)*(2) = (10,18,12) ({3}×{ })∧{ } triangular prism meet (3D/4D) (6,9,5)*(2) = (12,18,10) {3,3}∧{ } tetrahedral meet (3D/4D) (4,6,4)*(2) = (8,12,8) {3,3}∧{3} tetrahedron-triangle duomeet (4D/5D) (4,6,4)*(3,3) = (12,30,30,12) {3,4}∧{3} octahedron-triangle duomeet (4D/5D) (6,12,8)*(3,3) = (18,54,60,24) {4,3}∧{3} cube-triangle duomeet (4D/5D) (8,12,6)*(3,3) = (24,60,54,18) {3,4}∧{4} octahedron-square duomeet (4D/5D) (6,12,8)*(4,4) = (24,72,80,32) {4,3}∧{4} cube-square duomeet (4D/5D) (8,12,6)*(4,4) = (32,80,72,24) {3,3}∧{3,3} tetrahedral duomeet (5D/6D) (4,6,4)*(4,6,4) = (16,48,68,48,16)

Skew 1-polytopes

Skew polytopes can be topologically connected or unconnected. Skew 1-polytopes can be drawn disconnected, but when part of a k-face of a larger polytope, the interior can be filled to show their relatedness.

Meet operators allow polytopes to be defined by "polytope holes" so can produce skew polytopes with prism ridges as facets.

As well, an operator ~P implies a polytope P is reduced by rank by one, making a complex skew polytope.

1-polytopes are self-dual.

Skew 1-polytopes

Notation	{ }∧{ } = 2,2{ } = 4{ } = ~{4}	3{ }∧{ } = 3,2{ } = ~~{3}×{ }	{ }∧{ }∧{ }= 2,2,2{ } = ~~{4,3}	{ }∧{ }∧{ }∧{ }= 2,2,2,2{ } = ~~~{4,3,3}	3{ }∧3{ }=3,3{ } = ~~~{3}×{3}	3{ } = ~{3}	4{ } = ~{4}	5{ } = ~{5}	6{ } = ~{6}
Name	Tetron	Hexon	Octon	Hexadekon	Enneon	Trion	Tetron	Penton	Hexon
Dimension	2	3	4	4	2	2	2	2	2
f-vector	(2)*(2)=(4)	(3)*(2)=(6)	(2)3=(8)	(2)4=(16)	(3)2=(9)	(3)	(4)	(5)	(6)
Image

Prisms and meets

Pair composites

For example { }×{ }, is a topological square.

Rank	Operator	Name	f-vector	Vertices	Edges	χ	Image	Dual
2	{ }×{ } Regular {4}	Dion prism Square	(2,1)*(2,1) =(4,4,1)	4	4	0		{ }+{ }
1	{ }∧{ } =2,2{ } Regular 4{ }	Dion meet Tetron	(2)*(2) =(4)	4		4		Self-dual

Triple composites

For example { }×{ }×{ }, is a topological cube has three skew version with meet operators. There are 2 skew polygons and 1 skew 1-polytope sharing all the vertices.

All the skew forms are vertex-transitive, while 2 can be considered regular: polyhedron {4,3}, skew polygon ₄{ }×{ } and skew 1-polytope { }∧{ }∧{ } = _2,2,2{ }.

Rank	Operator	Name	f-vector	Vertices	Edges	Faces	χ	Image	Dual
3	{ }×{ }×{ } = { }3 {4}×{ } Regular {4,3}	Dion triprism Square prism Cube	(2,1)*(2,1)*(2,1) =(8,12,6,1)	8	12	6 {4}	2		{ }+{ }+{ }
2	({ }×{ })∧{ } Regular {4}∧{ }	Rectangle meet Square meet	(4,4)*(2) =(8,8)	8	8		0		Self-dual
2	({ }∧{ })×{ } 4{ }×{ }	Dion meet prism Tetron prism	(4,1)*(2,1) =(8,6,1)	8	6 4 {}, 2 4{}		2		({ }∧{ })+{ }
1	{ }∧{ }∧{ } = { }(3) Regular 2,2,2{ }	Dion tri-meet	(2)*(2)*(2) =(8)	8			8		Self-dual

Quadruple composites

For example { }×{ }×{ }×{ }, is a topological tesseract. There are 4 skew polyhedra and 4 skew polygons sharing all the vertices, and finally one skew 1-polytope with 16 points.

All the skew forms are vertex-transitive, while 5 can be considered regular: 4-polytope {4,3,3}, skew polyhedron {4}∧{4} = ₂{4}, skew polygon, 4}∧₄{ }, and skew 1-polytope { }∧{ }∧{ }∧{ } = _2,2,2,2{ } = _4,4{ }.

Rank	Operator	Name	f-vector	Vertices	Edges	Faces	Cells	χ	Image	Dual
4	{ }×{ }×{ }×{ } = { }4 {4}×{ }×{ } {4}×{4}={4}2 Regular {4,3,3}	Dion prism prism prism Square prism prism Square duoprism Tesseract, tes	(2,1)4 =(4,4,1)2 =(16,32,24,8,1)	16	32	24	8	0		{ }+{ }+{ }+{ }
3	({ }×{ })∧({ }×{ }) = ({ }2)(2) {4}∧({ }×{ }) {4}∧{4} Regular 2{4} ={4,4|4}	Rectangle duomeet Square-rectangle duomeet Square duomeet	(4,4)2 =(16,32,16)	16	32	16		0		Self-dual
3	({ }×{ }×{ })∧{ } ({4}×{ })∧{ } {4,3}∧{ }	Cuboid meet Square prism meet Cubic meet	(8,12,6)*(2) =(16,24,12)	16	24	12		4		{3,4}∧{ }
3	(({ }×{ })∧{ })×{ } ({4}∧{ })×{ }	Rectangle meet prism Square meet prism	(8,8,1)*(2,1) =(16,24,10,1)	16	24	10		2		({4}∧{ })+{ }
3	{ }×{ }×({ }∧{ }) {4}×({ }∧{ }) {4}×4{ }	Rectangle-(dion meet) duoprism Square-(dion meet) duoprism Square-tetron duoprism	(4,4,1)*(4,1) =(16,20,8,1)	16	20	8		4		{4}+4{ }
2	({ }×{ })∧{ }∧{ } {4}∧{ }∧{ } Regular {4}∧4{ }	Rectangle meet meet Square meet meet Square-tetron duomeet	(4,4)*(2)2 =(16,16)	16	16			0		Self-dual
2	(({ }∧{ })×{ })∧{ } (4{ }×{ })∧{ }	Tetron prism meet	(8,6)*(2) =(16,12)	16	12			4		(4{ }+{ })∧{ }
2	({ }∧{ }∧{ })×{ } 2,2,2{ }×{ } = 2,4{ }×{ }	Dion tri-meet prism Octon prism	(8,1)*(2,1) =(16,10,1)	16	10			6		2,4{ }+{ }
2	({ }∧{ })×({ }∧{ }) 4{ }×4{ }=4{ }2	Dion meet duoprism Tetron duoprism	(4,1)2 =(16,8,1)	16	8			8		({ }∧{ })+({ }∧{ })
1	{ }∧{ }∧{ }∧{ } = { }(4) 4{ }∧4{ } = 4{ }(2) Regular 4,4{ } or 2,2,2,2{ }	Tetron duomeet Dion tetra-meet	(2)4 =(16)	16				16		Self-dual