User:Tomruen/Complex polygons
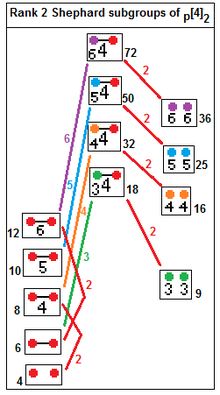
Rank 2
[edit]
Also p[4]q --> p[q]p, index q.

The symmetry of a regular complex polygon is p[q]r, called a Shephard group, analogous to a Coxeter group, while also allowing real and unitary reflections.
The rank 2 solutions that generate complex polygons are: 2[q]2, p[4]2, 3[3]3, 3[6]2, 3[4]3, 4[3]4, 3[8]2, 4[6]2, 4[4]3, 3[5]3, 5[3]5, 3[10]2, 5[6]2, and 5[4]3 or ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() .
.
Starry groups with whole q are ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() .
.
Enumeration of regular complex polygons
[edit]Coxeter enumerated this list of regular complex polygons in . Groups of the form p[2q]2 have a half symmetry p[q]p, so a regular polygon ![]()
![]()
![]()
![]() is the same as quasiregular
is the same as quasiregular ![]()
![]()
![]() .[2]
.[2]
| Group | Order | Image | Polygon | Vertices | Edges | Notes | ||
|---|---|---|---|---|---|---|---|---|
| 2[3]2 | 6 | 2{6}2 | |
3 | 3 | {} | equilateral triangle | |
| 2[q]2 | 2q | 2{q}2 | q | q | {} | regular polygons | ||
| 3[4]2 | 18 |  |
3{4}2 | 9 | 6 | 3{} | Same as 3{}×3{} or representation 3-3 duoprism | |
 |
2{4}3 | 6 | 9 | {} | representation as 3-3 duopyramid | |||
| 4[4]2 | 32 |  |
4{4}2 | 16 | 8 | 4{} | Same as 4{}×4{} or representation 4-4 duoprism or tesseract | |
 |
2{4}4 | 8 | 16 | {} | representation as 4-4 duopyramid, or 16-cell | |||
| 5[4]2 | 50 |  |
5{4}2 | 25 | 10 | 5{} | Same as 5{}×5{} or representation 5-5 duoprism | |
| 2{4}5 | 10 | 25 | {} | representation as 5-5 duopyramid | ||||
| p[4]2 | 2p2 | p{4}2 | p2 | 2p | p{} | Same as p{}×p{} or representation p-p duoprisms and {4,3,3} for p=4 | ||
| 2{4}p | 2p | p2 | {} | representation as p-p duopyramids and {3,3,4} with p=4 | ||||
| 3[3]3 | 24 |  |
3{3}3 | 8 | 8 | 3{} | representation as {3,3,4} Same as | |
| 3[6]2 | 48 |  |
3{6}2 | 24 | 16 | 3{} | Same as | |
| 2{6}3 | 16 | 24 | {} | representation as {4,3,3} | ||||
| 3[4]3 | 72 |  |
3{4}3 | 24 | 24 | 3{} | representation as {3,4,3} Same as | |
| 4[3]4 | 96 |  |
4{3}4 | 24 | 24 | 4{} | representation as {3,4,3} Same as | |
| 3[8]2 | 144 |  |
3{8}2 | 72 | 48 | 3{} | Same as | |
| 2{8}3 | 48 | 72 | {} | |||||
| 4[6]2 | 192 | 4{6}2 | 96 | 48 | 4{} | Same as | ||
| 2{6}4 | 48 | 96 | {} | |||||
| 4[4]3 | 288 | 4{4}3 | 96 | 72 | 4{} | |||
| 3{4}4 | 72 | 96 | 3{} | |||||
| 3[5]3 | 360 |  |
3{5}3 | 120 | 120 | 3{} | representation as {3,3,5} Same as | |
| 5[3]5 | 600 |  |
5{3}5 | 120 | 120 | 5{} | representation as {3,3,5} Same as | |
| 3[10]2 | 720 | 3{10}2 | 360 | 240 | 3{} | Same as | ||
| 2{10}3 | 240 | 360 | {} | |||||
| 5[6]2 | 1200 | 5{6}2 | 600 | 240 | 5{} | Same as representation as {5,3,3} | ||
| 2{6}5 | 240 | 600 | {} | |||||
| 5[4]3 | 1800 | 5{4}3 | 600 | 360 | 5{} | representation as {5,3,3} | ||
| 3{4}5 | 360 | 600 | 3{} | |||||
| Name | (p,r).m-gon | p{q}r | Cox | p | q | r | h | g | v | e | m |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Trionic square | (3,2).3-gon | 3{4}2 | 3 | 4 | 2 | 6 | 18 | 9 | 6 | 3 | |
| Trionous square | (2,3).3-gon | 2{4}3 | 2 | 4 | 3 | 6 | 18 | 6 | 9 | 3 | |
| Tetronic square | (4,2).4-gon | 4{4}2 | 4 | 4 | 2 | 8 | 32 | 16 | 8 | 4 | |
| Tetronus square | (2,4).4-gon | 2{4}4 | 2 | 4 | 4 | 8 | 32 | 8 | 16 | 4 | |
| Pentonic square | (5,2).5-gon | 5{4}2 | 5 | 4 | 2 | 10 | 50 | 25 | 10 | 5 | |
| Pentonous square | (2,5).5-gon | 2{4}5 | 2 | 4 | 5 | 10 | 50 | 10 | 25 | 5 | |
| Hexonic square | (6,2).6-gon | 6{4}2 | 6 | 4 | 2 | 12 | 72 | 36 | 12 | 6 | |
| Hexonous square | (2,6).6-gon | 2{4}6 | 2 | 4 | 6 | 12 | 72 | 12 | 36 | 6 | |
| Triadic octagon | 3{3}3 | 3 | 3 | 3 | 6 | 24 | 8 | 8 | 8/3 | ||
| (3,2).8-gon | 3{6}2 | 3 | 6 | 2 | 12 | 48 | 24 | 16 | 8 | ||
| (2,3).8-gon | 2{6}3 | 2 | 6 | 3 | 12 | 48 | 16 | 24 | 8 | ||
| Triadic 24-gon | 3{4}3 | 3 | 4 | 3 | 12 | 72 | 24 | 24 | 8 | ||
| Tetradic 24-gon | 4{3}4 | 4 | 3 | 4 | 12 | 96 | 24 | 24 | 6 | ||
| (3,2).24-gon | 3{8}2 | 3 | 8 | 2 | 24 | 144 | 72 | 48 | 24 | ||
| (2,3).24-gon | 2{8}3 | 2 | 8 | 3 | 24 | 144 | 48 | 72 | 24 | ||
| (4,2).24-gon | 4{6}2 | 4 | 6 | 2 | 24 | 192 | 96 | 48 | 24 | ||
| (2,4).24-gon | 2{6}4 | 2 | 6 | 4 | 24 | 192 | 48 | 96 | 24 | ||
| (4,3).24-gon | 4{4}3 | 4 | 4 | 3 | 24 | 288 | 96 | 72 | 24 | ||
| (3,4).24-gon | 3{4}4 | 3 | 4 | 4 | 24 | 288 | 72 | 96 | 24 | ||
| Triadic 120-gon | 3{5}3 | 3 | 5 | 3 | 30 | 360 | 120 | 120 | 40 | ||
| Pentadic 120-gon | 5{3}5 | 5 | 3 | 5 | 30 | 600 | 120 | 120 | 24 | ||
| (3,2).120-gon | 3{10}2 | 3 | 10 | 2 | 60 | 720 | 360 | 240 | 120 | ||
| (2,3).120-gon | 2{10}3 | 2 | 10 | 3 | 60 | 720 | 240 | 360 | 120 | ||
| (5,2).120-gon | 5{6}2 | 5 | 6 | 2 | 60 | 1200 | 600 | 240 | 120 | ||
| (2,5).120-gon | 2{6}5 | 2 | 6 | 5 | 60 | 1200 | 240 | 600 | 120 | ||
| (5,3).120-gon | 5{4}3 | 5 | 4 | 3 | 60 | 1800 | 600 | 360 | 120 | ||
| (3,5).120-gon | 3{4}5 | 3 | 4 | 5 | 60 | 1800 | 360 | 600 | 120 |
Enumeration of quasiregular complex polygons
[edit]The truncation of a regular complex polygon, ![]()
![]()
![]() is
is ![]()
![]()
![]() . It is quasiregular, alternating two types of edges. A regular polyhedron
. It is quasiregular, alternating two types of edges. A regular polyhedron ![]()
![]()
![]() with v vertices and e edges has qe vertices, and v+e edges of two types: v q{} edges, and e p{} edges.
with v vertices and e edges has qe vertices, and v+e edges of two types: v q{} edges, and e p{} edges.
| Group | Order | Image | Polygon | Vertices | Edges | Edge types | Notes | |
|---|---|---|---|---|---|---|---|---|
| 2[2]2 | 4 |  |
4 | 4 | 2 {} | 2 {} | Same as | |
| 2[3]2 | 6 |  |
6 | 6 | 3 {} | 3 {} | Same as | |
| 2[4]2 | 6 |  |
8 | 8 | 4 {} | 4 {} | Same as | |
| 2[5]2 | 5 |  |
10 | 10 | 5 {} | 5 {} | Same as | |
| 2[q]2 | 2q | 2q | 2q | q {} | q {} | Same as | ||
| 3[2]2 | 6 |  |
6 | 5 | 3 {} | 2 3{} | representation as triangular prism | |
| 4[2]2 | 8 |  |
8 | 6 | 4 {} | 2 4{} | representation as square prism | |
| 5[2]2 | 10 |  |
10 | 7 | 5 {} | 2 5{} | representation as pentagonal prism | |
| p[2]2 | 2p | 2p | p+2 | p {} | 2 p{} | representation as p-prism | ||
| 3[2]3 | 9 |  |
9 | 6 | 3 3{} | 3 3{} | representation as 3-3 duoprism Same as | |
| 3[2]4 | 12 |  |
12 | 7 | 3 4{} | 4 3{} | representation as 3-4 duoprism | |
| 4[2]4 | 16 |  |
16 | 8 | 4 4{} | 4 4{} | representation as 4-4 duoprism, tesseract | |
| 5[2]5 | 25 | 25 | 10 | 5 5{} | 5 5{} | representation as 5-5 duoprism Same as | ||
| p[2]q | pq | pq | p+q | p q{} | q p{} | representation as p-q duoprism Same as | ||
| 3[4]2 | 18 |  |
18 | 15 | 9 {} | 6 3{} | ||
| 4[4]2 | 32 |  |
32 | 24 | 16 {} | 8 4{} | ||
| p[4]2 | 2p2 | 2p2 | p2+2p | p2 {} | 2p p{} | |||
| 3[3]3 | 24 |  |
24 | 16 | 8 3{} | 8 3{} | Same as | |
| 3[6]2 | 48 | 48 | 40 | 16 3{} | ||||
| 3[4]3 | 72 |  |
72 | 48 | 24 3{} | 24 3{} | Same as | |
| 4[3]4 | 96 | 96 | 48 | 24 4{} | 24 4{} | Same as | ||
| 3[8]2 | 144 | 144 | 120 | 72 {} | 48 3{} | |||
| 4[6]2 | 192 | 192 | 144 | 96 {} | 48 4{} | |||
| 4[4]3 | 288 | 288 | 168 | 96 3{} | 72 4{} | |||
| 3[5]3 | 360 | 360 | 240 | 120 3{} | 120 3{} | Same as | ||
| 5[3]5 | 600 | 600 | 240 | 120 5{} | 120 5{} | Same as representation as {5,3,3} | ||
| 3[10]2 | 720 | 720 | 600 | 360 {} | 240 3{} | |||
| 5[6]2 | 1200 | 1200 | 840 | 600 {} | 240 5{} | |||
| 5[4]3 | 1800 | 1800 | 960 | 600 3{} | 360 5{} | |||
Enumeration of uniform complex polyhedra
[edit]3[3]3[3]3 family
[edit]| Polyhedron | Image | Vertices | Edges | Faces | Notes | ||||
|---|---|---|---|---|---|---|---|---|---|
(27) |
(72) |
(27) | |||||||
 |
27 | 72 |
Hessian polyhedron representation as 221 Same as | ||||||
 |
72 | 216 |
representation as 122 Same as | ||||||
| 216 |  |
||||||||
| 216 |  |
Same as | |||||||
| 648 |  |
 |
 |
Same as | |||||
3[3]3[4]2 family
[edit]| Polyhedron | Image | Vertices | Edges | Faces | Notes | |||
|---|---|---|---|---|---|---|---|---|
(54) |
(216) |
(72) | ||||||
 |
72 | 216 |
 |
Same as | ||||
| 216 |  |
 |
Same as Real representation r(221) | |||||
| 54 | 216 |
|||||||
| 648 |  |
 |
Same as | |||||
| 432 |  |
Real representation t(221) | ||||||
| 432 |  |
 |
||||||
| 1296 |  |
 |
||||||
2[3]2[4]3 family
[edit]| Polyhedron | Image | Vertices | Edges | Faces | Notes | |||
|---|---|---|---|---|---|---|---|---|
(27) |
(12) |
(9) | ||||||
| 9 | 27 |
Same as | ||||||
| 12 | ||||||||
| 27 | 27 |
 |
Same as | |||||
| 54 |  |
|||||||
| 81 | ||||||||
| 81 |  |
 |
||||||
| 162 |  |
 |
||||||
2[3]2[4]4 family
[edit]| Polyhedron | Image | Vertices | Edges | Faces | Notes | |||
|---|---|---|---|---|---|---|---|---|
(64) |
(48) |
(12) | ||||||
| 12 | 48 |
|||||||
| 48 | ||||||||
| 64 | 48 |
Same as | ||||||
| 96 |  |
|||||||
| 192 | ||||||||
| 192 | ||||||||
| 384 |  |
 |
||||||
Regular complex apeirogons
[edit]




 is a mixture of two regular apeirogons
is a mixture of two regular apeirogons 

 and
and 

 , seen here with blue and pink edges.
, seen here with blue and pink edges. 

 has only one color of edges because q is odd, making it a double covering.
has only one color of edges because q is odd, making it a double covering.Coxeter expresses them as δp,r
2 where q is constrained to satisfy q = 2/(1 – (p + r)/pr).[3]
Among the aperiogons, four are self-dual (when p = r), while eight exist as dual polytope pairs. Only one, {∞}, is real. The 12 pairs (p, r) as corresponding to aperiogons are (2,2), (3,2), (2,3), (3,3), (4,2), (2,4), (4,4), (6,2), (2,6), (6,3), (3,6), and (6,6).
Rank 2 complex apeirogons have symmetry p[q]r, where 1/p + 2/q + 1/r = 1. There are 8 solutions: 2[∞]2, 3[12]2, 4[8]2, 6[6]2, 3[6]3, 6[4]3, 4[4]4, and 6[3]6 or ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() .
.
Including affine nodes, there are 3 more infinite solutions: ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() , the first is an index 2 subgroup of the second, while the last is starry.
, the first is an index 2 subgroup of the second, while the last is starry.
A regular complex apeirogon p{q}r has p-edges and q-gonal vertex figures. The dual apeirogon of p{q}r is r{q}p. An apeirogon of the form p{q}p is self-dual. Groups of the form p[2q]2 have a half symmetry p[q]p, so a regular apeirogon ![]()
![]()
![]()
![]() is the same as quasiregular
is the same as quasiregular ![]()
![]()
![]() .[4]
.[4]
Apeirogons can be represented on the Argand plane share four different vertex arrangements. Apeirogons of the form 2[q]r have a vertex arrangement as {q/2,p}. The form p[q]2 have vertex arrangement as r{p,q/2}.
| Space | Group | Polygon | Edge type | rep.[5] | Picture | Notes | |
|---|---|---|---|---|---|---|---|
| 2[∞]2 = [∞] | δ2,2 2 = {∞} |
|
{} | Real apeirogon Same as | |||
| p[q]r | δp,r 2 = p{q}r |
p{} | |||||
| 3[12]2 | δ3,2 2 = 3{12}2 |
3{} | r{3,6} |  |
Same as | ||
| δ2,3 2 = 2{12}3 |
{} | {6,3} |  |
||||
| 3[6]3 | δ3,3 2 = 3{6}3 |
3{} | {3,6} | Same as | |||
| 4[8]2 | δ4,2 2 = 4{8}2 |
4{} | {4,4} |  |
Same as | ||
| δ2,4 2 = 2{8}4 |
{} | {4,4} |  |
||||
| 4[4]4 | δ4,4 2 = 4{4}4 |
4{} | {4,4} |  |
Same as | ||
| 6[6]2 | δ6,2 2 = 6{6}2 |
6{} | r{3,6} | Same as | |||
| δ2,6 2 = 2{6}6 |
{} | {3,6} | |||||
| 6[4]3 | δ6,3 2 = 6{4}3 |
6{} | {6,3} |  |
|||
| δ3,6 2 = 3{4}6 |
3{} | {3,6} | |||||
| 6[3]6 | δ6,6 2 = 6{3}6 |
6{} | {3,6} |  |
Same as | ||
Quasiregular apeirogons
[edit]| p[q]r |
p{q}r |
t(p{q}r) |
r{q}p |
|---|---|---|---|
| ∞[3[3]]∞ |  | ||
| ∞[2]∞ |  | ||
| ∞[4]2 |  | ||
| 4[4]4 |  |
 |
 |
| 4[8]2 |  |
 |
 |
| 6[6]2 |  |
 |
 |
| 6[4]3 |  |
 |
 |
| 3[12]2 |  |
 |
 |
| 3[6]3 |  |
 |
 |
| 6[3]6 |  |
 |
 |
Quasiregular
[edit]There are 7 quasiregular complex apeirogons which alternate edges between two dual complex apeirogons.
| p[q]r | 4[4]4 | 4[8]2 | 6[6]2 | 6[4]3 | 3[12]2 | 3[6]3 | 6[3]6 |
|---|---|---|---|---|---|---|---|
p{q}r (Regular) |
 |
 |
 |
 |
 |
 |
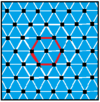 |
(Quasiregular) |
 |
 |
 |
 |
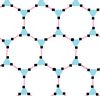 |
 |
 |
r{q}p (Regular dual) |
 |
 |
 |
 |
 |
 |
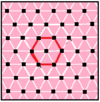 |
Rank 3
[edit]




 - 27
- 27

 - 54
- 54



 - 64
- 64


 - 96
- 96



 - 125
- 125


 - 150
- 150



 - 162
- 162

 - 336
- 336



 - 384
- 384



 - 648
- 648



 - 750
- 750



 - 1296
- 1296

 - 2160
- 2160

 - 2160
- 2160
References
[edit]- ^ Coxeter, Complex Regular Polytopes, p. 177, Table III
- ^ Regular Complex Polytopes, Table IV. The regular polygons. pp. 178-179
- ^ Coxeter, Regular Complex Polytopes, Table VI. The regular honeycombs. p. 111, 136.
- ^ Coxeter, Regular Complex Polytopes, Table IV. The regular polygons. pp. 178–179
- ^ Coxeter, Regular Complex Polytopes, 11.6 Apeirogons, pp. 111-112







