User:Tea2min/Scratch
Appearance
Polyhedra from equilateral triangles and squares only
[edit]-
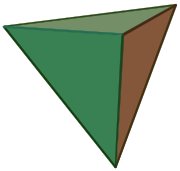
Tetrahedron (triangular pyramid)
Pyramids
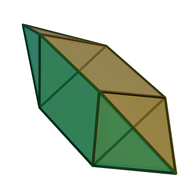
[edit]Elongated triangular pyramid
-
Tetrahedron (triangular pyramid)
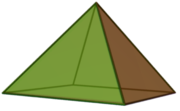
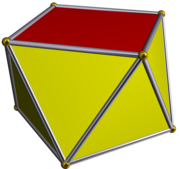
Square pyramid
-
Square pyramid (J1)
Bipyramids
[edit]-
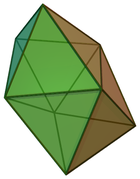
Square bipyramid (Octahedron)
-
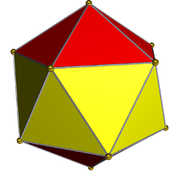
Pentagonal gyroelongated bipyramid (icosahedron)
Triangular prism
[edit]Triangular prism
Triangular prism
Triangular prism
Square antiprism
[edit]Square antiprism
-
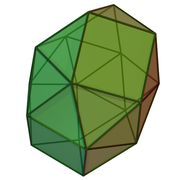
Snub disphenoid (J84)
-
Snub square antiprism (J85)
Bicupolae
[edit]Triangular bicupolae
-
Triangular orthobicupola (J27)
-
Triangular gyrobicupola (Cuboctahedron)
Square bicupolae
-
Square orthobicupola (J28)
-
Square gyrobicupola (J29)
Elongated triangular orthobicupola
Gyroelongated triangular bicupola
-
Triangular orthobicupola (J27)
-
Triangular gyrobicupola (Cuboctahedron)
Elongated square orthobicupola
-
Square orthobicupola (J28)
-
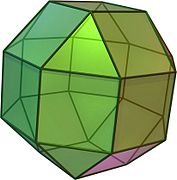
Elongated square orthobicupola (rhombicuboctahedron)
Elongated square gyrobicupola
-
Square gyrobicupola (J29)
Gyroelongated square bicupola
-
Square orthobicupola (J28)
-
Square gyrobicupola (J29)
Others
[edit]History of Scheme
[edit]Older standards
[edit]- RRS ("The Revised Report on Scheme", G.L. Steele et al., AI Memo 452, MIT, Jan 1978)
- R2RS ("The Revised Revised Report on the Algorithmic Language Scheme", Clinger, AI Memo 848, MIT Aug 1985)
- R3RS ("Dedicated to the Memory of ALGOL 60", Revised(3) Report on the Algorithmic Language Scheme)
- R4RS (Revised(4) Report on the Algorithmic Language Scheme)
R5RS and R6RS are already referenced from Scheme (programming language).
History of call/cc
[edit]- interaction with
dynamic-wind(R5RS call/cc & dynamic-wind in terms of r4rs, faking dynamic-wind, dynamic-wind, A new specification for dynamic-wind, call/wc, and call/nwc, implementing dynamic-wind) - interaction with
valuesandcall-with-values
Cosine powers
[edit]
Hermite polynomials
[edit]
Persons with first name Hanan
[edit]- Hanan al-Shaykh, a Lebanese author of contemporary Arab women's literature
- Hanan Ashrawi, a Palestinian legislator, activist, and scholar
- Hanan Habibzai, an Afghan journalist and writer
- Hanan Qassab Hassan, a prominent Syrian writer and academic
- Hanan Ahmed Khaled, an Egyptian female athlete
- Hanan Porat, a former Israeli politician
- Hanan Rubin, a German-born Israeli politician
- Hanan Tork, an Egyptian actress and former ballerina
Semimathematics
[edit]- Semicomputable function
- Semi-continuity
- Semi-deterministic Büchi automaton
- Semi-differentiability
- Semidirect product
- Semi-elliptic operator
- Semifield
- Semigroup
- Semigroup action
- Semigroupoid
- Semi-Hilbert space
- Semi-implicit Euler method
- Semi-infinite
- Semi-infinite programming
- Semilattice
- Semi-local ring
- Seminorm → Norm (mathematics)
- Seminormal subgroup
- Semiorder
- Semiperfect number
- Semiperfect ring
- Semipermutable subgroup
- Semiprime
- Semiprime ring
- Semiprimitive ring
- Semiregular space
- Semiring
- Semi-s-cobordism
- Semiset
- Semisimple algebra
- Semisimple algebraic group
- Semisimple Lie algebra
- Semisimple module
- Semi-simple operator
- Semistable abelian variety
- Semi-Thue system
Field of rational functions
[edit]In mathematics, given a field K, the field of rational functions K(X) is the field of all rational functions in the variable X with coefficients in K. It is the field of fractions of the polynomial ring K[X].
The field of rational functions is not to be confused with the field of rationals, which is the field of fractions for the ring of integers.
Given a field K, the ring K[X] of polynomials in the variable X with coefficients in K is an integral domain so that the field of fractions of K[X] can be constructed. K(X)/K is a field extension of infinite degree.
References
[edit]- David Dummit (2003). Abstract Algebra (third ed.). Wiley. ISBN 0-471-43334-9.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help)