User:Peter coxhead/Work/Phyletic terminology
| This is a Wikipedia user page. This is not an encyclopedia article or the talk page for an encyclopedia article. If you find this page on any site other than Wikipedia, you are viewing a mirror site. Be aware that the page may be outdated and that the user in whose space this page is located may have no personal affiliation with any site other than Wikipedia. The original page is located at https://en.wikipedia.org/wiki/User:Peter_coxhead/Work/Phyletic_terminology. |
The purpose of this page is to help me sort out in my own mind the confusion in the literature over the definitions of the terms "monophyly", "paraphyly" and "polyphyly". If and when (a) I'm clear (b) I'm convinced that there are suitable sources, I will try to edit the relevant articles.
Please leave any comments on the Talk page.
Comparison of terminology
[edit]It's clear that the meaning of some key terms, particularly "monophyly", has changed. The table below compares current terminology with the older terminology and an alternative terminology which some authors have supported.
| Type | Older/alternative | Current consensus | ||
|---|---|---|---|---|
| 1 | monophyletic | holophyletic | monophyletic | |
| 2 | paraphyletic | paraphyletic | non-monophyletic | |
| 3 | polyphyletic | polyphyletic | ||
Mayr & Bock (2002, p. 181f.) say that the original distinction was only between "monophyletic" and "polyphyletic" (or non-"monophyletic"), i.e. Types 1 and 2 in the table were not distinguished (see also Ashlock (1979, p. 443)). The introduction to the English-speaking world of the distinction between Types 1 and 2 and the changed terminology was due to Hennig (1966). He introduced the term "paraphyletic", reducing "monophyletic" to a narrower sense (i.e. only Type 1 in the table above).
In an attempt to maintain the wider sense of "monophyly", Ashlock (1971, p. 65) suggested "holophyly" as an alternative to the restricted Hennig sense of "monophyly". The older sense of "monophyly" would then include both "holophyly" and "paraphyly". The new term is commended by Mayr & Bock (2002, p. 175):
[Hennig (1950), Hennig (1966)] also transferred the traditional term monophyly to the new concept of phylogeny that caused great confusion [...]. To end this chaos, Ashlock (1971) introduced the term holophyly for Hennig’s new concept.
However, there's no evidence that this usage has entered the mainstream of biology. [PC comment: Hostility to the change of terminology and hostility to cladistics as a discipline – and in particular the insistence on holophyletic groups in classifications – seem to have become confused. Although related, logically these are distinct issues.]
The right-hand part of the table contains the current consensus usage (see, as just one example, Oosterbroek 1987).
In terms of the derivation of the words used, the older terminology is undoubtedly more logical: the binary alternative to 'mono' (one) is 'poly' (many), so whatever is not monophyletic should be polyphyletic. However, more logical or not, the terminology most used today is that shown on the right of the table. In this terminology, it is important to be clear that 'non-monophyletic' does not then mean polyphyletic but instead either paraphyletic or polyphyletic.
From this point on, the modern senses (right-hand part of the table above) are always meant.
"-phyly" vs. "-clady"
[edit]A common definition of "monophyletic" is that a monophyletic group is one that consists of an ancestor and all of its descendants (and nothing else).[citation needed]
However, there are definitions which do not require all the ancestors to be included in the group. Thus Nelson (1971) (cited in Podani 2010) defines a monophyletic group as one "into which have been placed all species or groups of species that are assumed to be descendants of a single hypothetical ancestral species". A definition which excludes all or some ancestors is more appropriate when considering cladograms which show only the branching pattern of the leaf nodes and in which the internal nodes are not taxa but serve only to define this pattern.
Podani (2010) suggested that the distinction between the inclusion and exclusion of ancestors should be recognized in a parallel set of terms to "monophyly", "paraphyly" and "polyphyly", namely "monoclady", "paraclady" and "polyclady". The former terms include ancestors, the latter ones do not. It's too soon to tell whether this distinction will catch on. Unless or until it does, it appears to be the case that sources will continue to use terms like "monophyletic" to either include or exclude ancestors.
Definitions
[edit]At this point, the focus is on definitions which are based solely on the shape (topology) of a cladogram, rather than on apomorphies or other characteristics. Discussion is also focussed on species, not individuals or higher level taxa.
Ancestors included or not?
[edit]Definitions can start from an ancestor or from its descendants. Starting with an ancestor, as noted above, a monophyletic group of species can be defined as the ancestral species plus all of its descendant species (and no other species).
The reverse direction is more appropriate when starting from a cladogram which represents the hypothesized phylogeny of a group of species. In such a cladogram, the internal nodes serve only to indicate the pattern of branching. The question is whether the leaf nodes form a monophyletic group. (Podani would call this a "monocladistic" group, but as he notes, the term "monophyletic" is regularly used in this situation.)
A group of leaf nodes in a cladogram are a monophyletic group if the branching pattern shows that they are all descendants of a common ancestor and there are no other descendants of this ancestor. By this definition, the common ancestor will be the nearest common ancestor.
Defining a paraphyletic group
[edit]A paraphyletic group of species has been defined as an otherwise monophyletic group lacking one or more smaller monophyletic groups.[citation needed]
When only one monophyletic group is removed, this definition is quite satisfactory. However, since any individual species is, by definition, monophyletic, apparently any random set of species can be removed from a monophyly to leave a paraphyly, meaning that there's no way of distinguishing between a paraphyly and polyphyly. Further, well-known polyphylies, such as mammals plus birds, appear to be paraphylies: in the case of mammals plus birds, a number of monophyletic groups from within the traditional reptiles are missing from an otherwise monophyletic group of amniotes.
The core idea needed to solve this problem was suggested by Nelson (1971) and is developed in detail in Oosterbroek (1987) (see also Podani 2010). The required definition is that a group of species is paraphyletic if it consists of the smallest monophyletic group which includes all of its members but from which one or more monophyletic groups are excluded and in each case the sister group of the excluded group is completely included. Note that when a single monophyletic group is removed its sister group is by definition included, so that the sister group qualification is only needed when more than one monophyletic group is excluded.
An alternative wording (closer to Oosterbroek's) is that a group of species is paraphyletic if it includes all the descendants of their most recent common ancestor excluding one or more monophyletic groups, for each of which the sister group is completely included in the group.
The reason for requiring the smallest monophyletic group or the most recent common ancestor is easier to explain with an example.
Artificial example
[edit]Consider the following set of taxa, where each of A, B, C, D, E and F could be single species or a monophyletic group of species. As is usual with cladograms of this form, we are only interested in the status of groups of the leaf nodes, excluding any hypothetical ancestors. The lines and internal nodes show only the branching patterns.
| |||||||||||||||||||||||||||||||
Given that ancestors are ignored, A+B+C+D+E form a monophyletic group, i.e. a clade. Now consider removing species from this group. The interesting cases are when at least part of the A+B and the C+D+E clades remain, since this doesn't alter the most recent common ancestor.
- Removing any one of A, B, C, D or E leaves a paraphyletic group, as does removing C+D.
- Removing B and E to leave A+C+D produces a paraphyletic group. The sister group of B is A; the sister group of E is C+D; both sister groups are included in A+C+D; hence A+C+D is paraphyletic.
- Removing B and C to leave A+D+E produces a paraphyletic group. The sister group of B is A; the sister group of C is D; both sister groups are included in A+D+E; hence A+D+E is paraphyletic.
- Removing B, C and E to leave A+D produces a polyphyletic group. The sister group of B is A; the sister group of C is D; the sister group of E is C+D; all three sister groups are not included in A+D as C is missing; hence A+D is polyphyletic.
The requirement to start from the smallest monophyletic group or all the descendants of the most recent common ancestor can be seen as follows. If B+C+D+E is treated as A+B+C+D+E minus A, then it forms a paraphyletic group. However, if B+C+D+E is treated as A+B+C+D+E+F minus A and F, then it would appear not to be a paraphyletic group, since the sister group of F, namely A+B+C+D+E, is not completely included.
Real example
[edit]Consider the cladogram used in the Cladistics article. Ignore any question of whether this cladogram is correct or not.
| |||||||||||||||||||||||||
- What is the status of Testudines+Lepidosauria+Crocodilia? The complete monophyletic group which includes their most recent common ancestor is Testudines+Lepidosauria+Crocodilia+Aves. Aves is excluded; its sister group is Crocodilia; this is included; hence Testudines+Lepidosauria+Crocodilia is a paraphyletic group.
- What is the status of Mammalia+Aves? The complete monophyletic group which includes their most recent common ancestor is Mammalia+Testudines+Lepidosauria+Crocodilia+Aves. Lepidosauria is one of the excluded taxa; its sister group is Crocodilia+Aves; Crocodilia is not included; hence Mammalia+Aves is a polyphyletic group.
Diagram to illustrate polyphyly
[edit]As of 15 August 2012, the diagram below is used in a number of articles to illustrate "polyphyly" (and other "phylies"), defined from the geometry (topology) of the cladogram rather than by apomorphies.
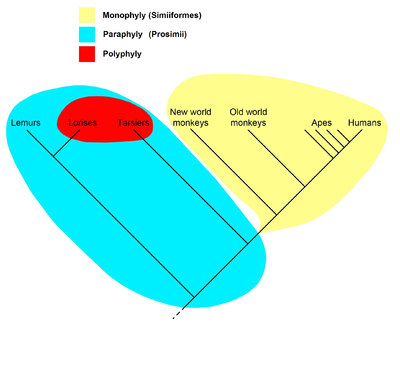
I'm interested in the "red group". Simplifying the diagram a bit, we have:

Why are (lorises+tarsiers) polyphyletic? According to one definition, because their last common ancestor (LCA) isn't included. But on this definition, monkeys represented as below are polyphyletic as well:

There's no material difference between Fig. 1 and Fig. 2 that I can see which makes them different kinds of "phylies".
Now add the ancestors to both:


Both are now paraphylies. (Lorises+tarsiers) are doubly paraphyletic: the clade of primates has two clades excluded: lemurs and simians. Monkeys are singly paraphyletic: the clade of simians has the clade of humanoids excluded.
But now consider this diagram.

What is the red group here? Based on the definition of paraphyly that it is a clade minus one or more clades which also includes its LCA, it's a quadruple paraphyly: the clade of primates has the clades lemurs, tarsiers, New World monkeys and Old World monkeys excluded.
Oosterbroek (1987) provided a tighter definition of paraphyly (see #Defining a paraphyletic group above), which rules out Fig. 5 as a paraphyly (because e.g. the sister group of the excluded tarsiers, namely the simians, is not wholly included). With his definition it's easy to illustrate a polyphyly. But his definition seems to be have been ignored by later workers. So the problem (at least for me) is that without Oosterbroek's qualification, any combination of terminal groups is paraphyletic by the current definition provided their LCA is included. So what is a polyphyly?
Discussion
[edit]Please feel free to add any comments here!
- Ok, here we go: The initial useses of the terms mono-, para- and polyphyly were quite exact. They were used fairly much like the tri-colour diagram suggests. The problem here is that this use was based on a basically Linnaean understanding of systematics, where a lot of assumptiosn are built in and not always clearly expressed. With the use of computer programs to find phylogeny, the race was on to find exact and explicit definitions, hence the "Clade A = critter a + critter b"-type of definitions, which eventually lead to the crown-group type definitions. With these, one need to be careful.
- The group New-World monkeys and Old World monkeys can be understood in three different ways: 1) The Linnaean parvorder Platyrrhini and the Linnaean family Cercopithecidae, 2) the phylogenetically defined group of e.g. Cebus + Macaca or 3) as two crown groups Cebus + Ateles and Macaca + Colobus. In proper Linnaean systematics, all animals should belong in a family, order etc, and preferably one that already exists , so that alternative 1 can be argued to represent the stem as well as the crown. This group also correspond to the common understanding of "monkey", effectively figure 4 (a grade). Alternative 2 is clearly a clade, the Simiiformes. Alternative 3 is obviously two separate crown groups with the common ancestor excluded, and is polyphyletic.
- To answer the basic question, there is no formal difference between the polyphyly of figure 1 and 2. The difference is that the expressed group "New-World monkeys and Old World monkeys" is very open to misinterpretation. There is formally and technically no reason not to use figure 2 as an example, but there are considerable practical reasons not to, unless we use it to illustrate the points above. The figure 1 has the benefit that it works to illustrate polyphyly independently of whether the reader is having a Linnaean or phylogenetic approach at the back of his/her mind. Petter Bøckman (talk) 11:47, 15 August 2012 (UTC)
- I've always accepted that polyphyly and paraphyly can only be distinguished by explicit exclusion or inclusion of the nodes (=common ancestors). In the 1990s, at least, this was a common argument against paraphyletic groups, since they differed from polyphyletic groups only through this explicit description.
- But the commonest knowledge-based use of paraphyletic groups is to represent evolutionary grades. A grade can be specified through specifying a clade and the included clades to be taken out of it. By this grade-focused definition, a paraphyletic group will always be continuous across a tree.
- Although I find all this interesting from a philosophical and biological standpoint, I think for Wikipedia purposes what we need is to list the irreconcilable different definitions of each of these terms, and discuss how these differences have played out in the literature.--Curtis Clark (talk) 14:25, 15 August 2012 (UTC)
- You're right. We also need to mention how the term polyphyly has been used to cover both poly- and paraphyly just for this reason. It is confusing to the layman (and quite irritating to me as a professional). Petter Bøckman (talk) 15:35, 15 August 2012 (UTC)
- Petter, it's very confusing and irritating to me, both as a lay biologist and as a professional computer scientist! Peter coxhead (talk) 23:10, 15 August 2012 (UTC)
- I suggest that the definitions of paraphyly and polyphyly, in the article leads, be based not on the geometries of cladograms but rather on the characterizations in Hennig 1965, pp. 103–104: paraphyly rests on symplesiomorphy and polyphyly on convergence. Hennig uses cladograms merely for illustration. Wikipedia articles can then go on to discuss geometric considerations and divergent definitions. WP:UNDUE prohibits us from presenting either the objection that Peter C. notes above or Oosterbroek's solution to it. To be sure, symplesiomorphies can be artificially constructed corresponding to polyphyletic groups, but only natural predicates are of value to science and only they are considered by Hennig. By "natural" I mean "projectible" in Nelson Goodman's sense (Schwartz, Scheffler & Goodman (1970)). The general reader need not be bothered with contorted predicates, defined only to make a theoretical point. "Nocturnal primate", however, is projectible; if the group arose by convergence in lorises and tarsiers, then it is polyphyletic, not paraphyletic. Monkeys, on the other hand, are paraphyletic, not polyphyletic. Peter M. Brown (talk) 16:02, 15 August 2012 (UTC)
Peter, I think that using Hennig's definitions as the main ones in the lead would not be right. Sure, this is how it started, and I entirely agree that the character-based definitions are coherent (whereas at present I don't think that the geometry-based ones are). However, the terms are not now defined or used this way in almost all current literature. Cladograms are built using computer programs and characters discussed, if at all, 'backwards' from the geometry.
- Look for example at how Stevens defines "paraphyletic" and "polyphyletic" on the very influential APweb site here. Characters aren't mentioned.
- Just to take one paper from an area I've been reading about recently (phylogeny of arthropods), when Carapelli et al. (2007) use "paraphyly" in their title "Phylogenetic analysis of mitochondrial protein coding genes confirms the reciprocal paraphyly of Hexapoda and Crustacea" they don't mean anything to do with characters (which would anyway be hardly comprehensible mitochondrial gene sequences) but that the geometry of their cladograms shows paraphyly.
Wikipedia articles must reflect the literature as it is, which means we need to explain current usage. Peter coxhead (talk) 17:12, 15 August 2012 (UTC)
- I have not (and don't expect to) read the Carappelli et al. article carefully enough to tell; are you sure that they're really not judging that certain characters of mitochondrial gene sequences are symplesiomorphic, thus using "paraphyly" in Hennig's sense?
- Do you suggest using the APweb definition in the Paraphyly lead? I thought that we had decided that the current text, which is more restrictive, was OK.
- Do I gather from their article title that the monophyly of Hexapoda is controversial? Neutrality would then require that we change both the Hexapoda and the Paraphyly articles.
- Peter M. Brown (talk) 18:08, 15 August 2012 (UTC)
- Instead of starting with a flat-out definition, could we take a historical approach?
- Paraphyly is a property of some groups of organisms and families of languages. The entomologist Willi Hennig coined the term paraphyletic for groups of organisms characterized by a symplesiomorphy, a trait or set of traits inherited from a common ancestor but not shared by all descendents of that ancestor. An example is the prokaryotes, organisms lacking a nucleus in their cells; all prokaryotes are descended from a primitive prokaryote, but other descendents—animals, for example—do have cells with nucleii and so are not prokaryotes. More recent writers have generally defined paraphyly solely in terms of ancestral relationships rather than mentioning traits. One such definition. . . .
- In this manner we could present an adequate definition while sticking to verifiable (historical) facts. Peter M. Brown (talk) 22:45, 15 August 2012 (UTC)
- Yes, I think that's the right approach, but it needs to be extended, to give not just "one such definition" (you may not have meant literally "one") but to give a number of competing definitions. However, I still have the problem that usage and definitions don't seem to match.
- Returning to your earlier points:
- Carappelli et al. are definitely not using paraphyly in Hennig's sense. The phrase "reciprocal paraphyly" gets about 90 hits in Google Scholar, mostly very recent (so this term should probably be in the Paraphyly article). Looking at some of the articles, this usage means that a monophyly is exhaustively divided into two (or more?) paraphylies. Thus (hexapods+crustaceans)=Pancrustacea are a clade, but neither hexapods nor crustaceans are a clade, with each group described as a "paraphyly". I think this is not possible given traditional definitions of paraphyly. Assuming this phylogeny of Pancrustacea is correct, traditional Crustacea is a paraphyly in Hennig's sense (their similarities are symplesiomorphies) whereas the hexapods represent separate and convergent evolution of six-leggedness + some adaptations to a terrestrial existence and so are a polyphyly in Hennig's sense. Some traditional geometrical definitions lead to a monophyly minus a paraphyly necessarily being a polyphyly (as Curtis Clark has argued elsewhere I seem to remember).
- (Aside) I think it's becoming a mainstream view as of 2012 that neither Hexapoda nor Crustacea as traditionally defined are monophyletic. Although details aren't clear, I don't think that this is particularly controversial at present (the Carappelli et al. article cites about 15 other papers as supporting this view). There seems to be a consensus view that the main hexapod groups, e.g. insects s.s., collembolans and diplurans, are probably separately nested inside the crustaceans as traditionally defined.
- So perhaps we can agree that:
- Discussion of the "phylies" needs to take a historical approach.
- Multiple definitions need to be given and illustrated, including when these conflict.
- Somehow we need to explain how the terms are currently used which may not be consistent with formal definitions.
- I think this approach strengthens my long held view that having three articles on Monophyly, Paraphyly and Polyphyly is a serious mistake. The last two cannot be understood independently of Monophyly and each other. Peter coxhead (talk) 23:03, 15 August 2012 (UTC)
- So perhaps we can agree that:
- (ec) That's indeed an effective way to get Hennig's definition in (and if it's not mentioned there, it should be mentioned later). I think it's important to cover both tree-based and character-based definitions. Is there an example of a character-based group that doesn't fit a tree-based definition? The only way I could envision that would be through imprecision of the term "symplesiomorphy".--Curtis Clark (talk) 23:13, 15 August 2012 (UTC)
- Just a note: This should be in terms understandable to the layman. I happen to be a zoologist, if I were not, very little of the above would be understandable. Petter Bøckman (talk) 08:28, 16 August 2012 (UTC)
- Absolutely! (But first we need to understand and agree among ourselves, which we seem now to be coming to do.) Peter coxhead (talk) 08:40, 16 August 2012 (UTC)
- @Curtis Clark: My feeling is that there isn't an example of a character-based group that doesn't fit a tree-based definition. Given a group based explicitly on characters, you can then draw a tree which represents that group. Of course the group and the resulting tree may be wrong as to the actual phylogeny (e.g. because the characters aren't actually synapomorphies or symplesiomorphies) but the tree and the characters will necessarily agree.
- I now think that Petter was right in his earlier comment above. In the late 2000s at least, those who work with computer-generated trees based on molecular data have effectively abandoned the distinction between paraphyly and polyphyly. There are monophyletic groups and non-monophyletic groups; non-monophyletic groups may then indifferently be called "paraphyletic", as in the example of "reciprocal paraphyly", or may be called "polyphyletic" when they are paraphyletic by older definitions.
- I believe that the reason is that, contrary to what I first thought, there is no purely geometrical way of differentiating paraphylies from polyphylies (with the sole exception of Oosterbroek's ignored definition). Geometrically, the red group in my Fig. 5 is a paraphyly by the definitions in current use (explicit or implicit). Only when you know what the terminals are do you realize that it isn't sensible to call this group a paraphyly, i.e. you need to know some characters to decide. Peter coxhead (talk) 08:40, 16 August 2012 (UTC)
- The "sensible rule" to me points up a crucial consideration: no modern biologist argues for the value of polyphyletic groups; they are identified in order to be eliminated. Fig. 5 would exist in modern biology only if someone believed it was a grade, which implies that there are characters to support it whether they are explicitly enumerated or not. Whether any of us think it is a good idea is another issue, but effectively irrelevant.--Curtis Clark (talk) 01:51, 17 August 2012 (UTC)
- If it can be sourced, the point that "those who work with computer-generated trees based on molecular data have effectively abandoned the distinction" should certainly be noted. It does not follow that, for the rest of us, non-monophyletic groups may indifferently be called paraphyletic or polyphyletic, nor that Oosterbroek's sister-group condition is the only geometric way of making the distinction. A group is paraphyletic if it can be represented geometrically as a clade minus a few subclades; it is polyphyletic if many subclades must be excluded in such a representation. The invertebrates are paraphyletic because only one subclade needs to be left out, while the flightless birds are polyphyletic because including both ostriches and penguins but no species of flying birds would require the exclusion of a large number of subclades of the Neognathae. To be sure, "few" and "many" are vague terms, so this vagueness is inherited by "paraphyletic" and "polyphyletic", and molecular geneticists perhaps cannot use the terms because they are operating in the gray area in between, but this need not trouble the rest of us. Most adjectives have some degree of vagueness. The distinction I propose is, I think, much closer to the traditional use of the -phyletic terms than one relying on the Oosterbroek criterion. It is unsourced and therefore cannot be used in an article (I still favor using character-based criteria, historically presented), but it does contest the claim that non-monophyletic groups, in general, may indifferently be called paraphyletic or polyphyletic unless characters are considered. Peter M. Brown (talk) 18:16, 16 August 2012 (UTC)
- I explicitly disagree with the "few subclades/many subclades" distinction, and I would not want it in the article without a clear reference to a reliable source. My biggest issue is "how many is many?" A subjective definition renders the term "paraphyletic" more or less useless, and I'm not willing to say that's the best we can do.--Curtis Clark (talk) 01:51, 17 August 2012 (UTC)
- If it can be sourced, the point that "those who work with computer-generated trees based on molecular data have effectively abandoned the distinction" should certainly be noted. It does not follow that, for the rest of us, non-monophyletic groups may indifferently be called paraphyletic or polyphyletic, nor that Oosterbroek's sister-group condition is the only geometric way of making the distinction. A group is paraphyletic if it can be represented geometrically as a clade minus a few subclades; it is polyphyletic if many subclades must be excluded in such a representation. The invertebrates are paraphyletic because only one subclade needs to be left out, while the flightless birds are polyphyletic because including both ostriches and penguins but no species of flying birds would require the exclusion of a large number of subclades of the Neognathae. To be sure, "few" and "many" are vague terms, so this vagueness is inherited by "paraphyletic" and "polyphyletic", and molecular geneticists perhaps cannot use the terms because they are operating in the gray area in between, but this need not trouble the rest of us. Most adjectives have some degree of vagueness. The distinction I propose is, I think, much closer to the traditional use of the -phyletic terms than one relying on the Oosterbroek criterion. It is unsourced and therefore cannot be used in an article (I still favor using character-based criteria, historically presented), but it does contest the claim that non-monophyletic groups, in general, may indifferently be called paraphyletic or polyphyletic unless characters are considered. Peter M. Brown (talk) 18:16, 16 August 2012 (UTC)
- Personally, i favour the tree analogy for explanation, simply because it (to me) is easier to visualize the problem that way rather than working against an abstract tree. Obviously though, both approaches must be mentioned. Petter Bøckman (talk) 19:57, 16 August 2012 (UTC)
- Actually, according to my proposal, Fig. 3 shows a paraphyletic group. It also satisfies the Oosterbroek condition. If the basal primates were nocturnal (this is controversial) and nocturnality was preserved in the lineages leading to lorises and tarsiers, I think that we would have to agree: nocturnality is plesiomorphic and the nocturnal primates are a paraphyletic group. Peter M. Brown (talk) 20:48, 16 August 2012 (UTC)
- True. One of my colleagues is the locak university expert on primates. I asked him about it, and he said it was not likely that the lorises and tarsiers are primitively nocturnal. But yes, if they are, and if we use the trait as the defining trait, they would be paraphyletic rather than polypyletic. Perhaps I need to find another trait to unite the two. Petter Bøckman (talk) 06:47, 17 August 2012 (UTC)
- This example precisely makes my point that the distinction between paraphyletic and polyphyletic cannot be made in terms of geometry [without Oosterbroek's ignored and hence irrelevant qualification]. Any set of the terminal nodes in my primate cladogram can be made into a paraphyly by including the LCA and claiming that there are symplesiomorphic characters uniting them.
- As a matter of practicality, I think that it's better to illustrate polyphyly by choosing a set which fits Oosterbroek's qualification, because this makes it harder to come up with plausible characters (as his approach was meant to, if you read the original paper). (Lemurs+Old World monkeys) is a possibility: diurnal Old World tailed primates. Peter coxhead (talk) 08:59, 17 August 2012 (UTC)
- True. One of my colleagues is the locak university expert on primates. I asked him about it, and he said it was not likely that the lorises and tarsiers are primitively nocturnal. But yes, if they are, and if we use the trait as the defining trait, they would be paraphyletic rather than polypyletic. Perhaps I need to find another trait to unite the two. Petter Bøckman (talk) 06:47, 17 August 2012 (UTC)
Perhaps the historical situation is this:
- Originally, both monophyletic and paraphyletic taxa were considered acceptable (indeed the term "monophyletic" was then used to cover both). This meant that the paraphyletic/polyphyletic distinction was important: paraphyletic (modern sense) was part of "good", polyphyletic was "bad".
- After Hennig's terminology and arguments became mainstream, the majority view switched to monophyletic = "good", everything else = "bad". The paraphyletic/polyphyletic distinction became unimportant, only distinguishing (for the majority) irrelevant degrees of "badness".
Anyway, this discussion has convinced me that there is no single coherent way of explaining the modern usage of "paraphyly" and "polyphyly"! Peter coxhead (talk) 08:59, 17 August 2012 (UTC)
- Peter, you're clearly going to be the one to do the bulk of the revision and, aside from details, the rest of us are not going to challenge you. My definition of "paraphyletic" above, however, is geometric, even though it does not incorporate Oosterbroek's condition. I think that it corresponds to the intuitions of most people who use the term, that it corresponds better than any definition based on symplesiomorphy, which is not that easy a concept. (I am unfamiliar with reciprocal paraphyly; perhaps this is a different meaning of the term corresponding to different intuitions.) On the other hand, I retract my proposal for "polyphyly", which—like the Oosterbroek criterion—is unintuitive. Unlike symplesiomorphy, convergence is an easy concept and I think that it is the basis of most uses of "polyphyletic". If you really don't like character-based definitions, you can define a polyphyletic group as one that is neither monophyletic nor paraphyletic, but I think that, when people use the term, they hardly ever consider and reject the other two predicates.
- I am very unhappy with Curtis' claim that my definition is subjective. To be subjective is to belong to the mind rather than to the object of thought, and my formulation is not remotely concerned with the mind. The fact that "how many is many?" lacks a precise answer shows merely that "paraphyletic" is a vague term, which is no criticism; most terms are somewhat vague, and my term "paraphyletic" has a leg up on Curtis' (and Wikipedia's) term "reliable" since there is no agreed-on metric to determine how reliable a source is while there is one to determine how many subclades a taxon excludes from the smallest clade that incorporates it. What is important is how closely the vagueness in my definition matches the vagueness in the term "paraphyletic" as commonly used.
- Consider the whales. No one would dispute the paraphyly of the group if the phylogeny of the Cetacea were like this:
|
Whales |
- This conclusion would not be based on any symplesiomorphy but simply on the geometry of the cladogram. The matter is actually much messier, however. Following Zhou et al. (2011)[1] and showing the whales in red:
| Cetacea |
| ||||||||||||||||||||||||||||||||||||||||||
- I don't think that anyone looking at this diagram who has not read this page would pronounce the whales paraphyletic. The reason is that, while the group is indeed a clade minus some subclades, the groups that need to be excluded are too many in number: three monophyletic dolphin groups and the porpoise group. On the other hand, a distinctive characteristic of whales is that they are large, at least as compared to dolphins; as this trait has evoloved independently in different whale groups, most people would readily grant that the group is polyphyletic.
- Whether or not my arguments for my preferred definitions are convincing, my negative points stand: a geometric definition of paraphyly does not require the Oosterbroek condition and, more importantly, vague terms are not necessarily subjective. "Subjective" is an overused term of opprobrium. Cladists congratulate themselves that they use taxonomic terms that are more precise than the "subjective" terms of Linnaean taxonomy, though the latter are simply vague, not subjective, and not necessarily less useful to researchers.
- Peter M. Brown (talk) 17:36, 17 August 2012 (UTC)
- Peter, I certainly hope that you, as a philosopher, don't think I was using "subjective" in a pejorative sense. When two different investigators apply a vague term and come up with two different "answers", their analyses are (at least as I understand the term) subjective. Not "bad", just subjective.
- Your example with whales very clearly illustrates what I think you are saying. To me, it points up the importance of the character-based view. If largeness is a symplesiomorphy, whales are paraphyletic; if it is convergence, they are polyphyletic. If it is convergence, and one draws a tree that connects all the basal nodes, the tree does not represent the characters. An inaccurate diagram is just that; it cannot be used to falsify a definition. (I have to add as a disclaimer that hundreds of scientists, all being misled by a bad diagram, can change a definition; I'm a descriptivist, not a prescriptivist, and the current definition of "monophyly" shows that I'm right.)
- And your example never has to deal with "few" or "many", but only with plesiomorphy and homoplasy. Symplesiomorphy is not a difficult concept. Like synapomorphy, it is shared homology: no homoplasy need apply. In symplesiomorphy, a character state transition obliterates a character state that would otherwise be used to diagnose a clade. A synapomorphy of the tetrapods is four limbs. Caecilians, snakes, and legless lizards (among others) have transitioned into a (±) limbless state. If we make a groups consisting of all the four-limbed tetrapods, it is paraphyletic, because we're basing it on aymplesiomorphy. If we understand the character state transformation, we include the legless tetrapods, and make a clade.
- Likewise, the dicots are flowering plants with two cotyledons. Two cotyledons is apparently a synapomorphy of the seed plants (or at least of the extant ones); it is transformed to one cotyledon in the monocots, so using it to make a paraphyletic dicot group is symplesiomorphy.
- It's quite true that "symplesiomorphy" is effectively meaningless in DNA sequence trees, but I hope we agree (since no one has a counterexample) that the character-based and node-based definitions are effectively identical (at least with respect to terminal taxa). And your whale example fits both criteria: if largeness is symplesiomorphy, an accurate diagram will include the nodes, and whales are paraphyletic. If instead it's convergence (hence homoplasy), and accurate diagram will not include the nodes, and whales are polyphyletic.--Curtis Clark (talk) 18:36, 17 August 2012 (UTC)
- @Peter. I think that you are implicitly using the Oosterbroek criterion. Yes, your very nice whale example shows geometrically and without characters (on this I agree with you against Curtis's comments above) that "whales" are polyphyletic. We don't need to know anything about their characters to see this. But it's not the number of omitted groups, but the way they are distributed in the cladogram that matters. Consider the groups defined by this colouring:
| Cetacea |
| ||||||||||||||||||||||||||||||||||||||||||
- The three groups are the same size as before, but now it's clear that the red group is a simple paraphyly (w.r.t. cetaceans minus Baleen whales). It's the "scattering" of excluded groups among the included groups that matters in your example and makes "whales" a polyphyly.
- Perhaps the real situation is this (new thought!). Groups defined from cladograms/phylograms are of four types:
- Monophylies – very clear, no problems in defining
- Single paraphylies (one excluded clade) – again, very clear, no problems in defining
- Multiple paraphylies (more than one excluded clade)
- Polyphylies
- (3) and (4) are treated as conceptually different by some authors (but not all, c.f. those who use the term "reciprocal paraphyly"), but are hard to separate; different definitions put problem cases into different categories. But this probably doesn't matter since no-one would now propose defining taxa which are complex paraphylies. Peter coxhead (talk) 21:37, 20 August 2012 (UTC)
- Perhaps the real situation is this (new thought!). Groups defined from cladograms/phylograms are of four types:
- I vehemently object to the suggestion that any group defined by symplesiomorphy should be called polyphyletic. It is a gross redefinition of the term. If you can clearly establish that use in the literature (show that someone has made that definition explicit, rather than simply created a situation that you could explain by it), then of course it should be in the article, but Wikipedia should not be stirring muddy waters any further.
- The fact that it is unlikely that a group with multiple excluded clades is based on symplesiomorphy is immaterial. I certainly agree that it is extremely unlikely. But in the unlikely case that such a group existed, your definition would effectively hide that fact. Making the unlikely semantically impossible is not a good way of doing science.--Curtis Clark (talk) 23:01, 20 August 2012 (UTC)
- Peter Coxhead is not trying to do science. He is trying to create one or more—his choice—articles to help the general public understand these concepts. Since the uses may not follow rigid rules and since, in any case, they correspond only roughly to definitions in the literature, he will have to make some compromises. An approach that is both effective and purist is probably impossible. I am confident that his choices will be intelligent, even if I will probably disagree with some of them. He created this page in the hope that we could provide some ideas that he will find useful; perhaps we have actually supplied some. Peter M. Brown (talk) 23:59, 20 August 2012 (UTC)
- I'm sorry I'm not making myself clear. What I am trying to avoid, and what I will continue to challenge until the day I retire from Wikipedia, is original research.
- If I were a reviewer of a paper that claimed that a group defined by symplesiomorphy was polyphyletic because there were too many excluded clades, I would recommend that it be changed, or if that were the crux of the article, rejected. I know at least a few other well-respected systematists who would agree. If such an argument has been explicitly published in a reliable source, we must of course include it, but we cannot give it undue weight against a long-standing tradition of consistent character-based and tree-based definitions. As Peter himself I believe pointed out in the controversy about tree, making a subject easier to understand is not license to make it misleading or wrong.
- And I contest that the traditional definitions are difficult to understand or apply. I've taught them to undergraduates for more than a quarter century. When I first started reading the discussions about paraphyly, I thought perhaps I was missing something, that someone had found a fatal flaw in the traditional definitions. That still may be true, but I have yet to see evidence of it.--Curtis Clark (talk) 00:51, 21 August 2012 (UTC)
- Peter C. has conclusively rebutted my proposal that lots of excluded clades make a group polyphyletic or at least not paraphyletic. That isn't even on the table. As far as the traditional definitions go, I proposed here (I have inserted an anchor) that Hennig's definitions be used; these are pretty much the "traditional definitions" you refer to, aren't they? He countered that "the terms are not now defined or used this way in almost all current literature." I still think that's a promising way to go: use the traditional definitions in the lead with a brief mention of the geometric options and then consider the latter more fully in a subsequent section, describing even the Oosterbroek criterion. (A different section might treat of reciprocal paraphyly.) If he does not favor that approach, though, we can be useful only by suggesting alternatives. Peter M. Brown (talk) 01:50, 21 August 2012 (UTC)
- @Curtis. I think that what Oosterbroek was trying to do was to come up with a purely geometric definition based only on terminal nodes that would make it impossible (or at least very unlikely) that there could be symplesiomorphies which could define a group that his definition called polyphyletic. So I think that he (and others at that time) would agree with you.
- Go back to Peter's first whale cladogram (which I repeat is a really good example).
| Cetacea |
| ||||||||||||||||||||||||||||||||||||||||||
- Consider the clade I've labelled "X". In traditional Hennig terms, there must be a synapomorphy of this entire clade which distinguishes it from the paraphyletic group (Baleen + Sperm whales). To put the Beaked whales and Beluga whales in the same paraphyletic group as Baleen and Sperm whales, you have to suppose that this synapomorphy was twice independently lost. It's not just that the "whales" retain symplesiomorphies of the ancestral cetacean; they must not have the apomorphies which define the other clades inside which they are nested. Beluga whales in particular would have to have lost so many apomorphies to be removed from their obvious position that it's highly implausible that they could share symplesiomorphies with the other "whales" while lacking the apomorphies of the groups which have separated from their most recent common ancestor. If you track the history of Oosterbroek's definition it comes precisely from the ideas of Farris and others about counting "reversals" of characters.
As far as I can see there's no flaw in traditional character-based definitions; the flaws are in the purely geometrical definitions which were intended to replace them and which don't seem to work in the case of multiple paraphyly – I think we agree on this now.
The problem is that the literature doesn't reflect our agreement (assuming we do all agree). Recent "reliable" sources give definitions which can quickly be shown to lead to unreasonable conclusions as to the kind of "phyly" a group is, but no-one seems to have published critiques of these definitions. Peter coxhead (talk) 10:53, 21 August 2012 (UTC)
Grades and paraphylies
[edit](Inserted subheading to break up the text for editing purposes. PC)
- In order to finally read the Oosterbroek paper, I guess I'm going to have to get a physical volume of Syst. Biol. from the library compactor storage; my library has no electronic access before 1992 (sigh). I'm not on campus much this summer, and it's a total PITA.
- With respect to your apomorphy arguments above, you really don't understand grades. There are apomorphies for the amniotes; the mammals and birds (sensu traditionalibus) didn't need to lose those apomorphies in order to leave a reptile grade. Grade transitions involve the origin of new apomorphies, not the loss of old ones. I have correspondence with a couple of folks who still defend paraphyletic groups (for different reasons), and I've thought a lot about grades (even come up with a skeleton system that could make a classification composed entirely of grades). (There's no shame in not understanding grades--even a lot of supporters of paraphyly have misunderstood them.) All it takes for your cladogram above is for the green and blue clades to each have an adaptive syndrome of apomorphies that marks, in someone's estimation, a grade boundary, putting them in separate grades from the ancestral whales. I'm willing to drop this for now, because I think the historical approach, below, is a more productive avenue.--Curtis Clark (talk) 02:50, 22 August 2012 (UTC)
- It seems I don't have access to the paper either, so I can't send it to you.
- The more I think about it, the more I think you are right about a grade being formed by the acquisition of a new trait. At least for the major, class-forming events in tetrapods that seems to be the case (feet, amnion, ear osicles and feathered flight respectively). When I wrote the lede for the list of transitional fossils I seem to have stumbled upon same thing, though not as explicitely (quote): The fossils are listed in series, showing the transition from one group to another, representing significant steps in the evolution of major features in various lines. These changes often represent major changes in anatomy, related to mode of life, like the acquisition of feathered wings for an aerial lifestyle in birds, or legs in the fish/tetrapod transition. When the two of us (and undoubtedly others) have independently come to the same conclusion, chances are we have nailed it down.
- I would like to suggest another point in the grade-forming event: The new trait must be one allowing for or be the direct result of a major shift in ecological niche, so that the descendant group finds a new mode of life not open to their ancestors, leading to rapid evolution away from the ancestral anatomy. In class-forming examples above, this criterion is fulfilled. I don't know if this is relevant for the -phyly article(s), but it certainly is for Evolutionary grade article.
- The question is, can we find a decent source for any of this? Petter Bøckman (talk) 08:01, 22 August 2012 (UTC)
- I think you are both shifting the ground here. The concept "grade" and the Hennigian concept "paraphyly" aren't the same, although they are related. Yes, a paraphyly, in Hennig's terms, is united only by a (sym)plesiomorphy – the (syn)apomorphy which distinquishes the paraphyly's enclosing clade from its sister. So, sure, all the "whales" possess the characters which distinguish cetaceans from their sister clade. But any random selection of subclades within the cetacean clade also has these characters; this isn't enough to define a paraphyletic taxon. We need the subclades making up the paraphyly not to have those apomorphies which separate off the excluded subclades, otherwise they would belong in one of them rather than in the "catch all" paraphyletic taxon.
- There's a difference, I think, between the precision of Hennig's clades and grades based on "traditional" classifications. If you don't draw the whole tree, then defining "whales" as what's left when more advanced grades emerge is ok:
| Cetacea |
| ||||||||||||||||||||||||
- But in the Hennigian method, every time sister groups separate from one another there has to a defining synapomorphy to "cause" the split. Once you draw the full tree, the situation is different from that shown above. Clade X must have an innovation/apomorphy distinguishing it from Sperm whales; the sister clade of South Asian river dolphins must have an innovation/apomorphy distinguishing it from South Asian river dolphins, and so on. To put Beluga whales "back" down the tree with Sperm whales and Baleen whales you have to suppose that all these innovations/apomorphies have been lost. As I understand it, Hennigian paraphylies are based on full trees and require:
- Possession of the symplesiomorphies of the enclosing clade
- Absence of the synapomorphies which separate off the excluded clades.
- Grades are a much less precise concept than Hennig's paraphylies. Peter coxhead (talk) 12:28, 22 August 2012 (UTC)
- But in the Hennigian method, every time sister groups separate from one another there has to a defining synapomorphy to "cause" the split. Once you draw the full tree, the situation is different from that shown above. Clade X must have an innovation/apomorphy distinguishing it from Sperm whales; the sister clade of South Asian river dolphins must have an innovation/apomorphy distinguishing it from South Asian river dolphins, and so on. To put Beluga whales "back" down the tree with Sperm whales and Baleen whales you have to suppose that all these innovations/apomorphies have been lost. As I understand it, Hennigian paraphylies are based on full trees and require:
- I quite agree. My comment above was to Curtis Clark and his definition of an evolutionary grade, not directed at paraphyly in general. The more I look into this, the more I agree that the three (or four) -phyly articles should be combined, and the grade article be given some attention to better make it stand on it's own feet. Petter Bøckman (talk) 17:55, 22 August 2012 (UTC)
- Grades are a subset of Hennig's paraphyly. Then, as now, grades were the primary reason people intentionally accepted paraphyletic groups.--Curtis Clark (talk) 19:18, 22 August 2012 (UTC)
- [ec] Peter, I think you're totally missing it, but I'm having so much trouble following you that I'm not sure. I'm confident that you don't really mean than synapomorphies cause evolution, but I think the rhetorical device causes confusion later on. especially with the "back down the tree", where you are invoking character reversals totally unnecessarily.
- Plesiomorphy is created through recognition of apomorphy. Reptiles (s. trad.) share the plesiomorphies of no hair, no feathers, no three-bone middle ear, no lactation, basically the absence of mammalian and avian traits. Setting aside the cotyledons, dicots share the plesiomorphies of no atactostele and no parallel leaf venation. Symplesiomorphy basically means "shared ancestral traits". They didn't get these features through convergence; they are part of their phylogenetic heritage.
- And the traditional Reptilia falsifies your whale conjecture: non-avian maniraptorans have all the synapomorphies of theropods, all the synapomorphies of saurischians, all the synapomorphies of archosaurs, and all the synapomorphies of diapsids; they need no character reversals to still be reptiles, and that still holds true if we remove the snake clade from Reptilia as well.
- It is true that not all paraphyletic groups can be convincingly described as grades. It is (IMO) true that grades are the only biologically useful paraphyletic groups, and they are the groups that are ordinarily trotted forth by proponents of paraphyly.
- But I'm perfectly willing to accept that I'm not addressing what you're saying.--Curtis Clark (talk) 19:16, 22 August 2012 (UTC)
I find it difficult to explain this without being able to draw diagrams as I talk! The whales example is crucially different from the reptiles example. Once a clade has been excluded from the reptiles (mammals, birds) it can't (and doesn't) have a subclade which is included "back" in the reptiles. Consider a very simplified cladogram (precise accuracy doesn't matter for the purpose of this discussion):
| |||||||||||||
Here it's clear that the clade birds can be defined by (syn)apomorphies not shared by the paraphyly (reptiles1 + reptiles2). (Reptiles1 + reptiles2) is defined by:
- the presence of ancestral plesiomorpies (also possessed by birds)
- the absence of the apomorphies which distinguish birds from reptiles2. (Of course there is some apomorphy which separates reptiles1 from (reptiles2 + birds) but this is not relevant to whether "reptiles" are a paraphyly.)
Now suppose some group had evolved from within birds which we also wanted to call "reptiles" (because they appeared not to have any bird-like characters). The cladogram might then be:
| |||||||||||||||||||||||||
This is essence of the geometry possessed by the whales example. Would "reptiles" = (reptiles1 + reptiles2 + reptiles3) now be a paraphyly? I believe the answer is no. It's a polyphyly. Reptiles3 possesses the apomorphy which distinguishes clade X, i.e "birds s.l.", from reptiles2. You can't put the genie back in the bottle; once clade X evolves characters we use to define birds, none of its subclades can go back to being "reptiles" because, crucially, "reptiles" cannot have the apomorphies which separate off birds, but reptiles3 would necessarily have these. The similarity between reptiles1 and reptiles2 is a matter of shared evolutionary history. The similarity between reptiles3 and reptiles1 or reptiles2 would not be; it's a convergence – a group of birds (reptiles3) would have independently evolved to appear like reptiles1 and reptiles2 by losing bird-like characters – quite a different evolutionary history from reptiles1 and reptiles2, which don't have any bird-like characters because they never evolved them.
Precisely the same applies to the whales example which has a parallel geometry, but it's harder to explain clearly because we don't have names for the relevant groups. Peter coxhead (talk) 22:27, 22 August 2012 (UTC)
- I think I see where the miscommunication is coming from. I'm saying, using your example, that if we decide that birds1 and birds2 each have their own apomorphies that separate them from reptiles, the remaining reptiles are paraphyletic. If we number the nodes 1-4 from the base of the tree, I'm saying that all four nodes would be reptiles; if I understand you correctly, you are saying that node 3 and possibly node 4 are birds. Based on your interpretation, yes, I agree that such cases would be polyphyly. I hope you understand why I think in my case reptiles would be paraphyletic. This exactly parallels character-based definitions: in my case, all reptiles have one or more synapomorphies; in your case, reptiles3 has a homoplasy. Are we on the same page?--Curtis Clark (talk) 23:45, 22 August 2012 (UTC)
- I think so, in this sense. What I'm trying to do is to use the definitions/approaches to defining paraphyly which arose in the 1960s-1980s, starting from Hennig and then extending through the debates involving people like Ashlock, Nelson, Farris, Charig and Oosterbroek (debates which I followed to some extent in the 1970s and 1980s, as I was then working on computational and statistical classification). I think our difference may be the following. The very strict Hennig-derived approach to constructing a cladogram, which I'm trying to use, requires prior identification of apomorphies at each split. Therefore there has to be at least one "substantive", "biologically real" apomorphy which the cladist can use to separate Clade X in my diagram from reptiles2. Once this apomorphy has been identified and used as a criterion for splitting, it can't be "undone", as I've argued, except by homoplasy as you note.
- Without knowledge of an apomorphy separating off Clade X (e.g. only being able to differentiate birds1 and birds2 separately from the rest as in your example) you can't construct the tree using the Hennig-derived step by step approach. Genetic methods are another kettle of fish. There could be a really minor genetic difference – even random drift – separating Clade X from reptiles2, a difference which traditionally would not be of relevance to classification at all, so that putting reptiles1, reptiles2 and reptiles3 together would be entirely sensible and fully justified. But modern dogma says that classification should be based strictly on evolutionary history regardless of whether there are any comprehensible morphological or behavioural characters associated with particular historical splits (dogma strenuously resisted by Mayr among others, but the resistors seem to have lost). So the shape of the tree should determine classification as if the tree had been constructed by strict Hennig-derived step by step methods with known apomorphies at each step. On this basis, the geometry says that "reptiles" composed of reptiles1 + reptiles2 + reptiles3 is a paraphyly. The real biology based on observable characters might well say something different – and Hennig would have agreed on this, I'm pretty sure. Peter coxhead (talk) 09:09, 23 August 2012 (UTC)
Personal view; not for Wikipedia! Grades are, I think, related to the often "ladder-like" shape of the tree of life rather than it being a more "balanced" binary tree. Suppose 4 clades A, B, C and D had evolved like this:
| |||||||||||||||||||||||||||||||||||||||||||
Then it's likely that there would have been no obvious morphological way of ordering A, B, C and D in terms of "advancement". Precisely this kind of shape puzzled the early biologists who thought in terms of advancing grades: how to relate mammals and birds? Actually they are on distinctly different branches of the tree of life, so ordering doesn't work.
But now suppose A to D evolved like this:
| |||||||||||||||||||||||||||||||||||||||||||||||||
A, B and C are paraphyletic, D is monophyletic according to modern terminology. Now there's likely to be an "obvious" ordering A → B → C → D, and prior to binary trees, the idea that "A evolved into B", "B evolved into C", etc. A, B, C and D represent clear grades. (Primates fit this pattern reasonably well, with A = traditional prosimians, B = traditional monkeys, C = traditional apes, D = humans.)
I draw two conclusions from this example.
- If all available character-based evidence made A, B, C and D "natural groups", it's questionable whether the fact that the historical pattern of evolution was ladder-like rather than balanced binary should influence classification.
- The frequence of ladder-like patterns in the tree of life suggests that "grades" are of real importance in understanding evolution.
However, neither view is currently fashionable and certainly not acceptable for Wikipedia! Peter coxhead (talk) 09:36, 23 August 2012 (UTC)
- Well, There are actual examples of this approach in print. I think both you Peter and Curtis would enjoy reading these two articles on animals[2] and plants[3].
Should articles be merged?
[edit]Question Should we push for the merger of the three articles Monophyly, Paraphyly and Polyphyly? Taking a historical approach in all three would just lead to a lot of repetition. Peter coxhead (talk) 08:40, 16 August 2012 (UTC)
- I have been against the merge, but I'm coming around to your POW. With the rich history now coming into focus, I think a merger is the best way to go about it. At least it will allow the article evolutionary grade stand more on it's own feet. Petter Bøckman (talk) 10:02, 16 August 2012 (UTC)
- I agree they should be merged.--Curtis Clark (talk) 01:51, 17 August 2012 (UTC)
@Peter: do you have a view on this? Peter coxhead (talk) 10:00, 21 August 2012 (UTC)
- Your sketch of the history here, which you have deleted for some reason, seems excellent. Since it doesn't make sense to tell the story three times, I would suggest one article. The lead need not contain an actual definition, just a brief characterization of the phylies: monophyly (mammals) indicates that the species involved are more closely related to each other than to anything else, paraphyly (reptiles) accommodates cases where groups have split off, and polyphyly (powered flight) handles the contrary situation where groups have come together in convergent evolution. Then, starting with the first section, you can go into the history as you have outlined it.
- I was planning to add to the paraphyly article (which defines the term geometrically) an explanation of the fact that convergent characters cannot delineate a paraphyletic group, so defined; the current article just takes that as obvious, which it isn't. I'll not proceed on that, though, since it looks like your work would supersede mine. Peter M. Brown (talk) 15:41, 21 August 2012 (UTC)
- Sounds good to me! Petter Bøckman (talk) 18:27, 21 August 2012 (UTC)
- @Peter: yes, please add this to the Paraphyly article. I simply don't have time at present (and probably won't have for about a month) to work on a merged article. Of course anyone else is free to do it! Peter coxhead (talk) 20:29, 21 August 2012 (UTC)
I'll be back
[edit]I'm reading the Oosterbroek paper, and there are some serious issues starting with Farris, but it's going to take me a few days to get my head around it all, and I have other things going on IRL. I'm starting to think that the whole thing was made overly complicated at some point, and all the work since has been an attempt to dig us out of that hole. I fear that the only way I'm going to be able to fix the Wikipedia article is to get a paper published in a reliable source that will clear things up.
One thing you might want to check out (and I'll eventually come up with a reference if one of you doesn't first) is the concept of "convex group" used by the character compatibility folks. At one time, convex groups were widely held to be the union set of monophyletic and paraphyletic groups, so that a convex group that was not monophyletic was thus paraphyletic.--Curtis Clark (talk) 01:41, 25 August 2012 (UTC)
- Here's the reference: Estabrook, G. F. 1978. Some concepts for the estimation of evolutionary relationships in systematic botany. Sysytematic Botany 3: 146-158 --Curtis Clark (talk) 01:48, 25 August 2012 (UTC)
I can't believe the mess that was created in the 1970s and 1980s with (IMO) unnecessarily complicated descriptions. It's no wonder that modern workers lump together para- and polyphyletic. I'm going to ask a colleague who is still a supporter of recognizing paraphyletic grades what he regards as the best definitions in the literature. I am going on the premise than any definition that could be read in a way to exclude the traditional Reptilia or Dicotyledonae is flawed.--Curtis Clark (talk) 01:15, 28 August 2012 (UTC)
Outline of history
[edit]As Peter noted above, I did start on an outline of how the history of this topic might be written. As I realized that I wouldn't have time to work on it for the next few weeks, I removed it. However, since Peter saw it, I'll put it back (slightly revised). I think these "phases" need to be included:
- Post-Darwin, the idea that taxa should reflect evolution, being based on ancestry. Taxa should be what was then called "monophyletic" but there was no requirement for all descendants to be included so that "monophyly" then included modern "paraphyly".
- Hennig's introduction of key ideas: plesiomorphies/apomorphies; clades (modern monophylies=holophylies to opponents) as all descendants of the most recent common ancestor. Manual construction of cladograms in the early days based on explicit identification and use of plesiomorphies/apomorphies.
- Rise of computer-based tree construction using parsimony, still based on morphological characters; however plesiomorphies/apomorphies defining groups might be identified "backwards" from the tree. Up to this point, there are clear, easily sourced definitions of the "phylies".
- Rise of computer-based tree construction using only extant species and based on molecular data. Published papers show little or no interest in characters of any kind; groups/taxa are identified purely from geometry with a focus on clades (i.e. no real interest in what non-clades are). The data used in the APG classifications are clear examples of this. Once taxa have been identified in this way, characters may be identified (e.g. as Stevens does in APweb) but these are not the characters used in the creation of the clades, so they don't have the same scientific status.
- My new understanding, and again thanks to you all for the input, is that in this "phase 4", although sources typically give definitions for paraphyly/polyphyly based on geometry rather than plesiomorphies/apomorphies – which they have to because they never explicitly consider characters – in the case of multiple paraphyly these definition cannot be made entirely consistent but this is actually of little practical importance.
Now 1-3 above are easy to reference (plus all the debates at each stage, e.g. Mayr against Hennig; attacks on purely molecular approaches; rearguard minority defence of paraphyletic taxa). What is OR/SYNTH is the analysis we seem to have reached of 4, so it seems that all we can do is to give some sourced definitions/usages and show that they are not entirely consistent with each other or the "traditional" character based definitions. Peter coxhead (talk) 20:29, 21 August 2012 (UTC)
- we're walking a fine line here, but we should at least be abl eto come up with some examples for point 4. Petter Bøckman (talk) 17:58, 22 August 2012 (UTC)
References/Bibliography
[edit]- Ashlock, Peter D. (1971), "Monophyly and Associated Terms", Systematic Zoology, 20 (1): 63–69, doi:10.2307/2412223, JSTOR 2412223, retrieved 2011-04-08
- Ashlock, Peter D. (1979), "An Evolutionary Systematist's View of Classification", Systematic Zoology, 28 (4): 441–450, doi:10.2307/2412559, JSTOR 2412559, retrieved 2011-02-04
- Barkley, Theodore M.; DePriest, Paula; Funk, Vicki; Kiger, Robert W. & John, W. (2004), "Linnaean Nomenclature in the 21st Century: A Report from a Workshop on Integrating Traditional Nomenclature and Phylogenetic Classification", Taxon, 53 (1): 153–158, doi:10.2307/4135501, JSTOR 4135501, retrieved 2011-10-03
{{citation}}: Text "Kress, Gerry Moore" ignored (help)
- Hennig, W. (1950), Grundzüge einer Theorie der Phylogenetischen Systematik, Berlin: Zentralverlag, cited in Mayr & Bock 2002
- Hennig, W. (1966), Phylogenetic Systematics, Urbana, IL: University of Illinois Press, OCLC 299927292, cited in Mayr & Bock 2002
- Mayr, Ernst & Bock, W.J. (2002), "Classifications and other ordering systems", J. Zool. Syst. Evol. Research, 40 (4): 169–94, doi:10.1046/j.1439-0469.2002.00211.x
- Nelson, G.J. (1971), "Paraphyly and polyphyly: Re-definitions", Systematic Zoology, 20: 471–472, doi:10.2307/2412125, JSTOR 2412125
- Oosterbroek, Pjotr (1987), "More Appropriate Definitions of Paraphyly and Polyphyly, with a Comment on the Farris 1974 Model", Systematic Biology, 36 (2): 103–108, doi:10.2307/2413263, JSTOR 2413263, retrieved 2011-02-11
- Podani, J. (2010), "Taxonomy in Evolutionary Perspective : An essay on the relationships between taxonomy and evolutionary theory", Synbiologia Hungarica, 6: 1–42, retrieved 2011-03-05
- Schwartz, Robert; Scheffler, Israel; Goodman, Nelson (1970), "An improvement in the theory of projectibility", Journal of Philosophy, 67 (18): 605–608, doi:10.2307/2024344, JSTOR 2024344
- Zhou, X; Xu, S; Yang, Y; Zhou, K; Yang, G (2011), "Phylogenomic analyses and improved resolution of Cetartiodactyla", Molecular Phylogenetics and Evolution, 61 (2): 255–264, doi:10.1016/j.ympev.2011.02.009, PMID 21315162
- ^ Zhou et al. 2011
- ^ Sperling, E. A.; Pisani, D.; Peterson, K. J. (1st January). "Poriferan paraphyly and its implications for Precambrian palaeobiology" (PDF). Geological Society, London, Special Publications. 286 (1): 355–368. doi:10.1144/SP286.25. Retrieved 22 August 2012.
{{cite journal}}: Check date values in:|date=and|year=/|date=mismatch (help) - ^ Donoghue, Michael J. (June 1st). "Key innovations, convergence, and success: macroevolutionary lessons from plant phylogeny" (PDF). Paleobiology. 31 (sp5): 77–93. doi:10.1666/0094-8373(2005)031[0077:KICASM]2.0.CO;2.
{{cite journal}}: Check date values in:|date=and|year=/|date=mismatch (help)
