User:Mencor/Consecutively Halved Positional Voting
| This is not a Wikipedia article: It is an individual user's work-in-progress page, and may be incomplete and/or unreliable. For guidance on developing this draft, see Wikipedia:So you made a userspace draft. Find sources: Google (books · news · scholar · free images · WP refs) · FENS · JSTOR · TWL |
Consecutively Halved Positional Voting
| A joint Politics and Economics series |
| Social choice and electoral systems |
|---|
 |
|
|
As its name indicates,consecutively halved positional voting (CHPV) is a type of positional voting system in which weightings are applied such that the lower of any two adjacent rank positions is worth half that of the higher one.[1] In single-winner contests, voters cast their preferences using a ranked ballot and the option gaining the most points overall wins.
In multiple-winner elections, CHPV is a highest averages party-list system in which the descending weights associated with the candidate rank positions on the party’s list are consecutively halved. Elections to the Legislative Assembly in Macau employ such weightings.
Ranked Ballot CHPV
[edit]Voting and counting
[edit]The single-winner version of CHPV is a ranked voting method. It is also a positional voting and geometric voting system.[1] Each voter inputs their preferences in the same manner as in other ranked ballot systems such as instant-runoff voting (alternative vote), Condorcet methods and the Borda count. Typically, the first preference is indicated by entering a ‘1’, the second preference by a ‘2’, the third preference a ‘3’ and so on.
The weighting of a first preference is unimportant in that it affects neither the ranking of the candidates nor on who wins the election.[2] Any convenient value for counting may be chosen but either the first or last preference is typically set at one. It is sometimes set at a half so that the sum-to-infinity of all the weightings equals one ‘vote’. Once fixed, every subsequent rank position is worth half that of the preceding one as CHPV is the special case of geometric voting where the common ratio (r) between adjacent rank positions has a value of one half (r = ½). The table below illustrates the weightings for a five-candidate election where the value of the first preference (a) is either 1 or 16.
| Ranking | Candidate | Formula | Weighting1 | Weighting2 |
|---|---|---|---|---|
| 1st | Andrew | a | 1 | 16 |
| 2nd | Brian | ar | 1/2 | 8 |
| 3rd | Catherine | ar2 | 1/4 | 4 |
| 4th | David | ar3 | 1/8 | 2 |
| 5th | Elizabeth | ar4 | 1/16 | 1 |
- where a = 1 and r = ½
- where a = 16 and r = ½
An example
[edit]
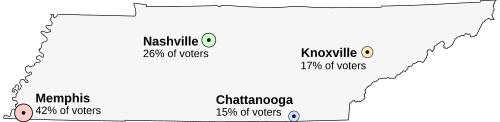
Suppose that Tennessee is holding an election on the location of its capital. The population is concentrated around four major cities. All voters want the capital to be as close to them as possible. The options are:
- Memphis, the largest city, but far from the others (42% of voters)
- Nashville, near the center of the state (26% of voters)
- Chattanooga, somewhat east (15% of voters)
- Knoxville, far to the northeast (17% of voters)
The preferences of each region's voters are:
| 42% of voters Far-West |
26% of voters Center |
15% of voters Center-East |
17% of voters Far-East |
|---|---|---|---|
|
|
|
|
If the various rankings given to each candidate are added up they are as follows.
| City | First | Second | Third | Fourth |
|---|---|---|---|---|
| Memphis | 42% | 0% | 0% | 58% |
| Nashville | 26% | 42% | 32% | 0% |
| Chattanooga | 15% | 43% | 42% | 0% |
| Knoxville | 17% | 15% | 26% | 42% |
It can be seen above, for example, that Chattanooga is ranked first by 15% of voters, second by 43%, third by 42%, and last by no voters at all. To give points to each candidate for these rankings this example uses the weightings above where a = 1 and r = 1/2. Thus, when Chattanooga's votes are added up, the results are calculated as (15/1) + (43/2) + (42/4) + (0/8) = 47. When the points for all candidates are added up, the results are as follows:
| City | First | Second | Third | Fourth | Total points |
|---|---|---|---|---|---|
| Memphis | 42/1 | 0/2 | 0/4 | 58/8 | 49.25 |
| Nashville | 26/1 | 42/2 | 32/4 | 0/8 | 55.00 |
| Chattanooga | 15/1 | 43/2 | 42/4 | 0/8 | 47.00 |
| Knoxville | 17/1 | 15/2 | 26/4 | 42/8 | 36.25 |
Result: Although it has fewer first preferences than Memphis, Nashville is the winner as it has sufficiently broad support - at the second and third preference ranks - to overtake it. Using the first-past-the-post system instead, Memphis would have been ranked first and not second. For the Borda count, Memphis would be placed third rather than second. As an option requires a combination of both strong and broad support to win, CHPV is an intermediate system between these two alternative methods.
Truncated ballots
[edit]After casting a first preference, truncation may or may not then be permitted.[3] Where it is allowed, voters can cease to express a preference for some or all of the remaining options. This usually occurs when voters are unable to distinguish between the ‘tail-end’ candidates or when they actively dislike them. Zero is awarded where no preference is cast.
Just voting for the first preference and thereby giving zero to all the other options is called bullet voting. This form of tactical voting is avoided when truncation is not permitted; so forcing all valid ballots to list every preference in rank order.
Evaluation by criteria
[edit]Ranked ballot CHPV passes the summability, consistency, participation, monotonicity, resolvability and Pareto criteria for a single-winner voting system.[4] It is not a Condorcet method and does not satisfy the Condorcet winner or loser criteria. Although it does not meet the majority condition, it does pass the two-thirds majority one.[5] It complies with Arrow's impossibility theorem as it meets all the necessary conditions for fairness except for the independence of irrelevant alternatives requirement.[6]
CHPV is a practical example of geometric voting as full accuracy is maintained throughout counting.[7] Weightings are always integers when the last preference is weighted as one. When the first preference is set at one or a half, either fractional or decimal numbers are generated during a manual count. However, the decimal numbers only require up to N decimal places for N-candidate elections. For electronic counting, binary numbers with N binary places are sufficient for such contests. No rounding is ever needed or permitted so only genuinely tied candidate rankings occur.
As an intermediate system
[edit]CHPV is a geometric voting (GV) system where the common ratio is one half (r = ½). First-past-the-post (FPTP) voting is directly equivalent to GV with a common ratio of zero (r = 0).[8] At the other end of the range, GV with a common ratio approaching one (r → 1) produces identical candidate rankings (but not tallies) to the Borda count.[9] CHPV is an intermediate system between these two other methods.
CHPV is the threshold GV variant for a three-way tie between a ‘consensus’ candidate with a second preference from every voter and two ‘polarised’ candidates who share all the first preferences equally between them.[10] This multiple tie occurs as two second preferences are worth the same as one first preference when r = ½. For the Borda count (or GV with r > ½) the consensus candidate would win here whereas for FPTP (or GV with r < ½) just the two polarised candidates would tie for first place.
It is possible for a consensus candidate with a unanimous but lower CHPV preference from every voter to beat all the other multiple candidates where they have an equal share of the other preferences.[11] This minimal winning preference has a weighting greater than the mean of all the N weightings employed and its rank position (n) is higher than the binary logarithm of the number of them (log2N). For example, in a six-candidate election, since n < log2 6 then n < 2.585 and the ‘high’ (above-mean-weighted) preferences are the first and second ones.
For FPTP, votes equate to first preferences and only this top rank (n = 1) matters. For the Borda count, the middle rank position (n = (N+1)/2) has the mean weighting so only the preceding ranks are of high preference. For a potentially winning candidate in any strictly ranked contest, gaining high preferences is essential while attracting low ones is a hindrance.
The table below gives the normalised1 weightings for an example six-candidate election. The high and low preferences are highlighted in bold and italic respectively for each of the three comparative voting systems.
| Rank (n) | FPTP weightings | CHPV weightings | Borda1 weightings |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 0 | 1/2 | 5/6 |
| 3 | 0 | 1/4 | 4/6 |
| 4 | 0 | 1/8 | 3/6 |
| 5 | 0 | 1/16 | 2/6 |
| 6 | 0 | 1/32 | 1/6 |
- Normalised through division by six.
To win, candidates ideally adopt a different campaign strategy in each system.[12] In FPTP, the rank (quality) of any preference is paramount as only the top one counts. Using the Borda count, it is almost invariably more advantageous to gain two second preferences than one first preference. Here, the focus is on maximising the quantity of high preferences rather than on their quality. As an intermediate system, CHPV requires a balanced focus between quality and quantity. Two preferences at one rank are consistently worth the same as one at the adjacent higher rank. Therefore, the campaign reward for converting a preference into the next higher rank is no different than obtaining an additional preference at the initial rank.
Combating teaming
[edit]Like other positional systems, CHPV fails to satisfy the independence of clones criterion and so is vulnerable to the strategic nomination of clones.[13] FPTP is susceptible to vote splitting but not teaming whereas the reverse is true for the Borda count. As an intermediate system, CHPV is affected by both - to a lesser extent - but voters can thwart attempts to win through teaming. An objective in teaming is to ‘bury’ opposition candidates by pushing them down in rank on the ballot and so reduce their tallies. This is achieved by nominating clones of the preferred candidate and awarding them a higher preference than the remaining candidates.
A party is said to introduce ‘fraternal’ clones when they are always ranked in the same order in adjacent positions by its supporters. This order can be listed on a ‘forward’ slate that is issued by a party to its supporters. Where no slate is issued, the resultant ‘identical’ clones are likely to have the same average rank position within the adjacent ranks due to their random ordering on each ballot. This lowers the tally for the sole preferred candidate prior to cloning. Identical cloning in CHPV results in self-harm through vote splitting while fraternal cloning seeks to gain an unfair advantage through teaming.[13]
The tables below illustrate an initial tie between two candidates A and B and three scenarios that may result from B nominating two clones of itself (B1 and B2) instead. By introducing identical clones, B has split its support equally between its two clones and handed victory to A. By promoting fraternal clones instead through the use of a forward slate, B successfully teams against A and wins. Supporters of candidate A may however successfully retaliate by using a ‘reverse’ slate and use B2 to bury B1 to the same degree that B2 is used to bury A. Unlike the Borda count, the tally for B2 is lower than for B1 so the original election outcome – a two-way tie - is rigorously maintained.
Preference table
| Prior to cloning | Identical cloning | Fraternal cloning | Teaming thwarted | ||
|---|---|---|---|---|---|
| Rank | Weighting | (No slate) | (Forward slate) | (Reverse slate) | |
| 1 | 1 | A.............B........ | A.....A......B1....B2 | A.....A......B1..... | A.............B1...... |
| 2 | 1/2 | B.............A........ | B1....B2....B2....B1 | B1....B2....B2..... | B2............B2..... |
| 3 | 1/4 | B2....B1....A......A | B2....B1....A....... | B1............A....... | |
| Votes | 8..............8........ | 4......4......4......4 | 4......4......8........ | 8..............8........ |
Candidate tally table
| Prior to cloning | Identical cloning | Fraternal cloning | Teaming thwarted | |
|---|---|---|---|---|
| Candidate | (No slate) | (Forward slate) | (Reverse slate) | |
| A | 12 | 10 | 10 | 10 |
| B / B1 | 12 | 9 | 11 | 10 |
| B2 | 9 | 7 | 8 |
Opposition supporters can thwart attempts at teaming by ranking the fraternal clones in the reverse order on their ballots. In CHPV, there is no incentive for a party to clone or to retaliate via cloning provided this reverse-slate strategy is enacted whenever necessary.[13] This tit-for-tat retaliation is not a consistently successful strategy in the inherently vulnerable Borda count or in geometric voting (GV) systems with common ratios greater than one half.[14] CHPV is the GV variant that is closest to the Borda count – and the furthest from FPTP - while still retaining the ability to combat teaming.
Party-list CHPV
[edit]For multiple-winner elections, the party-list version of CHPV may be employed.[15] It is a highest averages method where each party tally is divided by 1, 2, 4, 8 and so on (that is, consecutively halved) to determine the ‘average’ tally for the candidates that are first, second, third, fourth and so on in rank on the party’s list. Irrespective of party, the W candidates with the highest tallies are the victors in a W-winner election.
An example
[edit]The table below records the number of votes each of the six parties received from the 100,000 votes cast in a five-winner election. The following table shows the individual candidate tallies (for the top three ranks only). For example, the top-ranked Yellow candidate has 40,000 votes, the second Yellow one has 20,000 and the third has a tally of 10,000. The candidates with the five highest tallies are highlighted in bold. The final table indicates the order in which the five seats are filled.
Party votes table
| Party | Yellow | White | Red | Green | Blue | Pink |
|---|---|---|---|---|---|---|
| Votes | 40000 | 23000 | 16000 | 11000 | 6000 | 4000 |
Candidate tally table
| Party rank | Yellow | White | Red | Green | Blue | Pink |
|---|---|---|---|---|---|---|
| 1 | 40000 | 23000 | 16000 | 11000 | 6000 | 4000 |
| 2 | 20000 | 11500 | 8000 | 5500 | 3000 | 2000 |
| 3 | 10000 | 5750 | 4000 | 2750 | 1500 | 1000 |
Seat allocation table
| Seat | Yellow | White | Red | Green | Blue | Pink |
|---|---|---|---|---|---|---|
| 1 | 40000 | |||||
| 2 | 23000 | |||||
| 3 | 20000 | |||||
| 4 | 16000 | |||||
| 5 | 11500 |
Result: The Yellow and White parties have two seats each, Red has one and the others have none. On average, each winner represents one fifth of the voters with a tally of 20,000. Having two seats, Yellow receives its exact proportional share. With just over and just under 20,000 respectively, White and Red gain one seat each. However, there is still one remaining seat to fill and here it goes to White rather than to Green or Yellow.
The first four seats are allocated to the same parties whether the alternative D'Hondt or Sainte-Laguë highest averages systems are employed instead. Using the D'Hondt method in place of CHPV, the fifth seat would have gone to the larger party Yellow and not White (13,333 versus 11,500) and, with the Sainte-Laguë method, it would then have gone to the smaller party Green and not White (11,000 versus 7,666).
Party proportionality
[edit]As the weightings are consecutively halved, they rapidly become very small. Consequently, in multiple-winner elections, small parties gain their first seats too easily at the expense of the larger ones. As the number of winners increases, proportionality deteriorates markedly. Party-list CHPV is necessarily restricted to few-winner contests with generally no more than six seats.[16] As in single transferable vote contests, simultaneous elections across numerous few-winner constituencies are arranged when a large number of seats is required.
Other highest averages methods employ an arithmetic progression of divisors such as 1, 2, 3, 4… with D'Hondt and 1, 3, 5, 7… with Sainte-Laguë. Here, proportionality improves as the unlimited number of winners increases. However, the proportion of all possible election profiles yielding an optimal outcome (optimality) steadily declines. In contrast, with its geometric sequence of weightings, both the proportionality and optimality of CHPV peak within its limited few-winner range of values.[17][18]
Party-list CHPV is a less party-proportional system than the Sainte-Laguë one but, within its few-winner range, it is here more likely than the D'Hondt method to produce an optimally proportional result.[19][20] In some systems such as the unmodified Sainte-Laguë one (but not D'Hondt), a small party may gain more seats by cloning itself into two.[21][22] As an intermediate few-winner system, CHPV is more likely to be harmful than helpful to a small party splitting itself into two.[23]
In comparison with STV
[edit]Both the single transferable vote (STV) and party-list CHPV systems are categorised as examples of proportional representation and both are employed in concurrent few-winner elections across multiple local-area constituencies with all those elected having the same status (in contrast to mixed member systems). However, in STV elections, voters cast preferences for candidates whereas, in CHPV ones, they vote for their chosen party and thereby its closed list of candidates. In comparison with the multiple-round algorithm for STV, the transparent CHPV count process is simpler and quicker.
An option exists with party-list CHPV whereby voters for a party may additionally freely list their preferred candidates in rank order using the ranked ballot version of CHPV. Here, the allocation of seats to parties is based on a nominally closed list and the allocation of candidates to each party’s seats according to its free list.
History and Usage
[edit]Positional voting systems have been around for some time but it was not until 2012 that an evaluation and comparative analysis of consecutively halved positional voting was formally published. Although its weightings are synonymous with those of the long-established binary number system; it has yet to be adopted as a single-winner voting system.
The divisors used in the party-list CHPV system are also used in the twelve-seat highest averages system employed for legislative elections in Macau. Having exceeded the six-winner upper limit in CHPV, the largest party here has gained extra seats by splitting itself into two.
References
[edit]- ^ a b "Geometric voting and consecutively halved positional voting". Retrieved 25 August 2012.
- ^ "GV&CHPV". Weightings. Retrieved 25 August 2012.
- ^ "GV&CHPV". Voting. Retrieved 25 August 2012.
- ^ "GV&CHPV". General criteria. pp1-3. Retrieved 25 August 2012.
- ^ "GV&CHPV". Majority and related criteria. Retrieved 25 August 2012.
- ^ "GV&CHPV". Clones, teaming and independence criteria. pp1-2. Retrieved 25 August 2012.
- ^ "GV&CHPV". Countng. Retrieved 25 August 2012.
- ^ "GV&CHPV". Plurality (first-past-the-post). Retrieved 25 August 2012.
- ^ "GV&CHPV". Borda count – as an extreme variant of GV. Retrieved 25 August 2012.
- ^ "GV&CHPV". Majority and related criteria – consensus versus polarization. Retrieved 25 August 2012.
- ^ "GV&CHPV". Geometric voting – preference weightings and rankings for consensus. Retrieved 25 August 2012.
- ^ "GV&CHPV". Geometric voting – balancing polarization and consensus. Retrieved 25 August 2012.
- ^ a b c "GV&CHPV". Clones, teaming and independence criteria. pp3-6. Retrieved 25 August 2012.
- ^ "GV&CHPV". Teaming thresholds. pp1-6. Retrieved 25 August 2012.
- ^ "GV&CHPV". Party-list. Retrieved 25 August 2012.
- ^ "GV&CHPV". Proportionality of CHPV – party proportionality. Retrieved 25 August 2012.
- ^ "GV&CHPV". Proportionality of CHPV. pp1-3. Retrieved 25 August 2012.
- ^ "GV&CHPV". Optimality of CHPV. pp1-4. Retrieved 25 August 2012.
- ^ "GV&CHPV". Sainte Laguë ~ proportionality. Retrieved 25 August 2012.
- ^ "GV&CHPV". D'Hondt ~ proportionality. Retrieved 25 August 2012.
- ^ "GV&CHPV". Sainte Laguë ~ party cloning. Retrieved 25 August 2012.
- ^ "GV&CHPV". D'Hondt ~ party cloning. Retrieved 25 August 2012.
- ^ "GV&CHPV". Party cloning. pp1-2. Retrieved 25 August 2012.