User:Mark viking/Homology

Informal examples

Informally, the homology of a topological space $X$ is a set of topological invariants of $X$ represented by its homology groups

$H_{0}(X),H_{1}(X),H_{2}(X),\ldots$

where the $k^{\rm {th}}$ homology group $H_{k}(X)$ describes the $k$-dimensional holes in$X$. A 0-dimensional hole is simply a gap between two components, consequently $H_{0}(X)$ describes the path-connected components of $X$.

The circle or 1-sphere $S^{1}$

A one-dimensional sphere $S^{1}$ is a circle. It has a single connected component and a one-dimensional hole, but no higher dimensional holes. The corresponding homology groups are given as

$H_{k}(S^{1})=\left\{{\begin{array}{l}\mathbb {Z} {\rm {\ for\ }}k=0{\rm {\ and\ }}k=1,\\\{0\}{\rm {\ otherwise}}.\,\!\end{array}}\right.$

where $\mathbb {Z}$ is the group of integers and $\{0\}$ is the trivial group. The group $H_{1}(S^{1})=\mathbb {Z}$ represents a kind of one-dimensional vector space, with integer coefficients, that represents the single one-dimensional hole contained in a circle.

The 2-sphere $S^{2}$

A two-dimensional sphere $S^{2}$ has a single connected component, no one-dimensional holes, a two-dimensional hole, and no higher dimensional holes. The corresponding homology groups are

$H_{k}(S^{2})=\left\{{\begin{array}{l}\mathbb {Z} {\rm {\ for\ }}k=0{\rm {\ and\ }}k=2,\\\{0\}{\rm {\ otherwise}}.\,\!\end{array}}\right.$

In general for an $n$-dimensional sphere $S^{n}$, the homology groups are

$H_{k}(S^{n})=\left\{{\begin{array}{l}\mathbb {Z} {\rm {\ for\ }}k=0{\rm {\ and\ }}k=n,\\\{0\}{\rm {\ otherwise}}.\,\!\end{array}}\right.$

The solid disc or 1-ball $B^{1}$

A one-dimensional ball $B^{1}$ is a solid disc. It has a single connected component, but in contrast to the circle, has no one-dimensional or higher-dimensional holes. The corresponding homology groups are all trivial except for $H_{0}(B^{1})=\mathbb {Z}$. In general, for an $n$-dimensional ball $B^{n}$,

$H_{k}(B^{n})=\left\{{\begin{array}{l}\mathbb {Z} {\rm {\ for\ }}k=0,\\\{0\}{\rm {\ otherwise}}.\,\!\end{array}}\right.$

The torus $T=S^{1}\times S^{1}$

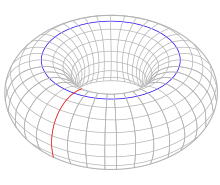
The torus is defined as a Cartesian product of two circles $T=S^{1}\times S^{1}$. The torus has a single connected component, two independent one-dimensional holes (indicated by circles in red and blue) and one two-dimensional hole as the interior of the torus. The corresponding homology groups are

$H_{k}(T)=\left\{{\begin{array}{l}\mathbb {Z} {\rm {\ for\ }}k=0,2\\\mathbb {Z} \times \mathbb {Z} {\rm {\ for\ }}k=1\\\{0\}{\rm {\ otherwise}}.\,\!\end{array}}\right.$

The two independent 1D holes form a two-dimensional vector space with integer coefficients, producing the Cartesian product group $\mathbb {Z} \times \mathbb {Z}$.