User:Makkabi~enwiki/sandbox
Salu's left-hand rule for Faraday’s law of induction
In 2013 Yehuda Salu proposed a new left-hand rule[1] that can serve as a simple and quick way of finding the directional relationships between the variables of Faraday's law, without using Lenz's law. Like other right and left hand rules that are already being used in electromagnetism [2][3], this rule is a visual mnemonic for a basic law of physics.
Faraday’s Law of Induction
[edit]Faraday’s law of induction deals with situations in which a magnetic field B crosses a surface A, enclosed by a line L. is the induced electromotive force (emf) and is the rate of change of the flux of the magnetic field B through the area A.
n is the normal to the area element dA. E is the induced electric field.
If the magnetic field is the same throughout the area, , (Figure 1).
The left hand rule for Faraday’s Law
[edit]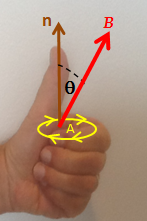
Align the curved fingers of the left hand with the loop of the conductor (Figure 1).
The stretched thumb represents the normal to the surface enclosed by the loop, and defines its positive direction.
If the change of flux ( ) is positive, the direction of the induced emf is the same as the direction of the curved fingers.
If the change of flux is negative, the direction of the induced emf is against the direction of the curved fingers.
Justification
[edit]Faraday’s Law is expressed in a right handed coordinate system as [4]: .
According to the convention of a right handed coordinate system, the direction of n (the normal to the area) is the direction of the stretched right thumb. The direction of the integration along L is the direction of the curved right fingers. The minus sign in Faraday’s Law is equivalent to changing the direction of the integration of the line integral, or to using a left handed coordinate system. Hence the left hand rule.
Example
[edit]
Let a uniform magnetic field that decreases with time point straight out of the paper (figure 2 a). Find the direction of the induce emf in a conducting ring that lies on the plane of the paper.
Answer. The left hand is set as in figure 2. b. Both the initial and final fluxes are positive. Since the magnetic field decreases with time, the change in flux ( ) is negative. Therefore, the direction of the induced emf is against the curved fingers, which is counterclockwise. (The induced emf would have the same direction whenever the flux decreases. e.g. if the ring starts to rotate around its diameter, or to shrink. )
See also
[edit]- Fleming's left hand rule for motors
- Maxwell–Faraday equation
- magnetic induction
- right hand rule
- Stokes' theorem
- Ampere's law
References
[edit]- ^ Salu, Y. A left-hand rule for Faraday’s Law. The Physics Teacher 52 (2014) 48. doi:10.1119/1.4849156
- ^ http://www.magnet.fsu.edu/education/tutorials/java/handrules/index.html
- ^ Fleming, John Ambrose (1902). Magnets and Electric Currents, 2nd Edition. London: E.& F. N. Spon. pp. 173–174 http://books.google.com/books?id=ASUYAAAAYAAJ&pg=PA173#v=onepage&q&f=false
- ^ Formula 17.3 http://www.feynmanlectures.caltech.edu/II_17.html








