User:Macumba/Wild Sandbox
Ion
[edit]Chemistry
[edit]Notation
[edit]Denoting the charged state
[edit]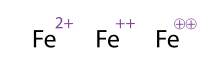
When writing the chemical formula for an ion, its net charge is written in superscript immediately after the chemical structure for the molecule/atom. The net charge is written with the magnitude before the sign; that is, a doubly charged cation is indicated as 2+ instead of +2. Conventionally the magnitude of the charge is omitted for singly charged molecules/atoms; for example, the sodium cation is indicated as Na+
and not Na+
.
An alternative (and acceptable) way of showing a molecule/atom with multiple charges is by drawing out the signs multiple times; this is often seen with transition metals. Chemists sometimes circle the sign; this is merely ornamental and does not alter the chemical meaning. All three representations of Fe2+
shown in the figure are thus equivalent.

Monatomic ions are sometimes also denoted with Roman numerals; for example, the Fe2+
example seen above is occasionally referred to as Fe(II) or FeII. The Roman numeral designates the formal oxidation state of an element, whereas the superscripted numerals denotes the net charge. The two notations are therefore exchangeable for monatomic ions, but the Roman numerals cannot be applied to polyatomic ions. It is however possible to mix the notations for the individual metal center with a polyatomic complex, as shown by the uranyl ion example.
Sub-classes
[edit]If an ion contains unpaired electrons, it is called a radical ion. Just like uncharged radicals, radical ions are very reactive. Polyatomic ions containing oxygen, such as carbonate and sulfate, are called oxyanions. Molecular ions that contain at least one carbon to hydrogen bond are called organic ions. If the charge in an organic ion is formally centered on a carbon, it is termed a carbocation (if positively charged) or carbanion (if negatively charged).
Astronomy
[edit]Stuff
[edit]The Clopper-Pearson interval is an exact interval since it is based directly on the binomial distribution rather than any approximation to the binomial distribution. This interval, however, can be conservative because of the discrete nature of the binomial distribution. For example, the true coverage rate of a 95% Clopper-Pearson interval may be well above 95%, depending on n and θ. Thus the interval may be wider than it needs to be to achieve 95% confidence. In contrast, it is worth noting that other confidence bounds may be narrower than their nominal confidence with, i.e., the Normal Approximation (or "Standard") Interval, Wilson Interval, Agresti-Coull Interval, etc, with a nominal coverage of 95% may in fact cover less than 95%.[1]
References
[edit]- ^ Lawrence D. Brown, T. Tony Cai and Anirban DasGupta, Interval Estimation for a Binomial Proportion, Statistical Science 2001, Vol. 16, No. 2, 101–133
