User:Jostylr/sandbox

The de Broglie–Bohm theory, also called the pilot-wave theory, Bohmian mechanics, and the causal interpretation, is a quantum theory describing point particles whose motion is determined by a wavefunction. Differently from ordinary quantum theory, these particles always have locations and the evolution of their location over time is deterministic. The evolution over time of the position of each particle (that is, each particle's velocity) arises from the gradient of the wavefunction (specifically from the guiding equation). The evolution of the wavefunction over time is given by Schrödinger's equation.

The de Broglie–Bohm theory is explicitly non-local. The velocity of any one particle depends on the value of the gradient of the wavefunction which is defined over configuration space and, thus, may depend on the simultaneous positions of any or all of the other particles in the universe.

This theory is deterministic and non-relativistic (relativistic extensions of this theory exist, though they tend to sacrifice determinism). It handles spin and curved spaces without difficulty. It can be modified to handle quantum field theory. Bell's theorem was inspired by Bell's discovery of the work of David Bohm and his subsequent wondering if the obvious non-locality of the theory could be removed.

This theory gives rise to a measurement formalism, analogous to thermodynamics for classical mechanics, which yields the standard quantum formalism generally associated with the Copenhagen interpretation. The measurement problem is resolved by this theory since the outcome of an experiment is registered by the configuration of the particles of the experimental apparatus after the experiment is completed. The familiar wavefunction collapse of standard quantum mechanics emerges from an analysis of subsystems and the quantum equilibrium hypothesis.

The theory has a number of equivalent mathematical formulations and has been presented under a number of different names.

The theory

De Broglie–Bohm theory is based on the following:

There are $N$ particles with positions $\mathbf {Q} _{k}$ that evolve according to the guiding equation

${\frac {d\mathbf {Q} _{k}}{dt}}={\frac {\hbar }{m_{k}}}Im\left({\frac {\nabla _{k}\psi }{\psi }}\right)$

There is a complex-valued wavefunction $\psi$ evolving according to Schrödinger's equation

$i\hbar {\frac {\partial }{\partial t}}\psi =-\sum _{k=1}^{N}{\frac {\hbar ^{2}}{2m_{k}}}\nabla _{k}^{2}\psi +V\psi$

That completes the specification of the theory for $N$ spinless particles. Incorporating spin is not difficult.

This theory will agree with the results of standard quantum mechanics if the initial positions of the particles are distributed according to $|\psi |^{2}$ which will typically be the case in any universe governed by this theory.

Results

Below are some highlights of the results that arise out of an analysis of de Broglie–Bohm theory. Experimental results agree with all of the standard predictions of quantum mechanics in so far as the latter has predictions. However, while standard quantum mechanics is limited to discussing experiments with human observers, de Broglie–Bohm theory is a theory which governs the dynamics of a system without the intervention of outside observers (p. 117 in Bell).

The basis for agreement with standard quantum mechanics is that the particles are distributed according to $|\psi |^{2}$. This is a statement of observer ignorance, but it can be proven that for a universe governed by this theory, this will typically be the case. There is apparent collapse of the wave function governing subsystems of the universe, but there is no collapse of the universal wavefunction.

Two-slit experiment

The Bohmian trajectories for an electron going through the two-slit experiment.

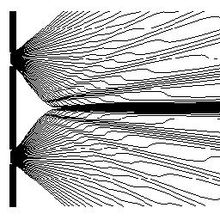
The double-slit experiment is an illustration of wave-particle duality. In it, a beam of particles (such as photons) travels through a barrier with two slits removed. If one puts a detector screen on the other side, the pattern of detected particles shows interference fringes characteristic of waves; however, the detector screen responds to particles. The system exhibits behaviour of both waves (interference patterns) and particles (dots on the screen).

If we modify this experiment so that one slit is closed, no interference pattern is observed. Thus, the state of both slits affects the final results. We can also arrange to have a minimally invasive detector at one of the slits to see which slit the particle went through. When we do that, the interference pattern disappears.

The Copenhagen interpretation states that the particles are not localised in space until they are detected, so that, if there is no detector on the slits, there is no matter of fact about what slit has the particle passed through. If one slit has a detector on it, then the wavefunction collapses due to that detection.

In de Broglie–Bohm theory, the wavefunction travels through both slits, but each particle has a well-defined trajectory and passes through exactly one of the slits. The final position of the particle on the detector screen and the slit through which the particle passes by is determined by the initial position of the particle. Such initial position is not controllable by the experimenter, so there is an appearance of randomness in the pattern of detection. The wave function interferes with itself and guides the particles in such a way that the particles avoid the regions in which the interference is destructive and are attracted to the regions in which the interference is constructive, giving rise to the interference pattern on the detector screen.

To explain the behavior when the particle is detected to go through one slit, one needs to appreciate the role of the conditional wavefunction and how it gives rise to the collapse of the wavefunction; this is explained below. The basic idea is that the environment registering the detection effectively separates the two wave packets in configuration space.

Measuring spin and polarization

According to ordinary quantum theory, it is not possible to measure the spin or polarization of a particle directly; instead, the component in one direction is measured; the outcome from a single particle may be 1, meaning that the particle is aligned with the measuring apparatus, or -1, meaning that it is aligned the opposite way. For an ensemble of particles, if we expect the particles to be aligned, the results are all 1. If we expect them to be aligned oppositely, the results are all -1. For other alignments, we expect some results to be 1 and some to be -1 with a probability that depends on the expected alignment. For a full explanation of this, see the Stern-Gerlach Experiment.

In de Broglie–Bohm theory, the results of a spin experiment cannot be analyzed without some knowledge of the experimental setup. It is possible to modify the setup so that the trajectory of the particle is unaffected, but that the particle with one setup registers as spin up while in the other setup it registers as spin down. Thus, for the de Broglie–Bohm theory, the particle's spin is not an intrinsic property of the particle -- instead spin is, so to speak, in the wave function of the particle in relation to the particular device being used to measure the spin. This is an illustration of what is sometimes referred to as contextuality, and is related to naive realism about operators.

Heisenberg's uncertainty principle

The Heisenberg uncertainty principle states that when two complementary measurements are made, there is a limit to the product of their accuracy. As an example, if one measures the position with an accuracy of $\Delta x$, and the momentum with an accuracy of $\Delta p$, then $\Delta x\Delta p\gtrsim h.$ If we make further measurements in order to get more information, we disturb the system and change the trajectory into a new one depending on the measurement setup; therefore, the measurement results are still subject to Heisenberg's uncertainty relation.

In de Broglie–Bohm theory, there is always a matter of fact about the position and momentum of a particle. Each particle has a well defined trajectory. Observers have limited knowledge as to what this trajectory is (and thus of the position and momentum). It is the lack knowledge of the particle's trajectory that accounts for the uncertainty relation. What one can know about a particle at any given time is described by the wavefunction. Since the uncertainty relation can be derived from the wavefunction in other interpretations of quantum mechanics, it can be likewise derived (in the epistemic sense mentioned above), on the de Broglie–Bohm theory.

To put the statement differently, the particles' positions are only known statistically. As in classical mechanics, successive observations of the particles' positions refine the experimenter's knowledge of the particles' initial conditions. Thus, with succeeding observations, the initial conditions become more and more restricted. This formalism is consistent with the normal use of the Schrödinger equation.

For the derivation of the uncertainty relation, see Heisenberg uncertainty principle, noting that it describes it from the viewpoint of the Copenhagen interpretation.

Quantum entanglement, Einstein-Podolsky-Rosen paradox, Bell's theorem, and nonlocality

De Broglie–Bohm theory highlighted the issue of nonlocality: it inspired John Stewart Bell to prove his now-famous theorem, which in turn led to the Bell test experiments.

In the Einstein-Podolsky-Rosen paradox, the authors point out that quantum mechanics allows the creation of pairs of particles in an entangled quantum state. They describe a thought-experiment one could perform on such a pair, the results of which they interpreted as indicating that quantum mechanics is an incomplete theory.

Decades later John Bell proved Bell's theorem (see p. 14 in Bell), in which he showed that, if they are to agree with the empirical predictions of quantum mechanics, all such "hidden-variable" completions of quantum mechanics must either be nonlocal (as the Bohm interpretation is) or give up the assumption that experiments produce unique results (see counterfactual definiteness and many-worlds interpretation). In particular, Bell proved that any local theory with unique results must make empirical predictions satisfying a statistical constraint called "Bell's inequality".

Alain Aspect performed a series of Bell test experiments that test Bell's inequality using an EPR-type setup. Aspect's results show experimentally that Bell's inequality is in fact violated -- meaning that the relevant quantum mechanical predictions are correct. In these Bell test experiments, entangled pairs of particles are created; the particles are separated, traveling to remote measuring apparatus. The orientation of the measuring apparatus can be changed while the particles are in flight, demonstrating the apparent non-locality of the effect.

The de Broglie–Bohm theory makes the same (empirically correct) predictions for the Bell test experiments as ordinary quantum mechanics. It is able to do this because it is manifestly nonlocal. It is often criticized or rejected based on this; Bell's attitude was: "It is a merit of the de Broglie–Bohm version to bring this [nonlocality] out so explicitly that it cannot be ignored."

The de Broglie–Bohm theory describes the physics in the Bell test experiments as follows: to understand the evolution of the particles, we need to set up a wave equation for both particles; the orientation of the apparatus affects the wavefunction. The particles in the experiment follow the guidance of the wavefunction. It is the wavefunction that carries the faster-than-light effect of changing the orientation of the apparatus. An analysis of exactly what kind of nonlocality is present and how it is compatible with relativity can be found in Maudlin. Note that in Bell's work, and in more detail in Maudlin's work, it is shown that the nonlocality does not allow for signaling at speeds faster than light.

Classical limit

Bohm's formulation of de Broglie–Bohm theory in terms of a classical-looking version has the merits that the emergence of classical behavior seems to follow immediately for any situation in which the quantum potential is negligible, as noted by Bohm in 1952. Modern methods of decoherence are relevant to an analysis of this limit. See Allori et al for steps towards a rigorous analysis.

History

De Broglie–Bohm theory has a history of different formulations and names. In this section, each stage is given a name and a main reference.

Pilot-wave theory

This was the theory which de Broglie presented at the 1927 Solvay Conference. At the conference, Wolfgang Pauli pointed out that it did not deal properly with the case of inelastic scattering. De Broglie was persuaded by this argument, and abandoned this theory. Later, in 1932, John von Neumann published a paper, claiming to prove that all hidden-variable theories are impossible. This clearly applied to de Broglie's theories.

This stage applies to many spin-less particles, and is deterministic, but lacks an adequate theory of measurement. An analysis of de Broglie's presentation is given in Bacciagaluppi et al.

Around this time Madelung also developed a hydrodynamic version of Schrödinger's equation which is the basis for the density current derivation of de Broglie–Bohm theory.

De Broglie–Bohm theory

This was described by Bohm's original papers 'A Suggested Interpretation of the Quantum Theory in Terms of "Hidden Variables" I and II' [Bohm 1952]. It extended the original Pilot Wave Theory to incorporate a consistent theory of measurement, and to address a criticism of Pauli that de Broglie did not properly respond to; it is taken to be deterministic (though Bohm hinted in the original papers that there should be disturbances to this, in the way Brownian motion disturbs Newtonian mechanics). This stage is known as the de Broglie–Bohm Theory in Bell's work [Bell 1987] and is the basis for 'The Quantum Theory of Motion' [Holland 1993].

This stage applies to multiple particles, and is deterministic.

The de Broglie–Bohm theory is an example of a hidden variables theory. Bohm originally hoped that hidden variables could provide a local, causal, objective description that would resolve or eliminate many of the paradoxes of quantum mechanics, such as Schrödinger's cat, the measurement problem and the collapse of the wavefunction. However, Bell's theorem complicates this hope, as it demonstrates that there can be no local hidden variable theory that is compatible with the predictions of quantum mechanics. The Bohmian interpretation is causal but not local.

Bohm became dissatisfied with the conventional interpretation of quantum mechanics, pointing out that, although it requires one to give up "the possibility of even conceiving what might determine the behaviour of an individual system at a quantum level", it does not prove that this requirement is necessary. Indeed, it was his understanding, given 44to him by Einstein, of the flawed nature of von Neumann's proof that inspired his papers.

Bohm's paper was largely ignored by other physicists; it was not supported by Albert Einstein (who was also dissatisfied with the prevailing orthodoxy and had discussed Bohm's ideas with him before publication). Bohm eventually abandoned it.

The cause was taken up by John Bell. In "Speakable and Unspeakable in Quantum Mechanics" [Bell 1987], several of the papers refer to hidden variables theories (which include Bohm's). Bell showed that Pauli's and von Neumann's objections amounted to showing that hidden variables theories are nonlocal, and that nonlocality is a feature of all quantum mechanical systems.

Bohmian mechanics

This term is used to describe the same theory, but with an emphasis on the notion of current flow. In particular, it is often used to include most of the further extensions past the spin-less version of Bohm. While de Broglie–Bohm theory has Lagrangians and Hamilton-Jacobi equations as a primary focus and backdrop, with the icon of the quantum potential, Bohmian mechanics considers the continuity equation as primary and has the guiding equation as its icon. They are mathematically equivalent in so far as the Hamilton-Jacobi formulation applies, i.e., spin-less particles. The papers of Dürr et al popularized the term.

All of non-relativistic quantum mechanics can be fully accounted for in this theory.

Causal interpretation and ontological interpretation

Bohm developed his original ideas, calling them the Causal Interpretation. Later he felt that causal sounded too much like deterministic and preferred to call his theory the Ontological Interpretation. The main reference is 'The Undivided Universe' [Bohm, Hiley 1993].

This stage covers work by Bohm and in collaboration with Vigier and Hiley. Bohm is clear that this theory is non-deterministic (the work with Hiley includes a stochastic theory). As such, this theory is not, strictly speaking, a formulation of the de Broglie–Bohm theory. However, it deserves mention here because the term "Bohm Interpretation" is ambiguous between this theory and the de Broglie–Bohm theory.

Hidden variables

De Broglie–Bohm theory is often referred to as a "hidden variable" theory. The alleged applicability of the term "hidden variable" comes from the fact that the particles postulated by Bohmian mechanics do not influence the evolution of the wavefunction. The argument is that, because adding particles does not have an effect on the wavefunction's evolution, such particles must not have effects at all and are, thus, unobservable, since they cannot have an effect on observers. There is no analogue of Newton's third law in this theory. The idea is supposed to be that, since particles cannot influence the wavefunction, and it is the wavefunction that determines measurement predictions through the Born rule, the particles are superfluous and unobservable.

Such an argument, however, arises from a fundamental misunderstanding of the relation between the ontology posited by the de Broglie–Bohm theory and the world of ordinary observation. In particular, the particles postulated by the de Broglie–Bohm theory are anything but "hidden" variables: they are what the cats and trees and tables and planets and pointers we see are made of! It is the wavefunction itself which is "hidden" in the sense of being invisible and not-directly-observable.

Thus, for example, when the wavefunction of some measuring apparatus is such that its pointer is superposed between pointing to the left and pointing to the right, what accounts for the fact that scientists, when they look at the apparatus, see the pointer pointing to the left (say) is the fact that the de Broglie–Bohmian particles that make up the pointer are actually pointed towards the left. While the exact details of how humans process such information and what it is based on is beyond the scope of the de Broglie–Bohm theory, the basic idea of any particle ontology is that if the particles in the theory appear where they seem to be from human observations, then it is considered a successful prediction.

Criticisms

Occam's razor criticism

Both Hugh Everett III and Bohm treated the wavefunction as a complex-valued but real field. Everett's many-worlds interpretation is an attempt to demonstrate that the wavefunction alone is sufficient to account for all our observations. When we see the particle detectors flash or hear the click of a Geiger counter or whatever then Everett's theory interprets this as our wavefunction responding to changes in the detector's wavefunction, which is responding in turn to the passage of another wavefunction (which we think of as a "particle", but is actually just another wave-packet). But no particle, in the Bohm sense of having a defined position and velocity, is involved in measurement. For this reason Everett sometimes referred to his approach as the "pure wave theory". Talking of Bohm's 1952 approach, Everett says:

“ Our main criticism of this view is on the grounds of simplicity - if one desires to hold the view that $\psi$ is a real field then the associated particle is superfluous since, as we have endeavored to illustrate, the pure wave theory is itself satisfactory. ”

In the Everettian view, then, the Bohm particles are unobservable entities, similar to, and equally as unnecessary as, for example, the luminiferous ether was found to be unnecessary in special relativity. We can remove the particles from Bohm's theory and still account for all our observations. The unobservability of the "hidden particles" stems from an asymmetry in the causal structure of the theory; the particles are influenced by a "force" exerted by the wavefunction and by each other, but the particles do not influence the time development of the wavefunction (i.e. there is no analogue of Newton's third law -- the particles do not react back onto the wavefunction) Thus, if we regard the wavefunction as real and the source of all experience, the particles do not make their presence known in any way; as the theory says, they are hidden, but in a far more profound way than de Broglie and Bohm had intended.

In the Everettian view the role of the Bohm particle is to tag, or select, just one branch of the universal wavefunction; the other branches are designated "empty" and implicitly assumed by Bohm, in what is called the "result assumption", to be devoid of conscious observers. H. Dieter Zeh comments on these "empty" branches:

“ It is usually overlooked that Bohm’s theory contains the same “many worlds” of dynamically separate branches as the Everett interpretation (now regarded as “empty” wave components), since it is based on precisely the same . . . global wave function . . . ”

David Deutsch has expressed the same point more "acerbically":

“ pilot-wave theories are parallel-universe theories in a state of chronic denial. ”

This argument of Everett's is sometimes called the "redundancy argument", since the superfluous particles are redundant in the sense of Occam's razor.

This conclusion has been challenged by pilot wave advocates, with a number of suggested resolutions; either make the "result assumption" explicit, deny that the wavefunction is as objectively real as the particles or dispute whether the Everett prescription is complete (e.g. can probabilities be derived from the wavefunction?)

The Theory

The ontology

This theory is a theory of particles moving in space-time. Each particle has a definite position $x$ at every time $t$. This is the starting point of the theory. The correspondence to our experiences is made by the identification of where the particles are and where we witness them to be, as in classical mechanics.

The difference between de Broglie–Bohm theory and classical mechanics is not in the ontology, but in the dynamics. In classical mechanics, the acceleration of the particles are given by forces. In de Broglie–Bohm theory, the velocities of the particles are given by the wavefunction.

In what follows below, we will give the setup for one particle moving in $\mathbb {R} ^{3}$ followed by the setup for $N$ particles moving in 3 dimensions. In the first instance, configuration space and real space are the same while in the second, real space is still $\mathbb {R} ^{3}$, but configuration space becomes $\mathbb {R} ^{3N}$. While the particle positions themselves are in real space, the velocity field and wavefunction are on configuration space which is how particles are entangled with each other in this theory.

Extensions to this theory include spin and more complicated configuration spaces.

We use variations of $\mathbf {Q}$ for particle positions while $\psi$ represents the complex-valued wavefunction on configuration space.

Guiding equation

For a single particle moving in $\mathbb {R} ^{3}$, the particle's velocity is given

${\frac {d\mathbf {Q} }{dt}}(t)={\frac {\hbar }{m}}Im\left({\frac {\nabla \psi }{\psi }}\right)(\mathbf {Q} ,t)$.

For many particles, we label them as $\mathbf {Q} _{k}$ for the $k$th particle and their velocities are given by

${\frac {d\mathbf {Q} _{k}}{dt}}(t)={\frac {\hbar }{m_{k}}}Im\left({\frac {\nabla _{k}\psi }{\psi }}\right)(\mathbf {Q} _{1},\mathbf {Q} _{2},\ldots ,\mathbf {Q} _{N},t)$.

The key fact to notice is that this velocity field depends on the actual positions of all of the $N$ particles in the universe. As explained below, in most experimental situations, the influence of all of those particles can be encapsulated into an effective wavefunction for a subsystem of the universe.

Schrödinger's equation

The one particle Schrödinger equation governs the time evolution of a complex-valued wavefunction on $\mathbb {R} ^{3}$. The equation represents a quantized version of the total energy of a classical system evolving under a real-valued potential function $V$ on $\mathbb {R} ^{3}$:

$i\hbar {\frac {\partial }{\partial t}}\psi =-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\psi +V\psi$

For many particles, the equation is the same except that $\psi$ and $V$ are now on configuration space, $\mathbb {R} ^{3N}$.

$i\hbar {\frac {\partial }{\partial t}}\psi =-\sum _{k=1}^{N}{\frac {\hbar ^{2}}{2m_{k}}}\nabla _{k}^{2}\psi +V\psi$

This is the same wavefunction of conventional quantum mechanics.

The Born Rule

In Bohm's original papers [Bohm 1952] , he discusses how de Broglie–Bohm theory gives rise to the usual measurement results of quantum mechanics. The key idea is that this is true if the positions of the particles satisfy the statistical distribution given by $|\psi |^{2}$. And that distribution is guaranteed to be true for all time under the guiding equation if the initial distribution of the particles satisfies $|\psi |^{2}$.

For a given experiment, we can postulate this as being true and verify experimentally that it does indeed hold true, as it does. But, as argued in Dürr et al, one needs to argue that this distribution for subsystems is typical. They argue that $|\psi |^{2}$ by virtue of its equivariance under the dynamical evolution of the system, is the appropriate measure of typicality for initial conditions of the positions of the particles. They then prove that the vast majority of possible initial configurations will give rise to Born rule (i.e., $|\psi |^{2}$) statistics for measurement outcomes. In short, in a universe governed by the de Broglie–Bohm dynamics, Born rule behavior is typical.

The situation is thus analogous to the situation in classical statistical physics. A low entropy initial condition will, with overwhelmingly high probability, evolve into a higher entropy state: behavior consistent with the second law of thermodynamics is typical. There are, of course, anomalous initial conditions which would give rise to violations of the second law. However, absent some very detailed evidence supporting the actual realization of one of those special initial conditions, it would be quite unreasonable to expect anything but the actually observed uniform increase of entropy. Similarly, in the de Broglie–Bohm theory, there are anomalous initial conditions which would produce measurement statistics in violation of the Born rule (i.e., in conflict with the predictions of standard quantum theory). But the typicality theorem shows that, absent some particular reason to believe one of those special initial conditions was in fact realized, Born rule behavior is what one should expect.

It is in that qualified sense that Born rule is, for the de Broglie–Bohm theory, a theorem rather than (as in ordinary quantum theory) an additional postulate.

The conditional wave function of a subsystem

In the formulation of the De Broglie–Bohm theory, there is only a wave function for the entire universe (which always evolves by the Schrödinger equation). However, once the theory is formulated, it is convenient to introduce a notion of wave function also for subsystems of the universe. Let us write the wave function of the universe as $\psi (t,q^{\mathrm {I} },q^{\mathrm {II} })$, where $q^{\mathrm {I} }$ denotes the configuration variables associated to some subsystem (I) of the universe and $q^{\mathrm {II} }$ denotes the remaining configuration variables. Denote, respectively, by $Q^{\mathrm {I} }(t)$ and by $Q^{\mathrm {II} }(t)$ the actual configuration of subsystem (I) and of the rest of the universe. For simplicity, we consider here only the spinless case. The conditional wave function of subsystem (I) is defined by:

$\psi ^{\mathrm {I} }(t,q^{\mathrm {I} })=\psi (t,q^{\mathrm {I} },Q^{\mathrm {II} }(t)).$

It follows immediately from the fact that $Q(t)=(Q^{\mathrm {I} }(t),Q^{\mathrm {II} }(t))$ satisfies the guiding equation that also the configuration $Q^{\mathrm {I} }(t)$ satisfies a guiding equation identical to the one presented in the formulation of the theory, with the universal wave function $\psi$ replaced with the conditional wave function $\psi ^{\mathrm {I} }$. Also, the fact that $Q(t)$ is random with probability density given by the square modulus of $\psi (t,\cdot )$ implies that the conditional probability density of $Q^{\mathrm {I} }(t)$ given $Q^{\mathrm {II} }(t)$ is given by the square modulus of the (normalized) conditional wave function $\psi ^{\mathrm {I} }(t,\cdot )$ (in the terminology of Dürr et. al this fact is called the fundamental conditional probability formula).

Unlike the universal wave function, the conditional wave function of a subsystem does not always evolves by the Schrödinger equation, but in many situations it does. For instance, if the universal wave function factors as:

$\psi (t,q^{\mathrm {I} },q^{\mathrm {II} })=\psi ^{\mathrm {I} }(t,q^{\mathrm {I} })\psi ^{\mathrm {II} }(t,q^{\mathrm {II} })$

then the conditional wave function of subsystem (I) is (up to an irrelevant scalar factor) equal to $\psi ^{\mathrm {I} }$ (this is what Standard Quantum Theory would regard as the wave function of subsystem (I)). If, in addition, the Hamiltonian does not contain an interaction term between subsystems (I) and (II) then $\psi ^{\mathrm {I} }$ does satisfy a Schrödinger equation. More generally, assume that the universal wave function $\psi$ can be written in the form:

$\psi (t,q^{\mathrm {I} },q^{\mathrm {II} })=\psi ^{\mathrm {I} }(t,q^{\mathrm {I} })\psi ^{\mathrm {II} }(t,q^{\mathrm {II} })+\phi (t,q^{\mathrm {I} },q^{\mathrm {II} }),$

where $\phi$ solves Schrödinger equation and $\phi (t,q^{\mathrm {I} },Q^{\mathrm {II} }(t))=0$ for all $t$ and $q^{\mathrm {I} }$. Then, again, the conditional wave function of subsystem (I) is (up to an irrelevant scalar factor) equal to $\psi ^{\mathrm {I} }$ and if the Hamiltonian does not contain an interaction term between subsystems (I) and (II), $\psi ^{\mathrm {I} }$ satisfies a Schrödinger equation.

The fact that the conditional wave function of a subsystem does not always evolve by the Schrödinger equation is related to the fact that the usual collapse rule of Standard Quantum Theory emerges from the Bohmian formalism when one considers conditional wave functions of subsystems.

Measurements, the quantum formalism, and observer independence

De Broglie–Bohm theory gives the same results as quantum mechanics. It treats the wavefunction as a fundamental object in the theory as the wavefunction describes how the particles move. This means that no experiment can distinguish between the two theories. This section outlines the ideas as to how the standard quantum formalism arises out of quantum mechanics. References include Bohm's original 1952 paper and Dürr et al.

Collapse of the wavefunction

De Broglie–Bohm theory is a theory that applies primarily to the whole universe. That is, there is a single wavefunction governing the motion of all of the particles in the universe according to the guiding equation. Theoretically, the motion of one particle depends on the positions of all of the other particles in the universe. In some situations, such as in experimental systems, we can represent the system itself in terms of a de Broglie–Bohm theory in which the wavefunction of the system is obtained by conditioning on the environment of the system. Thus, the system can be analyzed with Schrödinger's equation and the guiding equation, with an initial $|\psi |^{2}$ distribution for the particles in the system (see the section on the conditional wave function of a subsystem for details).

It requires a special setup for the conditional wavefunction of a system to obey a quantum evolution. When a system interacts with its environment, such as through a measurement, then the conditional wavefunction of the system evolves in a different way. The evolution of the universal wavefunction can become such that the wavefunction of the system appears to be in a superposition of distinct states. But if the environment has recorded the results of the experiment, then using the actual Bohmian configuration of the environment to condition on, the conditional wavefunction collapses to just one alternative, the one corresponding with the measurement results.

Collapse of the universal wavefunction never occurs in de Broglie–Bohm theory. Its entire evolution is governed by Schrödinger's equation and the particles' evolutions are governed by the guiding equation. Collapse only occurs in a phenomenological way for systems that seem to follow their own Schrödinger's equation. As this is an effective description of the system, it is a matter of choice as to what to define the experimental system to include and this will affect when "collapse" occurs.

Operators as observables

In the standard quantum formalism, measuring observables is generally thought of as measuring operators on the Hilbert space. For example, measuring position is considered to be a measurement of the position operator. This relationship between physical measurements and Hilbert space operators is, for standard quantum mechanics, an additional axiom of the theory. The de Broglie–Bohm theory, by contrast, requires no such measurement axioms (and measurement as such is not a dynamically distinct or special sub-category of physical processes in the theory). In particular, the usual operators-as-observables formalism is, for de Broglie–Bohm theory, a theorem. A major point of the analysis is that many of the measurements of the observables do not correspond to properties of the particles; they are (as in the case of spin discussed above) measurements of the wavefunction.

In the history of de Broglie–Bohm theory, the proponents have often had to deal with claims that this theory is impossible. Such arguments are generally based on inappropriate analysis of operators as observables. If one believes that spin measurements are indeed measuring the spin of a particle that existed prior to the measurement, then one does reach contradictions. De Broglie–Bohm theory deals with this by noting that spin is not a feature of the particle, but rather that of the wavefunction. As such, it only has a definite outcome once the experimental apparatus is chosen. Once that is taken into account, the impossibility theorems become irrelevant.

There have also been claims that experiments reject the Bohm trajectories [2] in favor of the standard QM lines. But as shown in [3] and [4], such experiments cited above only disprove a misinterpretation of the de Broglie–Bohm theory, not the theory itself.

There are also objections to this theory based on what it says about particular situations usually involving eigenstates of an operator. For example, the ground state of hydrogen is a real wavefunction. According to the guiding equation, this means that the electron is at rest when in this state. Nevertheless, it is distributed according to $|\psi |^{2}$ and no contradiction to experimental results is possible to detect.

Operators as observables leads many to believe that many operators are equivalent. De Broglie–Bohm theory, from this perspective, chooses the position observable as a favored observable rather than, say, the momentum observable. Again, the link to the position observable is a consequence of the dynamics. The motivation for de Broglie–Bohm theory is to describe a system of particles. This implies that the goal of the theory is to describe the positions of those particles at all times. Other observables do not have this compelling ontological status. Having definite positions explains having definite results such as flashes on a detector screen. Other observables would not lead to that conclusion, but there need not be any problem in defining a mathematical theory for other observables; see Hyman et al for an exploration of the fact that a probability density and probability current can be defined for any set of commuting operators.

Quantum trajectory method

Work by Robert Wyatt in the early 2000s attempted to use the Bohm "particles" as an adaptive mesh that follows the actual trajectory of a quantum state in time and space. In the "quantum trajectory" method, one samples the quantum wavefunction with a mesh of quadrature points. One then evolves the quadrature points in time according to the Bohm equations of motion. At each time-step, one then re-synthesizes the wavefunction from the points, recomputes the quantum forces, and continues the calculation. (Quick-time movies of this for H+H₂ reactive scattering can be found on the Wyatt group web-site at UT Austin.) This approach has been adapted, extended, and used by a number of researchers in the Chemical Physics community as a way to compute semi-classical and quasi-classical molecular dynamics. A recent (2007) issue of the Journal of Physical Chemistry A was dedicated to Prof. Wyatt and his work on "Computational Bohmian Dynamics".

Eric Bittner's group at the University of Houston has advanced a statistical variant of this approach that uses Bayesian sampling technique to sample the quantum density and compute the quantum potential on a structureless mesh of points. This technique was recently used to estimate quantum effects in the heat-capacity of small clusters Ne_n for n~100.

There remain difficulties using the Bohmian approach, mostly associated with the formation of singularities in the quantum potential due to nodes in the quantum wavefunction. In general, nodes forming due to interference effects lead to the case where ${\frac {1}{R}}\nabla ^{2}R\rightarrow \infty .$ This results in an infinite force on the sample particles forcing them to move away from the node and often crossing the path of other sample points (which violates single-valuedness). Various schemes have been developed to overcome this; however, no general solution has yet emerged.

These methods, as does Bohm's Hamilton-Jacobi formulation, do not apply to situations in which the full dynamics of spin need to be taken into account.

Derivations

De Broglie–Bohm theory has been derived many times and in many ways. Below are five derivations all of which are very different and lead to different ways of understanding and extending this theory.

• Schrödinger's equation can be derived by using Einstein's light quanta hypothesis: $E=\hbar \omega \;$ and de Broglie's hypothesis: $\mathbf {p} =\hbar \mathbf {k} \;$.

The guiding equation can be derived in a similar fashion. We assume a plane wave: $\psi (\mathbf {x} ,t)=Ae^{i(\mathbf {k} \cdot \mathbf {x} -\omega t)}$. Notice that $i\mathbf {k} =\nabla \psi /\psi$. Assuming that $\mathbf {p} =m\mathbf {v}$ for the particle's actual velocity, we have that $\mathbf {v} ={\frac {\hbar }{m}}Im\left({\frac {\nabla \psi }{\psi }}\right)$. Thus, we have the guiding equation.

Notice that this derivation does not use Schrödinger's equation.

• Preserving the density under the time evolution is another method of derivation. This is the method that Bell cites. It is this method which generalizes to many possible alternative theories. The starting point is the continuity equation $-{\frac {\partial \rho }{\partial t}}=\nabla \cdot (\rho v^{\psi })$ for the density $\rho =|\psi |^{2}$. This equation describes a probability flow along a current. We take the velocity field associated with this current as the velocity field whose integral curves yield the motion of the particle.
• A method applicable for particles without spin is to do a polar decomposition of the wavefunction and transform Schrödinger's equation into two coupled equations: the continuity equation from above and the Hamilton–Jacobi equation. This is the method used by Bohm in 1952. The decomposition and equations are as follows:

Decomposition: $\psi (\mathbf {x} ,t)=R(\mathbf {x} ,t)e^{iS(\mathbf {x} ,t)/\hbar }.$ Note $R^{2}(\mathbf {x} ,t)$ corresponds to the probability density $\rho (\mathbf {x} ,t)=|\psi (\mathbf {x} ,t)|^{2}$.

Continuity Equation: $-{\frac {\partial \rho (\mathbf {x} ,t)}{\partial t}}=\nabla \cdot \left(\rho (\mathbf {x} ,t){\frac {\nabla S(\mathbf {x} ,t)}{m}}\right)$

Hamilton–Jacobi Equation: ${\frac {\partial S(\mathbf {x} ,t)}{\partial t}}=-\left[V+{\frac {1}{2m}}(\nabla S(\mathbf {x} ,t))^{2}-{\frac {\hbar ^{2}}{2m}}{\frac {\nabla ^{2}R(\mathbf {x} ,t)}{R(\mathbf {x} ,t)}}\right].$

The Hamilton–Jacobi equation is the equation derived from a Newtonian system with potential $V-{\frac {\hbar ^{2}}{2m}}{\frac {\nabla ^{2}R}{R}}$ and velocity field ${\frac {\nabla S}{m}}.$ The potential $V$ is the classical potential that appears in Schrödinger's equation and the other term involving $R$ is the quantum potential, terminology introduced by Bohm.

This leads to viewing the quantum theory as particles moving under the classical force modified by a quantum force. However, unlike standard Newtonian mechanics, the initial velocity field is already specified by ${\frac {\nabla S}{m}}$ which is a symptom of this being a first-order theory, not a second-order theory.

• A fourth derivation was given by Dürr et al. In their derivation, they derive the velocity field by demanding the appropriate transformation properties given by the various symmetries that Schrödinger's equation satisfies, once the wavefunction is suitably transformed. The guiding equation is what emerges from that analysis.
• A fifth derivation, given by Dürr et al is appropriate for generalization to quantum field theory and the Dirac equation. The idea is that a velocity field can also be understood as a first order differential operator acting on functions. Thus, if we know how it acts on functions, we know what it is. Then given the Hamiltonian operator $H$, the equation to satisfy for all functions $f$ (with associated multiplication operator ${\hat {f}}$) is

$(v(f))(q)=\mathrm {Re} {\frac {(\psi ,{\frac {i}{\hbar }}[H,{\hat {f}}]\psi )}{(\psi ,\psi )}}(q)$ where $(v,w)$ is the local Hermitian inner product on the value space of the wavefunction.

This formulation allows for stochastic theories such as the creation and annihilation of particles.

Extensions

Spin

To incorporate spin, the wavefunction becomes complex-vector valued. The value space is called spin space; for a spin-1/2 particle, spin space can be taken to be $\mathbb {C} ^{2}$. The guiding equation is modified by taking inner products in spin space to reduce the complex vectors to complex numbers. The Schrödinger equation is modified by adding a Pauli spin term.

${\frac {d\mathbf {Q} _{k}}{dt}}(t)={\frac {\hbar }{m_{k}}}Im\left({\frac {(\psi ,D_{k}\psi )}{(\psi ,\psi )}}\right)(\mathbf {Q} _{1},\mathbf {Q} _{2},\ldots ,\mathbf {Q} _{N},t)$

$i\hbar {\frac {\partial }{\partial t}}\psi =-\sum _{k=1}^{N}{\frac {\hbar ^{2}}{2m_{k}}}D_{k}^{2}\psi +V\psi +\sum _{k=1}^{N}\mu _{k}\mathbf {S} ^{(k)}\cdot \mathbf {B} (\mathbf {q} _{k})$

where $\mu _{k}$ is the magnetic moment of the $k$th particle, $\mathbf {S} ^{(k)}$ is the appropriate spin operator acting on the $k$th particle's spin space, $D_{k}=\nabla _{k}-{\frac {ie_{k}}{c\hbar }}\mathbf {A} (\mathbf {q} _{k})$, $\mathbf {B}$ and $\mathbf {A}$ are, respectively, the magnetic field and the vector potential in $\mathbb {R} ^{3}$ (all other functions are fully on configuration space), $e_{k}$ is the charge of the $k$th particle, and $(\cdot ,\cdot )$ is the inner product in spin space $\mathbb {C} ^{d}$,

$(\phi ,\psi )=\sum _{s=1}^{d}\phi _{s}^{*}\psi _{s}.$

For an example of a spin space, a system consisting of two spin 1/2 particle and one spin 1 particle has a wavefunctions of the form $\psi :\mathbb {R} ^{9}\times \mathbb {R} \to \mathbb {C} ^{2}\otimes \mathbb {C} ^{2}\otimes \mathbb {C} ^{3}$. That is, its spin space is a 12 dimensional space.

Curved space

To extend de Broglie–Bohm theory to curved space (Riemannian manifolds in mathematical parlance), one simply notes that all of the elements of these equations make sense, such as gradients and Laplacians. Thus, we use equations that have the same form as above. Topological and boundary conditions may apply in supplementing the evolution of Schrödinger's equation.

For a de Broglie–Bohm theory on curved space with spin, the spin space becomes a vector bundle over configuration space and the potential in Schrödinger's equation becomes a local self-adjoint operator acting on that space.

Quantum field theory

In Dürr et al, the authors describe an extension of de Broglie–Bohm theory for handling creation and annihilation operators. The basic idea is that configuration space becomes the (disjoint) space of all possible configurations of any number of particles. For part of the time, the system evolves deterministically under the guiding equation with a fixed number of particles. But under a stochastic process, particles may be created and annihilated. The distribution of creation events is dictated by the wavefunction. The wavefunction itself is evolving at all times over the full multi-particle configuration space.

Exploiting nonlocality

Valentini has extended the de Broglie–Bohm theory to include signal nonlocality that would allow entanglement to be used as a stand-alone communication channel without a secondary classical "key" signal to "unlock" the message encoded in the entanglement. This violates orthodox quantum theory but it has the virtue that it makes the parallel universes of the chaotic inflation theory observable in principle.

Unlike de Broglie–Bohm theory, Valentini's theory has the wavefunction evolution also depend on the onotological variables. This introduces an instability, a feedback loop that pushes the hidden variables out of "sub-quantal heat death". The resulting theory becomes nonlinear and non-unitary.

Relativity

While Bell's theorem does suggest a certain amount of tension between quantum theory and relativity, it is possible to formulate models demonstrating the potential for relativistic theories. There has been work in developing nonlocal versions of de Broglie–Bohm theory. See Bohm and Hiley: The Undivided Universe, and [5], [6], and references therein. A quantum field theory treatment is given in [7] and [8]. Another approach is given in the work of Dürr et al in which they use Bohm-Dirac models and a Lorentz-invariant foliation of space-time.

See also

• David Bohm
• Interpretation of quantum mechanics
• Local hidden variable theory
• Quantum mechanics
• Pilot wave

References

• Albert, David Z. (May 1994). "Bohm's Alternative to Quantum Mechanics". Scientific American. 270 (5): 58–67. doi:10.1038/scientificamerican0594-58.
• Barbosa, G. D.; Pinto-Neto, N. (2003). "A Bohmian Interpretation for Noncommutative Scalar Field Theory and Quantum Mechanics". Physical Review D. 69: 065014. arXiv:hep-th/0304105. doi:10.1103/PhysRevD.69.065014. {{cite journal}}: Check date values in: |year= / |date= mismatch (help)
• Bohm, David (1952). "A Suggested Interpretation of the Quantum Theory in Terms of "Hidden Variables" I". Physical Review. 85 (2): 166–179. doi:10.1103/PhysRev.85.166.
• Bohm, David (1952). "A Suggested Interpretation of the Quantum Theory in Terms of "Hidden Variables", II". Physical Review. 85 (2): 180–193. doi:10.1103/PhysRev.85.180.
• Bohm, David (1990). "A new theory of the relationship of mind and matter". Philosophical Psychology. 3 (2): 271–286. doi:10.1080/09515089008573004.
• Bohm, David (1993). The Undivided Universe: An ontological interpretation of quantum theory. London: Routledge. ISBN 0-415-12185-X. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
• Dürr, D.; Goldstein, S.; Tumulka, R.; Zanghì, N. (December 2004). "Bohmian Mechanics" (PDF). Physical Review Letters. 93 (9): 090402. doi:10.1103/PhysRevLett.93.090402. ISSN 0031-9007. PMID 15447078.
• Goldstein, Sheldon (2001). "Bohmian Mechanics". Stanford Encyclopedia of Philosophy.
• Hall, Michael J.W. (2004). "Incompleteness of trajectory-based interpretations of quantum mechanics". Journal of Physics a Mathematical and General. 37 (40): 9549–9556. arXiv:quant-ph/0406054. doi:10.1088/0305-4470/37/40/015. (Demonstrates incompleteness of the Bohm interpretation in the face of fractal, differentialble-nowhere wavefunctions.)
• Holland, Peter R. (1993). The Quantum Theory of Motion : An Account of the de Broglie–Bohm Causal Interpretation of Quantum Mechanics. Cambridge: Cambridge University Press. ISBN 0-521-48543-6.
• Nikolic, H. (2004). "Relativistic quantum mechanics and the Bohmian interpretation". Foundations of Physics Letters. 18 (6): 549–561. arXiv:quant-ph/0406173. doi:10.1007/s10702-005-1128-1.
• Passon, Oliver (2004). "Why isn't every physicist a Bohmian?". arXiv:quant-ph/0412119. {{cite journal}}: Cite journal requires |journal= (help)
• Sanz, A. S.; Borondo, F. (2003). "A Bohmian view on quantum decoherence". The European Physical Journal D. 44: 319. arXiv:quant-ph/0310096. doi:10.1140/epjd/e2007-00191-8.{{cite journal}}: CS1 maint: date and year (link)
• Sanz, A.S. (2005). "A Bohmian approach to quantum fractals". J. Phys. A: Math. Gen. 38 (26): 6037–6049. doi:10.1088/0305-4470/38/26/013. (Describes a Bohmian resolution to the dilemma posed by non-differentiable wavefunctions.)
• Silverman, Mark P. (1993). And Yet It Moves: Strange Systems and Subtle Questions in Physics. Cambridge: Cambridge University Press. ISBN 0-521-44631-7.
• Streater, Ray F. (2003). "Bohmian mechanics is a "lost cause"". Retrieved 2006-06-25.
• Valentini, Antony (2004). "Dynamical origin of quantum probabilities". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 461 (2053): 253–272. arXiv:quant-ph/0403034. doi:10.1098/rspa.2004.1394. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
• Bohmian mechanics on arxiv.org

External links

• "Bohmian Mechanics" (Stanford Encyclopedia of Philosophy)
• "Pilot waves, Bohmian metaphysics, and the foundations of quantum mechanics", lecture course on Bohm interpretation by Mike Towler, Cambridge University.

Category:Interpretations of quantum mechanics Category:Quantum measurement