User:Johnjbarton/sandbox/introduction to eigenstates

Proposed new text below this line

This article is a non-technical introduction to the subject. For the main encyclopedia articles, see Eigenstates and Quantum state.

An eigenstate is a measured quantum state in which at least one quantifiable characteristics such as position or momentum has a determined value. A quantum system is a physical system viewed at the atomic or subatomic level and governed by quantum mechanics; a quantum state lists the properties and their values for all of the components of a quantum system. The properties include relative locations and velocities, as well as properties charactering internal states. The components of a quantum system are subatomic particles or combinations of them, like atoms and molecules. Experimental or simulated theoretical measurements determine the values of these properties, creating eigenstates.

In the everyday world, it is natural and intuitive to think of every object having simultaneously a definite position, a definite momentum; we expect that measurements of these objects will give a definite value and we can assign that measurement a definite time. We expect careful measurements of objects to leave them unaltered; we expect each object to be unique at least in some tiny way if examined carefully enough. Quantum mechanical objects do not fulfill these expectations.

In the quantum world we cannot directly sense the objects. Our only information comes from measurements. The results of measurements on the quantum world have unexpected and interesting properties. Physics uses the unusual word eigenstate to express the unusual character of these quantum measurements.

Measurements

Main article: Measurement in quantum mechanics

A quantum measurement produces an eigenstate, but more correctly, particular measurements produce particular eigenstates. For that reason, the correct description of an eigenstate always includes the particular measurement type. For example, measurement of $p_{x}$, the $x$ momentum, prepares an eigenstate of the $p_{x}$.

Repeated measurement of momentum $p_{x}$ for an eigenstate of $p_{x}$ momentum produces consistently repeatable results. The measurement may be a preliminary step performed to create an eigenstate for subsequent work. In that case the measurement may be called preparing an eigenstate.

Ordinary objects are measured by comparing them to standard objects, like rulers or protractors or stop watches. Atoms and elementary particles are far too small for direct comparisons, millions of times smaller than a human hair. Ordinary comparisons most often rely on visual comparisons that require light energy to bounce off the object. Light momentum pushes atoms around, changing the very thing we are trying to measure.

For these reasons quantum states are filtered to prepare for experiments and the measurements associated with eigenstates uses filtering rather than direct comparison. For example, position measurements may record the intensity of light or current through tiny apertures, sometimes using many thousands of apertures in parallel producing a 2D map of intensity versus position. Momentum measurements might deflect a charged particle beam in a constant magnetic field, collecting only those particles that exit though a slit. Particles with magnetic moments can be filtered with inhomogeneous magnet fields.

Experimental versus idealized mathematical eigenstates

Main articles: Quantum mechanics and Mathematical formulation of quantum mechanics

Physicists also use the word "eigenstate" as a synonym for "eigenfunction" or "eigenvector", mathematical entities used to describe experimental observations. These theoretical entities represent idealized measurements. The results of theoretical calculations rarely directly relate to observations; theoretical results typically need to be combined and averaged before comparisons.

In theoretical calculations a quantum state is "measured" by a mathematical filtering process. A mathematical representation of a measurement device, called an operator, modifies the solutions to, for example, Schrodingers equation producing both an eigenfunction and an associated number called an eigenvalue. These theoretical functions represent pure states and the eigenvalues represent idealized experimental results, as if the raw quantum state were filtered using all possible compatible measurements.. To compare to real experiments, the eigenvalues from theories need to be averaged into mixed quantum states, each value weighted by its probability; the result is called the expected value of the measurement according to the theory.

The uncertainty principle

Main article: Uncertainty relation

Unlike measurements of everyday objects, certain pairs of quantum measurements interact, with one such measurement altering eigenstates produced by the other member of the pair. For example, measurements of $p_{x}$, the momentum along the $x$ axis, creates an eigenstate of the $p_{x}$ momentum. Subsequent measurements of position along the $x$ axis, create an eigenstate of $x$ position. Going back and measuring $p_{x}$ momentum again, on this eigenstate of $x$ position, will not agree with the value before the $x$ position measurement. This is known as the uncertainty principle.

For a concrete example, the experiment of Matteucci, Ferrari, and Migliori, sent a parallel electron beam towards a tiny hole in a metal film mounted in a vacuum chamber. The parallel beam has very little momentum in directions across the beam: the apparatus has prepared an eigenstate of momentum in the two perpendicular directions. The hole creates an eigenstate of position for the two directions across the beam. Behind the metal film an electron microscope enlarges the image of the electron current emerging from the hole. Instead of a simple bright spot, the experiment shows a spread out circular pattern of electron current called an Airy disk.

Airy-pattern. This numerically calculated image matches the experimental result of Matteucci, Ferrari, and Migliori,

The incoming momentum eigenstate has been altered: the position measurement with the hole created motion perpendicular to the tube. The diameter of the circular pattern matches predictions of the uncertainty principle.

Interference

Main article: Wave interference

Schematic diagram of the Bach et al. experiment. Two slits are illuminated by a parallel electron beam.

Experimental electron double slit diffraction pattern. Across the middle of the image the intensity alternates from high to low showing interference in the signal from the two slits. From Roger Bach et al 2013 New J. Phys. 15 033018 Figure 3 cropped to top frame.

Splitting then recombining eigenstates produces interference patterns. Replace the tiny hole used in the example in the previous section with two tiny holes or slits. The two holes split the incoming eigenstate in two and they recombine on the detector. The combination is not the sum of intensity of two holes. Instead the detector shows a dramatic pattern light alternating with dark.

As a concrete example, the experiment of Bach et al. sent a parallel electron beam into a metal film with two tiny slits. As illustrated in the schematic diagram, the holes are close enough to allow recombination of the altered beam at an electron detector past the holes. The result is a pattern of higher and lower intensity across the detector as shown in the experimental photograph.

Probability

Main article: Measurement in quantum mechanics

Unlike everyday measurements, individual quantum measurements give random values. Large numbers of individual measurements must be combined. As more and more identical measurements are performed, some values appear more often that others. The state part of eigenstate signals this difference: in the quantum world measurements work on a quantum state rather than on definite objects.

For example, consider the electron version of the double-slit experiment discussed in the previous section. The alternating pattern of high and low intensity results from individual events appearing as single dots, seemingly randomly arranged, until many thousand of dots add up to pattern. A video of the same experiment shows the build up of the pattern:

Experimental electron double slit diffraction pattern. Across the middle of the image the intensity alternates from high to low showing interference in the signal from the two slits. From Roger Bach et al 2013 New J. Phys. 15 033018 Figure 3 cropped to top frame.

Matter wave double slit diffraction pattern building up electron by electron. Each white dot represents a single electron hitting a detector; with a statistically large number of electrons interference fringes appear.

Electron diffraction pattern and movie of its build up dot by dot.

The final pattern is only clear once many events have been averaged.

Entanglement

Main article: Quantum entanglement

Separate measurements of a split eigenstate give correlated results predicted by quantum theory but contrary to classical non-quantum results. This effect, called quantum entanglement, is under intense study as a possible basis for quantum computing.

Experimental work on quantum entanglement remains exceptionally sophisticated. For example, measurements demonstrating correlation of quantum states over 50km apart use Michelson interferometers, pulsed lasers, fiber optics, spontaneous parametric down conversion, and coincidence detection, among other technologies.

Quantum numbers

Main article: Quantum number

Position and momentum are continuous values, but some experiments, like the Stern-Gerlach experiment shown in the figure, produce results consistent with quantized, discrete eigenvalues.

Stern–Gerlach experiment: Silver atoms traveling through an inhomogeneous magnetic field, and being deflected up or down depending on their spin; (1) furnace, (2) beam of silver atoms, (3) inhomogeneous magnetic field, (4) classically expected result, (5) observed result

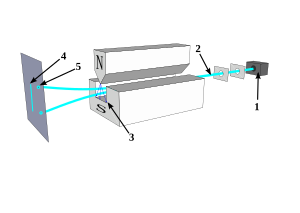
In such cases the eigenvalue is called a quantum number.

Quantum numbers also occur in bound systems like nuclei, atoms and molecules. They are revealed by indirect measurements such as spectroscopy where sudden jumps in the absorption or emission of light is interpreted as transition from or to bound eigenfunctions.

Multiple indistinguishable particles

Main article: Identical particles

Multiple particle bound systems like atoms and molecules have both internal eigenstates, call excited states, and eigenstates associated with their center of mass motion, called matter waves. Split and recombined eigenstates of both kinds given interference, for example, Ramsey interferometry for excited states and atom interferometry for center of mass.

Quantum particles are indistinguishable, altering the statistical properties of collections of particles. Quantum systems obey either Bose-Einstein statistics or Fermi-Dirac statistics, resulting in exotic phenomena like macroscopic quantum states called Bose–Einstein condensates, superconductivity, superfluidity, even white dwarf and neutron stars.

Origin of the word eigenstate

The words "eigenfunction" and "eigenvalue" have a long history in mathematics. Schrodinger's used of the word eigenwertproblem in the title of his first paper on the subject; his own translation of this word in his collected works was "problem of proper values".

See also

• Introduction to quantum mechanics
• Superposition principle
• List of textbooks on classical and quantum mechanics