User:Jaydavidmartin/Quantum computing

Quantum computing is the use of quantum-mechanical phenomena such as superposition and entanglement to perform computation. Computers that perform quantum computation are known as a quantum computers. Quantum computers are believed to be able to solve certain computational problems, such as the integer factorization that underlies RSA encryption, significantly faster than classical computers. The study of quantum computing is a subfield of quantum information science.

The field of quantum computing began in the early 1980s, when physicist Paul Benioff proposed a quantum mechanical model of the Turing machine. Richard Feynman and Yuri Manin later suggested that a quantum computer had the potential to simulate things that a classical computer could not. In 1994, Peter Shor developed a quantum algorithm for factoring integers that had the potential to decrypt RSA-encrypted communications. Despite ongoing experimental progress since the late 1990s, most researchers believe that "fault-tolerant quantum computing [is] still a rather distant dream". On 23 October 2019, Google AI, in partnership with the U.S. National Aeronautics and Space Administration (NASA), published a paper in which they claimed to have achieved quantum supremacy. While some have disputed this claim, it is still a significant milestone in the history of quantum computing.

Quantum computing is modeled by quantum circuits. Quantum circuits are based on the quantum bit, or "qubit", which is somewhat analogous to the bit in classical computation. Qubits can be in a 1 or 0 quantum state (much like the 0 and 1 states of classical bits), or they can be in a superposition of the 1 and 0 states. However, when qubits are measured the result is always either a 0 or a 1. The probabilities of these two outcomes depend on the quantum state that they were in immediately prior to the measurement. Computation is performed by manipulating qubits with quantum logic gates, which are somewhat analogous to classical logic gates.

There are currently two main approaches to physically implementing quantum computers: analog and digital (both of which make use of qubits). Analog approaches are further divided into quantum simulation, quantum annealing, and adiabatic quantum computation. Digital quantum computers use quantum logic gates to do computation.

Any computational problem that can be solved by a classical computer can also, in principle, be solved by a quantum computer. Conversely, quantum computers obey the Church–Turing thesis; that is, any computational problem that can be solved by a quantum computer can also be solved by a classical computer. While this means that quantum computers provide no additional power over classical computers in terms of computability, they do in theory provide additional power when it comes to the time complexity of solving certain problems. Notably, quantum computers are believed to be able to quickly solve certain problems that no classical computer could solve in any feasible amount of time—a feat known as "quantum supremacy". The study of the computational complexity of problems with respect to quantum computers is known as quantum complexity theory.

Motivation (Quantum Computing)

In principle, quantum computers are able to solve certain computational problems dramatically faster than classical computers.

Basic principles (Quantum Computing)

The fundamental unit of information in conventional computers is the bit, and classical computation can be fully described in terms of networks of logic gates, called circuits, operating on these bits. Similarly, the fundamental unit of information in quantum computers is the quantum bit, or "qubit", and quantum computation can be fully described in terms of networks of quantum logic gates, called quantum circuits, operating on these qubits. More explicitly, a quantum computer operates by taking as input some number of qubits and then manipulating those qubits with a fixed sequence of quantum logic gates. The particular sequence of gates applied to the qubits is called a quantum algorithm. While this basic structure of quantum circuits is highly similar to the structure of classical circuits, significant differences arise with how quantum circuits take advantage of the principles of quantum mechanics.

The fundamental distinction between classical bits and quantum bits is that while a classical bit can only exist in only one of two states (0 or 1), a qubit can exist in a quantum superposition of these two states. That is, [sentence]. Qubits possess this added capability over classical bits by taking advantage of a fundamental feature of quantum mechanics: physical parameters (such as energy or location) exist not as...

Single bits on their own are not very useful—hardly any algorithms can be run with only a single bit. For this reason, multiple bits are grouped together to form a register. Similarly, qubits can be combined together into quantum registers. [something something]

Yet simply having qubits available isn't sufficient to run algorithms—there must also be some way to manipulate the states of qubits. In the quantum circuit model, this function is performed by quantum logic gates, the quantum analog to classical logic gates like the AND gate, OR gate, and so on. Quantum gates thus serve as the basic building blocks of quantum computation. [something something]

A more technical description of quantum computation is provided in the section below.

Technical foundations

There are a number of theoretical models of quantum computation, such as the quantum circuit model, the quantum Turing machine, and the topological quantum computer. The most widely used of these is the quantum circuit, which is the subject of this section. The quantum circuit model describes quantum computation in terms of a network of quantum logic gates that operate on quantum bits, or "qubits". This is similar in many ways to the circuit model of classical computation, in which computation is described in terms of a network of logic gate that operate on (classical) bits.

The technical description of quantum computing can be summarized as follows: all quantum algorithms can be represented as quantum circuits. A quantum circuit takes as input the state of one or multiple qubits. Unlike classical bits, which can only exist in the states 0 or 1, a qubit can exist as a quantum superposition of these two states (represented as a linear combination of the computational basis states $|0\rangle$ and $|1\rangle$). The circuit performs computations on these qubits using quantum logic gates, which manipulate the states of the qubits. These gates are represented mathematically as unitary matrices, and their application to qubits corresponds to matrix multiplication on the vectors representing the states of the qubits. A quantum circuit is thus mathematically equivalent to a series of matrix multiplications. The state present at the end of the computation is the output state. The application of quantum logic gates proceeds deterministically, however [Measurement].

Qubits

Main article: Qubit

The Bloch sphere is a representation of a qubit, the fundamental building block of quantum computers.

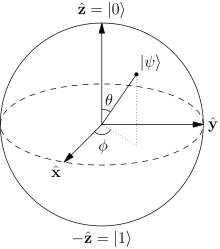
Just as the bit is the basic unit of information in classical computation, the quantum bit or "qubit" is the basic unit of information in quantum computation. In the theory of computation, qubits are represented as mathematical objects, which allows a theory of quantum computation to be constructed independently of the physical implementation of qubits—relying only on the principles of computation and quantum mechanics.

Representation and basic properties

The state of a qubit is represented as a unit vector in the two-dimensional complex Hilbert space ${\textstyle \mathbb {C} ^{2}}$. Generally, the state is expressed as a linear superposition of two orthonormal basis states called the computational basis states, represented in bra–ket notation as $|0\rangle ={\bigl [}{\begin{smallmatrix}1\\0\end{smallmatrix}}{\bigr ]}$ and $|1\rangle ={\bigl [}{\begin{smallmatrix}0\\1\end{smallmatrix}}{\bigr ]}$, corresponding to the two classical bit states 0 and 1, respectively. Hence, the state $|\psi \rangle$ of a qubit is represented mathematically as the linear combination:

$|\psi \rangle =\alpha |0\rangle +\beta |1\rangle ={\begin{bmatrix}\alpha \\\beta \end{bmatrix}}$

where $\alpha$ and $\beta$ are complex probability amplitudes. These probability amplitudes, or more precisely the squares of their norms, correspond to the probabilities of measuring the qubit as having value 0 or 1. This feature is a consequence of a basic feature of quantum mechanics called the Born rule: the quantum state of a qubit cannot be directly measured (that is, there is no way to precisely determine the values of $\alpha$ and $\beta$). Rather, when a qubit is measured the result of the measurement is always 0, with probability $|\alpha |^{2}$, or 1, with probability $|\beta |^{2}$. Because these are probabilities it follows that $|\alpha |^{2}+|\beta |^{2}=1$ (this is called the "normalization constraint").

What this representation indicates is that — unlike classical bits, which can only exist in the state 0 or the state 1 — the quantum properties of qubits enable them to exist in a continuum of states between $|0\rangle$ and $|1\rangle$—at least until the qubit is observed, at which point it probabilistically collapses to either 0 or 1.

Two important theorems relating to basic properties of qubits are the no-cloning theorem and the no-deleting theorem.

Quantum register

The single-qubit representation can be extended to multiple qubits, where a system of multiple qubits is known as a quantum register, by taking the tensor product of the qubits in the quantum register. For an ${\textstyle n}$-qubit quantum register, this results in a unit vector in the ${\textstyle 2^{n}}$-dimensional Hilbert space ${\textstyle \mathbb {C} ^{2^{n}}}$. For example, consider a two-qubit register. This register has has the computational basis $\{|00\rangle$, $|01\rangle$, $|10\rangle$, $|11\rangle \}$, where $$|00\rangle =|0\rangle \otimes |0\rangle ={\begin{bmatrix}1\\0\\0\\0\end{bmatrix}};\quad |01\rangle =|0\rangle \otimes |1\rangle ={\begin{bmatrix}0\\1\\0\\0\end{bmatrix}};\quad |10\rangle =|1\rangle \otimes |0\rangle ={\begin{bmatrix}0\\0\\1\\0\end{bmatrix}};\quad |11\rangle =|1\rangle \otimes |1\rangle ={\begin{bmatrix}0\\0\\0\\1\end{bmatrix}}.$$

A pair of qubits existing in a superposition of these states is then represented by the state vector:

$|\psi \rangle =\alpha _{00}|00\rangle +\alpha _{01}|01\rangle +\alpha _{10}|10\rangle +\alpha _{11}|11\rangle$.

where ${\textstyle \alpha _{00},\alpha _{01},\alpha _{10},\alpha _{11}}$ are the probability amplitudes. Similarly, the state of a three-qubit system is represented as a superposition of the basis states $|000\rangle$, $|001\rangle$, $|010\rangle$, $|011\rangle$, $|100\rangle$, $|101\rangle$, $|110\rangle$, and $|111\rangle$, and similarly for any $n$-qubit system.

Compare this to a classical register. For an ${\textstyle n}$-bit register, the state of the register is represented as a string in ${\textstyle \{0,1\}^{n}}$ (for example, all of the possible states of a three-bit register are: 000, 001, 010, 011, 100, 101, 110, and 111). That is, precisely defining the state of an ${\textstyle n}$-bit register requires a state space of dimensionality ${\textstyle n}$. As described above, the state of an ${\textstyle n}$-qubit quantum register, by contrast, requires a state space of dimensionality $2^{n}$. This means that whereas the dimensionality of the state space corresponding to classical bits grows linearly with the number of bits, the dimensionality of the state space corresponding to quantum bits grows exponentially with the number of qubits. More concretely, [concrete example]. This number grows quickly—for ${\textstyle n=500}$, [from concrete example] is larger than the estimated number of atoms in the universe.

Quantum logic gates

Main article: Quantum logic gates

Analogously to how classical computation can be fully described as a network of logic gates operating on bits, quantum computation can be fully described as a network of quantum logic gates operating on qubits. In this representation, qubits are abstracted as vectors, quantum logic gates are abstracted as unitary matrices, and the application of quantum logic gates to qubits corresponds to matrix multiplication.

Representation and basic properties

Quantum logic gates are represented as unitary matrices and their application to the states of qubits corresponds to matrix multiplication. More precisely, the application of a quantum logic gate ${\textstyle U}$ to a state ${\textstyle |\psi \rangle }$ corresponds to the matrix multiplication ${\textstyle U|\psi \rangle }$, which results in a new state ${\textstyle |\psi '\rangle }$. There is only one constraint on the type of matrices that can correspond to quantum logic gates: they must be unitary. This is the necessary condition for quantum logic gates to be norm-preserving. Furthermore, as this is the only constraint, any unitary matrix specifies a theoretically-valid quantum gate.

From the unitary constraint as well as the principles of quantum mechanics, there are several basic properties of quantum gates:

• Linearity: Quantum logic gates are linear operators; that is, a quantum logic gate ${\textstyle U}$ acts on a state ${\textstyle \alpha |0\rangle +\beta |1\rangle }$ in the following way: ${\textstyle U(\alpha |0\rangle +\beta |1\rangle )=\alpha U|0\rangle +\beta U|1\rangle }$. This is a consequence of the basic feature of quantum mechanics that every observable corresponds to a linear operator.
• Reversibility: An important feature of quantum gates that distinguish them from classical gates is that all quantum gates are reversible, whereas many classical gates, such as the XOR gate, are irreversible. This property follows directly from the requirement that quantum logic gates be unitary, as it is a basic property of unitary matrices that their inverses are also unitary.

Single qubit gates

The state of a single qubit can be manipulated by applying single-qubit quantum logic gates. A single-qubit quantum logic gates is represented as a 2x2 unitary matrix. For instance, one important gate for both classical and quantum computation is the NOT gate. The classical NOT gate takes 0 to 1 and 1 to 0; analogously, the quantum NOT gate (also called the Pauli-X gate) takes ${\textstyle |0\rangle }$ to ${\textstyle |1\rangle }$ and ${\textstyle |1\rangle }$ to ${\textstyle |0\rangle }$. This is represented by the matrix: $$X:={\begin{bmatrix}0&1\\1&0\end{bmatrix}}.$$

By matrix multiplication, ${\textstyle X|0\rangle =|1\rangle }$ and ${\textstyle X|1\rangle =|0\rangle }$. Naturally, quantum gates act not only on the basis states but also on superpositions of the basis states. The CNOT gate acts on an arbitary state ${\textstyle |\psi \rangle =\alpha |0\rangle +\beta |1\rangle }$ as follows: ${\textstyle X(\alpha |0\rangle +\beta |1\rangle )=\alpha X|0\rangle +\beta X|1\rangle =\alpha |1\rangle +\beta |0\rangle }$.

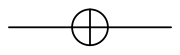
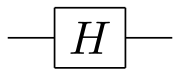
Notably, while there is only one non-trivial single-bit classical gate (the classical NOT gate), there are many non-trivial single-qubit gates, such as the quantum NOT gate described above, the square root of NOT gate, the highly important Hadamard gate, the Pauli gates, and the phase shift gates. These gates all have matrix representations like that for the NOT gate above; they can also be represented with quantum circuit symbols, much like the symbols for classical gates. Several of these are shown below. In this representation, the line moving from left to right is a quantum wire, and represents a single qubit.

• 
  Quantum NOT-gate
• 
  Square-root-of-NOT gate
• 
  Hadamard gate

Multiple qubit gates

The single-qubit representation can be extended to multi-qubit quantum operations: for an $n$-bit quantum register, a quantum operation acting on the state of the register is any $2^{n}\times 2^{n}$ unitary matrix. However, while quantum operations in principle can operate on states of an arbitrary number of qubits, in practice operations on a large number of qubits are impractical and instead circuit networks are made up of quantum gates that each act only on a small number of qubits. An example of such a gate is the two-qubit Controlled NOT or CNOT gate. With standard basis vectors, the CNOT gate is represented by the following matrix: $$CNOT:={\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{bmatrix}}.$$ It follows from matrix multiplication that ${\textstyle CNOT|00\rangle =|00\rangle }$, ${\textstyle CNOT|01\rangle =|01\rangle }$, ${\textstyle CNOT|10\rangle =|11\rangle }$, and ${\textstyle CNOT|11\rangle =|10\rangle }$. In other words, the CNOT applies a NOT gate (${\textstyle X}$ from above) to the second qubit if and only if the first qubit is in the state ${\textstyle |1\rangle }$. If the first qubit is ${\textstyle |0\rangle }$, nothing is done to either qubit.

Generally speaking, single-qubit gates are extended to multi-qubit gates in two important ways. The first way is simply to select a qubit and apply that gate to the target qubit while leaving the remainder of the memory unaffected. The second way is to apply the gate to its target only if another part of the memory is in a desired state.

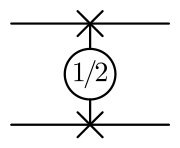
Important multi-qubit quantum gates include the Controlled NOT gate described above, the Toffoli gate, the SWAP gate, the square root of SWAP gate, and the Ising gates. As with single-qubit quantum gates, each of these gates has a quantum circuit symbol. Several are listed below. Recall that each quantum wire represents a single qubit.

• 
  Controlled NOT gate
• 
  Toffoli gate
• 
  SWAP gate
• 
  ${\sqrt {\mbox{SWAP}}}$ gate

Universal gate set

As noted above, quantum circuits are generally constructed out of a series of quantum gates, each operating on only a small number of qubits. This is theoretically sound, as it can be shown that any quantum computation can be represented as a network of quantum logic gates drawn from a fairly small family of gates.[source] This is similar to the fact that any classical computation can be performed with only AND, OR, and NOT gates.[source] A choice of gates that enables such a construction is known as a universal gate set. Furthermore, it turns out that any unitary operation can be decomposed in terms of only one- and two-qubit gates.

One common universal gate set includes all single-qubit gates as well as the CNOT gate. This means any quantum computation can be performed by executing a sequence of single-qubit gates together with CNOT gates. Though this gate set is infinite, it can be replaced with a finite gate set by appealing to the Solovay-Kitaev theorem.

Measurement

See also: Measurement in quantum mechanics

The manipulation of qubits by quantum gates is entirely deterministic. However, as a consequence of the laws of quantum mechanics, measurement of the state of a qubit is probabilistic. More precisely, when a qubit in an arbitrary state ${\textstyle \alpha |0\rangle +\beta |1\rangle }$ is measured, it will only appear as either the classical value '0', with probability ${\textstyle |\alpha |^{2}}$, or the classical value '1', with probability ${\textstyle |\beta |^{2}}$. For example, if a qubit were in the state ${\textstyle {\frac {1}{\sqrt {2}}}|0\rangle +{\frac {1}{\sqrt {2}}}|1\rangle }$, then when measured there is a 50% chance it would appear as a '0' and a 50% chance it would appear as a '1'.

Measurement is generally an irreversible process. In most cases, the state of the qubit prior to measurement cannot be recovered after the measurement. For instance, if a qubit in an arbitrary state ${\textstyle \alpha |0\rangle +\beta |1\rangle }$ is measured and appears as a '0', then not only is it observed as a '0' but the state of the qubit itself collapses to $|0\rangle$. Hence, if left undisturbed there is a 100% chance that any future measurement of the qubit would yield the value '0' ${\textstyle ({\text{since }}|\alpha |^{2}=1{\text{ and }}|\beta |^{2}=0)}$. Similarly, if the qubit is measured as having value '1' then the state of the qubit collapses to $|1\rangle$.

Measurements need not always be taken with respect to the familiar computational basis state. It is possible to perform a measurement with respect to any orthonormal basis. For example, measurements can be taken with respect to the orthonormal basis ${\textstyle \{|+\rangle ,|-\rangle \}}$, where ${\textstyle |+\rangle ={\frac {1}{\sqrt {2}}}|0\rangle +{\frac {1}{\sqrt {2}}}|1\rangle }$ and ${\textstyle |-\rangle ={\frac {1}{\sqrt {2}}}|0\rangle -{\frac {1}{\sqrt {2}}}|1\rangle }$. In this case, measurements always result in '$+$' with probability ${\textstyle |\alpha +\beta |^{2}/{\sqrt {2}}}$ or '$-$' with probability ${\textstyle |\alpha -\beta |^{2}/{\sqrt {2}}}$.

In a quantum circuit, any measurement can be deferred to the end of the computation, though often at a computational cost (this is known as the principle of deferred measurement). As a result, most quantum circuits depict networks consisting only of quantum logic gates, with measurement assumed to take place at the end. However, sometimes measurement is depicted in the circuit. The circuit symbol for measurement is depicted below.

• 
  Circuit representation of measurement. The two lines on the right-hand side represent a classical bit, and the single line on the left-hand side represents a qubit.

Quantum algorithms

Main article: Quantum algorithms

A quantum algorithm is an algorithm that can run on a quantum circuit or other equivalent model of quantum computation. The class of algorithms that can be represented by a quantum circuit includes all classical algorithms. Intuitively, this is the case because any classical algorithm can be represented by a classical circuit and any classical circuit can be converted into an equivalent quantum circuit.

There are several classes of algorithms for which quantum algorithms provide a time advantage over known classical algorithms. The first are algorithms based on the quantum Fourier transform, which includes the historically important Deutsch–Jozsa algorithm and the famous Shor's algorithm for integer factorization. The second class consists of quantum search algorithms, which includes Grover's algorithm and the subclass of algorithms based on amplitude amplification. The third class is quantum simulation, in which quantum computers simulate real quantum systems.

Quantum circuit example: teleportation

Quantum circuit for teleporting a qubit

One example of a useful quantum circuit is a circuit for quantum teleportation. Quantum teleportation is helpful in building quantum gates that are resistant to noise and is essential to the study of quantum error-correcting.

Quantum interactive proof system (separate page)

The classical interactive proof system can be extended to quantum computation. Interactive proof systems are abstract machines that model computation as the exchange of messages between two parties: a prover $P$ and a verifier $V$. The parties interact by exchanging messages, and an input string is accepted by the system if the verifier decides to accept the input on the basis of the messages it has received from the prover. The prover $P$ has unlimited computational power but is untrustworthy (this prevents all languages from being trivially recognized by the proof system by having the computationally unbounded prover determine if a string is in a language and then sending a trustworthy "YES" or "NO" to the verifier). The verifier must conduct an "interrogation" of the prover by "asking it" successive rounds of questions, accepting only if it develops a high degree of confidence that the string is in the language. Complexity classes are defined by placing resource bounds on the verifier. For example, the classical complexity class IP is defined as the set of problems that can be solved (with bounded error) by an interactive proof system that has as the verifier a polynomial-time probabilistic Turing machine.

The complexity class QIP is the quantum analog to the classical complexity class IP. More specifically, QIP is the set of problems that can be solved with bounded error by an interactive proof