∫
a
b
f
(
x
)
d
x
{\displaystyle \int _{a}^{b}\!f(x)\,dx\,}
∫
a
b
f
(
x
)
d
x
=
F
(
b
)
−
F
(
a
)
{\displaystyle \int _{a}^{b}\!f(x)\,dx=F(b)-F(a)\,}
Isaac Newton used a small vertical bar above a variable to indicate integration, or placed the variable inside a box. The vertical bar was easily confused with
x
˙
{\displaystyle {\dot {x}}}
x
′
{\displaystyle x'\,\!}
∫
a
b
f
(
x
)
d
x
.
{\displaystyle \int _{a}^{b}f(x)\,dx.}
∫
0
1
x
d
x
.
{\displaystyle \int _{0}^{1}{\sqrt {x}}\,dx\,\!.}
1
5
(
1
5
−
0
)
+
2
5
(
2
5
−
1
5
)
+
⋯
+
5
5
(
5
5
−
4
5
)
≈
0.7497.
{\displaystyle \textstyle {\sqrt {\frac {1}{5}}}\left({\frac {1}{5}}-0\right)+{\sqrt {\frac {2}{5}}}\left({\frac {2}{5}}-{\frac {1}{5}}\right)+\cdots +{\sqrt {\frac {5}{5}}}\left({\frac {5}{5}}-{\frac {4}{5}}\right)\approx 0.7497.\,\!}
∫
0
1
x
d
x
=
∫
0
1
x
1
2
d
x
=
F
(
1
)
−
F
(
0
)
=
2
3
.
{\displaystyle \int _{0}^{1}{\sqrt {x}}\,dx=\int _{0}^{1}x^{\frac {1}{2}}\,dx=F(1)-F(0)={\textstyle {\frac {2}{3}}}.}
∫
f
(
x
)
d
x
{\displaystyle \int f(x)\,dx\,\!}
∫
A
f
(
x
)
d
μ
{\displaystyle \int _{A}f(x)\,d\mu \,\!}
∫
A
d
ω
=
∫
∂
A
ω
,
{\displaystyle \int _{A}d\omega =\int _{\partial A}\omega ,\,\!}
a
=
x
0
≤
t
1
≤
x
1
≤
t
2
≤
x
2
≤
⋯
≤
x
n
−
1
≤
t
n
≤
x
n
=
b
.
{\displaystyle a=x_{0}\leq t_{1}\leq x_{1}\leq t_{2}\leq x_{2}\leq \cdots \leq x_{n-1}\leq t_{n}\leq x_{n}=b.\,\!}
∑
i
=
1
n
f
(
t
i
)
Δ
i
;
{\displaystyle \sum _{i=1}^{n}f(t_{i})\Delta _{i};}
|
S
−
∑
i
=
1
n
f
(
t
i
)
Δ
i
|
<
ϵ
.
{\displaystyle \left|S-\sum _{i=1}^{n}f(t_{i})\Delta _{i}\right|<\epsilon .}
∫
1
A
d
μ
=
μ
(
A
)
{\displaystyle \int 1_{A}d\mu =\mu (A)}
∫
s
d
μ
=
∫
(
∑
i
=
1
n
a
i
1
A
i
)
d
μ
=
∑
i
=
1
n
a
i
∫
1
A
i
d
μ
=
∑
i
=
1
n
a
i
μ
(
A
i
)
{\displaystyle {\begin{aligned}\int s\,d\mu &{}=\int \left(\sum _{i=1}^{n}a_{i}1_{A_{i}}\right)d\mu \\&{}=\sum _{i=1}^{n}a_{i}\int 1_{A_{i}}\,d\mu \\&{}=\sum _{i=1}^{n}a_{i}\,\mu (A_{i})\end{aligned}}}
∫
E
s
d
μ
=
∑
i
=
1
n
a
i
μ
(
A
i
∩
E
)
.
{\displaystyle \int _{E}s\,d\mu =\sum _{i=1}^{n}a_{i}\,\mu (A_{i}\cap E).}
∫
E
f
d
μ
=
sup
{
∫
E
s
d
μ
:
0
≤
s
≤
f
and
s
is a simple function
}
;
{\displaystyle \int _{E}f\,d\mu =\sup \left\{\int _{E}s\,d\mu \,\colon 0\leq s\leq f{\text{ and }}s{\text{ is a simple function}}\right\};}
f
+
(
x
)
=
{
f
(
x
)
,
if
f
(
x
)
>
0
0
,
otherwise
f
−
(
x
)
=
{
−
f
(
x
)
,
if
f
(
x
)
<
0
0
,
otherwise
{\displaystyle {\begin{aligned}f^{+}(x)&{}={\begin{cases}f(x),&{\text{if }}f(x)>0\\0,&{\text{otherwise}}\end{cases}}\\f^{-}(x)&{}={\begin{cases}-f(x),&{\text{if }}f(x)<0\\0,&{\text{otherwise}}\end{cases}}\end{aligned}}}
∫
E
|
f
|
d
μ
<
∞
,
{\displaystyle \int _{E}|f|\,d\mu <\infty ,\,\!}
∫
E
f
d
μ
=
∫
E
f
+
d
μ
−
∫
E
f
−
d
μ
.
{\displaystyle \int _{E}f\,d\mu =\int _{E}f^{+}\,d\mu -\int _{E}f^{-}\,d\mu .\,\!}
f
↦
∫
a
b
f
d
x
{\displaystyle f\mapsto \int _{a}^{b}f\;dx}
∫
a
b
(
α
f
+
β
g
)
(
x
)
d
x
=
α
∫
a
b
f
(
x
)
d
x
+
β
∫
a
b
g
(
x
)
d
x
.
{\displaystyle \int _{a}^{b}(\alpha f+\beta g)(x)\,dx=\alpha \int _{a}^{b}f(x)\,dx+\beta \int _{a}^{b}g(x)\,dx.\,}
f
↦
∫
E
f
d
μ
{\displaystyle f\mapsto \int _{E}fd\mu }
∫
E
(
α
f
+
β
g
)
d
μ
=
α
∫
E
f
d
μ
+
β
∫
E
g
d
μ
.
{\displaystyle \int _{E}(\alpha f+\beta g)\,d\mu =\alpha \int _{E}f\,d\mu +\beta \int _{E}g\,d\mu .}
f
↦
∫
E
f
d
μ
,
{\displaystyle f\mapsto \int _{E}fd\mu ,\,}
m
(
b
−
a
)
≤
∫
a
b
f
(
x
)
d
x
≤
M
(
b
−
a
)
.
{\displaystyle m(b-a)\leq \int _{a}^{b}f(x)\,dx\leq M(b-a).}
∫
a
b
f
(
x
)
d
x
≤
∫
a
b
g
(
x
)
d
x
.
{\displaystyle \int _{a}^{b}f(x)\,dx\leq \int _{a}^{b}g(x)\,dx.}
∫
a
b
f
(
x
)
d
x
<
∫
a
b
g
(
x
)
d
x
.
{\displaystyle \int _{a}^{b}f(x)\,dx<\int _{a}^{b}g(x)\,dx.}
∫
c
d
f
(
x
)
d
x
≤
∫
a
b
f
(
x
)
d
x
.
{\displaystyle \int _{c}^{d}f(x)\,dx\leq \int _{a}^{b}f(x)\,dx.}
(
f
g
)
(
x
)
=
f
(
x
)
g
(
x
)
,
f
2
(
x
)
=
(
f
(
x
)
)
2
,
|
f
|
(
x
)
=
|
f
(
x
)
|
.
{\displaystyle (fg)(x)=f(x)g(x),\;f^{2}(x)=(f(x))^{2},\;|f|(x)=|f(x)|.\,}
|
∫
a
b
f
(
x
)
d
x
|
≤
∫
a
b
|
f
(
x
)
|
d
x
.
{\displaystyle \left|\int _{a}^{b}f(x)\,dx\right|\leq \int _{a}^{b}|f(x)|\,dx.}
(
∫
a
b
(
f
g
)
(
x
)
d
x
)
2
≤
(
∫
a
b
f
(
x
)
2
d
x
)
(
∫
a
b
g
(
x
)
2
d
x
)
.
{\displaystyle \left(\int _{a}^{b}(fg)(x)\,dx\right)^{2}\leq \left(\int _{a}^{b}f(x)^{2}\,dx\right)\left(\int _{a}^{b}g(x)^{2}\,dx\right).}
|
∫
f
(
x
)
g
(
x
)
d
x
|
≤
(
∫
|
f
(
x
)
|
p
d
x
)
1
/
p
(
∫
|
g
(
x
)
|
q
d
x
)
1
/
q
.
{\displaystyle \left|\int f(x)g(x)\,dx\right|\leq \left(\int \left|f(x)\right|^{p}\,dx\right)^{1/p}\left(\int \left|g(x)\right|^{q}\,dx\right)^{1/q}.}
(
∫
|
f
(
x
)
+
g
(
x
)
|
p
d
x
)
1
/
p
≤
(
∫
|
f
(
x
)
|
p
d
x
)
1
/
p
+
(
∫
|
g
(
x
)
|
p
d
x
)
1
/
p
.
{\displaystyle \left(\int \left|f(x)+g(x)\right|^{p}\,dx\right)^{1/p}\leq \left(\int \left|f(x)\right|^{p}\,dx\right)^{1/p}+\left(\int \left|g(x)\right|^{p}\,dx\right)^{1/p}.}
∫
a
b
f
(
x
)
d
x
{\displaystyle \int _{a}^{b}f(x)\,dx}
∫
a
b
f
(
x
)
d
x
=
−
∫
b
a
f
(
x
)
d
x
.
{\displaystyle \int _{a}^{b}f(x)\,dx=-\int _{b}^{a}f(x)\,dx.}
∫
a
a
f
(
x
)
d
x
=
0.
{\displaystyle \int _{a}^{a}f(x)\,dx=0.}
∫
a
b
f
(
x
)
d
x
=
∫
a
c
f
(
x
)
d
x
+
∫
c
b
f
(
x
)
d
x
.
{\displaystyle \int _{a}^{b}f(x)\,dx=\int _{a}^{c}f(x)\,dx+\int _{c}^{b}f(x)\,dx.}
∫
a
c
f
(
x
)
d
x
=
∫
a
b
f
(
x
)
d
x
−
∫
c
b
f
(
x
)
d
x
=
∫
a
b
f
(
x
)
d
x
+
∫
b
c
f
(
x
)
d
x
{\displaystyle {\begin{aligned}\int _{a}^{c}f(x)\,dx&{}=\int _{a}^{b}f(x)\,dx-\int _{c}^{b}f(x)\,dx\\&{}=\int _{a}^{b}f(x)\,dx+\int _{b}^{c}f(x)\,dx\end{aligned}}}
∫
M
ω
=
−
∫
M
′
ω
.
{\displaystyle \int _{M}\omega =-\int _{M'}\omega \,.}
These conventions correspond to interpreting the integrand as a differential form, integrated over a chain . In measure theory , by contrast, one interprets the integrand as a function f with respect to a measure
μ
,
{\displaystyle \mu ,}
A, without any notion of orientation; one writes
∫
A
f
d
μ
=
∫
[
a
,
b
]
f
d
μ
{\displaystyle \textstyle {\int _{A}f\,d\mu =\int _{[a,b]}f\,d\mu }}
A. This is a minor distinction in one dimension, but becomes subtler on higher dimensional manifolds; see Differential form: Relation with measures for details.
F
(
x
)
=
∫
a
x
f
(
t
)
d
t
.
{\displaystyle F(x)=\int _{a}^{x}f(t)\,dt.}
∫
a
b
f
(
t
)
d
t
=
F
(
b
)
−
F
(
a
)
.
{\displaystyle \int _{a}^{b}f(t)\,dt=F(b)-F(a).}
The improper integral
∫
0
∞
d
x
(
x
+
1
)
x
=
π
{\displaystyle \int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi }
∫
a
∞
f
(
x
)
d
x
=
lim
b
→
∞
∫
a
b
f
(
x
)
d
x
{\displaystyle \int _{a}^{\infty }f(x)dx=\lim _{b\to \infty }\int _{a}^{b}f(x)dx}
∫
a
b
f
(
x
)
d
x
=
lim
ϵ
→
0
∫
a
+
ϵ
b
f
(
x
)
d
x
{\displaystyle \int _{a}^{b}f(x)dx=\lim _{\epsilon \to 0}\int _{a+\epsilon }^{b}f(x)dx}
Consider, for example, the function
1
(
x
+
1
)
x
{\displaystyle {\tfrac {1}{(x+1){\sqrt {x}}}}}
x goes to 0 the function goes to 8, and the upper bound is itself 8, though the function goes to 0. Thus this is a doubly improper integral. Integrated, say, from 1 to 3, an ordinary Riemann sum suffices to produce a result of
π
6
{\displaystyle {\tfrac {\pi }{6}}}
t (with t > 1), gives a well-defined result,
π
2
−
2
arctan
1
t
{\displaystyle {\tfrac {\pi }{2}}-2\arctan {\tfrac {1}{\sqrt {t}}}}
t goes to infinity, namely
π
2
{\displaystyle {\tfrac {\pi }{2}}}
1 /3 to 1 allows a Riemann sum as well, coincidentally again producing
π
6
{\displaystyle {\tfrac {\pi }{6}}}
1 /3 by an arbitrary positive value s (with s < 1) is equally safe, giving
−
π
2
+
2
arctan
1
s
{\displaystyle -{\tfrac {\pi }{2}}+2\arctan {\tfrac {1}{\sqrt {s}}}}
s goes to zero, namely
π
2
{\displaystyle {\tfrac {\pi }{2}}}
∫
0
∞
d
x
(
x
+
1
)
x
=
lim
s
→
0
∫
s
1
d
x
(
x
+
1
)
x
+
lim
t
→
∞
∫
1
t
d
x
(
x
+
1
)
x
=
lim
s
→
0
(
−
π
2
+
2
arctan
1
s
)
+
lim
t
→
∞
(
π
2
−
2
arctan
1
t
)
=
π
2
+
π
2
=
π
.
{\displaystyle {\begin{aligned}\int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}&{}=\lim _{s\to 0}\int _{s}^{1}{\frac {dx}{(x+1){\sqrt {x}}}}+\lim _{t\to \infty }\int _{1}^{t}{\frac {dx}{(x+1){\sqrt {x}}}}\\&{}=\lim _{s\to 0}\left(-{\frac {\pi }{2}}+2\arctan {\frac {1}{\sqrt {s}}}\right)+\lim _{t\to \infty }\left({\frac {\pi }{2}}-2\arctan {\frac {1}{\sqrt {t}}}\right)\\&{}={\frac {\pi }{2}}+{\frac {\pi }{2}}\\&{}=\pi .\end{aligned}}}
This process does not guarantee success; a limit may fail to exist, or may be unbounded. For example, over the bounded interval 0 to 1 the integral of
1
x
{\displaystyle {\tfrac {1}{x}}}
1
x
{\displaystyle {\tfrac {1}{\sqrt {x}}}}
The improper integral
∫
−
1
1
d
x
x
2
3
=
6
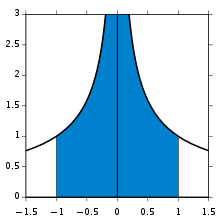
{\displaystyle \int _{-1}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}=6}
∫
−
1
1
d
x
x
2
3
=
lim
s
→
0
∫
−
1
−
s
d
x
x
2
3
+
lim
t
→
0
∫
t
1
d
x
x
2
3
=
lim
s
→
0
3
(
1
−
s
3
)
+
lim
t
→
0
3
(
1
−
t
3
)
=
3
+
3
=
6.
{\displaystyle {\begin{aligned}\int _{-1}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}&{}=\lim _{s\to 0}\int _{-1}^{-s}{\frac {dx}{\sqrt[{3}]{x^{2}}}}+\lim _{t\to 0}\int _{t}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}\\&{}=\lim _{s\to 0}3(1-{\sqrt[{3}]{s}})+\lim _{t\to 0}3(1-{\sqrt[{3}]{t}})\\&{}=3+3\\&{}=6.\end{aligned}}}
∫
−
1
1
d
x
x
{\displaystyle \int _{-1}^{1}{\frac {dx}{x}}\,\!}
∫
E
f
(
x
)
d
x
.
{\displaystyle \int _{E}f(x)\,dx.}
∬
D
5
d
x
d
y
{\displaystyle \iint _{D}5\ dx\,dy}
∫
4
9
∫
2
7
5
d
x
d
y
{\displaystyle \int _{4}^{9}\int _{2}^{7}\ 5\ dx\,dy}
From here, integration is conducted with respect to either x or y first; in this example, integration is first done with respect to x as the interval corresponding to x is the inner integral. Once the first integration is completed via the
F
(
b
)
−
F
(
a
)
{\displaystyle F(b)-F(a)}
∭
c
u
b
o
i
d
1
d
x
d
y
d
z
{\displaystyle \iiint _{\mathrm {cuboid} }1\,dx\,dy\,dz}
W
=
F
→
⋅
s
→
.
{\displaystyle W={\vec {F}}\cdot {\vec {s}}.}
For an object moving along a path in a vector field
F
→
{\displaystyle {\vec {F}}}
electric field or gravitational field , the total work done by the field on the object is obtained by summing up the differential work done in moving from
s
→
{\displaystyle {\vec {s}}}
s
→
+
d
s
→
{\displaystyle {\vec {s}}+d{\vec {s}}}
W
=
∫
C
F
→
⋅
d
s
→
.
{\displaystyle W=\int _{C}{\vec {F}}\cdot d{\vec {s}}.}
∫
S
v
⋅
d
S
.
{\displaystyle \int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }.}
∫
S
f
d
x
1
⋯
d
x
m
.
{\displaystyle \int _{S}f\,dx^{1}\cdots dx^{m}.}
d
x
a
∧
d
x
a
=
0
{\displaystyle dx^{a}\wedge dx^{a}=0\,\!}
d
ω
=
∑
i
=
1
n
∂
f
∂
x
i
d
x
i
∧
d
x
a
.
{\displaystyle d\omega =\sum _{i=1}^{n}{\frac {\partial f}{\partial x_{i}}}dx^{i}\wedge dx^{a}.}
∫
Ω
d
ω
=
∫
∂
Ω
ω
{\displaystyle \int _{\Omega }d\omega =\int _{\partial \Omega }\omega \,\!}
The most basic technique for computing definite integrals of one real variable is based on the fundamental theorem of calculus . Let f (x ) be the function of x to be integrated over a given interval [a , b ]. Then, find an antiderivative of f ; that is, a function F such that F' = f on the interval. By the fundamental theorem of calculus—provided the integrand and integral have no singularities on the path of integration—
∫
a
b
f
(
x
)
d
x
=
F
(
b
)
−
F
(
a
)
.
{\displaystyle \textstyle \int _{a}^{b}f(x)\,dx=F(b)-F(a).}
∫
−
2
2
1
5
(
1
100
(
322
+
3
x
(
98
+
x
(
37
+
x
)
)
)
−
24
x
1
+
x
2
)
d
x
,
{\displaystyle \int _{-2}^{2}{\tfrac {1}{5}}\left({\tfrac {1}{100}}(322+3x(98+x(37+x)))-24{\frac {x}{1+x^{2}}}\right)dx,}
| colspan="4" |
∫
−
2.25
1.75
f
(
x
)
d
x
=
4.1639019006585897075
…
{\displaystyle \textstyle \int _{-2.25}^{1.75}f(x)\,dx=4.1639019006585897075\ldots }
∫
a
b
f
(
x
)
d
x
≈
b
−
a
6
[
f
(
a
)
+
4
f
(
a
+
b
2
)
+
f
(
b
)
]
,
{\displaystyle \int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{6}}\left[f(a)+4f\left({\frac {a+b}{2}}\right)+f(b)\right],}
|
−
(
b
−
a
)
5
2880
f
(
4
)
(
ξ
)
|
.
{\displaystyle \left|-{\frac {(b-a)^{5}}{2880}}f^{(4)}(\xi )\right|.}












































![{\displaystyle \textstyle {\int _{A}f\,d\mu =\int _{[a,b]}f\,d\mu }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef1984db89ae7541827773297d337757fbe18a61)













![{\displaystyle \int _{-1}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}=6}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd73b4f0af904c14ed328dffa7434256e9f32eca)
![{\displaystyle {\begin{aligned}\int _{-1}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}&{}=\lim _{s\to 0}\int _{-1}^{-s}{\frac {dx}{\sqrt[{3}]{x^{2}}}}+\lim _{t\to 0}\int _{t}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}\\&{}=\lim _{s\to 0}3(1-{\sqrt[{3}]{s}})+\lim _{t\to 0}3(1-{\sqrt[{3}]{t}})\\&{}=3+3\\&{}=6.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4348fbc3e4bf3a5345fc4c8ca5e93e87307799c)



















![{\displaystyle \int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{6}}\left[f(a)+4f\left({\frac {a+b}{2}}\right)+f(b)\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/097ff187f17f0d29e4a5d52839b814d49bdad4ef)
