User:Indnwkybrd/sandbox

This is the user sandbox of Indnwkybrd. A user sandbox is a subpage of the user's user page. It serves as a testing spot and page development space for the user and is not an encyclopedia article. Create or edit your own sandbox here.

Other sandboxes: Main sandbox | Template sandbox

Finished writing a draft article? Are you ready to request review of it by an experienced editor for possible inclusion in Wikipedia? Submit your draft for review!


type	from	gates/delay
XOR	NAND	fewer
XOR	NAND	more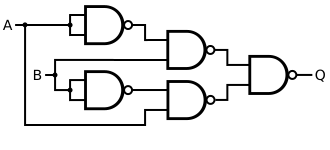
XOR	NOR	less
XOR	NOR	more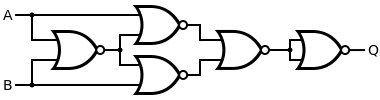
XNOR	NAND	less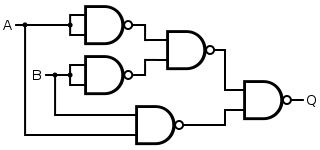
XNOR	NAND	more
XNOR	NOR	fewer
XNOR	NOR	more

$\sin 5\theta =\sin ^{5}\theta -10\sin ^{3}\theta \cos ^{2}\theta +5\cos ^{4}\theta \sin \theta$

$\cos 5\theta =\cos ^{5}\theta -10\cos ^{3}\theta \sin ^{2}\theta +5\sin ^{4}\theta \cos \theta$

The separating hyperplane theorem has a central application in mathematical microeconomics. If you've studied it or taken some micro courses, then you might recognize this diagram:

If not: this is an Edgeworth box, a visualization tool used in economics. It models a simple case of general equilibrium theory, a pure exchange economy with 2 agents O and A (apparently, also known as Octavio and Abby), and 2 goods X and Y. This particular example abstracts away from production of the goods, in order to focus on "pure exchange"; hence, the quantity of each good in overall economy is constant at Ω_X and Ω_Y. Each agent starts with a part of this overall quantity which is his/her endowment. In vector form, O has endowment (ω_X, ω_Y), and A has (Ω_X - ω_X, Ω_Y - ω_Y). The goods can both be subdivided into any real-valued amount.

What we are interested in, is whether O and A might like to barter some of their endowments with one another, in a way that makes both of them feel more satisfied with making a deal than with not making one. Therefore, the last piece of the model is a pair of preference relations, which quantify the notion of "more satisfied": two binary relations $(\succsim _{O},\succsim _{A})$ on $X\times Y$ the set of possible have-able quantities of goods.

utility functions: one for each agent, U_O and U_A, to quantify the notion of "more satisfied". The utility function is

Side note: you do not really need to assume that U_O and U_A exist a priori as such; you can show their existence as a consequence of some binary

makes each of them more satisfied with making a deal than s/he would have been with not making one.

Therefore we need one more element of the model: a pair of utility functions UO

 The point prominently marked by the arrows,

https://web.stanford.edu/~jdlevin/Econ%20202/General%20Equilibrium.pdf