User:Hoyda1

This is the user sandbox of Hoyda1. A user sandbox is a subpage of the user's user page. It serves as a testing spot and page development space for the user and is not an encyclopedia article. Create or edit your own sandbox here.

Other sandboxes: Main sandbox | Template sandbox

Finished writing a draft article? Are you ready to request review of it by an experienced editor for possible inclusion in Wikipedia? Submit your draft for review!

Մինիմաքս (երբեմն մինմաքս) որոշումներ ընդունելու կանոն է, որը օգտագործվում է որոշումների թեորեմում, խաղային թեորեմում, ստատիստիկայում և ֆիլիսոֆիայում մինիմայզինգի համար հնարավոր է կորուստ վատագույն դեպքում (մաքսիմում կորուստ) սցենարով: Հերթականությամբ, այն կարող է մաքսիմալացնել մինիմում ստացումը (մաքսիմին). Օրիգինալը նախատեսված էր երկու խաղացողների զրո-գումար խաղային թեորեմ, լուսաբանում է երկու դեպքերում էլ, երբ խաղացողն ընտրում է այլընտրանքային շարժումներ և դրանց միջոցով նրանք ստեղծում են միաժամանակյա շարժումներ, այն նաև ընդլայնվում է ավելի շատ կոմլեքս խաղերի և գլխավոր որոշումներ ընդունելու համար անորոշության առկայությամբ:

Խաղային թեորեմ

Այն վարկածում, որ միաժամանակյա խաղեր, մինիմաքսի ռազմավարությունը խառը ռազմավարություն որը զրո-գումարային խաղերի լուծման մասերից է: Զրո-գումարային խաղեր, մինիմաքս լուծումը նույն է ինչպես Նաշ հավասարակշռությունը.

Մինիմաքս թեորեմ

Մինիմաքս խաղային թեորեմը^[1]

Ամեն երկու հոգու համար,զրո-գումարային խաղը ռազմավարության վերջնական քանակությամբ,գոյություն ունի V արժեքը և խառը ռազմավարություն յուրաքանչյուր խաղացողի համար, ինչպիսին են՝
(a) Տրված է խաղացողին 2-րդ ռազմավարության, լավագույն հետադարձը հնարավոր առաջին խաղացողի համար V-է, և

(b) Տրված է առաջին ռազմավարությունը, լավագույն հետադարձը երկրորդ խաղացողի համար −V է:

Հավասար է նրան,որ առաջին խացաղողի ռազմավարությունը երաշխավորում է հաղթանակ V-ով զղջալով երկրորդ խաղացողին, և նույնապես երկրորդ խաղացողը կարող է երաշխավորել իր հաղթանակը −V-ով: Մինիմաքս անունը ծագում է քանի որ յուրաքանչյուր խաղացող մինիմալի է հասցնում մաքսիմում ելքի հնարավորությունը հնարավր է նաև ուրիշներինը:

Այս թեորեմը ստեղծվել է, Ջոն վոն Նեուման-ի կողմից,^[2] ով ասել է՝ "Ինչքան որ ես կարող եմ տեսնել, կարող է չլինել խաղերի թեորեմ, ես մտածում էի, որ որինչ չարժի այդ հրատարակումը մինչև Մինիմաքս թեորեմը հրատարակվեց".^[3]

Տեսե՛քSion's minimax theorem և Parthasarathy's theoremընդհանրացման համար; տեսե՛ք նաև example of a game without a value.

Օրինակ

	B chooses B1	B chooses B2	B chooses B3
A chooses A1	+3	−2	+2
A chooses A2	−1	0	+4
A chooses A3	−4	−3	+1

Հետևյալը զրո-գումարային խաղի օրինակ է,որտեղ A և B կատարում են համաշարժ գործողություններ, իլուստրացնում է մինիմաքս լուծումներ: Ենթադրենք յուրաքանչուր խաղացող ունի երեք ընտրություն և որոշում է payoff matrix-ը A -ի համար և ցուցադրում է այն աջից: Ենթադրենք որ, ելքային մատրիքսը B-ի համար նույն մատրիքսն է արտացոլվող սիմվոլի հետ միասին (այսինքն եթե ընտրություներն են A1-ը և B1-ը ուրեմնք B-ն տալիս է 3 դեպիA): Հետո, մինիմաքս ընտրությունը A-ի համար A2-ն է մինչ հնարավար վատագույն արդյունքը, հետո ստիպված է տալ 1, մինչդեռ պարզագույն մինիմաքս ընտրանքը B-ի համար B2-է մինչ հնարավոր վատագույն արդյունքը չի ունենում հետադարձում: Քանի որ, այս լուծումը ստաբիլ չէ, Այնպես ինչպես B հավատում է A-ին կընտրի A2-ը հետո B կընտրի B1-ին ստաբալու համար 1 արժեքը; հետո եթե A հավատում է B-ին կընտրի B1-ին հետո A կընտրի A1-ին ստանալու համար 3 արժեքը; և հետո B կընտրի B2-ին; և վերջնական արդյունքում խաղացողներից երկուսնել կգիտակցեն որոշում կայացնելու դժվարությունը: Այսպիսով ավելի ստաբիլ ռազմավարությունն է անհրաժեշտ:

Որոշ ընտրություններ գերակշռում են մյուսների կողմից և կարող են վերացվել: A չի ընտրի A3-ին մինչև և՛ A1-ը, և՛ A2-ը, կարտադրեն ավելի լավ արդյունք, նշանակություն չունի B ընտրանքը; B-ն չի ընտրի B3-ին մինչ B1-ի և B2-ի որոշ խառնուրդներ չարտադրեն ավելի լավ արդյունք,կապ չունի ինչ է A-ն ընտրում:

A -ն կարող է խուսափել ստիպված լինելուց կատարելու սպասված ելք ավելի քան 1/3 դեպքերում, ընտրելով A1-ը 1/6 հավանականությամբ և A2-ը 5/6 հավանականությամբ, կապ չունի B-ի ընտրությունը: B-ն կարող է ապահոցել սպասված ստացում 1/3 վերջնականորեն օգտագործելով ռանդոմիզացված ռազմավարություն B1-ի ընտրությամբ 1/3 հավանականությամբ և B2-ի ընտրությամբ 2/3 հավանականությամվ, կապ չունի A-ի ընտրությունը:Հետևյալ ընտրությունները՝ խառնված մինիմքաս ռազմավարությունները այժմ ստաբիլ են և չեն կարող հերքվել:

Մաքսիմին

Հաճախ է խաղի տեսության,մաքսիմին տարբերվում է մինիմաքս: Մինիմաքս օգտագործվում է զրոյական գումար խաղերի իմաստներով նվազագույնի հասցնելով է մրցակցի առավելագույն անսպասելի արդյունք: Մի զրոյական ելքով խաղ է, սա նույնական նվազագույնի հասցնելով սեփական առավելագույն կորուստը, եւ maximizing սեփական նվազագույն շահ:

"Մաքսիմին" ը տերմինը լայնորեն կիրառվում է ոչ զրոյական գումար խաղերի նկարագրել ռազմավարությունը, որը maximizes սեփական նվազագույն աշխատավարձի վճարում: Ոչ զրոյական գումար խաղերի, սա ընդհանուր առմամբ նույնն է, նվազագույնի հասցնելով, որ մրցակցի առավելագույն շահ, ոչ թե նույն, որպես Նաշ հավասարակշռության ռազմավարություն:

Համակցային խաղի տեսությունը

Համակցական խաղը տեսությունը-ում, կա մինիմաքս, ալգորիթմ է խաղի լուծումների. A '' պարզ տարբերակը minimax ալգորիթմի, - ասել է ստորեւ, զբաղվում է խաղերով, ինչպիսիք են տիկ-tac-ծայր, որտեղ յուրաքանչյուր խաղացող կարող է հաղթել, կորցնում են, կամ ոչ ոքի: Եթե խաղացողը Ա' կարող է հաղթել մի քայլին, նրա ամեն քայլը, որ հաղթող քայլը. Եթե խաղացողը B գիտի, որ մի քայլը կհանգեցնի իրավիճակի, երբ խաղացողը Ա' կարող է հաղթել մի քայլ, իսկ մյուս քայլը կհանգեցնի իրավիճակի, երբ խաղացողը Ա կարող է լավագույն ոքի, ապա B-նվագարկիչ լավագույն քայլը չէ մեկը տանում է ոչ ոքի: Ուշ խաղի, դա հեշտ է տեսնել, թե ինչ է "լավագույն" քայլ է. The Minimax ալգորիթմը օգնում է գտնել լավագույն քայլը, ըստ աշխատանքային հետընթաց է ավարտին խաղի. Յուրաքանչյուր քայլ, այն ենթադրում է, որ խաղացող ա փորձում է 'մեծացնելու հնարավորությունները A շահումները իսկ հաջորդ հերթին նվագարկիչ Բ - ն փորձում է 'նվազեցնելու հնարավորությունները A շահումները (այսինքն, մինչեւ առավելագույնի հասցնելու Բ սեփական հնարավորությունները հաղթելու):

Մինիմաքս ալգորիթմ և ալտերնատիվ քայլեր

Մինիմաքս ալգորիթմ^[4] ռեկուրսիվ է ալգորիթմ ընտրելու համար խաղացողխաղ,արժեքը, որը կապված է յուրաքանչյուր պաշտոնի կամ պետության խաղի. Այս արժեքը հաշվարկվում միջոցովդիրքային հավասարման ֆունկցիա եւ այն ցույց է տալիս, թե որքան լավ կլիներ, մի խաղացողի հասնել այդ դիրքը: Խաղացողը, ապա դարձնում քայլը, որ maximizes նվազագույն արժեքը դիրքորոշման արդյունքում հակառակորդի հետ հնարավոր է հետեւյալ քայլերի: Եթե A's շարժվում է , A-ն արժեքե տալիս յուրաքանչյուրին:

Հնարավոր տեղաբաշխումը մեթոդը կայանում է նշանակվում որոշակի հաղթելու համարA ինչպես +1 և B -ի համար −1. This leads to համակցային խաղային տեսություն զարգացվել է John Horton Conway-ի կողմից: Այլընտրանքային օգտագործում կանոն, որ եթե արդյունք քայլ է անմիջական հաղթանակը համար A դա նշանակվում է դրական եւ Ինֆինիտի, եթե այն անմիջական հաղթանակը համար B, բացասական արժեք: Արժեքը, ինչպես նաեւ A որեւէ այլ քայլ է առնվազն արժեքների արդյունքում յուրաքանչյուր B's հնարավոր պատասխան: Այս պատճառով, A-ն անվանում է մաքսիմալացնող խաղացող իսկ B կոչվում է նվազեցնող խաղացող, անունը մինիմաքս ալգորիթմ: Վերը ալգորիթմը չի հանձնարարել է արժեքը, դրական կամ բացասական Ինֆինիտի որեւէ պաշտոնի, քանի որ արժեքը յուրաքանչյուր դիրքում կլինի արժեքը մոտ վերջնական շահելու կամ կորցնելու դիրքորոշումը: Հաճախ դա ընդհանրապես հնարավոր է միայն այն ժամանակ հենց վերջի բարդ խաղերի, ինչպիսիք են շախմատ կամ գնալ, քանի որ դա իրագործելի ամբողջությամբ նայել առաջ որքանով ավարտից խաղի, բացի դեպի վերջ, եւ դրա փոխարեն պաշտոններ են վերջավոր արժեքները որպես գնահատականների վրա աստիճանի համոզմամբ, որ դրանք կհանգեցնեն հաղթելու է մեկ խաղացող, կամ մյուսը:

Սա կարող է երկարաձգվել, եթե մենք կարող ենք մատակարարել է էվրիստիկյանգնահատման գործառույթը, որը հնարավորություն է տալիս արժեքները ոչ վերջնական Խաղի պետությունների առանց հաշվի առնելու բոլոր հնարավոր են հետեւյալ ամբողջական: Մենք կարող սահմանափակել minimax ալգորիթմ նայելու միայն որոշակի շարք քայլերի առաջ: Այս թիվը կոչվում է "անցողակի հայացք առաջ", չափվում "խաղեր": Օրինակ, շախմատի համակարգչային խորը կապույտ (ընտրել Garry Kasparov) նայեց առաջ առնվազն 12 խաղեր, ապա կիրառվում են մի heuristic գնահատման գործառույթը: Իսկ ալգորիթմը կարելի է մտածել, ինչպես նաեւ ուսումնասիրելու է հանգույց խաղ երեք-ի. էֆֆեկտիվ բռանկյան գործառույթ այն ծառի է միջին թվաքանակը երեխաներ ամեն հանգույց (այսինքն,միջին քանակի լեգալ շարժումներ դիրքում): Թիվն հանգույցների է ուսումնասիրված սովորաբար էկսպենցիոնալ աճ խաղացողների թվով(դա ավելի քիչ է պաշտպանված շարժում կամ դիրքեր): Թիվն հանգույցների է ուսումնասիրված համար վերլուծության խաղը Հետեւաբար մոտավորապես Ճյուղավորման գործոնը բարձրացնում է իշխանության թվի խաղում է, այնուամենայնիվ քչախոսությունլրիվ վերլուծել խաղերը, ինչպիսիք են շախմատի օգտագործելով մինիմաքս ալգորիթմ:

Կատարման միամիտ մինիմաքս ալգորիթմի կարող են բարելավվել կտրուկ, առանց ազդում արդյունքը, ըստ օգտագործման ալֆա-բետա պրունինգ: Ուրիշ մեթոդները նույնպես կարող են աշխատել:

Լուա օրինակ

function minimax(node,depth)
   if depth <= 0 then
      -- positive values are good for the maximizing player
      -- negative values are good for the minimizing player
      return objective_value(node)
   end
   -- maximizing player is (+1)
   -- minimizing player is (-1)
   local alpha = -node.player * INFINITY
   
   local child = next_child(node,nil)
   while child = ~nil do
      local score = minimax(child,depth-1)
      alpha = node.player==1 and math.max(alpha,score) or math.min(alpha,score)
      child = next_child(node,child)
   end

   return alpha
end

Ծածկաբառ

Պսեվդակոդ Negamax-ի համար մինիմաքս ալգորիթմի տեսակ (օգտագործվում է հավասարակշռության ընթացքում) բերված է ստորև:

Կոդը հիմնված է հետազոտությունների վրա $\max(a,b)=-\min(-a,-b)$ :Այս խուսափում անհրաժեշտությունը համար ալգորիթմի է բուժել երկու խաղացողներ առանձին - առանձին, սակայն, չեն կարող օգտագործվել խաղերին, որտեղ խաղացողը կարող է ունենալ երկու անցնում է ժառանգաբար:

function integer minimax(node, depth)
    if node is a terminal node or depth <= 0:
        return the heuristic value of node
    α = -∞
    for child in node:                       # evaluation is identical for both players 
        α = max(α, -minimax(child, depth-1))
    return α

Օրինակ

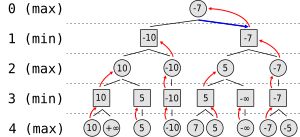
ենթադրում խաղը են խաղացել միայն առավելագույնը երկու հնարավոր քայլերի մեկ խաղացող ամեն հերթն է: Ալգորիթմը առաջացնում the երեք աջ կողմում,որտեղ շրջանակները ներկայացնում են քայլեր է խաղացողի վարող ալգորիթմ (մաքսիմալացնող խաղացող)եւ հրապարակներ ներկայացնելու քայլեր են հակառակորդի,(մինիմալացնող ալգորիթմ):Քանի որ սահմանափակման հաշվարկ ռեսուրսների, ինչպես բացատրված վերը ծառը սահմանափակվում է նայում `առաջ 4 քայլերի.

Ալգորիթմը հաշվարկում է յուրաքանչյուրը հանգույցօգտագործելով գնահատման գործառույթը ստանալով շահույթ: Մաթեմատիկայում և ինֆորմատիկայում, ալգորիթմը (ստեղծվել է հռչակավոր մաթեմատիկոս Ալ-Խորեզմիի կողմից) քայլ առ քայլ հաշվարկային գործընթաց է: Ալգորիթմը օգտագործվում է հաշվարկներում, տվյալների մշակման և մտահանգումների ավտոմատացման ժամանաակ: Ավելի ճշգրիտ, ալգորիթմը ֆունկցիայի հաշվարկման որոշակի լավ սահմանված արդյունավետ մեթոդ է <ref>"Օրինակ, յուրաքանչյուր դասական մաթեմատիկական ալգորիթմ կարող է նկարագրվել վերջավոր թվով անգլիական բառերով:" որը նաև կոչվում է տրանսպոտային ցանց, ուղղված գրաֆ է, որտեղ ամեն ծայրը ունի որոշակի թողունակություն, և որտեղ այդ ծայրերը ստանում են հոսք: Հոսքի քանակը եզրերի վրա չի կարող գերազանցել եզրի թողունակությունը: Հաճախ գործառնությունների հետազոտությունում (Operations Research) ուղիղ գրաֆն անվանվում է «ցանց», գագաթները կոչվում են «հանգույցներ», իսկ եզրերը կոչվում են «աղեղներ»:

Հոսքը պետք է բավարարի այն սահմանափակումները, որ որոշ հոսքերի գումարը դեպի հանգույց հավասար է դրանից դուրս եկող հոսքեի գումարին, բացառությամբ այն դեպքերի, երբ դա «աղբյուրն» է` հիմքը, որն ունի ավելի շատ դուրս եկող հոսք, կամ ընդունիչն է, վերջինս էլ ունի ավելի շատ մուտքային հոսք: Ցանցը կարող է օգտագործվել որպես երթևեկության մոդել ճանապարհային համակարգի մեջ, հեղուկներ խողովակների մեջ, հոսանքներ էլեկտրական միացման մեջ կամ որևէ նման մի բան, որի մեջ ինչ-որ բան «ճանապարհորդում» է ցանցային հանգույցների միջոցով:

Մինիմաքսը անհատական որոշումների համար

Մինիմաքսը դեմ առ դեմ անորոշությանը

Մինիմաքս տեսությունը տարածվում է նաեւ որոշումների, որտեղ չկա խաղացող, բայց որտեղ հետեւանքները որոշումները կախված են անհայտ փաստերի Օրինակ, որոշում են հեռանկարի համար հանքանյութերի կհանգեցնի ծախսերը, որը պետք է ապարդյուն, եթե հանքային չեն ներկայացել, այլ կբերի խոշոր պարգեւներով, եթե դրանք:Մի մոտեցում է վերաբերվի որպես խաղի դեմ բնություն (տեսնելշարժվել բնությամվ), եւ օգտագործելով համանման մտածողության `որպես Murphy's law, որը մեծացնում է մինիմալ սպասվող կորուստը:

Մինիմաքսը վիճակագրության տեսությունում

Դասական ստատիստիկ որոշումների տեսությունը, մենք ունենք մեկ գնահատող $\delta$ որն օգտագործվում է հաշվելու պարամետրը $\theta \in \Theta$ : Մենք նույնպես հաշվում ենք ռիսկի ֆունկցիան $R(\theta ,\delta )$ , սովորաբար հաշվարկված որպես ինտեգրալ կորստի ֆունկցիա:Այս շրջանակներում ${\tilde {\delta }}$ is called մինիմաքս եթե այն համընկնում է

Ոչ հավանական որոշման տեսություն

Բանալային ապագան: Պատկերացնենք մի շարք ջրատար խողովակներ ցանցին համապատասխան: Յուրաքանչյուր խողովակ ունի որոշակի տրամագիծ, այսպիսով այն կարող է օժանդակել որոշ քանակությամբ ջրի հոսքը:Այնտեղ, որտեղ խողովակները հանդիպում են, ջրի ամբողջ քանակությունը լցվում է դրանց մեջ, և այդ միացումը պետք է հավասար լինի ջրի դուրս եկող քանակությանը: Մենք ունենք ջրի մուտք, որը մեր սկզբնաղբյուրն է (source), և ջրի ելք, որը մեր ընդունիչն է: Հոսքն էլ պետք է լինի ջրելու այն հնարավոր եղանակը, որպեսզի հասնենք մուտքից դեպի ելքին:

Հոսքեր կարող ենք համարել տրանսպորտային ցանցում մարդկանց,կամ էլեկտրականությունը էլեկտարական բաշխման համակարգում: Նմանատիպ ֆիզիկական ցանցերում մուտքային հոսքը ցանկացած միջանկյալ հանգույցում, պետք է հավասար լինի այդ հանգույցի ելքային հոսքին: Այս պաշտպանության սահմանափակումը ձևակերպվում է որպես Կիրչհոֆի հոսանքի օրենք (Kirchhoff's current law):

Հոսքային ցանցերը կիրառվում են նաև էկոլոգիայում:Ցանցային էկոհամակարգի դաշտի վերլուծությունը` մշակված Ռոբերտ ՈՒլյանովիչի և ուրիշների կողմից, ներառում է իր մեջ հասկացություններ ինֆորմացիայի տեսությունից և ջերմադինամիկաից ուսումնասիրելու այս ցանցերի էվոլյուցիան ժամանակի ընթացքում:

Ամենապարզ և ամենատարածված խնդիրրը, որը լուծվում է օգտագործելով ցանցային հոսքերը, դա այսպես կոչված մաքսիմում հոսքը գտնելն է, վերջինս էլ տրված գրաֆում ապահովում է ամենաշատ հնարավոր հոսքը աղբյուրից դեպի ընդունիչ: Կան շատ ուրիշ խնդիներ, որոնք լուծվում են մաքսիմում հոսքի ալգորիթմի օգնությամբ: Մաքսիմում հոսքի խնդիրները կարող են լուծվել Ֆորդ-Ֆուլկերսոնի ալգորիթմի հիման վրա: Մաքսիմում հոսքի մինիմում կրճատման թեորեմը ապացուցում է, որ մաքսիմում ցանցային հոսքը գտնելը հավասարազոր է մինիմում թողունակության կրճատումը գտնելուն, որը առանձնացնում է աղբյուրն ու ընդունիչը:

Բազմապրանքային հոսքերի խնդրում մենք ունենք բազմաթիվ աղբյուրներ և ընդունիչներ, և տարբեր "ապրանքատեսակներ", որոնք հոսքեր են տրված աղբյուրից դեպի ընդունիչը: Այսպիսի օրինակ կարող են հանդիսանալ տարբեր ապրանքները, որոնք արտադրվել են տարբեր գործարաններում և պետք է մատակարարվեն տարբեր հաճախորդներին նույն տրանսպորտային ցանցով:

Տես նաև

Նշումներ

^ Osborne, Martin J., և Ariel Rubinstein. Խաղային թեորեմի կուրս. Cambridge, MA: MIT, 1994. Print.
^ Von Neumann, J: Zur Theorie der Gesellschaftsspiele Math. Annalen. 100 (1928) 295-320
^ John L Casti (1996). Five golden rules: great theories of 20th-century mathematics – and why they matter. New York: Wiley-Interscience. p. 19. ISBN 0-471-00261-5.
^ Russell, Stuart J.; Norvig, Peter (2003), Artificial Intelligence: A Modern Approach (2nd ed.), Upper Saddle River, New Jersey: Prentice Hall, pp. 163–171, ISBN 0-13-790395-2

Անհրաժեշտ հղումներ

Խաղային տեսություն

Category:Detection theory Category:Game artificial intelligence Category:Graph algorithms Category:Optimization algorithms and methods Category:Search algorithms Category:Game theory Category:Mathematical and quantitative methods (economics) Category:Theorems in discrete mathematics Category:Decision theory Category:Fixed points (mathematics)

pt:Minimax]] [[zh:极小化极大算法

[Osborne-1] Osborne, Martin J., և Ariel Rubinstein. Խաղային թեորեմի կուրս. Cambridge, MA: MIT, 1994. Print.

[2] Von Neumann, J: Zur Theorie der Gesellschaftsspiele Math. Annalen. 100 (1928) 295-320

[Casti-3] John L Casti (1996). Five golden rules: great theories of 20th-century mathematics – and why they matter. New York: Wiley-Interscience. p. 19. ISBN 0-471-00261-5.

[4] Russell, Stuart J.; Norvig, Peter (2003), Artificial Intelligence: A Modern Approach (2nd ed.), Upper Saddle River, New Jersey: Prentice Hall, pp. 163–171, ISBN 0-13-790395-2

[1]

[2]

[3]

[4]