User:Halibutt/Spacetime/Reference frames

Reference frames

Click here for a brief section summary

Figure 2-2. Galilean diagram of two frames of reference in standard configuration.

Figure 2-3. (a) Galilean diagram of two frames of reference in standard configuration. (b) spacetime diagram of two frames of reference. (c) spacetime diagram showing the path of a reflected light pulse.

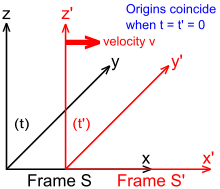
In comparing measurements made by relatively moving observers in different reference frames, it is useful to work with the frames in a standard configuration. In Fig. 2‑2, two Galilean reference frames (i.e. conventional 3-space frames) are displayed in relative motion. Frame S belongs to a first observer O, and frame S′ (pronounced "S prime") belongs to a second observer O′.

• The x, y, z axes of frame S are oriented parallel to the respective primed axes of frame S′.
• Frame S′ moves in the x-direction of frame S with a constant velocity v as measured in frame S.
• The origins of frames S and S′ are coincident when time t = 0 for frame S and t′ = 0 for frame S′.

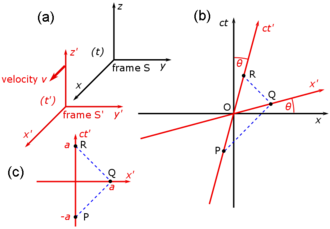
Fig. 2‑3a redraws Fig. 2‑2 in a different orientation. Fig. 2‑3b illustrates a spacetime diagram from the viewpoint of observer O. Since S and S′ are in standard configuration, their origins coincide at times t = 0 in frame S and t′ = 0 in frame S'. The ct′ axis passes through the events in frame S′ which have x′ = 0. But the points with x′ = 0 are moving in the x-direction of frame S with velocity v, so that they are not coincident with the ct axis at any time other than zero. Therefore, the ct′ axis is tilted with respect to the ct axis by an angle θ given by

$\tan \ \theta =v/c.$

The x′ axis is also tilted with respect to the x axis. To determine the angle of this tilt, we recall that the slope of the world line of a light pulse is always ±1. Fig. 2‑3c presents a spacetime diagram from the viewpoint of observer O′. Event P represents the emission of a light pulse at x′ = 0, ct′ = −a. The pulse is reflected from a mirror situated a distance a from the light source (event Q), and returns to the light source at x′ = 0, ct′ = a (event R).

The same events P, Q, R are plotted in Fig. 2‑3b in the frame of observer O. The light paths have slopes = 1 and −1 so that ΔPQR forms a right triangle. Since OP = OQ = OR, the angle between x′ and x must also be θ.

While the rest frame has space and time axes that meet at right angles, the moving frame is drawn with axes that meet at an acute angle. The frames are actually equivalent. The asymmetry is due to unavoidable distortions in how spacetime coordinates can map onto a Cartesian plane, and should be considered no stranger than the manner in which, on a Mercator projection of the Earth, the relative sizes of land masses near the poles (Greenland and Antarctica) are highly exaggerated relative to land masses near the Equator.

Return to Introduction

Light cone

Main article: light cone

Click here for a brief section summary

Figure 2-4. The light cone centered on an event divides the rest of spacetime into the future, the past, and "elsewhere".

In Fig. 2-4, event O is at the origin of a spacetime diagram, and the two diagonal lines represent all events that have zero spacetime interval with respect to the origin event. These two lines form what is called the light cone of the event O, since adding a second spatial dimension (Fig. 2‑5) makes the appearance that of two right circular cones meeting with their apices at O. One cone extends into the future (t>0), the other into the past (t<0).

Figure 2-5. Light cone in 2D space plus a time dimension.

A light (double) cone divides spacetime into separate regions with respect to its apex. The interior of the future light cone consists of all events that are separated from the apex by more time (temporal distance) than necessary to cross their spatial distance at lightspeed; these events comprise the timelike future of the event O. Likewise, the timelike past comprises the interior events of the past light cone. So in timelike intervals Δct is greater than Δx, making timelike intervals positive. The region exterior to the light cone consists of events that are separated from the event O by more space than can be crossed at lightspeed in the given time. These events comprise the so-called spacelike region of the event O, denoted "Elsewhere" in Fig. 2‑4. Events on the light cone itself are said to be lightlike (or null separated) from O. Because of the invariance of the spacetime interval, all observers will assign the same light cone to any given event, and thus will agree on this division of spacetime.

The light cone has an essential role within the concept of causality. It is possible for a not-faster-than-light-speed signal to travel from the position and time of O to the position and time of D (Fig. 2‑4). It is hence possible for event O to have a causal influence on event D. The future light cone contains all the events that could be causally influenced by O. Likewise, it is possible for a not-faster-than-light-speed signal to travel from the position and time of A, to the position and time of O. The past light cone contains all the events that could have a causal influence on O. In contrast, assuming that signals cannot travel faster than the speed of light, any event, like e.g. B or C, in the spacelike region (Elsewhere), cannot either effect event O, nor can they be affected by event O employing such signalling. Under this assumption any causal relationship between event O and any events in the spacelike region of a light cone is excluded.

Return to Introduction