User:Halibutt/Spacetime/Four-momentum

Four-momentum

Because of the close relationship between mass and energy, the four-momentum (also called 4‑momentum) is also called the energy-momentum 4‑vector. Using an uppercase P to represent the four-momentum and a lowercase p to denote the spatial momentum, the four-momentum may be written as

$P\equiv (E/c,{\vec {p}})=(E/c,p_{x},p_{y},p_{z})$ or alternatively,

$P\equiv (E,{\vec {p}})=(E,p_{x},p_{y},p_{z})$ using the convention that $c=1.$

Return to Introduction

Conservation laws

Main article: Conservation law

Click here for a brief section summary

In physics, conservation laws state that certain particular measurable properties of an isolated physical system do not change as the system evolves over time. In 1915, Emmy Noether discovered that underlying each conservation law is a fundamental symmetry of nature. The fact that physical processes don't care where in space they take place (space translation symmetry) yields conservation of momentum, the fact that such processes don't care when they take place (time translation symmetry) yields conservation of energy, and so on. In this section, we examine the Newtonian views of conservation of mass, momentum and energy from a relativistic perspective.

Total momentum

Figure 3-10. Relativistic conservation of momentum

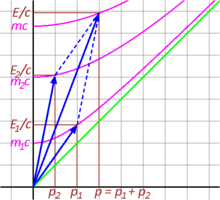
To understand how the Newtonian view of conservation of momentum needs to be modified in a relativistic context, we examine the problem of two colliding bodies limited to a single dimension.

In Newtonian mechanics, two extreme cases of this problem may be distinguished yielding mathematics of minimum complexity: (1) The two bodies rebound from each other in a completely elastic collision. (2) The two bodies stick together and continue moving as a single particle. This second case is the case of completely inelastic collision. For both cases (1) and (2), momentum, mass, and total energy are conserved. However, kinetic energy is not conserved in cases of inelastic collision. A certain fraction of the initial kinetic energy is converted to heat.

In case (2), two masses with momentums p₁ = m₁v₁ and p₂ = m₂v₂ collide to produce a single particle of conserved mass m = m₁ + m₂ traveling at the center of mass velocity of the original system, v_cm = (m₁v₁ + m₂v₂)/(m₁ + m₂). The total momentum p = p₁ + p₂ is conserved.

Fig. 3‑10 illustrates the inelastic collision of two particles from a relativistic perspective. The time components E₁/c and E₂/c add up to total E/c of the resultant vector, meaning that energy is conserved. Likewise, the space components p₁ and p₂ add up to form p of the resultant vector. The four-momentum is, as expected, a conserved quantity. However, the invariant mass of the fused particle, given by the point where the invariant hyperbola of the total momentum intersects the energy axis, is not equal to the sum of the invariant masses of the individual particles that collided. Indeed, it is larger than the sum of the individual masses: m > m₁ + m₂.

Looking at the events of this scenario in reverse sequence, we see that non-conservation of mass is a common occurrence: when an unstable elementary particle spontaneously decays into two lighter particles, total energy is conserved, but the mass is not. Part of the mass is converted into kinetic energy.

Return to Introduction

Choice of reference frames

Figure 3-11.
(above) Lab Frame.
(right) Center of Momentum Frame

The freedom to choose any frame in which to perform an analysis allows us to pick one which may be particularly convenient. For analysis of momentum and energy problems, the most convenient frame is usually the "center-of-momentum frame" (also called the zero-momentum frame, or COM frame). This is the frame in which the space component of the system's total momentum is zero. Fig. 3‑11 illustrates the breakup of a high speed particle into two daughter particles. In the lab frame, the daughter particles are preferentially emitted in a direction oriented along the original particle's trajectory. In the COM frame, however, the two daughter particles are emitted in opposite directions, although their masses and the magnitude of their velocities are generally not the same.

Return to Introduction

Energy and momentum conservation

In a Newtonian analysis of interacting particles, transformation between frames is simple because all that is necessary is to apply the Galilean transformation to all velocities. Since v' = v − u, the momentum p' = p − mu. If the total momentum of an interacting system of particles is observed to be conserved in one frame, it will likewise be observed to be conserved in any other frame.

Conservation of momentum in the COM frame amounts to the requirement that p = 0 both before and after collision. In the Newtonian analysis, conservation of mass dictates that m = m₁ + m₂. In the simplified, one-dimensional scenarios that we have been considering, only one additional constraint is necessary before the outgoing momenta of the particles can be determined—an energy condition. In the one-dimensional case of a completely elastic collision with no loss of kinetic energy, the outgoing velocities of the rebounding particles in the COM frame will be precisely equal and opposite to their incoming velocities. In the case of a completely inelastic collision with total loss of kinetic energy, the outgoing velocities of the rebounding particles will be zero.

Newtonian momenta, calculated as p = mv, fail to behave properly under Lorentzian transformation. The linear transformation of velocities v' = v − u is replaced by the highly nonlinear v' = (v − u)/(1 − vu/c²), so that a calculation demonstrating conservation of momentum in one frame will be invalid in other frames. Einstein was faced with either having to give up conservation of momentum, or to change the definition of momentum. As we have discussed in the previous section on four-momentum, this second option was what he chose.

Figure 3-12a. Energy-momentum diagram for decay of a charged pion

Figure 3-12b. Graphing calculator analysis of charged pion decay.

The relativistic conservation law for energy and momentum replaces the three classical conservation laws for energy, momentum and mass. Mass is no longer conserved independently, because it has been subsumed into the total relativistic energy. This makes the relativistic conservation of energy a simpler concept than in nonrelativistic mechanics, because the total energy is conserved without any qualifications. Kinetic energy converted into heat or internal potential energy shows up as an increase in mass.

Example: Because of the equivalence of mass and energy, elementary particle masses are customarily stated in energy units, where 1 MeV = 1×10⁶ electron volts. A charged pion is a particle of mass 139.57 MeV (approx. 273 times the electron mass). It is unstable, and decays into a muon of mass 105.66 MeV (approx. 207 times the electron mass) and an antineutrino, which has an almost negligible mass. The difference between the pion mass and the muon mass is 33.91 MeV.

π⁻
→
μ⁻
+
ν
_μ

Fig. 3‑12a illustrates the energy-momentum diagram for this decay reaction in the rest frame of the pion. Because of its negligible mass, a neutrino travels at very nearly the speed of light. The relativistic expression for its energy, like that of the photon, is E_ν = pc, which is also the value of the space component of its momentum. To conserve momentum, the muon has the same value of the space component of the neutrino's momentum, but in the opposite direction.

Algebraic analyses of the energetics of this decay reaction are available online, so Fig. 3‑12b presents instead a graphing calculator solution. The energy of the neutrino is 29.79 MeV, and the energy of the muon is 33.91 − 29.79 = 4.12 MeV. Interestingly, most of the energy is carried off by the near-zero-mass neutrino.

Return to Introduction

Beyond the basics

The topics in this section are of significantly greater technical difficulty than those in the preceding sections and are not essential for understanding Introduction to curved spacetime.

Rapidity

Main article: Rapidity

Click here for a brief section summary
Note: To avoid navigation issues with the internal wikilinks, mobile phone users should pre-expand all sections from Section Summaries back to the Introduction.

Figure 4-1a. A ray through the unit circle x² + y² = 1 in the point (cos a, sin a), where a is twice the area between the ray, the circle, and the x-axis.

Figure 4-1b. A ray through the unit hyperbola x² - y² = 1 in the point (cosh a, sinh a), where a is twice the area between the ray, the hyperbola, and the x-axis.

Figure 4-2. Plot of the three basic Hyperbolic functions: hyperbolic sine (sinh), hyperbolic cosine (cosh) and hyperbolic tangent (tanh). Sinh is red, cosh is blue and tanh is green.

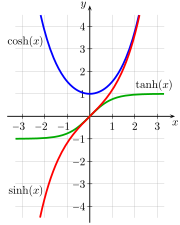
Lorentz transformations relate coordinates of events in one reference frame to those of another frame. Relativistic composition of velocities is used to add two velocities together. The formulas to perform the latter computations are nonlinear, making them more complex than the corresponding Galilean formulas.

This nonlinearity is an artifact of our choice of parameters. We have previously noted that in an x–ct spacetime diagram, the points at some constant spacetime interval from the origin form an invariant hyperbola. We have also noted that the coordinate systems of two spacetime reference frames in standard configuration are hyperbolically rotated with respect to each other.

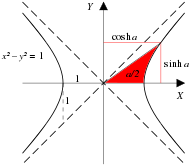
The natural functions for expressing these relationships are the hyperbolic analogs of the trigonometric functions. Fig. 4‑1a shows a unit circle with sin(a) and cos(a), the only difference between this diagram and the familiar unit circle of elementary trigonometry being that a is interpreted, not as the angle between the ray and the x-axis, but as twice the area of the sector swept out by the ray from the x-axis. (Numerically, the angle and 2 × area measures for the unit circle are identical.) Fig. 4‑1b shows a unit hyperbola with sinh(a) and cosh(a), where a is likewise interpreted as twice the tinted area. Fig. 4‑2 presents plots of the sinh, cosh, and tanh functions.

For the unit circle, the slope of the ray is given by

${\text{slope}}=\tan a={\frac {\sin a}{\cos a}}.$

In the Cartesian plane, rotation of point (x, y) into point (x', y') by angle θ is given by

${\begin{pmatrix}x'\\y'\\\end{pmatrix}}={\begin{pmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{pmatrix}}{\begin{pmatrix}x\\y\\\end{pmatrix}}.$

In a spacetime diagram, the velocity parameter $\beta$ is the analog of slope. The rapidity, φ, is defined by

$\beta \equiv \tanh \phi \equiv {\frac {v}{c}},$

where

$\tanh \phi ={\frac {\sinh \phi }{\cosh \phi }}={\frac {e^{\phi }-e^{-\phi }}{e^{\phi }+e^{-\phi }}}.$

The rapidity defined above is very useful in special relativity because many expressions take on a considerably simpler form when expressed in terms of it. For example, rapidity is simply additive in the collinear velocity-addition formula;

$\beta ={\frac {\beta _{1}+\beta _{2}}{1+\beta _{1}\beta _{2}}}=$ ${\frac {\tanh \phi _{1}+\tanh \phi _{2}}{1+\tanh \phi _{1}\tanh \phi _{2}}}=$ $\tanh(\phi _{1}+\phi _{2}),$

or in other words, $\phi =\phi _{1}+\phi _{2}.$

The Lorentz transformations take a simple form when expressed in terms of rapidity. The γ factor can be written as

$\gamma ={\frac {1}{\sqrt {1-\beta ^{2}}}}={\frac {1}{\sqrt {1-\tanh ^{2}\phi }}}$ $=\cosh \phi ,$

$\gamma \beta ={\frac {\beta }{\sqrt {1-\beta ^{2}}}}={\frac {\tanh \phi }{\sqrt {1-\tanh ^{2}\phi }}}$ $=\sinh \phi .$

Transformations describing relative motion with uniform velocity and without rotation of the space coordinate axes are called boosts.

Substituting γ and γβ into the transformations as previously presented and rewriting in matrix form, the Lorentz boost in the x direction may be written as

${\begin{pmatrix}ct'\\x'\end{pmatrix}}={\begin{pmatrix}\cosh \phi &-\sinh \phi \\-\sinh \phi &\cosh \phi \end{pmatrix}}{\begin{pmatrix}ct\\x\end{pmatrix}},$

and the inverse Lorentz boost in the x direction may be written as

${\begin{pmatrix}ct\\x\end{pmatrix}}={\begin{pmatrix}\cosh \phi &\sinh \phi \\\sinh \phi &\cosh \phi \end{pmatrix}}{\begin{pmatrix}ct'\\x'\end{pmatrix}}.$

In other words, Lorentz boosts represent hyperbolic rotations in Minkowski spacetime.

The advantages of using hyperbolic functions are such that some textbooks such as the classic ones by Taylor and Wheeler introduce their use at a very early stage.

Return to Introduction

4‑vectors

Main article: Four-vector

Click here for a brief section summary

Four‑vectors have been mentioned above in context of the energy-momentum 4‑vector, but without any great emphasis. Indeed, none of the elementary derivations of special relativity require them. But once understood, 4‑vectors, and more generally tensors, greatly simplify the mathematics and conceptual understanding of special relativity. Working exclusively with such objects leads to formulas that are manifestly relativistically invariant, which is a considerable advantage in non-trivial contexts. For instance, demonstrating relativistic invariance of Maxwell's equations in their usual form is not trivial, while it is merely a routine calculation (really no more than an observation) using the field strength tensor formulation. On the other hand, general relativity, from the outset, relies heavily on 4‑vectors, and more generally tensors, representing physically relevant entities. Relating these via equations that do not rely on specific coordinates requires tensors, capable of connecting such 4‑vectors even within a curved spacetime, and not just within a flat one as in special relativity. The study of tensors is outside the scope of this article, which provides only a basic discussion of spacetime.

Definition of 4-vectors

A 4-tuple, A = (A₀, A₁, A₂, A₃) is a "4-vector" if its component A_i transform between frames according the Lorentz transformation.

If using (ct, x, y, z) coordinates, A is a 4–vector if it transforms (in the x-direction) according to

${\begin{aligned}A_{0}'&=\gamma \left(A_{0}-(v/c)A_{1}\right)\\A_{1}'&=\gamma \left(A_{1}-(v/c)A_{0}\right)\\A_{2}'&=A_{2}\\A_{3}'&=A_{3}\end{aligned}}$

which comes from simply replacing ct with A₀ and x with A₁ in the earlier presentation of the Lorentz transformation.

As usual, when we write x, t, etc. we generally mean Δx, Δt etc.

The last three components of a 4–vector must be a standard vector in three-dimensional space. Therefore, a 4–vector must transform like (c Δt, Δx, Δy, Δz) under Lorentz transformations as well as rotations.

Return to Introduction

Properties of 4-vectors

• Closure under linear combination: If A and B are 4-vectors, then C = aA + aB is also a 4-vector.
• Inner-product invariance: If A and B are 4-vectors, then their inner product (scalar product) is invariant, i.e. their inner product is independent of the frame in which it is calculated. Note how the calculation of inner product differs from the calculation of the inner product of a 3-vector. In the following, ${\vec {A}}$ and ${\vec {B}}$ are 3-vectors:

$A\cdot B\equiv$ $A_{0}B_{0}-A_{1}B_{1}-A_{2}B_{2}-A_{3}B_{3}\equiv$ $A_{0}B_{0}-{\vec {A}}\cdot {\vec {B}}$

In addition to being invariant under Lorentz transformation, the above inner product is also invariant under rotation in 3-space.

Two vectors are said to be orthogonal if $A\cdot B=0.$ Unlike the case with 3-vectors, orthogonal 4-vectors are not necessarily at right angles with each other. The rule is that two 4-vectors are orthogonal if they are offset by equal and opposite angles from the 45° line which is the world line of a light ray. This implies that a lightlike 4-vector is orthogonal with itself.

• Invariance of the magnitude of a vector: The magnitude of a vector is the inner product of a 4-vector with itself, and is a frame-independent property. As with intervals, the magnitude may be positive, negative or zero, so that the vectors are referred to as timelike, spacelike or null (lightlike). Note that a null vector is not the same as a zero vector. A null vector is one for which $A\cdot A=0,$ while a zero vector is one whose components are all zero. Special cases illustrating the invariance of the norm include the invariant interval $c^{2}t^{2}-x^{2}$ and the invariant length of the relativistic momentum vector $E^{2}-p^{2}c^{2}.$

Return to Introduction

Examples of 4-vectors

• Displacement 4-vector: Otherwise known as the spacetime separation, this is (Δt, Δx, Δy, Δz), or for infinitesimal separations, (dt, dx, dy, dz).

$dS\equiv (dt,dx,dy,dz)$

• Velocity 4-vector: This results when the displacement 4-vector is divided by $d\tau$, where $d\tau$ is the proper time between the two events that yield dt, dx, dy, and dz.

$V\equiv {\frac {dS}{d\tau }}={\frac {(dt,dx,dy,dz)}{dt/\gamma }}=$ $\gamma \left(1,{\frac {dx}{dt}},{\frac {dy}{dt}},{\frac {dz}{dt}}\right)=$ $(\gamma ,\gamma {\vec {v}})$

Figure 4-3a. The momentarily comoving reference frames of a rapidly accelerating particle as observed from a stationary frame.

Figure 4-3b. The momentarily comoving reference frames along the trajectory of a rapidly accelerating observer (center).

The 4-velocity is tangent to the world line of a particle, and has a length equal to one unit of time in the frame of the particle.

An accelerated particle does not have an inertial frame in which it is always at rest. However, as stated before in the earlier discussion of the transverse Doppler effect, an inertial frame can always be found which is momentarily comoving with the particle. This frame, the momentarily comoving reference frame (MCRF), enables application of special relativity to the analysis of accelerated particles.

Since photons move on null lines, $d\tau =0$ for a photon, and a 4-velocity cannot be defined. There is no frame in which a photon is at rest, and no MCRF can be established along a photon's path.

• Energy-momentum 4-vector: As discussed in the section on Energy and momentum,

$P\equiv (E/c,{\vec {p}})=(E/c,p_{x},p_{y},p_{z})$

As indicated before, there are varying treatments for the energy-momentum 4-vector so that one may also see it expressed as $(E,{\vec {p}})$ or $(E,{\vec {p}}c).$ The first component is the total energy (including mass) of the particle (or system of particles) in a given frame, while the remaining components are its spatial momentum. The energy-momentum 4-vector is a conserved quantity.

• Acceleration 4-vector: This results from taking the derivative of the velocity 4-vector with respect to $\tau .$

$A\equiv {\frac {dV}{d\tau }}=$ ${\frac {d}{d\tau }}(\gamma ,\gamma {\vec {v}})=$ $\gamma \left({\frac {d\gamma }{dt}},{\frac {d(\gamma {\vec {v}})}{dt}}\right)$

• Force 4-vector: This is the derivative of the momentum 4-vector with respect to $\tau .$

$F\equiv {\frac {dP}{d\tau }}=$ $\gamma \left({\frac {dE}{dt}},{\frac {d{\vec {p}}}{dt}}\right)=$ $\gamma \left({\frac {dE}{dt}},{\vec {f}}\right)$

As expected, the final components of the above 4-vectors are all standard 3-vectors corresponding to spatial 3-momentum, 3-force etc.

Return to Introduction