User:Halibutt/Spacetime/Active, passive and inertial

• Active, passive, and inertial mass

Before discussing the experimental evidence regarding these other sources of gravity, we need first to discuss Bondi's distinctions between different possible types of mass: (1) active mass ($m_{a}$) is the mass which acts as the source of a gravitational field; (2) passive mass ($m_{p}$) is the mass which reacts to a gravitational field; (3) inertial mass ($m_{i}$) is the mass which reacts to acceleration.

• $m_{p}$ is the same as what we have earlier termed gravitational mass ($m_{g}$) in our discussion of the equivalence principle in the Basic propositions section.

In Newtonian theory,

• The third law of action and reaction dictates that $m_{a}$ and $m_{p}$ must be the same.
• On the other hand, whether $m_{p}$ and $m_{i}$ are equal is an empirical result.

In general relativity,

• The equality of $m_{p}$ and $m_{i}$ is dictated by the equivalence principle.
• There is no "action and reaction" principle dictating any necessary relationship between $m_{a}$ and $m_{p}$.

Return to Introduction

• Pressure as a gravitational source

Figure 5-9. (A) Cavendish experiment (B) Kreuzer experiment

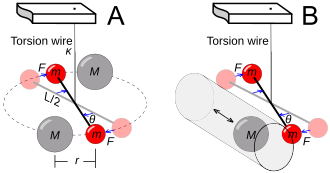
The classic experiment to measure the strength of a gravitational source (i.e. its active mass) was first conducted in 1797 by Henry Cavendish (Fig. 5‑9a). Two small but dense balls are suspended on a fine wire, making a torsion balance. Bringing two large test masses close to the balls introduces a detectable torque. Given the dimensions of the apparatus and the measurable spring constant of the torsion wire, the gravitational constant G can be determined.

To study pressure effects by compressing the test masses is hopeless, because attainable laboratory pressures are insignificant in comparison with the mass-energy of a metal ball.

However, the repulsive electromagnetic pressures resulting from protons being tightly squeezed inside atomic nuclei are typically on the order of 10²⁸ atm ≈ 10³³ Pa ≈ 10³³ kg·s⁻²m⁻¹. This amounts to about 1% of the nuclear mass density of approximately 10¹⁸kg/m³ (after factoring in c² ≈ 9×10¹⁶m²s⁻²).

Figure 5-10. Lunar laser ranging experiment. (left) This retroreflector was left on the Moon by astronauts on the Apollo 11 mission. (right) Astronomers all over the world have bounced laser light off the retroreflectors left by Apollo astronauts and Russian lunar rovers to measure precisely the Earth-Moon distance.

If pressure does not act as a gravitational source, then the ratio $m_{a}/m_{p}$ should be lower for nuclei with higher atomic number Z, in which the electrostatic pressures are higher. L. B. Kreuzer (1968) did a Cavendish experiment using a Teflon mass suspended in a mixture of the liquids trichloroethylene and dibromoethane having the same buoyant density as the Teflon (Fig. 5‑9b). Fluorine has atomic number Z = 9, while bromine has Z = 35. Kreuzer found that repositioning the Teflon mass caused no differential deflection of the torsion bar, hence establishing active mass and passive mass to be equivalent to a precision of 5×10⁻⁵.

Although Kreuzer originally considered this experiment merely to be a test of the ratio of active mass to passive mass, Clifford Will (1976) reinterpreted the experiment as a fundamental test of the coupling of sources to gravitational fields.

In 1986, Bartlett and Van Buren noted that lunar laser ranging had detected a 2-km offset between the moon’s center of figure and its center of mass. This indicates an asymmetry in the distribution of Fe (abundant in the Moon's core) and Al (abundant in its crust and mantle). If pressure did not contribute equally to spacetime curvature as does mass-energy, the moon would not be in the orbit predicted by classical mechanics. They used their measurements to tighten the limits on any discrepancies between active and passive mass to about 1×10⁻¹².

Return to Introduction

• Gravitomagnetism

Figure 5-11. Gravity Probe B confirmed the existence of gravitomagnetism.

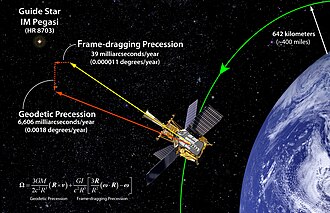
The existence of gravitomagnetism was proven by Gravity Probe B (GP-B), a satellite-based mission which launched on 20 April 2004. The spaceflight phase lasted until 2005. The mission aim was to measure spacetime curvature near Earth, with particular emphasis on gravitomagnetism.

Initial results confirmed the relatively large geodetic effect (which is due to simple spacetime curvature, and is also known as de Sitter precession) to an accuracy of about 1%. The much smaller frame-dragging effect (which is due to gravitomagnetism, and is also known as Lense–Thirring precession) was difficult to measure because of unexpected charge effects causing variable drift in the gyroscopes. Nevertheless, by August 2008, the frame-dragging effect had been confirmed to within 15% of the expected result, while the geodetic effect was confirmed to better than 0.5%.

Subsequent measurements of frame dragging by laser-ranging observations of the LARES, LAGEOS-1 and LAGEOS-2 satellites has improved on the GP-B measurement, with results (as of 2016) demonstrating the effect to within 5% of its theoretical value, although there has been some disagreement on the accuracy of this result.

Another effort, the Gyroscopes in General Relativity (GINGER) experiment, seeks to use three 6 m ring lasers mounted at right angles to each other 1400 m below the Earth's surface to measure this effect.

Return to Introduction

Technical topics

Riemannian geometry

Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, defined as smooth manifolds with a Riemannian metric (an inner product on the tangent space at each point that varies smoothly from point to point). This gives, in particular, local notions of angle, length of curves, surface area and volume. From those, some other global quantities can be derived by integrating local contributions.

Riemannian geometry originated with the vision of Bernhard Riemann expressed in his inaugural lecture "Ueber die Hypothesen, welche der Geometrie zu Grunde liegen" ("On the Hypotheses on which Geometry is Based"). It is a very broad and abstract generalization of the differential geometry of surfaces in R³. Development of Riemannian geometry resulted in synthesis of diverse results concerning the geometry of surfaces and the behavior of geodesics on them, with techniques that can be applied to the study of differentiable manifolds of higher dimensions. It enabled the formulation of Einstein's general theory of relativity, made profound impact on group theory and representation theory, as well as analysis, and spurred the development of algebraic and differential topology.

Return to Introduction

Curved manifolds

Main articles: Manifold, Lorentzian manifold, and Differentiable manifold

For physical reasons, a spacetime continuum is mathematically defined as a four-dimensional, smooth, connected Lorentzian manifold $(M,g)$. This means the smooth Lorentz metric $g$ has signature $(3,1)$. The metric determines the geometry of spacetime, as well as determining the geodesics of particles and light beams. About each point (event) on this manifold, coordinate charts are used to represent observers in reference frames. Usually, Cartesian coordinates $(x,y,z,t)$ are used. Moreover, for simplicity's sake, units of measurement are usually chosen such that the speed of light $c$ is equal to 1.

A reference frame (observer) can be identified with one of these coordinate charts; any such observer can describe any event $p$. Another reference frame may be identified by a second coordinate chart about $p$. Two observers (one in each reference frame) may describe the same event $p$ but obtain different descriptions.

Usually, many overlapping coordinate charts are needed to cover a manifold. Given two coordinate charts, one containing $p$ (representing an observer) and another containing $q$ (representing another observer), the intersection of the charts represents the region of spacetime in which both observers can measure physical quantities and hence compare results. The relation between the two sets of measurements is given by a non-singular coordinate transformation on this intersection. The idea of coordinate charts as local observers who can perform measurements in their vicinity also makes good physical sense, as this is how one actually collects physical data—locally.

For example, two observers, one of whom is on Earth, but the other one who is on a fast rocket to Jupiter, may observe a comet crashing into Jupiter (this is the event $p$). In general, they will disagree about the exact location and timing of this impact, i.e., they will have different 4-tuples $(x,y,z,t)$ (as they are using different coordinate systems). Although their kinematic descriptions will differ, dynamical (physical) laws, such as momentum conservation and the first law of thermodynamics, will still hold. In fact, relativity theory requires more than this in the sense that it stipulates these (and all other physical) laws must take the same form in all coordinate systems. This introduces tensors into relativity, by which all physical quantities are represented.

Geodesics are said to be time-like, null, or space-like if the tangent vector to one point of the geodesic is of this nature. Paths of particles and light beams in spacetime are represented by time-like and null (light-like) geodesics, respectively.

Return to Introduction

Privileged character of 3+1 spacetime

Properties of (n + m)-dimensional spacetimes

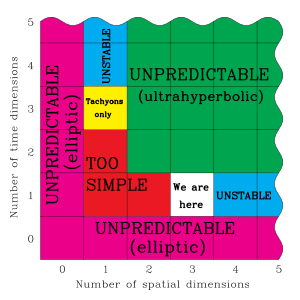
There are two kinds of dimensions: spatial (bidirectional) and temporal (unidirectional). Let the number of spatial dimensions be N and the number of temporal dimensions be T. That N = 3 and T = 1, setting aside the compactified dimensions invoked by string theory and undetectable to date, can be explained by appealing to the physical consequences of letting N differ from 3 and T differ from 1. The argument is often of an anthropic character and possibly the first of its kind, albeit before the complete concept came into vogue.

The implicit notion that the dimensionality of the universe is special is first attributed to Gottfried Wilhelm Leibniz, who in the Discourse on Metaphysics suggested that the world is "the one which is at the same time the simplest in hypothesis and the richest in phenomena". Immanuel Kant argued that 3-dimensional space was a consequence of the inverse square law of universal gravitation. While Kant's argument is historically important, John D. Barrow said that it "gets the punch-line back to front: it is the three-dimensionality of space that explains why we see inverse-square force laws in Nature, not vice-versa" (Barrow 2002:204).

In 1920, Paul Ehrenfest showed that if there is only a single time dimension and more than three spatial dimensions, the orbit of a planet about its Sun cannot remain stable. The same is true of a star's orbit around the center of its galaxy. Ehrenfest also showed that if there are an even number of spatial dimensions, then the different parts of a wave impulse will travel at different speeds. If there are $5+2k$ spatial dimensions, where k is a positive whole number, then wave impulses become distorted. In 1922, Hermann Weyl claimed that Maxwell's theory of electromagnetism can be expressed in terms of an action only for a four-dimensional manifold. Finally, Tangherlini showed in 1963 that when there are more than three spatial dimensions, electron orbitals around nuclei cannot be stable; electrons would either fall into the nucleus or disperse.

Max Tegmark expands on the preceding argument in the following anthropic manner. If T differs from 1, the behavior of physical systems could not be predicted reliably from knowledge of the relevant partial differential equations. In such a universe, intelligent life capable of manipulating technology could not emerge. Moreover, if T > 1, Tegmark maintains that protons and electrons would be unstable and could decay into particles having greater mass than themselves. (This is not a problem if the particles have a sufficiently low temperature.) Lastly, if N < 3, gravitation of any kind becomes problematic, and the universe would probably be too simple to contain observers. For example, when N < 3, nerves cannot cross without intersecting. Hence anthropic and other arguments rule out all cases except N = 3 and T = 1, which describes the world around us.

On the other hand, in view of creating black holes from an ideal monatomic gas under its self-gravity, Wei-Xiang Feng showed that (3 + 1)-dimensional spacetime is the marginal dimensionality. Moreover, it is the unique dimensionality that can afford a "stable" gas sphere with a "positive" cosmological constant. However, a self-gravitating gas cannot be stably bound if the mass sphere is larger than ~10²¹ solar masses, due to the small positivity of the cosmological constant observed.

In 2019, James Scargill argued that complex life may be possible with two spatial dimensions. According to Scargill, a purely scalar theory of gravity may enable a local gravitational force, and 2D networks may be sufficient for complex neural networks.

Return to Introduction

Section summaries

Introduction summary

^Definitions (click here to return to main)

• In classical mechanics, time is separate from space. In special relativity, time and space are fused together into a single 4-dimensional "manifold" called spacetime.
• The technical term "manifold" and the great speed of light imply that at ordinary speeds, there is little that humans might observe which is noticeably different from what they would observe if the world followed the geometry of "common sense."
• Things that happen in spacetime are called "events". Events are idealized, four-dimensional points. There is no such thing as an event in motion.
• The path of a particle in spacetime traces out a succession of events, which is called the particle's "world line".
• In special relativity, to "observe" or "measure" an event means to ascertain its position and time against a hypothetical infinite latticework of synchronized clocks. To "observe" an event is not the same as to "see" an event.

^History (click here to return to main)

• To mid-1800s scientists, the wave nature of light implied a medium that waved. Much research was directed to elucidate the properties of this hypothetical medium, called the "luminiferous aether". Experiments provided contradictory results. For example, stellar aberration implied no coupling between matter and the aether, while the Michelson–Morley experiment demanded complete coupling between matter and the aether.
• FitzGerald and Lorentz independently proposed the length contraction hypothesis, a desperate ad hoc proposal that particles of matter, when traveling through the aether, are physically compressed in their direction of travel.
• Henri Poincaré was to come closer than any other of Einstein's predecessors to arriving at what is currently known as the special theory of relativity.
• "The special theory of relativity ... was ripe for discovery in 1905."
• Einstein's theory of special relativity (1905), which was based on kinematics and a careful examination of the meaning of measurement, was the first to completely explain the experimental difficulties associated with measurements of light. It represented not merely a theory of electrodynamics, but a fundamental re-conception of the nature of space and time.
• Having been scooped by Einstein, Hermann Minkowski spent several years developing his own interpretation of relativity. Between 1907 and 1908, he presented his geometric interpretation of special relativity, which has come to be known as Minkowski space, or spacetime.

Return to Introduction

Spacetime in special relativity summary

^Spacetime interval (click here to return to main)

• Time by itself and length by itself are not invariants, since observers in relative motion will disagree on the time between events or the distance between events.
• On the other hand, observers in relative motion will agree on the measure of a particular combination of distance and time called the "spacetime interval."
• Spacetime intervals can be positive, negative or zero. Particles moving at the speed of light have zero spacetime intervals and do not age.
• Spacetime diagrams are typically drawn with only a single space and a single time coordinate. The time axis is scaled by $c$ so that the space and time coordinates have the same units (meters).

^Reference frames (click here to return to main)

• To simplify analyses of two reference frames in relative motion, Galilean (i.e. conventional 3-space) diagrams of the frames may be set in a standard configuration with aligned axes whose origins coincide when t = 0.
• A spacetime diagram in standard configuration is typically drawn with only a single space and a single time coordinate. The "unprimed frame" will have orthogonal x and ct axes. The axes of the "primed frame" will share a common origin with the unprimed axes, but its x' and ct' axes will be inclined by equal and opposite angles from the x and ct axes.
• Although the axes of the unprimed frame are orthogonal and the axes of the primed frame are inclined, the frames are actually equivalent. The asymmetry is due to unavoidable mapping distortions, and should be considered no stranger than the mapping distortions that occur, say, when mapping a spherical Earth onto a flat map.

^Light cone (click here to return to main)

• On a spacetime diagram, two 45° diagonal lines crossing the origin represent light signals to and from the origin. In a diagram with an extra space direction, the diagonal lines form a "light cone".
• The light cone divides spacetime into a "timelike future" (separated from the origin by more time than space), a "timelike past", and an "elsewhere" region (separated from the origin by a "spacelike" interval with more space than time).
• Events in the future and past light cones are causally related to the origin. Events in the elsewhere region do not have a causal relationship with the origin.

^Relativity of simultaneity (click here to return to main)

• If two events are timelike separated (causally related), then their before-after ordering is fixed for all observers.
• If two events are spacelike separated (non-causally related), then different observers with different relative motions may have reverse judgments on which event occurred before the other.
• Simultaneous events are necessarily spacelike separated.
• The spacetime interval between two simultaneous events gives the "proper distance". The spacetime interval measured along a world line gives the "proper time".

^Invariant hyperbola (click here to return to main)

• In a plane, the set of points equidistant from the origin form a circle.
• In a spacetime diagram, a set of points at a fixed spacetime interval from the origin forms an invariant hyperbola.
• The loci of points at constant spacelike and timelike intervals from the origin form timelike and spacelike invariant hyperbolae.

^Time dilation and length contraction (click here to return to main)

• If frame S' is in relative motion to frame S, its ct' axis is tilted with respect to ct.
• Because of this tilt, one light-second on the ct' axis maps to greater than one light-second on the ct axis. Likewise, one light-second on the ct axis maps to greater than one light-second on the ct' axis. Each observer measures the other's clocks as running slow.
• The world sheet of a rod one light-second in length aligned parallel to the x' axis projects to less than one light-second on the x axis. Likewise, the world sheet of a rod one light-second in length aligned parallel to the x axis projects to less than one light-second on the x' axis. Each observer measures the other's rulers as being foreshortened.

^Mutual time dilation and the twin paradox (click here to return to main)

^Mutual time dilation (click here to return to main)

• To beginners, mutual time dilation seems self-contradictory because two observers in relative motion will each measure the other's clock as running more slowly.
• Careful consideration of how time measurements are performed reveals that there is no inherent necessity for the two observers' measurements to be reciprocally "consistent."
• In order to measure the rate of ticking of one of B's clocks, observer A must use two of his own clocks to record the time where B's clock made a first tick, and the time where B's clock made a second tick, so that a grand total of three clocks are involved in the measurement. Conversely, observer B uses three clocks to measure the rate of ticking of one of A's clocks. A and B are not doing the same measurement with the same clocks.

^Twin paradox (click here to return to main)

• In the twin paradox, one twin A makes a journey into space in a high-speed rocket, returning home to find that the twin B who remained on Earth has aged more.
• The twin paradox is not a paradox because the twins' paths through spacetime are not equivalent.
• Throughout both the outbound and the inbound legs of the traveling twin's journey, A measures B's clocks as running slower than A's own. But during the turnaround, a shift takes place in the events of A's world line that B considers to be simultaneous with his own.

^Gravitation (click here to return to main)

• In the absence of gravity, spacetime is flat, is uniform throughout, and serves as nothing more than a static background for the events that take place in it.
• Gravity greatly complicates the description of spacetime. In general relativity, spacetime is no longer a static background, but actively interacts with the physical systems that it contains.

Return to Introduction